Unit - 2
Product of two subgroups
Definition of subgroup-
Let G = {a, b, c,….} be a group with respect to o. Any non-empty subset G’ of G is called a subgroup of G if G’ is itself a group with respect to o.
Clearly G’ = {u}, where u is the identity element of G, and G itself are subgroups of any group G.
They will be called improper subgroups; other subgroups of G, if any, will be called proper. We note in passing that every subgroup of G contains u as its identity element.
Note-
- A non-empty subset G0 of a group G is a subgroup of G if and only if (i) G’ is closed with respect to o, (ii) G’ contains the inverse of each of its elements.
- Let a be an element of a group G. The set G’ =
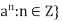 of all integral powers of a is a subgroup of G.
of all integral powers of a is a subgroup of G. - If S is any set of subgroups of G, the intersection of these subgroups is also a subgroup of G.
Product of two subgroups
Let H = 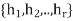 and K =
and K =  be subgroups of a group G and define the ‘‘product’’
be subgroups of a group G and define the ‘‘product’’
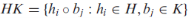
Note- If H and K are invariant subgroups of a group G, so also is HK.
Key takeaways
- Let G = {a, b, c,….} be a group with respect to o. Any non-empty subset G’ of G is called a subgroup of G if G’ is itself a group with respect to o.
- If S is any set of subgroups of G, the intersection of these subgroups is also a subgroup of G.
Cyclic group- A group G is said to be cyclic if G = [a] = 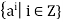 for some
for some 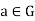 .
.
For example: the additive group Z of integers and the additive groups Z/(n) of integers modulo n.
G is a cyclic group generated by a is written as- G = [a]
Note- A cyclic group is necessarily Abelian.
Example: The additive group J of integers is an infinite cyclic group, the integer, 1 being the generator.
Theorem: Every cyclic group is isomorphic to Z or to Z/(n) for some 
Proof:
If G = [a] is an infinite cyclic group, consider the mapping 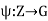 given by
given by 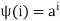 .
.
It is clear that 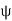 is a surjective homomorphism.
is a surjective homomorphism.
Moreover, 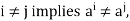 for otherwise “a” would be of finite order.
for otherwise “a” would be of finite order.
Hence 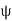 is injective.
is injective.
Therefore 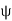 is an isomorphism.
is an isomorphism.
Now let G = [a] is a cyclic group of finite order n.
Then G = 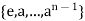 and o(a) = n.
and o(a) = n.
Consider the mapping 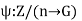 given by
given by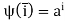 .
.
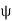 is well defined and also injective, for let
is well defined and also injective, for let 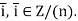
Then
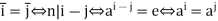
Here clearly 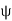 is surjective.
is surjective.
Further,
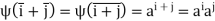
Hence  is an isomorphism.
is an isomorphism.
Note- Any two cyclic groups of the same order are isomorphic.
Theorem: (Fundamental theorem of cyclic groups)- every subgroup of a cyclic group is cyclic.
Proof:
Suppose G = [a] be a cyclic group, and let H be a subgroup of G.
If H is a trivial subgroup, the result is obvious.
So let H is a proper subgroup of G.
If 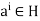 then
then 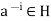 . Hence, there is a least positive integer m such that
. Hence, there is a least positive integer m such that  .
.
We prove that H = [b].
Let 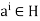 by using division algorithm,
by using division algorithm,
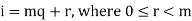
Then
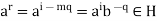
Hence r = 0, therefore, 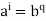 , that proves H = [b].
, that proves H = [b].
Theorem: Let G be a finite cyclic group of order n, and let d be a positive divisor of n. Then G has exactly one subgroup of order d.
Proof:
The result holds trivially if d = 1 or d = n, so let 1 < d < n and put n/d = m. Let G = [a], then b = 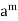 is of order d. Hence, [b] is a cyclic subgroup of order d.
is of order d. Hence, [b] is a cyclic subgroup of order d.
To prove the uniqueness, let H be any subgroup of G of order d.
Then by the above theorem, H is generated by an element c = 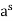 . Then
. Then 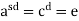 . Hence n|sd, that is md|sd and so m|s.
. Hence n|sd, that is md|sd and so m|s.
Let mq = s, this yields 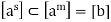 . But since each of the subgroups [
. But since each of the subgroups [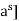 and [
and [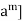 is of order d, [
is of order d, [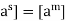 . Which proves H = [b].
. Which proves H = [b].
Example: Suppose H = [a] and K = [b] be cyclic groups of order m and n respectively, such that (m, n) = 1. Then H  is a cyclic group of order mn.
is a cyclic group of order mn.
Sol:
Suppose order of a, b is d. Now 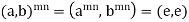 implies d|mn.
implies d|mn.
Also (e, e) = 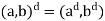 implies
implies 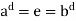 , so m|d and n|d. Therefore mn|d. Consequently, mn = d, since | H
, so m|d and n|d. Therefore mn|d. Consequently, mn = d, since | H 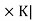 = mn, it follows that (a, b) generates the group H
= mn, it follows that (a, b) generates the group H 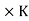 .
.
Key takeaways:
- A group G is said to be cyclic if G = [a] =
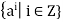 for some
for some 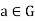 .
. - For example: the additive group Z of integers and the additive groups Z/(n) of integers modulo n.
- A cyclic group is necessarily Abelian.
- Every cyclic group is isomorphic to Z or to Z/(n) for some
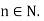 every subgroup of a cyclic group is cyclic.
every subgroup of a cyclic group is cyclic.
Here we will consider the case for infinite and finite cyclic groups respectively.
1. Case-1 (infinite cyclic group)-
We are going to prove that every proper subgroup of an infinite cyclic group is itself an infinite cyclic group and accordingly isomorphic to the group itself.
Each member of a proper subgroup H of a cyclic group
G = {a}
Is some power of a.
Let m is the smallest non-negative integer such that
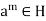
And 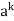 is any arbitrary element of H.
is any arbitrary element of H.
There exists integers q and r such that

So that

Hence r = 0 and we have
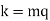
So that k is a multiple of m.
Also, conversely, if k is any multiple of m, we have
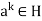
Thus
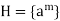
Consisting, as it does, of the elements.
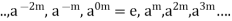
The equality of any two members of the set will imply that
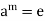
Which, however not the case. Thus H is an infinite cyclic group.
2. Case-1 (finite cyclic group)-
Here we will prove that every subgroup of a finite cyclic group is cyclic and to every divisor l of the order of the group, there corresponds one and only one subgroup of that order
Let

Be a cyclic group of order n, so that it consists of the n elements
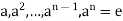
As in first case, we may show that if m be the smallest positive integer such that 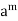 belongs to a given subgroup H of G.
belongs to a given subgroup H of G.
Then H consists of the powers of 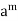 so that
so that
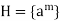
And is accordingly cyclic.
Let l be the order of H so that l is the least positive integer such that
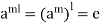
And H consists of the l distinct elements
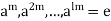
Of course, by Lagrange’s theorem, l is a divisor of n.
Thus every subgroup is cyclic.
Suppose now that l is any divisor of n and let n = lm.
Then

Is a subgroup of G of order l.
It can be obtained on taking the mth power of each element of G.
We have now to show that this is the only subgroup of order l.
This is a consequence of the fact that a subgroup of order l is obtained when we take the mth powers of the elements of G where m =n/l so that its relationship to G is given in terms of the order l only.
Theorem: every group of prime order is cyclic.
Assume that the order is greater than one, let a be any element other than the identity,
Then
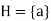
Is a cyclic subgroup of the given group.
The order of H being a divisor of p, other than 1, is necessarily p and as such, we have
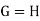
Theorem: Every finite group of composite order possesses proper subgroups.
Suppose G is a finite group of order lm where l and m are not 1.
If G is cyclic and a is any generator thereof, then
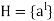
Is a proper subgroup of G, being of order m.
Now suppose G is not cyclic, then each independent generating system of G will contain atleast 2 elements.
Then the cyclic group generated by any member of an independent generating system is a proper subgroup of the given group.
Key takeaways
- Every group of prime order is cyclic.
- Every finite group of composite order possesses proper subgroups.
Introduction
Cyclic notation was first introduced by the great French mathematician Cauchy in 1815.
Let us consider the permutation
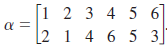
We can present these as-
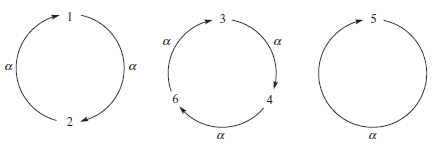
Although mathematically satisfactory, such diagrams are cumbersome.
Instead, we leave out the arrows and simply write  = (1, 2) (3, 4, 6)(5).
= (1, 2) (3, 4, 6)(5).
Example, consider
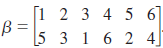
In cycle notation, 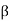 can be written (2, 3, 1, 5)(6, 4) or (4, 6)(3, 1, 5, 2), since both of these unambiguously specify the function
can be written (2, 3, 1, 5)(6, 4) or (4, 6)(3, 1, 5, 2), since both of these unambiguously specify the function 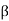 . An expression of the form
. An expression of the form 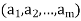 is called a cycle of length m.
is called a cycle of length m.
A multiplication of cycles can be introduced by a cycle as a permutation that fixes any symbol not appearing in the cycle.
Thus, the cycle (4, 6) can be thought of as representing the permutation

In this manner, we can multiply cycles by thinking of them as permutations given in array form.
If array notations for 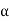 and
and 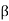 , respectively, are
, respectively, are
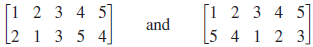
Then, in cycle notation,  = (12)(3)(45),
= (12)(3)(45),  (153)(24), and
(153)(24), and 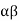 = (12)(3)(45)(153)(24).
= (12)(3)(45)(153)(24).
To put 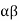 in disjoint cycle form, observe that (24) fixes 1; (153) sends 1 to 5; (45) sends 5 to 4; and (3) and (12) both fix 4. So,
in disjoint cycle form, observe that (24) fixes 1; (153) sends 1 to 5; (45) sends 5 to 4; and (3) and (12) both fix 4. So,  sends 1 to 4. Continuing in this way we obtain
sends 1 to 4. Continuing in this way we obtain 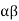 5 (14)(253).
5 (14)(253).
One can convert  back to array form without converting each cycle of
back to array form without converting each cycle of  into array form by simply observing that (14) means 1 goes to 4 and 4 goes to 1; (253) means 2
into array form by simply observing that (14) means 1 goes to 4 and 4 goes to 1; (253) means 2 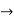 5, 5
5, 5 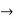 3, 3
3, 3 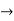 2.
2.
Theorem- Every permutation of a finite set can be written as a cycle or as a product of disjoint cycles.
Proof:
Let 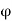 be a permutation on A = {1, 2, . . . , n}. To write a in disjoint cycle form, we start by choosing any member of A, say
be a permutation on A = {1, 2, . . . , n}. To write a in disjoint cycle form, we start by choosing any member of A, say 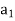 , and let
, and let
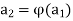
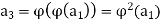
…………
…………
…………
…………
And so on, until we arrive at 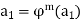 for some m. We know that such an m exists because the sequence
for some m. We know that such an m exists because the sequence  ,
,  . . . . Must be finite so there must eventually be a repetition, say
. . . . Must be finite so there must eventually be a repetition, say 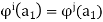 for some i and j with i < j. Then
for some i and j with i < j. Then
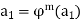
Where m = j - i. We express this relationship among 
The three dots at the end indicate the possibility that we may not have exhausted the set A in this process. In such a case, we merely choose any element 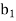 of A not appearing in the first cycle and proceed to create a new cycle as before.
of A not appearing in the first cycle and proceed to create a new cycle as before.
That is, we let

And so on, until we reach 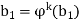 for some k. This new cycle will have no elements in common with the previously constructed cycle. For, if so, then
for some k. This new cycle will have no elements in common with the previously constructed cycle. For, if so, then
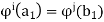
For some i and j. But then
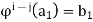
And therefore
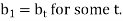
This contradicts the way 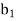 was chosen. Continuing this process until we run out of elements of A, our permutation will appear as
was chosen. Continuing this process until we run out of elements of A, our permutation will appear as

In this manner, we see that every permutation can be written as a product
Of disjoint cycles.
Theorem: If the pair of cycles 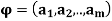 and
and 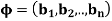 have no entries in common, then
have no entries in common, then 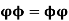
Proof:
Suppose 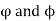 are permutations of the set
are permutations of the set

Where the c’s are the members of S left fixed by both 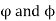 .
.
To prove 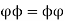 we must show that
we must show that 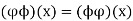 for all x in S. If x is one of the a elements, say
for all x in S. If x is one of the a elements, say 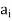 then
then
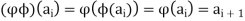
Since 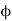 fixes all a elements.
fixes all a elements.
For the same reason,
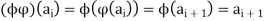
Hence, the functions of 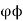 and
and  agree on the a elements. A similar argument shows that
agree on the a elements. A similar argument shows that  and
and 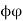 agree on the b elements as well.
agree on the b elements as well.
Finally, suppose that x is a c element, say ci. Then, since both 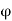 and
and 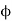
Fix c elements, we have
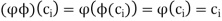
And
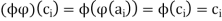
Which is the proof:
Note- (Order of a permutation)- The order of a permutation of a finite set written in disjoint cycle form is the least common multiple of the lengths of the cycles.
Theorem: Every permutation in 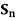 , n > 1, is a product of 2-cycles
, n > 1, is a product of 2-cycles
Proof:
First, note that the identity can be expressed as (12)(12), and so it is a product of 2-cycles, By first theorem, we know that every permutation can be written in the form

A direct computation shows that this is the same as
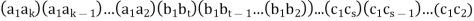
Even and odd permutations:
Definition:
A permutation that can be expressed as a product of an even number of 2-cycles is called an even permutation. A permutation that can be expressed as a product of an odd number of 2-cycles is called an odd permutation.
Note- The set of even permutations in 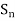 forms a subgroup of
forms a subgroup of  .
.
The group of even permutations of n symbols is denoted by 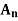 and is called the alternating group of degree n.
and is called the alternating group of degree n.
Theorem: For n . 1, An has order n!/2.
Proof:
For each odd permutation a, the permutation (12)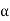 is even and (12)
is even and (12)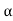
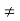 (12)
(12) when
when 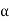
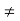
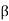 . Thus, there are at least as many even permutations as there are odd ones. On the other hand, for each even permutation a, the permutation (12)
. Thus, there are at least as many even permutations as there are odd ones. On the other hand, for each even permutation a, the permutation (12) is odd and (12)
is odd and (12)
 (12)
(12) when
when 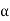
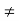
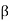 . Thus, there are at least as many odd permutations as there are even ones. It follows that there are equal numbers of even and odd permutations. Since |Sn| = n!, we have |An| = n!/2.
. Thus, there are at least as many odd permutations as there are even ones. It follows that there are equal numbers of even and odd permutations. Since |Sn| = n!, we have |An| = n!/2.
The names for the symmetric group and the alternating group of degree n come from the study of polynomials over n variables. A symmetric polynomial in the variables x1, x2, . . . , xn is one that is unchanged under any transposition of two of the variables. An alternating polynomial is one that changes signs under any transposition of two of the variables.
Key takeaways
- Every permutation of a finite set can be written as a cycle or as a product of disjoint cycles.
- If the pair of cycles
 and
and 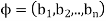 have no entries in common, then
have no entries in common, then 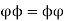
- The order of a permutation of a finite set written in disjoint cycle form is the least common multiple of the lengths of the cycles.
- The set of even permutations in
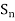 forms a subgroup of
forms a subgroup of 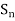 .
.
References:
1. Contemporary abstract algebra, Joseph A. Gallian
2. Schaum’s abstract algebra
3. Basic abstract algebra by P.B. Bhattacharay, SK jain, S.R. Nagpaul
4. Modern abstract algebra by Shanti narayan, S.Chand & Co.