Unit - 3
Properties of cosets
Definition of cosets
Coset of H in G-
Let G be a group and let H be a subset of G. For any a 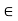 G, the set {ah | h
G, the set {ah | h 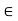 H} is denoted by aH. Analogously, Ha = {ha | h
H} is denoted by aH. Analogously, Ha = {ha | h 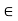 H} and aH
H} and aH 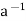 = {ah
= {ah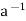 | h
| h 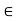 H}. When H is a subgroup of G, the set aH is called the left coset of H in G containing a, whereas Ha is called the right coset of H in G containing a. In this case, the element a is called the coset representative of aH (or Ha). We use |aH| to denote the number of elements in the set aH, and |Ha| to denote the number of elements in Ha.
H}. When H is a subgroup of G, the set aH is called the left coset of H in G containing a, whereas Ha is called the right coset of H in G containing a. In this case, the element a is called the coset representative of aH (or Ha). We use |aH| to denote the number of elements in the set aH, and |Ha| to denote the number of elements in Ha.
Example: Let H 5 {0, 3, 6} in Z9 under addition. In the case that the group operation is addition, we use the notation a + H instead of aH. Then the cosets of H in Z9 are
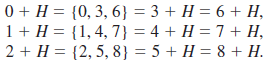
Properties of Cosets
Let H be a subgroup of G, and let a and b belong to G. Then,
1. a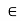 aH,
aH,
2. AH = H if and only if a 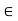 H,
H,
3. AH = bH if and only if a 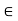 bH
bH
4. AH = bH or aH 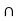 bH =
bH = 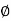 ,
,
5. AH = bH if and only if 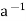 b [ H,
b [ H,
6. |aH| = |bH|,
7. AH = Ha if and only if H = aH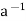 1,
1,
8. AH is a subgroup of G if and only if a 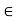 H.
H.
Proof of the above properties
1. a = ae 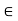 aH.
aH.
2. To verify property 2, we first suppose that aH = H. Then a = ae 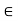 aH = H. Next, we assume that a
aH = H. Next, we assume that a 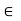 H and show that aH
H and show that aH 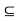 H and H
H and H 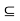 aH. The first inclusion follows directly from the closure of H. To show that H
aH. The first inclusion follows directly from the closure of H. To show that H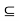 aH, let h
aH, let h 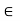 H. Then, since a
H. Then, since a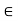 H and h
H and h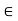 H, we know that
H, we know that 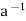 h
h 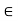 H. Thus, h = eh = (a
H. Thus, h = eh = (a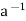 )h = a(
)h = a(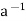 h)
h) 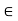 aH.
aH.
3. If aH = bH, then a = ae 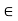 aH = bH. Conversely, if a
aH = bH. Conversely, if a 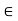 bH we have a = bh where h
bH we have a = bh where h 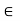 H, and therefore aH = (bh)H = b(hH) = bH.
H, and therefore aH = (bh)H = b(hH) = bH.
4. Property 4 follows directly from property 3, for if there is an element c in aH y bH, then cH = aH and cH = bH.
5. Observe that aH = bH if and only if H = 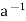 bH. The result now follows from property 2.
bH. The result now follows from property 2.
6. To prove that |aH| = |bH|, it suffices to define a one-to-one mapping from aH onto bH. Obviously, the correspondence ah → bh maps aH onto bH. That it is one-to-one follows directly from the cancellation property.
7. Note that aH = Ha if and only if (aH)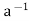 1 = (Ha)
1 = (Ha)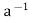 = H(a
= H(a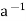 ) =
) =
H—that is, if and only if aH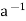 = H.
= H.
8. If aH is a subgroup, then it contains the identity e. Thus, aH 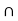 eH 2 0/; and, by property 4, we have aH = eH = H. Thus, from property 2, we have a
eH 2 0/; and, by property 4, we have aH = eH = H. Thus, from property 2, we have a 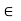 H. Conversely, if a
H. Conversely, if a 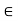 H, then, again by property 2, aH = H.
H, then, again by property 2, aH = H.
Note-
- Property-1 means that the left coset of H containing a does contain a.
- Property-2 means that the H “absorbs” an element if and only if the element belongs to H.
- Property-3 means that a left coset of H is uniquely determined by any one of its elements. In particular, any element of a left coset can be used to represent the coset.
- Property-4 means that two left cosets of H are either identical or disjoint.
- Property 5 shows how we may transfer a question about equality of left cosets of H to a question about H itself and vice versa.
- Property-6 means that all left cosets of H have the same size.
- Property 7 is analogous to property 5 in that it shows how a question about the equality of the left and right cosets of H containing a is equivalent to a question about the equality of two subgroups of G. The last property of the lemma says that H itself is the only coset of H that is a subgroup of G.
Definition of subgroup:
Let (G, .) be the group and let H be the subset of the group G.
H is called the subgroup of G, written H < G, if H is a group relative to the binary operation in G.
For any group G the singleton (e) and G itself are subgroup of G, called trivial subgroups.
A subgroup H of G is said to be proper subgroup if H is not equal to e and H and G are unequal.
It is seen that the identity element of a subgroup of a group must be same as that of the group.
Theorem: Let G be a group. A be non empty subset H of G is a subgroup of G iff either of the following rules holds
- For all a, b
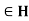 , ab
, ab 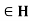 and inverse of a
and inverse of a 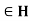
- For all a, b
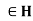 ,
, 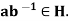
Proof:
If H is a subgroup the both the conditions above are true. Conversely suppose H satisfies the condition first then for any 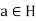 ,
, 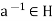 .
.
Hence, e = 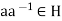 . Therefore, H is a subgroup.
. Therefore, H is a subgroup.
Now suppose that H follows the second rule.
Let 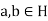 . Then
. Then 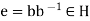 .
.
Hence 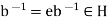 .
.
Therefore 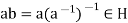 , which proves that H is a subgroup of G.
, which proves that H is a subgroup of G.
Theorem: let 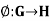 be a homomorphism of groups, then ker
be a homomorphism of groups, then ker 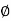 is a subgroup of G and Im
is a subgroup of G and Im 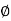 is a subgroup of H.
is a subgroup of H.
Proof:
Ker 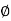 and Im
and Im 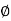 both are non empty. Let
both are non empty. Let 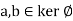 then
then 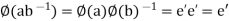 where e’ is the identity of G.
where e’ is the identity of G.
Hence 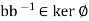 . This proves that ker
. This proves that ker 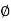 is a subgroup of G.
is a subgroup of G.
Now let 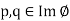 then
then 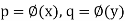 for some x, y
for some x, y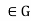 .
.
Hence 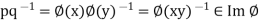 , which proves that Im
, which proves that Im 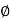 is the subgroup of H.
is the subgroup of H.
Definition of centre of a group:
The centre of a group G is the set of those elements in G that commute with every element in G, that is
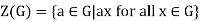
Theorem: the centre of a group G is a subgroup of G.
Proof:
Since ex= x = xe for all 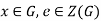 . Let a, b
. Let a, b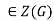 . Then for all
. Then for all 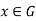
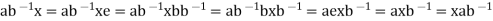
Hence, 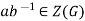 . Therefore, Z(G) is the subgroup of G.
. Therefore, Z(G) is the subgroup of G.
Theorem: let H and K be subgroups of a group (G, .), then HK is a subgroup of G iff HK = KH.
Proof:
Let HK = KH. Since e = ee 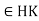 , HK is not empty.
, HK is not empty.
Let 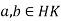 then
then 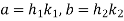 for some
for some 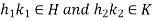 . Hence
. Hence
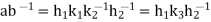
Where 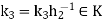 .
.
Now 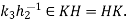 hence
hence 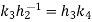 for some
for some 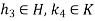 , therefore
, therefore
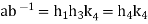
Where 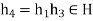 hence
hence 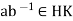 .
.
This proves that HK is a subgroup.
Conversely, suppose that HK is a subgroup, let 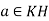 , so that a = kh for some
, so that a = kh for some 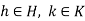 . Then
. Then 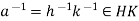 . Hence
. Hence 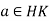 .
.
Therefore, KH is subgroup of HK.
Now let 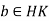 . Then
. Then 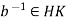 . Hence
. Hence 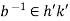 for some
for some 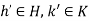 . Therefore
. Therefore 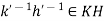 . Hence HK
. Hence HK 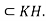
Theorem: Let G be a group and 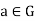
- If
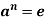 for some integer
for some integer 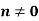 then o(a)|n
then o(a)|n - If o(a) = m, then for all integers I,
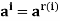 , where r(i) is the remainder of I modulo m.
, where r(i) is the remainder of I modulo m. - [a] is of order m iff o(a) = m
Proof:
Part-1: if 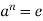 then
then 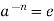 , hence
, hence 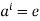 for some i > 0. Therefore by the well ordering property of N, there is a least +ve integer m = 0(a) such that
for some i > 0. Therefore by the well ordering property of N, there is a least +ve integer m = 0(a) such that 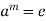 .
.
By using division algorithm, n = mq + r, 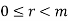 .
.
Hence 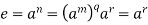 . Therefore r = 0 and m|n.
. Therefore r = 0 and m|n.
Part-2: again using division algorithm, for any 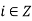 , i = mq + r,
, i = mq + r, 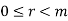 . Hence
. Hence 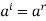 , where r = r(i) is the remainder of i modulo m.
, where r = r(i) is the remainder of i modulo m.
Part-3: Let o(a) = m then 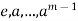 are distinct, for otherwise
are distinct, for otherwise 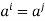 for some I, j,
for some I, j, 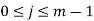 . Hence,
. Hence, 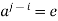 , a contradiction.
, a contradiction.
Let H = [a] be the cyclic subgroup generated by a.
For any 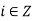 ,
, 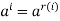 . This implies that H has exactly m elements
. This implies that H has exactly m elements 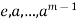 .
.
Conversely, suppose H is of finite order. Then 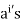 are not distinct for all
are not distinct for all 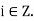
Hence 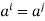 for some
for some 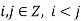 . Then
. Then 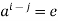 . Hence a is of finite order, say m but then H has exactly m elements as proved earlier.
. Hence a is of finite order, say m but then H has exactly m elements as proved earlier.
Left coset and right coset:
Let H be a subgroup of G. Given 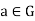 , the set
, the set
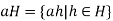
Is called the left coset of H determined by a.
A subset C of G is called a left coset of H in G if C = aH for some a in G.
The set of all cosets of H in G can be written as G/H.
A right coset Ha us defined similarly.
The set of all right cosets of H in G is written as H .
.
Definition: Let H be a subgroup of G. The cardinal number of the set of left and right cosets of H in G is called the index of H in G and it is denoted by [G:H].
Note- Let G be a finite group and let H be any subgroup of G. Let |G| = n and |H| = m then every left coset of H has m elements.
Since the distinct left coset of H are pairwise disjoint and their union is G, we must have n = km, where k is the number of left cosets of H in G.
Key takeaways
- Let (G, .) be the group and let H be the subset of the group G. H is called the subgroup of G, written H < G, if H is a group relative to the binary operation in G.
- Let
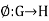 be a homomorphism of groups, then ker
be a homomorphism of groups, then ker 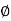 is a subgroup of G and Im
is a subgroup of G and Im 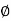 is a subgroup of H.
is a subgroup of H. - The centre of a group G is the set of those elements in G that commute with every element in G, that is
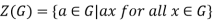
4. The centre of a group G is a subgroup of G.
5. Let H be a subgroup of G. Given 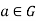 , the set
, the set
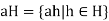 Is called the left coset of H determined by a.
Is called the left coset of H determined by a.
This theorem first stated by Lagrange in 1770 and the complete proof was given by Pietro Abbati.
Theorem- If G is a finite group and H is a subgroup of G, then |H| divides |G|. Moreover, the number of distinct left (right) cosets of H in G is |G|/|H|.
Proof:
Let 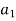 H,
H, 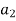 H, . . . ,
H, . . . , 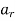 H denote the distinct left cosets of H in G. Then, for each a in G, we have aH =
H denote the distinct left cosets of H in G. Then, for each a in G, we have aH = 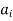 H for some i. Also, by property 1 of the lemma, a
H for some i. Also, by property 1 of the lemma, a 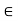 aH. Thus, each member of G belongs to one of the cosets aiH. In symbols,
aH. Thus, each member of G belongs to one of the cosets aiH. In symbols,
G = 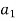 H
H 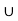 . . . .
. . . . 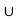
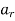 H.
H.
Now, property 4 of the lemma shows that this union is disjoint, so that
|G| = |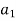 H| + |
H| + |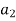 H| + ……+ |
H| + ……+ |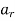 H|.
H|.
Finally, since |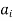 H| = |H| for each i, we have |G| = r|H|.
H| = |H| for each i, we have |G| = r|H|.
Note- The converse of Lagrange’s Theorem is false. For example, a group of order 12 need not have a subgroup of order 6.
The index of a subgroup H in G is the number of distinct left cosets of H in G. This number is denoted by |G:H|. As an immediate consequence of the proof of Lagrange’s Theorem, we have the following useful formula for the number of distinct left (or right) cosets of H in G.
Corollary- If G is a finite group and H is a subgroup of G, then |G:H| 5 |G|/|H|.
Corollary- In a finite group, the order of each element of the group divides the order of the group.
Corollary- A group of prime order is cyclic.
Corollary- Let G be a finite group, and let a 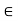 G. Then,
G. Then, 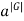 = e.
= e.
Fermat’s Little Theorem- For every integer a and every prime p, 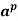 mod p = a mod p.
mod p = a mod p.
Proof:
By the division algorithm, a = pm + r, where 0 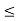 r , p. Thus, a mod p = r, and it suffices to prove that
r , p. Thus, a mod p = r, and it suffices to prove that 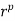 mod p = r. If r = 0, the result is trivial, so we may assume that r
mod p = r. If r = 0, the result is trivial, so we may assume that r 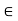 U(p). [Recall that U(p) = {1, 2, . . . , p 2 1} under multiplication modulo p.] Then, by the above corollary,
U(p). [Recall that U(p) = {1, 2, . . . , p 2 1} under multiplication modulo p.] Then, by the above corollary, 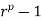 mod p = 1 and, therefore,
mod p = 1 and, therefore, 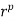 mod p 5 r.
mod p 5 r.
Note-
We use Fermat’s Little Theorem in conjunction with computers to test for primality of certain numbers. One case concerned the number p = 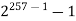 . If p is prime, then we know from Fermat’s Little Theorem that
. If p is prime, then we know from Fermat’s Little Theorem that 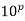 mod p = 10 mod p and, therefore,
mod p = 10 mod p and, therefore, 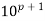 mod p 5 100 mod p. Using multiple precision and a simple loop, a computer was able to calculate
mod p 5 100 mod p. Using multiple precision and a simple loop, a computer was able to calculate 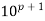 mod p =
mod p = 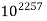 mod p in a few seconds. The result was not 100, and so p is not a prime.
mod p in a few seconds. The result was not 100, and so p is not a prime.
Theorem- An application of cosets to permutation groups
Stabilizer of a Point
Let G be a group of permutations of a set S. For each i in S, let stablizerG(i) = {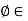 G |
G | 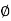 (i) = i}. We call stablizerG(i) the stabilizer of i in G.
(i) = i}. We call stablizerG(i) the stabilizer of i in G.
Orbit of a Point
Let G be a group of permutations of a set S. For each s in S, let orbG(s) = {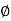 (s) |
(s) | 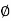
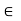 G}. The set orbitG(s) is a subset of S called the orbit of s under G. We use |orbG(s)| to denote the number of elements in orbG(s).
G}. The set orbitG(s) is a subset of S called the orbit of s under G. We use |orbG(s)| to denote the number of elements in orbG(s).
Example: Let G 5 {(1), (132)(465)(78), (132)(465), (123)(456), (123)(456)(78), (78)}.
Then
OrbG(1) 5 {1, 3, 2}, stabG(1) 5 {(1), (78)},
OrbG(2) 5 {2, 1, 3}, stabG(2) 5 {(1), (78)},
OrbG(4) 5 {4, 6, 5}, stabG(4) 5 {(1), (78)},
OrbG(7) 5 {7, 8}, stabG(7) 5 {(1), (132)(465), (123)(456)}.
Key takeaways
- If G is a finite group and H is a subgroup of G, then |H| divides |G|. Moreover, the number of distinct left (right) cosets of H in G is |G|/|H|.
- The converse of Lagrange’s Theorem is false. For example, a group of order 12 need not have a subgroup of order 6.
- If G is a finite group and H is a subgroup of G, then |G:H| 5 |G|/|H|.
- A group of prime order is cyclic.
External Direct Product
Let G1, G2, . . . , Gn be a finite collection of groups. The external direct product of G1, G2, . . . , Gn, written as G1  G2
G2  …
…  Gn, is the set of all n-tuples for which the ith component is an element of Gi and the operation is componentwise.
Gn, is the set of all n-tuples for which the ith component is an element of Gi and the operation is componentwise.
In symbols,
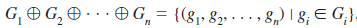
Where (g1, g2, . . . , gn)(g1’, g2’, . . . , gn’) is defined to be (g1g1’, g2g2’, . . . , gngn’). It is understood that each product gigi ‘ is performed with the operation of Gi.
Example:
U(8)  U(10) = {(1, 1), (1, 3), (1, 7), (1, 9), (3, 1), (3, 3), (3, 7), (3, 9), (5, 1), (5, 3), (5, 7), (5, 9), (7, 1),(7, 3), (7, 7), (7, 9)}.
U(10) = {(1, 1), (1, 3), (1, 7), (1, 9), (3, 1), (3, 3), (3, 7), (3, 9), (5, 1), (5, 3), (5, 7), (5, 9), (7, 1),(7, 3), (7, 7), (7, 9)}.
The product (3, 7)(7, 9) 5 (5, 3), since the first components are combined by multiplication modulo 8, whereas the second components are combined by multiplication modulo 10.
Example: Classification of Groups of Order 4
A group of order 4 is isomorphic to Z4 or Z2  Z2. To verify this, let G = {e, a, b, ab}. If G is not cyclic, then it follows from Lagrange’s Theorem that |a| = |b| = |ab| = 2. Then the mapping e
Z2. To verify this, let G = {e, a, b, ab}. If G is not cyclic, then it follows from Lagrange’s Theorem that |a| = |b| = |ab| = 2. Then the mapping e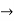 (0, 0), a
(0, 0), a 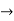 (1, 0), b
(1, 0), b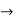 (0, 1), and ab
(0, 1), and ab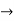 (1, 1) is an isomorphism from G onto Z2
(1, 1) is an isomorphism from G onto Z2  Z2.
Z2.
Theorem- Order of an Element in a Direct Product
The order of an element in a direct product of a finite number o finite groups is the least common multiple of the orders of the components of the element.
Symbolically
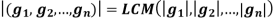
Proof:
Denote the identity of Gi by ei. Let S =
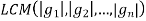
And
t = 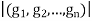
Because s is a multiple of each |gi| implies that
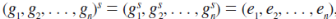
We know that t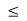 s. On the other hand, from
s. On the other hand, from
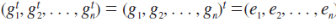
We see that t is a common multiple of 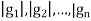 . Thus
. Thus  .
.
Theorem- Criterion for G H to be Cyclic
H to be Cyclic
Let G and H be finite cyclic groups. Then G  H is cyclic if and only if |G| and |H| are relatively prime.
H is cyclic if and only if |G| and |H| are relatively prime.
Proof:
Let |G| = m and |H| = n, so that |G  H| 5 mn. To prove the first half of the theorem, we assume G
H| 5 mn. To prove the first half of the theorem, we assume G  H is cyclic and show that m and n are relatively prime. Suppose that gcd(m, n) = d and (g, h) is a generator of G
H is cyclic and show that m and n are relatively prime. Suppose that gcd(m, n) = d and (g, h) is a generator of G  H. Since
H. Since 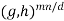 =
= 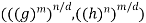 = (e, e), we have mn = |(g, h)|
= (e, e), we have mn = |(g, h)| 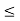 mn/d. Thus, d = 1. To prove the other half of the theorem, let G = <g> and H = <h> and suppose gcd(m, n) = 1. Then, |(g, h)| = lcm(m, n) = mn = |G
mn/d. Thus, d = 1. To prove the other half of the theorem, let G = <g> and H = <h> and suppose gcd(m, n) = 1. Then, |(g, h)| = lcm(m, n) = mn = |G  H|, so that (g, h) is a generator of G
H|, so that (g, h) is a generator of G 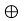 H.
H.
Corollary-1: Criterion for 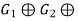 …
… 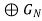 to Be Cyclic
to Be Cyclic
An external direct product 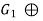
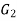
 …
… 
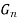 of a finite numberof finite cyclic groups is cyclic if and only if |
of a finite numberof finite cyclic groups is cyclic if and only if |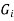 | and
| and 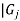 || are relatively prime when I and j are unequal.
|| are relatively prime when I and j are unequal.
Key takeaways
- Let G1, G2, . . . , Gn be a finite collection of groups. The external direct product of G1, G2, . . . , Gn, written as G1
 G2
G2  …
…  Gn, is the set of all n-tuples for which the ith component is an element of Gi and the operation is component wise.
Gn, is the set of all n-tuples for which the ith component is an element of Gi and the operation is component wise. - Let G and H be finite cyclic groups. Then G
 H is cyclic if and only if |G| and |H| are relatively prime.
H is cyclic if and only if |G| and |H| are relatively prime.
Definition of normal subgroup-
A subgroup H of a group G is called a normal subgroup of G if aH = Ha for all a in G. We denote this by H 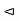 G.
G.
In other words we can define it as-
Let G be a group. A subgroup N of G is called a normal subgroup of G, written as N  G, if
G, if 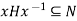 for every
for every 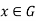 .
.
Note- If G is abelian then every subgroup of G is a normal subgroup, but the converse is not same.
A group in which every subgroup is normal is not necessarily abelian.
Note- “H is normal in G” means ah = ha for a 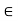 G and h
G and h 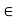 H. This is not what normality of H means; rather, it means that if a
H. This is not what normality of H means; rather, it means that if a 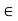 G and h
G and h 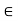 H, then there exist elements h’ and h’’ in H such that ah = h’a and ha = ah’’.
H, then there exist elements h’ and h’’ in H such that ah = h’a and ha = ah’’.
Theorem- (normal subgroup test)- A subgroup H of G is normal in G if and only if 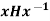
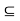 H for all x in G.
H for all x in G.
Proof:
If H is normal in G, then for any x [ G and h [ H there is an h’ in H such that xh = h’x. Thus, 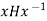 = h’, and therefore
= h’, and therefore 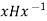
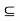 H.
H.
Conversely, if 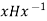
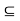 H for all x, then, letting x = a, we have
H for all x, then, letting x = a, we have 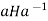
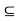 H or aH
H or aH 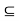 Ha. On the other hand, letting x =
Ha. On the other hand, letting x = 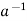 , we have
, we have 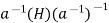 =
= 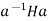
 H or Ha
H or Ha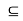 aH.
aH.
Note- Let N be a subgroup of a group G, then the following are equivalent-
- N
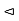 G
G 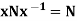 for every
for every 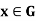
- XN = Nx for every
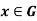
- (xN)(yN) = xyN for all x, y
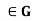
Theorem: let N be a normal subgroup of the group G. Then G/N is a group under multiplication. The mapping 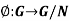 , given by
, given by 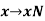 , is a surjective homomorphism and
, is a surjective homomorphism and 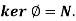
Proof:
By the properties above (xN)(Yn) = (xy)N for all 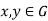 . Hence, G/N is closed under multiplication, because multiplication is associative in G, multiplication is also associative in G/N.
. Hence, G/N is closed under multiplication, because multiplication is associative in G, multiplication is also associative in G/N.
The coset eN = N is the identity for multiplication in G/N, and for any 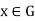 ,
,
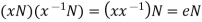
This proves that G/N is a group.
The mapping 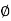 is a homomorphism. Further, xN = eN iff
is a homomorphism. Further, xN = eN iff 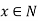 .
.
Hence ker 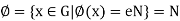 .
.
Theorem: Let G be a group. For any non-empty subset S of G, N(S) is a subgroup of G, further, for any subgroup H of G,
- N(H) is the largest subgroup of G in which H is normal
- If K is a subgroup of N(H), then H is a normal subgroup of KH.
Proof:
Clearly if 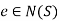 , if x, y
, if x, y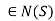 , then
, then
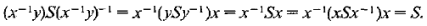
Hence 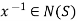 , therefore, N(S) is a subgroup of G.
, therefore, N(S) is a subgroup of G.
Let H is a subgroup of G, then 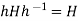 for all
for all 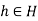 , therefore H is a subset, hence a subgroup of N(H).
, therefore H is a subset, hence a subgroup of N(H).
Further by the definition 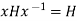 for all
for all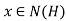 .
.
Hence H 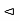 N(H).
N(H).
Let K be any subgroup of G such that H 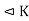 .
.
Then 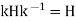 for all
for all 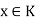 .
.
Hence K is subset of N(H). This proves that N(H) is the largest subgroup of G containing H as normal subgroup.
Let K be a subgroup of N(H), then for all 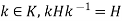 hence kH = Hk, therefore KH = HK.
hence kH = Hk, therefore KH = HK.
Hence by the theorem KH is a subgroup of N(H), and H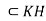 , consequently H
, consequently H 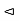 HK.
HK.
Theorem: Let G be a group, and let G’ be the derived group of G.
Then
- G’
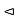 G.
G. - G/G’ is abelian
- If H
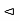 G, then G/H is abelian iff G’
G, then G/H is abelian iff G’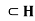 .
.
Proof:
- Suppose
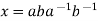 be any commutator in G. Then
be any commutator in G. Then 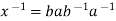 is also a commutator, moreover for any g in G,
is also a commutator, moreover for any g in G,
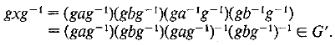
Now any element y in G’ is a product of a finite number of commutators,
Say
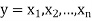
Where 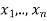 are commutators. Then for any
are commutators. Then for any 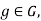
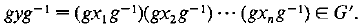
Hence, G’ is a normal subgroup of G.
2. For all 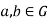
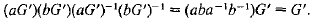
Hence (aG’)(bG’) = (bG’)(aG’). Therefore G/G’ is abelian.
3. Suppose G/H is abelian. Then for all 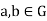
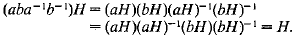
Hence, 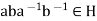 . This proves that
. This proves that 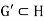 .
.
We can prove the converse similarly.
Example: If G is a group and H is a subgroup of index 2 in G, then H is a normal subgroup of G.
Sol:
If a does not belongs to H then by the hypothesis G = H 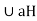 and aH
and aH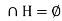 .
.
Also G = H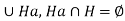 . Thus aH = Ha,
. Thus aH = Ha, 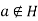 .
.
But clearly aH = Ha, for every 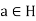 , hence for every
, hence for every 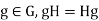 , proving that H is normal in G.
, proving that H is normal in G.
Example: If A < G and B 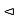 G, then A
G, then A 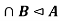 and AB < G.
and AB < G.
Sol:
Of course A 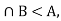 in order to prove the normality for this, suppose
in order to prove the normality for this, suppose 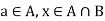 . Then
. Then 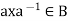 , because B
, because B 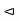 G, trivially,
G, trivially, 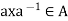 . Thus
. Thus
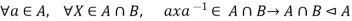
To prove AB < G, let a, 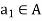 , b,
, b, 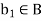 , then ab(
, then ab(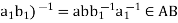 , because
, because 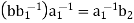 for some
for some 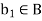 . Thus AB < G.
. Thus AB < G.
Example: If N and M are normal subgroups of G such that N 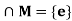 , then nm = mn,
, then nm = mn, 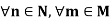 .
.
Sol:
If 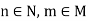 , then
, then
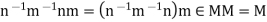
And also
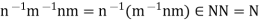
Thus,
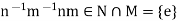
Hence, nm = mn.
Definition of quotient group: Let N be a normal subgroup of G. The group G/N is called the quotient group of G by N.
The homomorphism 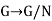 given by
given by 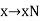 is called the canonical or natural homomorphism of G onto G/N.
is called the canonical or natural homomorphism of G onto G/N.
Definition of normalizer: let G be a group and S be a non-empty subset of G, the normalize of S in G is the set
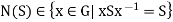
The normalizer of a singleton {a} is written as N(a).
Definition of commutator subgroup:
Let G be a group, for any  ,
,  is called a commutator in G. The subgroup of G generated by the set of all commutators in G is called the commutator subgroup of G. It is denoted by G’.
is called a commutator in G. The subgroup of G generated by the set of all commutators in G is called the commutator subgroup of G. It is denoted by G’.
Example: Every subgroup of an Abelian group is normal. (In this case, ah = ha for a in the group and h in the subgroup.)
Example: The center Z(G) of a group is always normal. [Again, ah = ha for any a 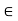 G and any h
G and any h 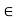 Z(G).
Z(G).
Factor group:
When the subgroup H of G is normal, then the set of left (or right) cosets of H in G is itself a group—called the factor group of G by H (or the quotient group of G by H).
Theorem: Let G be a group and let H be a normal subgroup of G. The set G/H = {aH | a 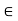 G} is a group under the operation (aH)(bH) = abH
G} is a group under the operation (aH)(bH) = abH
Proof:
First we need to show that the operation is well defined; that is, we must show that the correspondence defined above from G/H 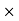 G/H into G/H is actually a function. To do this we assume that for some elements a, a’, b, and b’ from G, we have aH = a’H and bH = b’H and verify that aHbH = a9Hb’H. That is, verify that abh = a’b’H. (This shows that the definition of multiplication depends only on the cosets and not on the coset representatives.) From aH = a’H and bH = b’H , we have a’ = ah1 and b’ = bh2 for some h1, h2 in H, and therefore
G/H into G/H is actually a function. To do this we assume that for some elements a, a’, b, and b’ from G, we have aH = a’H and bH = b’H and verify that aHbH = a9Hb’H. That is, verify that abh = a’b’H. (This shows that the definition of multiplication depends only on the cosets and not on the coset representatives.) From aH = a’H and bH = b’H , we have a’ = ah1 and b’ = bh2 for some h1, h2 in H, and therefore
a’b’H = ah1bh2H = ah1bH = ah1Hb = aHb = abH. Here we have made multiple use of associativity, and the fact that H  G. EH = H is the identity;
G. EH = H is the identity; 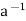 H is the inverse of aH; and (aHbH)cH = (ab)HcH = (ab)cH = a(bc)H = aH(bc)H = aH(bHcH). This proves that G/H is a group.
H is the inverse of aH; and (aHbH)cH = (ab)HcH = (ab)cH = a(bc)H = aH(bc)H = aH(bHcH). This proves that G/H is a group.
Theorem: (Cauchy’s Theorem for Abelian Groups) - Let G be a finite Abelian group and let p be a prime that divides the order of G. Then G has an element of order p.
Proof:
The statement is true for the case in which G has order 2. We prove the theorem by using the Second Principle of Mathematical Induction on |G|. That is, we assume that the statement is true for all Abelian groups with fewer elements than G and use this assumption to show that the statement is true for G as well. Certainly, G has elements of prime order, for if |x| = m and m = qn, where q is prime, then |; 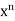 | = q. So let x be an element of G of some prime order q, say. If q = p, we are finished; so assume that q in not equals p. Since every subgroup of an Abelian group is normal, we may construct the factor group
| = q. So let x be an element of G of some prime order q, say. If q = p, we are finished; so assume that q in not equals p. Since every subgroup of an Abelian group is normal, we may construct the factor group 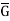 = G/<x>. Then
= G/<x>. Then 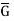 is Abelian and p divides |
is Abelian and p divides |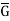 |, since |
|, since |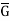 | = |G|/q. By induction, then,
| = |G|/q. By induction, then, 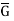 has an element—call it y<x> —of order p.
has an element—call it y<x> —of order p.
Definition Internal Direct Product of Hand K
We say that G is the internal direct product of H and K and write G = H 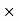 K if H and K are normal subgroups of G and
K if H and K are normal subgroups of G and
G = HK and H 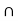 K = {e}.
K = {e}.
Note- We call G the internal direct product of H and K if H and K are subgroups of G, and if G is naturally isomorphic to the external direct product of H and K.
Key takeaways
- A subgroup H of a group G is called a normal subgroup of G if aH = Ha for all a in G. We denote this by H
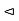 G.
G. - If G is abelian then every subgroup of G is a normal subgroup, but the converse is not same.
- A group in which every subgroup is normal is not necessarily abelian.
- Let N be a normal subgroup of G. The group G/N is called the quotient group of G by N.
- The normalizer of a singleton {a} is written as N(a).
References:
1. Contemporary abstract algebra, Joseph A. Gallian
2. Schaum’s abstract algebra
3. Basic abstract algebra by P.B. Bhattacharay, SK jain, S.R. Nagpaul
4. Modern abstract algebra by Shanti narayan, S.Chand & Co.