Unit - 4
Systems of linear differential equations
The general linear system of two first order differential equations in two unknown functions x and y is of the form
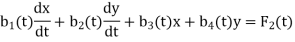
For example: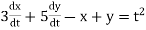 
Note- When a set of linear equations which is related to a group of functions to their derivative, then the system is called the system of linear differential equations.
The general linear system of three first-order differential equations in three unknown functions x, y and z can be defined as
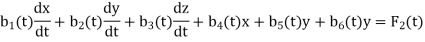
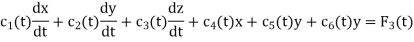
Example: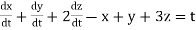 
The normal form in the case of two linear differential equations in two unknown functions are given as-
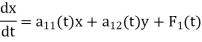
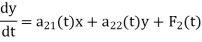
For example:
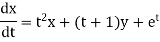
The normal form in the case of linear system of three differential equations in three unknown functions x,y and z are
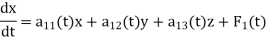
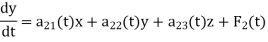
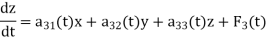
For example:
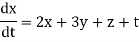
Normal form of LDE-
The normal form of in the case of two LDE in two unknown functions is-
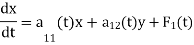
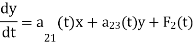
The normal form of in the case of a linear system of three differential equations in three unknown functions x, y and z is-
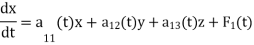
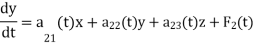
Matrix form of system of linear differential equations
Suppose the system of linear differential equations is gives as below
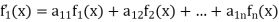
This system is written as
Where
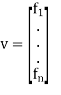
And
Key takeaways
- When a set of linear equations which is related to a group of functions to their derivative, then the system is called the system of linear differential equations.
- The normal form in the case of two linear differential equations in two unknown functions are given as-
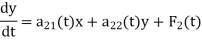
In order to solve a linear system with constant coefficient, we use symbolic operators.
Suppose x is n-times differentiable function of the independent variable t. We denote the operation of differentiation with respect to t by the symbol ‘D’ and we call it as differential operator.
In terms of this differential operator the derivative dx/dt is denoted by Dx.
Which is
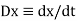
In same order we denote the second derivative of x with respect to t by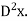 
The nth derivative of x with respect to t by 
That is
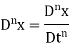
Extending the operator notations, we write
And
Where a, b and c are the constants.
In this notation the linear differential expression with constant coefficients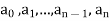 
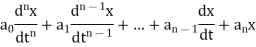
Can be written as-
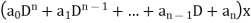
Here note that the operator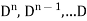 
in this expression do not represent quantities that are to be multiplied by the function x, but rather they indicate operations that are to be carried out upon this function.
The expression
Where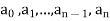 
are constants, is called linear differential operator with constant coefficients.
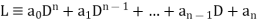
Where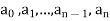 
are constants, now suppose 
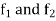are both n-times differentiable functions of t and 
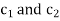are constants.
Then it can be written as
For example, if the operator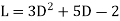 
is applied to 
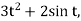then
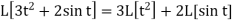
Or
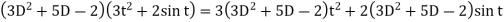
An operator method for linear system with constant coefficient
We consider a linear system of the form
Where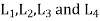 
are linear differential operators with constant coefficient.
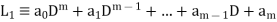
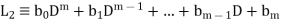
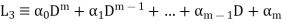
Where a, b,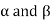 
are constants.
Example:
A simple example of a system which may be expressed in the form of (1) and (2) is provided by
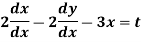
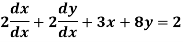
Let’s denote the above system in notation format
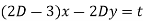
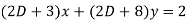
Where
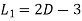
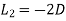
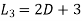
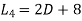
Now we apply the operator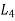 
to (1) and 
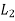to (2), we get
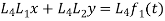
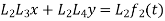
Now subtract the second of these equations from first, since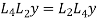 
We get
Or
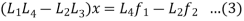
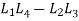is the left side of this equation is itself a linear differential operator with constant coefficients.
We assume that it is neither a zero nor a non-zero constant and denote it by 
.
And if we again assume that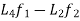 
is the right side and 
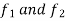are the members of this, then this member is some function let say 
.
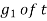Then the equation (3) becomes
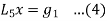
Equation (4) is a linear differential equation with constant coefficient in the single dependent variable x.
Hence we notice that the procedure has eliminated the other dependent variable y.
We now solve the differential equation (4) for x.
Suppose (4) is of order n. Then the general solution of (4) will be
Where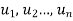 
are the n linearly dependent solutions of the homogenous linear equation 
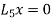and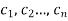 
are arbitrary constants and 
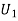is the particular solution (PI).
Now again we apply the operators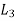 
and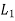 
to the equations (1) and (2) respectively.
The system becomes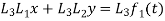
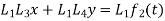
Subtracting, we get
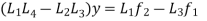
As same as above
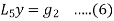
The general solution
Where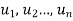 
are the n linearly dependent solutions of the homogenous linear equation 
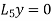and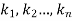 
are arbitrary constants and 
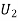is the particular solution (PI).
Key takeaways
- In terms of this differential operator the derivative dx/dt is denoted by Dx.
Which is
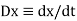
2. 
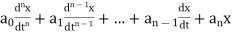
Can be written as-
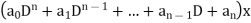
Let us consider a basic type of system of two linear differential equations in two unknown functions. This is of the form
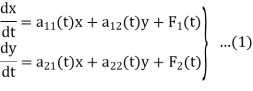
We will assume that the functions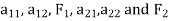 
are all continuous on a real interval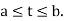 
If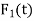 
and 
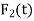are zero for all t, then the above system is called homogeneous, otherwise the system is called non-homogeneous.
For example:
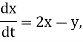
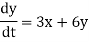
Is homogenous,
And the system
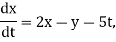
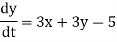
Is non-homogeneous.
We mean by the solution of equation (1), an ordered pair of real functions each having a continuous derivative on the real interval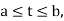 
such that
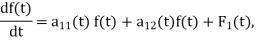
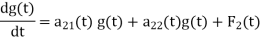
For all t such that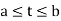 
,
In other words,
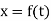
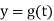
Simultaneously satisfy both equation of the system (1) identically for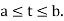 
Key takeaways
If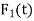 
and 
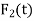are zero for all t, then the above system is called homogeneous, otherwise the system is called non-homogeneous.
Linear differential equation are those in which the independent variable and its derivative occur only in the first degree and are not multiplied together.
Thus the general linear differential equation of the n’th order is of the form
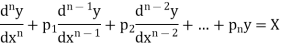
Where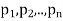 
and X are function of x.
Linear differential equation with constant co-efficient are of the form-
Where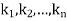 
are constants.
Rules to find the complementary function-
To solve the equation-
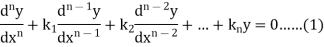
This can be written as in symbolic form-
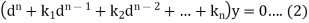
Or-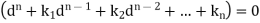
It is called the auxiliary equation.
Let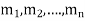 
be the roots-
Case-1: If all the roots are real and distinct, then equation (2) becomes,
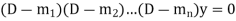
Now this equation will be satisfied by the solution of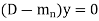 
This is a Leibnitz’s linear and I.F. =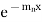 
Its solution is-
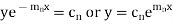
The complete solution will be-
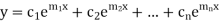
Case-2: If two roots are equal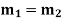 
Then complete solution is given by-
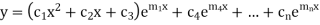
Case-3: If one pair of roots be imaginary, i.e.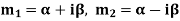 
then the complete solution is-
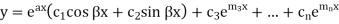
Where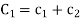 
and 
Case-4: If two points of imaginary roots be equal-
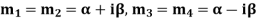
Then the complete solution is-
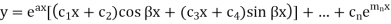
Example-Solve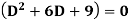 
Sol.
Its auxiliary equation is-
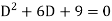
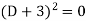
Where-
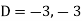
Therefore the complete solution is-
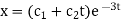
Inverse operator-
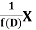is that function of x, not containing arbitrary constants which when operated upon gives X.
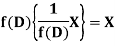
So that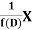 
satisfies the equation f(D)y = X and is, therefore, its P.I.
f(D) and 1/f(D) are inverse operator.
Note-
1. 
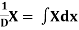
2. 
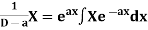
Rules for finding the particular integral-
Let us consider the equation-
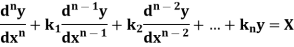
Or in symbolic form-
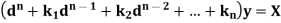
So that-
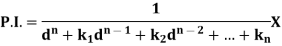
Now-
Case-1: When X =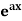 
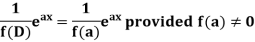
In case f(a) = 0, then we see that the above rule will not work,
So that-
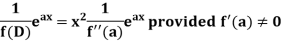
Example: Find the P.I. Of (D + 2)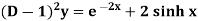
Sol.
P.I. =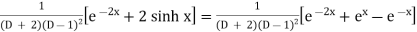 
Now we will evaluate each term separately-
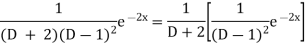
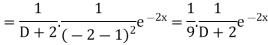
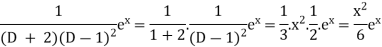
And
Therefore-
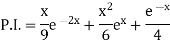
Example: Solve (D – D’ – 2 ) (D – D’ – 3) z = 
Sol.
The C.F. Will be given by-
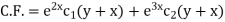
Particular integral-
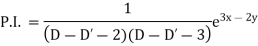
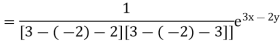
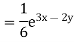
Therefore the complete solution is-
Case-2: when X = sin(ax + b) or cos (ax + b)
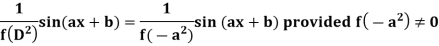
In case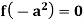 
then the above rule fails.
Now-
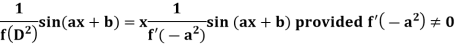
And if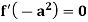 
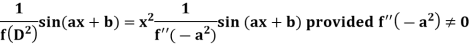
Similarly-
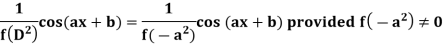
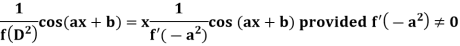
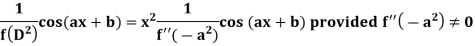
Example: Find the P.I. Of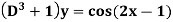 
Sol.
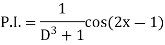
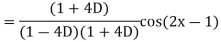
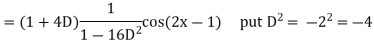
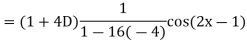
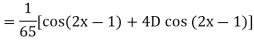
Example: Find the P.I. Of (D + 1) (D + D’ – 1)z = sin (x + 2y)
Sol.
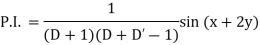
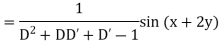
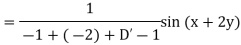
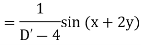
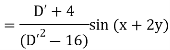
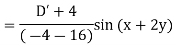
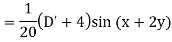
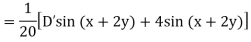
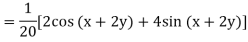
Example: Find P.I. Of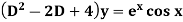
Sol. P.I =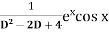 
Replace D by D+1
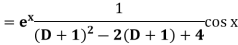
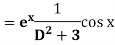
Put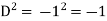 
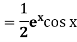
Problem:
Solve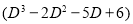 
Solution:
Auxiliary equation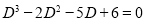 
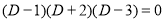
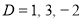
Complementary function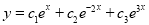 
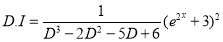
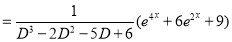
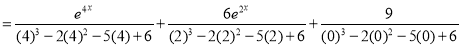
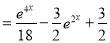
Complete Solution is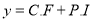 
Problem:
Solve 
Solution:
Auxiliary equation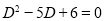 
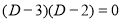
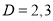
C.F is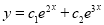 
[
]
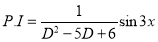
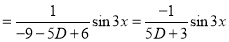
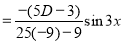
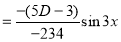
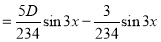
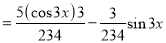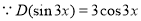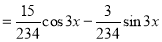
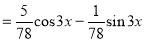
The Complete Solution is 
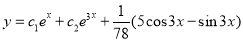
Example:
Solve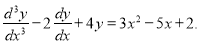 
Solution:
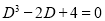
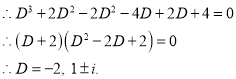
The Auxiliary equation is 
The C.F is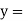 
P.I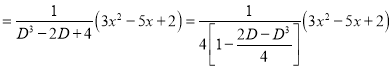 
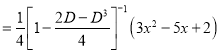
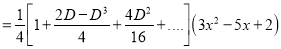
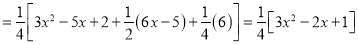
The Complete Solution is 
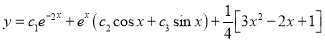
Example:
Solve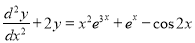 
Solution:
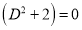
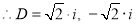
The Auxiliary equation is 
The C.F is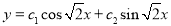
P.I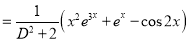 
Now, 
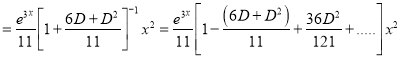
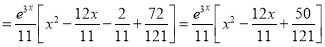
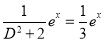
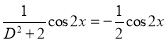
The Complete Solution is
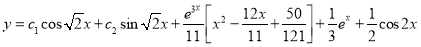
Example:
Solve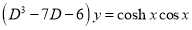 
Solution:
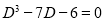
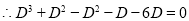
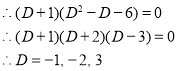
The auxiliary solution is 
The C.F is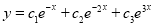
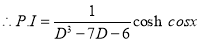
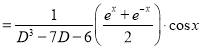
Now,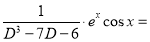 
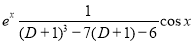
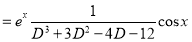
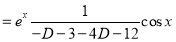[Putting 
]
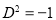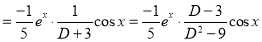
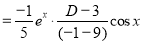
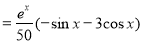
Similarly, we find that
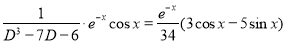
The Complete Solution is
Example:
Solve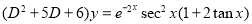 
Solution:
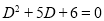
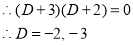
The auxiliary equation is 
The C.F is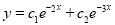 
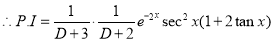
[Put 
]
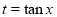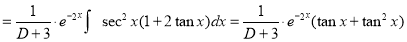
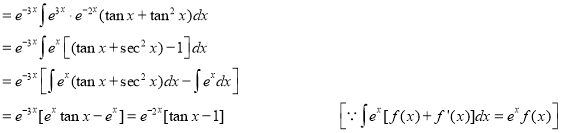
The Complete Solution is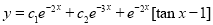 
Example:
Solve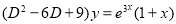 
Solution:
The auxiliary equation is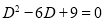 
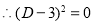
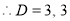
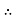The C.F is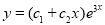
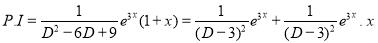
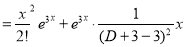
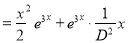
But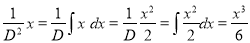 
The Complete Solution is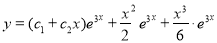 
Example:
Solve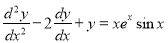 
Solution:
The auxiliary equation is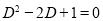
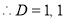
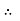The C.F is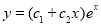
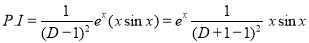
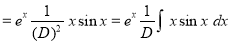
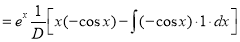[By parts]
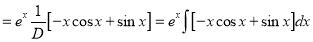
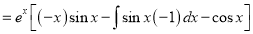
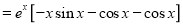
The Complete Solution is 
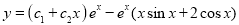
Example:
Solve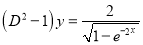 
Solution:
The auxiliary equation is 
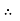The C.F is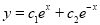
Here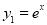 
, 
, 
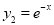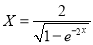. Let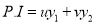 
Now,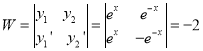 
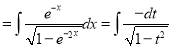Put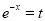 
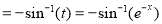
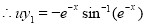
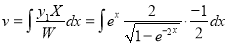
Multiply by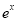 
in the numerator and denominator
Put 
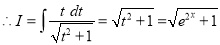
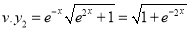
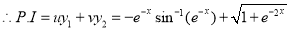
The Complete Solution is 
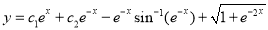
Example:
Solve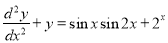 
Solution:
The auxiliary equation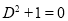 is
The C.F is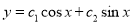
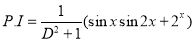
Now,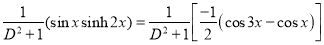 
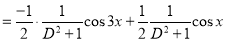
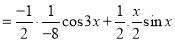
And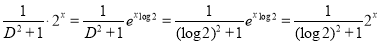 
The Complete Solution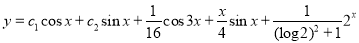 
Example:
Solve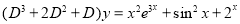 
Solution:
The auxiliary equation is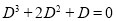
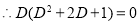
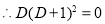
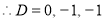
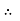The C.F is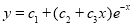
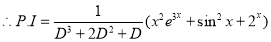
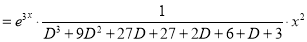
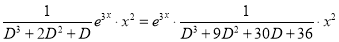
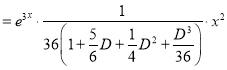
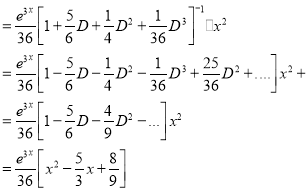
And,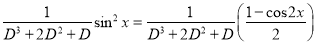 
Now,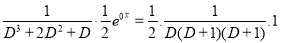 
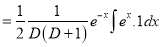
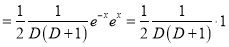
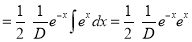
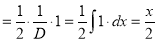
And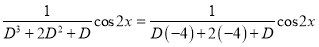 
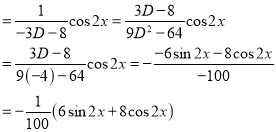
And 
The Complete Solution is
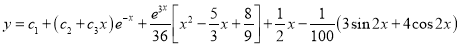
Key takeaways
- Linear differential equation with constant co-efficient are of the form-
Where 
are constants.
2. If all the roots are real and distinct, then equation (2) becomes,
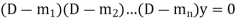
3. If two roots are equal 
Then complete solution is given by-
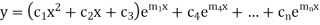
4. If one pair of roots be imaginary, i.e.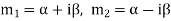 
then the complete solution is-
Where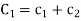 
and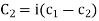 
5. If two points of imaginary roots be equal-
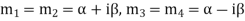
Then the complete solution is-
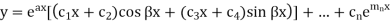
Suppose dy/dx = f(x, y) is a first order ODE and with the initial condition y(0) = 0 and if f and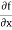 
are continuous on rectangle R for which the 
then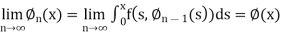 
where y = 
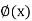is the unique solution to this initial value problem.
Now the functions 
are successive approximations of the unique solution y =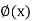 
.
Hence we begin with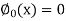 
, and the other functions can be find by using the formula given below
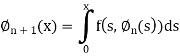
Example: By using the method of successive approximation find the functions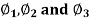 
of the following differential equation
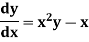
With the initial condition y(0) = 0.
Sol:
Suppose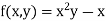 
, here f is continuous on all of 
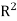and 
is continuous on all of 
, hence the unique solution exists.
Now define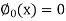 
Here we will calculate the three approximations,
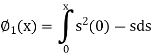
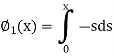
Similarly
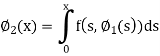
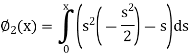
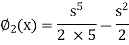
Now the third approximations will be
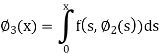
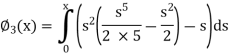
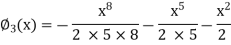
Example: By using the method of successive approximation find the functions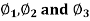 
of the following differential equation
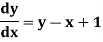
With the initial condition y(0) = 0.
Sol:
Suppose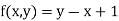 
, here f is continuous on all of 
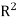and 
is continuous on all of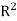 
, hence the unique solution exists.
Now define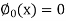 
Here we will calculate the three approximations,
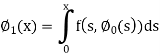
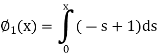
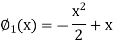
Now
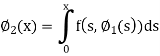
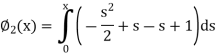
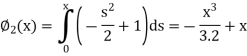
And
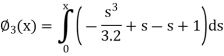
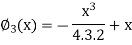
References:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. Advanced engineering mathematics, by HK Dass
3. Differential equations, Shepley L. Ross, Willey India.
4. Partial differential equations, Phoolan Prasad, Renuka ravindran, John Willey & Sons
