Unit - 4
Divisibility in integral domains
We said before that one of the reasons for the definition of integral domain was to capture some of the most important features of integers. This is at the heart of mathematics' abstraction and generalisation: distilling the important qualities of our objects of interest and investigating the ramifications of those properties. Cancellation is one of Z's most essential properties.
Theorem 2.3.1.
Let R be a ring. Then R is a domain if and only if for
All a,b,c∈R with c≠0 and ac=bc, we have a=b.
We may read Theorem 2.3.1 as saying that the defining property of an integral domain is the ability to cancel common nonzero factors. Note that we have not divided; division is not a binary operation, and nonzero elements of rings need not be units. However, as was the case in Z, there are notions of divisibility and factorization in rings.
Definition 2.3.2.
Let R be a commutative ring with identity, and let a,b∈R. We say aa divides b and write a∣b if there is a c∈R such that ac=b. We then say that ais a factor of b.
Investigation 2.3.1.
Find all factors of 2¯ in the following rings:
- Z5
- Z6
- Z10
Our definition of prime applies to domains as well. Indeed, our less-known formulation in Definition 1.3.1 is motivated by a wish to extend the familiar concept of prime from Z to any ring.
Definition 2.3.3.
Let R be a domain. We say a nonzero nonunit element a∈R is prime if whenever a∣bc for some b,c∈R, either a|b or a|c.
Irreducibility is a concept linked to primality. In fact, irreducibility may be considered a natural generalisation of the standard concept of prime found in classroom mathematics.
Definition 2.3.4.
Let R be a domain. We say a nonzero nonunit element a∈R is irreducible if whenever a=bc for some b,c∈R, one of b or c is a unit. (Note that in some areas of the literature, the word atom is used interchangeably with irreducible.)
Exploration 2.3.2.
Find the units, primes, and irreducibles in the following rings.
- R
- Z
- Z5
- Z6
In domains, all primes are irreducible.
Theorem 2.3.5.
Let R be a domain. If a∈R is prime, then a is irreducible.
In familiar settings, the notion of prime and irreducible exactly coincide.
Theorem 2.3.6.
Every irreducible in Z is prime.
Despite their similarity in appearance, primes and irreducibles are two different sorts of components. Not all primes are irreducible, as the following investigation illustrates. Furthermore, Exploration 2.3.4 will demonstrate that not all irreducibles, even in domains, are primes!
Exploration 2.3.3.
Find an example of a ring R and prime p∈R such that p is not irreducible.
Exploration 2.3.4.
Consider the set R of all polynomials in Z[x] for which the coefficient on the linear term is zero. That is,

(You don't need to prove that R is an integral domain; you only need to believe it.) Then, in R, discover an irreducible but non-prime polynomial of the type xn.
The concept of greatest common divisor is our final straightforward generalisation from Z's multiplicative structure. Our careful work in the case of Z generalises nicely to all domains, as our next definition indicates. Indeed, we didn't use in Definition 1.2.7 to determine the largest common divisor because not all rings have a natural order relation like Z.
Definition 2.3.7.
Let R be a domain, and let a,b∈R. A nonzero element d∈R is a greatest common divisor of a and b if
- d∣a and d∣b and,
- If e∈R with e∣a and e∣b, then e∣d.
Theorem 2.3.8.
Let R be a domain and a,b∈R and suppose d is a greatest common divisor of a and b. Then any associate of d is also a greatest common divisor of a and b. (Recall Definition 2.2.7.)
Numericals:
1) Consider D = 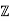 [d] = {a + b √ d : a, b ∈
[d] = {a + b √ d : a, b ∈ 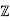 }, where d 6= 1 and not divisible by p2 for a prime.
}, where d 6= 1 and not divisible by p2 for a prime.
Define N(a + b √ d) = |a 2 – db2 |. Then
- N(x) = 0 if and only if x = 0; N(xy) = N(x)N(y);
- N(x) = 1 if and only if x is a unit;
- If N(x) is prime then x is irreducible in
 [ √ d].
[ √ d].
2) In D = 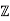 [−3] = {a + b √ −3 : a, b ∈
[−3] = {a + b √ −3 : a, b ∈ 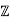 }, the element 2 is irreducible, but it is not a prime.
}, the element 2 is irreducible, but it is not a prime.
Proof. If 2 = bc and x, y ∈ D are not units, then 4 = N(2) = N(x)N(y). So, 2 = N(x) = N(a + b √ −3) = a 2 + 3b 2 , a contradiction.
Note that 4 = (1 + √ −3)(1 − √ −3) is divisible by 2, but none of (1 ± √ −3) is divisible by 2....
Key takeaways:
• An integral domain is a commutative ring with no zero-divisors and an identity (1 0). That example, ab = 0 (a = 0) or b = 0 (b = 0). Examples. The integral domain is the ring Z.
• If R = 0 (or 1 = 0), and r is a zero divisor in R, then R is an integral domain.
• An integral domain is a commutative ring with no zero-divisors and identity.
An element 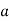 of a ring which is nonzero, not a unit, and whose only divisors are the trivial ones (i.e., the units and the products
of a ring which is nonzero, not a unit, and whose only divisors are the trivial ones (i.e., the units and the products 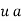 , where
, where  is a unit). Equivalently, an element
is a unit). Equivalently, an element 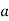 is irreducible if the only possible decompositions of
is irreducible if the only possible decompositions of 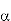 into the product of two factors are of the form
into the product of two factors are of the form
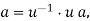
Where 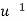 is the multiplicative inverse of
is the multiplicative inverse of  .
.
Irreducible elements include prime numbers and irreducible polynomials, for example. The irreducible elements are the generators of the nonzero prime ideals in a principal ideal domain, hence they are exactly the prime elements. However, the two concepts are not interchangeable in general.
Relationship with prime elements
Prime elements and irreducible elements are not the same thing. (In a commutative ring R, a non-zero non-unit element an is called prime if a|bc for some b and c in R, then a|b or a|c) Every prime element is irreducible in an integral domain, although this is not the case in general. For unique factorization domains, the opposite is true (or, more generally, GCD domains.)
Furthermore, whereas an ideal generated by a prime element is a prime ideal, an ideal created by an irreducible element is not an irreducible ideal in general. If D is a GCD domain and x is an irreducible element of D, then x is prime, and the ideal generated by x is a prime (thus irreducible) ideal of D, as stated above.
Example
In the quadratic integer ring 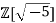 it can be shown using norm arguments that the number 3 is irreducible. However, it is not a prime element in this ring since, for example,
it can be shown using norm arguments that the number 3 is irreducible. However, it is not a prime element in this ring since, for example, 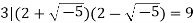
But 3 does not divide either of the two factors.
A prime number (or prime integer, often simply called a "prime" for short) is a positive integer  that has no positive integer divisors other than 1 and
that has no positive integer divisors other than 1 and 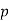 itself. More concisely, a prime number
itself. More concisely, a prime number 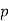 is a positive integer having exactly one positive divisor other than 1, meaning it is a number that cannot be factored. For example, the only divisors of 13 are 1 and 13, making 13 a prime number, while the number 24 has divisors 1, 2, 3, 4, 6, 8, 12, and 24 (corresponding to the factorization
is a positive integer having exactly one positive divisor other than 1, meaning it is a number that cannot be factored. For example, the only divisors of 13 are 1 and 13, making 13 a prime number, while the number 24 has divisors 1, 2, 3, 4, 6, 8, 12, and 24 (corresponding to the factorization 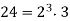 ), making 24 not a prime number. Positive integers other than 1 which are not prime are called composite numbers.
), making 24 not a prime number. Positive integers other than 1 which are not prime are called composite numbers.
While the word "prime number" is most usually used to refer to prime positive integers, other forms of primes, such as Gaussian primes, are also described.
The number one is a unique situation that is neither prime nor composite (Wells 1986, p. 31). Although the number 1 was once considered a prime (Goldbach 1742; Lehmer 1909, 1914; Hardy and Wright 1979, p. 11; Gardner 1984, pp. 86-87; Sloane and Plouffe 1995, p. 33; Hardy 1999, p. 46), it now necessitates special treatment in so many definitions and applications involving primes greater than or equal to 2, that it is usually placed into its own class. One rationale for not calling 1 a prime number is that if it were, the fundamental theorem of arithmetic would have to be changed because "in exactly one way" would be untrue. Because any  . In other words, unique factorization into a product of primes If the primes included 1, the problem would be solved. Tietze (1965, p. 2) gives a somewhat less revealing but mathematically true argument "Why is the number one treated differently? This is an issue that many schoolboys dispute about, yet it is not debatable because it is a question of definition." "2 pays its way [as a prime] on balance; 1 doesn't," Derbyshire (2004, p. 33) puts it more simply.
. In other words, unique factorization into a product of primes If the primes included 1, the problem would be solved. Tietze (1965, p. 2) gives a somewhat less revealing but mathematically true argument "Why is the number one treated differently? This is an issue that many schoolboys dispute about, yet it is not debatable because it is a question of definition." "2 pays its way [as a prime] on balance; 1 doesn't," Derbyshire (2004, p. 33) puts it more simply.
With 1 removed, the smallest prime number is 2. However, because 2 is the only even prime (which ironically makes it the "oddest" prime), it is unique, and the set of all primes except 2 is referred to as the "odd primes." It's also worth noting that while 2 is now considered a prime, it wasn't always (Tietze 1965, p. 18; Tropfke 1921, p. 96).
The nth prime number is commonly denoted 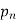 , so
, so 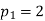 ,
, , and so on, and may be computed in the Wolfram Language as Prime[n].
, and so on, and may be computed in the Wolfram Language as Prime[n].
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37,... Are the first few primes (OEIS A000040; Hardy and Wright 1979, p. 3). "In the early morning, astronomers spiritualized nonmathematicians," is a mnemonic for remembering the first seven primes (G. L. Honaker, Jr., pers. Comm., Aug. 4, 2005). The protagonist Christopher in the novel The Curious Incident of the Dog in the Night-Time (Haddon 2003) amusingly numbers the chapters using prime numbers rather than the (far) more customary positive integers. In the NUMB3RS television crime drama's Season 1 episode "Prime Suspect" (2005), math genius Charlie Eppes realised that his character Ethan's daughter had been kidnapped because he was close to solving the Riemann hypothesis, which allegedly would allow the perpetrators to break virtually all internet security by factoring large numbers.
The numbers of decimal digits in 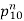 for
for  , 1, ... Is given by 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, ... (OEIS A099260).
, 1, ... Is given by 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, ... (OEIS A099260).
The set of primes is sometimes denoted 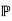 , represented in the Wolfram Language as Primes.
, represented in the Wolfram Language as Primes.

The first several primes are shown above as a binary bit sequence.
"Mathematicians have sought in vain to discover some order in the series of prime numbers to this day, and we have cause to suppose that it is a mystery into which the mind will never penetrate," Euler wrote (Havil 2003, p. 163). D. Zagier made a remark in a 1975 lecture "There are two truths regarding prime number distribution that I aim to persuade you of so strongly that they will be indelibly etched in your minds. The first is that, despite their straightforward definition and function as natural number building blocks, prime numbers spread like weeds among the natural numbers, seemingly obeying no other law than chance, and no one can anticipate where the next one will sprout. The second truth is even more amazing, because it states the exact opposite: that prime numbers are remarkably regular, that they follow laws that regulate their behaviour, and that they obey these laws with military precision " (Havil 2003, p. 171).
The 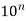 th prime for
th prime for  , 1, ... Is given by 2, 29, 541, 7919, 104729, 1299709, 15485863, 179424673, 2038074743, ... (OEIS A006988; Graham et al. 1990, p. 111).
, 1, ... Is given by 2, 29, 541, 7919, 104729, 1299709, 15485863, 179424673, 2038074743, ... (OEIS A006988; Graham et al. 1990, p. 111).
Large primes (Caldwell) include the large Mersenne primes, Ferrier's prime, and the 1521561 -digit counterexample 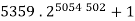 showing that 5359 is not a Sierpiński number of the second kind (Helm and Norris). The largest known prime as of December 2018 is the Mersenneprime
showing that 5359 is not a Sierpiński number of the second kind (Helm and Norris). The largest known prime as of December 2018 is the Mersenneprime  , which has a whopping 24 862 048 decimal digits.
, which has a whopping 24 862 048 decimal digits.
Prime numbers can be formed by sieving processes (such as Eratosthenes' sieve), and fortunate numbers, which are also generated through sieving, appear to have some intriguing asymptotic qualities in common with primes. Many unusual and amazing features are satisfied by prime numbers. Although there exist explicit prime formulas (i.e., formulas which either generate primes for all values or else the  th prime as a function of
th prime as a function of  ), they are contrived to such an extent that they are of little practical value.
), they are contrived to such an extent that they are of little practical value.
The Dirichlet generating function of the characteristic function of the prime numbers 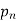 is given by
is given by
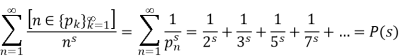
Where  is the prime zeta function and
is the prime zeta function and 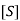 is an Iverson bracket.
is an Iverson bracket.
The function that gives the number of primes less than or equal to a number 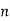 is denoted
is denoted 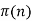 and is called the prime counting function. The theorem giving an asymptotic form for
and is called the prime counting function. The theorem giving an asymptotic form for 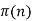 is called the prime number theorem. Similarly, the numbers of primes of the form
is called the prime number theorem. Similarly, the numbers of primes of the form  less than or equal to a number
less than or equal to a number  is denoted
is denoted 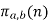 and is called the modular prime counting function.
and is called the modular prime counting function.
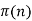 and
and 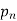 are inverse functions, so
are inverse functions, so
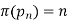 (4)
(4)
For all positive integers and
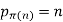 (5)
(5)
Iff n is a prime number.
For identifying the prime factors of a given number, a process known as factorization or prime factorization, many prime factorization methods have been invented. The level of sophistication and complexity varies greatly. Because creating a general-purpose algorithm for this computationally "hard" problem is extremely difficult, any additional information about the number in question or its factors can typically be leveraged to save a significant amount of time. It's worth noting that just because no efficient methods for factoring arbitrary integers are known, that doesn't mean they don't exist. As a result, it's possible that a sufficiently bright person could invent a generic way of factoring that would make the vast majority of encryption systems in use today, including those used by banks and governments, simply breakable.
Because of their importance in encryption algorithms such as RSA encryption, prime numbers can be important commercial commodities. In fact, R. Schlafly (1994) has obtained U.S. Patent 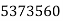 on the following two primes (expressed in hexadecimal notation):
on the following two primes (expressed in hexadecimal notation):
98A3DF52AEAE9799325CB25D767EBD1F4630398
9E21732A4AFB1624BA6DF911466AD8DA960586F4
A0D5E3C36AF099660BDDC1577E54A9F402334433
ACB14BCB
And
93E8965DAFD9DFECFD00B466B68F90EA68AF5DC9
FED915278D1B3A137471E65596C37FED0C7829FF
8F8331F81A2700438ECDCC09447DC397C685F397
294F722BCC484AEDF28BED25AAAB35D35A65DB1F
D62C9D7BA55844FEB1F9401E671340933EE43C54
E4DC4594007AD61248B83A2624835B31FFF2D95
95 A5B90B276E44F9
The fundamental theorem of arithmetic states that any positive integer can be represented in exactly one way as a product of primes. Euclid's second theorem demonstrated that there are an infinite number of primes. However, it is not known if there are an infinite number of primes of the form 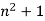 (Hardy and Wright 1979, p. 19; Ribenboim 1996, pp. 206-208), whether there are an infinite number of twin primes (the twin prime conjecture), or if a prime can always be found between
(Hardy and Wright 1979, p. 19; Ribenboim 1996, pp. 206-208), whether there are an infinite number of twin primes (the twin prime conjecture), or if a prime can always be found between 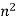 and
and  (Hardy and Wright 1979, p. 415; Ribenboim 1996, pp. 397-398). The latter two of these are two of Landau's problems.
(Hardy and Wright 1979, p. 415; Ribenboim 1996, pp. 397-398). The latter two of these are two of Landau's problems.
The "direct search factorization" method is the simplest way to locate factors (a.k.a. Trial division). This method involves testing all possible variables using trial division to check if they truly divide the given number. It is only feasible for relatively small groups. The elliptic curve factorization method and the number field sieve factorization method are two more general (and difficult) methods.
The set of prime numbers has been demonstrated to be a Diophantine set (Ribenboim 1991, pp. 106-107).
With the exception of 2 and 3, all primes are of the form  , i.e.,
, i.e., 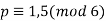 (Bungus 1599, p. 399, quoted in Peano 1908, p. 59; Wells 1986, p. 68). For
(Bungus 1599, p. 399, quoted in Peano 1908, p. 59; Wells 1986, p. 68). For 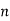 an integer
an integer 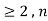 is prime iff the congruence equation
is prime iff the congruence equation
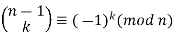 (8)
(8)
Holds for 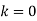 , 1, ...,
, 1, ..., 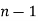 (Deutsch 1996), where
(Deutsch 1996), where 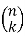 is a binomial coefficient. In addition, an integer
is a binomial coefficient. In addition, an integer 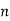 is prime iff
is prime iff
 (9)
(9)
The first few composite n for which
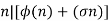
Are  , 560, 588, 1400, 23760, with a total of 18 such numbers less than
, 560, 588, 1400, 23760, with a total of 18 such numbers less than 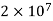 .
.
Chen (1979) showed that for  sufficiently large, there always exists a number with at least two prime factors between
sufficiently large, there always exists a number with at least two prime factors between  and
and  for
for  (Le Lionnais 1983, p. 26; Guy 2004, p. 34). In practice, this relation seems to hold for all
(Le Lionnais 1983, p. 26; Guy 2004, p. 34). In practice, this relation seems to hold for all 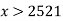 .
.
2, 3, 5, 7, 23, 67, 89, 4567, 78901,... Are primes with consecutive digits (considering 0 as occurring after 9). (OEIS A006510). 23, 37, 53, 73, 223, 227, 233, 257, 277, 337, 353, 373, 523, 557,... (OEIS A019546), which is one of the Smarandache sequences, are primes consisting of numbers that are themselves primes.
Because a prime number p has only the trivial factors 1 and 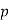 , in his In his book The Road Ahead, Bill Gates made an unintentional reference to a minor operation when he said "Because encryption is required for both the privacy of the system and the security of digital money, a breakthrough in mathematics or computer science that defeats the cryptographic system could be disastrous. The finding of an easy mechanism to factor huge prime numbers [emphasis added] would be an obvious mathematical advance." (Gates, p. 265, 1995).
, in his In his book The Road Ahead, Bill Gates made an unintentional reference to a minor operation when he said "Because encryption is required for both the privacy of the system and the security of digital money, a breakthrough in mathematics or computer science that defeats the cryptographic system could be disastrous. The finding of an easy mechanism to factor huge prime numbers [emphasis added] would be an obvious mathematical advance." (Gates, p. 265, 1995).
The "Top Ten" Record Primes
Rank | Prime | Digits | Who | When |
1 | 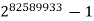 | 24862048 | G16 | 2018 |
2 | 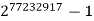 | 23249425 | G15 | 2018 |
3 | 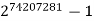 | 22338618 | G14 | 2016 |
4 | 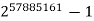 | 17425170 | G13 | 2013 |
5 |  | 12978189 | G10 | 2008 |
6 | 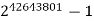 | 12837064 | G12 | 2009 |
7 | 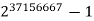 | 11185272 | G11 | 2008 |
8 | 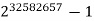 | 9808358 | G9 | 2006 |
9 |  | 9383761 | SB12 | 2016 |
10 | 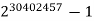 | 9152052 | G9 | 2005 |
Key takeaways:
- Prime numbers are utilised in a variety of computer programmes, including public-key cryptography, which relies on the difficulty of factoring huge integers into prime factors.
- Prime elements and prime ideals are objects that behave like prime numbers in a generalised fashion.
- Primes are extremely essential to number theorists because they are the fundamental building blocks of whole numbers, and they are also extremely significant to the rest of the world since their peculiar mathematical features make them ideal for our contemporary applications.
4.4.1 Introduction:
In mathematics, a unique factorization domain (UFD) is a ring in which a statement comparable to the fundamental theorem of arithmetic holds (also known as a factorial ring in Bourbaki's nomenclature). A UFD is a nontrivial commutative ring in which the product of any two non-zero elements is non-zero. Every non-zero non-unit element can be expressed as a product of prime elements (or irreducible elements), uniquely up to order and units.
Integers and polynomial rings in one or more variables with coefficients derived from integers or fields are good examples of UFDs.
4.4.2 Definition:
Formally, a unique factorization domain is defined to be an integral domain R in which every non-zero element x of R can be written as a product (an empty product if x is a unit) of irreducible elements pi of R and a unit u:
x = u p1 p2 ⋅⋅⋅ pn with n ≥ 0
And this representation is unique in the following sense: If q1, ..., qm are irreducible elements of R and w is a unit such that
x = w q1 q2 ⋅⋅⋅ qm with m ≥ 0,
Then m = n, and there exists a bijective map φ : {1, ..., n} → {1, ..., m} such
That pi is associated to qφ(i) for i ∈ {1, ..., n}.
Because the uniqueness portion is often difficult to verify, the following equivalent definition is useful:
Every non-zero element of an integral domain R can be expressed as a product of a unit and prime elements of R.
4.4.3 Examples
UFDs are the most common rings in elementary mathematics:
- UFDs are all major ideal domains, and thus all Euclidean domains. The integers (also known as the fundamental theorem of arithmetic), Gaussian integers, and Eisenstein integers are examples of UFDs.
- R[X], the ring of polynomials with coefficients in R, is a UFD if R is a UFD. R[X] is not a principal ideal domain unless R is a field. A polynomial ring in any number of variables over any UFD (and especially over a field or the integers) is a UFD by induction.
- The formal power series ring K[[X1,...,Xn]] over a field K (or more generally over a regular UFD such as a PID) is a UFD. On the other hand, the formal power series ring over a UFD need not be a UFD, even if the UFD is local. For example, if R is the localization of k[x,y,z]/(x2 + y3 + z7) at the prime ideal (x,y,z) then R is a local ring that is a UFD, but the formal power series ring R[[X]] over R is not a UFD.
- The Auslander–Buchsbaum theorem states that every regular local ring is a UFD.
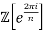 is a UFD for all integers 1 ≤ n ≤ 22, but not for n = 23.
is a UFD for all integers 1 ≤ n ≤ 22, but not for n = 23.- Mori showed that if the completion of a Zariski ring, such as a Noetherian local ring, is a UFD, then the ring is a UFD.[1] The converse of this is not true: there are Noetherian local rings that are UFDs but whose completions are not. The question of when this happens is rather subtle: for example, for the localization of k[x,y,z]/(x2 + y3 + z5) at the prime ideal (x,y,z), both the local ring and its completion are UFDs, but in the apparently similar example of the localization of k[x,y,z]/(x2 + y3 + z7) at the prime ideal (x,y,z) the local ring is a UFD but its completion is not.
- Let be a field of any characteristic other than 2. Klein and Nagata showed that the ring R[X1,...,Xn]/Q is a UFD whenever Q is a nonsingular quadratic form in the X's and n is at least 5. When n=4 the ring need not be a UFD. For example,
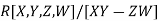
 is not a UFD, because the element XY equals the element 𝑍W so that 𝑋Y and 𝑍W are two different factorizations of the same element into irreducibles.
is not a UFD, because the element XY equals the element 𝑍W so that 𝑋Y and 𝑍W are two different factorizations of the same element into irreducibles. - The ring Q[x,y]/(x2 + 2y2 + 1) is a UFD, but the ring Q(i)[x,y]/(x2 + 2y2 + 1) is not. On the other hand, The ring Q[x,y]/(x2 + y2 – 1) is not a UFD, but the ring Q(i)[x,y]/(x2 + y2 – 1) is (Samuel 1964, p.35). Similarly the coordinate ring R[X,Y,Z]/(X2 + Y2 + Z2 − 1) of the 2-dimensional real sphere is a UFD, but the coordinate ring C[X,Y,Z]/(X2 + Y2 + Z2 − 1) of the complex sphere is not.
- Suppose that the variables Xi are given weights wi, and F(X1,...,Xn) is a homogeneous polynomial of weight w. Then if c is coprime to w and R is a UFD and either every finitely generated projective module over R is free or c is 1 mod w, the ring R[X1,...,Xn,Z]/(Zc − F(X1,...,Xn)) is a UFD.
4.4.4 Properties
Some concepts defined for integers can be generalized to UFDs:
- In UFDs, every irreducible element is prime. (In any integral domain, every prime element is irreducible, but the converse does not always hold. For instance, the element
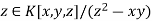
 is irreducible, but not prime.) Note that this has a partial converse: a domain satisfying the ACCP is a UFD if and only if every irreducible element is prime.
is irreducible, but not prime.) Note that this has a partial converse: a domain satisfying the ACCP is a UFD if and only if every irreducible element is prime. - Any two elements of a UFD have a greatest common divisor and a least common multiple. Here, a greatest common divisor of a and b is an element d which divides both a and b, and such that every other common divisor of a and b divides d.
All greatest common divisors of a and b are associated.
- Any UFD is integrally closed.
In other words, if R is a UFD with quotient field K, and if an element k in K is a root of a monic polynomial with coefficients in R, then k is an element of R.
- Let S be a multiplicatively closed subset of a UFD A.
Then the localization  is a UFD. A partial converse to this also holds; see below.
is a UFD. A partial converse to this also holds; see below.
Equivalent conditions for a ring to be a UFD
If and only if every height 1 prime ideal is primary, a Noetherian integral domain is a UFD (a proof is given at the end). A Dedekind domain is also a UFD if and only if the ideal class group of the domain is trivial. It is, in fact, a primary ideal domain in this situation.
The following criteria are identical in general for an integral domain A:
1. A is a user-defined function.
2. There is a prime element in every nonzero prime ideal of A. (Kaplansky)
3. The localization meets the ascending chain condition on principal ideals (ACCP). S1A is a UFD, where S is a prime element-generated multiplicatively closed subset of A. (Criteria of Nagata)
4. A fulfils ACCP, and all irreducibles are prime.
5. Every irreducible is prime, and A is atomic.
6. A is a GCD domain (one in which any two items have the same greatest common divisor) that satisfies (ACCP).
7. A is an atomic Schreier domain.
8. A is an atomic and pre-Schreier domain.
9. There is a divisor theory in which each divisor is a primary divisor.
Every divisorial ideal is principal in the Krull domain A. (in fact, this is the definition of UFD in Bourbaki.)
Every prime ideal of height 1 is principal in the Krull domain A.
(2) and (3) are the most useful conditions to check in practise. Because every prime ideal in a PID is formed by a prime element, it follows directly from (2) that a PID is a UFD.
Consider the case of a Noetherian integral domain in which one prime ideal is principal at each height. Because every prime ideal has a finite height, it contains one principal prime ideal (induction on height). The ring is a UFD according to (2).
A Euclidean domain (or Euclidean ring) is a ring that can be solved using the Euclidean algorithm.
In formal terms, a ring is a Euclidean domain if:
- It is an integral domain.
- There a function
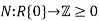 called a Norm such that for all nonzero
called a Norm such that for all nonzero 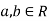 there are
there are 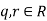 such that
such that 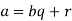 and either
and either 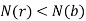 or
or 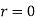 .
.
Some common examples of Euclidean domains are:
- The ring of integers
 with norm given by
with norm given by 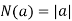 .
. - The ring of Gaussian integers
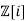 with norm given by
with norm given by  .
. - The ring of polynomials
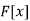 over any field
over any field 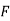 with norm given by
with norm given by 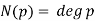
It can be easily shown through infinite descent that any Euclidian domain is also a principal ideal domain. Indeed, let  be any ideal of a Euclidean domain
be any ideal of a Euclidean domain 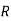 and take some
and take some 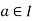 with minimal norm. We claim that
with minimal norm. We claim that  . Clearly
. Clearly 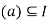 , because
, because 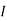 is an ideal. Now assume
is an ideal. Now assume 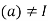 and consider any
and consider any 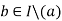 . Applying the division algorithm we get that there are
. Applying the division algorithm we get that there are 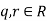 such that
such that  with (we cannot have
with (we cannot have 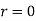 as
as 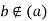 ). But now as
). But now as 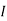 is an ideal, and
is an ideal, and  , we must have
, we must have 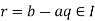 , contradicting the minimality of
, contradicting the minimality of  . Hence
. Hence  and
and 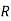 is indeed a principle ideal domain.
is indeed a principle ideal domain.
4.5.1 Examples
Examples of Euclidean domains include:
- Any field. Define f (x) = 1 for all nonzero x.
- Z, the ring of integers. Define f (n) = |n|, the absolute value of n.[3]
- Z[ i ], the ring of Gaussian integers. Define f (a + bi) = a2 + b2, the norm of the Gaussian integer a + bi.
- Z[ω] (where ω is a primitive (non-real) cube root of unity), the ring of Eisenstein integers. Define f (a + bω) = a2 − ab + b2, the norm of the Eisenstein integer a + bω.
- K [X], the ring of polynomials over a field K. For each nonzero polynomial P, define f (P) to be the degree of P.[4]
- K [[X]], the ring of formal power series over the field K. For each nonzero power series P, define f (P) as the order of P, that is the degree of the smallest power of X occurring in P. In particular, for two nonzero power series P and Q, f (P) ≤ f (Q) if and only if P divides Q.
- Any discrete valuation ring. Define f (x) to be the highest power of the maximal ideal M containing x. Equivalently, let g be a generator of M, and v be the unique integer such that g v is an associate of x, then define f (x) = v. The previous example K [[X]] is a special case of this.
- A Dedekind domain with finitely many nonzero prime ideals P1, ..., Pn. Define
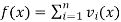
 , where vi is the discrete valuation corresponding to the ideal Pi .
, where vi is the discrete valuation corresponding to the ideal Pi . - Examples of domains that are not Euclidean domains include:
- Every domain that is not a principal ideal domain, such as the ring of polynomials in at least two indeterminates over a field, or the ring of univariate polynomials with integer coefficients, or the number ring
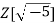
- The ring of integers of
 , consisting of the numbers
, consisting of the numbers 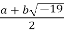 where a and b are integers and both even or both odd. It is a principal ideal domain that is not Euclidean.
where a and b are integers and both even or both odd. It is a principal ideal domain that is not Euclidean. - The ring A = R[X, Y]/(X2 + Y2 + 1) is also a principal ideal domain that is not Euclidean. To see that it is not a Euclidean domain, it suffices to show that for every non-zero prime
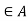 , the map
, the map  induced by the quotient map
induced by the quotient map  is not surjective.
is not surjective.
4.5.2 Properties:
Let R be a domain and f a Euclidean function on R. Then:
- R is a principal ideal domain (PID). In fact, if I is a nonzero ideal of R then any element a of I\{0} with minimal value (on that set) of f(a) is a generator of I. As a consequence R is also a unique factorization domain and a Noetherian ring. With respect to general principal ideal domains, the existence of factorizations (i.e., that R is an atomic domain) is particularly easy to prove in Euclidean domains: choosing a Euclidean function f satisfying (EF2), x cannot have any decomposition into more than f(x) nonunit factors, so starting with x and repeatedly decomposing reducible factors is bound to produce a factorization into irreducible elements.
- Any element of R at which f takes its globally minimal value is invertible in R. If an f satisfying (EF2) is chosen, then the converse also holds, and f takes its minimal value exactly at the invertible elements of R.
- If the Euclidean property is algorithmic, i.e., if there is a division algorithm that for given a and nonzero b produces a quotient q and remainder r with a = bq + r and either r = 0 or f(r) < f(b), then an extended Euclidean algorithm can be defined in terms of this division operation.
- If a Euclidean domain is not a field then it has an element a with the following property: any element x not divisible by a can be written as x=ay+u for some unit u and some element y. This follows by taking a to be a non-unit with f(a) as small as possible. This strange property can be used to show that some principal ideal domains are not Euclidean domains, as not all PIDs have this property. For example, for d = −19, −43, −67, −163, the ring of integers of
 is a PID which is not Euclidean, but the cases d = −1, −2, −3, −7, −11 are Euclidean.
is a PID which is not Euclidean, but the cases d = −1, −2, −3, −7, −11 are Euclidean.
However, in many finite extensions of Q with trivial class group, the ring of integers is Euclidean (not necessarily with respect to the absolute value of the field norm; see below). Assuming the extended Riemann hypothesis, if K is a finite extension of Q and the ring of integers of K is a PID with an infinite number of units, then the ring of integers is Euclidean. In particular this applies to the case of totally real quadratic number fields with trivial class group. In addition (and without assuming ERH), if the field K is a Galois extension of Q, has trivial class group and unit rank strictly greater than three, then the ring of integers is Euclidean. An immediate corollary of this is that if the number field is Galois over Q, its class group is trivial and the extension has degree greater than 8 then the ring of integers is necessarily Euclidean.
Numericals:
Let's start with an integer example. Begin with the numbers 750 and 144.

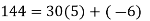

We begin by ascending Euclid's algorithm and substituting:
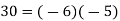
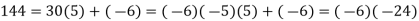

To see that 144 and 750 have a common divisor of 6.
Then we follow Euclid's formula:
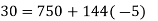
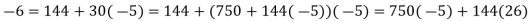
6 is a linear combination of 750 and 144, as shown.
After that, we'll look at a polynomial example. Begin with
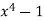 and
and 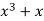 in
in 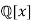
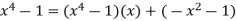

We begin by ascending Euclid's algorithm and substituting:

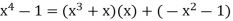
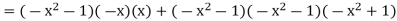
x 2 1 is a common divisor, as you can see. Then we descend:

To see that the polynomials -x 2 -1 are a linear combination
2) There are two possible prime factorizations of 15:
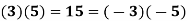
And 3 is connected to -3 and 5 is connected to -5.
In Q[x], there are multiple prime factorizations of x 2 - 1. Examples:
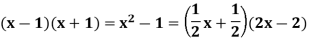
And x - 1 is linked to 2x - 2, and x + 1 is linked to 2x 3.

Key takeaways:
- All rings in this note are commutative. 1. Euclidean Domains Definition: Integral Domain is a ring with no zero divisors (except 0).
- Any field is euclidean domain: 1) d(xy)≥d(y) holds for any nonzero x,y∈F.
References:
1. M. Artin, Abstract Algebra, 2nd Ed., Pearson, 2011.
2. Joseph 1. Rotman, An Introduction to the Theory of Groups, 4th Ed., Springer Verlag, 1995.
3. I. N. Herstein, Topics in Algebra, Wiley Eastern Limited, India, 1975.