Unit - 1

Metric spaces

1.1 Metric space

Overview: The notion of function, the concept of limit and the related concept of continuity play an important role in the study of mathematical analysis. The notion of limit can be formulated entirely in terms of distance. For example, a sequence 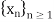of real numbers converges to x if and only if for all e > 0 there exists a positive integer n0 such that 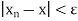whenever n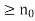. A discerning reader will note that the above definition of convergence depends only on the properties of the distance |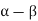| between pairs a, b of real numbers, and that the algebraic properties of real numbers have no bearing on it, except insofar as they determine properties of the distance such as,

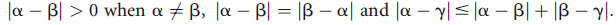
There are many other sets of elements for which ‘‘distance between pairs of elements’’ can be defined, and doing so provides a general setting in which the notions of convergence and continuity can be studied. Such a setting is called a metric space.

Definition:

A set in which we talk about the distance between two elements, is said to be metric space.

Suppose there is a non-empty set X. A function 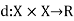is said to be a metric space if d satisfies the conditions given below-

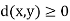1. for all X and d(x, y) = 0 if an only if x = y.
2. d(x , y) = d(y , x) for all x , y E X.
3. d(x, z) < d(x, y) + d(y, z) for all x, y, z E X. This is called the triangle inequality.

For x, y E X, d(x, y) is called the distance between x and y.

The pair (X, d) is then called a metric space.

The above properties can also be defined as-

1. The distance between x and y is non-negative and it is equal to zero when and only when x and y coincide,
2. The distance between x and y is the same as the distance between y and x. This is the property of symmetry.
3. The distance between x and y is not more than the distances between x and z and that between z and y, added together. This is called the triangle inequality.

Note that the triangle inequality follows from the inequality

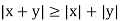
Example: Consider the function 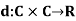such that .

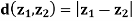Here we know that the absolute function on C follows the properties given below-

1. |z| and |z|=O if and only if z = 0
2. |-z| = |z|

Hence it is very easy to verify that d satisfies conditions (I) and (2) in Definition of metric space.

To show the triangular inequality 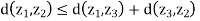we use the inequality

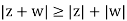with z = 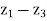, w = 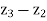, we can verify this inequality.

This shows that d is a metric.

Example: The function d: R 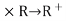defined by d(x, y) = |x – y| is a metric on R,

For any x, y, z 2 R,

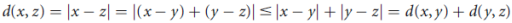
It is known as the usual or standard metric on R.

1.2 Sequences in metric space

Definition-

Let (X,d) be a metric space. A sequence of points in X is a function f from N into X.

Or

In other words, a sequence assigns to each n 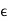N a uniquely determined element

Of X. If f (n) = 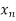, it is customary to denote the sequence by the symbol 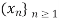or

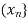or by x1, x2, . . . , xn, . . . .

Definition-

Let d be a metric on a set X and 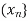be a sequence in the set X. An element x 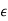X is said to be a limit of  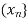 if, for every e > 0, there exists a natural number 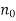such that

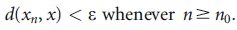
In this case, we also say that 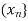   converges to x, and write it in symbols as 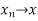. If there is no such x, we say that the sequence diverges. A sequence is said to be convergent if it converges to some limit, and divergent otherwise.

Note-

1. In case there are two or more metrics on the set X, then it is necessary to specify which metric is intended to be used in applying the definition of convergence.
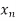
2. By comparing the above with the definition of convergence in R (or C), we find that x if and only if where d denotes the usual metric in R (or C).

1.3 Cauchy sequence

Let d be a metric on a set X. A sequence 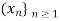in the set X is said to be a Cauchy sequence if, for every 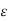> 0, there exists a natural number n0 such that

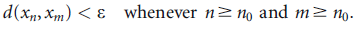
Example: The sequence 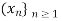, where 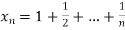does not satisfy Cauchy’s criterion of convergence. Indeed, 

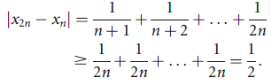
So, it is not the case here that 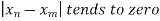for large m and n.

Example: In C[0,1], the sequence f1, f2, f3, . . . Given by

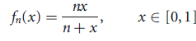
Is Cauchy in the uniform metric. For m n the function

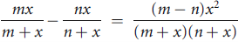
being continuous on [0, 1], assumes its maximum at some point x0 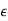[0,1]. So,

For large m and n. Moreover, the sequence 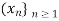converges to some limit. For f(x) = x

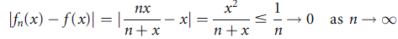
Therefore, 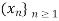  converges to the limit f, where f (x) = x for all x 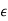[0, 1].

Note- A convergent sequence in a metric space is a Cauchy sequence.

1.4 Complete metric space

Definition- A metric space (X,d) is said to be complete if every Cauchy sequence in X is convergent.

Definition- let 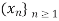be a given sequence in a metric space (X,d) and let 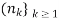be a sequence of positive integers such that  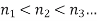 Then the sequence  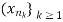is called a subsequence o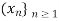f . If 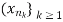converges, its limit is called a sub-sequential limit of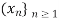

It is clear that a sequence 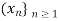 in X converges to x if and only if every subsequence of it converges to x.

Proposition- The metric space X = 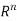with the metric given by

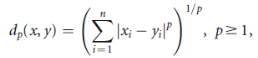
Where x = (x1, x2, . . . , xn) and y = (y1, y2, . . . , yn) are in 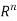, is a complete metric space.

Proof: Let 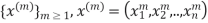denote a Cauchy sequence in

(X,d), I.e. 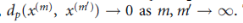Then, for a given 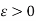there exists

An integer 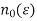such that

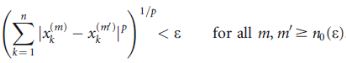………………(1)

For all 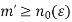letting 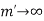in equation (2), we have-

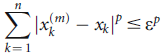
For all 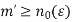which means 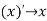in (X, d).

Completion of a metric space-

Definition-

Let (X, d) be an arbitrary metric space. A complete metric space (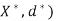is said to be a completion of the metric space (X, d) if-

1. X is a subspace of
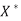
2. Every point of 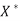is the limit of some sequence in X.

Note-

The space of all real numbers is the completion of the space of rationals. Also, the closed interval [0,1] is the completion of (0,1), [0,1), (0,1] and itself.

Definition-

Let (X, d) and (X’,d’) be two metric space. A mapping f of X into X’ is an isometry if

d’(f(x), f(y)) = d(x, y)

For all x, y X. The mapping f is also called an isometric embedding of X into X’. If, however, the mapping is onto, the spaces X and X’ themselves, between which there exists an isometric mapping, are said to be isometric. It may be noted that an isometry is always one-to-one.

Note- Every metric space has a completion and any two completions are isometric to each other.

1.5 Open and closed balls, Neighbourhood

Definition of open and closed balls-

Let (X, d) be a metric space. The set

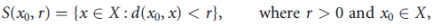
Is called the open ball of radius r and centre x0. The set

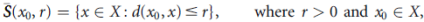
Is called the closed ball of radius r and centre x0.

Definition-

Let (X, d) be a metric space. A neighbourhood of the point x0 belongs to X is any open ball in (X, d) with centre x0.

Definition-

A subset G of a metric space (X, d) is said to be open if given any point x 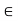G, there exists r > 0 such that S(x, r) 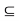G, i.e., each point of G is the centre of some open ball contained in G. Equivalently, every point of the set has a neighbourhood contained in the set.

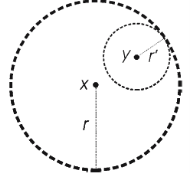
Theorem- In any metric space (X, d), each open ball is an open set.

Proof:

First observe that S(x,r) is nonempty, since x 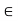S(x, r). Let y 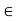S(x, r), so that d(y, x) < r, and let r’ = r – d(y, x) > 0. We shall show that S(y, r’) 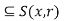as illustrated in figure. Consider any x 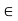S(x, r’), Then we have

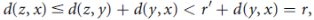
Which means z 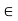S(x, r). Thus, for each y S(x, r), there is an open ball S(y, r’) 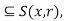Therefore S(x, r) is an open subset of X.

Theorem- A subset G in a metric space (X, d) is open if and only if it is the union of all open balls contained in G.

Proof:

Suppose that G is open. If G is empty, then there are no open balls contained in it. Thus, the union of all open balls contained in G is a union of an empty class, which is empty and therefore equal to G. If G is nonempty, then since G is open, each of its points is the centre of an open ball contained entirely in G. So, G is the union of all open balls contained in it.

1.6 Open set, interior of set, limit point of set, closed set, diameter of a set

Definition-

Let A be a subset of a metric space (X, d). A point x 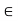X is called an interior point of A if there exists an open ball with centre x contained in A, which means-

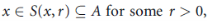
Or equivalently, if x has a neighbourhood contained in A. The set of all interior points of A is called the interior of A and is denoted either by Int(A) or , Thus

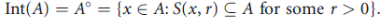
Observe that Int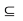(A) A.

Example: The interior of the subset [0, 1] 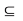R can be shown to be (0, 1). Let x (0, 1). Since (0, 1) is open, there exists r > 0 such that (x - r, x + r) 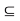[0, 1]. So, x is an interior point of [0,1]. Also, 0 is not an interior point of [0,1], because there exists no r > 0 such that (-r, r) [0, 1]. Similarly, 1 is also not an interior point of [0, 1].

Theorem-

Let A be a subset of a metric space (X, d). Then

(i) 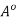is an open subset of A that contains every open subset of A;

(ii) A is open if and only if A =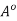

Proof:

Let x 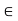 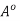 be arbitrary. Then, by definition, there exists an open ball S(x, r) 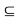A. But S(x,r) being an open set, each point of it is the centre of some open ball contained in S(x,r) and consequently also contained in A. Therefore each point of S(x,r) is an interior point of A, i.e., S(x, r) 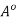Thus, x is the centre of an open ball contained in 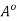Since x 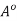  is arbitrary, it follows that each x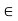 has the property of being the centre of an open ball contained in 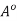Hence, 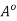is open.

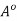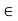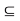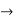It remains to show that contains every open subset G A. Let x G. Since G is open, there exists an open ball S(x, r) G A. So x 2 A This shows that x G x 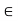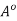In other words, G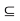 (ii) is immediate from (i).

Theorem- Let (X, d) be a metric space and A, B be subsets of X. Then

(i) A 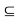B )   ;

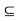
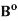(ii) (  =   ;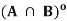

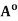
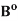(iii)   ; .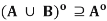

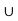
Proof:

(i)                Let x 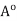. Then there exists an r > 0 such that S(x, r) 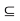A. Since A 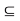B, we have S(x, r) 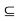B, i.e., x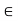

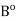
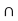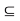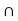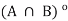
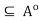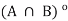
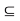
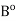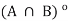
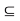
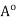
(ii)              A B A as well as A B B. It follows from (i) that as well as    , which implies that   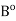    . On the other hand, let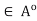 x     . Then x 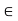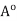and x 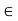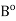. Therefore, there exist r1 > 0 and r2 > 0 such that S(x, r1) 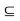A and S(x, r2) 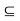B. Let r =  min {r1, r2}. Clearly, r > 0 and S(x, r) 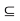A 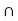B, i.e., x

(iii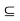)           A A 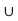B  as well as B 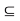A B. Now apply first condition.

1.7 Cantor’s theorem

Theorem- If A is any set, then  <

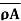
Proof:

First, we need to show that 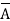< 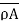: define an injection f:A→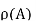by f(a)={a}. Now we need to show that there is no bijection g:A→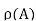. For a contradiction, suppose gg is such a bijection. Let

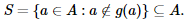
Since S ∈ 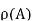, S = g(x), for some x ∈ A, because g is a surjection. There are two possibilities: x ∈S and x ∉ S

If x ∈ S, then x ∉ g(x)=S, i.e., x ∉ S, a contradiction.

2. If x ∉ S, then x ∈ g(x) = S, i.e., x ∈ S, a contradiction.

Therefore, no such bijection is possible

Cantor's theorem implies that there are infinitely many infinite cardinal numbers, and that there is no largest cardinal number. It also has the following interesting consequence:

It also has the following interesting consequence:

There is no such thing as the "set of all sets''.

References:

1. S. Kumaresan, Topology of Metric Spaces, Narosa Publishing House, Second Edition 2011
2. Topology of metric spaces, S. Kumarsen, Alpha science international Ltd.
3. Metric spaces, Satish shirali and Harkrishan L. Vasudeva, Springer.