Unit - 2

Matrix representation of a linear transformation

2.1 Matrix representation of a linear transformation

Linear transformation

Let V and U be vector spaces over the same field K. A mapping F : V 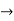U is called a linear mapping or linear transformation if it satisfies the following two conditions:

(1) For any vectors v; w 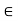V, F(v + w) = F(v) + F(w)

(2) For any scalar k and vector v 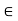V, F(kv) = k F(v)

Now for any scalars a, b 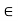   K and any vector v, w  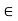  V, we obtain

F (av + bw) = F(av) + F(bw) = a F(v) + b F(w)

Matrix representation of a linear transformation

Ordered basis- Let V be a finite-dimensional vector space. An ordered basis for V is a basis for V endowed with a specific order; that is, an ordered basis for V is a finite sequence of linearly independent vectors in V that generates V.

Definition:

Let 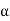= {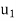,,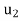 . . . , 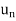} be an ordered basis for a finite dimensional vector space V. For x ∈ V, let 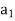, , 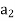. . . , 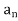be the unique scalars such that

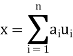
We define the coordinate vector of x relative to 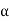, we denote it by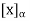

Example: Let V = P2(R), and let β = {1, x, 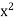} be the standard ordered basis for V. If

f(x) = 4+6x − 7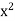, then

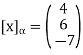
Example: let given by

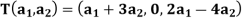
Let be the standard ordered bases for 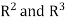, respectively. Now

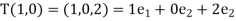
And

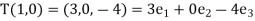
Hence

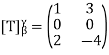
If we suppose 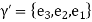, then

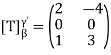
Example: be the linear operator defined by F(x, y) = (2x + 3y, 4x – 5y).

Find the matrix representation of F relative to the basis S = { 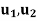} = {(1, 2), (2, 5)}

(1) First find F(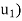, and then write it as a linear combination of the basis vectors 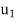and 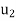. (For notational convenience, we use column vectors.) We have

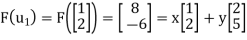
And

X + 2y = 8

2x + 5y = -6

Solve the system to obtain x = 52, y =-22. Hence,

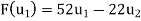
Now

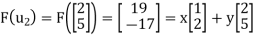
X + 2y = 19

2x + 5y = -17

Solve the system to obtain x = 129, y =-55. Hence,

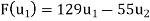
Now write the coordinates of 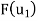and 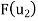as columns to obtain the matrix

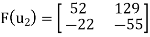
Steps to find Matrix Representations:

The input is a linear operator T on a vector space V and a basis S = {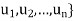 of V. The output is the matrix representation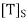

Step 0- Find a formula for the coordinates of an arbitrary vector relative to the basis S.

Step 1- Repeat for each basis vector 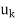in S:

(a) Find T(.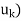

(b) Write T(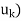 as a linear combination of the basis vectors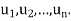

Step 2- Form the matrix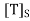 whose columns are the coordinate vectors in Step 1(b).

Example: 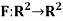be the linear operator defined by F(x, y) = (2x + 3y, 4x – 5y).

Find the matrix representation 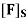of F relative to the basis S = { 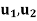} = {(1, -2), (2, -5)}

Sol:

Step 0 - First find the coordinates of 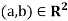relative to the basis S. We have

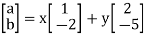
Or

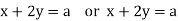
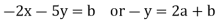
Solving for x and y in terms of a and b yields x = 5a + 2b,  y = -2a – b, thus

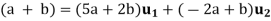
Step 1- Now we find 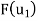and write it as a linear combination of 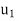and 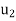using the above formula for (a, b). And then we repeat the process for 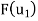. We have

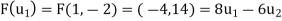
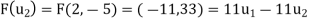
Step 2-  Now, we write the coordinates of 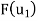and 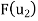as columns to obtain the required matrix:

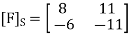
Key takeaways:

1. V be a finite-dimensional vector space. An ordered basis for V is a basis for V endowed with a specific order
2. We define the coordinate vector of x relative to 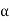, we denote it by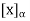

2.2 Algebra of linear transformations

Definition:
Let V, W be vector spaces over F and let S, T ∈ 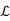(V;W). Then, we define the point-wise

1. Sum of S and T, denoted S + T, by (S + T)(v) = S(v) + T(v), for all v ∈ V.

2. Scalar multiplication, denoted c T for c ∈ F, by (c T)(v) = c (T(v)), for all v ∈ V

Theorem:
Let V be a vector space over F with dim(V) = n. If S,T ∈ 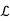(V) then

1. Nullity(T) + Nullity(S) 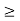Nullity(ST) 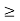max {Nullity(T), Nullity(S)}

2. Min Rank(S), Rank(T)g 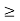Rank(ST) 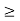n - Rank(S) - Rank(T).

Definition:

Let f : S → T be any function. Then

1. A function g : T → S is called a left inverse of f if (g o f)(x) = x, for all x ∈ S. That is, g o f = Id, the identity function on S.

2. A function h : T → S is called a right inverse of f if (f o h)(y) = y, for all y ∈ T. That is, f 0 h = Id, the identity function on T.

3. f is said to be invertible if it has a right inverse and a left inverse.

Note- Let f : S → T be invertible. Then, it can be easily shown that any right inverse and any left inverse are the same. Thus, the inverse function is unique and is denoted by 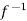. It is well known that f is invertible if and only if f is both one-one and onto.

Definition:

Let V and W be vector spaces over F and let T → 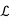(V;W). If T is one-one and onto then, the map 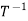: W → V is also a linear transformation. The map 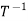.  Is called the inverse linear transform of T and is defined by 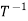(w) = v whenever T(v) = w.

Note- Let V and W be vector spaces over F and let T ∈ 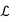(V;W).

Then the following statements are equivalent.

1. T is one-one.

2. T is non-singular.

3. Whenever S 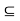V is linearly independent then T(S) is necessarily linearly independent.

Theorem:

Let V, W, and Z be vector spaces over the same field F, and let T: V → W and U: W → Z be linear. Then UT: V → Z is linear.

Proof.

Let x, y ∈ V and a ∈ F. Then UT(ax + y) = U(T(ax + y)) = U(aT(x) + T(y))

= aU(T(x)) + U(T(y)) = a(UT)(x) + UT(y).

The following theorem lists some of the properties of the composition of linear transformations.

Theorem:

Let V be a vector space. Let T,U1,U2 ∈ L(V). Then

(a) T(U1 + U2) = TU1 + TU2 and (U1 + U2)T = U1T + U2T

(b) T(U1U2) = (TU1)U2

(c) TI = IT = T

(d) a(U1U2) = (aU1)U2 = U1(aU2) for all scalars a.

Definition:

Let A be an m × n matrix and B be an n × p matrix. We define the product of A and B, denoted AB, to be the m × p matrix such that

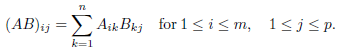
Note- (AB)ij is the sum of products of corresponding entries from the

Ith row of A and the jth column of B.

Example:

We have

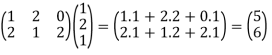
Key takeaways:

1. Let V be a vector space over F with dim(V) = n. If S,T ∈ 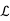(V) then

1. Nullity(T) + Nullity(S) 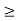Nullity(ST) 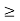max {Nullity(T), Nullity(S)}

2. Min Rank(S), Rank(T)g 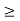Rank(ST) 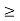n - Rank(S) - Rank(T).

Let f : S → T be any function. Then

2. A function g : T → S is called a left inverse of f if (g o f)(x) = x, for all x ∈ S. That is, g o f = Id, the identity function on S.

3. f is said to be invertible if it has a right inverse and a left inverse

2.3 Isomorphisms, Isomorphism theorems, invertibility and isomorphisms

Definition: Let V and W be vector spaces, and let T: V → W be linear.

A function U: W → V is said to be an inverse of T if TU = 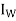and UT = IV.

If T has an inverse, then T is said to be invertible. As noted in Appendix B,

If T is invertible, then the inverse of T is unique and is denoted by .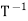

The following conditions hold for invertible functions T and U.

1. = .

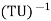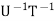2. 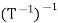= T; in particular, 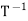is invertible.

3. Let T: V → W be a linear transformation, where V and W are finite dimensional spaces of equal dimension. Then T is invertible if and only

If rank(T) = dim(V).

Theorem: Let V and W be vector spaces, and let T: V → W be linear and invertible. Then T−1 : W → V is linear.

Proof. Let 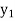, 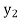∈ W and c ∈ F. Since T is onto and one-to-one, there

Exist unique vectors x1 and x2 such that T(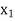) = 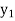and T(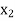) = 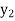. Thus

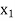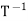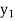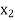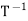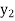= () and = (); so

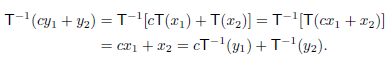
Note- if T is a linear transformation between vector spaces of equal (finite) dimension, then the conditions of being invertible, one-to-one, and onto are all equivalent.

Definition: Let A be an n × n matrix. Then A is invertible if there exists an n × n matrix B such that AB = BA = I. If A is invertible, then the matrix B such that AB = BA = I is unique. (If C were another such matrix, then C = CI = C(AB) = (CA)B = IB = B.) The matrix B is called the inverse of A and is denoted by .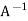

Lemma: Let T be an invertible linear transformation from V to W. Then V is finite-dimensional if and only if W is finite-dimensional. In this case,

Dim(V) = dim(W).

Theorem: Let V and W be finite-dimensional vector spaces with ordered bases β and γ, respectively. Let T: V → W be linear. Then T is invertible if and only if 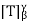is invertible.

Proof:

Suppose that T is invertible. By the lemma, we have dim(V) = dim(W). Let n = dim(V). So 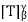is an n × n matrix. Now 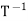: W → V

Satisfies T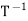 = IW and 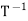T = IV. Thus

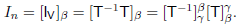
Similarly, 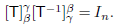so 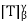is invertible and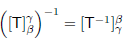

Now suppose that A = 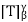is invertible. Then there exists an n × n

Matrix B such that AB = BA = In. By Theorem-, there exists

U ∈ L(W,V) such that

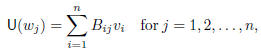
Where γ = {w1, w2, . . . , wn} and β = {v1, v2, . . . , vn}. It follows that 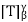= B. To show that U =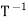, observe that

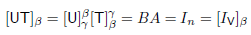
By Theorem- So UT = 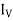, and similarly, TU = .

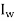Definition: Let V and W be vector spaces. We say that V is isomorphic to W if there exists a linear transformation T: V → W that is invertible. Such a linear transformation is called an isomorphism from V onto W.

Example: Define

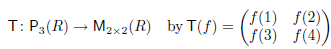
It is easily verified that T is linear. By use of the Lagrange interpolation formula, it can be shown that T(f) = O only when f is the zero polynomial. Thus T is one-to-one. Moreover, because dim(P3(R)) = dim(M2×2(R)), it follows that

T is invertible. We conclude that P3(R) is isomorphic to M2×2(R).

Theorem: Let V and W be finite-dimensional vector spaces (over the same field). Then V is isomorphic to W if and only if dim (V) = dim (W).

Proof:

Suppose that V is isomorphic to W and that T: V → W is an isomorphism from V to W. By the lemma, we have that dim(V) = dim(W).

Now suppose that dim(V) = dim(W), and let 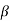= {v1, v2, . . . , vn}. And 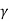= {w1, w2, . . . , wn} be bases for V and W, respectively

There exists T: V → W such that T is linear and T(vi) = wi for i = 1, 2, . . . , n. We have

R(T) = span(T(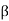)) = span(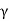) = W.

So T is onto.

We have that T is also one-to-one. Hence T is an isomorphism.

Note- Let V be a vector space over F. Then V is isomorphic to 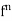if and only if dim(V) = n.

Key takeaways:

1. Let V and W be vector spaces, and let T: V → W be linear.
2. A function U: W → V is said to be an inverse of T if TU = 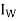and UT = IV
3. Let V and W be vector spaces, and let T: V → W be linear and invertible. Then T−1 : W → V is linear.
4. Let A be an n × n matrix. Then A is invertible if there exists an n × n matrix B such that AB = BA = I

2.4 Change of coordinate

Theorem: Let β and β’ be two ordered bases for a finite-dimensional vector space V, and let Q = 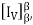then

(a) Q is invertible.

(b) For any v ∈ V,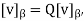

Now the matrix Q = 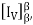is called a change of coordinate matrix. Because (b) of the theorem, we say that Q changes β’- coordinates into β-coordinates. Observe that if 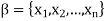and 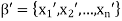, then

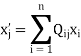
For j = 1, 2, . . . , n; that is, the jth column of Q is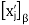

Note- if Q changes β’ - coordinates into β-coordinates, then 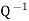changes β-coordinates into β’-coordinates.

Example: In 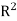let β = {(1, 1), (1, -1)} and β’ = {(2, 4), (3, 1)}, since

(2,4) = 3(1, 1) − 1(1,−1) and (3, 1) = 2(1, 1) + 1(1,−1),

The matrix that changes β’-coordinates into β-coordinates is

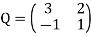
Thus, for instance,

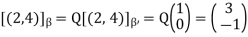
Theorem: Let T be a linear operator on a finite-dimensional vector space V, and let β and β’ be ordered bases for V. Suppose that Q is the change of coordinate matrix that changes β’-coordinates into β-coordinates. Then

2.5 Matrix, Dual spaces, dual basis, double dual

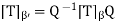
Linear functional and the Dual Space

Let V be a vector space over a field K. A mapping 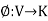is called a linear functional if, for every u, v 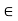V and every a, b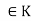

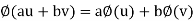
Note- A linear functional on V is a linear mapping from V into K.

The set of linear functionals on a vector space V over a field K is also a vector space over K, with addition and scalar multiplication defined by

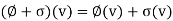
And

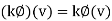
Where 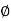and 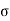are linear functionals on V and k belongs to K. This space is called the dual space of V and is denoted by V*.

Example: Let V be the vector space of continuous real-valued functions on the interval

[0, 2π]. Fix a function g ∈ V. The function h: V → R defined by

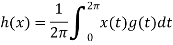
Is a linear functional on V. In the cases that g(t) equals sin nt or cos nt, h(x) is often called the nth Fourier coefficient of x.

Definition of dual Space:

For a vector space V over F, we define the dual space of V to be the vector space 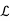(V, F), denoted by .

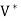Note-

1. Thus 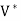is the vector space consisting of all linear functionals on V with the operations of addition and scalar multiplication
2. If V is finite-dimensional, then- dim(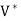) = dim 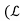(V, F)) = dim(V)· dim(F) = dim(V).

Theorem: Suppose that V is a finite-dimensional vector space with the ordered basis β = {x1, x2, . . . , xn}. Let fi (1 ≤ i ≤ n) be the ith coordinate function with respect to β as just defined, and let β∗ = {f1, f2, . . . , fn}. Then β∗ is an ordered basis for V∗, and, for any f ∈ V∗, we have

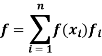
Proof:

Let f ∈  V*. Since dim(V*) = n, we need only show that

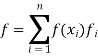
From which it follows that β∗  generates V*, and hence is a basis

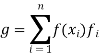
For 1 ≤ j ≤ n, we have

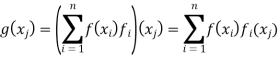
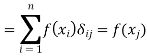
Therefore f = g.

Definition of dual basis:

We call the ordered basis β∗ = {f1, f2, . . . , fn} of V∗ that satisfies fi(xj) = 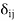(1 ≤ i, j ≤ n) the dual basis of β.

Note- Let V be a finite-dimensional vector space with dual space V*. Then every ordered basis for V* is the dual basis for some basis for V.

Key takeaways:

1. Let V be a vector space over a field K. A mapping 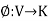is called a linear functional if, for every u, v 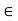V and every a, b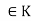

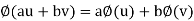
2.     For a vector space V over F, we define the dual space of V to be the vector space 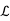(V, F), denoted by .

2.6 Transpose of a linear transformation and its matrix in the dual basis

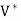Let T :V 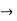U be an arbitrary linear mapping from a vector space V into a vector space U. Now for any linear functional  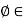U*, the composition 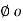T is a linear mapping from V into K:

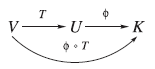
That is, 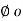T 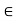V*. Thus, the correspondence

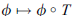
Is a mapping from

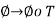
Is a mapping from U* into V*; we denote it by Tt and call it the transpose of T. In other words,

Tt :U* 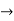V* is defined by

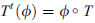
Theorem: The transpose mapping 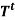defined above is linear.

Proof:

For any scalars a; b 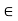K and any linear functionals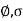 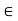U*,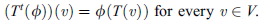

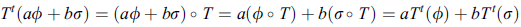
That is, 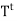is linear

Theorem: Let T :V 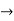U be linear, and let A be the matrix representation of T relative to bases { 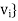of V and 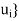of U. Then the transpose matrix 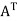is the matrix representation of 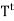: U* 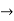V* relative to the bases dual to { 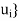 and {

2.7 Annihilators, Basics of Fields

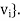
Annihilators-

Let W be a subset (not necessarily a subspace) of a vector space V. A linear functional 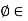V* is called an annihilator of W if 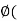w) = 0 for every w 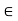W, that is, if 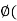w) = {0}. We show that the set of all such mappings, denoted by 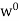and called the annihilator of W, is a subspace of V*. Clearly, 0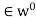

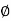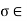
Now suppose ,  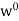. Then, for any scalars a, b 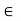K and for any 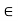w W,

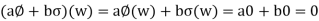
Thus 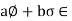 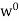 and so 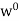is a subspace of V*.

Theorem: Suppose V has finite dimension and W is a subspace of V. Then

1. Dim W +
2. 

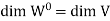
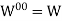
Note-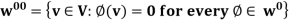

Basics of field-

Definition of integral domain:

A commutative ring R with a unit element is called an integral domain if R has no zero divisors—that is, if ab = 0 implies a = 0 or b = 0.

Field:

Definition:

A field F is a set on which two operations + and · (called addition and multiplication, respectively) are defined so that, for each pair of elements x, y in F, there are unique elements x+y and x·y in F for which the following conditions hold for all elements a, b, c in F.

(1) a + b = b + a and a·b = b·a

(commutativity of addition and multiplication)

(2) (a + b) + c = a + (b + c) and (a·b)·c = a· (b·c)

(associativity of addition and multiplication)

(3) There exist distinct elements 0 and 1 in F such that

0 + a = a and 1·a = a

(existence of identity elements for addition and multiplication)

(4) For each element a in F and each nonzero element b in F, there exist

Elements c and d in F such that

a + c = 0 and b·d = 1

(existence of inverses for addition and multiplication)

(5) a·(b + c) = a·b + a·c

(distributivity of multiplication over addition)

The elements x + y and x·y are called the sum and product, respectively, of x and y. The elements 0 and 1 mentioned in (3) are called identity elements for addition and multiplication, respectively, and the elements c and d referred to in (4) are called an additive inverse for a and a multiplicative inverse for b, respectively

Example 1 The set of real numbers R with the usual definitions of addition and multiplication is a field.

Example 2- The set of rational numbers with the usual definitions of addition and multiplication is a field.

Example 3- Neither the set of positive integers nor the set of integers with the usual definitions of addition and multiplication is a field, for in either case (4) does not hold.

Theorem(Cancellation Laws). For arbitrary elements a, b, and c in a field, the following statements are true.

(a) If a + b = c + b, then a = c.

(b) If a·b = c·b and b _= 0, then a = c.

Proof. (a) The proof of (a) is left as an exercise.

(b) If b 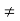0, then (4) guarantees the existence of an element d in the

Field such that b·d = 1. Multiply both sides of the equality a·b = c · b by d

To obtain (a·b)·d = (c·b)·d. Consider the left side of this equality: By (2)

And (3), we have

(a·b)·d = a· (b·d) = a·1 = a.

Similarly, the right side of the equality reduces to c. Thus a = c.

Each element b in a field has a unique additive inverse and, if b 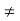0, a unique multiplicative inverse.)

The additive inverse and the multiplicative inverse of b are denoted by −b and 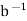, respectively. Note that

−(−b) = b and 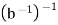= b. Subtraction and division can be defined in terms of addition and multiplication by using the additive and multiplicative inverses. Specifically, subtraction of b is defined to be addition of −b and division by b _= 0 is defined to be multiplication by 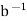; that is,

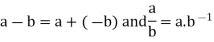
Theorem:

Let a and b be arbitrary elements of a field. Then each of the following statements are true.

(a) a·0 = 0.

(b) (−a)·b = a· (−b) = −(a·b).

(c) (−a)· (−b) = a·b

Proof. (a) Since 0 + 0 = 0, (F 5) shows that

0 + a·0 = a·0 = a·(0 + 0) = a·0 + a·0.

Thus 0 = a·0 by above theorem.

b) By definition, −(a·b) is the unique element of F with the property a·b + [−(a·b)] = 0. So in order to prove that (−a)·b = −(a·b), it suffices to show that a·b + (−a)·b = 0. But −a is the element of F such that

a + (−a) = 0; so

a·b + (−a)·b = [a + (−a)]·b = 0·b = b·0 = 0

By (5) and (a). Thus (−a)·b = −(a·b). The proof that a· (−b) = −(a·b) is similar.

(c) By applying (b) twice, we find that (−a)· (−b) = −[a· (−b)] = −[−(a·b)] = a· b.

Note- A field may also be viewed as a commutative ring in which the nonzero elements form a group under multiplication.

Key takeaways:

1. Let W be a subset (not necessarily a subspace) of a vector space V. A linear functional 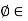V* is called an annihilator of W if 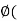w) = 0 for every w 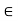W
2. 
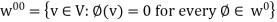
3. A commutative ring R with a unit element is called an integral domain if R has no zero divisors—that is, if ab = 0 implies a = 0 or b = 0.
4. The set of rational numbers with the usual definitions of addition and multiplication is a field.
5. A field may also be viewed as a commutative ring in which the nonzero elements form a group under multiplication.

References:

1. Rao A R and Bhim Sankaram Linear Algebra Hindustan Publishing house.

2.Gilbert Strang, Linear Algebra and its Applications, Thomson, 2007.

3. Stephen H. Friedberg, Arnold J. Insel, Lawrence E. Spence, Linear Algebra (4th Edition), Pearson, 2018.

4. Linear Algebra, Seymour Lipschutz, Marc Lars Lipson, Schaum’s Outline Series