Unit - 1
Introduction to linear Programming problem
Introduction:
Optimization may be a way of life. We all have limited resources and time and need to form the foremost of them. Everything from using time productively to solving problems in your company's supply chain uses optimization. This is often a very interesting and relevant topic in data science.
This is also a really interesting topic. It starts with an easy problem, but it are often very complicated. For instance, sharing a chocolate candy between siblings may be a simple optimization problem. While solving it, we do not think mathematically. On the opposite hand, devising an e-tailer inventory and warehousing strategy are often very complex. Many SKUs with different popularity in several regions are delivered at defined times and resources.
Linear programming (LP) is one among the simplest ways to perform optimization. Making some simplified assumptions will assist you solve some very complex optimization problems. Analysts will encounter applications and problems that are solved by applied mathematics.
For some reason, LPs do not get enough attention while learning data science. So I wanted to form this excellent technique justice. i made a decision to write down a piece of writing that explains applied mathematics in simple English. The content is as simple as possible. The thought is to urge excited about applied mathematics for the primary time.
Note-If you would like to find out this during a course format, we curate this free course-Linear programming for data science professionals
What’s linear programming?
So what's linear programming? Applied mathematics may be a simple technique that uses linear functions to represent complex relationships and find the simplest points. The important words within the preamble are drawn. The particular relationship could also be far more complicated, but it is often simplified to a linear relationship.
Linear programming applications are everywhere around you. Use applied mathematics on a private and professional side. If you're driving from home to figure and need to use the shortest route, you're using applied mathematics. Or, when delivering a project, develop a technique to figure efficiently in order that your team can deliver on time.
Applications of LP
Linear programming and optimization are used in a variety of industries. Manufacturing and service industries regularly use linear programming.
- Manufacturing uses linear programming to analyse supply chain operations. Their motivation is to maximize efficiency with minimal operating costs. Following the recommendations of the linear programming model, manufacturers can reconfigure their storage layouts and adjust their employees to reduce bottlenecks. This is a case study of Cequent's small warehouse based in the United States. Watch this video for a clearer understanding.
- Linear programming is also used in retail stores organized to optimize shelf space. With the number of products on the market growing exponentially, it's important to understand what your customers want. Optimization is actively used in stores such as Wal-Mart, Hyper city, Reliance, and Big Bazaar. The products in the store are strategically placed with the customer's shopping patterns in mind. The goal is to make it easier for customers to find and select the right product. This has limitations such as limited shelf space and various products.
- Optimization is also used to optimize delivery routes. The service industry uses optimization to find the best route for multiple salespeople travelling to multiple cities. With the help of clustering and greedy algorithms, delivery routes are determined by companies such as FedEx and Amazon. The goal is to minimize operational costs and time.
- Optimization is also used in machine learning. Supervised learning addresses the basics of linear programming. The system is trained to fit a mathematical model of a function from labelled input data that can predict values from unknown test data.
The application of linear programming does not end here. There are many other real-world linear programming applications, such as those applied by shareholders, sports, stock markets, and more. Please continue to explore further.
Important definitions-
Linear programming problem-
We need to optimize the linear function Z subject to certain conditions, these types of problems are called Linear programming problem or in short LPP.
Objective functions-
This is a linear function of several variables, subject to the conditions.
Optimal value-
This is a maximum or minimum value of a object function which is to be calculated in a LPP.
Formulation of LPP-
Let’s consider the following example with case studies to understand the concept of linear programming problems-
Case study-1
Example: A manufacturer produces two types of products ‘P’ and ‘Q’. Each ‘P’ type of product required 4 hours of grinding and 2 hrs of polishing, where ‘Q’ product requires 2 hrs of grinding and 5hrs of polishing.
The manufacturer has 2 grinders and 3 polishers. Each grinder works for 80hrs a week and each polisher works for 180hrs a week. Profit on ‘P’ product is Rs. 3 and profit on ‘Q’ is Rs. 4.Whatever is produced in a week is sold in the market.
How should the manufacturer allocate his capacity of production of two types of products so that he may make the maximum profit and minimum loss in a week?
Now we formulate this problem in mathematical terms as explained below-
Suppose 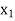 is the number of ‘P’ product and
is the number of ‘P’ product and 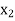 is the number of ‘Q’ product produced weekly.
is the number of ‘Q’ product produced weekly.
Then the weekly profit is-
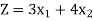
Here ‘Z’ is called the objective function which is to be maximize or minimize.
Now, to produce these number of products, the total number of grinding hours needed weekly is-
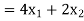
And the total number of polishing hours needed per week is-
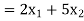
Here the number of grinding hours is not more than 80 and the number of polishing hours is not more than 180, so that we write,
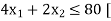 This is called the first constraint]
This is called the first constraint]
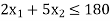 [This is the second constraint]
[This is the second constraint]
Since the number of product is non-negative, then we can write-
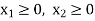
This is called the third constraint.
Hence we form the problem mathematically as follows-
To maximize-
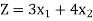
Subject to the constraints:
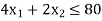
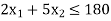
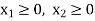
This expression is called as mathematical formulation.
Note- The variables that enter into the problem are called ‘decision variables’.
Case study-2
Example: A dietician mixes together two kinds of food, say, A and B in such a way that the mixture contains at least 6 units of vitamin P, 7 units of vitamin Q, 12 units of vitamin R and 9 units of vitamin S. The vitamin contents of 1 kg of food A and 1 kg of food B are given below:
Cost | Vitamin-P | Vitamin-Q | Vitamin-R | Vitamin-S |
Food-A | 1 | 1 | 1 | 2 |
Food-B | 2 | 1 | 3 | 1 |
One kg of food X costs Rs. 5, whereas one kg of food Y costs Rs. 8. Formulate the linear programming problem.
Sol.
Decision variables- Here decision variables are units of food A and B.
Let food A in the mixture be 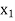 and food B in the mixture
and food B in the mixture 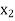 .
.
Objective function- To minimize the cost,
Total cost of food A and B = 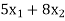
Or
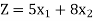
Now we will write the constraints one by one-
Constraint-1: 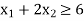
Constraint-2: 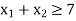
Constraint-3: 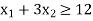
Constraint-4: 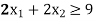
Constraint-5: 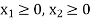
Mathematical formation will be as follows-
To minimize,
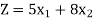
Subject to the constraints-
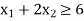

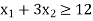
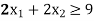

Case study-3
Example: A manufacturer has 3 machines 1, 2 and 3. Machines 1 and 2 are capable of being operated for at the most 12 hours whereas machine 3 must be operated at least for 5 hours a day. He produces two items each requiring the use of the three machines.
The number of hours required for producing 1 unit of each of the items X and Y on the three machines are given below:
Items | Numbers of hours required on the machines 1 2 3 |
X | 1 2 1 |
Y | 2 1 5/4 |
She makes a profit of Rs. 60 on item X and Rs. 40 on item Y. Assuming that he can sell all that he produces, how many of each item should be produced so as to maximize the profit. Formulate the above as L.P.P.
Sol.
Decision variables- Here decision variables are item X and Y.
Let the production of item X be 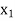 and the production of item Y be
and the production of item Y be 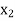 .
.
Objective function- To maximize the profit,
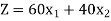
Now we will write the constraints one by one-
Constraint-1: 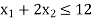
Constraint-2: 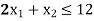
Constraint-3: 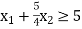
Constraint-4: 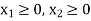
Mathematical formation will be as follows-
To maximize,
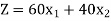
Subject to the constraints-
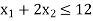
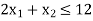

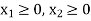
Case study-4
Example: Consider a chocolate manufacturer that produces only two sorts of chocolate, A and B. Both chocolates only require milk and chocolate. To manufacture each of the A and B units, you would like the subsequent quantities:
Each unit during a requires 1 unit of milk and three units of chocolate
Each unit in B requires 1 unit of milk and a couple of units of chocolate.
The company's kitchen features a total of 5 units of milk and 12 units of chocolate. With each sale, the corporate makes a profit
Rs6 per unit A sold
Rs5 per unit B sold.
Now the corporate wants to maximise profits. What percentage units of A and B does one got to produce respectively?
Solution: the primary thing to try to is to tabulate the matter for better understanding.
Milk | Chocó | Profit per unit | |
A | 1 | 3 | Rs 6 |
B | 1 | 2 | Rs 5 |
Total | 5 | 12 |
|
Let = X be the entire number of units generated by A.
Let = Y be the entire number of units generated by B.
Now, the entire profit is represented by Z
The company's gross profit margin is that the total number of A and B units produced multiplied by the profit per Rs6 and Rs5 units, respectively.
Profit: Maximum Z = 6X + 5Y
That is, you would like to maximize Z.
The company will attempt to produce as many A and B units as possible to maximize profits. However, Milk and Chocó resources are available in limited quantities.
As shown within the table above, each unit A and B requires 1 unit of milk. The entire amount of milk available is 5 units. To precise this mathematically,
X + Y ≤ 5
Also, each unit A and B requires 3 units and a couple of units of Chocó, respectively. The entire number of chocolates sold is 12. To precise this mathematically,
3X + 2Y ≤ 12
Also, the unit value of A can only be an integer.
Therefore, there are two constraints, X ≥ 0 and Y ≥ 0.
Steps in Solving LP Problems
The steps involved in forming a linear programming problem are as follows:
Step 1 → Identify the decision variables that the decision maker is interested in and represent them as x1, x2, x3 ………
Step 2 → Determine the purpose for the decision maker to decide whether to minimize or maximize.
Step 3 → Check the cost (for minimization problem) or profit (for maximization problem) per unit of each decision variable.
Step 4 → Check the constraints that represent maximum availability or minimum commitment or equivalence and represent them as less than or equal to (≤) type inequalities or greater than or equal to (≥) type inequalities or as "equal" (=) type equivalence.
Key takeaways
- LPP is the popular mathematical technique which is used to make maximum profit and minimum loss.
- The variables that enter into the problem are called ‘decision variables’
Graphical method to solve LPP:
LPP having two variables can be easily solved by graphical method which provides a pictorial representation of the solution and we get insights into the basic concept used in solve LPP.
Step by step procedure to solve LPP graphically-
- First we need to formulate the given problem as a LPP in mathematical form.
- Now plot the given constraints on
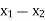 coordinate plane and find the convex region.
coordinate plane and find the convex region. - Now determine the convex region and find the value of the objective function at each vertex. The vertex which gives the max or min value of the objective function gives the optimal solution of the LPP.
Note- The region satisfying all the constraints is called feasible region.
Example: Solve the following LPP graphically-
Maximize-
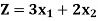
Subject to the constraints-

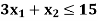

Sol.
Change the given constraints into equations-
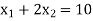
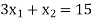
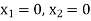
The line 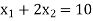 meets the x-axis at the point A(10,0) and meets the y-axis at the point B(0,5). Join A and B to get the graph for the line.
meets the x-axis at the point A(10,0) and meets the y-axis at the point B(0,5). Join A and B to get the graph for the line.
Hence origin (0,0) satisfies the inequality 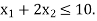 so that half plane containing the origin represent the solution set of
so that half plane containing the origin represent the solution set of 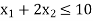 .
.
And
The line 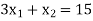 meets the x-axis at the point C(5,0) and meets the y-axis at the point D(0,15). Join C and D to get the graph for the line.
meets the x-axis at the point C(5,0) and meets the y-axis at the point D(0,15). Join C and D to get the graph for the line.
Hence origin (0,0) satisfies the inequality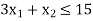 so that half plane containing the origin represent the solution set of
so that half plane containing the origin represent the solution set of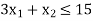 .
.
Now all the points in first quadrant satisfies 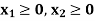 .
.
So that first quadrant is the region represented by 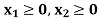
Hence the region OCEBO satisfies all the inequalities.
And each point on the region is the feasible solution of the problem.
Feasible solution-
Here in this problem the feasible solution is (5,0), (4,3) and (0,5).
Now we can obtain the optimal solution of the problem.
As we know that any point in the feasible region that gives the optimal value is called an optimal solution.
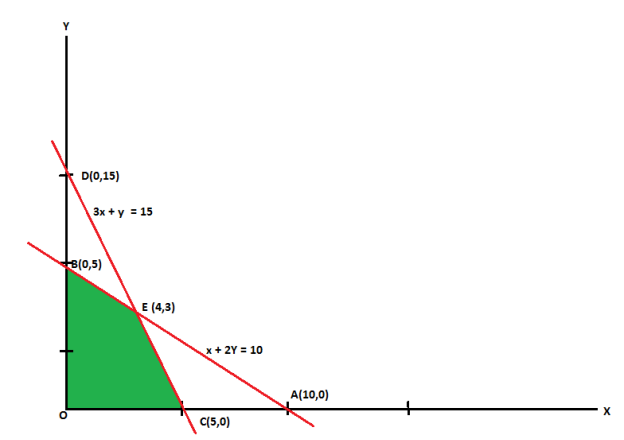
The value of the objective function 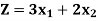 at corner points of the feasible region is given below-
at corner points of the feasible region is given below-
Vertex [ feasible region ] | Value of 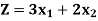 |
O(0,0) | 0 |
C(5,0) | 15 |
E(4,3) | 18 [Maximum] |
B(0,5) | 10 |
Here we see that the maximum value of Z is 18.

Note-
- This method is called corner point method-
- The optimal value of objective function must occur at a corner point (vertex) of the feasible region
- If the feasible region is bounded then the objective function Z has both maximum and minimum values on corner points of the bounded region.
Key takeaways:
- Linear programming problem-We need to optimize the linear function Z subject to certain conditions, these types of problems are called Linear programming problem or in short LPP.
- Objective functions- This is a linear function of several variables, subject to the conditions.
- Optimal value- This is a maximum or minimum value of a object function which is to be calculated in a LPP.
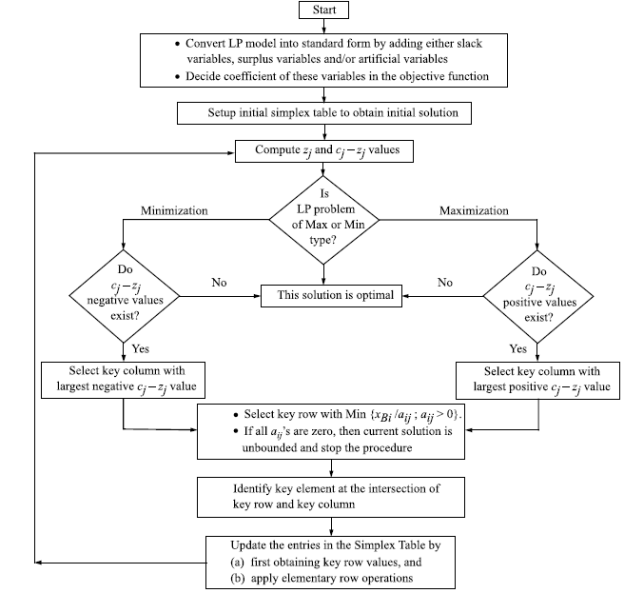
The simplex method is very popular and widely used in operations research.
This method of analysis was developed by one American Mathematician by name George B. Dantzig, during 1947. This method provides an algorithm (a procedure which is iterative) which is based on fundamental theorems of Linear Programming. It helps in moving from one basic feasible solution to another in a prescribed manner such that the value of the objective function is improved. This procedure of jumping from one vertex to another vertex is repeated.
Step by step method:
1. Convert the inequalities into equalities by adding slack variables, surplus variables or artificial variables, as the case may be.
2. Identify the coefficient of equalities and put them into a matrix form AX = B Where "A" represents a matrix of coefficient, "X" represents a vector of unknown quantities and B represents a vector of constants, leads to AX = B.
3. Set the data into the first iteration of Simplex Method.
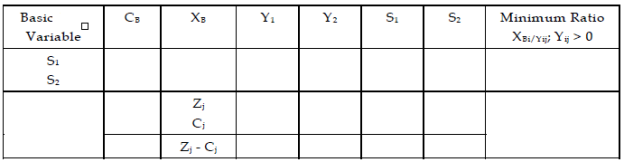
(a) Cj is the coefficient of unknown quantities in the objective function.  (Multiples and additions of coefficients in the table, i.e.,
(Multiples and additions of coefficients in the table, i.e.,  ×
×  +
+ ×
× 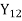 )
)
(b) Identify the Key or Pivotal column with the minimum element of Zj - Cj denoted as 'KC' throughout to the problems in the chapter.
(c) Find the 'Minimum Ratio' i.e., XBi/Yij.
(d) Identify the key row with the minimum element in a minimum ratio column. Key row is denoted as 'KP'.
(e) Identify the key element at the intersecting point of key column and key row, which is put into a box throughout to the problems in the chapter.
4. Reinstate the entries to the next iteration of the simplex method.
(a) The pivotal or key row is to be adjusted by making the key element as '1' and dividing the other elements in the row by the same number.
(b) The key column must be adjusted such that the other elements other than key elements should be made zero.
(c) The same multiple should be used to other elements in the row to adjust the rest of the elements. But, the adjusted key row elements should be used for deducting out of the earlier iteration row.
(d) The same iteration is continued until the values of Zj – Cj become either '0' or positive.
5. Find the 'Z' value given by  ,
, 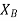 .
.
Example: Maximize
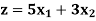
Subject to-

By using simplex method.
Sol. Here all b’s are positive and the objective function is to be maximized.
Step-1: Now express the problem in the standard form-
Let 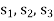 are slack variables then the problem in standard form becomes-
are slack variables then the problem in standard form becomes-
Maximize-
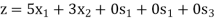
Subject to
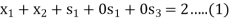

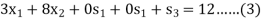
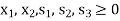
Step-2: Find the initial basic feasible solution-
There are three equations having 5 unknowns and for obtaining the solution we assign zero value to any two of the three variables.
We start with a basic solution for which we set 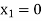 and
and 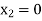 .
.
Putting
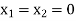 in the above three equations-
in the above three equations-
We get-
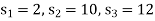
Here all
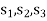 are positive, the basic solution is also feasible and non-degeneate.
are positive, the basic solution is also feasible and non-degeneate.
The BFS is-
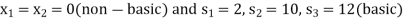
Initial BFS is given by the table below-
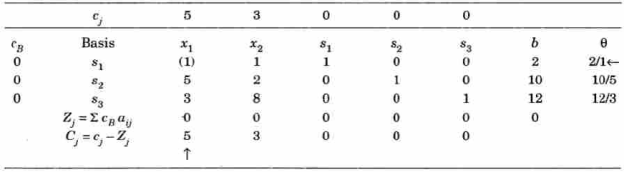
For 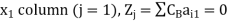
For 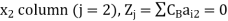
Similarly-
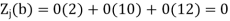
Now apply the optimality test-
As 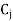 is positive under some columns, the IBFS is not optimal, we move to the next step-
is positive under some columns, the IBFS is not optimal, we move to the next step-
Step- Identify the outgoing and incoming variables-
By the above table 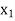 is the incoming variable as its incremental contribution
is the incoming variable as its incremental contribution  is max. And the column in which it appears is the key column.
is max. And the column in which it appears is the key column.
Dividing the elements under b-column by the corresponding elements of key-column we find the min.positive ratio 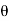 in two rows.
in two rows.
Therefore we arbitrarily choose the row containing 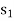 as the key row.
as the key row.
The elements at the intersection of key row and the key column is the key element.
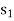 is therefore the outgoing variable which will now become non-basic.
is therefore the outgoing variable which will now become non-basic.
Having decided that 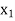 is to enter the solution we have tried to find as to what maximum under
is to enter the solution we have tried to find as to what maximum under 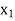 could have without violating the constraints.
could have without violating the constraints.
So that removing 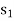 , the new basis will contain
, the new basis will contain 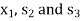 as the basic variables.
as the basic variables.
Now iterate towards the optimal solution-
To transform the intial set of equations with a BFS into an equivalent set of equatins with a different BFS, we make the key element unity.
We retain the key row as it is. Then to make all other elements in key column zero, we subtract proper multiples of the key row from the other rows.
Here we subtract five times the elements of key row from the second row and three times the element of key row from the third row.
These become the second and the third of the next table.
We also change the corresponding value under 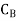 column from 0 to 5.
column from 0 to 5.
While relacing 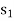 by
by 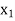 under the basis.
under the basis.
Thus the second BFS is given below-

As 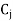 is either zero or negative under all columns, the above table gives the optimal BFS.
is either zero or negative under all columns, the above table gives the optimal BFS.
This optimal BFS is-

Example: Maximize-
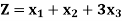
Subject to-
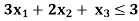
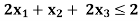
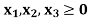
By using simplex method.
Sol.
Here we have

And the inequalities-
 ...... (1)
...... (1)
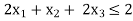 ........ (2)
........ (2)
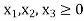 ..........(3)
..........(3)
By adding  we get-
we get-
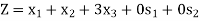 ...... (4)
...... (4)
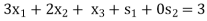 ....... (5)
....... (5)
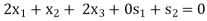 ...... (6)
...... (6)
Putting decision variables 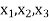 equals to zero, we get-
equals to zero, we get-
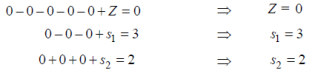
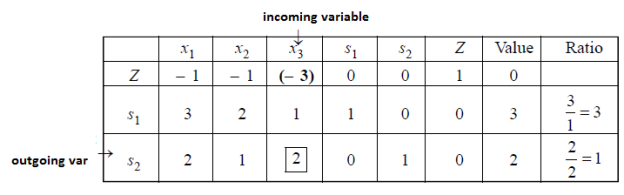
Since coefficient (–3) of 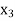 is most negative, so x3 is entering variable.
is most negative, so x3 is entering variable.
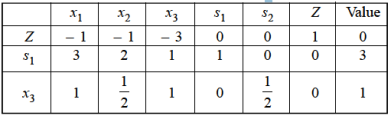
The smallest ratio is 1 in the s2-row, therefore s2 is departing variable. The pivot entry (2) is at the intersection of x3-column and s2-row.
To make pivot entry (1), we multiply third row by ½, we get-
Applying R1 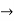 R1 + 3R3 and R2
R1 + 3R3 and R2  R2 - R1, we get
R2 - R1, we get
Since, Z row of the table has non-negative entries in the column of variables, therefore, this is the case of optimal solution. From the last column of the table we have x1 = 0, x2 = 0 and x3 = 1 and the maximum value of Z = 3.
Example: Maximise ‘Z’ = 2x1 + 3x2
Subject to constraints
x1 + x2 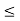 1
1
3x1 + x2 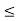 4
4
Where, x1, x2 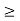 0
0
Sol:
Step 1: Conversion of inequalities into equalities by adding slack variables.
x1 + x2 + x3 = 1
3x1 + x2 + x4 = 4
Where x3 and x4 are slack variables.
Step 2: Identify the coefficients.
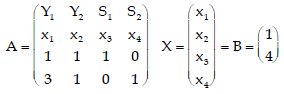
Step 3: First iteration of Simplex Method.

Therefore
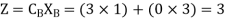
Therefore, Maximum value of ‘Z’ = 3
Example: Example:
Maximise ‘Z’ = 4x1 + 3x2
Subject to constraints
2x1 + x2 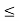 30
30
x1 + x2 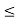 24
24
Where, x1, x2 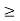 0
0
Sol:
Step 1: Convert the inequalities into equalities adding slack variables.
2x1 + x2 + x3 = 30
x1 + x2 + x4 = 24
Where x3 and x4 are slack variables.
Step 2: Fit the data into a matrix form.
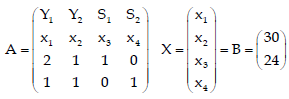
Step 3: First iteration of Simplex Method.
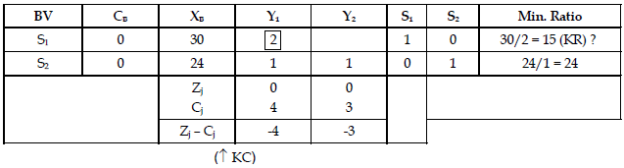
Therefore, Z = (0 × 30) + (0 × 24)
= 0
Step 4: Second iteration of Simplex Method.
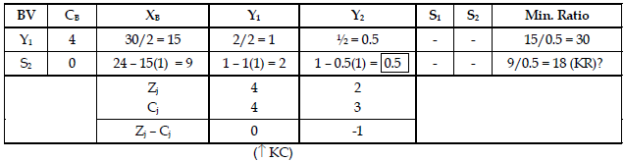
Therefore
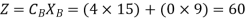
Step 5: Third iteration of Simplex Method.
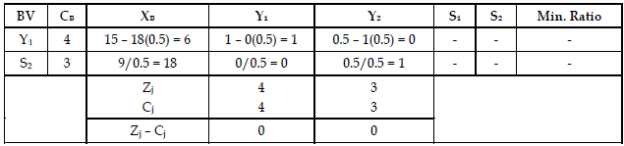
Therefore
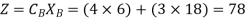
Z = 78
Example: Maximise ‘Z’ = 5x1 + 3x2
Subject to constraints
= 3x1 + 5x2 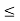 15
15
= 5x1 + 2x2 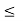 10
10
Where, x1, x2  0
0
Step 1: Convert the inequalities into equalities by adding the slack variables.
3x1 + 5x2 + x3 = 15
5x1 + 2x2 + x4 = 10
Where, x3 and x4 are slack variables.
Step 2: Fit the data into a matrix form.
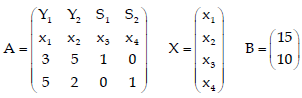
Step 3: First iteration of Simplex Method.
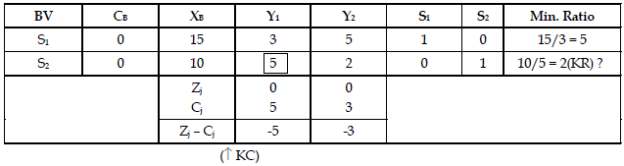
Therefore
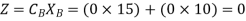
Step 4: Second iteration of Simplex Method.
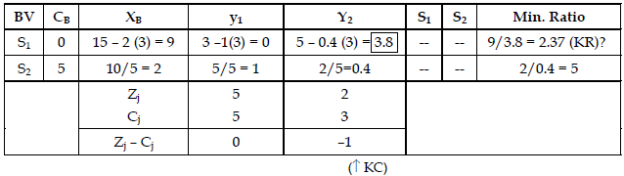
Therefore
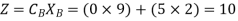
Step 5: Third iteration of Simplex Method.
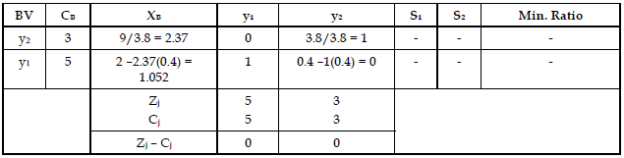
Therefore
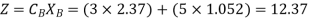
Maximum value of ‘Z’ = 12.37
Key takeaways:
- The simplex method is one of the most powerful and popular linear programming methods.
- The simplex method is an iterative procedure to get the most viable solution. This method keeps transforming the values of the fundamental variables to get the maximum value of the objective function.
- Linear programming functions are in standard form when trying to maximize the objective function.
In many LPP’s it is difficult to find an initial basic feasible solution of the given LP problem. Such cases arise
(i) When the constraints are of the ≤ type,
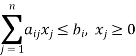
And value of few right-hand side constants is negative. After adding the non-negative slack variable si (i = 1, 2, . . ., m), the initial solution so obtained will be si = – bi for a particular resource, i. This solution is not feasible because it does not satisfy non-negativity conditions of slack variables.
(ii) When the constraints are of the ≥ type,
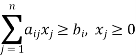
After adding surplus (negative slack) variable si, the initial solution so obtained will be – si = bi or
Si = –bi
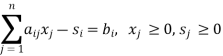
This solution is not feasible because it does not satisfy non-negativity conditions of surplus variables. In such a case, artificial variables, Ai (i = 1, 2, . . ., m) are added to get an initial basic feasible solution. The resulting system of equations then becomes
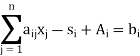
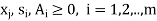
These are m simultaneous equations with (n + m + m) variables (n decision variables, m artificial variables and m surplus variables). An initial basic feasible solution of LP problem with such constraints can be obtained by equating (n + 2m – m) = (n + m) variables equal to zero. Thus the new solution to the given LP problem is: Ai = bi (i = 1, 2, . . . , m), which is not the solution to the original system of equations because the two systems of equations are not equivalent. In order to get back to the original problem, artificial variables should be removed from the optimal solution.
Two methods are used to remove the artificial variables,
- Two-phase method
- Big-M method
The simplex algorithm (for both minimization and the maximization LPP) can be stated as below-
Artificial variable techniques:
After reducing the given LPP into standard form, many times we note that some of the variables in the standard form are surplus variables and the corresponding column vectors do not provide unit vectors for the initial basis and hence the column which form unit matrix are missing in the initial simplex table. Such a situation is usually observed if the constraints equation(s) is (are) of the type “≥”. In order to have unit vectors in the basis, we introduce new type of variable (s) known as artificial variable(s). These are added to act as basic variable. They have no physical meaning and are used only to initiate the solution so that the simplex procedure may be adopted as usual till the optimal solution is obtained. The artificial variables are eliminated from the simplex table as and when they become non-basic variables. This technique is called the artificial variable technique for solving LPP.
There are two methods for solving LPPs involving artificial variables.
i) Big-M
Ii) Two-Phase Method
Two-Phase Method
In the first phase of this method, the sum of the artificial variables is minimized subject to the given constraints in order to get a basic feasible solution of the LP problem. The second phase minimizes the original objective function starting with the basic feasible solution obtained at the end of the first phase.
Since the solution of the LP problem is completed in two phases, this method is called the two-phase method.
Step by step method- (Phase-I)
Step-1:
(a) If all the constraints in the given LP problem are ‘less than or equal to’ (≤) type, then Phase II can be directly used to solve the problem. Otherwise, the necessary number of surplus and artificial variables are added to convert constraints into equality constraints.
(b) If the given LP problem is of minimization, then convert it to the maximization type by the usual method.
Step-2: Assign zero coefficient to each of the decision variables (xj) and to the surplus variables; and assign – 1 coefficient to each of the artificial variables. This yields the following auxiliary LP problem.

Subject to the constraints
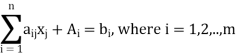
And
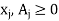
Step 3: Apply the simplex algorithm to solve this auxiliary LP problem. The following three cases may arise at optimality.
(a) Max Z * = 0 and at least one artificial variable is present in the basis with positive value. This means
That no feasible solution exists for the original LP problem.
(b) Max Z * = 0 and no artificial variable is present in the basis. This means that only decision variables
(xj’s) are present in the basis and hence proceed to Phase II to obtain an optimal basic feasible solution on the original LP problem.
(c) Max Z * = 0 and at least one artificial variable is present in the basis at zero value. This means that a feasible solution to the auxiliary LP problem is also a feasible solution to the original LP problem. In order to arrive at the basic feasible solution, proceed directly to Phase II or else eliminate the artificial basic variable and then proceed to second phase.
Second phase- Assign actual coefficients to the variables in the objective function and zero coefficient to the artificial variables which appear at zero value in the basis at the end of Phase I. The last simplex table of Phase I can be used as the initial simplex table for Phase II. Then apply the usual simplex algorithm to the modified simplex table in order to get the optimal solution to the original problem. Artificial variables that do not appear in the basis may be removed.
Example: By using two phase method solve the following LPP,
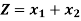
Subject to the constraints,
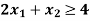
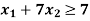
And
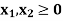
Sol:
Convert the function into maximization form and add surplus variables 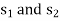 and artificial variables
and artificial variables  and
and 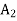 in the constraints, it becomes,
in the constraints, it becomes,
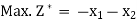
Subject to the constraints
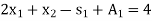
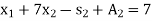
And
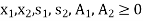
Where,
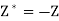
First phase-
This phase starts by considering the following auxiliary LP problem:
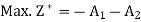
Subject to the constraints
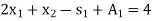
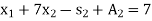
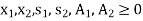
The initial solution is given in table,
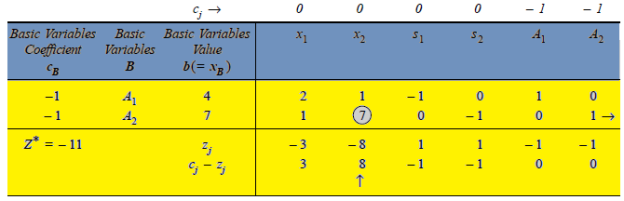
Artificial variables  and
and 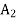 are now removed, one after the other, maintaining the feasibility of the solution.
are now removed, one after the other, maintaining the feasibility of the solution.
First iteration- Applying the following row operations to get an improved solution by entering variable 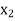 in the basis and first removing variable
in the basis and first removing variable 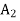 from the basis. The improved solution is shown in next table
from the basis. The improved solution is shown in next table
Note-the variable 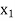 cannot be entered into the basis as this would lead to an infeasible solution.
cannot be entered into the basis as this would lead to an infeasible solution.

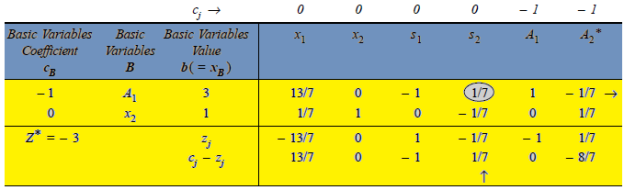
*- we can permanently remove this column at this stage
Second iteration: To remove 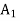 from the solution shown in above, we enter variable s2 in the basis by applying the following row operations. The new solution is shown in next table. It may be noted that if instead of
from the solution shown in above, we enter variable s2 in the basis by applying the following row operations. The new solution is shown in next table. It may be noted that if instead of 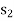 , variable
, variable 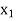 is chosen to be entered into the basis, it will lead to an infeasible solution
is chosen to be entered into the basis, it will lead to an infeasible solution
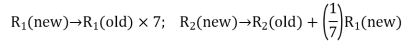
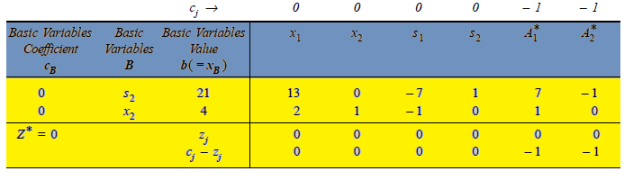
* Remove columns  and
and  from table
from table
Since all  –
–
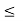 0 correspond to non-basic variables, the optimal solution:
0 correspond to non-basic variables, the optimal solution:  = 0,
= 0, 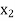 = 4,
= 4,
 = 0,
= 0, 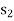 = 21,
= 21, 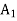 = 0,
= 0,  = 0 with Z* = 0 is arrived at. However, this solution may or may not be the basic feasible solution to the original LP problem. Thus, we have to move to Phase 2 to get an optimal solution to our original LP problem.
= 0 with Z* = 0 is arrived at. However, this solution may or may not be the basic feasible solution to the original LP problem. Thus, we have to move to Phase 2 to get an optimal solution to our original LP problem.
Second phase-
The modified simplex table obtained from Table given above is
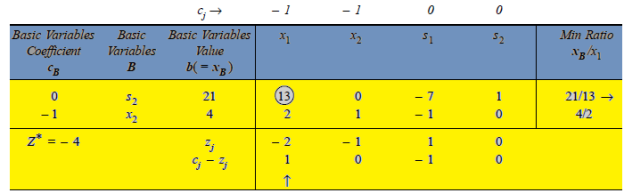
First iteration:
Introducing variable 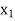 into the basis and removing variable
into the basis and removing variable 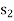 from the basis by applying the following row operations:
from the basis by applying the following row operations:
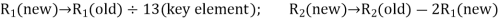
The improved basic feasible solution so obtained is given in next table. Since in next table, 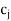 –
–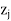
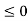 for all non-basic variables, the current solution is optimal. Thus, the optimal basic feasible solution to the given
for all non-basic variables, the current solution is optimal. Thus, the optimal basic feasible solution to the given
LP problem is: 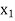 = 21/13,
= 21/13, 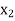 = 10/13 and Max
= 10/13 and Max 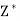 = – 31/13 or Min Z = 31/13.
= – 31/13 or Min Z = 31/13.
Big-M method:
This is the second method of removing artificial variables from the basis.
Large undesirable (unacceptable penalty) coefficients to artificial variables are assigned from the point of view
Of the objective function. If the objective function Z is to be minimized, then a very large positive price (penalty) is assigned to each artificial variable. Similarly, if Z is to be maximized, then a very large negative price (penalty) is assigned to each of these variables. The penalty is supposed to be designated by – M, for a maximization problem, and + M, for a minimization problem, where M > 0.
Steps for Big-M method:
Step-I: Express the LPP in the standard form by adding slack variables, surplus variables and/or artificial variables. Assign a zero coefficient to both slack and surplus variables. Then assign a very large coefficient + M (minimization case) and – M (maximization case) to artificial variable in the objective function.
Step-II: The initial basic feasible solution is obtained by assigning zero value to decision variables, 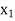 ,
, 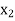 , ..., etc.
, ..., etc.
Step-III: Calculate the values of 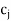 –
–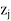 in last row of the simplex table and examine these values.
in last row of the simplex table and examine these values.
(i) If all 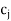 –
–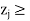 0, then the current basic feasible solution is optimal.
0, then the current basic feasible solution is optimal.
(ii) If for a column, k, 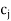 –
–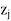 is most negative and all entries in this column are negative, then the problem has an unbounded optimal solution.
is most negative and all entries in this column are negative, then the problem has an unbounded optimal solution.
(iii) If one or more 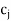 –
–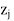 < 0 (minimization case), then select the variable to enter into the basis (solution mix) with the largest negative
< 0 (minimization case), then select the variable to enter into the basis (solution mix) with the largest negative  –
–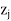 value.
value.
This value also represents the opportunity cost of not having one unit of the variable in the solution. That is,
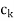 –
–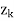 = Min {
= Min {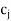 –
–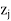 :
:  –
–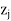 < 0}
< 0}
Step-IV: Determine the key row and key element in the same manner as discussed in the simplex algorithm for the maximization case.
Step-V: Continue with the procedure to update solution at each iteration till optimal solution is obtained.
Note-
- If at least one artificial variable is a basic variable (i.e., variable that is present in the basis) with zero value and the coefficient it M in each
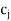 –
–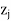 ( j = 1, 2, . . ., n) values is non-negative, then the given LP problem has no solution.
( j = 1, 2, . . ., n) values is non-negative, then the given LP problem has no solution. - If at least one artificial variable is present in the basis with a positive value and the coefficients M in each
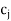 –
–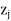 ( j = 1, 2, . . ., n) values is non-negative, then the given LP problem has no optimum basic feasible solution.
( j = 1, 2, . . ., n) values is non-negative, then the given LP problem has no optimum basic feasible solution.
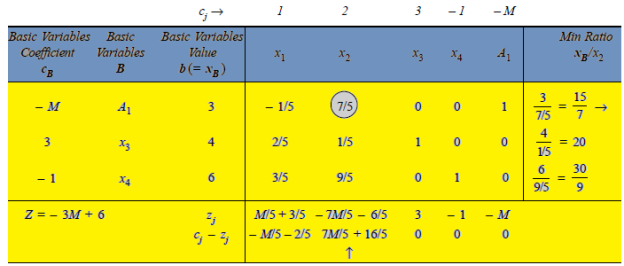
Example: Solve the following LPP by using Big-M method:
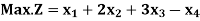
Subject to the constraints,


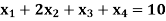
And
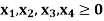
Sol:
Here all constraints of the given LPP are equations, therefore only artificial variables 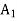 and
and  are added in the constraints to convert given LP problem to its standard form. The standard form of the problem is stated as follows:
are added in the constraints to convert given LP problem to its standard form. The standard form of the problem is stated as follows:
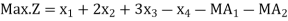
Subject to the constraints,
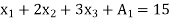

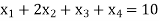
And
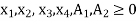
An initial basic feasible solution is-
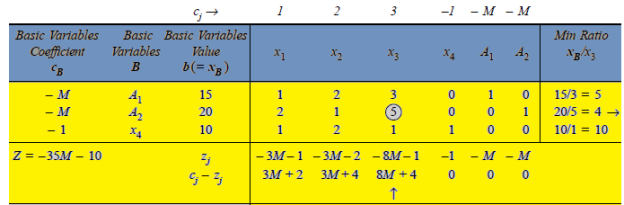
Since value of 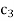 –
–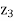 in Table given above is the largest positive value, the non-basic variable x3 is chosen to replace the artificial variable A2 in the basis. Thus, to get an improved solution, apply the following row operations.
in Table given above is the largest positive value, the non-basic variable x3 is chosen to replace the artificial variable A2 in the basis. Thus, to get an improved solution, apply the following row operations.


The improved basic feasible solution will be
Since value of  –
–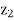 > 0 (positive) in Table above, the non-basic variable x2 is chosen to replace the artificial variable A1 in the basis. Thus, to get an improved basic feasible solution, apply the following row operations:
> 0 (positive) in Table above, the non-basic variable x2 is chosen to replace the artificial variable A1 in the basis. Thus, to get an improved basic feasible solution, apply the following row operations:
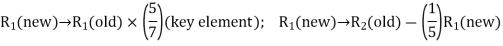
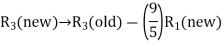
The improved basic feasible solution will be

Once again, the solution shown in Table above is not optimal as 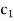 –
–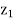 > 0 in
> 0 in 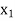 -column. Thus, applying the following row operations for replacing non-basic variable
-column. Thus, applying the following row operations for replacing non-basic variable 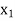 in the basis with basic variable x4:
in the basis with basic variable x4:
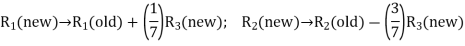
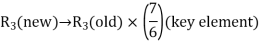
The improved basic feasible solution will be,
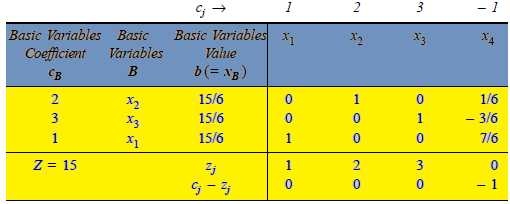
Since all  –
–
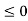 , therefore, we get an optimal solution with value of variables as:
, therefore, we get an optimal solution with value of variables as: 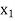 = 15/6,
= 15/6, 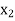 = 15/6,
= 15/6,  = 15/6 and Max Z = 15.
= 15/6 and Max Z = 15.
Case study
Example: A publication company (printing) is facing a tight financial squeeze and is attempting to cut costs wherever possible. At present it has only one printing contract, and luckily, the book is selling well in both the hardcover and the paperback editions. It has just received a request to print more copies of this book in either the hardcover or the paperback form. The printing cost for the hardcover books is Rs 600 per 100 books while that for paperback is only Rs 500 per 100. Although the company is attempting to economize, it does not wish to lay off any employee. Therefore, it feels obliged to run its two printing presses – I and II, at least 80 and 60 hours per week, respectively. Press I can produce 100 hardcover books in 2 hours or 100 paperback books in 1 hour. Press II can produce 100 hardcover books in 1 hour or 100 paperbacks books in 2 hours. Determine how many books of each type should be printed in order to minimize costs.
Sol:
Suppose  and
and 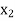 be the number of batches containing 100 hard cover and paperback books, to
be the number of batches containing 100 hard cover and paperback books, to
Be printed respectively. The LP problem can then be formulated as follows.
Minimize Z = 600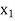 + 500
+ 500
Subject to the constraints
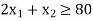
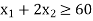
And
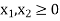
Adding surplus variables 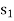 ,
, 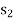 and artificial variables
and artificial variables 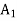 ,
,  in the the constraints, the standard form of the LP problem becomes
in the the constraints, the standard form of the LP problem becomes
Minimize Z = 600 + 500
+ 500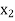 + 0
+ 0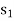 + 0
+ 0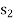 + M
+ M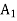 + M
+ M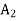
Subject to the constraints
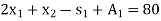
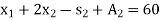
And
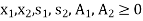
Solution by simplex method:
The initial basic feasible solution: 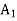 = 80,
= 80, 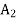 = 60 and Min Z = 80M + 60M = 140M obtained by putting
= 60 and Min Z = 80M + 60M = 140M obtained by putting 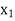 =
= 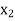 =
= 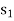 =
= 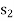 = 0 is shown in Table
= 0 is shown in Table

Since 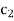 –
– value in
value in 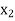 -column of Table above is the largest negative, therefore non-basic variable
-column of Table above is the largest negative, therefore non-basic variable 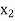 is chosen to replace basic variable
is chosen to replace basic variable 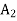 in the basis. For this, apply following row operations.
in the basis. For this, apply following row operations.
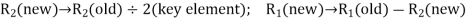
To get an improved basic feasible solution as shown in table below
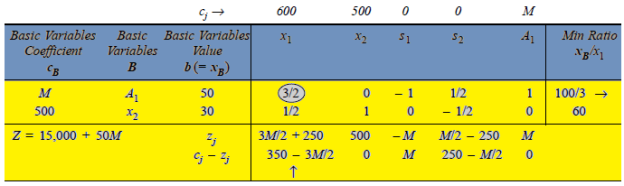
Again, since value  –
– of in x1-column of Table above is the largest negative, non-basic variable
of in x1-column of Table above is the largest negative, non-basic variable  is chosen to replace basic variable
is chosen to replace basic variable 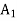 in the basis. For this, apply following row operations:
in the basis. For this, apply following row operations:
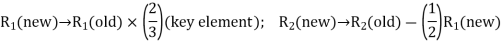
To get an improved basic feasible solution as shown in Table below
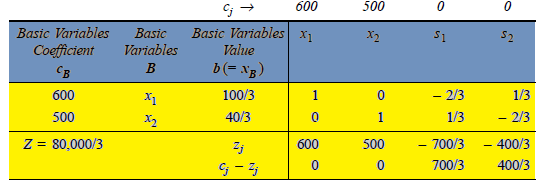
In above Table, all 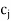 –
–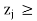 0 and no artificial variable is present in the basis (solution mix). Hence, an optimum solution is arrived at with
0 and no artificial variable is present in the basis (solution mix). Hence, an optimum solution is arrived at with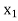 = 100/3 batches of hardcover books,
= 100/3 batches of hardcover books, 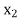 = 40/3 batches of paperback books, at a total minimum cost,
= 40/3 batches of paperback books, at a total minimum cost,
Z = Rs. 80,000/3.
Practice case study-1:
Mr. Krishna, the marketing manager of ABC Typewriter Company is trying to decide how he should allocate his salesmen to the company’s three primary markets. Market I is in the urban area and the salesman can sell, on the average, 40 typewriters a week. Salesmen in the other two markets, II and III can sell, on the average, 36 and 25 typewriters per week, respectively. For the coming week, three of the salesmen will be on vacation, leaving only 12 men available for duty. Also because of lack of company care, a maximum of 5 salesmen can be allocated to market area I. The selling expenses per week for salesmen in each area are Rs 800 per week for area I, Rs 700 per week for area II, and Rs 500 per week for area III. The budget for the next week is Rs 7,500. The profit margin per typewriter is Rs 150. Determine how many salesmen should be assigned to each area in order to maximize profits?
Practice case study-2:
A transport company is considering the purchase of new vehicles for providing transportation between the Delhi Airport and hotels in the city. There are three vehicles under consideration: Station wagons, minibuses and large buses. The purchase price would be Rs 1,45,000 for each station wagon, Rs 2,50,000 for each minibus and Rs 4,00,000 for each large bus. The board of directors has authorized a maximum amount of Rs 50,00,000 for these purchases. Because of the heavy air travel, the new vehicles would be utilized at maximum capacity, regardless of the type of vehicles purchased. The expected net annual profit would be Rs 15,000 for the station wagon, Rs 35,000 for the minibus and Rs 45,000 for the large bus. The company has hired 30 new drivers for the new vehicles. They are qualified drivers for all three types of vehicles. The maintenance department has the capacity to handle an additional 80 station wagons. A minibus is equivalent to 1.67 station wagons and each large bus is equivalent to 2 station wagons in terms of their use of the maintenance department. Determine the number of each type of vehicle that should be purchased in order to maximize profit.
Key takeaways:
- Big M method can be used to find the existence of feasible solution. But it is difficult and many a time one gets confused during computation because of manipulation of constant M. In two–phase method big M is eliminated and calculations will become easy.
- If at least one artificial variable is a basic variable (i.e., variable that is present in the basis) with zero value and the coefficient it M in each
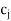 –
–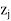 ( j = 1, 2, . . ., n) values is non-negative, then the given LP problem has no solution.
( j = 1, 2, . . ., n) values is non-negative, then the given LP problem has no solution. - If at least one artificial variable is present in the basis with a positive value and the coefficients M in each
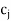 –
– ( j = 1, 2, . . ., n) values is non-negative, then the given LP problem has no optimum basic feasible solution.
( j = 1, 2, . . ., n) values is non-negative, then the given LP problem has no optimum basic feasible solution.
References:
- Operations research- theory and application, JK Sharma, trinity press
- Operations research, P. Rama Murthy, new age international publishers
- Higher engineering mathematics, B.S. Grewal