Unit - 2

Duality

2.1 Duality, formulation of the dual problem, primal-dual relationships

In linear programming, duality implies that each linear programming problem can be analyzed in two different ways but would have equivalent solutions. Any LP problem (either maximization and minimization) can be stated in another equivalent form based on the same data. The new LP problem is called dual linear programming problem.

Definition: each maximization problem in LP has its corresponding problem, called the dual, which is a minimization problem. Similarly, each minimization problem has its corresponding dual, a maximization problem.

An optimal solution from the primal and the dual problem would be same as they both originate from the same set of data.

Note- The necessary and sufficient condition for any LPP and its dual to have optimal solutions is that both have feasible solutions.

Note- The shadow price is also defined as the rate of change in the optimal objective function value with respect to the unit change in the availability of a resource. To be more precise for any constraint, we have

Shadow price = Change in optimal objective function value/Unit change in the availability of resource

Formation of the dual problem:

We use the following steps to convert primal problem into its dual.

Simplex method is used to obtain the optimal solution for both primal and dual form.

Step 1: For each constraint, in primal problem there is an associated variable in the dual problem.

Step 2: The elements of right-hand side of the constraints will be taken as the coefficients of the objective function in the dual problem.

Step 3: If the primal problem is maximization, then its dual problem will be minimization and vice versa.

Step 4: The inequalities of the constraints should be interchanged from ³ to  and vice versa and the variables in both the problems are non-negative.

Step 5: The rows of primal problem are changed to columns in the dual problem. In other words, the matrix A of the primal problem will be changed to its transpose (A) for the dual problem.

Step 6: The coefficients of the objective function will be taken to the right hand side of the constraints of the dual problem.

Advantages of Duality

1. It is advantageous to solve the dual of a primal having less number of constraints because the number of constraints usually equals the number of iterations required to solve the problem.

2. It avoids the necessity for adding surplus or artificial variables and solves the problem quickly (the technique is known as the primal-dual method).

3. The dual variables provide an important economic interpretation of the final solution of an LP problem.

4. It is quite useful when investigating changes in the parameters of an LPP (the technique known as sensitivity analysis).

5. Duality is used to solve an LPP by the simplex method in which the initial solution is infeasible.

Example: Write the dual of the following problem.

Maximise

Z = –6x1 + 7x2

Subject to, –x1 + 2x2 –5

3x1 + 4x2 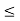7

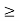x1, x2 0

Sol:

The given problem is considered as primal linear programming problem. To convert it into dual, the following procedure is adopted.

Step 1: There are 2 constraints and hence the dual problem will have 2 variables. Let us denote them as y1 and y2.

Step 2: The right hand side of the constraints are –5 and 7 which are taken as the coefficients of the variables y1 and y2 in the objective function.

Step 3: The primal objective problem is maximization and hence the dual seeks minimization for the objective function. Hence, the objective functions for the dual problem is given by

Minimise Z = –5y1 + 7y2

Step 4: The inequalities of the constraints for the primal problem are of the type (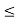). Hence, the inequalities for the dual constraints will be of the type ().

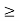Step 5: The coefficient matrix for the primal problem is

The transpose of this matrix which serves as the coefficient matrix for the dual problem is given

By.

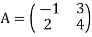
Step 6: The coefficients of the objective function for the given primal are –6 and 7. They are taken on the right hand side of the constraints for the dual problem. Hence, the constraints for the dual problem are represented as

–y1 + 3y2 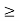–6

2y1 + 4y2 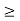7

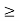y1, y2 0

Example: Find the dual of the following problem:

Minimise Z = 3x1 + 4x2 + 5x3

Subject to

x1 + x3 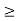3

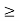x2 + x3 4

x1,x2,x3 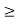0

Sol:
Let the given problem be denoted as primal. The objective of the primal is minimization and hence the objective of the dual is maximization. There are two constraints for the primal problem. Hence, the problem has 2 variables namely, y1 and y2. The right hand side of the constraints are 3 and 4 which are the coefficients for y1 and y2 in the objective function for the dual problem given as

Maximise Z = 3y1 + 4y2

The coefficient of the objective function in the primal problem are 3, 4 and 5 which serve as the

Right hand side of the constraints for the dual problem. The inequalities of the constraints of the type (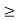) are converted as () type for the dual problem. The coefficient matrix for primal problem is

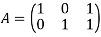
And hence the coefficient matrix for the dual problem is

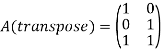
Hence, the dual problem is represented as

Maximise ‘Z’ = 3y1 + 4y2

Subject to

Is

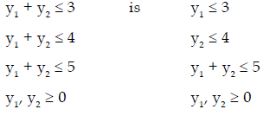
Primal-dual relationship:

The relation between primal and dual LPP can be explained as below

If Primal	If dual
Objective is to maximize	Objective is to minimize
Jth primal variable,	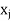Jth dual constraint
Ith primal constraint	Ith dual variable,
Primal variable 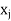unrestricted in sign	Dual constraint j is = type
Primal constraint i is = type	Dual variable 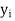is unrestricted in sign
Primal constraints 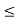type	Dual constraints ≥ type

Key takeaways:

1. Each maximization problem in LP has its corresponding problem, called the dual, which is a minimization problem. Similarly, each minimization problem has its corresponding dual, a maximization problem.
2. An optimal solution from the primal and the dual problem would be same as they both originate from the same set of data.
3. The necessary and sufficient condition for any LPP and its dual to have optimal solutions is that both have feasible solutions.
4. Shadow price = Change in optimal objective function value/Unit change in the availability of resource

2.2 Fundamental Theorem of Duality, economic interpretation of the dual

There are two important forms of primal and dual LP problems-

1. Symmetrical (canonical) form
2. Standard form.

Symmetrical Form:

Suppose the primal LPP is given in the form

Subject to the constraints,

………………

………………

………………

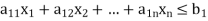
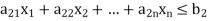
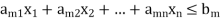
And

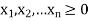
Then the corresponding dual LP problem is written as:

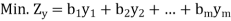
Subject to the constraints,

………………

………………

………………

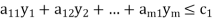
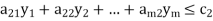
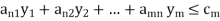
And

Economic Interpretation of Dual Variables:

Parameters:

Z = return,

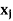= number units of variable j

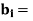maximum units of resource, i available

Primal LPP

Subject to the constraints

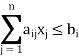
And

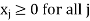
Dual LPP

Minimize (cost)

Subject to the constraints

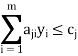
And

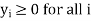
Economic Interpretation of Dual Constraints:

A we know that the dual constraints are expressed as,

Since coefficients 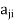represents the amount of resource 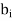consumed by per unit of activity 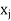, and the dual variable 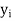represents shadow price per unit of resource , the quantity 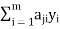(=) should be total shadow price of all resources required to produce one unit of activity .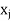

For maximization LP problem, if – 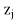> 0 value corresponds to any non-basic variable, then the value of objective function can be increased. This implies that the value of variable, 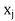 can be increased from zero to a positive level provided its unit profit 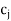is more than its shadow price, i.e.

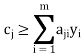
Profit per unit of activity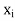 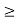Shadow price of resources used per unit of activity, .

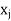Procedure to convert into dual from primal:

1. A dual variable is defined corresponds to each constraint in the primal LP problem and vice versa. Thus, for a primal LP problem with m constraints and n variables, there exists a dual LP problem with m variables and n constraints and vice-versa.
2. The right-hand side constants 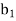, , 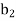. . ., 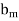of the primal LP problem becomes the coefficients of the dual variables 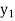, , 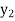. . ., in the dual objective function 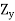. Also the coefficients , , 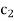. . ., 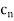of the primal variables 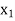, , . . ., 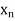in the objective function become the right-hand side constants in the dual LP problem.
3. For a maximization primal LP problem with all type constraints, there exists a minimization dual LP problem with all 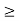type constraints and vice versa. Thus, the inequality sign is reversed in all the constraints except the non-negativity conditions.
4. The matrix of the coefficients of variables in the constraints of dual is the transpose of the matrix of coefficients of variables in the constraints of primal and vice versa.
5. If the objective function of a primal LP problem is to be maximized, the objective function of the dual is to be minimized and vice versa.
6. If the ith primal constraint is = (equality) type, then the ith dual variables is unrestricted in sign and vice versa.

Example: Obtain the dual LP problem of the following primal LP problem:

Minimize Z = 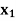+ 2

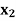
Subject to the constraints

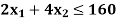
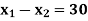
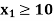
And

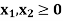
Sol:

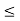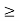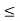Since the objective function of the primal LP problem is of minimization, change all type constraints to type constraints by multiplying the constraint on both sides by –1. Also write = type constraint equivalent to two constraints of the type and Then the given primal LP problem can be rewritten as:

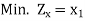+ 2

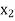
Subject to the constraint

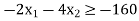
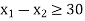
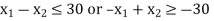
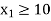
And

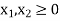
Suppose 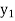, , 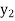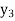and 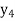be the dual variables corresponding to the four constraints in the given order.

The dual of the given primal LP problem can then be formulated as follows:

Subject to the constraints,

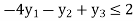
And

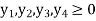
Let y =

The dual problem then reduces to the form

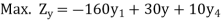
Subject to the constraints

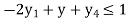
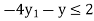
And

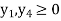
Example: Obtain the dual of the following primal LPP

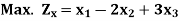
Subject to the constraints

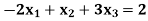
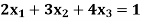
And

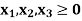
Sol:

Since both the primal constraints are of the equality type, the corresponding dual variables and , will be unrestricted in sign. Following the rules of duality formulation, the dual of the given primal

LP problem is

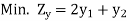
Subject to the constraints

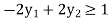
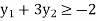
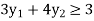
And

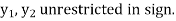
Key takeaways:

1. One part of a Linear Programming Problem (LPP) is called the Primal and the other part is called the Dual. In other words, each maximization problem in LP has its corresponding problem, called the dual, which is a minimization problem.
2. Dual Problem: In the dual problem, the dual vector multiplies the constants that determine the positions of the constraints in the primal.
3. Duality principle: In optimization theory, the duality principle states that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem.
4. Primal Problems: In the primal problem, the objective function is a linear combination of n variables.

References:

1. Operations research- theory and application, JK Sharma, trinity press
2. Operations research, P. Rama Murthy, new age international publishers
3. Operations research by kanti swarup