Unit - 3

Special probability distributions

3.1 Special probability distributions: Discrete Uniform distribution

Discrete uniform distribution is considered as one of the simplest probability distributions.

The discrete random variable assumes each of its values with the same (equal) probability. In this equiprobable or uniform space each sample point is assigned equal probabilities.

Example 1: In the tossing of a fair die, each sample point in the sample space {1, 2, 3, 4, 5, 6} is assigned with the same (uniform) probability 1

6 i.e. p(x) = 1/6 for x = 1, 2, 3, 4, 5, 6. In particular, if the sample space S contains k points, then probability of each point is 1/k . Thus in the discrete uniform distribution, the discrete random variable X assigns equal probabilities to all possible values of X. Therefore the probability mass function f (X) has the form

Here the constant K which is the parameter completely determines the discrete uniform distribution.

(1). The mean and variance of (1) are given by

And

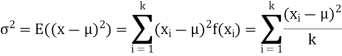
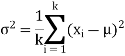
Example: Find the mean and variance of a number on an unbiased die when thrown.

Sol:

Suppose X be the number on an unbiased die when thrown,

Then X can take the values 1, 2, 3, 4, 5, 6 with

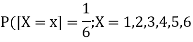
By uniform distribution, we have

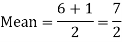
And

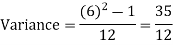
Example: If a ticket is drawn from a box containing 10 tickets numbered 1 to 10 inclusive. Find the probability that the number x drawn is (a) less that 4

(b) even number (c) prime number (d) find the mean and variance of the random variable X.

Sol:

(a) Since each ticket has the same probability for being drawn, the probability distribution is discrete uniform distribution given by f (x) =1/10 for x = 1, 2, 3, . . . , 10. Now

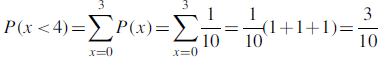
(b) 2, 4, 6, 8, 10 are even numbers each with probability 1/10 probability of even number

= 5/10 = 1/2

(c) 2, 3, 5, 7 are prime prob. Of prime = 4/10 = 2/5 .

(d) Mean = E(x) =

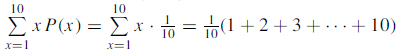
Mean =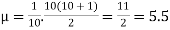

Variance

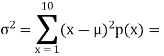
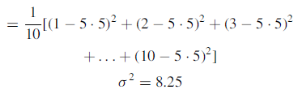
Key takeaways:

1. The discrete uniform distribution-

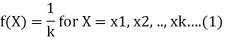
2.    

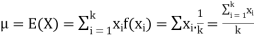
3.    

3.2 Binomial distribution

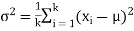
A probability distribution is an arithmetical function which defines completely possible values &possibilities that a random variable can take in a given range. This range will be bounded between the minimum and maximum possible values. But exactly where the possible value is possible to be plotted on the probability distribution depends on a number of influences. These factors include the distribution's mean, SD, Skewness, and kurtosis.

It was discovered by a Swiss Mathematician Jacob James Bernoulli in the year 1700.

This distribution is concerned with trials of a repetitive nature in which only the occurrence or non-occurrence, success or failure, acceptance or rejection, yes or no of a particular event is of interest.

For convenience, we shall call the occurrence of the event ‘a success’ and its non-occurrence ‘a failure’.

Let there be n independent trials in an experiment. Let a random variable X denote the number of successes in these n trials. Let p be the probability of a success and q that of a failure in a single trial so that p + q = 1. Let the trials be independent and p be constant for every trial.

BINOMIAL DISTRIBUTION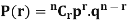

To find the probability of the happening of an event once, twice, thrice,…r times ….exactly in n trails.

Let the probability of the happening of an event A in one trial be p and its probability of not happening be 1 – p – q.

We assume that there are n trials and the happening of the event A is r times and its not happening is n – r times.

This may be shown as follows

AA……A                                 

r times                                       n – r times                          (1)

A indicates its happening 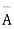its failure and P (A) =p and P (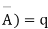

We see that (1) has the probability

Pp…p qq….q=

r times              n-r times                                                       (2)

Clearly (1) is merely one order of arranging r A’S.

The probability of (1) =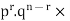Number of different arrangements of r A’s and (n-r)’s

The number of different arrangements of r A’s and (n-r)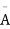’s

Probability of the happening of an event r times =

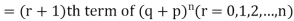
If r = 0, probability of happening of an event 0 times

If r = 1,probability of happening of an event 1 times

If r = 2,probability of happening of an event 2 times

If r = 3,probability of happening of an event 3 times and so on.

These terms are clearly the successive terms in the expansion of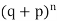

Hence it is called Binomial Distribution.

Note - n and p occurring in the binomial distribution are called the parameters of the distribution.

Note - In a binomial distribution:

(i) n, the number of trials is finite.

(ii) each trial has only two possible outcomes usually called success and failure.

(iii) all the trials are independent.

(iv) p (and hence q) is constant for all the trials.

Applications of binomial distribution:

1. In problems concerning no. Of defectives in a sample production line.

2. In estimation of reliability of systems.

3. No. Of rounds fired from a gun hitting a target.

4. In Radar detection

Example. If on an average one ship in every ten is wrecked. Find the probability that out of 5 ships expected to arrive, 4 at least we will arrive safely.

Solution. Out of 10 ships one ship is wrecked.

I.e. nine ships out of 10 ships are safe, P (safety) =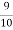

P (at least 4 ships out of 5 are safe) = P (4 or 5) = P (4) + P(5)

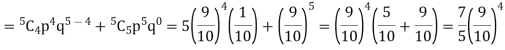
Example. The overall percentage of failures in a certain examination is 20. If 6 candidates appear in the examination what is the probability that at least five pass the examination?

Solution. Probability of failures = 20%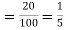

Probability of (P) =

Probability of at least 5 pass = P(5 or 6)

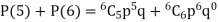
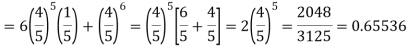
Example. The probability that a man aged 60 will live to be 70 is 0.65. What is the probability that out of 10 men, now 60, at least seven will live to be 70?

Solution. The probability that a man aged 60 will live to be 70

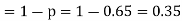
Number of men= n = 10

Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10)

= P (7)+ P(8)+ P(9) + P(10) =

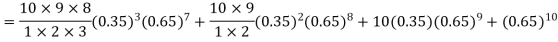
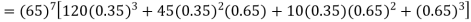
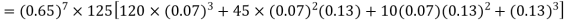
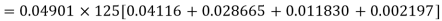
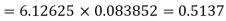
Example. Assuming that 20% of the population of a city are literate so that the chance of an individual being literate is and assuming that hundred investigators each take 10 individuals to see whether they are illiterate, how many investigators would you expect to report 3 or less were literate.

Solution.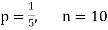

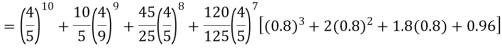
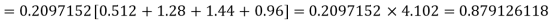
Required number of investigators = 0.879126118× 100 =87.9126118

= 88 approximate

Mean or binomial distribution

Successors r	Frequency f	Rf
0		0
1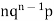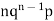
2		n(n-1)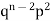
3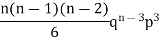
…..	……	….
n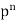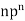

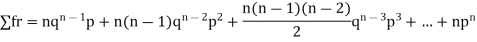
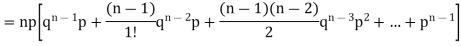
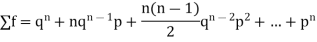
Since,

STANDARD DEVIATION OF BINOMIAL DISTRIBUTION

Successors r	Frequency f
0		0
1
2		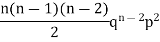2n(n-1)
3
…..	……	….
n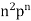

We know that 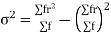          (1)

r is the deviation of items (successes) from 0.

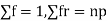
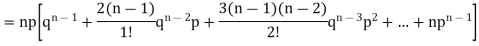
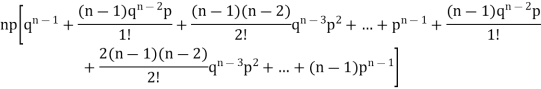
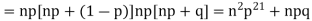
Putting these values in (1) we have

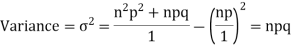
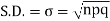
Hence for the binomial distribution, Mean

Example. A die is tossed thrice. A success is getting 1 or 6 on a TOSS. Find the mean and variance of the number of successes.

Solution.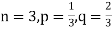

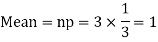
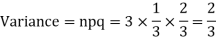
RECURRENCE RELATION FOR THE BINOMIAL DISTRIBUTION

By Binomial Distribution

On dividing (2) by (1) , we get

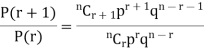
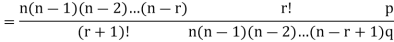
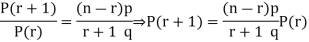
Key takeaways:

1. BINOMIAL DISTRIBUTION
2. n and p occurring in the binomial distribution are called the parameters of the distribution.
3. 
4. 

3.3 Negative binomial, Geometric, Hypergeometric distributions

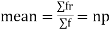
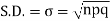
Negative binomial distribution:

Negative binomial distribution is a probability distribution of number of occurences of successes and failures in a sequence of independent trails before a specific number of success occurs. Following are the key points to be noted about a negative binomial experiment.

1. The experiment should be of x repeated trials.
2. Each trail have two possible outcome, one for success, another for failure.
3. Probability of success is same on every trial.
4. Output of one trial is independent of output of another trail.
5. Experiment should be carried out until r successes are observed, where r is mentioned beforehand.

Negative binomial distribution probability can be calculated by using-

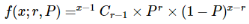
Where −

1. x = Total number of trials.
2. r  = Number of occurences of success.
3. P = Probability of success on each occurence.
4. 1−P= Probability of failure on each occurence.
5. f(x;r,P)= Negative binomial probability, the probability that an x-trial negative binomial experiment results in the rth success on the xth trial, when the probability of success on each trial is P.
6. NCr = Combination of n items taken r at a time.

Example: Ronaldo is a football player. His success rate of goal hitting is 70%. What is the probability that Ronaldo hits his third goal on his fifth attempt?

Sol:

Here probability of success, P is 0.70. Number of trials, x is 5 and number of successes, r is 3. Using negative binomial distribution formula, let's compute the probability of hitting third goal in fifth attempt

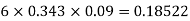
Geometric distribution: The geometric distribution is a special case of the negative binomial distribution. It deals with the number of trials required for a single success. Thus, the geometric distribution is a negative binomial distribution where the number of successes (r) is equal to 1.

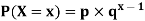
Where −

1. p = probability of success for single trial.
2. q = probability of failure for a single trial (1-p)
3. x = the number of failures before a success.
4. P(X−x) = Probability of x successes in n trials.

Example: In an amusement fair, a competitor is entitled for a prize if he throws a ring on a peg from a certain distance. It is observed that only 30% of the competitors are able to do this. If someone is given 5 chances, what is the probability of his winning the prize when he has already missed 4 chances?

Sol:

If someone has already missed four chances and has to win in the fifth chance, then it is a probability experiment of getting the first success in 5 trials. The problem statement also suggests the probability distribution to be geometric. The probability of success is given by the geometric distribution formula:

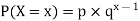
Where −

• p=30%=0.3p=30%=0.3
• x= 5 = the number of failures before a success.

Therefore, the required probability:

Hyper-geometric distribution

When the population is finite and the sampling is done without replacement, so that the events are stochastically dependent, although random, we obtain hyper-geometric distribution.

Suppose a urn contains N balls, of which M are white and N-M are black.

Of these, n balls are chosen at random without replacement. Let X be a random variable that denote the number of white balls drawn. Then, the probability of X = x white balls among the n balls drawn is given by

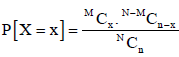
[For x = 0, 1, 2,..., n (n M) or x = 0, 1, 2,...,M (n > M)]

The probability function of discrete random variable X given above is known as the Hyper-geometric distribution.

The conditions for hyper-geometric distributions

1. There are finite number of dependent trials
2. A single trial has one of the two possible outcomes-Success or Failure
3. Sampling is done without replacement

Definition: A random variable X is said to follow the hypergeometric distribution with parameters N, M and n if it assumes only non-negative integer values and its probability mass function is given by

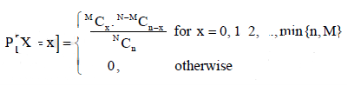
Where n, M, N are positive integers such that n ≤ N, M ≤ N.

Mean of the Hyper-geometric distribution is given as-

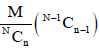
And the variance is

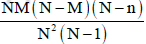
Example: A 5 members committee is drawn at random from a voters’ list of 100 persons, out of which 60 are non-graduates and 40 are graduates. What is the probability that the committee will consist of 3 graduates?

Sol:

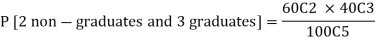
Key takeaways:

1. Negative binomial distribution probability can be calculated by using-

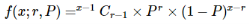
2.     Geometric distribution-

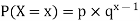
3.     Hyper-geometric distribution-

Let X be a random variable that denote the number of white balls drawn. Then, the probability of X = x white balls among the n balls drawn is given by

3.5 Poisson, multinomial distribution

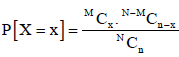
Poisson Distribution-

Poisson distribution is a particular limiting form of the Binomial distribution when p (or q) is very small and n is large enough.

Poisson distribution is

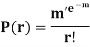
Where m is the mean of the distribution.

Proof. In Binomial Distribution

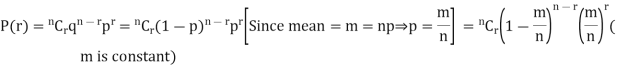
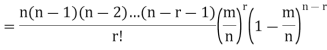
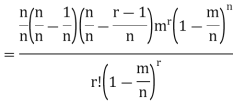
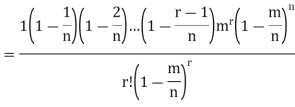
Taking limits when n tends to infinity

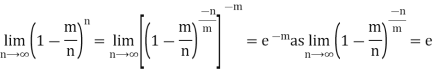
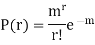
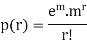
MEAN OF POISSON DISTRIBUTION

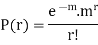
Success r	Frequency f	f.r
0		0
1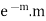
2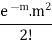
3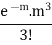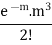
…	…	…
r
…	…	…

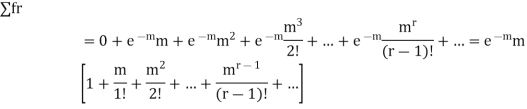
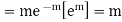
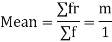
STANDARD DEVIATION OF POISSON DISTRIBUTION

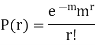
Successive r	Frequency f	Product rf	Product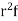
0		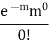0	0
1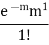
2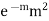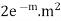
3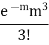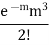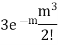
…….	……..	……..	……..
r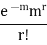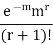
……..	…….	……..	…….

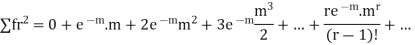
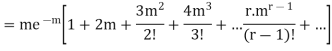
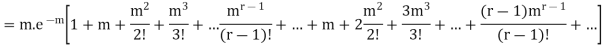
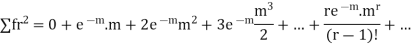
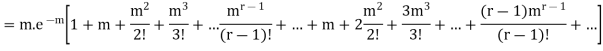
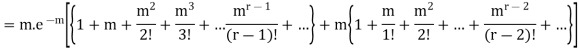
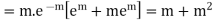
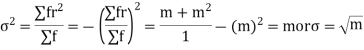
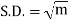
Hence mean and variance of a Poisson distribution are equal to m. Similarly we can obtain,

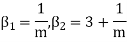
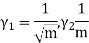
MEAN DEVIATION

Show that in a Poisson distribution with unit mean, and the mean deviation about the mean is 2/e times the standard deviation.

Solution. 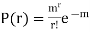But mean = 1 i.e. m =1 and S.D. =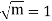

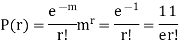
r	P (r)	|r-1|	P(r)|r-1|
0		1
1		0	0
2		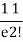1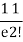
3		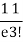2
4		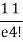3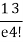
…..	…..	…..	…..
r		r-1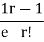

Mean Deviation =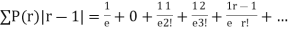

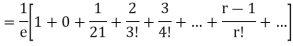
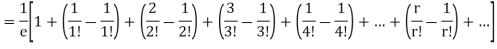
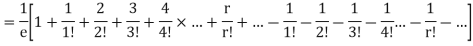
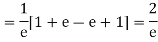
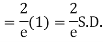
MOMENT GENERATING FUNCTION OF POISSON DISTRIBUTION

Solution.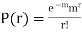

Let 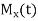be the moment generating function then

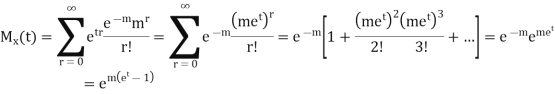
CUMULANTS

The cumulant generating function is given by

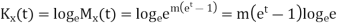
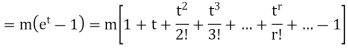
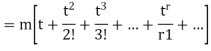
Now 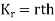cumulant =coefficient of in K (t) = m

i.e. , where r = 1,2,3,…

Mean =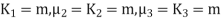

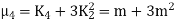
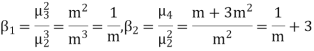
RECURRENCE FORMULA FOR POISSON DISTRIBUTION

SOLUTION. By Poisson distribution

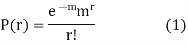
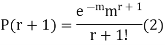
On dividing (2) by (1) we get

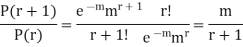
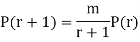
Example. Assume that the probability of an individual coal miner being killed in a mine accident during a year is 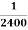. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.

Solution.

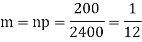
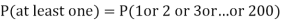
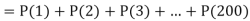
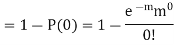
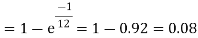
Example. Suppose 3% of bolts made by a machine are defective, the defects occuring at random during production. If bolts are packaged 50 per box, find

(a)  Exact probability and

(b)  Poisson approximation to it, that a given box will contain 5 defectives.

Solution.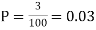

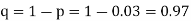
(a)  Hence the probability for 5 defectives bolts in a lot of 50.

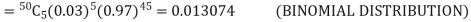
(b) To get Poisson approximation m = np =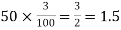

Required Poisson approximation=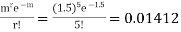

Example. In a certain factory producing cycle tyres, there is a smallchance of 1 in 500 tyres to be defective. The tyres are supplied in lots of 10. Using Poisson distribution, calculate the approximate number of lots containing no defective, one defective and two defective tyres, respectively, in a consignment of 10,000 lots.

Solution.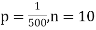

S.No.	Probability of defective	Number of lots containing defective
1.
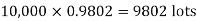2.
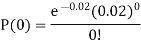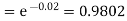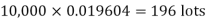3.

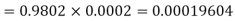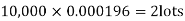Key takeaways:

1. Poisson distribution is

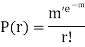
Where m is the mean of the distribution.

2.    

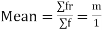
3.    

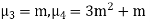
4.    

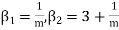
5.    

6.     In a Poisson distribution with unit mean, and the mean deviation about the mean is 2/e times the standard deviation.

3.6 Multinomial, Special probability densities

Multinomial experiments consists of the following properties-

1. The trials are independent.

2. Each trial has discrete number of possible outcomes.

3. The Experiments consists of n repeated trials.

Note- Binomial distribution is a special case of multinomial distribution.

Multinomial distribution-

A multinomial distribution is the probability distribution of the outcomes from a multinomial experiment.

The multinomial formula defines the probability of any outcome from a multinomial experiment.

Multinomial formula-

Suppose there are n trials in a multinomial experiment and each trial can result in any of k possible outcomes 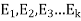. Now suppose each outcome can occur with probabilities .

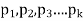Then the probability 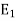occurs times, 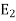occurs 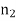times and occurs times

Is-

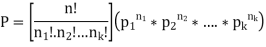
Example1:

You are given a bag of marble. Inside the bag are 5 red marble, 4 white marble, 3 blue marble. Calculate the probability that with 6 trials you choose 3 marbles that are red, 1 marble that is white and 2 marble is blue. Replacing each marble after it is chosen.

Solution:

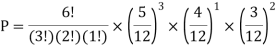
Example2:

You are randomly drawing cards from an ordinary deck of cards. Every time you pick one you place it back in the deck. You do this 5 times. What is the probability of drawing 1 heart, 1 spade, 1club, and 2 diamonds?

Solution:

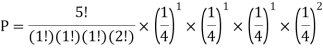
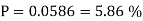
Example3:

A die weighed or loaded so that the number of spots X that appear on the up face when the die is rolled has pmf

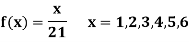
If this loaded die is rolled 21 times. Find the probability of rolling one one, two twos, three threes, four fours, five fives, six sixes.

Solution:

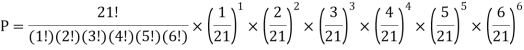
Example4:

If we have 10 balls in a bag, in which 2 are red, 3 are green and remaining are blue colour balls. Then we select 4 balls randomly form the bag with replacement, then what will be the probability of selecting 2 green balls and 2 blue balls.

Sol.

Here this experiment has 4 trials so n = 4.

The required probability will be-

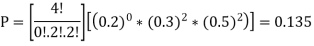
So that-

Key takeaways:

1. A multinomial distribution is the probability distribution of the outcomes from a multinomial experiment.

3.7 Uniform distribution, exponential, gamma, chi-square, beta distribution

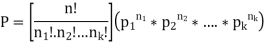
Continuous uniform distribution

A random variable X is said to follow a continuous uniform distribution over an interval (a, b) if its probability density function is given by

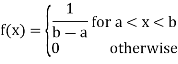
Mean and Variance of the continuous uniform Distribution

Example: Find the coefficient of variation for the rectangular distribution in (0, 12).

Sol:

Here a = 0, b = 12

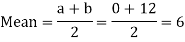
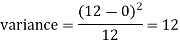
Then the SD will be-

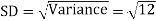
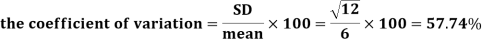
Example: Buses are scheduled every 5 minutes at a certain bus stand. A person comes to the stand at a random time. Let the random variable X count the number of minutes he/she has to wait for the next bus. Assume X has a uniform distribution over the interval (0, 5). Find the probability that he/she has to wait at least 3 minutes for the bus.

Sol:

As X follows uniform distribution over the interval (0, 5), probability density function of X is

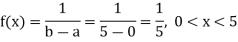
Thus, the desired probability

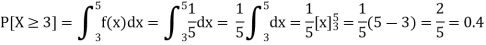
The probability that he/she has to wait at least 3 minutes for the bus is 0.4.

Gamma density

Consider the distribution of the sum of 2autonomous Exponential(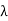) R.V.

Density of the form:

Density is known Gamma (2,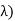 density. In common the gamma density is precise with 2 reasons (t,  as being non zero on the +ve reals and called:

Where F (t) is the endless which symbols integral of the density quantity to one:
 

By integration by parts we presented the significant recurrence relative:

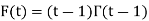
Because 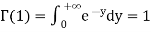, we have for integer t=m

The specific case of the integer t can be linked to the sum of n independent exponential, it is the waiting time to the nth event, it is the matching of the negative binomial.

From that we can estimate what the estimated value and the variance are going to be: If all the Xi's are independent exponential (, then if we sum n of them we

Have  and if they are independent: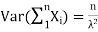 

This simplifies to the non-integer t case:

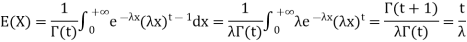
Example1: Following probability distribution

X	0	1	2	3	4	5	6	7
P(x)	0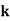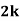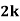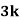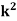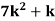

Find: (i) k   (ii)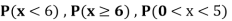

(i)                Distribution function

(ii)             If 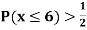  find minimum value of C

(iii)          Find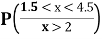

Solution:

If P(x) is p.m.f –

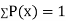
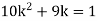
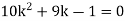
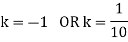
(i)

X	0	1	2	3	4	5	6	7
P(x)	0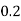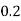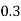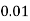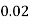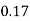

(ii)

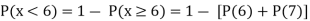
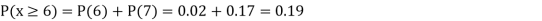
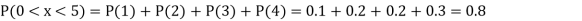
(iii)

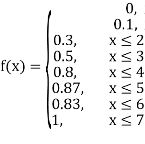
(iv)

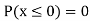
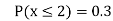
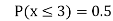
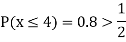
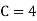
(v)

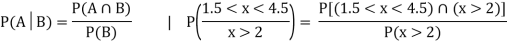
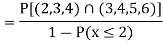
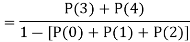
Example 2. I choose real number uniformly at random in the interval [a, b], and call it X. Buy uniformly at random, we mean all intervals in [a, b] that have the same length must have the same probability. Find the CDF of X.

Solution.

Since 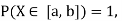we conclude

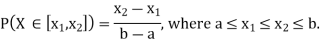
Now, let us find the CDF. By definition thus immediately have

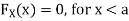
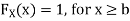
For

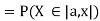
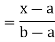
Thus, to summarize

Note that hear it does not matter if we use “<” or “≤” as each individual point has probability zero, so for example Figure 4.1 shows the CDF of X. As we expect the CDF starts at 0 at end at 1.

Example 3.

Find the mean value μ and the median m of the exponential distribution

Solution. The mean value μ is determined by the integral

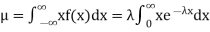
Integrating by parts we have

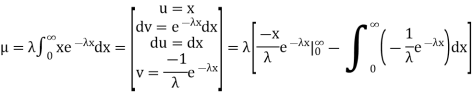
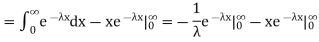
We evaluate the second term with the help of 1 Hospital's Rule:

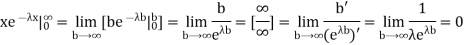
Hence the mean (average) value of the exponential distribution is

Determine the median m

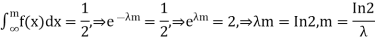
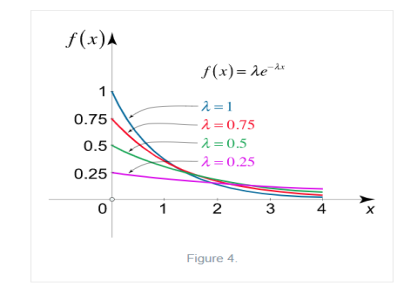
Exponential Distribution:

The exponential distribution is a C.D. Which is usually used to define to come time till some precise event happens. Like, the amount of time until a storm or other unsafe weather event occurs follows an exponential distribution law.

The one-parameter exponential distribution of the probability density function PDF is defined:

f(x)=λ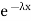,x≥0

Where, the rate λ signifies the

Normal amount of events in single time.

The mean value is μ = 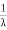. The median of the exponential distribution is m = 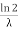, and the variance is shown by .

Note-

If 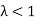, then mean < Variance

If 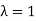, then mean = Variance

If 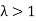, then mean > Variance

The memoryless Property of Exponential Distribution

It can be stated as below

If X has an exponential distribution, then for every constant a 0, one has P[X 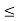x + a | X a] = P[X 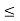x] for all x i.e. the conditional probability of waiting up to the time 'x + a ' given that it exceeds ‘a’ is same as the probability of waiting up to the time ‘ x ’.

Chi-square distribution:

When a fair coin is tossed 80 times we expect from the theoretical considerations that heads will appear 40 times and tail 40 times. But this never happens in practice that is the results obtained in an experiment do not agree exactly with the theoretical results. The magnitude of discrepancy between observations and theory is given by the quantity 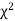(pronounced as chi squares). If 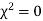the observed and theoretical frequencies completely agree. As the value of 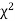increases, the discrepancy between the observed and theoretical frequencies increases.

(1)  Definition. If and 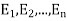be the corresponding set of expected (theoretical) frequencies, then is defined by the relation

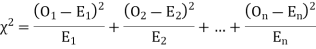
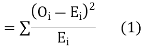
(2)  Chi – square distribution

If 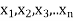be n independent normal variates with mean zero and s.d. Unity, then it can be shown that is a random variate having 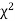distribution with ndf.

The equation of the 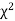curve is

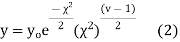
(3)  Properties of 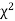distribution

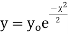1. If v = 1, the curve (2) reduces to which is the exponential distribution.
2. If this curve is tangential to x – axis at the origin and is positively skewed as the mean is at v and mode at v-2.
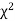3. The probability P that the value of from a random sample will exceed 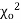is given by

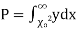
have been tabulated for various values of P and for values of v from 1 to 30. (Table V Appendix 2)

,the curve approximates to the normal curve and we should refer to normal distribution tables for significant values of .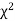

IV.             Since the equation of curve does not involve any parameters of the population, this distribution does not dependent on the form of the population.

V.                Mean = and variance =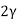

Goodness of fit

The values of 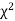is used to test whether the deviations of the observed frequencies from the expected frequencies are significant or not. It is also used to test how will a set of observations fit given distribution therefore provides a test of goodness of fit and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between the theory and fact.

This is a nonparametric distribution free test since in this we make no assumptions about the distribution of the parent population.

Procedure to test significance and goodness of fit

(i)                Set up a null hypothesis and calculate

(ii)              Find the df and read the corresponding values of at a prescribed significance level from table V.

(iii)           From table, we can also find the probability P corresponding to the calculated values of for the given d.f.

(iv)            If P<0.05, the observed value of is significant at 5% level of significance

If P<0.01 the value is significant at 1% level.

If P>0.05, it is a good faith and the value is not significant.

Example. A set of five similar coins is tossed 320 times and the result is

Solution. For v = 5, we have

P, probability of getting a head=1/2;q, probability of getting a tail=1/2.

Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion

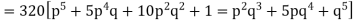
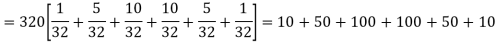
Thus the theoretical frequencies are 10, 50, 100, 100, 50, 10.

Hence,

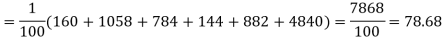
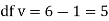
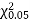Since the calculated value of is much greater than the hypothesis that the data follow the binomial law is rejected.

Example. Fit a Poisson distribution to the following data and test for its goodness of fit at level of significance 0.05.

Solution. Mean m =

Hence, the theoretical frequency are

Hence,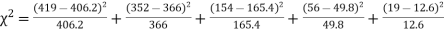

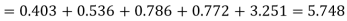
Since the mean of the theoretical distribution has been estimated from the given data and the totals have been made to agree, there are two constraints so that the number of degrees of freedom v = 5- 2=3

For v = 3, we have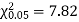

Since the calculated value of 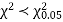the agreement between the fact and theory is good and hence the Poisson distribution can be fitted to the data.

Key takeaways:

Continuous uniform distribution

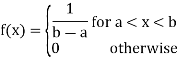
Mean and Variance of the continuous uniform Distribution

Exponential Distribution:

f(x)=λ,x≥0

3.8 Normal, normal approximation to binomial

Normal Distribution

Normal distribution is a continuous distribution. It is derived as the limiting form of the Binomial distribution for large values of n and p and q are not very small.

The normal distribution is given by the equation

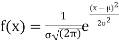    (1)

Where 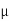= mean, 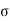= standard deviation, 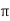=3.14159…e=2.71828…

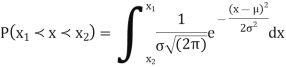
On substitution in (1) we get 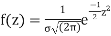     (2)

Here mean = 0, standard deviation = 1

(2) is known as standard form of normal distribution.

MEAN FOR NORMAL DISTRIBUTION

Mean 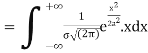        [Putting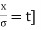

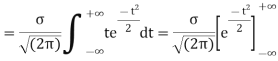
STANDARD DEVIATION FOR NORMAL DISTRIBUTION

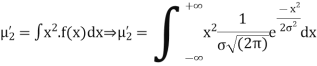
Put,

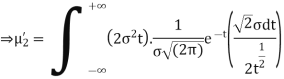
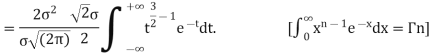
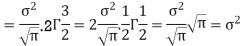
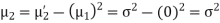
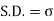
MEDIAN OF THE NORMAL DISTRIBUTION

If a is the median then it divides the total area into two equal halves so that

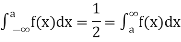
Where,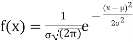

Suppose mea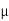n, then

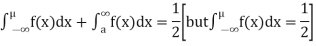
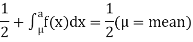
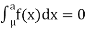
Thus,

Similarly, when 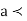mean, we have a =

Thus, median = mean =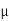

MEA DEVIATION ABOUT THE MEAN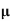

Mean deviation

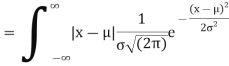
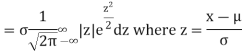
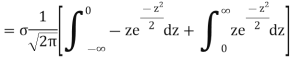
MODE OF THE NORMAL DISTRIBUTION

We know that mode is the value of the variate x for which f (x) is maximum. Thus by differential calculus f (x) is maximum if and

Where,

Thus mode is 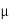and model ordinate =

NORMAL CURVE

Let us show binomial distribution graphically. The probabilities of heads in 1 tosses are

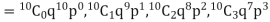
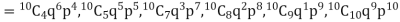
. It is shown in the given figure.

If the variates (head here) are treated as if they were continuous, the required probability curve will be a normal curve as shown in the above figure by dotted lines.

Properties of the normal curve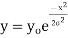

1. The curve is symmetrical about the y- axis. The mean, median and mode coincide at the origin.
2. The curve is drawn, if mean (origin of x) and standard deviation are given. The value of 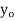can be calculated from the fact that the area of the curve must be equal to the total number of observations.
3. y decreases rapidly as x increases numerically. The curve extends to infinity on either side of the origin.
4. (a)

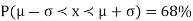
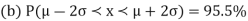
AREA UNDER THE NORMAL CURVE

By taking 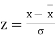the standard normal curve is formed.

The total area under this curve is 1. The area under the curve is divided into two equal parts by z = 0. Left hand side area and right hand side area to z = 0 is 0.5. The area between the ordinate z = 0.

Example. On a final examination in mathematics, the mean was 72, and the standard deviation was 15. Determine the standard scores of students receiving graders.

(a)  60

(b)  93

(c)  72

Solution. (a)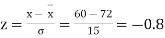

(b)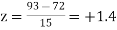

(c)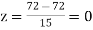

Example. Find the area under the normal curve in each of the cases

(a)  Z = 0 and z = 1.2

(b)  Z = -0.68 and z = 0

(c)  Z = -0.46 and z = -2.21

(d)  Z = 0.81 and z = 1.94

(e)  To the left of z = -0.6

(f)    Right of z = -1.28

Solution. (a) Area between Z = 0 and z = 1.2 =0.3849

(b)Area between z = 0 and z = -0.68 = 0.2518

(c)Required area = (Area between z = 0 and z = 2.21) + (Area between z = 0 and z =-0.46)\

= (Area between z = 0 and z = 2.21)+ (Area between z = 0 and z = 0.46)

=0.4865 + 0.1772 = 0.6637

(d)Required area = (Area between z = 0 and z = 1.+-(Area between z = 0 and z = 0.81)

= 0.4738-0.2910=0.1828

(e) Required area = 0.5-(Area between z = 0 and z = 0.6)

= 0.5-0.2257=0.2743

(f)Required area = (Area between z = 0 and z = -1.28)+0.5

= 0.3997+0.5

= 0.8997

Example. The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise the washers are considered defective. Determine the percentage of defective washers produced by the machine assuming the diameters are normally distributed.

Solution.

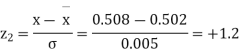
Area for non – defective washers = Area between z = -1.2

And z = +1.2

=2 Area between z = 0 and z = 1.2

=2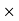 (0.3849)-0.7698=76.98%

Percentage of defective washers = 100-76.98=23.02%

Example. A manufacturer knows from experience that the resistance of resistors he produces is normal with mean 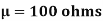and standard deviation 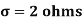. What percentage of resistors will have resistance between 98 ohms and 102 ohms?

Solution. ,

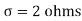
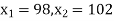
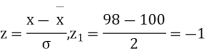
Area between

= (Area between z = 0 and z = +1)

= 2 (Area between z = 0 and z = +1)=2 0.3413 = 0.6826

Percentage of resistors having resistance between 98 ohms and 102 ohms = 68.26

Example. In a normal distribution, 31% of the items are 45 and 8% are over 64. Find the mean and standard deviation of the distribution.

Solution. Let 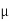be the mean and the S.D.

If x = 45,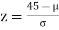

If x = 64,

Area between 0 and

[From the table, for the area 0.19, z = 0.496)

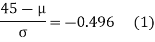
Area between z = 0 and z =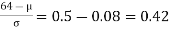

(from the table for area 0.42, z = 1.405)

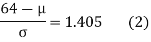
Solving (1) and (2) we get

Normal approximation to binomial

Let N be the binomial distribution. If p = q then p = q = ½ (since p + q = 1) and consequently the binomial distribution is symmetrical. Let n be an even integer say 2k, k being an integer. Since n 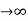∞, the frequencies of r and r + 1 successes can be written in following forms:

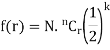
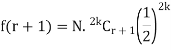
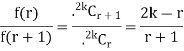
The frequency of r successes will be greater than the frequency of (r + 1) successes if

f (r) > f (r + 1)

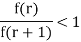
2k – r < r + 1

r > k – ½   .... (1)

In a similar way, the frequency of r successes will be greater than the frequencies of

(r – 1) successes if r < k + ½  ..    (2)

In view of (1) and (2), we observe that if k - 1/2 < r < k + 1/2 the frequency corresponding to r successes will be the greatest. Clearly, r = k is the value of the success corresponding to which the frequency is maximum. Suppose it is y0. Then, we have

Let yx be the frequency of k + x successes then, we have

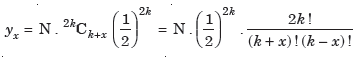
Now

Take log on both sides

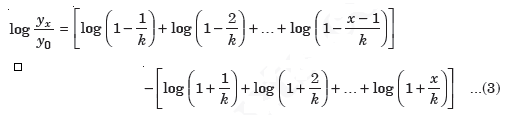
Now, writing expression for each term and neglecting higher powers of x/k (very small quantity), we get from (3),

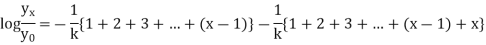
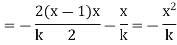
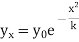
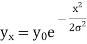
Which is normal distribution.

Key takeaways-

Probability of the happening of an event r times =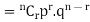

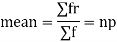
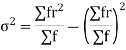
1. RECURRENCE RELATION FOR THE BINOMIAL DISTRIBUTION

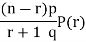
2.     Poisson distribution is

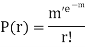
Where m is the mean of the distribution.

3.    

4.     MOMENT GENERATING FUNCTION OF POISSON DISTRIBUTION

5.     RECURRENCE FORMULA FOR POISSON DISTRIBUTION

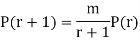
6.     Normal Distribution

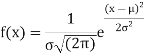
7.      median = mean =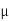

3.9 Bivariate normal

A bivariate distribution, set only, is the probability that a definite event will happen when there are 2 independent random variables in your scenario. E.g, having two bowls, individually complete with 2dissimilarkinds of candies, and drawing one candy from each bowl gives you 2 independent random variables, the 2dissimilar candies. Since you are pulling one candy from each bowl at the same time, you have a bivariate distribution when calculating your probability of finish up with specific types of candies.

Properties:

Properties 1. Two random variables X and Y are said to be bivariate normal, or jointly normal distribution for all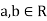

Properties 2:

Two random variables X and Y are set to have the standard bivariate normal distribution with correlation efficient if their joint PDF is given by

Where 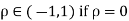then we just say X and Y have the standard by will it normal distribution.

Properties 3:

Two random variables X and Y are set to have a bivariate normal distribution with parameters 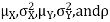if their joint PDF is given by

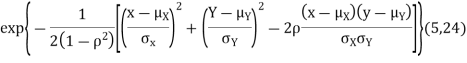
Where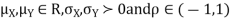 are all constants.

Properties 4:

Suppose X and Y are jointly normal random variables with parameters 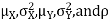. Then given X = x, Y is normally distributed with

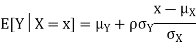
Example.

Let 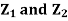be two independent N (0, 1) random variables. Define

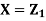
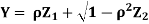
Where 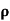is a real number in (-1, 1).

1. Show that X and Y are bivariate normal.
2. Find the joint PDF of X and Y.
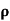3. Find (X,Y)

Solution.

First note that since 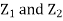are normal and independent they are jointly normal with the joint PDF

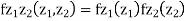
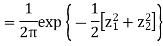
1. We need to show aX + bY is normal for all. We have

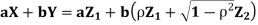
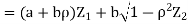
Which is the linear combination of and thus it is normal.

b.     We can use the method of transformations (theorem 5.1) to find the joint PDF of X and Y. The inverse transformation is given by

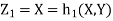
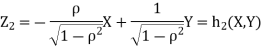
We have

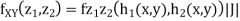
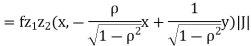
Where,

Thus we conclude that

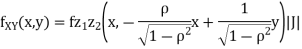
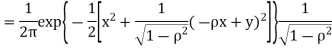
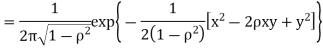
c.      To find 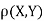FIRST NOTE

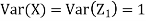
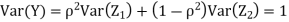
Therefore,

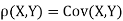
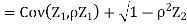
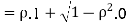
Example: Let X and Y be jointly normal random variable with parameters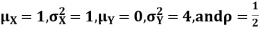

1. Find P (2X+ Y≤3)
2. Find
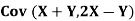
3. Find

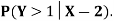
Solution.

1. Since X and Y are jointly normal the random variables V =2 X +Y is normal. We have

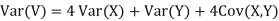
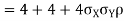
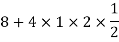
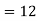
Thus V ~ N (2, 12). Therefore,

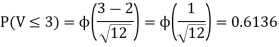
b.     Note that Cov (X,Y)= 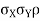(X,Y) =1. We have

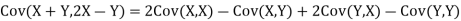
c.      Using properties we conclude that given X =2, Y is normally distributed with

3.10 Functions of random variables

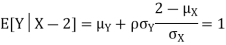
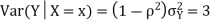
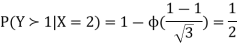
Random variables

It is a real valued function which assigns a real number to each sample point in the sample space.

A random variable X is a function defined on the sample space 5 of an experiment S of an experiment. Its value are real numbers. For every number a the probability

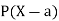
With which X assumes a is defined. Similarly for any interval l the probability

With which X assumes any value in I is defined.

Example:

Tossing a fair coin thrice then-

Sample Space(S) = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

Roll a dice

Sample Space(S) = {1,2,3,4,5,6}

A random variable is a real-valued function whose domain is a set of possible outcomes of a random experiment and range is a sub-set of the set of real numbers and has the following properties:

i) Each particular value of the random variable can be assigned some probability

Ii) Uniting all the probabilities associated with all the different values of the random variable gives the value 1.

A random variable is denoted by X, Y, Z etc.

For example if a random experiment E consists of tossing a pair of dice, the sum X of the two numbers which turn up have the value 2,3,4,…12 depending on chance. Then X is a random variable 

Discrete random variable-

A random variable is said to be discrete if it has either a finite or a countable number of values. Countable number of values means the values which can be arranged in a sequence.

Note- if a random variable takes a finite set of values it is called discrete and if if a random variable takes an infinite number of uncountable values it is called continuous variable.

Discrete probability distributions-

Let X be a discrete variate which is the outcome of some experiments. If the probability that X takes the values of x is , then-

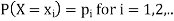
Where-

1.

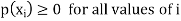
2.

The set of values 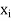with their probabilities makes a discrete probability distribution of the discrete random variable X.

Probability distribution of a random variable X can be exhibited as follows-

X		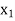	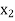and so on
P(x)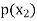

Example: Find the probability distribution of the number of heads when three coins are tossed simultaneously.

Sol.

Let be the number of heads in the toss of three coints

The sample space will be-

{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

Here variable X can take the values 0, 1, 2, 3 with the following probabilities-

P[X= 0] = P[TTT] = 1/8

P[X = 1] = P [HTT, THH, TTH] = 3/8

P[X = 2] = P[HHT, HTH, THH] = 3/8

P[X = 3] = P[HHH] = 1/8

Hence the probability distribution of X will be-

X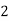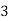
P(x)

Example: For the following probability distribution of a discrete random variable X,

Find-

1. The value of c.

2. P[1<x<4]

Sol,

1. We know that-

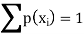
So that-

0 + c + c + 2c + 3c + c = 1

8c = 1

Then c = 1/8

Now, 2. P[1<x<4] = P[X = 2] + P[X = 3] = c + 2c = 3c = 3× 1/8 = 3/8

Probability density function

Probability density function (PDF) is a arithmetical appearance which gives a probability distribution for a discrete random variable as opposite to a continuous random variable. The difference among a discrete random variable is that we check an exact value of the variable. Like, the value for the variable, a stock worth, only goes two decimal points outside the decimal (Example 32.22), while a continuous variable have an countless number of values (Example 32.22564879…).

When the PDF is graphically characterized, the area under the curve will show the interval in which the variable will decline. The total area in this interval of the graph equals the probability of a discrete random variable happening. More exactly, since the absolute prospect of a continuous random variable taking on any exact value is zero owing to the endless set of possible values existing, the value of a PDF can be used to determine the likelihood of a random variable dropping within a exact range of values.

Example: The probability density function of a variable X is

(i)                Find

(ii)             What will be e minimum value of k so that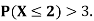

Solution

(i) If X is a random variable then

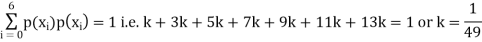
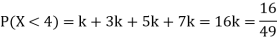
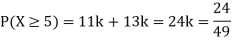
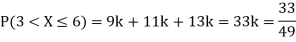
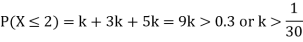
(iii)           Thus minimum value of k=1/30.

Example: A random variate X has the following probability function

x	0	1	2	3	4	5	6	7
P (x)	0	k	2k	2k	3k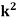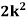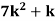

(i)                Find the value of the k.

(ii)            

Solution. (i) If X is a random variable then

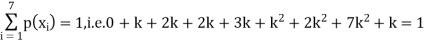
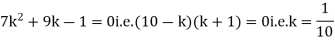
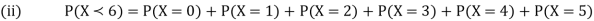
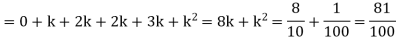
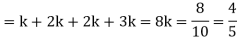
Continuous probability distribution

When a variate X takes every value in an interval it gives rise to continuous distribution of X. The distribution defined by the vidiots like heights or weights are continuous distributions.

a major conceptual difference however exist between discrete and continuous probabilities. When thinking in discrete terms the probability associated with an event is meaningful. With continuous events however where the number of events is infinitely large, the probability that a specific event will occur is practically zero. For this reason continuous probability statements on must be worth did some work differently from discrete ones. Instead of finding the probability that x equals some value, we find the probability of x falling in a small interval.

Thus the probability distribution of a continuous variate x is defined by a function f (x) such that the probability of the variate x falling in the small interval 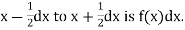Symbolically it can be expressed as 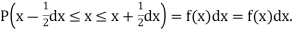Thus f (x) is called the probability density function and then continuous curve y = f(x) is called the probability of curve.

The range of the variable may be finite or infinite. But even when the range is finite, it is convenient to consider it as infinite by opposing the density function to be zero outside the given range. Thus if f (x) =(x) be the density function denoted for the variate x in the interval (a,b), then it can be written as

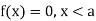
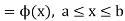
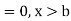
The density function f (x) is always positive and 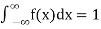(i.e. the total area under the probability curve and the the x-axis is is unity which corresponds to the requirements that the total probability of happening of an event is unity).

(2) Distribution function

If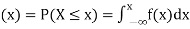

Then F(x) is defined as the commutative distribution function or simply the distribution function the continuous variate X. It is the probability that the value of the variate X will be ≤x. The graph of F(x) in this case is as shown in figure 26.3 (b).

The distribution function F (x) has the following properties

(i)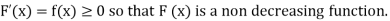               

(ii)             

(iii)          

(iv)            P(a ≤x ≤b)= 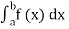= =F (b) – F (a).

Example.

(i)                Is the function defined as follows a density function.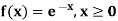

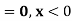
(ii)             If so determine the probability that the variate having this density will fall in the interval (1.2).

(iii)          Also find the cumulative probability function F (2)?

Solution. (i) f (x) is clearly ≥0 for every x in (1,2) and

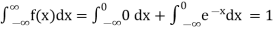
Hence the function f (x) satisfies the requirements for a density function.

(ii)Required probability =

This probability is equal to the shaded area in figure 26.3 (a).

(iii)Cumulative probability function F(2)

Example: Show that the following function can be defined as a density function and then find .

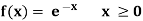
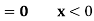
Sol.

Here

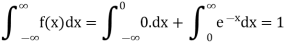
So that, the function can be defined as a density function.

Now.

Example: Let X be a continuous random variable with PDF given by

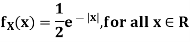
If , find the CDF of Y.

Solution. First we note that , we have

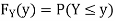
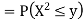
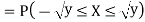
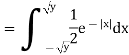
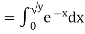
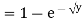
Thus,
 

Example: Let X be a continuous random variable with PDF

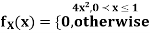
Find .

Solution. We have

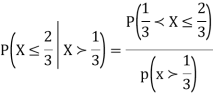
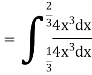
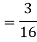
Key takeaways-

1. A random variable is said to be discrete if it has either a finite or a countable number of values. Countable number of values means the values which can be arranged in a sequence.

2.

Where-

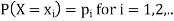
3.11 Distribution function technique, transformation technique-one variable, several variables, moment generating function technique

In addition to considering the probability distributions of random variables simultaneously using joint distribution functions, there is also occasion to consider the probability distribution of functions applied to random variables as the following example demonstrates.

One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a continuous random variable:

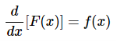
Derivative of cdf = pdf

Let X be uniform on [0,1].  We find the pdf of Y=X^2

Recall that the pdf for a uniform[0,1]random variable is fX(x)=1, for 0≤x≤10≤x≤1, and that the cdf is

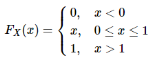
Note that the possible values of Y are 0≤y≤1

First, we find the cdf of Y, for 0≤y≤1

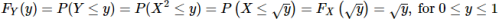
Now we differentiate the cdf to get the pdf of YY:

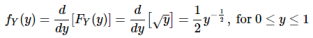
Change-of-Variable Technique

Suppose that X is a continuous random variable with pdf fX(x), which is nonzero on interval II.

Further suppose that gg is a differentiable function that is strictly monotonic on II.

Then the pdf of Y=g(X)is given by

Example: Recall that the random variable X denotes the amount of gas stocked. We now let Y denote the total cost of delivery for the gas stocked, i.e., Y=30000X+2000Y. We know that the pdf of X is given by

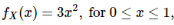
So that I=[0,1], using the notation of the Change-of-Variable technique. We also have that y=g(x)=30000x+2000y, and note that g is increasing on the interval I. Thus, the Change-of-Variable technique can be applied, and so we find the inverse of g and its derivative:

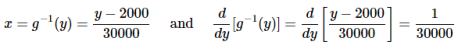
So, applying Change-of-Variable formula given

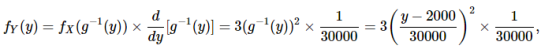
Informally, the Change-of-Variable technique can be restated as follows.

1. Find the cdf of Y=g(X) in terms of the cdf for X using the inverse of g, i.e., isolate X.
2. Take the derivative of the cdf of Y to get the pdf of Y using the chain rule.  An absolute value is needed if g is decreasing.

The advantage of the Change-of-Variable technique is that we do not have to find the cdf of X in order to find the pdf of Y, as the next example demonstrates.

Let the random variable X have pdf given by fX(x)=5x^4for 0≤x≤1, i.e., I=[0,1]. Also, let g(x)=1−x2. To find the pdf for Y= g(X) =1−X2, we first find g−1

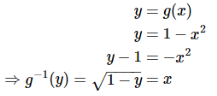
Now we can find the derivative of g−1

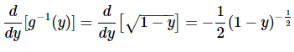
Applying the change of variable formula, we get

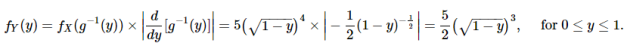
Moment generating function technique

There is another approach to finding the probability distribution of functions of random variables, which involves moment-generating functions.  Recall the following properties of mgf's.

Theorem: The mgf MX(t) of random variable X uniquely determines the probability distribution of X.  In other words, if random variables X and Y have the same mgf, MX(t)=MY(t), then X and Y have the same probability distribution.

Let X be a random variable with mgf MX(t), and let a,b be constants.  If random variable Y=aX+b, then the mgf of Y is given by

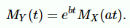
Example: suppose that X∼N(μ,σ).  It can be shown that the mgf of XX is given by

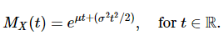
Using this mgf formula, we can show that Z=X−μσZ=X−μσ has the standard normal distribution

1. Note that if Z∼N(0,1)Z∼N(0,1), then the mgf is 
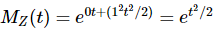
2. Also note that , so by

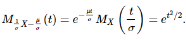
Thus, we have shown that Z and X−μ/σ have the same mgf, which by Theorem says that they have the same distribution.

Now suppose X1,…,Xn  are each independent normally distributed with means μ1,…,μn and sd's σ1,…,σn, respectively.

Let's find the probability distribution of the sum Y=a1X1+⋯+anXn (a1,…,an constants) using the mgf technique:

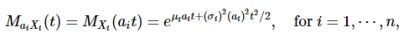
Thus by theorem, Y∼N(μy,σy)

References:

1. E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.

2. P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.

3. S. Ross, “A First Course in Probability”, Pearson Education India, 2002.

4. W. Feller, “An Introduction to Probability Theory and its Applications”, Vol. 1, Wiley, 1968.

5. N.P. Bali and M. Goyal, “A text book of Engineering Mathematics”, Laxmi Publications, 2010.

6. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.

7. T. Veerarajan, “Engineering Mathematics”, Tata McGraw-Hill, New Delhi, 2010.

8. BV ramana mathematics.