Unit - 3
Morera’s theorem
We use standard texts like Spiegel (1964) or Levinson and Redheffer in this case (1970).
If for each closed contour C within a complicated area R and
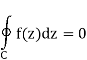
Then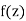 
is analytic everywhere in 𝑅.
Proof:
Assume that the hypothesis is false, and that there is a contour in some part of R such that
Where 𝐴 is nonzero.
We assume that the real and imaginary parts of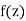 
are continuously differentiable in 𝑅, (otherwise df(z)/dz would not exist at some points in 𝑅 and 
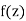would not be analytic by the definition of analyticity.)
Rewriting the integral by substituting real and imaginary parts
f(z) = u(x,y) +iv(x,y) and dz =dx + idy we obtain
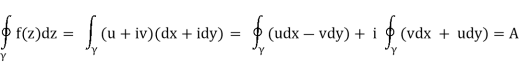
Because the partial derivatives of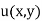 
and 
exist, we may invoke the 2D version of Green's theorem for the real and imaginary parts
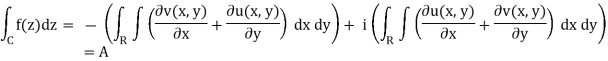
Because A = a + ib ≠ 0 at least one of the Cauchy-Riemann equations is not satisfied, and the theorem is proven. However, this proof is less satisfactory, because we had to assume that the real and imaginary parts of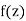 
were differentiable.
The fact that if fj is a sequence of holomorphic functions on a planar domain and the sequence converges uniformly on compact subsets of is a standard and well-known fact from complex function theory. Certainly, this conclusion is one of the explanations for the compact-open topology being applied to the space of holomorphic functions on (see also [LUR], where this point of view is developed in detail from the perspective of functional analysis).
The following result of William Fogg Osgood [ OSG] is even less widely known:
1st Theorem: Let fj be a holomorphic function sequence on a planar domain. Assume that the fj pointwise converge to the limit function f on. Then on a dense, open subset of, f is holomorphic. On compact subsets of the dense, open set, convergence is uniform.
This finding isn't immediately apparent; yet, it is undoubtedly surprising and intriguing. For the sake of completeness, here is a proof of the theorem:
Proof of the Theorem: Let U be a nonempty open subset of Ω with compact closure in Ω. Define, for k = 1,2,...
Sk =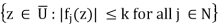 
Since the fj converge at each z ∈ U, certainly the set {fj(z): j ∈ N} is bounded for each fixed z. So each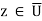 
lies in some Sk. In other words,
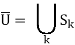
Because U is a full metric space (in the Euclidean sense), the Baire category theorem states that some Sk must be “somewhere dense” in U. Sk will therefore have a nontrivial Euclidean metric ball (or disc) in U. B is the name of the ball. It's now just a matter of using Montel's theorem to B to discover a subsequence fjk that converges uniformly to a limit function g on compact sets. But, of course, g and f must be the same, and g (and so f) must be holomorphic on B.
Because the choice of U in the preceding arguments was arbitrary, the theorem's conclusion follows.
Remark: An alternative approach, which avoids the explicit use of Montel’s theorem, is as follows. Once one has identified an Skwhose closure contains a ball or disc D(P,r), let γ be a simple closed curve in D(P,r). Then of course the image γ of γ is a compact set. Let > 0. By Lusin’s theorem, the sequence fj converges uniformly on some subset E ⊆γe with the property that the linear measure of γ \ E is less than. Let K be a compact subset of the open region surrounded by γ, and let δ> 0 be the Euclidean distance of K to γ. Let ∗> 0 and choose J > 0 so large that when j,k> J then
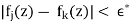
For all z ∈ E. Then, for w ∈ K,
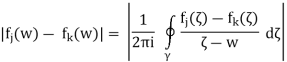
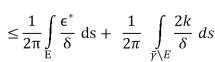
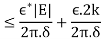
Thus we see that we have uniform convergence on K. And the holomorphicity follows as usual.
More Results on Planar Domains
Harmonic functions are the subject of our first new result for planar domains:
Theorem number two Let fj denote a succession of harmonic functions on a plane. Assume that the fj pointwise converge to the limit function f on.
Then on a dense open subset of, f is harmonic.
A sketch of the theorem's proof is as follows: Proceed as in the holomorphic functions verification of the result. It is unmistakably true that a subsequence of harmonic functions on a planar domain that is uniformly bounded on compact sets will converge uniformly on compact sets. This is based on simple Poisson kernel estimates. The rest of the argument is identical to the previous one.
3rd Theorem On a planar domain, let L be a uniformly elliptic operator of order 2. Let fj represent a set of functions that L on annihilates. Assume that the fj pointwise converge to the limit function f on. Then, on a dense open subset of, L annihilates f.
The proof is identical to the previous finding. The only thing to look for is a subsequence that converges uniformly on compact sets given a collection of functions annihilated by L that is bounded on compact sets. This follows from the Poisson formula for L, just as it did in the harmonic case. The remainder of the argument is identical.
4th Theorem Let fj be a holomorphic function sequence on a planar domain. Assume that for all j and all z, there is a constant M > 0 such that |fj(z)| M. Assume that the fj pointwise converge to the limit function f on. Then all of is holomorphic to f.
Remark: Of course, the new feature of Stieltjes [STElast]'s theorem is that we assume the family fj is uniformly limited. This Tauberian hypothesis leads to a more conclusive result. This time, the proof will be a little different.
Assume that U is an open subset of. Then the argument from Theorem 1's proof applies to U right away. As a result, the limit function on U is holomorphic. We're done because the choice of U was arbitrary.
In reality, a much weaker condition (than in the previous theorem) yields the same result:
Theorem No. 5 Let fj be a holomorphic function sequence on a planar domain. Assume that for all j and all z, there is a nonnegative, integrable function g on such that |fj(z)| g(z). Assume that the fj pointwise converge to the limit function f on. Then, on a set of measure zero, f can be rectified so that it is holomorphic on all of.
The proof is simplicity itself. Let ϕ be a Cc∞ function on Ω. Then
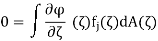
For each j. Here dA is Lebesgue area measure on C. Now the Lebesgue dominated convergence theorem allows us to let j → ∞ and infer that
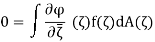
As a result, f is a holomorphic function with a weak holomorphic property. But, according to Weyl's lemma, f can be corrected on a set of measure zero, making it holomorphic in the classical sense.
The 6th Theorem Let fj be a pointwise convergent sequence of univalent holomorphic functions on a domain. The limit function is therefore holomorphic over all.
To prove that, one must first notice that each fj's picture is missing an arc (this is a standard fact about univalent functions that follows simply from the topology of the Riemann sphere and the open mapping principle). Then each fj is postcomposed with an automorphism j of the Riemann sphere, resulting in two complex values p and q being ignored by all the fj. [These automorphisms will, by necessity, converge to the identity.] The family j fj is then normal, according to Montel's classic theorem (see [MON]). We can observe that the original family fj is normal after unravelling the rationale.
The outcome is obvious right away.
Results in Several Complex Variables
In Cn, the first result is as follows.
Theorem No. 7 Let fj denote a set of holomorphic functions on the domain Cn. Assume that the fj pointwise converge to the limit function f on. Then on a dense open subset of, f is holomorphic. On compact subsets of the dense open set, the convergence is also uniform.
The reasoning for Theorem 2 is the same as for Theorem 1. We merely need to remember that Montel's theorem still holds true. The remainder of the argument is identical.
Remark: We might use the Henkin-Ramirez integral formula on small balls (see [KRA, Ch. 8]) to give an alternate proof of this result, much as we did in the Remark following the demonstration of Theorem 1.
Theorem no. 8 Let fj denote a set of holomorphic functions on the domain Cn. Assume that the fj pointwise converge to the limit function f on. In Cn, let be any complex line. Then on a dense open subset of, the limit function f is holomorphic.
Proof: Of course, we just use the logic from Theorem 1's proof to.
Note that this is a more powerful result than Theorem 6. Something similar may be demonstrated if "complex line" was replaced by "complex analytic variety." It's unclear what the best outcome would be.
Concluding Remarks
There's little doubt that there's more to learn about the multiple complicated variable setting. We'd need a result that has a good likelihood of being sharp, so that the exceptional convergence set can be identified (as in [SIC] for one complex variable). Future publications will go deeper into this topic.
Integration of holomorphic functions
We can try to integrate holomorphic functions because they are continuous functions. The complex plane provides us more flexibility in defining such integrals than the real line: integrating g: RR from a real number a to a larger real number b is clear, but integrating g: RR from a holomorphic function to a bigger real number b is not. f : C→C To understand the integral, we must provide a path from a complex number a C to a complex number b C. In other words, we can write Z b.
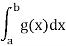
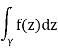
Then one can inquire as to how this is affected by the path taken from point a to point b. The most essential property of holomorphic functions for physics and engineering is revealed here:
(3) If 0 can be deformed into 1 using a set of t pathways with the same endpoints and constant dependence on t, then
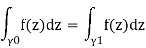
This results in a highly powerful way for computing integrals, because you can choose to make your life as simple as possible.
Example (Contour integration). If γ(0) = γ(1) and γ can be deformed in Ω to a constant map while keeping its endpoints fixed, then
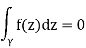
Surprising, as γ could be some large circle.
Numericals:
1) Prove that f(z) =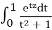 
is holomorphic.
The simplest argument might be to invoke Morera’s theorem after changing order of integration. The change of order is easily justifiable, since one is looking at a continuous function of two variables. That is, for each t ∈ [0, 1], the function z→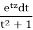 
is holomorphic, and the function of two variables is continuous. Thus, letting γ be a small triangle,
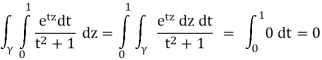
By applying Cauchy’s theorem to z→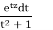 
By Morera, 
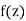is continuous.
Another approach is to view the integral as a uniform limit of a sequence of finite (Riemann) sums, each of which is holomorphic, being a finite sum of holomorphic functions, and then invoke the holomorphy of uniform (on compacts) limits of holomorphic functions.
2) Prove that f(z) =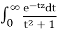 
is holomorphic for Re (z) > 0
Using the previous example, it would suffice to show that the sequence of finite integrals
fn(z) =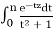 
Converges uniformly to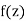 
for z in compact subsets of Re (z) > 0, since these finite integrals are holomorphic functions, via Morera.
For fixed δ> 0 and Re (z) ≥δ, for N ≤ m ≤ n,
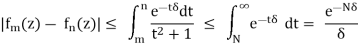
This can be made smaller than a given δ> 0 by taking N sufficiently large
Suppose that f is an analytic function which is defined in the upper half-disk {|z|2 < 1, I[z]>0}. Assume that this extends to a continuous function on the real axis that accepts real values on the real axis. The formula can then be expanded to an analytic function on the entire disc.
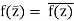
And the reflections of across the real axis are the values for reflected across the real axis. In the interior of the lower half-disk, it is simple to check that the above function is complex differentiable. What's interesting is that, despite no assumptions of differentiability, the resulting function must be analytic along the real axis as well.
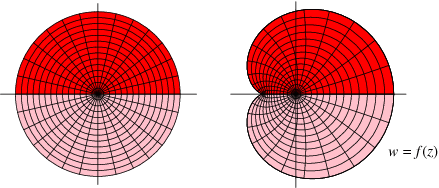
The Schwarz reflection principle, often known as Schwarz's symmetric principle, is an example of this (Needham 2000, p. 257). The reflection concept is illustrated in the diagram above for a function developed for the upper half-disk (left figure; red) and its image (right figure; red). Because the function is real on the real axis, it can be extended to the reflected domain (left and right figures; pink).
The values at the boundary must be continuous and fall on the line being reflected for the reflected function to be continuous. The notion of reflection also applies to reflecting along any line, not simply the real axis, in which case the function must take values along a line in the range. In fact, any arc that is biholomorphic to a straight line in its neighbourhood can be reflected across. The basic example is the boundary of the unit circle which is mapped to the real axis by z → (iz+1)/(z+i) .
A harmonic function that extends continuously to the zero function on its boundary can also be reflected using the reflection principle. For example, in this case negative y, defining
v(x, y) = - v(x, -y)
Extends v to a harmonic function on the reflected domain. Again note that it is necessary for v(x, 0) = 0. . This result provides a way of extending a harmonic function from a given open set to a larger open set.
Application of Schwarz’s reflection principle:
As an application of Schwarz's reflection principle, we show that a holomorphic map between two domains can expand into a holomorphic map between neighbourhoods of both domains if the domain boundaries are analytic curves.
A curve φ: [T0,T1] →C is called an analytic curve if φ is analytic function (i.e., it has power series expansion at each point). φ is called non-singular if φ′(t) =6 0, ∀t ∈ [T0,T1].
We could write φ(t) = φ1(t) + iφ2(t) where φ1 and φ2 are real-valued functions. Thenφ is analytic ⇐⇒φ1 and φ2 are analytic
φ is non-singular ⟺ (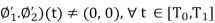 
.
Theorem 24.2 Let D1,D2 ⊂C be domains and z1 ∈ ∂ D1 and z2 ∈ ∂D2. Let f : D1 → D2 be a holomorphic map such that f is continuous up to ∂D1∩Uz1 where Uz1 is a neighborhood of z1 in C, that f(z1) = z2, and that f(∂D1 ∩Uz1) ⊂ ∂D2 ∩Uz2. Suppose that ∂D1 ∩Uz1 and
∂D2 ∩ Uz2 are non-singular analytic curves. Then there exist neighborhoods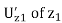
and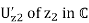 
such that f : D1 → D2 extends to a holomorphic map f : 
.
Proof: By the definition of real analytic curves, we consider the following commutative diagram
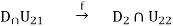
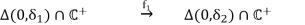
Where φ1(0) = z1,φ2(0) = z2, C+ = {z ∈ C | Im(z) > 0}. Here we may shrink Uz1 and Uz2 if necessary. By Schwarz reflection principle, f2 can extend holomorphically to
∆(0,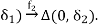 
Therefore, we have proved the desired holomorphic extension.
Key takeaways:
The one-complex-variable Schwarz Reflection Principle is a theorem describing holomorphic mappings' border behaviour. In the C°° category, stating a fair equivalent of the reflection principle is simple, and proving it is not difficult.
By definition, a point singularity of a function f is a complex numberz0 such that f is defined in a neighborhood of z0 but not at the pointz0 itself. We shall also call such points isolated singularities. Forexample, if the function f is defined only on the punctured plane byf(z) = z, then the origin is a point singularity. Of course, in that case,the function f can actually be defined at 0 by setting f(0) = 0, so thatthe resulting extension is continuous and in fact entire. (Such pointsare then called removable singularities.) More interesting is the caseof the function g(z) = 1/z defined in the punctured plane. It is clearnow that g cannot be defined as a continuous function, much less asa holomorphic function, at the point 0. In fact, g(z) grows to infinityas z approaches 0, and we shall say that the origin is a pole singularity.
Finally, the case of the function h(z) =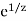 
on the punctured plane showsthat removable singularities and poles do not tell the whole story. Indeed,the function h(z) grows indefinitely as z approaches 0 on the positive realline, while h approaches 0 as z goes to 0 on the negative real axis. Finallyh oscillates rapidly, yet remains bounded, as z approaches the origin onthe imaginary axis.
Since singularities often appear because the denominator of a fractionvanishes, we begin with a local study of the zeros of a holomorphicfunction.
A complex number z0 is a zero for the holomorphic function f iff(z0) = 0. In particular, analytic continuation shows that the zeros ofa non-trivial holomorphic function are isolated. In other words, if f isholomorphic in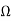 
and f(z0) = 0 for some z0 ∈
, then there exists an open neighborhood U of z0 such that f(z) _= 0 for all z ∈U − {z0}, unlessf is identically zero. We start with a local description of a holomorphic function near a zero.
Theorem: Suppose that f is holomorphic in a connected open set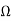 
,has a zero at a point z0 ∈
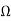, and does not vanish identically in 
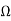. Thenthere exists a neighborhood U ⊂
of z0, a non-vanishing holomorphicfunction g on U, and a unique positive integer n such that
f(z) = (z- z0)n g(z) for all z ∈ U
Proof:
Since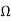 
is connected and f is not identically zero, we concludethat f is not identically zero in a neighborhood of z0. In a small disccentered at z0 the function f has a power series expansion,
f(z) = 
Since f is not identically zero near z0, there exists a smallest integer nsuch that an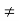 
0. Then, we can write
f(z) = (z – z0 )n [ an + an+1 (z – z0 ) + … ] = (z – z0 )n g(z)
Where g is defined by the series in brackets, and hence is holomorphic,and is nowhere vanishing for all z close to z0 (since an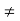 
0). To provethe uniqueness of the integer n, suppose that we can also write
f(z) = (z – z0)n g(z) = (z – z0)m h(z)
Where h(z0)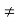 
0. If m> n, then we may divide by (z – z0)n to see thatand letting z →z0 yields g(z0) = 0, a contradiction. If m < n a similarargument gives h(z0) = 0, which is also a contradiction. We concludethat m = n, thus h = g, and the theorem is proved.
In the case of the above theorem, we say that f has a zero of order n (or multiplicity n) at z0. If a zero is of order 1, we say that it is simple. We observe that, quantitatively, the order describes the rate atwhich the function vanishes.
The importance of the previous theorem comes from the fact that we can now describe precisely the type of singularity possessed by the function 1/f at z0. For this purpose, it is now convenient to define a deleted neighborhood of z0 to be an open disc centered at z0, minus the point z0, that is, the set
{ z : 0 < | z – z0| < r}
For some r >0. Then, we say that a function f defined in a deleted neighborhood of z0 has a pole at z0, if the function 1/f, defined to be zero at z0, is holomorphic in a full neighborhood of z0.
Theorem: If f has a pole at z0 ∈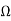
, then in a neighborhood of thatpoint there exist a non-vanishing holomorphic function h and a uniquepositive integer n such that
f(z) = (z – z0 ) –n h(z)
Proof:
By the previous theorem we have 1/f(z) = (z – z0)n g(z) ,where g is holomorphic and non-vanishing in a neighborhood of z0, sothe result follows with h(z) = 1/g(z).
The integer n is called the order (or multiplicity) of the pole, anddescribes the rate at which the function grows near z0. If the pole is oforder 1, we say that it is simple.
The next theorem should be reminiscent of power series expansion, except that now we allow terms of negative order, to account for thepresence of a pole.
Theorem: If f has a pole of order n at z0, then
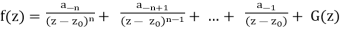…….. (1)
Where G is a holomorphic function in a neighborhood of z0.
Proof. The proof follows from the multiplicative statement in theprevious theorem. Indeed, the function h has a power series expansion
h(z) = A0 + A1 (z – z0) + …
So that
f(z) = (z – z0)-n (A0 + A1 (z – z0) + …)
= 
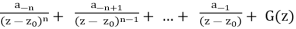
The sum
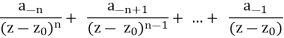
Is called the principal part of f at the pole z0, and the coefficient a−1 is the residue of f at that pole. We write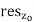 
= 
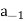. The importance ofthe residue comes from the fact that all the other terms in the principalpart, that is, those of order strictly greater than 1, have primitives in adeleted neighborhood of z0. Therefore, if P(z) denotes the principal partabove and C is any circle centered at z0, we get
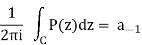
We shall return to this important point in the section on the residueformula.
As we shall see, in many cases, the evaluation of integrals reduces tothe calculation of residues. In the case when f has a simple pole at z0,it is clear that
Resz0 f =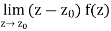 
If the pole is of higher order, a similar formula holds, one that involvesdifferentiation as well as taking a limit.
References:
1. Elias M. Stein & Rami Shakarchi, Complex Analysis, Princeton University press, Princeton and Oxford, 2003.
2. James Ward Brown and Ruel V. Churchill, Complex Variables and Applications (Eighth Edition), McGraw - Hill International Edition, 2009.
3. G. F. Simmons, Introduction to Topology and Modern Analysis, Mcgraw-Hill, Edition 2004.
4. Joseph Bak and Donald Newman, Complex analysis (2ndEdition), Undergraduate Texts in Mathematics, Springer-Verlag New York, Inc., New York, 1997.
5. COMPLEX ANALYSIS Elias M. Stein& Rami Shakarchi PRINCETON
