Unit - 4

Meromorphic Functions and the Logarithm

4.1 Meromorphic Functions and the Logarithm: The residue formula, Examples

4.1.1 Residue Theorem

Poles and zeros

We'd like to remind you of the following terms: Assume that f(z) is analytic at z0.

f(z) = an(z −z0)n + an+1(z −z0)n+1 + ...,

6 = 0 withan Then we say that f has an order n zero at z0. We call z0 a simple zero if n = 1. Assume that f has an isolated singularity at z0 and that the Laurent series exists.

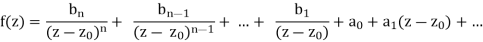
Which culminates in 0 <|z −z0| < R and with bn=6 0. Then we say that f has an order n pole at z0. We call z0 a simple pole if n = 1.

Example

f(z) =

Singularities have been isolated at z = 0,±i and a zero at z = −1. We will show that z = 0 is a pole of order 3, z = ±i are poles of order 1 and z = −1 is a zero of order 1. The style of argument is the same in each case.

At z = 0:

f(z) =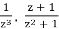

The second element is referred to as g. (z). It has a Taylor Series since g(z) is analytic at z = 0 and g(0) = 1.

g(z) =

Therefore

f(x) =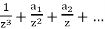

This demonstrates that z = 0 is a third-order pole.

At z = i;    f(z) = . Call the second factor g(z). Since g(z) is analytic at z = i, it has a Taylor series

g(z) = 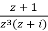= a0 + a1 (z – i) + a2 (z – i)2 + ...

Wherea0 = g(i) 6= 0. Therefore

f(z) =

This demonstrates that z = I is a first-order pole.

The arguments for z = −i and z = −1 are similar.

4.1.2 Words: Holomorphic and meromorphic

Definition. Holomorphic on A refers to a function that is analytic on a region A.

Meromorphic on A is a function that is analytic on A except for a collection of finite order poles.

Example

Let

f(z) =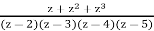

With (simple) poles at z = 2,3,4,5, this is meromorphic on C.

4.1.3 Behavior of functions near zeros and poles

The essential assumption is that a function behaves like this near a zero of order n. (z −z0)n A function acts like this near a pole of order n. 1/(z −z0)n. This is made a little more precise by the following.

Behavior near a zero. If f has an order n zero at z0, then it is near z0.

f(z) ≈ an(z −z0)n,

For some constant an.

Proof. By definition, f has a Taylor series of the form around z0.

f(z) = an (z- z0)n + an+1 (z – z0)n+1 + ...

= an (z – z0)n ( a+

The claim follows because the second factor equals 1 at z0.

Behavior near a finite pole. If f has a pole of order n at z0 then near z0,

f(z) ≈ ,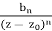

For some constant bn.

Proof. This argument is virtually identical to the one before it. By definition, f has a Laurent series of the form around z0.

f(z) =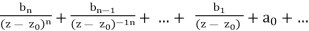

=

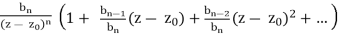
The claim follows because the second factor equals 1 at z0.

Picard’s theorem and essential singularities

Picard's theorem can be found near an essential singularity. This theorem will not be proved or used in 18.04. Nonetheless, we believe it is attractive enough to show you.

Picard’s theorem. If f(z) has an essential singularity at z0, then f(z) takes on all conceivable values infinitely many times in every neighbourhood of z0, with the possible exception of one value.

Example. It is easy to see that in any neighborhood of z = 0 the function w = e1/z takes every value except w = 0.

Quotients of functions

The following is a statement concerning function quotients. If one or both functions had a pole instead of a zero, we might make similar statements.

Theorem. Suppose f has a zero of order m at z0 and g has a zero of order n at z0. Let

h(z) = f(z)/g(z)

Then

• If n > m then h(z) has a pole of order n −m at z0. • If n < m then h(z) has a zero of order m −n at z0.
• If n = m then h(z) is analytic and nonzero at z0.

At z0, we can deduce that h(z) has a ‘pole' of order n -m. The ‘pole' is truly a zero if n -m is negative.

Proof. You should be able to provide proof of your claim. It's almost identical to the previous proofs: Take the quotient by expressing f and g as Taylor series.

Example. Let

h(z) = sin(z)/z2.

We know that sin(z) has a first-order zero at z = 0 and z2 has a second-order zero. At z = 0, h(z) has a pole of order 1. Of course, using the Taylor series, we can clearly see this.

h(z) = 

4.1.4 Residues

We'll look at how to calculate residues in this part. We've already seen enough to know that this will be beneficial. When we look at the residue theorem in the next part, we'll see this much more clearly.

Definition. Consider the function f(z) with an isolated singularity at z0, i.e. defined on the region 0 <|z −z0| < r and with Laurent series (on that region)

f(z) =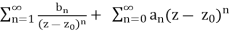

Residue of fat z0 is b1. This is denoted Res(f,z0) = b1 or Res f = b1. z=z0

What is the importance of the residue? If γis a small, simple closed curve that goes counterclockwise around b1 then

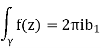
Γ small enough to be inside |z −z0| < r, surround z0 and contain no other singularity of f.

Integrating the Laurent series term by term demonstrates this. The phrase b1/z contains the only nonzero integral.

Example

f(z) =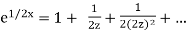

At 0 has an isolated singularity Res(f,0) = 1/2, according to the Laurent series.

Example

(i)            Let

f(z) =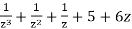

Has a pole of order 3 at z = 0 and Res(f,0) = 4.

(ii)            Suppose

f(z) = ,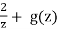

At z = 0, g is analytic. Res(f,0) = 2 if f has a simple pole at 0.

(iii)            Let f(z) = cos(z) = 1 −z2/2! + ....

At z = 0, f is analytic, and Res(f,0) = 0.

(iv)            Let

f(z) =

So, when z = 0, f has a detachable singularity and Res(f,0) = 0.

Example

Using partial fractions. Let

f(z) =

Locate f's poles and residues.

Solution:  We write partial fractions using partial fractions.

f(z) =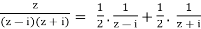

At z = I the poles are located. We calculate the residues at each pole as follows:

At z = i:

f(z) =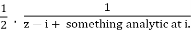

As a result, Res(f,i) = 1/2 and the pole is simple.

At z = −i:

f(z) =

As a result, Res(f,i) = 1/2 and the pole is simple. Exercising 8.8 A word of caution! Let

f(z) =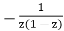

The Laurent expansions for f near z = 0 are as follows.

On 0 <|z| <1:

f(z) =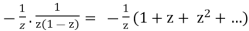

As a result, the pole at z = 0 is straightforward, and Res(f,0) = -1.

On 1 <|z| <∞:

f(z) =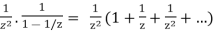

Despite the fact that this is a valid Laurent expansion, it cannot be used to compute the residue at 0. This is because the Laurent series on the area 0 |z z0| r is required by the definition of residue.

Example

Let f(z) = log(1 + z).

This has a singularity at z = −1, but it is not isolated, so not a pole and therefore there is no residue at z = −1.

Residues at simple poles

Simple poles occur frequently enough that we'll spend some time looking at how to compute their residues. There are several methods for locating a simple pole and calculating its residue. All of them have a reason that can be traced back to the Laurent series.

Assume that f(z) contains a singularity at z = z0. Then there are the properties listed below. Property 1: If f(zLaurent )'s series is of the type

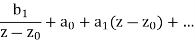
Thenfhas a simple pole at z0 and Res(f,z0) = b1.

Property 2 If g(z) = (z z0)f(z) at z0 is analytic, z0 is either a simple pole or a detachable singularity. Res(f,z0) = g in either case (z0). (In the event of a detachable singularity, the residue is zero.) Proof. For f near z0, directly from the Laurent series.

Property 3: If f at z0 has a simple pole,

Lim (z −z0)f(z) = Res(f,z0) z→z0

This proves that the limit exists and that the residue equals the limit. If the limit is present, either the pole is simple or f is analytic at z0. The limit is equal to the residue in both circumstances.

Proof. For f near z0, directly from the Laurent series.

Property 4. Res(fg,z0) = g(z0)Res(fg,z0) = g(z0)Res(fg,z0) = g(z0)Res(fg,z0) = g(z0)Res(fg,z0) = g(z0)Res(fg,z0) = g(z0) (f,z0).

If g(z0) 6 equals 0, then

Res(f/g, z0 ) = Res(f,z0).

Proof. Since z0 is a simple pole,

f(z) =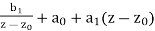

Since g is analytic,

g(z) = c0 + c1(z −z0) + ...,

When c0 equals g (z0). When these series are multiplied together, Res(fg,z0) = c0b1 = g(z0)Res (f,z0). QED

Because 1/g is analytic at z0, the statement concerning quotients f/g follows from the proof for products.

Property 5. 1/g(z) has a simple pole at z0 if g(z) has a simple zero at z0. And

Res(1/g, z0) = .

Proof. The algebra for this is very similar to what we've done previously. For g, the Taylor expansion is

g(z) = a1(z −z0) + a2(z −z0)2 + ...,

Wherea1 = g0(z0). So

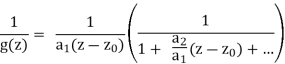
At z0, the second right-hand factor is analytic and equals 1. As a result, we know that 1/g's Laurent expansion is

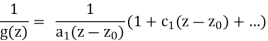
Clearly the residue is 1/a1 = 1/g0(z0). QED.

Example

Let

f(z) =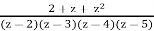

Demonstrate that all of the poles are simple, and calculate their residues.

The poles are located at z = 2,3,4,5. They're all on their own. We'll look at z = 2, although the others are comparable. When we multiply by z2, we obtain

g(z) = (z-2) f(z) =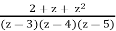

This is analytic at z = 2 and

g(2) =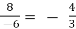

So the pole is simple and Res(f,2) = −4/3.

Example

Let

f(z) =

Locate all of the poles as well as their remnants.

Solution: The zeros of sin(z), i.e. n for an integer n, are the poles of f(z). Thezeros are straightforward since the derivative sin0(n) = cos(n) 6= 0 and by Property 5 above.

Res(f, nπ) =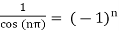

Example

Let

f(z) = .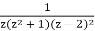

Determine which poles are simple by identifying all of the poles.

Solution: The poles are clearly at z = 0,i,2.

g(z) = zf at z = 0 (z)

At 0 and g(0) = 1/4, is analytic. As a result, the pole is straightforward, and the residual equals g(0) = 1/4.

When z equals I

g(z) = (z-i) f(z) =

The pole is simple, and the residue is g. Is analytic at I the pole is simple, and the residue is g. (i).

At z = I the following is true: This is analogous to the scenario where z = i. The pole is straightforward.

At z = 2, the following is true:

g(z) = (z-2) f(z) =

The pole is not simple because is not analytic at 2. ( It should be self-evident that this is a pole of authority.

Example

At z = z0, let p(z) and q(z) be analytic. Assume p(z0)=0, q(z0)=0, and q0(z0)=0. Find

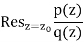
Solution: Since q0(z0) 6= 0, q has a simple zero at z0. So 1/q has a simple pole at z0 and

Res(1/q, z0) =

Since p(z0) 6= 0 we know

Res(p/q,z0) = p(z0)Res(1/q, z0) = .

Residues at finite poles

We can make statements comparable to those for simple poles for higher-order poles, but the formulas and computations are more complicated. The following is the general principle: Poles of higher order. If at z0, f(z) has a pole of order k, then

g(z) = (z −z0)kf(z)

Is analytic at z0 and if

g(z) = a0 + a1(z −z0) + ...

Then

f,z0) = ak-1

Proof. Usingthe Taylor and Laurent series for g and f, this is obvious.

Example

Let

f(z) =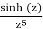

And at z = 0 find the residue

Solution: The Taylor series is well-known for

Sinh(z) = z + z3/3! + z5/5! + ...

(You can find this using sinh(z) = (ez−e−z)/2 and the Taylor series for ez.) Therefore,

f(z) =

Res(f,0) = 0 is what we see.

It's worth noting that we might have deduced this by noting that f(z) is an even function.

Example

Let

f(z) =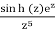

At z = 0, find the residue.

The coefficient of z4 in the Taylor expansion of sinh(z)ez is clearly equal to Res(f,0). This is calculated immediately as

Sinh(z)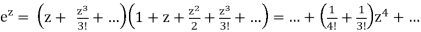

So

Res(f,0) = .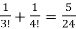

Example

Find the residue of

f(z) =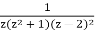

Atz= 2.

Solution:g(z) = (z-2)2 f(z) =   is analytic at z = 2. So, the residue we want is the

a1term in its Taylor series, i.e.g0(2). This is easy, if dull, to compute

Res(f,2) = g’(2) = -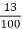

Cot(z)

In practise, the function cot(z) has shown to be extremely beneficial. This is owing to the fact that it has simple poles at all multiples of and the residue at each pole is one. That is the first thing we demonstrate.

Fact. For an integer n, f(z) = cot(z) has simple poles at n, and Res(f,n) = 1.

Proof.

f(z) =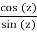

At the zeros of sin, i.e. at z = n, this has poles. f is of the form p/q at the poles, with q having a simple zero at z0 and p(z0) 6= 0. As a result, we can use the formula.

Res(f, z0) = .

In our case, we have

Res(f, nπ) = ,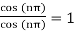

As claimed.

In the Laurent expansion of cot, we sometimes need more words (z). Although there is no simple formula for the terms, we can easily compute as many as we need using the technique below.

Example Calculate the first few terms of cot(zLaurent)'s expansion around z = 0.

Solution: We know that cot(z) has a simple pole at 0 since it has a simple pole.

Cot(z) =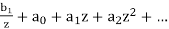

We also know

Cot(z) =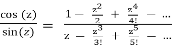

When we add the two expressions together, we obtain

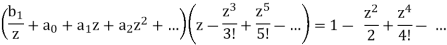
We can multiply the coefficients of like powers of z and equate them.

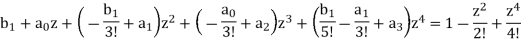
So, starting from b1 = 1 and a0 = 0, we get

−b1/3! + a1 = −1/2! ⇒ a1 = −1/3

−a0/3! + a2 = 0 ⇒ a2 = 0

b1/5! −a1/3! + a3 = 1/4! ⇒ a3 = −1/45.

As previously stated, all of the even terms are zero, as they should be. We've got

Cot(z) = ½ - z/3 – z/45 + ... 3

4.1.5 Residue at ∞

The residue at ∞ is a clever mechanism that allows us to substitute the computation of several residues with the computation of a single residue in specific cases.

Assume that f is analytic in C with the exception of a small number of singularities. Let C be a big, positively oriented curve that contains all of the singularities.

All of the fare poles are contained inside C Definition. The fat infinite residue is defined as

Res(f, ∞) = -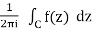

We should start by explaining the concept. As you navigate a simple closed curve, everything to the left is the inside. Because curve C is counterclockwise, its interior contains all of f's poles. The residue theorem states that the residues of these poles define the integral over C.

The interior of the curve C, on the other hand, is everything outside of C. There are no fin poles in that area. The only choice is to have a residue at and define it as we did if we want the residue theorem to hold (which we do –it's that critical).

All of the poles of fare inside C are assumed in the definition of the residual at infinity. As a result, the residue theorem entails

Res(f,∞) = −X the residues of f.

We'll need a way to compute the residue directly to make this usable. The following theorem proves this.

Theorem. If f is analytic in C except for a finite number of singularities then

Res(f,∞) = −Res .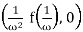

Proof. The proof is just a change of variables: w = 1/z.

Change of variable: w = 1/z

That z = 1/w and dz= −(1/w2)dw.

The map w = 1/z, on the other hand, transports the positively oriented z-circle of radius R to the negatively oriented w-circle of radius 1/R. (Observe how the circled points 1, 2, 3, 4 on C in the z-plane are transferred to points on C in the w-plane to see the orientiation.) Thus,

Res(f, ∞) = -

Finally, all the poles inside the circle C are mapped to points outside the circle C by z = 1/w. So w = 0 is the only feasible pole of (1/w2)f(1/w) that is inside C. The residue theorem argues that because C is oriented clockwise,

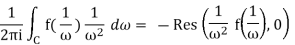
Comparing this with the equation just above finishes the proof.

Example. Let

f(z) = .

Earlier we computed

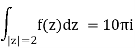
Calculate residues at z = 0 and z = 1 Calculate a single residue at infinity to recalculate this integral.

Solution:

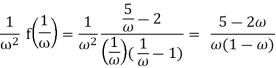
We easily compute that

Res(f,∞) = −Res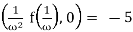

Since |z| = 2 contains all the singularities of fwe have

4.2 Singularities and meromorphic functions

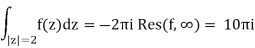
4.2.1 Meromorphic function:

A function on a domain Ω is called meromorphic, if there exists a sequence of points p1,p2,···with no limit point in Ω such that if we denote Ω∗= Ω \{p1,···}

• f : Ω∗→C is holomorphic.
• F has poles at p1,p2···.

It is often useful to think of z = ∞ on the same footing as other points in the complex plane, and to define the extended complex plane

Cˆ = C∪∞.

We can then think of meromorphic functions f : Ω \{p1,···,pj,···}→C, as functions f : Ω →Cˆ, by defining

f(pj) = ∞

Pjs for all the poles Similarly, while considering meromorphic functions on C, it's also a good idea to think about the function's own extension to C. If z = 0 is a pole (resp. Detachable or essential singularity) for the function, we say z = is a pole (resp. Removable or essential singularity).

fˆ(z) = f(1/z).

If a meromorphic function on C does not have an essential singularity at z =∞, we say it is meromorphic on the extended plane. Meromorphic functions on C can be classified, it turns out. Remember that a rational function on C is a form function.

R(z) =

Where both P(z) and Q(z) are polynomials.

Lemma 0.1. At infinity, a rational function possesses a pole or detachable singularity. If and only if degQ≥ degP, it possesses a detachable singularity.

Theorem 0.1. The only meromorphic functions on Cˆ are rational functions.

Proof. Let F :Cˆ→Cˆ be a meromorphic function.

Claim-1. F has only finitely many poles {p1,···,pn} in the complex plane C.

To see this, note that F(1/z) has either a pole or zero at z = 0. In either case there is a small neighborhood|z| <εwhich has no other pole. Which is the same as saying that F has no finite pole in |z| >1/ε. But |z|≤ 1/εis compact, and since all poles are isolated, this shows that there are only finitely many poles. Now, corresponding to each of the poles pk∈C there exists a polynomial Pk(see Remark 0.2 in Lecture-20) such that

F(z) = Pk

WhereGkis holomorphic on pk's whole neighbourhood (including at the point pk). In the same way, we may write

F,

Where as before, G(z) is holomorphic in a neighborhood of z = 0. Claim number two is that the function

H(z) = F(z) - P∞(z) –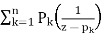

Is an entire and bounded function.

Assuming the claim, Liouville's theorem shows that H(z) is a constant, and so F(z) must be rational, proving the theorem. To demonstrate the assertion, first notice that H(z) is obviously holomorphic away from p1,•••,pn. At some z = pk, Pj(1/z −pj) is holomorphic for all j =6k. On the other hand, near pk,

F(z) – Pk

That is, it is holomorphic. This demonstrates that H(z) is complete. As a result, we only need to show boundedness on |z| > R for some large R to demonstrate boundedness. To see this, remember that Pkare polynomials are polynomials.

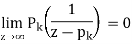
Hence it is enough to show that F(z)−P∞(z) is bounded near infinity. But this follows immediately from noting that

G∞(z) = F(1/z) - P∞ (1/z)

Is holomorphic near z = 0 and hence is bounded on |z| <εfor some ε>0. In particular F(z) −P∞(z) is bounded on |z| >1/ε. This proves the claim, and hence completes the proof of the theorem.

The following theorem on partial fraction decomposition is a simple consequence of the proof, which we take for granted as an important tool in integration theory but never see the evidence of.

Corollary 0.1. For any rational function R(z) = P(z)/Q(z) has a partial fraction decomposition of the form

R(z) = P∞(z) +

Wherepkis a root of Q(z) of order mk, Pkis a polynomial of degree mk, and degP∞ = degP−degQ.

4.2.2 Singularities:

A singularity is a point when an equation, surface, or other object blows up or degenerates. Singularities are also referred to as singular points.

Singularities play a crucial role in complex analysis, as they define the range of conceivable behaviours for analytic functions. Complex singularities are spots in a function's domain where the function fails to be analytic. Poles, essential singularities, logarithmic singularities, and detachable singularities are all types of isolated singularities. Natural boundaries or branch cuttings can produce nonisolated singularities.

Consider the ordinary differential equation of second order.

y’’ + P(x)y’ + Q(x) y = 0

If P(x) and Q(x) remain finite at x= x0, then x0 is called an ordinary point. If either P(x) or Q(x) diverges as x→ x0, then x0  is called a singular point. Singular points are further classified as follows:

1. If either  P(x) or Q(x) diverges as x→ x0 but (x-x0)P(x) and (x- x0)2 Q(x)  remain finite as x→ x0, then x=x0 is called a regular singular point (or nonessential singularity).

2. If P(x) diverges more quickly than 1/(x – x0), so (x-x0) P(x) approaches infinity as x→ x0, or Q(x) diverges more quickly than 1/(x-x0)2 Q so that (x – x0)2 Q(x)  goes to infinity as x→ x0 , then x0 is called an irregular singularity (or essential singularity).

A pole of order m is a point z0 of f(z) such that the Laurent series of f(z) has an=0 for n < - m and a-m ≠ 0.

Essential singularities are poles of infinite order. A pole of order n is a singularity z0 of f(z) for which the function (z – z0)n f(z) is nonsingular and for which (z – z0)k f(z) is singular for k = 0, 1, ..., n-1. 

A logarithmic singularity is a singularity of an analytic function whose main z-dependent term is of order O(ln z), O(ln ln z), etc.

Removable singularities are singularities for which it is possible to assign a complex number in such a way that f(z) becomes analytic. For example, the function f(z) = z2/z has a removable singularity at 0, since f(z)=z everywhere but 0, and f(z) can be set equal to 0 at z=0. Removable singularities are not poles.

For example, the function f(z) = csc(1/z) has the following singularities: poles at z=1/(2πn), and a nonisolated singularity at 0.

4.3 The argument principle and applications

4.3.1 Argument Principle

Introduction

The argument principle (or argument principle) is a result of the residue theorem. It links a curve's winding number to the number of zeros and poles within the curve. This is useful in applications (both mathematical and non-mathematical) when we need to know where the zeros and poles are located.

Principle of the argument Setup.

A basic closed curve that is oriented counterclockwise.

Except for (potentially) some finite poles inside (not on) and some zeros inside (not on), f(z) is analytic on and inside.

Let p1, ...,pm be the poles of f inside γ.

Let z1, ...,zn be the zeros of f inside γ.

Write mult(zk) = the multiplicity of the zero at zk. Likewise write mult(pk) = the order of the pole at pk.

We begin with a theory that will lead to the principle of argumentation. Theorem 11.1 is the first of a series of theorems With the arrangement described above,

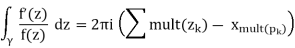
Proof. To prove this theorem we need to understand the poles and residues of f0(z)/f(z). With this in mind, suppose f(z) has a zero of order m at z0. The Taylor series for f(z) near z0 is f(z) = (z −z0)mg(z)

Whereg(z) is analytic and never 0 on a small neighborhood of z0. This implies

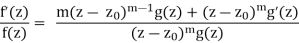
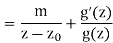
Since g(z) is never 0, g0(z)/g(z) is analytic near z0. This implies that z0 is a simple pole of f0(z)/f(z) and

Res 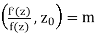= mult(z0).

Likewise, if z0 is a pole of order m then the Laurent series for f(z) near z0 is

f(z) = (z −z0)−mg(z)

Whereg(z) is analytic and never 0 on a small neighborhood of z0. Thus,

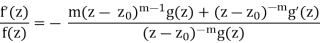
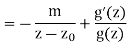
Again we have that z0 is a simple pole of f0(z)/f(z) and

Res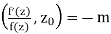 = - mult(z0).

The following theorem comes directly from the Residue Theorem:

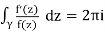    sum of the residues

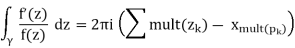
Definition. We write Zf,γfor the sum of multiplicities of the zerosoffinsideγ. Likewise for Pf,γ. So the Theorem 11.1 says,

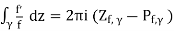 (1)

Definition. Winding number. We have an intuition for what this means. We define it formally via Cauchy’s formula. If γis a closed curve then its winding number (or index) about z0 is defined as

Ind(γ, z0) =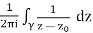

Mapping curves: f ◦γ

One of the key notions in this topic is mapping one curve to another. That is, if z = γ(t) is a curve and w = f(z) is a function, then w = f ◦γ(t) = f(γ(t)) is another curve. We say f maps γtof◦γ. We've done it before, but it's significant enough to us now that we'll pause and offer a few examples. This is a crucial notion in the reasoning principle, so make sure you understand it completely.

Example 11.1. Let γ(t) = eitwith 0 ≤ t ≤ 2π (the unit circle). Let f(z) = z2. Describe the curve f ◦γ.

Solution: Clearly f ◦γ(t) = e2it traverses the unit circle twice as tgoes from 0 to 2π.

Example 11.2. Let γ(t) = it with −∞< t <∞ (the y-axis). Let f(z) = 1/(z + 1).

Describe the curve f ◦γ(t).

Solution: f(z) is a fractional linear transformation that transfers the line given by to the circle centred at 1/2 through the origin. By double-checking a few points:

f(-i) =      f(0) = 1,       f(i) = ,      f(∞) = 0

We see that the circle is traversed in a clockwise manner as tgoes from −∞to ∞.

Im(z)Im(w)

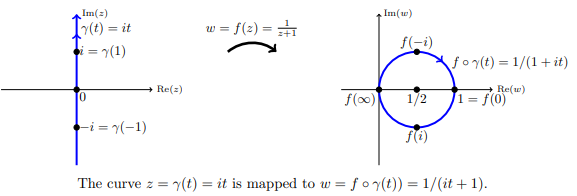
The curve z = γ(t) = it is mapped to ω = f o γ(t) = 1/(it+1)

Argument principle

This is also known as the principle of the argument.

Theorem 11.3. The premise of the argument With the same setup as before, for f

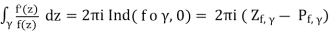           (2)

Proof. Theorem 11.1 demonstrates that

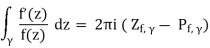
As a result, we must show that the integral also equals the provided winding number. The change of variables w = f is all there is to it (z). With this change of variables the countourz= γ(t) becomes w = f ◦γ(t) and dw= f0(z)dzso

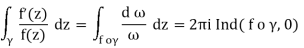
The preceding equation's final equivalence comes from the definition of a winding number.

Note that by assumption γdoes not go through any zerosof f, so w = f(γ(t)) is never zero and 1/w in the integral is not a problem.

Here is an easy corollary to the argument principle that will be useful to us later.

Corollary. Assuming that f ◦γdoes not go through −1, i.e. there are no zeros of 1+f(z) on γthen

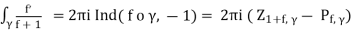 (3)

Proof. When we apply Equation 2's argument principle to the function 1 + f(z), we get

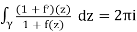  Ind(1 + f ◦γ,0) = 2πi(Z 1+f,γ−P1+f,γ)

We can now compare each term in this equation to the terms in Equation 3:

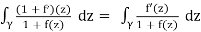      (because (1 + f)0 = f0 )

Ind(1 + f ◦γ,0) = Ind(f ◦γ,−1) (1 + f winds around 0 ⇔f winds around -1)

Z1+f,γ= Z1+f,γ (same in both equations)

P1+f,γ= Pf,γ (poles of f = poles of 1 + f)

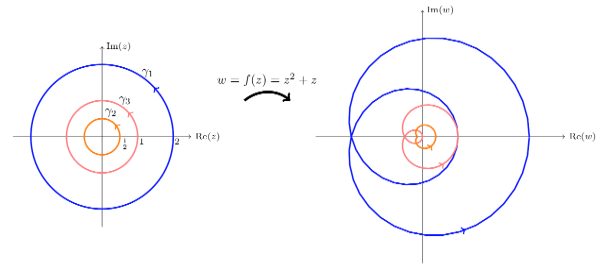
Example 11.4. Let f(z) = z2 + z Find the winding number of f ◦γaround 0 for each of the following curves.

1. γ1 = circle of radius 2.
2. γ2 = circle of radius 1 / 2.
3. γ3 = circle of radius 1.

Answers. f(z) has zeros at 0, −1. It has no poles.

So, f has no poles and two zeros inside γ1. The argument principle says Ind(f ◦γ1,0) = Zf,γ1 −Pf,γ= 2

Likewisef has no poles and one zero inside γ2, so Ind(f ◦γ2,0) = 1 −0 = 1

For γ3 a zero of fis on the curve, i.e.f(−1) = 0, so the argument principle doesn’t apply. The image of γ3 is shown in the figure below – it goes through 0.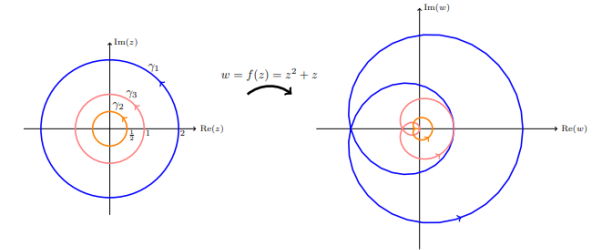

The image of 3 different circles under =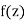

Rouch´e’s theorem

Theorem 11.5. Theorem of Rouch. Consider the following scenarios:

Except for some finite poles, is a simple closed curve f,hare analytic functions on and within.

There are no poles of f and h on γ.

|h| <|f| everywhere on γ.

Then

Ind(f ◦γ,0) = Ind((f + h) ◦γ,0).

That is,

Zf,γ−Pf,γ= Zf+h,γ−Pf+h,γ (4)

Proof. We demonstrated a heuristic proof in class using a person walking a dog.  f ◦γon a leash of length h ◦γ. Here is the analytic proof.

The argument principle requires the function to have no zeros or poles on γ. So we first show that this is true of f, f + h, (f + h)/f. The argument is goes as follows.

Zeros: The fact that 0 ≤|h| <|f| on γimpliesf has no zeros on γ. It also implies f + h has no zeros on γ, since the value of h is never big enough to cancel that of f. Since f and f + h have no zeros, neither does (f + h)/f.

Poles: Assuming that f and h have no poles on, f +h also has no poles. (f + h)/f has no poles on because f has no zeros. The argument principle can now be used to f and f + h.

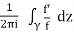= Ind(f  ◦γ, 0) = Z f,γ−Pf,γ (5)

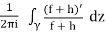= Ind((f + h) ◦γ,0) = Z f+h,γ−Pf+h,γ. (6)

Next, by assumption |h/f| < 1, so (h/f) o γ  is inside the unit circle. . This means that

1+h/f = maps γ to the inside of the unit disk centered at 1. This implies that

Ind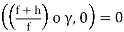

Let g = 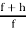. The above says Ind(g o γ, 0) = 0. So, 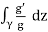= 0. (We showed above that g has no zeros or poles on γ.)

Now, it’s easy to compute that 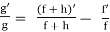. So, using

Ind(g o γ, 0) = 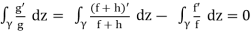⟹ Ind((f +h)◦γ,0) = Ind(f ◦γ,0).

Now equations 5 and 6 tell us Zf,γ−Pf,γ= Zf+h,γ−Pf+h,γ, i.e. we have proved Rouch´es theorem.

Corollary. Under the same hypotheses, Ifh and f are analytic (no poles) then

Zf,γ= Zf+h,γ.

Proof. Since the functions are analytic Pf,γandPf+h,γare both 0. So Equation 4 shows Zf= Zf+h. QED.

We think of h as a small perturbation of f.

Example 11.6. Show all 5 zeros of z5 + 3z + 1 are inside the curve C2 :|z| = 2.

Solution: Let f(z) = z5 and h(z) = 3z + 1. Clearly all 5 roots of f (really one root with multiplicity 5) are inside C2. Also clearly, |h| <7 <32 = |f| on C2. The corollary to Rouch´es theorem says all 5 roots of f + h = z5 + 3z + 1 must also be inside the curve.

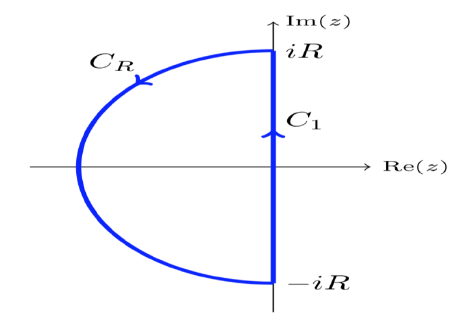
Example 11.7. Show z + 3 + 2ez has one root in the left half-plane.

Solution: Let f(z) = z + 3, h(z) = 2ez. Consider the contour from −iRtoiRalong the y-axis and then the left semicircle of radius R back to −iR. That is, the contour C1 + CR shown below.

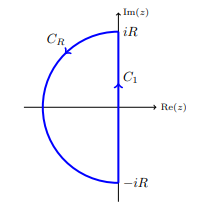
In order to apply the corollary to Rouch's theorem, we must first make sure that (for R large) |h| <|f| on C1 + CR. On C1, z = iy, so

|f(z)| = |3 + iy|≥ 3, |h(z)| = 2|eiy| = 2.

So |h| <|f| on C1.

On CR, z = x + iywithx<0 and |z| = R. So,

|f(z)| > R −3 for R large, |h(z)| = 2|ex+iy| = 2ex <2 (since x <0).

So |h| <|f| on CR.

The only zero of fis at z = −3, which lies inside the contour.

As a result of the Rouch es theorem's Corollary, f + h has the same number of roots as f inside the contour, which is 1. Allow R to reach infinity, then we can see that f + h has just one root in the half-plane.

Theorem. Fundamental theorem of algebra.

The following is how Rouch's theorem can be used to show the fundamental theorem of algebra.

Proof. Let

P(z) = zn+ an−1zn−1 + ... + a0

Be an nth order polynomial. Let f(z) = znandh = P −f. Choose an R such that

R >max(1,n|an−1|,...,n|a0|). Then on |z| = R we have

|h| ≤ | an-1| Rn-1 + | an-2 | Rn-2 + ... + | a0 | ≤ R/n Rn-1 + R/n Rn-2 + ... + R/n < Rn

On |z| = R we have |f(z)| = Rn, so we have shown |h| <|f| on the curve. Thus, the corollary to Rouch´es theorem says f + h and f have the same number of zeros inside |z| = R. Since we know f has exactly n zeros inside the curve the same is true for the polynomial f + h. Now let R go to infinity, we’ve shown that f + h has exactly n zeros in the entire plane.

Note. The proof establishes a simple bound on the size of the zeros: they are all less than or equal to max in magnitude.  (1,n|an−1|,...,n|a0|).

4.4 The complex logarithm

4.4.1 Review of the properties of the argument of a complex number

Before we get started, let's go through the attributes of the argument of a non-zero complex number z, represented by argz (a multi-valued function), and the principal value of the argument, Argz, which is single-valued and typically defined as follows:

−π <Argz≤ π (1)

The argument of a complex number is covered in detail in the class handout. We'll go through a few of the findings from that handout here. Argz can be thought of as a collection of the following elements:

Argz= Argz+ 2πn, n = 0, ±1, ±2, ±3, ... ,−π <Argz≤ π . (2)

One can also express Argzin terms of argzas follows:

Arg z = arg z + 2π , (3)

The biggest integer function is denoted by [ ]. That is, the greatest integer less than or equal to the real number x is defined as [x]. As a result, [x] is the only integer that fulfils the inequality.

x−1 <[x] ≤ x, for real x and integer [x]. (4)

For example, [1.5] = [1] = 1 and [−0.5] = −1. It is possible to verify that Argz, as defined in eq. (3), falls within the primary interval defined by eq (1). The properties of the multi-valued function argz are as follows:

Arg(z1z2) = argz1 + argz2 , (5)

Arg . (6)

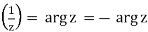Arg  . (7)

Eqs. (5)–(7) should be regarded as set equalities, i.e. the elements of the sets represented by the left-hand and right-hand sides of the above identities are the same. The following outcomes, however, are not set equalities:

Arg z + arg z ≠ 2 arg z,                       arg z – arg z ≠ 0,                 (8)

Which, by virtue of eqs. (5) and (6), yield:

Arg z2 = arg z + arg z ≠ 2 arg z,                         arg(1) = arg z – arg z ≠ 0,      (9)

For example,      arg(1) = 2πn, for n = 0 ±1, ±2, ..... More generally,

Arg zn = arg z + arg z + ... + arg z ≠ n arg z.                      (10)

|----------- n -----------------|

We also take notice of various aspects of the argument's principal value.

Arg (z1 z2) = Arg z1 + Arg z2 + 2π N+ ,                              (11)

Arg (z1 / z2) = Arg z1 -  Arg z2 + 2π N- ,                              (12)

Where the integers N± are determined as follows:

N± =                (13)

When we set z1 to 1 in eq. (12), we get

Arg (1/z) = Arg 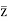=      (14)

Note that for z real, both 1/z and z are also real so that in this case z = z and Arg(1/z) = Argz= Argz. In addition, in contrast to eq. (10), we have

Arg(zn) = nArgz+ 2πNn, (15)

Where the integer Nnis given by:

Nn  =

And [ ] is the greatest integer bracket function introduced in eq. (4).

4.4.2 Properties of the real-valued logarithm, exponential and power functions

Consider a positive real number's logarithm.

The quantity of properties:

This function fulfils a requirement. 

eln x = x,                                                       (17)

Ln (ea) = a,                                                   (18)

Ln(xy) = ln(x) + ln (y),                              (19)

Ln (x/y) = ln(x) – ln(y),                             (20)

Ln(1/x) = - ln (x)                                         (21)

Ln xp = p ln x                                               (22)

x and y are positive real values, whereas a and p are arbitrary real numbers. Similarly, the power function defined over real numbers satisfies the following conditions:

xa = ea ln x ,                                                           (23)

xa xb = xa+b,                                                         (24)

xa/xb = xa-b,                                                         (25)

1/ xa = x-a,                                                            (26)

(xa)b = xab,                                                           (27)

(xy)a = xaya,                                                         (28)

(x/y)a = xay-a ,                                                     (29)                               

x and y are positive real values, whereas a and b are random real numbers. The generalised exponential function defined over real numbers is closely connected to the power function. This function fits the following criteria:

ax = ex ln a,                                                                  (30)

axay = ax+y,                                                                 (31)

ax/ay = ax-y,                                                                (32)

1/ ax = a-x,                                                                  (33)

(ax)y = axy,                                                                  (34)

(ab)x = axbx,                                                               (35)

(a/b)x = axb-x,                                                             (36)

For positive real numbers a and b and arbitrary real numbers x and y.

We would like to know which of these relations are satisfied when these functions are extended to the complex plane. It is dangerous to assume that all of the above relations are valid in the complex plane without modification, as this assumption can lead to seemingly paradoxical conclusions. Here are three examples:

1. Since 1/(−1) = (−1)/1 = −1 ,

Hence, 1/i= iori2 = 1. But i2 = −1, so we have proven that 1 = −1.

2.     Since 1 = (−1)(−1) ,

1 = 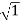=  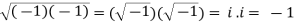(38)

3.     To prove that ln(−z) = ln(z) for all z =6 0, we proceed as follows:

Ln(z2) = ln[(−z)2],

Ln(z) + ln(z) = ln(−z) + ln(−z),

2ln(z) = 2ln(−z), ln(z) = ln(−z).

All of these "proofs" are, of course, false. The first two proofs contain a fallacy due to eqs. (28) and (29), which are true for real-valued functions but not for complex-valued functions in general. The third proof's mistake is more subtle, and it will be addressed later in these comments. A thorough understanding of the complex logarithm, power, and exponential functions will explain how to adjust eqs. (17)–(36) correctly and avoid common mistakes that can lead to incorrect results.

4.4.3 Definition of the complex exponential function

We'll start with the complex exponential function, which has the following power series:

ez = ,

Where z is a complex number of any type. Using this definition of a power series, one may verify that:

ez1 + z2  = ez1 ez2,                            for all complex z1 and z2.           (39)

If z = x + iy, where x and y are real numbers, it follows that

ez= ex+iy= ex eiy= ex(cosy + isiny).

The complex exponential function can be used to quickly verify that eqs. (30)–(33) are met. Furthermore, when the outer exponent is an integer, eq. (34) holds:

(ez)n = enz, n = 0, ±1, ±2, ... . (40)

The resulting equation is a multivalued power function if the outer exponent is a non-integer. In section 8, we'll go over this case in further depth.

Before we continue, there is one important property of the complex exponential to note:

e2πin = 1, n = 0, ±1, ±2, ±3, ... . (41)

4.4.4 Definition of the complex logarithm

The complex logarithm must be defined by solving the complex equation:

z = ew, (42)

Forw, where z is any complex number that is not zero. If we write w = u + iv, we may write eq. (42) as

Eueiv= |z|eiargz . (43)

Eq. (43) implies that:

|z| = eu, v = argz .

The equation |z| = euis a real equation, so we can write u = ln|z|, where ln|z| is the ordinary logarithm evaluated with positive real number arguments. Thus,

w = u + iv = ln|z| + iargz= ln|z| + i(Argz+ 2πn), n = 0, ±1, ±2, ±3, ...(44)

The complex logarithm is denoted by the symbol w, which is written as w = lnz. Since we have used the symbol ln for the real logarithm in eq. (44) this is an uncomfortable notation. The real logarithm in eq. (44) will be denoted by the symbol Ln to solve this notational conundrum. That is, the ordinary real logarithm of |z| will be denoted as Ln|z|. We may rephrase eq. (44) using this notational convention:

Lnz= Ln|z| + iargz= Ln|z| + i(Argz+ 2πn), n = 0, ±1, ±2, ±3, ... (45)

For any complex number z that is not zero

Lnzi is clearly a multi-valued function (as its value depends on the integer n). It is useful to define a single-valued complex function, Ln z, called the principal value of lnzas follows:

Lnz= Ln|z| + iArgz , −π <Argz≤ π , (46)

Which extends the definition of Ln z to the entire complex plane (excluding the origin, z = 0, where the logarithmic function is singular). In particular, eq. (46) implies that Ln(−1) = iπ. Note that for real positive z, we have Argz= 0, so that eq. (46) simply reduces to the usual real logarithmic function in this limit. The relation between lnzand its principal value is simple:

Lnz= Ln z + 2πin, n = 0, ±1, ±2, ±3, ... .

4.4.5 Properties of the complex logarithm

Now we'll look at whether of the properties in equations (17)–(22) apply to the complex logarithm. We should look at the properties of both the multi-valued function lnz and the single-valued function Ln z now that we've defined them. Let's start with the lnz multi-valued function. First, we'll look at eq (17). Using eq. (45), we can deduce:

Elnz= eLn|z|eiArgze2πin = |z|eiArgz= z . (47)

Thus, eq. (17) is satisfied. Next, we examine eq. (18) for z = x + iy:

Ln(ez) = Ln|ez| + i(argez) = Ln(ex) + i(y + 2πk) = x + iy+ 2πik= z + 2πik ,

Wherekis an arbitrary integer. In deriving this result, we used the fact that ez= exeiy, which implies that arg(ez) = y + 2πk.‡ Thus,

Ln(ez) = z + 2πik=6 z , unless k = 0. (48)

This is not surprising, since ln(ez) is a multi-valued function, which cannot be equal to the single-valued function z. Indeed eq. (18) is false for the multi-valued complex logarithm.

As a check, let us compute ln(elnz) in two different ways. First, using eq. (47) , it follows that ln(elnz) = lnz. Second, using eq. (48), ln(elnz) = lnz+ 2πik. This seems to imply that lnz= lnz+ 2πik. In fact, the latter is completely valid as a set equality in light of eq. (45).

Now we'll look at the properties shown in eqs. (19)–(20). (22). Equations (19)–(21) are satisfied as set equalities using the definition of multi-valued complex logarithms and the properties of argz given in eqs. (5)–(7):

Ln (z1z2) = ln z1 + ln z2

Ln (z1/ z2 ) = ln z1 – ln z2

Ln (1/z) = - ln z, (51)

However, one must be careful in employing these results. One should not make the mistake of writing, for example, lnz+ lnz=? 2lnz or lnz−lnz=? 0. For the same reason that eqs. (8) and (9) are not identities under set equality, both of these claims are untrue. When p is an integer n, the multi-valued complex logarithm does not meet eq. (22):

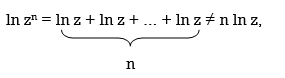(52)

Which is inferred from eq (10). If p is not an integer, zp is a complex multivalued function, then the validity of eq. (22) requires more investigation. In section 6, we'll show [see eq. (62)] that the complex logarithm can only satisfy eq. (22) if p = 1/n, where n is an integer. In this instance,

Ln ( z1/n) = 1/n ln z,                            n = 1, 2, 3, ...                                (53)

The properties of the single-valued function Ln z are next investigated. We look at the six qualities given by eqs. (17)– (19) once again (22). For starters, eq. (17) is easily met since

eLn z  = eLn |z| ei Arg z = | z| ei Arg z = z                                                      (54)

However, eq. (18) is frequently incorrect. Given example, for z = x + iy

Ln(ez) = Ln |ez| + i ( Arg ez) = Ln (ex) + i (Arg eiy) = x + i  Arg (eiy)

= x+ i arg(eiy)+ 2πi

= z + 2πi 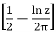                                                     (55)

After using eq. (3), where [ ] is the greatest integer bracket function defined in eq. (4). Thus, eq. (18) is satisfied only when −π < y ≤ π. For values of y outside the principal interval, eq. (18) contains an additive correction term as shown in eq. (55).

As a check, let us compute Ln(eLnz) in two different ways. First, using eq. (54) , it follows that Ln(eLnz) = Ln z. Second, using eq. (55) ,

Ln (eLn z) = Ln z + 2πi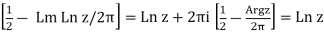

Where we have used Im Ln z = Argz[see eq. (46)]. In the last step, we noted that

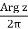0 ≤ ½ - <1,

Due to eq. (1), which implies that the integer part of ½ - 1/2π Argzis zero. Thus, the two computations agree.

Now we'll look at the properties shown in eqs. (19)–(20). (22). Because the complex logarithm's primary value must be within the interval, Ln z may not meet any of these requirements.  −π <Im Ln z ≤ π. Using the results of eqs. (11)–(16), it follows that

Ln (z1z2) = Ln z1 + Ln z2 + 2πiN+ , (56)

Ln (z1/z2) = Ln z1 −Ln z2 + 2πiN−, (57)

Ln(zn) = nLnz+ 2πiNn (integer n), (58)

Where the integers N± = −1, 0 or +1 and Nnare determined by eqs. (13) and

(16), respectively, and

Ln(1/z) =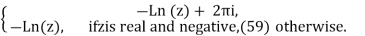

Note that eq. (19) is satisfied if Rez1 >0 and Re z2 >0 (in which case N+ = 0). In other cases, N+ =6 0 and eq. (19) fails. Similar considerations also apply to eqs. (20)–(22). For example, eq. (21) is satisfied by Ln z unless Argz= π (equivalently for negative real values of z), as indicated by eq. (59). In particular, one may use eq. (58) to verify that:

Ln[(−1)−1] = −Ln(−1) + 2πi= −πi+ 2πi= πi= Ln(−1),

As expected, since (−1)−1 = −1.

We can't examine whether eq. (22) holds if p is a non-integer because zp is a multi-valued function in this situation. As a result, we'll now focus on the complicated power functions (and the related generalised exponential functions).

4.4.6 Definition of the generalized power and exponential functions

The equation for the generalised complex power function is as follows:

ω = zc = ec ln z ,                   z ≠ 0,                                         (60)

To justify this definition, consider that if c = k is an integer, then z = |z|eiargz is an integer.

Zk= |z|kekiargz= ekLn|z|ekiargz= ek(Ln|z|+iargz) = eklnz .

In this case, w = zkis a single-valued function, since

Zk= eklnz= ek(Ln z +2πin) = ekLnz .

If c = 1/k (where k is an integer), then we have:

z1/k= |z|1/keiarg(z)/k = eLn|z|/keiarg(z)/k = e(Ln|z|+iargz)/k = eln(z)/k ,

Where|z|1/k refers to the real kth root of |z| that is positive. We can easily prove that eq. (60) holds for any rational real number c by combining the two conclusions just obtained. Because any irrational real number can be approximated (to any desirable degree of precision) by a rational number, eq. (60) must hold for any real number c. These considerations motivate the use of eq. (60) to define the generalised complex power function for any complex power c.

Note that due to the multi-valued nature of lnz, it follows that w = zc= eclnzis also multi-valued for any non-integer value of c, with a branch point at z = 0:

w = zc= eclnz= ecLnze2πinc, n = 0, ±1, ±2, ±3,···. (61)

If c is a rational number, then it can always be expressed in the form c = m/k, where m is an integer and k is a positive integer such that m and k possess no common divisor. One can then assume that n = 0,1,2,...,k−1 in eq. (61), since other values of n will not produce any new values of zm/k. It follows that the multi-valued function w = zm/k has precisely k distinct branches. If c is irrational or complex, then the number of branches is infinite (with one branch for each possible choice of integer n).

Having defined the multi-valued complex power function, we are now able to compute ln(zc). In light of eq. (48) ,

Ln (zc) = ln(ec ln z) = c ln z + 2πik = c (ln z +

Wherekis an arbitrary integer. Thus, ln(zc) = clnzin the sense of set equality ( in which case the sets corresponding to lnzand lnz+2πik/c coincide) if and only if k/c is an integer for all values of k. Taking c = 1/n, where n is an integer, is the only way to satisfy this criterion. As a result, eq. (53) has been verified.

We can define a single-valued power function by selecting the principal value of lnzin eq. (60). Consequently, the principal value of zcis defined by

Zc = ecLn z,               z ≠ 0,                                          (63)

For lack of a better notation, I'll capitalise the variable Z as shown above to represent the principal value. The principal value definition of zccan lead to some unexpected results. For example, consider the principal value of the cube root function w = Z1/3 = eLn(z)/3. Then, for z = −1, the principal value of

This may have surprised you, if you were expecting that . To obtain the latter result would require a different choice of the principal interval in the definition of the principal value of z1/3.

In the case where both the complex logarithm and the complex power function are specified by their principal values, we can now check eq. (22). To put it another way, we compute:

Ln(Zc) = Ln(ecLnz) = cLnz+ 2πiNc, (64)

Following the application of eq. (55), where Ncis is an integer defined by

Nc ≡ [ ½ -

The biggest integer bracket function defined in eq. Is [ ]. (4). It is possible to assess Nc by noticing that:

Im (cLnz) = Im{c(Ln|z| + iArgz)} = ArgzRe c + Ln|z|Imc.

It's worth noting that if c = n and n is an integer, eq. (64) simplifies to eq. (58) as expected. We conclude that both the multi-valued complex logarithm and its primary value are erroneous in eq. (22).

The generalised exponential function is a function that is comparable to the complicated power function in several ways. The generalised exponential function for c =6 0 could be defined as follows:

ω = cz = ez ln c  = ez(Ln c + 2π i n ),                       n = 0, ±1, ±2, ±3, ......                     (66)

The multivalued nature of this function, however, differs from the multivalued power function in some ways. The generalised exponential function, in contrast to the latter, has no branch point (or any other sort of singularity) in the finite complex z-plane. For each value of n, eq. (66) can be thought of as creating a set of independent single-valued functions. The n = 0 case is usually the most practical, in which case we simply define:

ω = cz = ez ln c ,                                c≠0.                                 (67)

This matches our concept of the exponential function in section 3 (c = e). We'll use eq. (67) as the single-valued generalised exponential function definition from now on.

Some of the results for the complex power function's principal value can be applied to the generalised exponential function right away. For example, a nearly identical computation as in eqs. (64) and (65) yields the following results:

Ln (cz) = Ln (ez Ln c) = z Ln c + 2πi N’c ,                           (68)                          

Where N’c is an integer determined by:

N’c = [ ½ - lm (z Ln c)/2π]                                                (69)

4.4.7 Properties of the generalized power function

Let's take a look at the properties listed in eqs (29). The complex power function is defined by Eq. (23) It's all too easy to write:

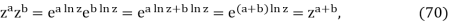
However, consider the case of non-integer aandbwhere a + b is an integer. In this case, eq. (70) cannot be correct since it would equate a multi-valued function zazbwith a single-valued function za+b. In fact, the questionable step in eq. (70) is false:

a ln z + b ln z = (a+b) ln z                  [ FALSE!!],                        (71)

In the case of a = b = 1 [cf. Eq. (8)], we already know that eq. (71) is untrue. A more thorough calculation yields:

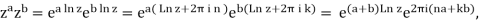
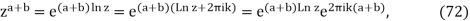
Wherekand n are arbitrary integers. Hence, za+bis a subset of zazb. Whether the set of values for zazbandza+bdoes or does not coincide depends on aandb.

However, in general, eq. (24) does not hold.

Similarly,

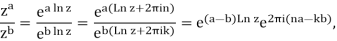
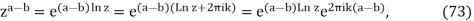
In practice, many textbooks treat the generalized exponential function as a single-valued function, cz= ezLnc, only when c is a positive real number. For any other value of c, the multi-valued function cz= ezlncis preferred. We shall not pursue this approach in these notes.

Wherekand n are arbitrary integers. Hence, za−b is a subset of za/zb. Whether the set of values za/zbandza−b does or does not coincide depends on aandb. However, in general, eq. (25) does not hold. Setting a = b in eq. (73) yields the expected result:

z0 = 1, z =6 0

For any complex number z that is not zero The set equality is obtained by setting a = 0 in eq. (73):

z-b = 1/zb,             (74)

i.e., the set of values for z−b and 1/zbcoincide. Thus, eq. (26) is satisfied. Note, however, that

Zaz−a = ealnze−alnz= ea(lnz−lnz) = ealn1 = e2πika ,

Wherekis an arbitrary integer. Hence, if a is a non-integer, then zaz−a =6 1 for k =6 0. This is not in conflict with the set equality given in eq. (74) since there always exists at least one value of k (namely k = 0) for which zaz−a = 1. To show that eq. (27) can fail, we use eq. (48) to conclude that

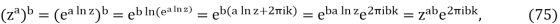
Where k is a random number. When we use the principal value of the generalised power function, which is described in eq. (63), we get eqs. (61) and (75).

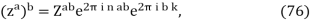
k and n are both arbitrary integers. Thus, zabis a subset of (za)b. Note that the elements of zaband (za)b coincide if a = ±1 and/or b is an integer.¶In contrast, if z = a = b = i, then zab= −i, whereas eq. (75) yields,

(ii)i = ii . i e-2πk  = i- 1 e- 2πk = - i e-2 πk,                 k = 0, ±1, ±2, ......            (78)

The multi-valued power function, on the other hand, satisfies eqs. (28) and (29) because

(z1z2)a = ea ln (z 1 z 2 ) = ea( ln z1 + ln z2) = ealn z1 ea ln z2 = za1 za2

(z1 /z2)a = ea ln (z 1 /z 2 ) = ea( ln z1 - ln z2) = ealn z1 e -a ln z2 = za1 z -a2

Other special cases exist in which the elements of zaband (za)bcoincide. For example, if a = 3/2 and b = 1/2, then one can check that allowing for all possible integer values of n and k in eqs. (76) and (77) yields (za)b= zab= {Zab,−Zab,iZab,−iZab}.

We now repeat the above analysis for the principal value of the power function, Zc= ecLnz. In this case, the results are somewhat reversed from the case of the multi-valued power function. In particular, eqs. (24)–(26) are satisfied, whereas eqs. (27)–(29) may be violated. For example, for the single-valued power function,

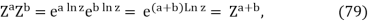
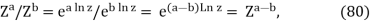
As expected, setting a = b in eq. (80) results in Z0 = 1 (for z 6=0). Since eq. (55) implies that, eq. (27) may be broken.

(Zc)b= (ecLnz)b = ebLn(ecLnz) = eb(cLnz+2πiNc) = ebcLnz e2πibNc= Zcb e2πibNc ,

WhereNcis an integer determined by eq. (65). As an example, if z = b = c = i, eq. (65) gives Nc= 0, which yields the principal value of (ii)i= ii·i= i−1 = −i. However, in general Nc=6 0 is possible in which case (Zc)b6=Zcb[i.e., eq. (27) does not hold] unless bNcis an integer. For example, if z is real and negative and c = −1, then Nc= 1 and (Z−1)b= Z−be2πib[which provides a resolution for the paradox of eq. (37)]. That is, if z is real and negative then (Z−1)b6=Z−b unless b is an integer.

Eqs. (28) and (29) may also be violated since eqs. (56) and (57) imply that

(Z1Z2)a = ea ln (z 1 z 2 ) = ea( ln z1 + ln z2 + 2πiN+) = Za1 Za2 e2πi a N - ,                      (82)

(Z1 /Z2)a = ea ln (z 1 /z 2 ) = ea( ln z1 - ln z2 + 2πiN -) = Za1 e2πi a N -/Za2 ,                  (83)

Where the integers N± are determined from eq. (13).

4.4.8 Properties of the generalized exponential function

The single-valued generalised exponential function w = cz(c =6 0) is defined by eq (67). One can rapidly examine whether eqs. (31)–(36) hold in the complex plane using this formulation and the features of the complex exponential function ez.Eqs. (31)–(33) are virtually identical to eqs. (79)–(81) in terms of proof:

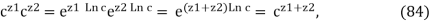
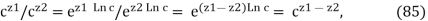
However, eq. (34) does not generally hold. Using eq. (68) ,

(cz1)z2= ez2 Ln(cz1) = ez2(z1 Ln c+2πiNc′) = ez2z1 Ln c e2πiz2Nc′= cz1z2 e2πiz2Nc′, (87) where N’c is determined by eq. (69) [with z replaced by z1]. The case of c = e is noteworthy. Eq. (87) reduces to:

(ez1)z2 = ez1 z2 e2π i z 2 N’c ,     N’c ≡ [1/2 – lm z1/2π]                                 (88)

If z2 = n where n is any integer, then e2πinNe′= 1 (since N’c is an integer by definition of the bracket notation). Thus, we recover eq. (40).

Us test eq. (88) by substituting z1 = −iπ. Then, N’c = 1 and hence (e−πi)z = eiπz .

This result may seem strange, but it is a consequence of our definition of the generalized exponential function, cz= ezLnc, which employs the principal value of the logarithm. Indeed

(e-i π)z = (-1)z = ez Ln (-1) = ei πz,

Since Ln(−1) = iπ. We conclude that eq. (34) can be violated, even for the ordinary exponential function.

Ultimately, the real difficulty with (cz1)z2is that it is simultaneously a generalized exponential function and a generalized power function. Thus, if z2 is a non-integer, it may be more convenient to treat (cz1)z2as a multi-valued function. That is, in this latter convention, we treat the generalized exponential function cz1 = ez1 Ln c as a single-valued function (using the principal value definition of the logarithm in the exponent), whereas we treat the generalized power function (cz1)z2= ez2 ln(cz1) as a possible multi-valued function:

(cz1)z2= ez2 ln(cz1) = ez2 ln(ez1 Ln c) = ez2(z1 Ln c+2πik) = ez2z1 Ln c e2πiz2k = cz1z2 e2πikz2 ,

Wherekis an arbitrary integer [see eq. (48)]. In particular, for z2 a non-integer, (cz1)z2is a multi-valued function, with branches corresponding to different choices of k. For example, for c = z1 = z2 = i, we recover eq. (78). One might be tempted to call the k = 0 branch the principal value of (cz1)z2, in which case eq. (34) would be valid. Clearly, we must define our conventions carefully if we wish to manipulate expressions involving exponentials of exponentials.

Finally, the equations (35) and (36) may be broken. The procedure is roughly identical to that described in equations (82) and (83):

(ab)z = ez Ln (ab) = ez ( Ln a + Ln b + 2π i N + ) = azbze2πizN+

(a/b)z = ez Ln (a/b) = ez ( Ln a - Ln b + 2π i N - ) = az e2πizN -/bz

Where N± is calculated by eq. (13) [where z1 and z2 are replaced by a and b, respectively]. N = 0, and eqs. (35) and (36) are met if Re a >0 and Re b >0.

NUMERICALS:

1) Express log (2 − 3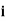) in Cartesian form.

Solution:

Since |2 − 3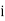| = 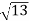, and arg (2 − 3i)=2kπ− Tan−1(3/2),

Log (2 – 3i) = ln √13 + [ 2kπ – Tan-1(3/2)]i = ½ ln 13 + [ 2k π – Tan -1 (3/2)]i.

Some of the properties of the real logarithm function have counterparts in the complex logarithm. For example, if , then

elog z  = eln r + θi = eln r eθ i  = r eθi = z,                                             (3.22a)

(as should be expected from the definition of 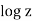), and

Log (ez ) = log (ex+yi) = ln (ex) + (y+ 2 kπ ) i                     ( k an integer)

= x + yi + 2kπi

= z + 2kπi.                                                    (3.22b)

In real analysis the counterpart of this equation is 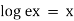. The 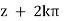on the right side of 3.22b is a reflection of the facts that log z is multiple-valued and the logarithm is the last operation on the left side of the equation.

If 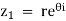and 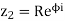, then

Log(z1z2) = log [ r Re(θ+ϕ)i] = ln (rR) + (θ + ϕ+ 2pπ)i                      (p an integer)

= (ln r + θi) + (ln R + ϕi) + 2pπi.

But 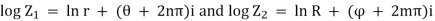. Hence,

Log(z1z2) = (log z1 – 2n π i ) + (log z2 – 2mπi) + 2pπi

= log z1 + log z2 + 2(p – n – m) πi

= log z1 + log z2 + 2kπi.                                           (3.23a)

Similarly,

Log(z1/ z2) = log z1 – log z2 + 2kπi.                                       (3.23b)

The last two results must be approached with care. Because the logarithm function is multiple-valued, each equation must be interpreted as saying that given values for the logarithm terms, there is a value of k for which the equation holds. It is also possible to write these equations in the forms

Log(z1z2) = log z1 + log z2,                            (3.24 a)

Log (z1/z2) = log z1 – log z2.                          (3.24b)

We interpret them as saying that given values for two of the logarithm terms, there is a value of the third logarithm for which the equation is valid.

Multiple-valued functions cannot be analytic. To see why, consider the derivative of ,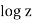

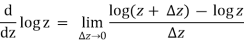
This limit must exist, be unique, and be independent of the mode of approach of 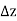to 0. But this is impossible if there is an infinity of possible choices for and for 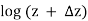for each value of 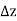. Thus, only single-valued functions can have derivatives. We therefore ask if it is possible to restrict the range of the logarithm function to obtain an analytic function; that is, can we make 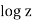single-valued in such a way that it will have a derivative. The answer is yes, and there are many ways to do it. The most natural way to make log z single-valued is to restrict 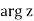in equation 3.21 to its principal value 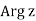. When this is done, we denote the resulting single-valued function by

Log z = ln |z| + (Arg z)i,       z ≠ 0.                (3.25)

Is Log z an analytic function? The answer is yes in a suitably restricted domain. To see this, we note that at any point on the negative real axis, the imaginary part of Log z is a discontinuous function. Theorem 2.4 implies therefore that 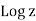is discontinuous at points on the negative real axis, and Log z cannot be differentiable thereon. Suppose we consider the domain . f we express Log z in the form

Log z = ln r + θi,           - π < θ < π

Partial derivatives of its real and imaginary parts are

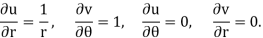
Since these derivatives satisfy Cauchy-Riemann equations 2.22 and are continuous in the domain 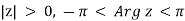, it follows that Log z is an analytic function in this domain. According to formula 2.23a, the derivative of 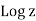is

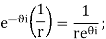
That is,

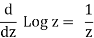
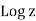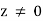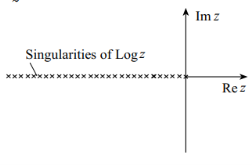
Thus, is analytic in the domain |z| > 0, −π< Arg z <π. It is defined for all , but analytic only in the aforementioned domain. Points on the negative real axis and are singularities of , but they are not isolated singularities.

The restriction of arg z to Arg z in the definition of Log z produced a branch of the multiple-valued logarithm function called the principal branch of log z. Other choices for arg z lead to different branches. For example, we could restrict arg z to argφz. When this is done, we denote the resulting branch of the logarithm function by

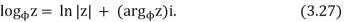
These branches are analytic in any domain that does not contain z = 0, the branch point, or points on the branch cut, the half-line through z = 0 making an angle of φ radians with the positive real axis

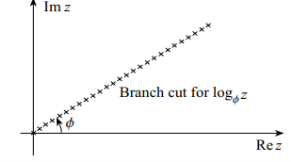
In real variable work, the notation 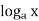indicates that a is the base of the logarithm function. This is not the case in complex function theory. Only e is used as the base for logarithms, and φ in indicates a particular branch of the function.

2) Find branch points and branch cuts for the function log3π/2(3 − 5z).

Solution:

Branch points occur at the zeros of 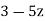, there being only one . Branch cuts occur where one of the arguments of 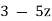is equal to 3π/2. If we set , then . If θ is an argument of this complex number, then

For θ to be equal to 3π/2, the first of these requires x = 3/5, and then the second implies that

The branch cut is therefore the vertical half-line above z = 3/5, including z = 3/5, (Figure 3.22).

Q. Let f(z)=z2+zf(z)=z2+z Find the winding number of f∘γf∘γ around 0 for each of the following curves.

1. γ1γ1 = circle of radius 2.
2. γ2γ2 = circle of radius 1/2.
3. γ3γ3 = circle of radius 1.

Solution:

f(z)f(z) has zeros at 0, −1. It has no poles.

So, ff has no poles and two zeros inside γ1γ1.

The argument principle says Ind(f∘γ1,0)=Zf,γ1−Pf,γ=2Ind(f∘γ1,0)=Zf,γ1−Pf,γ=2

Likewise ff has no poles and one zero inside 

γ2γ2, so Ind(f∘γ2,0)=1−0=1Ind(f∘γ2,0)=1−0=1

For γ3γ3 a zero of ff is on the curve, i.e., f(−1)=0f(−1)=0, so the argument principle doesn’t apply. The image of γ3γ3 is shown in the figure below – it goes through 0.

The image of 3 different circles under f(z)=z2+zf(z)=z2+z.

Q. Show all 5 zeros of z5+3z+1z5+3z+1 are inside the curve C2:|z|=2C2:|z|=2.

Solution:

Let f(z)=z5f(z)=z5 and h(z)=3z+1h(z)=3z+1. Clearly all 5 roots of ff (really one root with multiplicity 5) are inside C2C2.

Also, clearly, |h|<7<32=|f||h|<7<32=|f| on C2C2. The corollary to Rouchés theorem says all 5 roots of f+h=z5+3z+1f+h=z5+3z+1 must also be inside the curve.

Q. Show z+3+2ezz+3+2ez has one root in the left half-plane.

Solution:

Let f(z)=z+3f(z)=z+3, h(z)=2ezh(z)=2ez.

Consider the contour from −iR−iR to iRiR along the yy-axis and then the left semicircle of radius RR back to −iR−iR. That is, the contour C1+CRC1+CR shown below.

To apply the corollary to Rouchés theorem we need to check that

(for RR large) |h|<|f||h|<|f| on C1+CRC1+CR. On C1C1, z=iyz=iy, so

|f(z)|=|3+iy|≥3,   |h(z)|=2|eiy|=2.(12.1.23)(12.1.23)|f(z)|=|3+iy|≥3,   |h(z)|=2|eiy|=2.

So |h|<|f||h|<|f| on C1C1.

On CRCR, z=x+iyz=x+iy with x<0x<0 and |z|=R|z|=R. So,

|f(z)|>R−3 for R large, |h(z)|=2|ex+iy|=2ex<2 (since x<0).(12.1.24)(12.1.24)|f(z)|>R−3 for R large, |h(z)|=2|ex+iy|=2ex<2 (since x<0).

So |h|<|f||h|<|f| on CRCR.

The only zero of ff ia at z=−3z=−3, which lies inside the contour.

Therefore, by the Corollary to Rouchés theorem, f+hf+h has the same number of roots as ff inside the contour, that is 1. Now let RR go to infinity and we see that f+hf+h has only one root in the entire half-plane.

References:

1. Elias M. Stein & Rami Shakarchi, Complex Analysis, Princeton University press, Princeton and Oxford, 2003.

2. G. F. Simmons, Introduction to Topology and Modern Analysis, Mcgraw-Hill, Edition 2004.

3. Joseph Bak and Donald Newman, Complex analysis (2ndEdition), Undergraduate Texts in Mathematics, Springer-Verlag New York, Inc., New York, 1997.

4. COMPLEX ANALYSIS Elias M. Stein& Rami ShakarchiPRINCETON