Unit - 1
Automorphism
1.1.1 Automorphism
An automorphism in mathematics is an isomorphism from one mathematical object to another. It's a symmetry of the object in some ways, as well as a way of mapping the object to itself while keeping all of its structure. The automorphism group is the collection of all an object's automorphisms. It is, in a broad sense, the object's symmetry group.
In mathematics, an automorphism is an isomorphism between two mathematical objects. In some aspects, it's a symmetry of the thing, as well as a method of mapping the object to itself while maintaining all of its structure. All of an object's automorphisms are collected in the automorphism group. It is, in a general sense, the symmetry group of the item.
The specific definition of an automorphism is determined by the sort of "mathematical object" in question, as well as what defines a "isomorphism" of that object. The most general context in which these concepts have meaning is category theory, an abstract field of mathematics. Abstract objects and morphisms between them are the focus of category theory.
An automorphism is a type of automorphism in category theory.
An automorphism preserves the structural properties of a group, e.g.
- The type of "mathematical object" in question, as well as what determines a "isomorphism" of that object, dictate the specific definition of an automorphism. Category theory, an abstract subject of mathematics, is the most general environment in which these concepts have meaning. Category theory is concerned with abstract objects and their morphisms.
- An automorphism is a type of automorphism in which one object transforms into another one.
- In set theory, an automorphism is an arbitrary permutation of the elements of a set X. The symmetric group on X is sometimes known as the automorphism group of X. The set of integers Z, viewed as a group under addition in elementary arithmetic, has a single nontrivial automorphism: negation. However, when viewed as a ring, it merely has the trivial automorphism. Negation is a word that is used to express the absence of something.
- An automorphism of a graph is a permutation of nodes that preserves edges and non-edges in graph theory. If two nodes are connected by an edge, their pictures are also connected by the permutation.
- In geometry, an automorphism is referred to as a space motion. There is also specialised terminology:
- An automorphism is a self-isometry in metric geometry. The automorphism group is a subset of the automorphism group.
- An automorphism is a biholomorphic map (also known as a conformal map) from a surface to itself in the category of Riemann surfaces. The automorphisms of the Riemann sphere, for example, are Möbius transformations.
- A differentiable manifold's automorphism M is a diffeomorphism between M and M. Diff is another name for the automorphism group (M).
Continuous mappings are morphisms between topological spaces in topology, and an automorphism of a topological space is a space's homeomorphism to itself, also known as self-homeomorphism (see homeomorphism group). It is not necessary for a morphism to be bijective in this situation to be an isomorphism.
Numericals:
1) The identity on real numbers is called ϕ automorphism.
We complete the proof of the problem in this assertion.
Let x be any positive integer.
Seeking a contradiction, assume that ϕ(x)≠x.
Consider the following two scenarios:
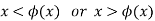
First, suppose that x<ϕ(x). Then there is a rational number q that is equal to
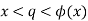
Then there's
ϕ(x)<ϕ(q) by Claim 2 since x<q
= Claim 4 applies to q because q is reasonable.
<ϕ(x) by the choice of q,
This is an inconsistency. Consider the following scenario. When x>ϕ(x).
There is a rational number q that has the property of
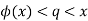
Then, using the same logic as before, we arrive at
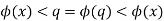
Which is a contradiction. As a result, in any instance, we arrived at a contradiction, and as a result,
We must have ϕ(x)=x for all real numbers x. This proves that the automorphism ϕ: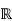
→
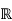is the identity map.
2) Determine the automorphism group of 
over Q.
Let σ∈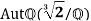
be an automorphism of 
over Q.
Then σ is determined by the value σ(
since any element α of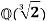 
can be written as 
for some a,b,c∈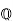
and
=
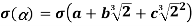
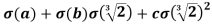
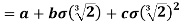
Because Q's elements are σ fixed
Note that σ(
is a root of the minimal polynomial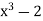 
and
.
But the roots of 
are not real except 
, hence not in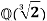 
.
Thus we must have σ(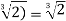
.
Hence σ is trivial.
In conclusion, we have
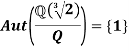
1.1.2 Inner automorphism
In abstract algebra an inner automorphism is an automorphism of a group, ring, or algebra given by the conjugation action of a fixed element, called the conjugating element. These inner automorphisms form a subgroup of the automorphism group, and the quotient of the automorphism group by this subgroup gives rise to the concept of the outer automorphism group.
If G is a group and g is an element of G (alternatively, if G is a ring, and g is a unit), then the function
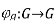
g refers to this as (right) conjugation (see also conjugacy class). For every, this function is an endomorphism of G:
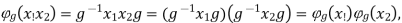
Where the second equality is given by the insertion of the identity between X1 and X2 Furthermore, it has a left and right inverse, namely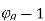 
Thus, 
is bijective, and so an isomorphism of G with itself, i.e. an automorphism. An inner automorphism is any automorphism that arises from conjugation.[1]
When discussing right conjugation, the expression 
is often denoted exponentially by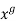 
This notation is used because composition of conjugations satisfies the identity: 
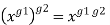for all 
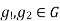This shows that conjugation gives a right action of G on itself.
1.1.3 Automorphism group
If an object's automorphisms constitute a set (rather than a proper class), they form a group under morphism composition. The automorphism group of X is the name given to this group.
Closure
Another automorphism is the composition of two automorphisms.
Associativity
The associative nature of morphism composition is part of the notion of a category.
Identity
The identity morphism from an item to itself, which is an automorphism, is called the identity.
Inverses
Every isomorphism has an inverse, which is also an isomorphism, and the inverse is an automorphism because it is also an endomorphism of the same object.
If the category C is evident from context, the automorphism group of an object X in that category is called AutC(X), or simply Aut(X).
Key takeaways:
- In some cases, the identity morphism (identity mapping) is referred to as the trivial automorphism.
- A graph automorphism is a symmetry in which the graph is mapped onto itself while maintaining the edge–vertex connectivity.
Numericals
1.Prove that the automorphisms of G form a group Aut(G) under composition.
ANSWER-
Let φ and ψ be automorphisms of G.
We need to check that φ ◦ ψ is also an automorphism.
But the composition of group homomorphisms is a group homomorphism, and a composition of bijections is a bijection, so
φ ◦ ψ
Is an isomorphism from G to G.
We then need to verify that it satisfies the axioms of a group.
It is associative, because composition of any kind of functions always is (Proposition from the Appendix). It has an identity, namely the identity map. And by definition, being an automorphism, it has an inverse. So Aut(G) is a group.
2.Let G = G1 × G2 be a finite group with gcd(|G1|, |G2|)) = 1. Then every subgroup H of G is of the form H = H1 × H2 where Hi is a subgroup of Gi for i = 1, 2.
ANSWER-
Let H be a subgroup of G.
Let π be the natural projection from G to Gi .
Then the restriction of πi to H gives homomorphisms from H to Gi for i = 1, 2. Let Hi = πi(H) for i = 1, 2. Then clearly H ≤ H1 × H2 and Hi ≤ Gi for i = 1, 2.
Then H/Ker(π1) ∼= H1 implies that |H1| | |H| similarly |H2| | |H|.
But gcd(|H1|, |H2|) = 1 implies that |H1||H2| | |H|.
So H = H1 × H2. 2.6. Let H ✂ G and K ✂ G. Then H ∩ K ✂ G.
3. Show that we can define a map ϕ
ANSWER-
G/H ∩ K −→ G/H × G/K g(H ∩ K) → (gH, gK)
For all g ∈ G and that ϕ is an injective homomorphism.
Thus G/(H ∩ K) can be embedded in G/H ×G/K.
Deduce that if G/H and G/K or both abelian,
Then G/H ∩ K abelian.
1.2.1 Finite automorphism groups
THEOREM 1. A finitely generated group G has a finite automorphism group if and only if it has a central cyclic subgroup of finite index.
PROOF: First, we'll show that these requirements are sufficient. We can assume that G is infinite and so a finite and central extension of an infinite cyclic group if we do so. The centre Z of G has a finite index in G, hence it is finitely generated according to Schreier's subgroup theorem. As a result, Z is the direct sum of an infinite cyclic group and a finite abelian group T. As a result, Hom(G/if, Z) = HomGjZ, T) and Aut(G/Z) are finite. Finally, once we prove that Aut(Z) is finite, we can use the following Corollary. This, however, is the result of another application of the Corollary. If Aut(G) is finite, then GZ is finite because it is isomorphic to G's inner automorphism group. Z will be finitely generated again, thanks to Schreier's theorem. In opposition to the theorem, we can assume that Z contains two or more infinite cyclic components in a direct decomposition into cyclic groups. Let Z = W x () x (6) be the subgroups produced by components a and b, respectively. Write ma> = wa> + rta + ta>b for the factor set M, where w>e W, sa>, and ta> are all integers. Let (w) = wor w W, (a) = ma + rib, (b) = pa + qb be the automorphism of Z, where m,n,p, and q are all integers, and mq— np = 1. The factor set (M) can thus be expressed as (ma) = wt + s r.a + t'b, where s'a =msΛtβ + ptob3 and Vatβ = nsa>β +
QtΛtβ. As a result, So = s>, To = tat, SO = s, and To = trt are GZ factor sets with integral values, and SQ — mS0 + pT0, To = nS0 + qT0. The proof is now reduced to the following problem by Lemmas 1 and 2: Find as many quadruplets (m, n, p, q) of integers as possible. The factor sets mS0 + pT0 and nS0 + qT0 are equal to the factor sets So and To, respectively, and mq — np = 1. To put it another way, the factor sets (m —)SO + pT0 and nS0 + (q —)T0 are both trivial factor sets. If GjZ has order h, however, hS0 and hT0 are both equal to the trivial factor set (3; p. 223).
As a result, for every integer k, the following values for m, n, p, and q suffice: h p = -h2 k -hk2 -h q = hk + l m = -h2 - hk + 1 n — h p = -h2 k -hk2 -h q = hk + l m = -h2 - hk + 1 n — h p = -h2 k -hk2 -h q
1.2.2 Infinite Cyclic Group
An infinite cyclic group is a cyclic group G such that
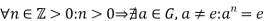
An infinite cyclic group is a cyclic group G such that:
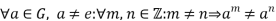
Where e denotes G's identity element.
That is, so that all of a's powers are distinct.
An infinite cyclic group is represented as follows:
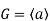
This states that G is generated by a single infinite-order element.
The additive group of integers (Z,+) creates an infinite cyclic group from Integers under Addition form Infinite Cyclic Group. As a result, the infinite cyclic group is frequently denoted by the letter Z. This is supported by the fact that, according to Cyclic Groups of the Same Order are Isomorphic, Z is isomorphic to a.
A cyclic group is also known as a free group on one generator.
If aG generates an infinite cyclic group, then aa is an infinite order element, and all powers of an are different.
Thus:
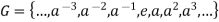
1.2.3 Applications of factor groups to automorphism groups
- Virtually cyclic groups
If a group contains a finite index cyclic subgroup, it is said to be virtually cyclic (the number of cosets that the subgroup has). To put it another way, each element in a nearly cyclic group can be obtained by multiplying a cyclic subgroup member with a member of a finite set. Every cyclic group, like every finite group, is nearly cyclic. The direct product of Z/nZ and Z, in which the factor Z has finite index n, is an example of an infinite group that is nearly cyclic if and only if it is finitely produced and has exactly two ends. A Gromov hyperbolic group's abelian subgroups are all virtually cyclic.
- Locally cyclic groups
A locally cyclic group is one whose finitely produced subgroups are all cyclic. The additive group of rational numbers, for example, is a set of integer multiples of a single unit fraction, the inverse of their lowest common denominator, which forms a cyclic group of integer multiples of this unit fraction as a subgroup. Locally, a group is cyclic.
- Cyclically ordered groups
A cyclically ordered group is one that has a cyclic order that is maintained by the group structure. Every cyclic group can be given a structure that is consistent with the ordering of the integers as a cyclically ordered group (or the integers modulo the order of the group). A cyclically ordered group's finite subgroups are all cyclic.
- Metacyclic and polycyclic groups
A metacyclic group is one that contains a cyclic normal subgroup with a cyclic quotient. The cyclic groups, dicyclic groups, and direct products of two cyclic groups are among these groups.
- Cyclic group
A cyclic group or monogenous group is a group produced by a single element in n group theory, a branch of abstract algebra. It's a collection of invertible items with a single associative binary operation, in other words and it contains an element g such that by repeatedly applying the group operation to g or its inverse, every other element of the group may be obtained. Each element can be expressed as a multiple of g in additive notation or as a power of g in multiplicative notation. The element g is referred to as a group generator. Every infinite cyclic group is isomorphic to Z, the integers' additive group. The additive group of Z/nZ, the integers modulo n, is isomorphic to any finite cyclic group of rank n. Every cyclic group is an abelian group (i.e., it has a commutative group operation), and every finitely produced abelian group is a direct product of cyclic groups. Every prime-order cyclic group is a simple group that cannot be subdivided into smaller ones. The cyclic groups of prime order are one of the three infinite classes in the classification of finite simple groups. The prime order cyclic groups are thus among the basic blocks from which all groups can be constructed.
- Symmetric group
The symmetric group defined over any set in abstract algebra is the group whose elements are all the bijections from the set to itself and whose group operation is function composition. The permutations that can be done on the n symbols make up the finite symmetric group defined over a finite set of n symbols. [1] Because there are ( factorial) permutations,
Despite the fact that symmetric groups can be created on infinite sets, this article focuses on finite symmetric groups, including their applications, elements, conjugacy classes, finite presentations, subgroups, automorphism groups, and representation theory. The term "symmetric group" will be used throughout this text to refer to a symmetric group on a finite set.
The symmetric group has applications in Galois theory, invariant theory, Lie group representation theory, and combinatorics, among other fields of mathematics. According to Cayley's theorem, every group G is isomorphic to a subgroup of the symmetric group on (the underlying set of) G.
- Applications
The Galois group of the general polynomial of degree n is the symmetric group on a set of size n, and it plays an important role in Galois theory. The symmetric group works on the variables of a multi-variate function in invariant theory, and the functions left invariant are known as symmetric functions. Through the concepts of Schurfunctors, the representation theory of the symmetric group plays a crucial role in the representation theory of Lie groups. The symmetric group is the Coxeter group of type An, which appears as the Weyl group of the generic linear group in Coxeter group theory. The symmetric groups, their elements (permutations), and their representations provide information in combinatorics. As well as the Bruhat order. Permutation groups are subgroups of symmetric groups that are researched extensively due to their usefulness in understanding group actions, homogeneous spaces, and automorphism groups of graphs, such as the Higman–Sims group and the Higman–Sims graph.
Numericals-
1.Suppose that F is a finite field with say |F| = p m = q and that V has finite dimension n over F. Then find the order of GL(V ).
ANSWER-
Let F be a finite field with say |F| = p m = q and that V has finite dimension n over F.
Then |V | = q n for any base w1, w2, ..., wn of V ,
There is unique linear map θ : V → V such that viθ = wi for i = 1, 2, ..., n.
Hence |GL(V )| is equal to the number of ordered bases of V , in forming a base w1, w2, ..., wn of V we may first choose w1 to be any nonzero vector of V then w2 be any vector other than a scalar multiple of w1. Then w3 to be any vector other than a linear combination of w1 and w2 and so on. Hence |GL(V )| = (q n − 1)(q n − q)(q n − q 2 )....(q n − q n−1 ).
2. Let α ∈ Aut G and let H = {g ∈ G : g α = g}. Prove that H is a subgroup of G, it is called the fixed point subgroup of G under α.
ANSWER-
Let g1, g2 ∈ H.
Then g α 1 = g1 and g α 2 = g2.
Now (g1g2) α = g α 1 g α 2 = g1g2 (g −1 2 ) α = (g α 2 ) −1 = g −1 2 ∈ H.
So H is a subgroup.
3. Let n be a positive integer and F a field. For any n×n matrix y with entries in F let y t denote the transpose of y. Show that the map
ANSWER-
φ : GLn(F) → GLn(F)
x → (x −1 ) t
For all x ∈ GLn(F) is an automorphism of GLn(F) and that the corresponding fixed point subgroup consist of all orthogonal n × n matrices with entries in F. ( That is matrices y such that y t y = 1)
Solution
φ(x1x2) = [(x1x2) −1 ] t
= [x −1 2 x −1 1 ] t
= (x −1 1 ) t (x −1 2 ) t
= φ(x1)φ(x2)
Now if φ(x1) = 1 = (x −1 1 ) t , then x −1 1 = 1.
Hence x1 = 1. So φ is a monomorphism.
For all x ∈ GLn(F) there exists x1 ∈ GLn(F) such that φ(x1) = x. Let x1 = (x −1 ) t .
So we obtain φ is an automorphism. Let H = {x ∈ GLn(F) : φ(x) = x}.
We show in the previous exercise that H is a subgroup of GLn(F).
Now for x ∈ H φ(x) = x = (x −1 ) t implies xxt = 1.
That is the set of the orthogonal matrices.
Recall that if G = G1 × G2, then the subgroup H of G may not be of the form H1 × H2
As H = {(0, 0),(1, 1)} is a subgroup of Z2 × Z2 but H is not of the form H1 × H2 where Hi is a subgroup of Gi .
But the following question shows that if |G1| and |G2| are relatively prime,
Then every subgroup of G is of the form H1 × H2.
A typical subgroup of a group is one that maintains its stability despite all automorphisms. Any characteristic subgroup of is also a normal subgroup of for every because the map is an automorphism (especially an inner automorphism) on.
Examples
Every group has a characteristic subgroup, and the trivial subgroup of a group is also characteristic.
Assume that is a natural number that divides the order of. The set of elements for which divides is thus a distinctive subgroup of. Because each subgroup of a cyclic group is cyclic, each subgroup of a cyclic group is also a characteristic group.
However, not every cyclic group of an Abelian group is characteristic in general. Because any permutation of its non-identity elements is an automorphism, the Klein 4-group has no non-trivial characteristic subgroups. The group also has no nontrivial characteristic subgroups for an odd prime.
Indeed, the mapping is an automorphism for every reasonably prime to, as is the mapping. As a result, if ( ) is a member of a characteristic subgroup, then so is, and these two clearly create; and if ( ) is an element of a characteristic subgroup, then setting, we see that is an element of this characteristic subgroup; so is all of.
This idea also shows that there are no non-trivial characteristic subgroups for any natural number. In actuality, the characteristic subgroups of are of the form for some integer.
1.3.1 Fully characteristic subgroup
A fully characteristic subgroup (also, fully invariant subgroup; cf. Invariant subgroup), H, of a group G is a group that remains invariant under every endomorphism of G; that is, a fully characteristic subgroup (also, fully invariant subgroup; cf. Invariant subgroup) of G is a group that remains invariant under every endomorphism of G.
∀φ∈End(G)：φ[H] ≤ H.
Every group is divided into two separate subgroups: the unsuitable subgroup and the trivial subgroup. The commutator subgroup of a group is always a fully distinctive subgroup.
Every G endomorphism gives rise to a G/H endomorphism, yielding a map End(G) End(G/H).
1.3.2 Characteristic Subgroups of Normal Subgroups
Theorem 1. Let's say there's a group, and there's a normal subgroup of it. Assume that is a typical subgroup of Then is a normal subgroup of; also, if is a characteristic subgroup of, then is a subgroup of Proof. Assume that is a (inner) automorphismon. Then is typical (normal) in if and only if is an automorphismon.
Theorem 2. If and only if is equivalent to for some characteristic subgroup of, an equivalence relation is compatible with the group law on and every automorphism on.
Proof. Obviously, must be of the form, where is the set of elements that is identical to under. A characteristic subgroup exists for any and all automorphisms on.
If is a distinctive subgroup, on the other hand, the relationship is compatible with the group rule; it also entails.
Functions giving subgroups
The group as a whole, as well as the trivial subset, are distinctive. Any process that produces a distinct subgroup of a given group must also produce a characteristic subgroup. A distinctive subgroup, for example, is found at the centre of a group. The collection of elements that commute with all other elements is referred to as the centre. It is distinctive in that the attribute of commuting with all elements does not alter when automorphisms are performed. Similarly, because any automorphism will take a maximal subgroup to a maximal subgroup, the Frattini subgroup, which is defined as the intersection of all maximal subgroups, is distinctive.
Because an automorphism permutes the generating commutators, the commutator subgroup is distinctive.
Non-examples
Because every characteristic subgroup is normal, finding non-characteristic subgroups is a simple way to uncover examples of non-characteristic subgroups. For example, in the symmetric group on three elements, the subgroup of order two is a non-normal subgroup.
There are also examples of non-characteristic normal subgroups. The following are the most basic instances. Take any G that isn't trivial. Consider G to be a subset of. Because it is not invariant under the exchange automorphism, the initial copy G is a normal subgroup but not a characteristic one.
Numericals:
1) Let H be a subgroup of a group G. We call H characteristic in G if for any automorphism σ∈Aut(G), we have σ(H)=H.
(a) Prove that if σ(H)⊂H for all σ∈Aut(G), then H is characteristic in G.
(b) Demonstrate that G's centre Z(G) is characteristic.
Solution:
(a) If σ(H)⊂H for all σ∈Aut(G), then H is characteristic in G
Because σ is an automorphism of G, the inverse σ−1 is likewise an automorphism of G.
Based on the assumption
As a result of our σ application, we have
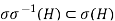
After that, we get
Because both endpoints of the line are H, the inclusion is actually the equality.
As a result, we get
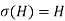
In the group G, the subgroup H is distinctive.
(b) In G, the centre Z(G) is distinctive.
By part (a), it suffices to prove that σ(Z(G))⊂Z(G) for every
Automorphism σ∈Aut(G) of G.
Let x∈σ(Z(G)). Then there exists y∈Z(G) such that x=σ(y).
To show that x∈Z(G), consider an arbitrary g∈G.
Then since σ is an automorphism, we have G=σ(G).
Thus there exists g′ such that g=σ(g′).
We have
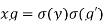
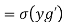(since is a homomorphism)
(since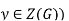 
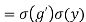(since is a homorphism)
Since this is true for all g∈G, it follows that x∈Z(G), and thus
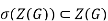
The proof is now complete.
2) Prove the following.
(a) If H is a normal subgroup of G, then H is a characteristic subgroup of G.
(b) H is typical in G if it is the only subgroup of G of a particular order.
(c) Assume that a subgroup K in a group H is characteristic, and that H is a normal subgroup of G. Then in G, K is a normal subgroup.
Solution:
(a) If H is a normal subgroup of G, then H is a characteristic subgroup of G.
For each g∈G, define a map ϕg:G→G defined by ϕg(x)=gxg−1. This is an automorphism of G with the inverse ϕg−1.
Since H is characteristic, we have ϕg(H)=H, equivalently we have gHg−1=H.
Therefore H is a normal subgroup of G.
(b) H is typical in G if it is the only subgroup of G of a particular order.
For any automorphism ϕ∈Aut(G), we have ϕ(H)⊂ϕ(G)=G and |H|=|ϕ(H)|. The uniqueness of H implies that H=ϕ(H) and thus H is characteristic.
(c) K is characteristic in H and H is normalG. Then K is a normal subgroup in G.
For each g∈G, consider the automorphism ϕg of G defined in the proof of (a).
Since H◃G, we have ϕg(H)=H.
Hence the restriction ϕg|H belongs to Aut(H).
Now since K is characteristic in H, we have ϕg|H(K)=K, or equivalently we have gKg−1=K and K is normal in G.
References:
1. M. Artin, Abstract Algebra, 2nd Ed., Pearson, 2011.
2. David S. Dummit and Richard M. Foote, Abstract Algebra, 3rd Ed., John Wiley and Sons (Asia) Pvt. Ltd., Singapore, 2004.
3. J.R. Durbin, Modern Algebra, John Wiley & Sons, New York Inc., 2000.
