Unit - 2
Commutator subgroup and its properties
2.1.1 The Commutator Subgroup
Let G stand for any group. If a, b G, then the element aba1 b 1 is the commutator of a and b. Naturally, if a and b commute, aba1 b 1 = e. Define C as the set C = x1x2 •••xn | n 1 | n I where xi is a commutator in G.
In other words, C is the set of all finite commutator products in G. After that, there's Proposition 1. If G is any group, then C C G is the answer. Proof. First, we have e = eee1 e 1 C, and then we have e = eee1 e 1 C.
As a result, C is nonempty and holds the identity
If c, d are both C, we get c = x1x2 •••xn and d = y1y2 •••ym, with each xi and yj being a commutator in G.
Cd = x1x2 ••• xny1y2 •••ym C, then
Since this is just another finite commutator product
We also have d −1 = (x1x2 ···xn) −1 = x −1 n ··· x −1 2 x −1 1.
If xi = aibia−1 i b −1 i, then x −1 i = biaib−1 i a −1 i,
Which is also a commutator.
Thus c −1 ∈ C, and C ≤ G.
To prove C is a normal subgroup of G, let g ∈ G, and c = x1x2 ···xn∈ C.
Then we have gcg−1 = gx1x2 ···xng−1 = (gx1g −1 )(gx2g −1 )···(gxng−1 ),
- Where we have just inserted gg−1 = e between xi and xi+1 for each i< n.
- Now, if xi = aibia−1 i b −1 i , then we have gxig−1 = gaibia−1 i b −1 i g −1 = (gaig−1 )(gbig−1 )(ga−1 i g −1 )(gb−1 i g −1 )
Now note that
(gaig−1 ) −1 = (g −1 )−1a −1 i g −1 = ga−1 i g −1 ,
If we substitute ai with bi, we get the same statement. So there you have it.
Gxig−1 = (gaig−1 )(gbig−1 )(gaig−1 ) −1 (gbig−1 ) −1 ,
Which is a commutator.
Now, from (1), we have
Gcg−1
Is a product of commutators, and so gcg−1 ∈ C.
C C G is the result. The commutator subgroup of G is also known as the derived subgroup of G. It is indicated by C = G0 or C = [G, G], and it is also denoted as C = G0 or C = [G, G]. In one sense, the commutator subgroup can be used as a measure of how distant a group is from being Abelian, because if G is Abelian, then C = e. We get the following result in particular.
Theorem 1
Assume G is a group, and C is the commutator subgroup of G.
Assume that N C G. If and only if C N, G/N is Abelian. G/C is Abelian in particular.
Proof.
First assume that G/N is Abelian.
Let a, b ∈ G.
Because we assume G/N is Abelian, (aN)(bN) = (bN)(aN), and abN = baN according to the concept of coset multiplication in the factor group.
Now, we know
AbN = baN implies ab(ba) −1 ∈ N, where ab(ba) −1 = aba−1 b −1 , and so aba−1 b −1 ∈ N.
Any commutator in G is an element of N, and since N is a subgroup of G, any finite product of commutators in G is an element of N. As a result, C = N. Assume that C N, and that a, b, and G are all positive.
Then aba1 b 1 N and ab(ba) 1 N come next.
This means that abN = baN, or (aN)(bN) = (bN) (aN).
Because a and b were picked at random, G/N Abelian holds for any elements aN, bN G/N.
2.1.2 Commutator Subgroup properties
Early in the nineteenth century, the study of groups developed from the study of theoretical equations, notably from the endeavour to determine roots of a polynomial in terms of its coefficients. The theory of groups, which had previously been applied to practically every discipline of mathematics, has evolved in a variety of directions. It becomes crucial in a variety of mathematical specialties.
I've looked into Commutators, which are an important aspect of groups that are related to solvable groups. In this paper, I've examined commutator properties and plan to provide some of the most important commutator theorems in relation to solvable groups. Throughout the work, I have assumed that the group G is a finite group.
- Property- 1: Let xy∈G be elements of a group G, the (y,x) = (x,y)-1 [3]
Proof:
L.H.S: (y,x) = y-1x-1yx = (x-1y-1xy)-1 = y-1x-1yx
Hence, (y,x) = (x,y)-1
- Property-2:
Let x,y,z∈G be elements of a group G then
(xy,z) = (x,z)y(y,z) = (x,z)(x,z,y)(y,z) [4]
Proof:
Consider, (xy,z) = (xy)-1z-1(xy)z = y-1x-1z-1xyz
Consider, (x,z)y(y,z) = y-1(x,z)y(y,z)
= y-1x-1z-1xzyy-1z-1yz
= y-1x-1z-1xyz
Again, (x,z)(x,z,y)(y,z)
= x-1z-1xz(x,z)-1y-1(x,z)yy-1z-1yz
= x-1z-1xzz-1x-1zxy-1x-1z-1xzyy-1z-1yz
= y-1x-1z-1xyz
Hence, (xy,z) = (x,z)y(y,z) = (x,z)(x,z,y)(y,z)
- Property-3: Let x,y,z be elements of a group G. Then
(x,yz)=(x,z)(x,y)z=(x,z)(x,y)(x,y,z) [5]
Proof:
Consider, (x,yz) = x-1(yz)-1xyz = x-1z-1y-1xyz
Consider, (x,z)(x,y)z = (x,z)z-1(x,y)z
= x-1z-1xzz-1x-1y-1xyz
= x-1z-1y-1xyz
Again (x,z)(x,y)(x,y,z) = x-1z-1xzx-1y-1xyx-1(y,z)-1x(y,z)
=x-1z-1xzx-1y-1xyy-1x-1yxz-1x-1y-1xyz
= x-1z-1y-1xyz
Hence, (x,yz) = (x,z)(x,y)z = (x,z)(x,y)(x,y,z)
- Property-4:
Let x,y,z be elements of a group G, Then
(x,y-1,z)y(y,z-1,x)z(z,x-1,y)x = e, the identity of G. [6]
Proof:
Consider (x,y-1,z)y = y-1(x,y-1,z)y
= y-1(x,y-1)-1z-1(x,y-1)zy
= y-1yx-1yxz-1x-1yxy-1zy
= x-1yxz-1x-1y xy-1zy (a)
Similarly, (y,z-1,x)z = z-1(y,z-1,x)z
= z-1(y,z-1)-1x-1(y,z-1)xz
= z-1zy-1z-1yx-1y-1zyz-1xz
=y-1z-1yx-1y-1zyz-1xz (b) Again,
(z,x-1,y)x = x-1(z,x-1,y)x
= x-1(z,x-1)-1y-1(z,x-1)yx
= x-1xz-1x-1zy-1z-1xzx-1yx
=z-1x-1zy-1z-1xzx-1yx (c)
Now, Combining (a),(b),(c), we get
x-1y-1xz-1x-1yxy-1zy y-1z-1yx-1y-1zyz-1xz z-1x-1zy-1z-1xzx-1yx =e(identity)
Hence, (x,y-1,z)y(y,z-1,x)z(z,x-1,y)x = e, the identity of G.
- Property-5:
Let x,y,z be elements of a group G, then
(x,y,z)(y,z,x)(z,x,y)=(y,x)(z,x)(z,y)x(x,y)(x,z)y(y,z)x(x,z)(z,x)y [7]
Proof:
L.H.S. (x,y,z)(y,z,x)(z,x,y)
= (x,y)-1z-1(x,y)z(y,z)-1x-1(y,z)x(z,x)-1y-1(z,x)y
= y-1x-1yxz-1x-1y-1xyzz-1y-1zyx-1y-1z-1yzxx-1z-1xzy-1z-1x-1zxy
= y-1x-1yxz-1x-1y-1xzyx-1y-1z-1yxzy-1z-1x-1zxy
R.H.S. (y,x)(z,x)(z,y)x(x,y)(x,z)y(y,z)x(x,z)(z,x)y
= (y,x)(z,x)x-1(z,y)x(x,y)y-1(x,z)yx-1(y,z)x(x,z)y-1(z,x)y
= y-1x-1yxz-1x-1zxx-1z-1y-1zyxx-1y-1xyy-1x-1z-1xzyx-1y-1z-1yzxx-1z-1xzy-1z-1x-1zxy
= y-1x-1yxz-1x-1y-1xzyx-1y-1z-1yxzy-1z-1x-1zxy
Therefore, L.H.S. = R.H.S
- Property-6:
Let x,y,z be elements of a group G, then
(x,y,z) = ((z,x-1,y-1)xy)-1((y-1,z-1,x)zy)-1 [8]
Proof:
L.H.S (x,y,z) = (x,y)-1z-1(x,y)z
= y-1x-1yxz-1 x-1y-1xyz
R.H.S. ((z,x-1,y-1)xy)-1 = [(xy)-1(z,x-1,y-1)xy)]-1
= [y-1x-1(z,x-1)-1(y-1)-1(z,x-1)y-1xy]-1
= (y-1x-1xz-1x-1zyz-1xzx-1y-1xy)-1
= y-1x-1yxz-1x-1zy-1z-1xzx-1xy
=y-1x-1yxz-1x-1zy-1z-1xzy (a)
Again,
((y-1,z-1,x)zy)-1 = [(zy)-1(y-1,z-1,x)zy]-1
= [y-1z-1(y-1,z-1)-1x-1(y-1,z-1)xzy]-1
= [y-1z-1zyz-1y-1x-1 yzy-1z-1xzy]-1
= [z-1y-1x-1 yzy-1z-1xzy]-1
= y-1z-1x-1zyz-1y-1xyz (b)
Combining (a) and (b) we get
y-1x-1yxz-1x-1zy-1z-1xzyy-1z-1x-1zyz-1y-1xyz = y-1x-1yxz-1x-1y-1xyz
Hence, L.H.S=R.H.S and the proof follows:
- Property-7:
Let x,y be elements of a group G and suppose that z = (x,y) commutes with both x and y
Then (i)(xi,yj) = zij for all j [9]
(ii) 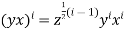 for all I [10]
for all I [10]
Proof:
Since x-1y-1xy = z, then we have y-1xy = xz where y-1xiy = (y-1xy)i = (xz)i = xizi as x and z commute. Conjugating by y which gives that
y-1(y-1xiy)y = y-1 (xizi)y = (xizi)zi = xiz2i
As y and z commute.
Repeating this argument j times. We conclude that
y-jxiyj = xizij and (xi,yj) = zij
Again, (ii) holds, for j=1, assuming the result for (i-1), we have

Since, by then follows at once, that is,
Hence 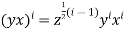 for all i
for all i
- Property-8:
Let x,y,z be element of a group G then
(i) If is commutes with z and if (x,G) is abelian then
(x,y,z)=(x,z,y) [11]
(ii) If (x,y) commutes with both x and y then
(xy-1)-1=(x-1,y)=(x,y-1) [12]
Proof:
First (x,y,z ) = (x,y)-1z-1(x,y)(z)
= y-1x-1yxz-1x-1y-1xyz
= x-1(xy-1x-1y)(xz-1x-1z)(z-1y-1xyz)
Furthermore, xy-1xy = (x-1,y) = (xm,y) for some positive integer m, we conclude easily by p-2 that (xm,y)∈(x,G) .
Thus, xy-1x-1y, and likewise xz-1x-1z lies in (x,G).
Hence, by hypothesis these two elements commute. It follows, therefore, that
(x,y,z) = x-1(xy-1x-1y)(xz-1x-1z)(z-1y-1xyz)
Since, y and z commute by assumption, this reduces to
(x,y,z) = z-1x-1zxy-1x-1z-1xzy
= (x,z,y)
Which proves (i)
We have, e = (xx-1,y )= (x,y)(x,y,x-1)(x-1,y)
But, (x,y,x-1) = ((x,y),x-1) and (x,y) commute with x by hypothesis, whence (x,y,x-1) = e
Hence, e = (x,y)(x-1,y) and consequently, (x,y)-1 = (x-1,y)
Similarly, by p-3, we obtain(x,y)-1 = (x,y-1) by (i ) holds.
Numericals:
1) Let G be a simple non-abelian group. The commutator subgroup of G is D(G)=[G,G]. Demonstrate that G=D (G).
ANSWER
It's worth noting that the commutator subgroup D(G) is a regular one.
Any normal subgroup of G is either the trivial group e or G itself, because G is simple. As a result, D(G)=e or D(G)=G is the case.
If D(G)=e, then the commutator [a,b]D(G)=e for any two elements a,bG.
As a result, 
Therefore we have ab=ba for any a,b∈G. This means that the group G is abelian, which contradicts with the assumption that G is non-abelian.
Therefore, we must have D(G)=G as required.
2) Let K and N be normal subgroups of G. Assume that both the quotient groups G/K and G/N are abelian.
Then demonstrate that the group is cohesive.
ANSWER
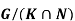
G/K is an abelian group if and only if the commutator subgroup D(G)=[G,G] is included in K, according to the above lemma.
D(G) is also contained in N because G/N is abelian.
As a result, the commutator subgroup D(G)KN is formed. This implies, once again, that the quotient group exists.
G/(K∩N)
3. Prove that a group of order 25 has an element of order 5.
ANSWER
- Let G be a group with |G|=25. The order of each element of a group G must dived the order of G (Theorem from the class). Therefore the only possible orders of elements of G are: 1,5,25
- The identity e is the only element in G with |e|=1
- Since G has more then one element, there must be another element a
 G and
G and  .
. - Since
 we have that
we have that 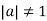 .
. - Therefore |a|=5 or |a|=25
- If |a|=5 we are done, since we wanted to show that there is an element n G of order 5.
- If |a|=25, let
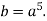 Then =
Then =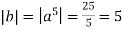 . (Remember the rule for the order of elements in cyclic groups:
. (Remember the rule for the order of elements in cyclic groups: 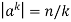 in cyclic group <a>, where |a|=n if k|n).
in cyclic group <a>, where |a|=n if k|n). - Therefore G has an element of order 5
4. Let G be a group of order pq, where p and q are primes. Prove that any proper subgroup of G is cyclic.
ANSWER
- Let G be a group with |G|=pq, where p,q are primes.
- Order of any subgroup of G must divide order of the group |G|=pq
- The only possible orders of subgroups of G are: 1,p,q,pq.
- Let H be a proper subgroup of G. Then
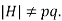 Then |H|=1,p,q.
Then |H|=1,p,q. - If
 then
then 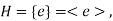 hence H is cyclic
hence H is cyclic - |H|=p or |H|=q then H is cyclic since every group of prime order is cyclic. (As stated in class)
2.2.1 Properties
Theorem (8.1 — An Element's Order in a Direct Product). The lcm of the orders of the components of the elements is the order of an element in a direct product of a finite number of finite groups: |(g1, g2,..., gn)| = lcm(|g1|, |g2|,..., |gn|).
Proof.
Consider the instance of a direct product with two components. Let (g1, g2) 2 G1G2 be the answer. Let t = |(g1, g2)| and s = lcm(|g1|, |g2|). Then (g1, g2) s = (gs 1, gs 2) = (e, e) = (e, e) = (e, e) = (e, e) = (e, e) = (e, e) = ( (Theorem 4.1, Corollary 2) t|s. As a result, t s. However, (gt 1, gt 2) = (g1, g2) t = (e, e) =) |g1| t and |g2| t are equal. Since s = lcm(|g1|, |g2|), t is a common multiple of |g1| and |g2| =) s t. As a result, s = t, and |(g1, g2)| = lcm(|g1|, |g2|).
Assume that the result holds for G1 G2 ••• Gn1 in the general case. However, because G1 G2 ••• Gn1 Gn = G1 G2 ••• Gn1 Gn, the result holds for G1 G2 ••• Gn by induction. ⇤ Example. Determine how many elements of order 7 there are in Z49 Z7. Solution. 7 = |(a, b)| = lcm(|a|, |b|) for each such element
Theorem 8.1. There are three mutually exclusive cases:
(1) |a| = 7 and |b| = 7. There are 6 choices for a (7, 14, 21, 28, 35, 42) and 6 for b (1, 2, 3, 4, 5, 6) for a total of 36.
(2) |a| = 7 and |b| = 1. We have 6 choices for a and 1 for b, a total of 6.
(3) |a| = 1 and |b| = 7. Another 6 choices. Thus Z49 Z7 has 48 elements of order 7.
Example. Find the number of cyclic subgroups of order 14 in Z196 Z49.
Solution.
We count the elements (a, b) of order 14:
(1) |a| = 14 and |b| = 7 or 1. Z196 has a unique cyclic subroup of order 14 and this has (14) = 6 generators (Theorem 4.4), so we have 6 choices for a and 7 for b, a total of 42 for (a, b).
(2) |a| = 2 and |b| = 7. By Theorem 4.4, since 2|196, there is (2) = 1 subgroup of order 2, and thus element of order 2. There are 6 choices for b, so 6 overall.
Thus we have 48 elements of order 14.
There are 48/6 = 8 cyclic subgroups of order 14 since each cyclic group has 6 elements of order 14 and no two cyclic groups can share an element of order 14.
Example. h8i h4i is a subgroup of order 24 in Z48 Z16 because |8| = 6 in Z48 and |4| = 4 in Z16. Theorem (8.2): The criterion for G H being cyclic. Consider the finite cyclic groups G and H. Then G H is cyclic () since |G| and |H| are prime.
Proof.
Let |G| = m and |H| = n, so |G H| = mn.
(=)) Assume GH is cyclic. Suppose gcd(m, n) = d and
(g, h) is a generator of G H. Now (g, h) mn d = (gm) n d ,(hn) m d = (e, e) =) mn = |(g, h)| mn d =) d = 1.
Thus |G| and |H| are relatively prime.
(=) Suppose G = hgi and H = hhi, and gcd(m, n) = 1. Then |(g, h)| = lcm(m, n) = mn = |G H|,
So (g, h) is a generator of G H =) G H is cyclic.
⇤ Corollary (1 — Criterion for G1 G2 ···Gn to be Cyclic). An external direct product G1 G2 ···Gn of a finite number of finite cyclic groups is cyclic () |Gi|and|Gj| are relatively prime when i 6= j.
U(n) as an External Direct Product
If k|n, let Uk(n) = {x 2 U(n)|x mod k = 1}.
Example.
U(21) = {1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20}, so
U3(21) = {1, 4, 10, 13, 16, 19} and
U7(21) = {1, 8}. Lemma.
Ifk|n, Uk(n) U(n).
Proof.
For a, b 2 Uk(n), a mod k = 1 and b mod k = 1 =)
(ab) mod k = (a mod k)(b mod k) = 1 · 1 = 1,
SoUk(n) is closed under multiplication mod k.
Since 1 2 Uk(n), Uk(n) 6= ;, Uk(n) U(n) by the Finite Subgroup test.
NUMERICALS
1. Let |G| = 15. If G has only one subgroup of order 3 and only one of order 5, prove that G is cyclic.
ANSWER
- Elements of G have orders 1,3,5,15
- |e|=1 Identity is the only element of order 1.
- Let H be a subgroup of order 3. Since 3 is prime, H is cycle, hence H=<a> with |a|=3 Elements of H are H{
 }.
}. - Let K be a subgroup of order 5. Since 5 is prime, K is cyclic hence K=<b> with |b|=5. Elements of K are K=
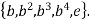
- H∪K =
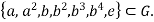
- Since |G|=15 there must be some other elements in G.
- Let c
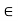 G\(H∪K), ie, c
G\(H∪K), ie, c G but c
G but c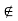 H∪K.
H∪K.
- If |c|=1 then
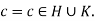 Therefore
Therefore 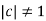 .
. - If |c|=3 then |<c>|=3 and <c>
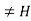 since
since 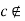 H). This is contradiction to the assumption that H is the only subgroup of order 3. Therefore |c|
H). This is contradiction to the assumption that H is the only subgroup of order 3. Therefore |c|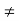 3.
3. - If |c|=5 then |<c>|=5 and <c>
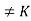 since
since 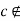 K). This is contradiction to the assumption that K is the only subgroup of order 5. Therefore |c|
K). This is contradiction to the assumption that K is the only subgroup of order 5. Therefore |c|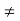 5.
5.
- Since
 it follows that
it follows that 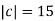
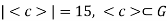 and |G|=15 implies <c>=G
and |G|=15 implies <c>=G- Therefore G is cyclic group. q.e.d
2. Consider external direct product: Z6 ⊕ Z12.
(a) Find a subgroup of order 4 which is cyclic.
ANSWER
- To find a cyclic subgroup of order 4, need to find an element of order 4.
- Order of(a,b) is |(a,b)|=lcm(|a|,|b|)
- Order of
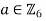 must divide 6, hence |a|=1,2,3,6
must divide 6, hence |a|=1,2,3,6 - Order of b
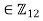 must divide 12, hence |b|=1,2,3,4,6,12
must divide 12, hence |b|=1,2,3,4,6,12 - The only possibilities are: lcm(1,4)=lcm(2,4)=4
- For example:
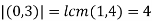 . Therefore <(0,3)> is a cyclic group of order 4.
. Therefore <(0,3)> is a cyclic group of order 4. - Another example:
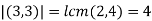 . Therefore <(3,3)> is a cyclic group of order 4.
. Therefore <(3,3)> is a cyclic group of order 4.
(b) Find a subgroup of order 4 which is not cyclic.
ANSWER
Subgroup of order 4, which is not cyclic has no elements of order 4. So all elements must have order 1 or 2.
The only element of order 1 is (0, 0).
Elements of order (2) are
(0,6) since |(0,6)|=lcm(1,2)=2
(3,0) since |(3,0)|=lcm(2,1)=2
(3,6) since |(3,6)|=lcm(2,2)=2
Check that the set H:= {(0, 0),(0, 6),(3, 0),(3, 6)} forms a subgroup of Z6 ⊕ Z12. – By definition all elements of H are in Z6⊕Z12, therefore H is a subset of Z6⊕Z12. – Since H is a finite subset, it is enough to check that it is closed under operation. This can be checked by forming the Cayley table and noticing that no new elements are introduced:
| (0,0) | (0,6) | (3,0) | (3,6) |
(0,0) | (0,0) | (0,6) | (3,0) | (3,6) |
(0,6) | (0,6) | (0,0) | (3,6) | (3,0) |
(3,0) | (3,0) | (3,6) | (0,0) | (0,6) |
(3,6) | (3,6) | (3,0) | (0,6) | (0,0) |
3. Is Z6 ⊕ Z15 isomorphic to Z90?
ANSWER
- Order of (a,b) is |a,b|=lcm(|a|,|b|)
- Orders of
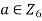 must divide 6, hence |a|=1,2,3,6.
must divide 6, hence |a|=1,2,3,6. - Orders of b
 must divide 15, hence |b|=1,3,5,15
must divide 15, hence |b|=1,3,5,15 - The only [ossibilities for the orders |(a,b)| are:

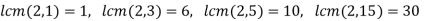
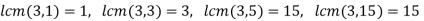
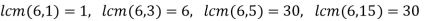
Since no elements in 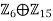 have order 90 and
have order 90 and  has elements of order 90 (for example 1
has elements of order 90 (for example 1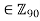 ) these tow groups cannot be isomorphic. Isomorphic groups have the same numbers of elements of same order
) these tow groups cannot be isomorphic. Isomorphic groups have the same numbers of elements of same order
2.3.1 Multiplicative group of integers modulo n
The multiplicative group of integers modulo n is formed by multiplying the integers coprime (roughly prime) to n from the set of n non-negative integers in modular arithmetic. The constituents of this group are equivalently thought of as coprimeto n congruence classes, commonly known as residues modulo n. As a result, the group of primitive residue classes modulo is another name for it.
It is defined as the group of units of the ring of integers modulo n in ring theory, a part of abstract algebra. In this ring, units refers to elements with a multiplicative inverse, which are all coprimeto n.
In number theory, this group, which is commonly designated, is crucial. It's used in cryptography, integer factorization, and primality testing, among other things. It's an abelian, finite group with Euler's totient function as its order: The group is cyclic for prime n, and the structure is simple to define in general, however no universal formula for locating generators exists for prime n.
U(n) as an External Direct Product
If k|n, let
Uk(n) = {x 2 U(n)|x mod k = 1}.
Example.
U(21) = {1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20}, so
U3(21) = {1, 4, 10, 13, 16, 19} and
U7(21) = {1, 8}.
Lemma. If k|n, Uk(n) U(n).
Proof.
For a, b 2 Uk(n), a mod k = 1 and b mod k = 1 =)
(ab) mod k = (a mod k)(b mod k) = 1 · 1 = 1,
SoUk(n) is closed under multiplication mod k.
Since 1 2 Uk(n), Uk(n) 6= ;, Uk(n) U(n) by the Finite Subgroup test.
NUMERICALS
1.Is Z2 ⊕ Z45 isomorphic to Z90?
ANSWER
- Order of (a,b) is |a,b|=lcm(|a|,|b|)
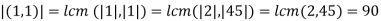
- Therefore <(1,1)> is cyclic group of order 90
- <(1,1)> is a subgroup of
 , which is also a group with 90 elements.
, which is also a group with 90 elements. - Therefore, <(1,1)> =
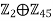 ,
, - Therefore,
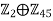 is a cyclic group order 90.
is a cyclic group order 90. - Every cyclic group of order 90 is isomorphic to
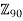
- Therefore,
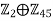 is isomorphic to
is isomorphic to 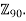
2.4.1 INTERNAL DIRECT PRODUCT
Here is the definition of internal direct product from the text:
Definition 1: Assume HiCG for i1,..., n. [Please note that Hi must be normal!] If any g G, then G is the internal direct product of the Hi's! hi, in which g = h1 • h2 •••hn.
The characteristics I used to determine if a group is isomorphic to the (external) direct product of a finite number of its subgroups are as follows:
Definition 2. Let Hi ≤ G for i∈ {1, . . . , n}. Then the sets Hi satisfy the IDP properties if:
(1) Hi C G, for all i;
(2) G = H1 ···Hndef = {h1 ···hn : hi ∈ Hi};
(3) if Hˆ idef = H1 ··· Hi−1 · Hi+1 ···Hn, then Hi ∩ Hˆi = {1}. [Note that if n = 2, then Hˆ 1 = H2 and Hˆ 2 = H1.]
We'll show that the definitions are identical, meaning that G is the internal direct product of the Hi's if and only if the Hi's satisfy the IDP properties. [Theorem 5 is shown below.]
We need the following lemma.
Lemma 3. If Hi ≤ G for i∈ {1, . . . , n} satisfy IDP properties, then hihj = hjhi for all hi ∈ Hi and hj∈Hj with i 6= j.
Proof. Since h −1 i∈ Hi C G, we have that hjh−1 i h −1 j ∈Hi . So, hi(hjh−1 i h −1 j ) ∈ Hi . Similarly, since hj∈Hj C G, we have that hihjh−1 i∈Hj . So, (hihjh−1 i )h−1 j ∈Hj.
Thus, we have that hihjh−1 i h −1 j ∈ Hi ∩Hj . But since i 6= j, we have that Hj⊆ Hˆi , and so Hi ∩Hj⊆ Hi ∩ Hˆi . Moreover, by property (3), we have that Hi ∩ Hˆi = {1}.
Hence, hihjh−1 i h −1 j ∈ Hi ∩Hj⊆ Hi ∩ Hˆi = {1}, which implies that hihjh−1 i h −1 j = 1, i.e., hihj = hjhi.
We then have:
- Theorem 4. Let H1, . . . ,Hn ≤ G. Then, φ : H1 ×···×Hn→ G defined by φ(h1, . . . , hn) = h1 ···hn is an isomorphism if and only if the Hi’s satisfy the IDP properties.
Proof. [⇒:] Assume that φ [as in the statement] is an isomorphism. Let G˜ def = H1 × ···×Hn and H˜idef = {1} ×··· {1} × Hi × {1} ×···× {1} ≤ G˜ [with Hi in the i-th coordinate]. Then, clearly φ(H˜i) = Hi . Since H˜i C G˜ [easy exercise!], we have that Hi C G, as φ is an isomorphism [by assumption]. [This was a problem in the exam.]
Thus, IDP property (1) is proved.
Since φ is an isomorphism [and hence onto] and φ(G˜) = H1 ···Hn [by definition of φ and the product of groups], we have that G = H1 ···Hn, proving property (2).
Now, let H ˆ˜ idef = H1 × ···× Hi−1 × {1} × Hi+1 ×···×Hn. Then, clearly φ(H ˆ˜i) = Hˆi [with Hˆi as in Definition 2] and H˜i∩ H ˆ˜i = {(1, . . . , 1)}. Thus
{1} = φ({(1, . . . , 1)})
= φ(H˜i∩ H ˆ˜i) [as noted above]
= φ(H˜i) ∩φ(H ˆ˜i) [as φ is a bijection– this is a Math 300 exercise]
= Hi ∩ Hˆi [as noted above]
Hence, property (3) is also satisfied.
[⇐:] Assume now that the Hi ’s satisfy the IDP property. Then, φ is a homomorphism by Lemma 3. It is onto by property (2) [as φ(H1 ×···×Hn) = H1 ···Hn by definition of φ].
Now we show that φ is injective. Suppose that φ(h1, . . . , hn) = 1. This means that h1 ···hn = 1, or h −1 1 = h2 ···hn. Since the left hand side is in H1 and the right hand side is in Hˆ 1, property (3) tells us that h1 = 1 and h2 ···hn = 1. Then, h −1 2 = h3 ···hn and now the left hand side is in H2 and the right hand side is in Hˆ 2. As before, we obtain h2 = 1 and h3 ···hn = 1. Inductively, we obtain that hi = 1 for all i. Hence, kerφ = {(1, . . . , 1)} and φ is injective.
Now, we can prove that equivalency of the Definitions 1 and 2:
Theorem 5. Assume Hi C G for i1,..., n. [Note that we've already assumed that the Hi's are normal because they appear in both definitions!] If and only if the Hi's satisfy the IDP characteristics, we obtain that G is the internal direct product of the Hi.
Proof. [⇒:] Assume that G is the Hi's internal direct product. IDP properties (1) and (2) are clearly satisfied.
Now, let hi ∈ Hi ∩ Hˆi . Then, since hi ∈ Hˆi , we have, by definition, that
1 ··· 1 · hi · 1 ··· 1 = hi = x1 ··· xi−1 · 1 · xi+1 ···xn,
Wherexj∈Hj . By the unique representation hypothesis, we have that hi = 1. Thus Hi ∩ Hˆi = {1}, i.e., property (3) is also satisfied.
[⇐:] Assume that the Hi satisfies the IDP properties at this point. [By (1), we'd deduce that the Hi's are normal, but we're assuming that already.] Then, according to (2), any element g G can be expressed as g = h1 •••hn with hi Hi. [We must demonstrate our individuality.]
Now assume that
h1 ···hn = x1 ···xn, with hi , xi ∈ Hi .
As in Theorem 4's statement [which we can apply because we're assuming IDP characteristics], we have that
φ(h1, . . . , hn) = φ(x1, . . . , xn).
We know that hi = xi for all I since is an isomorphism [and so one-to-one], and thus the representation is unique.
This gives us:
Corollary number six. G is the internal direct product of the Hi's for I 1,..., n [and thus Hi C G by assumption!] H1 •••Hn G defined by (h1,..., hn) = h1 •••hn is an isomorphism if and only if
Proof. Because of Theorem 4, we know that Hi satisfying IDP is equal to [as in the sentence] being an isomorphism. Because the former is identical to G, which is the internal direct product of the Hi's subgroups [by Theorem 5], the result follows.
2.5.1 The Fundamental Theorem of Finite Abelian Groups
1. The Fundamental Theorem of Finite Abelian Groups is a categorising theorem that categorises all finite Abelian groups.
2.Theorem: For prime p, every finite Abelian group is the external direct product of cyclic groups of the form Zp. Furthermore, any two of these groups are isomorphic, with ZaZbZab whenever gcd (a, b) = 1. Omit the proof. QED
3. To demonstrate how this allows us to enumerate all distinct (up to isomorphism) finite Abelian groups of order n, consider the following:
(a) Step 1: Let's start with the order n = p. If we divide into nonincreasing sums, we get:
α = β1 + β2 + ... + βk with β1 ≥β2 ≥ ... ≥βk
Then, for each partition, a distinct Abelian group emerges:
Zpβ1 ⊕Zpβ2 ⊕ ... ⊕Zpβk
Example: To find all distinct finite Abelian groups of order 16 = 24 we first list all partitions of 4:
4
3 + 1
2 + 2
2 + 1 + 1
1 + 1 + 1 + 1
This then yields distinct groups:
Z2 4 = Z16
Z2 3 ⊕ Z2 1 = Z8 ⊕ Z2
Z22 ⊕ Z2 2 = Z4 ⊕ Z4
Z2 2 ⊕ Z2 1 ⊕ Z2 1 = Z4 ⊕ Z2 ⊕ Z2
Z2 1 ⊕ Z2 1 ⊕ Z2 1 ⊕ Z2 1 = Z2 ⊕ Z2 ⊕ Z2 ⊕ Z2
(b) Step 2: We find the prime factorization of n that are not merely of order n = p.
n: n = p α1 1 ...p αk k
After that, apply the preceding result to each p ii, and then make all conceivable combinations of them.
Example: To find all distinct finite Abelian groups of order 72 = 23 ·3 2 we first list those for 23 using partitions 3 = 3 = 2 + 1 = 1 + 1:
Z8
Z4 ⊕ Z2
Z2 ⊕ Z2 ⊕ Z2
And then for 32 using partitions 2 = 2 = 1 + 1:
Z9
Z3 ⊕ Z3
Then we create all possible combinations:
Z8 ⊕ Z9
Z8 ⊕ Z3 ⊕ Z3
Z4 ⊕ Z2 ⊕ Z9
Z4 ⊕ Z2 ⊕ Z3 ⊕ Z3
Z2 ⊕ Z2 ⊕ Z2 ⊕ Z9
Z2 ⊕ Z2 ⊕ Z2 ⊕ Z3 ⊕ Z3
(c) Example: Consider U(13) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} with multiplication mod 13. Since U(13) is Abelian and |U(13)| = 12 we must have either U(13) ≈ Z4 ⊕ Z3 or U(13) ≈ Z2 ⊕ Z2 ⊕ Z3. To figure out which we could try a variety of things. One option: The elements in Z4 ⊕Z3 can have order 1,2,3,4,6,12 and the elements in Z2 ⊕Z2 ⊕Z3 can have order 1,2,3,6,12. Thus if U(13) has an element of order 4 then it must be isomorphic to Z4 ⊕ Z3. In fact in U(13) we have |5| = 4 and so U(13) ≈ Z4 ⊕ Z3. Interestingly since Z4 ⊕ Z3 ≈ Z12 this also tells us that U(13) ≈ Z12 which means it’s cyclic.
(d) Note: Apply the previous result to each p ii, and then create all possible combinations of them.
4.If m | n = |G| and G is a finite Abelian group, then G has a subgroup of order m.
Proof: On n = |G|, the proof is (interestingly) by strong induction. If |G| = 1, the result is self-evident; thus, suppose m | n for Abelian groups of order smaller than n. Assume m > 1 because the solution is also trivial if m = 1. Assume that p is a prime and that p | m. Then p | n, and since G Zp + G0 for some G0 and by cyclic group characteristics, we know there is some
K ≤Zpα with |K| = p. Put K = K ⊕ {0} Then G/K is an Abelian group of order n/p. Since m | n we know (m/p) | (n/p) and hence by induction G/K has a subgroup of order m/p which has the form H/K with H ≤ G (*). Then since |H/K| = m/p and |H/K| = |H|/|K| = |H|/p we have |H| = p(m/p) = m. QED
(*)It is not clear, but not difficult to prove, that a subgroup of G/N must have the form H/N where H g.
Example: An Abelian group of order 100 must have subgroups of orders 1,2,4,5,10,20,50 and 100.
Numericals:
Let G be an abelian group and let f:G→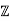 be a surjective group homomorphism.
be a surjective group homomorphism.
Prove that we have an isomorphism of groups:
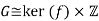
Solution:
Since f:G→Z is surjective, there exists an element a∈G such that

Let H=⟨a⟩be the subgroup of G generated by the element a.
We show that G≅ker(f)×H
To prove this isomorphism, it suffices to prove the following three conditions.
- The subgroups ker(f) and H are normal in G.
- The intersection is trivial: ker(f)∩H={e}, where e is the identity element of G.
- Every element of G is a product of elements of ker(f) and H. That is, G=ker(f)H.
The first condition follows immediately since the group G is abelian, hence all the subgroups of G are normal.
To check condition 2, let x∈ker(f)∩H.
Then x=an for some n∈Z and we have
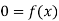 since
since 
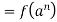
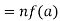 since f is a homomorphism
since f is a homomorphism
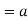 since f(a)=1
since f(a)=1
Thus, as a result we have x=a0=e, and hence ker(f)∩H={e}.
As a result, condition 2 is satisfied.
Let b be any arbitrary element in G to prove condition 3.
Let n=f(b)∈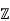 . Then we have
. Then we have
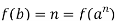
And thus we have

It follows that ba−n∈ker(f).
So there exists z∈ker(f) such that ba−n=z.
Therefore we have
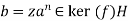
This implies that G=ker(f)H.
As a result of proving all of the prerequisites, we are able to obtain.
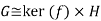
H is isomorphic to Z because it is an infinite-order cyclic group.
(There exists a positive integer n such that an=e if H has a finite order.) Then there's
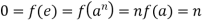
And this is in opposition to n's positivity.)
When these isomorphisms are combined, we get
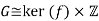
As required.
NUMERICALS
1. Consider external direct product: Z6 ⊕ Z15
(a) What is the order of (2, 3) ∈ Z6 ⊕ Z15?
ANSWER-
- Order of (a,b) is |a,b|=lcm(|a|,|b|)
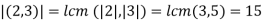 . Since |2|=6/2=3 in
. Since |2|=6/2=3 in 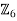 and
and 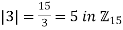
(b) What is the order of (2, 12) ∈ Z6 ⊕ Z15?
ANSWER-
- Order of (a,b) is |a,b|=lcm(|a|,|b|)
- |2|=6/2=3 in
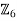
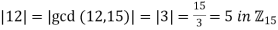
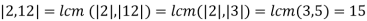
(c) What is the order of (4, 12) ∈ Z6 ⊕ Z15?
ANSWER-
- Order of (a,b) is |a,b|=lcm(|a|,|b|)
- |4|=|gcd(4,6)|=2=6/2=4 in


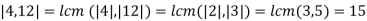
References:
1. M. Artin, Abstract Algebra, 2nd Ed., Pearson, 2011.
2. David S. Dummit and Richard M. Foote, Abstract Algebra, 3rd Ed., John Wiley and Sons (Asia) Pvt. Ltd., Singapore, 2004.
3. J.R. Durbin, Modern Algebra, John Wiley & Sons, New York Inc., 2000.