Unit - 3
Group actions
3.1.1 Group action
A group action on a space in mathematics is a group homomorphism of a given group into the space's group of transformations. A group action on a mathematical structure is the same as a group homomorphism of a group into the structure's automorphism group. The group is believed to have an effect on the space or structure. When a group operates on a structure, it almost always acts on the objects that are created from that structure. The group of Euclidean isometries, for example, has an effect on Euclidean space and the figures drawn in it. It has an effect on the set of all triangles in particular. A polyhedron's group of symmetries acts on the polyhedron's vertices, edges, and faces in the same way.
A representation of the group is a group action on a (finite-dimensional) vector space. It enables the identification of a large number of groups with subgroups of GL(n, K), the group of invertible matrices of dimension n over a field K.
By permuting the set's elements, the symmetric group Sn acts on any set with n elements. Although the group of all permutations of a set is theoretically dependent on the set, the idea of group action allows one to investigate the permutations of all sets with the same cardinality as a single group.
3.1.2 Left group action
A (left) group action of G on X is a function if G is a group with identity element e and X is a set.
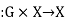
(with α(g, x) often shortened to gx or g ⋅ x when the action being considered is clear from context)
That satisfies the following two axioms:[1]
Identity: 
Compatibility:
For all g and h in G, as well as all x in X
The G group is considered to be influenced by X. (from the left). A (left) G-set is a combination of a set X and a G action.
From these two axioms, it follows that the function from X to itself that maps x to g x is a bijection for any fixed g in G, with inverse bijection being the corresponding map for g1. As a result, a group action of G on X can be defined as a group homomorphism from G to the symmetric group Sym(X) of all bijections from X to itself.
3.1.3 Right group action
Likewise, a right group action of G on X is a function
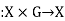
(with α(x, g) often shortened to xg or x ⋅ g when the action being considered is clear from context)
That satisfies the analogous axioms:
Identity: 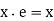
Compatibility: 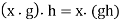
For all g and h in G and all x in X.
The difference between left and right actions is in the order in which a product gh acts on x. For a left action, h acts first, followed by g second. For a right action, g acts first, followed by h second. Because of the formula (gh)−1 = h−1g−1 By composing with the group's inverse operation, a left action can be created from a right action. A right action of a group G on X can also be thought of as a left action of the opposite group Gop on X.
As a result, considering solely left actions is sufficient for proving general features of group actions. In other circumstances, however, this is not possible. Multiplication of a group, for example, causes both a left and a right action on the group itself—left and right multiplication, respectively.
By definition, the groups Sn, An, and (for n 3) Dn behave as permutations on specific sets. Because stiff motions of the vertices influence where the rest of the n-gon goes, the groups Sn and An both permute the set 1, 2,..., n, therefore Dn can be considered a group of permutations of a regular n-gon, or even just of its n vertices. Dn can be seen as a subgroup of Sn if the vertices of the n-gon are labelled in a specified manner with numbers ranging from 1 to n. For example, the 90 degree counterclockwise rotation r in D4 is (1234), while the reflection s over the horizontal line bisecting the square is (1234). (24). The rest of the elements of D4, as permutations of the vertices, are in the table below the square.
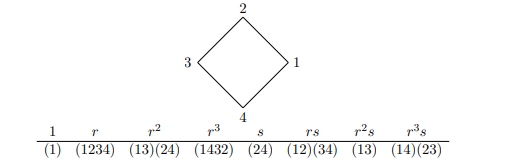
If we label the vertices in a different way (e.g., swap the labels 1 and 2), we turn the elements of D4 into a different subgroup of S4. More abstractly, if we are given a set X (not necessarily the set of vertices of a square), then the set Sym(X) of all permutations of X is a group under composition, and the subgroup Alt(X) of even permutations of X is a group under composition. If we list the elements of X in a definite order, say as X = {x1, . . . , xn}, then we can think about Sym(X) as Sn and Alt(X) as An, but a listing in a different order leads to different identifications of Sym(X) with Sn and Alt(X) with An. 1 The “abstract” symmetric groups Sym(X) really do arise naturally:
Key takeaways:
• Some theorems about groups, such as the Sylow Theorems, which (can) require group actions to prove them, can help us comprehend groups even more.
• We can think about a group operating on itself to figure out what properties it has.
• A group action is a representation of a group's elements as set symmetries.
Numericals:
1) Assume that S is any set, and that G is any subgroup of A. (S). Then G does the following action toward S. For each f ∈ G ⊆ A(S) and each x ∈ S, we define
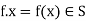 . Note that f : S → S is a (bijective) function since f ∈ A(S). Thus this makes sense and condition (0) is verified. For condition (1), note that e ∈ G is the identity function id : S → S, and id .x = id(x) = x as desired. Finally we verify (2), note that if f, g ∈ G, then f.(g.x) = f(g.x) = f(g(x)) = (f ◦ g)(x) = (fg).x as desired.
. Note that f : S → S is a (bijective) function since f ∈ A(S). Thus this makes sense and condition (0) is verified. For condition (1), note that e ∈ G is the identity function id : S → S, and id .x = id(x) = x as desired. Finally we verify (2), note that if f, g ∈ G, then f.(g.x) = f(g.x) = f(g(x)) = (f ◦ g)(x) = (fg).x as desired.
The identical scenario is now considered in a little more explicit framework.
2) Assume that G = S4, the permutation group on the set S = 1, 2, 3, 4. The action of G on S is demonstrated in the following examples:
(a) (12)(34).3=4
(b) (12)(34).2=1
(c) (1234).2=3
(d) (132)(12).2=3
(e) (132)(12).4=4
Finally, we show how matrices interact with vectors.
3) Assume that G is a set of 22 matrices.

ANSWER-
Under matrix multiplication. These are the matrices that rotate a column vector v clockwise by when multiplied by. This gives us an action of G on 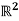 , by A.v = Av. For example, if θ = π/2
, by A.v = Av. For example, if θ = π/2
And  , then consider the matrix acting on the vector
, then consider the matrix acting on the vector
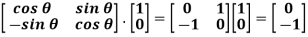
It's simple to confirm that this is a group action. It's worth noting that the identity matrix is in G (corresponding to 0), and the identity matrix sends vectors to itself. It's also worth noting that B.(A.v) = B(Av) = (BA)v = (BA).v, completing the proof.
3.2.1 Stabilizers
Consider the actions of a group G on a set X. The set of elements in X to which an element x can be transported by the elements of G is called the orbit of an element x in X. Gx is the symbol for x's orbit:
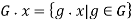
The defining features of a group guarantee that under the action of G, the set of orbits of (points x in) X form a partition of X. If and only if there is a g in G with gx = y, the related equivalence relation is defined as x y. Under this relation, the orbits are the equivalence classes; two elements x and y are equal if and only if their orbits are the same, i.e., Gx = Gy.
If and only if the group action has precisely one orbit, that is, if there is x in X with Gx = X, then it is transitive. If and only if Gx = X for all x in X, this is the case (given that X is non-empty).
The quotient of the action is the set of all orbits of X under the action of G, denoted as X/G (or, less frequently: GX). It is known as the orbit space in geometric settings and the space of coinvariants in algebraic situations, and is denoted XG, in contrast to the invariants (fixed points), which are denoted XG: the coinvariants are a quotient while the invariants are a subset. In group cohomology and group homology, which employ the same superscript/subscript standard, coinvariant terminology and notation are very useful.
3.2.2 Kernels
The kernel of a group homomorphism  is the set of all elements of
is the set of all elements of  which are mapped to the identity element of
which are mapped to the identity element of  . The kernel is a normal subgroup of
. The kernel is a normal subgroup of 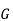 , and always contains the identity element of
, and always contains the identity element of  . It is reduced to the identity element iff
. It is reduced to the identity element iff 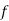 is injective.
is injective.
Theorem
Let G be a group whose identity is e.
Let Xbe a set.
Let ϕ:G×X→X be a group action.
Let G0 denote the kernel of ϕ.
Then G0 is a normal subgroup of G.
Proof
Let h∈G0.
|
|
|
|
| h | ∈ |
|
|
| G0 |
|
|
|
|
|
| ↭ |
|
| h | ∈ |
|
|
| {g∈G:∀x∈X:g⋅x=x} |
|
| Definition of Kernel of Group Action |
|
|
| ↭ |
| ∀x∈X: | h | ∈∈ |
|
|
| {g∈G:g⋅x=x}{g∈G:g⋅x=x} |
|
|
|
|
|
| ↭ |
| ∀x∈X: | h | ∈ |
|
|
| Stab(x) |
|
|
|
|
|
| ↭ |
|
| h | ∈ |
|
|
| ⋂x∈XStab(x) |
|
|
|
|
|
| ↭ |
|
| G0 | == |
|
|
| ⋂x∈XStab(x) |
|
|
|
|
From Stabilizer is Subgroup:
Stab(x)≤GStab(x)≤G
Thus G0 is the intersection of subgroups.
By Intersection of Subgroups is Subgroup:
G0≤G
To prove normality it is sufficient to show:
∀g∈G:gG0g−1=G0
Let h∈G0,g∈G be arbitrary.
Then:
|
|
|
|
| (ghg−1)⋅x | = |
|
|
| g⋅(h⋅(g−1⋅x)) |
|
| Group Action Associates with Group Operation: Group Action Axiom GA1GA1 |
|
|
|
|
|
|
| == |
|
|
| g⋅(g−1⋅x) |
|
| Because h∈Stab(g−1⋅x)h∈Stab(g−1⋅x) |
|
|
|
|
|
|
| == |
|
|
| (g⋅g−1)⋅x |
|
| Group Action Associates with Group Operation: Group Action Axiom GA1GA1 |
|
|
|
|
|
|
| == |
|
|
| xx |
|
| e⋅x=xe⋅x=x: Group Action Axiom GA2GA2 |
|
Therefore:
Ghg−1∈G0
So:
GG0g−1⊆G0
Conversely suppose that h∈G0h∈G0.
Then by the above:
h′=g−1hg∈G0
Therefore:
h=gh′g−1∈gG0g−1
And so:
G0⊆gG0g−1
This concludes the proof.
Key takeaways:
• A diagnosis that describes or characterizes the nature of the problem.
• An overarching policy for dealing with the problem.
• A series of well-coordinated actions intended to carry out the guiding policy.
3.3.1 Permutation representation
For G a group (tyically a finite group), consider a G-set (S,ρ)), hence
a set S (typically a finite set), equipped with an action of G
ρ:G×S⟶S
Equivalently this is a group homomorphism
ρ:G⟶AutSet(S)
From G to the group of permutations of elements of S. As such it is a representation of G “by permutations”.
Specifically, if SS is a finite set and an isomorphism S≃{1,2,3,⋯,n}is understood, it is equivalently a group homomorphism
ρ:G⟶Sn
To the symmetric group Sn on n elements.
This G-action can be linearized to a k-linear representation of G in an obvious fashion for k any field (or, more broadly, any commutative ring, but one usually concerns fields):
3.3.2 Associated with a given group action
The linear permutation representation of a G-set (S,ρ)) is the following k-linear representation of G:
- The underlying k-vector space is the freely spanned vector space k[S], whose elements (vectors) are the formal linear combinations
k[S]={v=∑s ∈ Sf in⊂ Sv ss| Sf infinite sub set, vs ∈ k}
Of elements of S with coefficients in k, hence is the k-vector space for which S is a canonical linear basis.
2. The linear G-action
k[ρ]:G×k[C]⟶k[C]
Is given on linear basis-elements s∈S↪k[S]s by ρ, which uniquely defines it by linearity to act on a general vector as
k[ρ](g):v↦∑s∈Sfin⊂Svsρ(g)(s).
This concept immediately generalizes to groupoid representations and so forth, see also at infinity-action the section
3.3.3 Virtual permutation representations
We'll look at some examples of the canonical ring homomorphism operation of constructing virtual linear permutation representations (Remark 2.3).

From Def. 2.2.
For emphasis, note that linear permutation representations are a minor sub-class of plain linear representations, i.e. a linear representation is not a linear permutation representation in general. However, when we move to virtual representations, this assertion may change dramatically:
If the ring homomorphism β (Def. 2.2) is a surjective function, this means that in fact all virtual linear G-representation are virtual linear permutation representations. This is not the case for all groups, but it is the case for large classes of groups! This is the content of Prop. 3.3 below.
Notice that when this is the case, it signifies that the provided group's representation theory is wholly combinatorial, or, in the context of (1), that it is fully specified over the absolute ground field. F1
3.3.4 Comparison from Burnside- to representation ring
Assume that GG is a finite group and that all G-sets and linear representations in the following are finite dimensional.
Consider
- The Burnside ring A(G), which is the Grothendieck ring of the rig-category (GSet,⊔,×) of finite G-sets;
- The representation ring R(G), which is the Grothendieck ring of the rig category (GRep,⊕,⊗) of finite-dimensional linear G-representations.
Definition 2.2. (permutation representations make ring homomorphism from Burnside ring to representation ring)
Since forming k-linear permutation representation is a rig-functor GSet−→−k[−]GRep, under passing to Grothendieck rings it induces a ring homomorphism
K(k[−]):K(GSet,⊔,×)=A(G)−→−−βR(G)=K(GRep,⊕,⊗)
From the Burnside ring of GG to its representation ring.
This homomorphism is traditionally denoted β\beta, as shown.
Its kernel is known as the Brauer relations.
Numericals:
1) Prove that every order 24 group has a typical order 4 or 8 subgroup.
ANSWER-
Let G be a 24th-order group.
It's worth noting that 24=233.
Assume G has a Sylow 2-subgroup P. Then |P| equals 8.
Consider the operation of the group G via left multiplication on the left cosets G/P.
A permutation representation homomorphism results as a result of this.
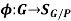
SG/P denotes a collection of bijective maps (permutations) on G/P.
The homomorphism is defined as follows:
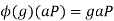
For g∈G and aP∈G/P.
Then by the first isomorphism theorem, we see that
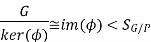
This implies that the order of G/ker(ϕ) divides the order of SG/P. Note that as |G/P|=3, we have |SG/P|=|S3|=6. Thus, we must have 4∣|kerϕ|4∣.
Also note that ker(ϕ)<P. To see this let x∈ker(ϕ). Then we have
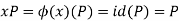
Here id is the identity map from G/P to itself. Hence x∈P. It follows that |ker(ϕ)| divides |P|=8.
Combining these restrictions, we see that |ker(ϕ)|=4,8.
Being the kernel of a homomorphism, ker(ϕ) is a normal subgroup of G.
Hence the group G of order 24 has a normal subgroup of order 4 or 8.
3.4.1 Group actions
A group action on a space in mathematics is a group homomorphism of a given group into the space's group of transformations. A group action on a mathematical structure is the same as a group homomorphism of a group into the structure's automorphism group. The group is believed to have an effect on the space or structure. When a group operates on a structure, it almost always acts on the objects that are created from that structure. The group of Euclidean isometries, for example, has an effect on Euclidean space and the figures drawn in it. It has an effect on the set of all triangles in particular. A polyhedron's group of symmetries acts on the polyhedron's vertices, edges, and faces in the same way.
A representation of the group is a group action on a (finite-dimensional) vector space. It enables the identification of a large number of groups with subgroups of GL(n, K), the group of invertible matrices of dimension n over a field K.
By permuting the set's elements, the symmetric group Sn acts on any set with n elements. Although the group of all permutations of a set is theoretically dependent on the set, the idea of group action allows one to investigate the permutations of all sets with the same cardinality as a single group.
Numericals:
1) Let G be a finite group and let S be a non-empty set.
Suppose that G acts on S freely and transitively. Prove that |G|=|S|. That is, the number of elements in G and S are the same.
ANSWER-
We simply denote by gs the action of g∈G on s∈S.
We add an element s0S to SS because it isn't empty. Create a map
ϕ:G→S
By sending g∈G to gs0∈S.
We prove that the map ϕ is bijective. Suppose that we have ϕ(g)=ϕ(h) for some g,h∈G.
Then it gives gs0=hs0, and since the action is free this implies that g=h.
Thus ϕ is injective.
To show that ϕ is surjective, let s be an arbitrary element in S.
Since the action is transitive, there exists g∈G such that gs0=s.
Hence we have ϕ(g)=s, and ϕ is surjective.
Therefore the map ϕ:G→S is bijective, and we conclude that |G|=|S|.
2) Prove that every finite group of order 72 is not a simple group.
ANSWER-
Keep an eye on the prime factorization. 72=23⋅32
Let G be a 72-order group.
The number of Sylow 3-subgroups in G is n3.
We know that n3 satisfies Sylow's theorem.
n3≡1(mod3) and
n3 divides 8.
The first condition results in n3 being 1,4,7,...
Only n3=1,4 meets the second requirement.
If n3=1, a single Sylow 3-subgroup exists, which is a normal subgroup of order 9.
As a result, the group G is not simple in this example.
It is still necessary to investigate the case where n3=4.
G is divided into four Sylow 3-subgroups.
Sylow's theorem states that these subgroups are not regular.
By conjugation, the group G acts on the set of these four Sylow 3-subgroups.
As a result, a permutation representation homomorphism is possible.
f:G→S4,
Where S4 is the degree 4 symmetric group.
By the first isomorphism theorem, we have
G/kerf<S4.
Thus, the order of G/kerf divides the order of S4.
Since |S4|=4!=23⋅3, the order |kerf| must be divisible by 3 (otherwise |G/kerf| doesnotdivide|S_4|),hence),ker f$ is not the trivial group.
We claim that kerf≠G.
If kerf=G, then it means that the action given by the conjugation by any element g∈G is trivial.
That is, gPg−1=P for any g∈G and for any Sylow 3-subgroup P.
Since those Sylow 3-subgroups are not normal, this is a contradiction.
Thus, kerf≠G.
Because a homomorphism's kernel is a normal subgroup, kerf is a nontrivial proper normal subgroup of G, implying that G is not a simple group.
3.4.2 Cayley's theorem
Cayley's theorem, named for Arthur Cayley, states that any group G is isomorphic to a subgroup of the symmetric group acting on G in group theory. [1] This might be interpreted as an illustration of G's group action on G's constituents. [2] The theorem can be proved by explicitly creating the representation within the regular representation of the symmetric group of permutation matrices.
A permutation of a set G is any bijective function taking G onto G. The set of all permutations of G forms a group under function composition, called the symmetric group on G, and written as Sym(G).[3]
By viewing any group (including infinite groups like (R,+)) as a permutation group of some underlying set, Cayley's theorem equalises all groups. As a result, theorems that hold for subgroups of permutation groups also hold for groups as a whole. Despite this, Alperin and Bell state that "the notion that finite groups are embedded in symmetric groups has had no effect on the methods employed to investigate finite groups in general."
The regular action used in the usual proof of Cayley's theorem does not create a minimal-order permutation group representation of G. The regular action, for example, would represent S3, which is already a symmetric group of order 6, as a subgroup of S6 (a group of order 720). Indeed, the direct sum of all irreducible representations with multiplicity equal to their dimension yields the complex regular representation of finite groups. Finding a group's embedding in a minimal-order symmetric group is a challenging task to solve.
If g is any element of a group G with operation ∗, consider the function fg : G → G, defined by fg(x) = g ∗ x. By the existence of inverses, this function has a two-sided inverse, 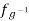 . So multiplication by g acts as a bijective function. Thus, fg is a permutation of G, and so is a member of Sym(G).
. So multiplication by g acts as a bijective function. Thus, fg is a permutation of G, and so is a member of Sym(G).
The set K = {fg : g ∈ G} is a subgroup of Sym(G) that is isomorphic to G. The fastest way to establish this is to consider the function T : G →Sym(G) with T(g) = fg for every g in G. T is a group homomorphism because (using · to denote composition in Sym(G)):
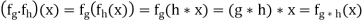
For all x in G, and hence:

The homomorphism T is injective since T(g) = idG (the identity element of Sym(G)) implies that g ∗ x = x for all x in G, and taking x to be the identity element e of G yields g = g ∗ e = e, i.e. the kernel is trivial. Alternatively, T is also injective since g ∗ x = g′∗ x implies that g = g′ (because every group is cancellative).
As a result, G is isomorphic to T, which is the subgroup K.
The normal representation of G is sometimes referred to as T.
3.4.3 Index theorem
The number of left cosets of H in G, or equivalently, the number of right cosets of H in G, is the index of a subgroup H in a group G in mathematics, specifically group theory. The index is denoted 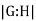 or
or 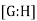 or
or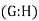 . Because G is the disjoint union of the left cosets and because each left coset has the same size as H, the index is related to the orders of the two groups by the formula
. Because G is the disjoint union of the left cosets and because each left coset has the same size as H, the index is related to the orders of the two groups by the formula
(interpret the quantities as cardinal numbers if some of them are infinite). Thus the index 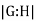 measures the "relative sizes" of G and H.
measures the "relative sizes" of G and H.
For example, let G=Z be the group of integers under addition, and let H=2Z be the subgroup consisting of the even integers. Then 2Z has two cosets in Z, namely the set of even integers and the set of odd integers, so the index 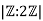 is 2. More generally,
is 2. More generally,  for any positive integer n.
for any positive integer n.
When G is finite, the formula may be written as 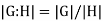 , and it implies Lagrange's theorem that |H| divides |G|.
, and it implies Lagrange's theorem that |H| divides |G|.
When G is infinite, |G:H| is a nonzero cardinal number that may be finite or infinite. For example, |Z:2Z|=2, but |R:Z| is infinite.
Because the underlying set of G/N is the set of G/N cosets of N in G, |G:N| is equal to the order of the quotient group if N is a normal subgroup of G.
References:
1. M. Artin, Abstract Algebra, 2nd Ed., Pearson, 2011.
2. David S. Dummit and Richard M. Foote, Abstract Algebra, 3rd Ed., John Wiley and Sons (Asia) Pvt. Ltd., Singapore, 2004.
3. J.R. Durbin, Modern Algebra, John Wiley & Sons, New York Inc., 2000.