Unit - 3
Dielectric Properties of Matter & Electromagnetic Induction
In dielectric material molecules are tightly bounded to the nucleus and not able to move freely as in case of conductor. But when a dielectric material is placed in an electric field, electric charges do not flow through the material as they flow in case of an electrical conductor but only slightly shift from their average equilibrium positions causing dielectric polarization. Because of dielectric polarization, positive charges are displaced in the direction of the field and negative charges shift in the direction opposite to the field. In dielectric molecules are tightly bound to the nucleus and not able to move freely as in case of conductors. The dielectric material is largely used in the manufacturing of capacitor.
Response of Dielectric to External Electric Field
In case of Polar Molecules -When the electric field is not present, it causes the electric dipole moment of these molecules in a random direction. This is why the average dipole moment is zero. If the external electric field is present, the molecules align themselves in the direction electric field and resulted in having dipole moment.
In case of Non-Polar Molecules – As we know nonpolar molecule has zero dipole moment. In spite of zero dipole, when a dielectric nonpolar material is placed in an electric field. The positive and the negative charges in a nonpolar molecule experience forces in opposite directions. This force causes the separation between the charges and hence nonpolar molecule experiences induced dipole moment.
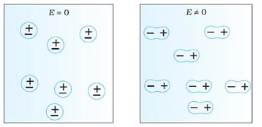
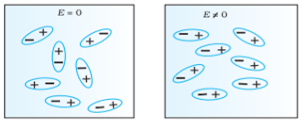
Figure 1 (a) (left) Non Polar Molecule Figure 1 (b) (right) Polar Molecule
In previous section we have seen about the dielectric material’s behaviour and we have seen that when the dielectric material is placed in an electric field, then the molecule of polar and non-polar dielectric gains the dipole moment. Then the dielectric is said to be polarised.
Definition:
The diploe moment per unit volume of dielectric material is called the electric polarization of dielectric. It is represented by vector P.
In S.I. System, unit of polarization is C/m2.
When an external electric field is applied to a dielectric material, its behaviour can be determined and is known as Dielectric Polarization that can be understood by the displacement of charges(positive and negative) when an electric field is applied
The main task of the dielectric polarization is to relate macroscopic properties to microscopic properties. Where macroscopic property can be dielectric constant to polarizability.
Polarization occurs through the action of an electric field or other external factors, such as mechanical stress in the case of piezoelectric crystals (piezoelectric crystals are those solid materials which accumulates electric charge within them). Dielectric Polarization can also arise spontaneously in pyroelectric crystals, particularly in ferroelectrics (Ferroelectricity is a property of certain materials that have a spontaneous electric polarization that can be reversed by the application of an external electric field).
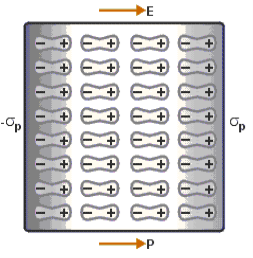
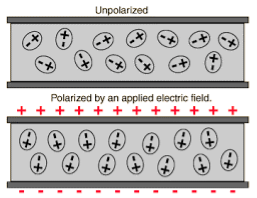
Figure 2: Polarisation of dielectric molecules
Above figure explains the polarisation of dielectric molecules when the electric field is applied.
Dielectric polarization occurs when a dipole moment is formed in an insulating material because of an externally applied electric field. When a current interacts with a dielectric material, the dielectric material will respond with a shift in charge distribution with the positive charges aligning with the electric field and the negative charges aligning against it.
Polarization
"When a dielectric material placed in external electrical field, it's molecule gain electric dipole moment and dielectric said to be polarised"
"The induce moment per unit volume of dielectric material is called the electric polarization of dielectric." It is represented by vector p.
Type of dielectric polarization
There are four types of dielectric polarization
1. Electronic polarization
2. Ionic polarization
3. Orientational polarization
4. Space charge polarization
Electric Polarization
Electronic polarization refers to the separation of centre of positive charge and centre of negative charge in a material.This separation is caused by high electric field.
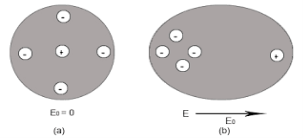
Figure 3: (a) shows thecharge distribution of an atom in absence of electric field while figure (b) show the charge distribution in presence of external electrical field.
Let us consider a single atom of atomic number Z. +e coulomb is the charge of each proton in the nucleus and -e coulomb is the charge of each electron surrounds the nucleus. All electrons in the atom form a spherical cloud of negative charge surrounds the positively charged nucleus. The charge of nucleus is +Ze coulombs and charge of the negative cloud of electrons is -Ze coulombs.
Let us also assume that the negative charge of the electrons cloud is homogeneously distributed on a sphere of radius R. In the absence of external electric field, the center of this sphere and center of nucleus of the atom coincide.
When an external electric field E is applied to the atom. Because of this external electric field the nucleus of the atom is shifted towards negative intensity of the field and the electron cloud is shifted towards the positive intensity of the field.
As due to influence of external electric field the center of nucleus and center of electrons cloud are separated, there will be an attractive force between them according to Coulomb’s law.
Let us suppose x is distance of separation between positive charge nucleus and electron cloud.
Also Nucleus is considered as point charge. Hence, the electrostatic force acting on the nucleus =+EZe …….(1)
As we know nucleus has been shifted from the center of electrons cloud by a distance x.
By using Gauss’s theorem
The force is only due to electron cloud acting upon nucleus would only be due to the portion of the cloud enclosed by the sphere of radius x. Portion outside the sphere of radius x does not apply any force on the nucleus.
Volume of the sphere of radius x = (4/3)πx3 and
Volume of the sphere of radius R = (4/3)πR3
Now total negative charge of the electron cloud is -Ze …..(2)
Hence, the quantity of negative charge enclosed by the sphere of radius x is,
[-Ze/(4/3)πR3] * (4/3)πx3 = -Ze (x3/ R3) ……..(3)
According to coulomb’s law = q1q2 /4 πR2
Here it becomes charge on electrons q1=-Ze (x3/ R3)
Charge on nucleus q2= Ze
So coulomb’s force = {-Ze (x3/ R3) * Ze}/4πƐox2 = Z2e2x/4πƐo R3 ……(4)
Note- magnitude is taken into account. Neglect negative sign.
i.e. At equilibrium Electrostatic force = Coulomb force
EZe = Z2e2x/4πƐoR3 ……..(5)
Upon simplify
x = {4πƐoR3/Ze} E
Now dipole moment = either charge * separation between charges i.e. x
= Ze *{4πƐoR3/Ze} E
= 4πƐoR3E
Polarization is number of dipole moment per unit volume. Let us suppose N is the number of dipoles per unit volume so
Pe=4πƐoR3EN
So it is clear that polarization depends upon radius of atom or volume of atom and number of atoms present per unit volume.
Key Takeaways
- A dielectric is non-conducting material which stores electrical charges.
- The molecules of a dielectric is of two types Polar molecules and Non-polar molecules
- The diploe moment per unit volume of dielectric material is called the electric polarization of dielectric. It is represented by vector P. In S.I. System, unit of polarization is C/m2.
- There are four types of dielectric polarization 1. Electronic polarization 2. Ionic polarization 3. Orientational polarization 4. Space charge polarization
- Electronic polarization refers to the separation of centre of positive charge and centre of negative charge in a material.This separation is caused by high electric field.
- Polarization is number of dipole moment per unit volume. Let us suppose N is the number of dipoles per unit volume so Pe=4πƐoR3EN.
Electric susceptibility
Susceptibility is the extent to which a given material gets polarised when it is kept in an electric field.
If the material gets polarised more, it will set up an internal field which opposes the external field which will then reduce the total electric flux through that material. Therefore, electric susceptibility affects the electric permittivity of the medium.
Greater the level of polarisation, lower will be the electric permittivity
For most linear dielectric materials, the polarization P is directly proportional to the average electric field strength E so that the ratio of the two, P/E, is a constant that expresses an intrinsic property of the material.
The electric susceptibility, χe, in the centimetre-gram-second (cgs) system, is defined by this ratio; that is,
χe = P/E.
In the metre-kilogram-second (mks) system, electric susceptibility is defined slightly differently by including the constant permittivity of a vacuum, ε0, in the expression; that is,
χe = P/(ε0E).
In both systems the electric susceptibility is always a dimensionless positive number. Because of the slight difference in definition, the value of the electric susceptibility of a given material in the mks system is 4π times its value in the cgs system.
Susceptibility of polar dielectric depends upon the temperature whereas Susceptibility of non-polar dielectric is independent of the temperature.
Dielectric constant
Dielectric constant it is a quantity measuring the ability of a substance to store electrical energy in an electric field.
Or
The ratio of the permittivity of the substance to the permittivity of the free space
Dielectric constant is also called Relative Permittivity Dielectric Constant is expressed by Greek letter kappa ‘κ’. It is dimensionless quantity.
It is mathematically expressed as:
κ = 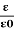
Where,
- κ is the dielectric constant
- 𝜺 is the permittivity of the substance
- 𝜺0 is the permittivity of the free space
Dielectric constant in terms of capacitance
Dielectric constant is equal to the ratio of the capacitance of a capacitor filled with the given material to the capacitance of an identical capacitor in a vacuum without the dielectric material.
If C is the value of the capacitance of a capacitor filled with a given dielectric and C0 is the capacitance of an identical capacitor in a vacuum, the dielectric constant κ, is simply expressed as
κ = 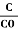
Dielectric Strength
It is defined as the maximum electric field which the material can sustain without breaking down.
When a high electric field is applied to the dielectric, the outer electrons get detached from their parent atoms. The dielectric then behaves as a conductor. In other words every dielectric starts conducting when if an external field is applied to it. This value of electric field depends on the nature of material of dielectric and is called dielectric strength.
Figure 4: Table - List of value of dielctric constant and dielectric strength of some material
Material | Dielectiric constant | Dielectric strength (kV/mm) |
Vacuum | 1.00000 | - |
Air (dry) | 1.00059 | 3 |
Polystyrene | 2.6 | 24 |
Paper | 3.6 | 16 |
Water | 80 | - |
Key Takeaways
- Susceptibility is the extent to which a given material gets polarised when it is kept in an electric field.
- Dielectric constant it is a quantity measuring the ability of a substance to store electrical energy in an electric field.
- Dielectric Strength is defined as the maximum electric field which the material can sustain without breaking down.
3.3.1 Capacitors and Capacitance
Capacitors: A capacitor is a two-terminal electrical device that possesses the ability to store energy in the form of an electric charge. It consists of two electrical conductors that are separated by a distance. The space between the conductors may be filled by vacuum or with an insulating material known as a dielectric.
Capacitors store energy by holding apart pairs of opposite charges. The simplest design for a capacitor is a parallel plate, which consists of two metal plates with a gap between them. But, there are different types of capacitors manufactured in many forms, styles, lengths, girths, and many materials.
Capacitance: The ability of the capacitor to store charges is known as capacitance.
Dielectric constant in terms of capacitance
Dielectric constant is equal to the ratio of the capacitance of a capacitor filled with the given material to the capacitance of an identical capacitor in a vacuum without the dielectric material.
If C is the value of the capacitance of a capacitor filled with a given dielectric and C0 is the capacitance of an identical capacitor in a vacuum, the dielectric constant κ, is simply expressed as
κ = 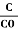
A dielectric, is an insulating material such as mineral oil or plastic, and is characterized by a numerical factor k, called the dielectric constant of the material.
Some dielectrics, such as strontium titanate, can increase the capacitance by more than two orders of magnitude. The introduction of a dielectric also limits the potential difference that can be applied between the plates to a certain value Vmax, called the breakdown potential.
Every dielectric material has a characteristic dielectric strength, which is the maximum value of the electric field that it can tolerate without breakdown.
3.3.2 Parallel plate capacitor filled with dielectric
Capacity of a parallel plate condenser which is partially filled with a dielectric medium- By the distance between the plates is d and in between the plates there is a dielectric medium of thick-ness t and dielectric constant K. If each plate is given a charge +q then surface charge.
σ=q/A
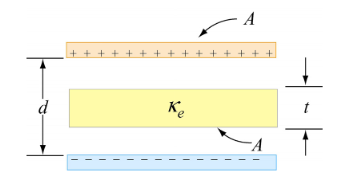
Figure 5: Parallel plate Capacitor filled with dielectric
Where A is the surface area of the plates. If the distance between the plates in negligible in comparison to their area then the intensity of electric field in the area filled with air between the plates.
Eo= σ / εo
Electric field intensity within the dielectric medium E= σ/ Kεo
By the definition of potential difference, the potential difference between the plates.
V= Work done in moving a unit charge from one plate (negative) to another (positive) plate.
= Work done in moving a unit charge a distance (d−t) in air and distance t in dielectric medium
V=Eo×(d−t)+Et
On substituting the values of Eo and E
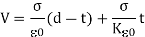
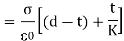
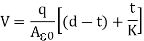
Hence capacity of the condenser
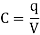
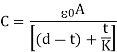
3.3.3 Spherical capacitor filled with dielectric
Consider there are two spheres, the inner and outer sphere as shown in figure. The inner radius of sphere is “a” and outer radius of sphere is “b”.
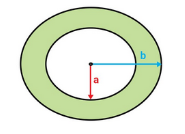
Figure 6: Spherical capacitor
Now if a charge of Q coulomb is supplied to the outer conductor shell of the capacitor where r is the radius of the sphere. Then the potential or voltage built at the surface of the capacitor is given by
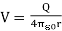 …… (1)
…… (1)
If we ground the outer surface of the capacitor and supply a positive charge of Q coulombs to the inner spheres.
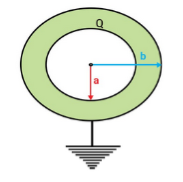
Figure 7: Spherical capacitor
Then a charge –Q is induced at the inner surface of the outer sphere and a charge +Q is induced at the outer surface of the outer sphere will be sent to the ground. Now the surface potential at the outer sphere due to its own charge
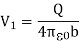
And the surface potential at the inner sphere due to its own charge
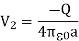
Thus, the potential difference between two spheres is

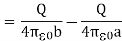
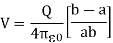
On arranging the equation, we get the ratio of Q and V which is equal to the capacitance.
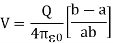

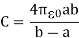
When we assume that there is no air between them means the vacuum is present then the equation of capacitance is given by
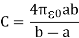
Now we assume that there is no vacuum between them. And we inserted dielectric material between them. Permittivity of the medium is 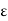

Figure 8: Spherical capacitor
Now the capacitance of the sphere with dielectric material in it is given as
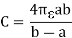
We know that Dielectric constant is also called Relative Permittivity Dielectric Constant is expressed by Greek letter kappa ‘κ’. It is dimensionless quantity.
It is mathematically expressed as:
K =κ = 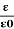
Where,
- κ is the dielectric constant
- 𝜺 is the permittivity of the substance
- 𝜺0 is the permittivity of the free space
Using it we get
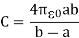
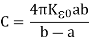
Which is the required value of spherical capacitance when dielectric material is inserted in it.
3.3.4 Cylindrical capacitor filled with dielectric
Consider there are two cylinders, the inner and outer cylinders as shown in figure. The length of both the cylinders is L. Also inner radius of cylinder is “a” and outer radius of cylinder is “b”.
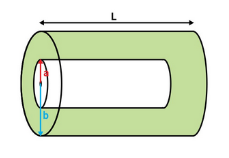
Figure 9: Cylindrical capacitor filled with dielectric
Consider charge per meter length of the cable on the outer surface the inner cylinder is +Q and on the inner surface the outer cylinder is –Q.
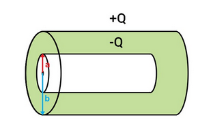
Figure 10: Cylindrical capacitor filled with dielectric
The surface area of the coaxial cylinder of radius x meters and length 1 meter is
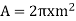
Electric field at a point x meters away from the center of the inner cylinder is
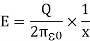
Thus potential difference developed between the plates or cylinder in the parallel plate capacitors V is given by
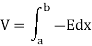
By putting the value of E
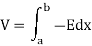
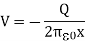
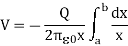
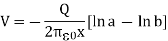
Thus capacitance is given by
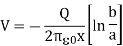
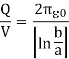
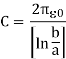
Thus capacitance is given by
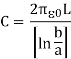
Insert the dielectric material. Now we assume that there is no vacuum between them. And we inserted dielectric material between them. Permittivity of the medium is 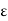 . Thus capacitance is given by
. Thus capacitance is given by
We know that Dielectric constant is also called Relative Permittivity Dielectric Constant is expressed by Greek letter kappa ‘κ’. It is dimensionless quantity.
It is mathematically expressed as:
K =κ = 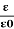
Where,
- κ is the dielectric constant
- 𝜺 is the permittivity of the substance
- 𝜺0 is the permittivity of the free space
Using it we get
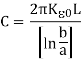
Which is the required value of cylindrical capacitance when dielectric material is inserted in it.
Key Takeaways
- Capacitance for parallel plate capacitor filled with dielectric is given by
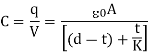
- The required value of spherical capacitance when dielectric material is inserted in it is given by
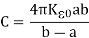
- Capacitance for cylindrical capacitor filled with dielectric is given by
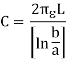
Besides the bound charges due to polarization, a dielectric material may also contain some extra charges which just happen to be there. For a lack of a better term, such extra charges are called free charges, just to contrast them from the bound charged due to polarization. Anyway, the net macroscopic electric field does not care for the origin of the electric charges or how we call them but only
 net(r) =
net(r) = free(r) +
free(r) +  bound(r);
bound(r); 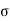 net(r) =
net(r) = 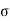 free(r) +
free(r) + 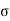 bound(r); ………(1)
bound(r); ………(1)
In particular, the Gauss Law in differential form says
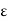 0
0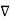 .E(r) =
.E(r) = 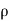 net(r) +
net(r) + 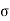 net
net 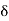 (coordinate ⟂ surface) + more
(coordinate ⟂ surface) + more 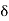 function terms due to linear and point charges ………(2)
function terms due to linear and point charges ………(2)
For simplicity, let's ignore for a moment the surface, line, and point charges and focus on just the volume charge density. This gives us
 0
0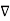 .E(r) =
.E(r) = 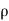 net(r) =
net(r) = 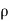 free(r) +
free(r) +  bound(r) =
bound(r) =  free(r) −∇ ·P
free(r) −∇ ·P
Which we may rewrite as
∇.(ε0E+P) =  free ………(3)
free ………(3)
In light of this formula, the combination
D(r) =ε0E(r) +P(r) ………(4)
Called the electric displacement field obeys the Gauss Law involving only the free charges but not the bound charges,
∇.D(r) =  free
free
The permittivity εo of free space is 8.854×10-12 farads/meter, where
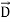 =εo
=εo 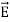 .
.
The permittivity ε of any material deviates from εo for free space if applied electric fields induce electric dipoles in the medium; such dipoles alter the applied electric field seen by neighbouring atoms.
Electric fields generally distort atoms because 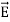 pulls on positively charged nuclei (f=q
pulls on positively charged nuclei (f=q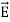 [N]) and repels the surrounding negatively charged electron clouds. The resulting small offset d of each atomic nucleus of charge +q relative to the center of its associated electron cloud produces a tiny electric dipole in each atom, as suggested in Figure: 11(a).
[N]) and repels the surrounding negatively charged electron clouds. The resulting small offset d of each atomic nucleus of charge +q relative to the center of its associated electron cloud produces a tiny electric dipole in each atom, as suggested in Figure: 11(a).
In addition, most asymmetric molecules are permanently polarized, such as H2O or NH3, and can rotate within fluids or gases to align with an applied field. Whether the dipole moments are induced, or permanent and free to rotate, the result is a complete or partial alignment of dipole moments as suggested in Figure: 11(b).
These polarization charges generally cancel inside the medium, as suggested in Figure: 11(b), but the immobile atomic dipoles on the outside surfaces of the medium are not fully cancelled and therefore contribute the surface polarization charge ρsp

Figure 11: Polarized media
Figure:11(c) suggests how two charged plates might provide an electric field 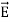 that polarizes a dielectric slab having permittivity ε > εo. The electric field
that polarizes a dielectric slab having permittivity ε > εo. The electric field 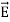 is the same in vacuum as it is inside the dielectric (assuming no air gaps) because the path integral of
is the same in vacuum as it is inside the dielectric (assuming no air gaps) because the path integral of  from plate to plate equals their voltage difference V in both cases. The electric displacement vector
from plate to plate equals their voltage difference V in both cases. The electric displacement vector 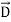 e =ε
e =ε  and therefore differs.] We associate the difference between
and therefore differs.] We associate the difference between  o =εo
o =εo (vacuum) and
(vacuum) and 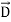 ε=ε
ε=ε (dielectric) with the electric polarization vector P , where:
(dielectric) with the electric polarization vector P , where:
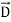 = ε
= ε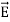 =εo
=εo 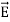 +
+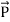 = εo
= εo 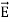 (1+
(1+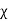 ) (8)
) (8)
The polarization vector 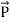 is defined by (8) and is normally parallel to
is defined by (8) and is normally parallel to 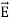 in the same direction, as shown in Figure: 11(c); it points from the negative surface polarization charge to the positive surface polarization charge (unlike
in the same direction, as shown in Figure: 11(c); it points from the negative surface polarization charge to the positive surface polarization charge (unlike  , which points from positive charges to negative ones).
, which points from positive charges to negative ones).
As suggested in (8), 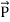 = εo
= εo 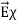 ,
,
Where χ is defined as the dimensionless susceptibility of the dielectric. Because nuclei are bound rather tightly to their electron clouds, χ is generally less than 3 for most atoms, although some molecules and crystals, particularly in fluid form, can exhibit much higher values.
Electric displacement, also known as dielectric displacement and usually denoted by D, is a vector field in a non-conducting medium, a dielectric.
In a dielectric material, the presence of an electric field E causes the bound positive and negative charges in the material to slightly separate, inducing a local electric dipole moment. The electric displacement field "D" is defined as
D= 𝜺0E+P
D =
Electric displacement
E = External electric field in which the dielectric is placed
𝜺0 = the permittivity of the free space
P = Polarization Density
In S.I. System, Unit of Electric displacement is C/m2.
D = 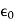 E+P
E+P
D= 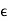 E and P =
E and P = 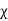 eE
eE
Relation between dielectric constant and susceptibility
Electric displacement, also known as dielectric displacement and usually denoted by D, is a vector field in a non-conducting medium, a dielectric.
In a dielectric material, the presence of an electric field E causes the bound positive and negative charges in the material to slightly separate, inducing a local electric dipole moment. The electric displacement field "D" is defined as
D= 𝜺0E+P
D =
Electric displacement
E = External electric field in which the dielectric is placed
𝜺0 = the permittivity of the free space
P = Polarization Density
In S.I. System, Unit of Electric displacement is C/m2.
D =  E+P
E+P
D= 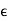 E and P =
E and P = 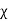 eE
eE
Substituting these values in eq (1), we get
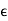 E =
E = 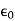 E+
E+ eE
eE
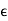 =
= 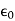 +
+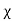 e
e
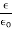 = 1 +
= 1 + 
But
κ = 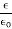 = Dielectric constant
= Dielectric constant
κ = 1 + 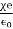
Clearly values of κ for all dielectric is greater than one, and for empty space 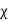 e=0 and κ =1.
e=0 and κ =1.
Key Takeaways
- The permittivity εo of free space is 8.854×10-12 farads/meter
- The electric displacement vector
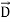 e =ε
e =ε 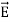 and therefore differs.] We associate the difference between
and therefore differs.] We associate the difference between 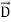 o =εo
o =εo (vacuum) and
(vacuum) and 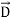 ε=ε
ε=ε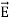 (dielectric) with the electric polarization vector P , where:
(dielectric) with the electric polarization vector P , where: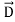 = ε
= ε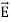 =εo
=εo 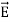 +
+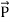 = εo
= εo  (1+
(1+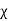 )
) - The electric displacement field "D" is defined as D= 𝜺0E+P
At far distances from the sphere, the field is uniform and is equal to
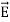 =
= ……….(1)
……….(1)
Which corresponds to a potential of
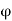 out =
out = ……….(2)
……….(2)
As before we can expand the potential inside and outside in terms of Legendre polynomials. Since the distant potential only has Legendre polynomial of order 1, we need to include only up to this order. Outside the sphere, the field is given by the potential.
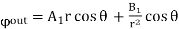 ……….(3)
……….(3)
Inside the sphere, the origin is included. Thus, inside the sphere, the potential cannot have a singularity at the origin and is given by
 ……….(4)
……….(4)
Comparing with the asymptotic limit at long distances, A1 =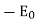
The potential itself is continuous at r=R
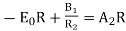 ……….(5)
……….(5)
Since there are no free charges on the surface, the normal component of the displacement vector is continuous across the surface. The normal component being the radial direction, we have,
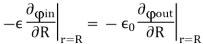
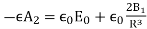 ……….(6)
……….(6)
Solving, we get,
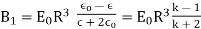 ……….(7)
……….(7)
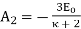 ……….(8)
……….(8)
So that
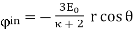 ……….(9)
……….(9)
And the electric field inside the dielectric is
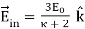 ……….(10)
……….(10)
It is seen that the due to the presence of dielectric the electric field inside is reduced by
 ……….(11)
……….(11)
We observe that if a dipole is kept at the origin of a sphere of radius R, since the radius of the sphere can be considered very large compared with the dimensions of the dipole, the field is given by
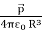 ……….(12)
……….(12)
Thus the effect of dielectric is the same as that of replacing the dielectric with a dipole of moment
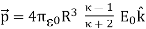 ……….(13)
……….(13)
The polarization of the sphere is then obtained by dividing this by the volume of the sphere, i.e.,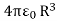 /3 by
/3 by
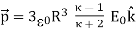 ……….(14)
……….(14)
Thus the field due to the dielectric can be written as
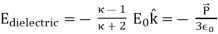 ……….(15)
……….(15)
Note that the polarization in the medium is uniform and is directed along the direction of the external field. The field lines approach the sphere from the left (negative z direction) and leave from the right, making the left face of the sphere negatively charged.
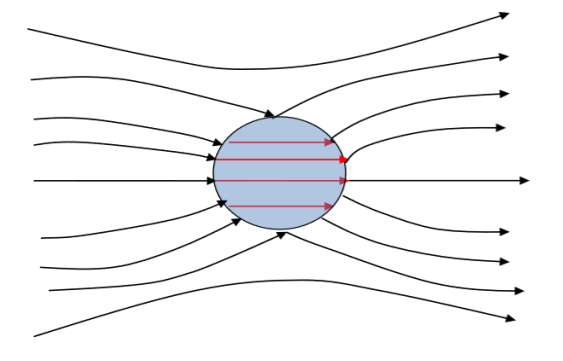
Figure 12: Gauss's law in the presence of a dielectric
Reduction in the electric field due to the presence of a dielectric
Consider a point charge in an isotropic dielectric with permittivity  . Taking the position of the charge at the origin, the field must be radial. The displacement field can be found from the Gauss’s law,
. Taking the position of the charge at the origin, the field must be radial. The displacement field can be found from the Gauss’s law,
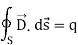
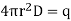 ……….(16)
……….(16)
So that 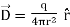 ……….(17)
……….(17)
Since the dielectric is uniform,
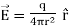 ……….(18)
……….(18)
Thus in the presence of a dielectric the electric field is reduced by a factor 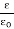 =k. The dielectric constant is a measure of the factor by which the electric field gets reduced in a linear dielectric medium. The polarization vector is given by
=k. The dielectric constant is a measure of the factor by which the electric field gets reduced in a linear dielectric medium. The polarization vector is given by
 ……….(19)
……….(19)
Consider a Gaussian sphere of radius r. We can calculate the volume charge density inside the volume by the negative divergence of the polarization vector

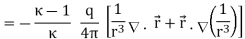
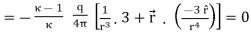 ……….(20)
……….(20)
However, there is a bound surface charge density. Since the dielectric is inside the sphere, the surface direction is inward 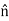 =
=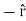 .
.
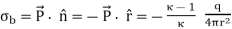 ……….(21)
……….(21)
Thus there exists a net negative bound charge. The total charge is obtained by multiplying the above with the surface area, 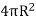 which gives qb=
which gives qb= 
As the total charge bound to the surface. The effective charge seen by a test charge is the sum of the original charge as reduced by this amount, i.e
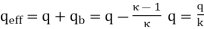 ……….(22)
……….(22)
.i.e., the test charge experiences the electric field due to an effective charge screened by a factor equal to the dielectric constant of the medium.
Key Takeaways
- There are no free charges on the surface, the normal component of the displacement vector is continuous across the surface.
- The dielectric constant is a measure of the factor by which the electric field gets reduced in a linear dielectric medium.
- The polarization vector is given by
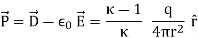
The magnetic effects in magnetic materials are due to atomic magnetic dipoles in the materials. These dipoles result from effective current loops of electrons in atomic orbits, from effects of electron spin & from the magnetic moments of atomic nuclei.
The electric currents in an atom are caused by orbital and spin motions of electrons and those of its nucleus. Since all these motions of charged particles form closed electric currents, they are equivalent to “magnetic dipoles”. When such dipoles are subjected to an external electric field, they experience a torque which tends to align their magnetic moments in the direction of the externally applied field.
Some Important Definitions
Magnetic dipole
Each tiny dimension of a magnetic material (or) atoms in magnetic materials is called magnetic dipole. This magnetic dipole produces magnetic moment depending on the alignment with respect to the applied magnetic field.
Magnetic flux (Ф)
It is defined as the amount of magnetic lines of forces passing perpendicularly through unit area of a given material. It is denoted by ‘Ф’
Ф=AB
Where A= Area of cross section of the material in m2
B = magnetic Induction in Wb/ m2
Units: Weber (Wb)
Intensity of Magnetization (M)
When a material is magnetized, it develops a net magnetic moment. The magnetic moment per unit volume is called Intensity of magnetization.
Magnetization (M) = 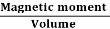
Units: Amp/m
Magnetic Induction (B)
Magnetic induction at a point is defined as the force experienced by a unit North Pole Placed at that point. It is denoted by ‘B’i.e.
B =
Unit is weber / m2
Magnetizing field strength (H)
When a medium is exposed to a magnetic field of intensity ‘H’, it causes an induction ‘B’ in the medium i.e. B H
B = μH
Where μ = absolute permeability of the medium. If the medium is air or vacuum B=μ0H
μ0=permeability of free space i.e. air or vacuum
μ0=4𝜋×10-7 H/m
Units for H: Amp /m
Permeability (μ)
It indicates with which the material allows magnetic lines of force to pass through it.
Or
It is the ability of the medium to pass magnetic lines of forces through it.
There are three Permeabilities i.e. μ1,μ0, μr
μ = μ0μr
Where μ = Absolute permeability of the medium
μ0 = Permeability of free space i.e. air or vacuum
μr = Relative permeability of the medium
Magnetic moment
Magnetic moment μm = (current) × (area of circulating orbit)
μm = (I) × (𝜋r2)
Units: Amp-m2
When the magnetic dipoles (atoms consisting of charged particles like protons & neutrons) undergo orbital motion (or) spin motion produces a magnetic moment. Since motion of charged particles is considered as closed electric current loops which in turn produces a magnetic moment.
Magnetic susceptibility (χ)
If H is the applied magnetizing field intensity and M is the amount of magnetization of the material,
Then χ = 
χ = 0 in vacuum
χ = +ve for paramagnetic and Ferro magnetic materials
χ = -ve for diamagnetic materials
Units: It has no units.
Relation between B, H and M
We know
B = μH ……. (1)
Also we know μ = μ0μr ……. (2)
Using (2)
B = μ0μrH ……. (3)
Adding and subtracting μ0H to equation (3)
B = μ0μrH + μ0H - μ0H
B = μ0H (μr -1) +μ0H
B = μ0M +μ0H
B = μ0 (M +H) ……. (4)
This is the relation between B, H and M
Now M= H (μr -1)
So we know that μ = μ0μr
We know μr = μ / μ0
Now μr= (B/H) /(B/H+M)
As B = μH and B = μ0 (M +H)
Therefore μr=1+M/H
μr-1=M/H
M=H(μr -1) ……. (5)
Key Takeaways
- The magnetic effects in magnetic materials are due to atomic magnetic dipoles in the materials. These dipoles result from effective current loops of electrons in atomic orbits,
- The electric currents in an atom are caused by orbital and spin motions of electrons and those of its nucleus.
- Relation between B, H and M is B = μ0 (M +H)
A ferromagnetic material is made up of smaller regions, called ferromagnetic domain. Within each domain, the magnetic moments are spontaneously aligned in a direction. This alignment is caused by strong interaction arising from electron spin which depends on the inter-atomic distance. Each domain has net magnetisation in a direction. However the direction of magnetisation varies from domain to domain and thus net magnetisation of the specimen is zero.
In the presence of external magnetic field, two processes take place
1. The domains having magnetic moments parallel to the field grow in size
2. The other domains (not parallel to field) are rotated so that they are aligned with the field.
As a result of these mechanisms, there is a strong net magnetisation of the material in the direction of the applied field
This magnetic domain theory for ferromagnetic was first proposed by Pierre-Ernest Weiss in 1906. The microscopic ordering of electron spins characteristic of ferromagnetic materials leads to the formation of regions of magnetic alignment called domains.
The magnetic moments of atoms dictate the magnetic properties of a material. In ferromagnetic materials, long-range alignments of magnetic moments, called domains, contain magnetic moments that all point in the same direction.
However, if material were to have all of its magnetic moments pointed in the same direction, this would create a very large external magnetic field. This field is not energetically minimizing as it stores large amounts of magnetostatic energy in the field.
Thus, for the system to minimize its internal energy, it must minimize the external field produced. To do this, the material creates different domains within itself to redirect the magnetic field. The regions in-between these domains are known as domain walls.
Interactions of a material's exchange interaction, magnetocrystalline anisotropy, and minimization of external magnetic field determine the domain structure of a material.
The magnetisation within the domain is saturated and will always lie in the easy direction of magnetisation when there is no externally applied field. The direction of the domain alignment across a large volume of material is more or less random and hence the magnetisation of a specimen can be zero.
Magnetic domains exist to reduce the energy of the system. A uniformly magnetized specimen as shown in figure 12a) has large magnetostatic energy associated with it. This is the result of the presence of magnetic free poles at the surface of the specimen generating a demagnetizing field, Hd. From the convention adopted for the definition of the magnetic moment for a magnetic dipole the magnetisation within the specimen points from the south pole to the north pole, while the direction of the magnetic field points from north to south. Therefore, the demagnetizing field is in opposition to the magnetisation of the specimen. The magnitude of Hd is dependent on the geometry and magnetisation of the specimen.
In general, if the sample has a high length to diameter ratio (and is magnetized in the long axis) then the demagnetizing field and the magnetostatic energy will be low.
The break-up of the magnetisation into two domains as illustrated in figure 13(b) reduces the magnetostatic energy by half. In fact, if the magnet breaks down into N domains then the magnetostatic energy is reduced by a factor of 1/N, hence figure13(c) has a quarter of the magnetostatic energy of figure 13(a). Figure 13(d) shows a closure domain structure where the magnetostatic energy is zero, however, this is only possible for materials that do not have a strong uniaxial anisotropy, and the neighbouring domains do not have to be at 180º to each other.
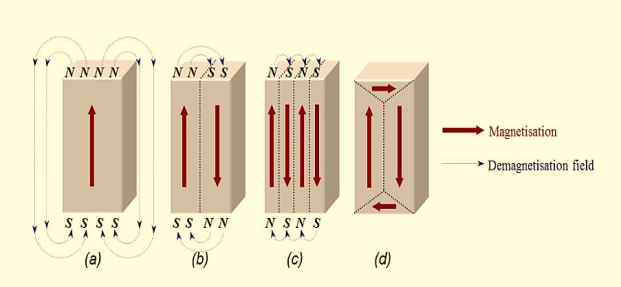
Figure 13: Schematic illustration of the break-up of magnetisation into domains: (a) single domain; (b) two domains; (c) four domains; (d) closure domains.
The introduction of a domain raises the overall energy of the system, therefore the division into domains only continues while the reduction in magnetostatic energy is greater than the energy required to form the domain wall.
The energy associated with a domain wall is proportional to its area. The schematic representation of the domain wall, shown in figure 13, illustrates that the dipole moments of the atoms within the wall are not pointing in the easy direction of magnetisation and hence are in a higher energy state.
Also, the atomic dipoles within the wall are not at 180º to each other and so the exchange energy is also raised within the wall. Therefore, the domain wall energy is an intrinsic property of material depending on the degree of magnetocrystalline anisotropy and the strength of the exchange interaction between neighbouring atoms. The thickness of the wall will also vary in relation to these parameters, as a strong magnetocrystalline anisotropy will favour a narrow wall, whereas a strong exchange interaction will favour a wider wall.
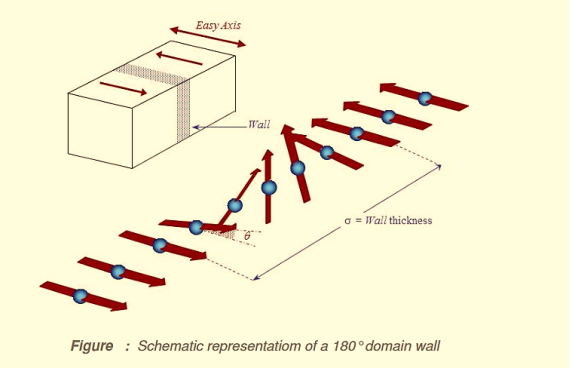
Figure 14: Schematic representation of a 180o domain wall
Minimum energy can therefore be achieved with a specific number of domains within a specimen. This number of domains will depend on the size and shape of the sample (which will affect the magnetostatic energy) and the intrinsic magnetic properties of the material (which will affect the magnetostatic energy and the domain wall energy).
The main implication of the domains is that there is already a high degree of magnetization in ferromagnetic materials within individual domains, but that in the absence of external magnetic fields those domains are randomly oriented. A modest applied magnetic field can cause a larger degree of alignment of the magnetic moments with the external field, giving a large multiplication of the applied field.
These illustrations of domains are conceptual only and not meant to give an accurate scale of the size or shape of domains.
The microscopic evidence about magnetization indicates that the net magnetization of ferromagnetic materials in response to an external magnetic field may occur more by the growth of the domains parallel to the applied field at the expense of other domains rather than the reorientation of the domains themselves as implied in the sketch.
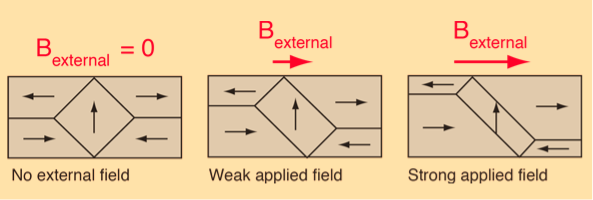
Figure 15: Domain Alignment
The internal magnetic fields which come from the long-range ordering of the electron spins are much stronger, sometimes hundreds of times stronger, than the external magnetic fields required to produce these changes in domain alignment.
Key Takeaways
- The microscopic ordering of electron spins characteristic of ferromagnetic materials leads to the formation of regions of magnetic alignment called domains.
- For the system to minimize its internal energy, it must minimize the external field produced. To do this, the material creates different domains within itself to redirect the magnetic field. The regions in-between these domains are known as domain walls.
- This number of domains will depend on the size and shape of the sample and the intrinsic magnetic properties of the material.
Magnetic Hysteresis
The lag or delay of a magnetic material known commonly as Magnetic Hysteresis relates to the magnetization properties of a material by which it first becomes magnetized and then de-magnetized.
The set of magnetization curves, M above represents an example of the relationship between B and H for soft-iron and steel cores but every type of core material will have its own set of magnetic hysteresis curves. You may notice that the flux density increases in proportion to the field strength until it reaches a certain value where it cannot increase any more becoming almost level and constant as the field strength continues to increase.
This is because there is a limit to the amount of flux density that can be generated by the core as all the domains in the iron are perfectly aligned. Any further increase will not affect the value of M, and the point on the graph where the flux density reaches its limit is called Magnetic Saturation also known as Saturation of the Core and in our simple example above the saturation point of the steel, the curve begins at about 3000 ampere-turns per metre.
As the magnetic field strength, ( H ) increases these molecular magnets become more and more aligned until they reach perfect alignment producing maximum flux density, and an increase in the magnetic field strength due to an increase in the electrical current flowing through the coil will have little or no effect.
Retentivity
Let’s assume that we have an electromagnetic coil with a high field strength due to the current flowing through it and that the ferromagnetic core material has reached its saturation point, maximum flux density. If we now open a switch and remove the magnetizing current flowing through the coil we would expect the magnetic field around the coil to disappear as the magnetic flux reduced to zero.
However, the magnetic flux does not completely disappear as the electromagnetic core material still retains some of its magnetism even when the current has stopped flowing in the coil. This ability for a coil to retain some of its magnetism within the core after the magnetization process has stopped is called Retentivity or remanence, while the amount of flux density remaining in the core is called Residual Magnetism, BR.
The reason for this that some of the tiny molecular magnets do not return to a completely random pattern and still point in the direction of the original magnetizing field giving them a sort of “memory”. Some ferromagnetic materials have a high retentivity (magnetically hard) making them excellent for producing permanent magnets.
While other ferromagnetic materials have low retentivity (magnetically soft) making them ideal for use in electromagnets, solenoids, or relays. One way to reduce this residual flux density to zero is by reversing the direction of the current flowing through the coil, thereby making the value of H, the magnetic field strength negative. This effect is called a Coercive Force, HC.
If this reverse current is increased further the flux density will also increase in the reverse direction until the ferromagnetic core reaches saturation again but in the reverse direction from before. Reducing the magnetizing current, i once again to zero will produce a similar amount of residual magnetism but in the reverse direction.
Then by constantly changing the direction of the magnetizing current through the coil from a positive direction to a negative direction, as would be the case in an AC supply, a Magnetic Hysteresis loop of the ferromagnetic core can be produced.
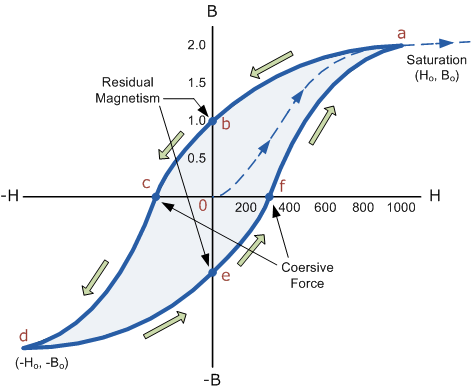
Figure 16: B-H Curve
The B-H Curve or Magnetic Hysteresis loop above shows the behaviour of a ferromagnetic core graphically as the relationship between B and H is non-linear.
Starting with an unmagnetized core both B and H will be at zero, point 0 on the magnetization curve.
If the magnetization current, i is increased in a positive direction to some value the magnetic field strength H increases linearly with i and the flux density B will also increase as shown by the curve from point 0 to point a as it heads towards saturation.
Now if the magnetizing current in the coil is reduced to zero, the magnetic field circulating around the core also reduces to zero. However, the coils magnetic flux will not reach zero due to the residual magnetism present within the core and this is shown on the curve from point a to point b.
To reduce the flux density at point b to zero we need to reverse the current flowing through the coil. The magnetising force which must be applied to null the residual flux density is called a “Coercive Force”. This coercive force reverses the magnetic field re-arranging the molecular magnets until the core becomes unmagnetised at point c.
An increase in this reverse current causes the core to be magnetised in the opposite direction and increasing this magnetisation current further will cause the core to reach its saturation point but in the opposite direction, point d on the curve.
This point is symmetrical to point b. If the magnetising current is reduced again to zero the residual magnetism present in the core will be equal to the previous value but in reverse at point e.
Again reversing the magnetising current flowing through the coil this time into a positive direction will cause the magnetic flux to reach zero, point f on the curve and as before increasing the magnetisation current further in a positive direction will cause the core to reach saturation at point a.
Then the B-H curve follows the path of a-b-c-d-e-f-a as the magnetising current flowing through the coil alternates between a positive and negative value such as the cycle of an AC voltage. This path is called a B-H Curve or Magnetic Hysteresis Loop.
The effect of magnetic hysteresis shows that the magnetisation process of a ferromagnetic core and therefore the flux density depends on which part of the curve the ferromagnetic core is magnetised on as this depends upon the circuits past history giving the core a form of “memory”. Then ferromagnetic materials have memory because they remain magnetised after the external magnetic field has been removed.
However, soft ferromagnetic materials such as iron or silicon steel have very narrow magnetic hysteresis loops resulting in very small amounts of residual magnetism making them ideal for use in relays, solenoids, and transformers as they can be easily magnetised and demagnetised.
Since a coercive force must be applied to overcome this residual magnetism, work must be done in closing the hysteresis loop with the energy being used being dissipated as heat in the magnetic material. This heat is known as hysteresis loss, the amount of loss depends on the material’s value of coercive force.
By adding additives to the iron metal such as silicon, materials with a very small coercive force can be made that have a very narrow hysteresis loop. Materials with narrow hysteresis loops are easily magnetised and demagnetised and known as soft magnetic materials.
Magnetic Hysteresis Loops for Soft and Hard Materials
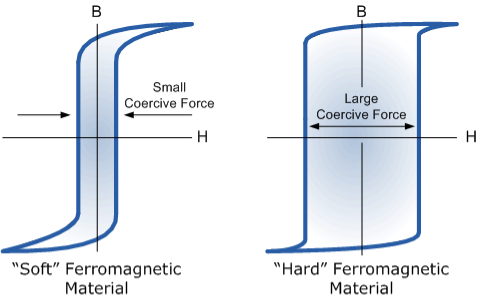
Figure 17: Magnetic Hysteresis Loops for Soft and Hard Materials
Magnetic Hysteresis results in the dissipation of wasted energy in the form of heat with the energy wasted being in proportion to the area of the magnetic hysteresis loop. Hysteresis losses will always be a problem in AC transformers where the current is constantly changing direction and thus the magnetic poles in the core will cause losses because they constantly reverse direction.
Rotating coils in DC machines will also incur hysteresis losses as they are alternately passing north the south magnetic poles. As said previously, the shape of the hysteresis loop depends upon the nature of the iron or steel used and in the case of iron which is subjected to massive reversals of magnetism, for example, transformer cores, the B-H hysteresis loop must be as small as possible.
Key Takeaways
- The lag or delay of a magnetic material known commonly as Magnetic Hysteresis relates to the magnetization properties of a material by which it first becomes magnetized and then de-magnetized.
- There is a limit to the amount of flux density that can be generated by the core as all the domains in the iron are perfectly aligned. Any further increase will not affect the value of M, and the point on the graph where the flux density reaches its limit is called Magnetic Saturation also known as Saturation of the Core.
- This ability for a coil to retain some of its magnetism within the core after the magnetization process has stopped is called Retentivity or remanence, while the amount of flux density remaining in the core is called Residual Magnetism, BR.
- One way to reduce this residual flux density to zero is by reversing the direction of the current flowing through the coil, thereby making the value of H, the magnetic field strength negative. This effect is called a Coercive Force, HC.
- Materials with narrow hysteresis loops are easily magnetised and demagnetised and known as soft magnetic materials.
Faraday’s law of electromagnetic induction (referred to as Faraday’s law) is a basic law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (EMF). This phenomenon is known as electromagnetic induction.
Faraday’s law states that a current will be induced in a conductor which is exposed to a changing magnetic field. Lenz’s law of electromagnetic induction states that the direction of this induced current will be such that the magnetic field created by the induced current opposes the initial changing magnetic field which produced it. The direction of this current flow can be determined using Fleming’s right-hand rule.
Let us understand Faraday’s law by faraday‘s experiment.
Faraday’s Experiment
In this experiment, Faraday takes a magnet and a coil and connects a galvanometer across the coil. At starting, the magnet is at rest, so there is no deflection in the galvanometer i.e. the needle of the galvanometer is at the center or zero position. When the magnet is moved towards the coil, the needle of the galvanometer deflects in one direction.
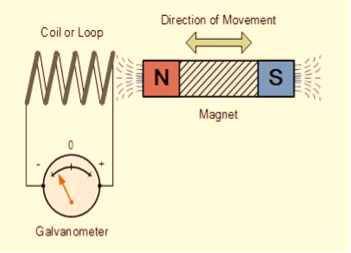
Figure 18: Faraday’s law of electromagnetic induction
When the magnet is held stationary at that position, the needle of galvanometer returns to zero position. Now when the magnet moves away from the coil, there is some deflection in the needle but opposite direction, and again when the magnet becomes stationary, at that point respect to the coil, the needle of the galvanometer returns to the zero position.
Similarly, if the magnet is held stationary and the coil moves away, and towards the magnet, the galvanometer similarly shows deflection. It is also seen that the faster the change in the magnetic field, the greater will be the induced EMF or voltage in the coil.
Let us take a look at the following table. This table is showing the observation of faraday’s experiment.
Position of magnet | Deflection in galvanometer |
Magnet at rest | No deflection in the galvanometer |
Magnet moves towards the coil | Deflection in galvanometer in one direction |
Magnet is held stationary at same position (near the coil) | No deflection in the galvanometer |
Magnet moves away from the coil | Deflection in galvanometer but in the opposite direction |
Magnet is held stationary at the same position (away from the coil) | No deflection in the galvanometer |
Conclusion
From this experiment, Faraday concluded that whenever there is relative motion between a conductor and a magnetic field, the flux linkage with a coil changes and this change in flux induces a voltage across a coil.
Michael Faraday formulated two laws on the basis of the above experiments. These laws are called Faraday’s laws of electromagnetic induction.
Faraday’s First Law
Any change in the magnetic field of a coil of wire will cause an emf to be induced in the coil. This emf induced is called induced emf and if the conductor circuit is closed, the current will also circulate through the circuit and this current is called induced current.
Method to change the magnetic field:
- By moving a magnet towards or away from the coil
- By moving the coil into or out of the magnetic field
- By changing the area of a coil placed in the magnetic field
- By rotating the coil relative to the magnet
Faraday’s Second Law
It states that the magnitude of emf induced in the coil is equal to the rate of change of flux that linkages with the coil. The flux linkage of the coil is the product of the number of turns in the coil and flux associated with the coil.
According to Faraday’s law of electromagnetic induction, the rate of change of flux linkage is equal to induced emf.
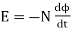 ………..(9)
………..(9)
Considering Lenz’s Law
Where:
- Flux Φ in Wb = B.A
- B = magnetic field strength
- A = area of the coil
Factors on which induced emf depend
- By increasing the number of turns in the coil i.e. N, from the formulae derived above it is easily seen that if the number of turns in a coil is increased, the induced emf also gets increased.
- By increasing magnetic field strength i.e. B surrounding the coil- Mathematically, if magnetic field increases, flux increases and if flux increases emf induced will also get increased. Theoretically, if the coil is passed through a stronger magnetic field, there will be more lines of force for the coil to cut and hence there will be more emf induced.
- By increasing the speed of the relative motion between the coil and the magnet – If the relative speed between the coil and magnet is increased from its previous value, the coil will cut the lines of flux at a faster rate, so more induced emf would be produced.
Applications of faraday’s law
Faraday law is one of the most basic and important laws of electromagnetism. This law finds its application in most of the electrical machines, industries, and the medical field, etc.
- Power transformers function based on Faraday’s law
- The basic working principle of the electrical generator is Faraday’s law of mutual induction.
- The Induction cooker is the fastest way of cooking. It also works on the principle of mutual induction. When current flows through the coil of copper wire placed below a cooking container, it produces a changing magnetic field. This alternating or changing magnetic field induces an emf and hence the current in the conductive container, and we know that the flow of current always produces heat in it.
- Electromagnetic Flow Meter is used to measure the velocity of certain fluids. When a magnetic field is applied to an electrically insulated pipe in which conducting fluids are flowing, then according to Faraday’s law, an electromotive force is induced in it. This induced emf is proportional to the velocity of fluid flowing.
- From bases of Electromagnetic theory, Faraday’s idea lines of force is used in well-known Maxwell’s equations. According to Faraday’s law, change in magnetic field gives rise to change in electric field and the converse of this is used in Maxwell’s equations.
- It is also used in musical instruments like an electric guitar, electric violin, etc.
Key Takeaways
- Any change in the magnetic field of a coil of wire will cause an emf to be induced in the coil. This emf induced is called induced emf .
- If the conductor circuit is closed, the current will also circulate through the circuit and this current is called induced current.
- Magnetic field can be change by moving a magnet towards or away from the coil, by moving the coil into or out of the magnetic field, by changing the area of a coil placed in the magnetic field, by rotating the coil relative to the magnet.
- Faraday’s law states that the magnitude of emf induced in the coil is equal to the rate of change of flux that linkages with the coil.
- The flux linkage of the coil is the product of the number of turns in the coil and flux associated with the coil.
Lenz’s Law
Lenz’s law states that the direction of the current induced in a conductor by a changing magnetic field is such that the magnetic field created by the induced current opposes the initial changing magnetic field which produced it.
Lenz’s Law is named after the German scientist H. F. E. Lenz in 1834.
Lenz’s law formula
Lenz’s law states that when an EMF is generated by a change in magnetic flux according to Faraday’s Law, the polarity of the induced EMF is such, that it produces an induced current whose magnetic field opposes the initial changing magnetic field which produced it
The negative sign used in Faraday’s law of electromagnetic induction, indicates that the induced EMF (ε) and the change in magnetic flux (δΦB) have opposite signs. The formula for Lenz’s law is shown below
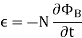
Where:
- ε = Induced emf
- δΦB = change in magnetic flux
- N = Number of turns in coil
Lenz’s law can also be understood as follow. We already know that when a current is induced by a magnetic field, the magnetic field that this induced current produces will create its own magnetic field. This magnetic field will always be such that it opposes the magnetic field that originally created it. In the example below, if the magnetic field “B” is increasing – as shown in (1) – the induced magnetic field will act in opposition to it.
When the magnetic field “B” is decreasing – as shown in (2) – the induced magnetic field will again act in opposition to it. But this time ‘in opposition’ means that it is acting to increase the field – since it is opposing the decreasing rate of change.
Lenz’s law is based on Faraday’s law of induction. Faraday’s law tells us that a changing magnetic field will induce a current in a conductor. Lenz’s law tells us the direction of this induced current, which opposes the initial changing magnetic field which produced it. This is signified in the formula for Faraday’s law by the negative sign (‘–’).
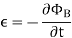
Figure 19: Lenz’s law
This change in the magnetic field may be caused by changing the magnetic field strength by moving a magnet towards or away from the coil, or moving the coil into or out of the magnetic field. In other words, we can say that the magnitude of the EMF induced in the circuit is proportional to the rate of change of flux.
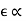
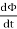
Key Takeaways
- Lenz’s law states that the direction of the current induced in a conductor by a changing magnetic field is such that the magnetic field created by the induced current opposes the initial changing magnetic field which produced it.
- Lenz’s Law is named after the German scientist H. F. E. Lenz in 1834.
- The formula for Lenz’s law is shown below
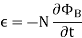
3.12.1 Self Inductance
According to Lenz's law the direction of this induced e.m.f. Will be so as to oppose the cause producing it. The cause is the current I hence the self-induced e.m.f. Will try to set up a current which is in opposite direction to that of current I. When current is increased, self-induced e.m.f. Reduces the current tries to keep it to its original value. If current is decreased, self-induced e.m.f. Increases the current and tries to maintain it back to its original value. So any change in current through coil is opposed by the coil.
This property of the coil which opposes any change in current passing through it is called Self-Inductance or Only Inductance.
It is analogous to electrical inertia or electromagnetic inertia.
Magnitude of Self Induced E.M.F.
From the Faraday's law of electromagnetic induction, self-induced e.m.f. Can be expressed as
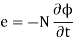
This negative sign indicates that direction of this e.m.f. Is opposing change in current due to which it exists.
The flux can be expressed as,
 = ( Flux / Ampere )x Ampere
= ( Flux / Ampere )x Ampere
Now for a circuit, as long as permeability is constant, ratio of flux to current (i.e. B/H) remains constant.
Rate of change of flux = 
 rate of change of current
rate of change of current

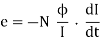
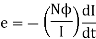
The constant 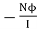 in this expression is nothing but the quantitative measure of the property due to which coil opposes any change in current. So this constant is called coefficient of self inductance and denoted by L.
in this expression is nothing but the quantitative measure of the property due to which coil opposes any change in current. So this constant is called coefficient of self inductance and denoted by L.
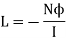
It can be define as flux linkage per ampere current. Its units is henry
A circuit possess a one henry inductance when a current through the coil changes uniformly at the rate on 1 ampere per second including an opposing e.m.f. Of 1 volt in it.
Also
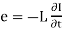
Expression for coefficient of self-inductance
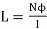
But 
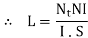
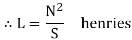
Now 
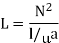
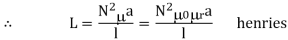
Where L is the length of the magnetic circuit and a is the area of cross section through which the flux passes
Factors Affecting Self Inductance of a Coil
We can define factors on which self-inductance of a coil depends as,
- It is directly proportional to the square of number of turns of a coil. This means for same length, if number of turns are more then self-inductance of coil will be more.
- It is directly proportional to the cross-sectional area of the magnetic circuit.
- It is inversely proportional to the length of the magnetic circuit.
- It is directly proportional to the relative permeability of the core. So for iron and other magnetic materials inductance is high as their relative permeabilities are high.
- For air cored or non-magnetic cored magnetic circuits, μr=1 and constant, hence self-inductance coefficient is also small and always constant. As against this for magnetic materials, as current i.e. magnetic field strength H is changed, it μr also changes. Due to this change in current, must change In value of self-Inductance. So for magnetic materials It is not constant but varies with current.
- Since the relative permeability of iron varies with respect to flux density, the coefficient of self-inductance varies with respect to flux density.
- Lf the conductor is bent back on itself, then magnetic fields produced by current through it will be opposite to each other and hence will neutralize each other. Hence inductance will be zero under such condition.
3.12.2 Mutual Inductance
Mutually induced e.m.f.
If the flux produced by one coil is getting linked with another coil and due to change in this flux produced by first coil, there is induced e.m.f. In the second coil, then such an e.m.f. Is called mutually induced e.m.f.
Figure Consider two coils which are placed adjacent to each other as shown in the Figure. The coil A has N1 turns while coil B has N2 number of turns. The coil A has switch S, variable resistance R and battery of 'E' volts in series with it. A galvanometer is connected across coil B to sense induced e.m.f. And current because of it.
Current I1through coil A is h producing flux 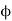 1 . Part of this flux will link with coil B i.e. will complete its path through coil B as shown in the Figure. This is the mutual flux
1 . Part of this flux will link with coil B i.e. will complete its path through coil B as shown in the Figure. This is the mutual flux  2.
2.
Now if current through coil A is changed by means of variable resistance R then flux 1 changes. Due to this, flux associated with coil B, which is mutual flux
1 changes. Due to this, flux associated with coil B, which is mutual flux  2. also changes.
2. also changes.
Due to Faraday's law there will be induced e.m.f. In coil B which will set up a current through coil B, which will be detected by galvanometer G.
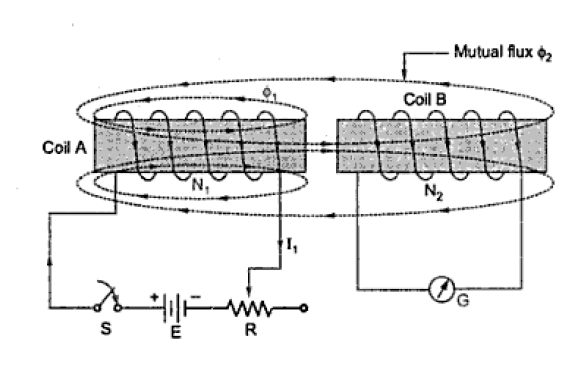
Figure 20: Mutually induced e.m.f.
Magnitude of Mutually Induced E.M.F.
Let N1= Number of turns of coil A
N2 = Number of turns of coil B
I1 = Current flowing through coil A
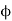 1 = Flux produced due to current II in webers.
1 = Flux produced due to current II in webers.
 2= Flux linking with coil B
2= Flux linking with coil B
According to Faraday's law, the induced e.m.f. In coil B

Negative sign indicates that this e.m.f. Will set up a current which will oppose the change of flux linking with it.
Now
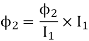
If permeability of the surroundings is assumed constant then  2
2  I1 and hence
I1 and hence 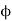 2 / I1 is constant.
2 / I1 is constant.
Rate of change of 2 =(
2 =(  2 / I1)x Rate of change of current I1
2 / I1)x Rate of change of current I1
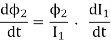
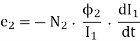
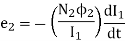
Here - (N2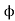 2 / I1) is called coefficient of mutual inductance denoted by M.
2 / I1) is called coefficient of mutual inductance denoted by M.
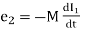 volts
volts
Coefficient of mutual inductance is defined as the property by which e.m.f. Gets induced in the second coil because of change in current through rust coil. Coefficient of mutual inductance is also called mutual inductance. It has unit’s henries.
Expressions for mutual inductance
1.
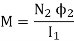
2. 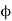 2 is the part of the flux
2 is the part of the flux 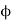 1 produced to I1. Let K1 be thethe fraction of flux
1 produced to I1. Let K1 be thethe fraction of flux 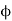 1 which is linking with the coil B
1 which is linking with the coil B
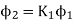
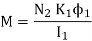
3. The flux 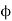 1 can be expressed as
1 can be expressed as
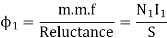
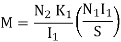
If all the flux produced by the coil A links with coil B then K1 =1
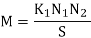
4. Now
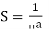 and
and 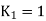
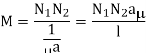
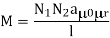
5. If the second coil producing current I2 and flux 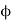 2, the part of which link with coil A i.e.
2, the part of which link with coil A i.e. 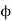 1, Then
1, Then
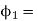
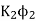 and
and 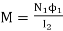
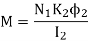
Now 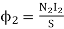
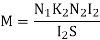
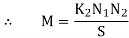
If the entire flux produced by the coil B2 links with the coil 1, K2 =1, Hence
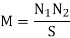
Coefficient of coupling or magnetic coupling coefficient
We know that

Multiplying the two expressions of M
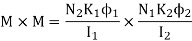
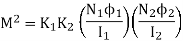
But  Self inductance of coil 1=
Self inductance of coil 1=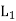
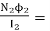 Self inductance of coil 2=
Self inductance of coil 2=
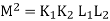

Where
K=
The K is called coefficient of coupling. If entire flux produced by one coil links with other then K = K1= K2 = 1 and maximum mutual inductance existing between the coil is
M = K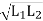
This gives an idea about magnetic coupling between the two coils. When entire flux produced by one coil links with other, this coefficient is maximum i.e. Unity. It can be defined as the ratio of the actual mutual inductance present between the two coils to the maximum possible value of the mutual inductance. The expression for K is,
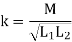
Key Takeaways
- This property of the coil which opposes any change in current passing through it is called Self-Inductance or Only Inductance.
- The constant is called coefficient of self-inductance and denoted by L.
- It is given by
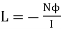
- If the flux produced by one coil is getting linked with another coil and due to change in this flux produced by first coil, there is induced e.m.f. In the second coil, then such an e.m.f. Is called mutually induced e.m.f.
Suppose two coils are placed near each other, And current I1 is passed through coil 1, then there is magnetic field (B1) produced in it. Using right hand thumb rule, we can see the direction of Magnetic field. As the current is AC, the field also changes, and Field (B1) times number of turn N1 is magnetic flux(Φ), so flux changes,
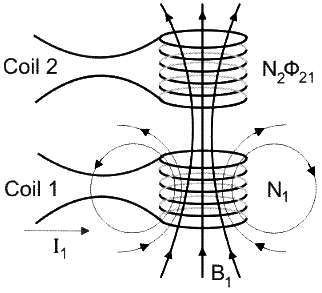
Figure 21: Reciprocity Theorem
Since the two coils are close to each other, some of the magnetic field lines through coil 1 will also pass through coil 2.Then there will be an induced emf associated with the changing magnetic flux in the second coil, given by Faraday's Law:
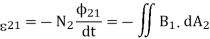
The rate of change of magnetic flux in coil 2 is proportional to the time rate of change of the current in coil 1:
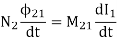
Where the proportionality constant M21 is called the mutual inductance. It can also be written as
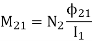
Similarly if we pass current from coil two:

Figure 22: Reciprocity Theorem
There will be production of emf in first coil due to AC current in coil 1, given by
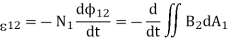
And comparing it to the emf generated due to a inductor's changing current
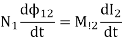
So mutual inductance is
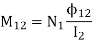
By principle of reciprocity means Mutual inductance is reciprocate from one side to other in equal manner.
Experiments and calculations that combine Ampere’s law and Biot-Savart law confirm that the two constants, M21 and M12 are equal in the absence of material medium between the two coils.
M12 = M21
This property is called reciprocity and by using reciprocity theorem, we can simply write the mutual inductance between two coils as;
M12 = M21 =M
Key Takeaways
- By principle of reciprocity means Mutual inductance is reciprocate from one side to other in equal manner.
- By using reciprocity theorem, we can simply write the mutual inductance between two coils as;
M12 = M21 =M
Let the induced e.m.f. In a coil be
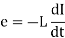
This opposes a supply voltage. So supply voltage 'V' supplies energy to overcome this, which ultimately gets stored in the magnetic field.
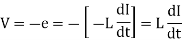
Power supplied

Energy supplied in time dt is,
E = Power 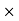 Time
Time
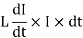
= L di  I joules.
I joules.
This is energy supplied for change in current of cil but actually current changes from zero to I.
Integrating above total energy stored is
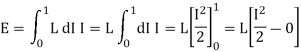

Energy stored per unit volume
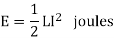
Now, 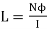

Now 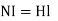 ampere-turns
ampere-turns
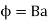
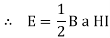
But a 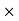 l = area
l = area  length = Volume of magnetic circuit
length = Volume of magnetic circuit
Energy stored per unit volume = ½ BH
But B = μ H
Thus Energy stored per unit volume becomes

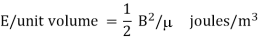
Where 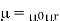
In case of inductive circuit when circuit is opened with the help of switch then current decays and finally becomes zero. In such case energy stored is recovered and if there is resistance in the circuit, appears in the form of heat across the resistance.
While if the resistance is not present then this energy appears in the form of an arc across the switch, when switch is opened
If the medium is air, µr = 1 hence µ = µ0 must be used in the above expressions of energy.
Key Takeaways
- The induced e.m.f. In a coil be
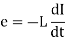
- Energy stored per unit volume becomes
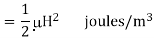
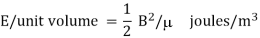
Where 
Maxwell equations are of fundamental importance since they describe the whole of classical electromagnetic phenomena.
From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization.
We are just to stating these equations without derivation. Since our goal is simply to apply them, the usual approach will be followed.
Maxwell’s four equations are given by
∇·E = ρ/ε0 (1)
∇×E = −∂B/∂t (2)
∇×H = J + ∂D/∂t (3)
∇·B = 0 (4)
These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation,
∇=(∂/∂x, ∂/∂y, ∂/∂z)
E is the electric vector
B is the magnetic induction
ρ is the electric charge density
j is the electric current density
ε0 is the permittivity of free space
c is the speed of light.
In addition to Maxwell equations, the following identities are useful:
J = σE (5)
D = εE (6)
B = μH (7)
Here,
D is the electric displacement
H is the magnetic vector
σ is the specific conductivity
ε is the dielectric constant (or permittivity)
μ is the magnetic permeability
In the Gaussian systems of units, Maxwell equations are given in the form of
∇·B=0 (8)
∇·E=4πρ (9)
∇×H=(1/c)(∂D/∂t+4πj) (10)
∇×E=−(1/c)(∂B/∂t) (11)
Free space or non-conducting medium. We know that non-conducting medium means no current so conductivity is zero i.e. σ=0.
So current density J=σE will also become zero as σ=0 Also free space means no charges which leads to ρ=0. These points mentioned below.
(a) No condition current i.e σ=0, thus J=0 ( J=σE)
(b) No charges (i.e ρ=0)
For the case of no charges or currents, that is, j = 0 and ρ = 0, and a homogeneous medium. Using these the Maxwell equation can rewritten as
∇.D=0 or ∇.E=0 as ρ=0 (12)
∇ x E= -dB/dt or ∇ x E= -μ dH/dt because B = μH (13)
∇ x H=d D/dt or ∇ x H = ε dE/dt (J=0) and D = εE (14)
∇.B=0 (15)
Maxwell's Equations are a set of 4 complicated equations that describe the world of electromagnetics. These equations describe how electric and magnetic fields propagate, interact, and how they are influenced by objects.
Maxwell was one of the first to determine the speed of propagation of electromagnetic (EM) waves was the same as the speed of light - and hence to conclude that EM waves and visible light were really the same thing.
These equations are rules the universe uses to govern the behaviour of electric and magnetic fields. A flow of electric current will produce a magnetic field. If the current flow varies with time (as in any wave or periodic signal), the magnetic field will also give rise to an electric field. Maxwell's Equations shows that separated charge (positive and negative) gives rise to an electric field - and if this is varying in time as well will give rise to a propagating electric field, further giving rise to a propagating magnetic field.
From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization.
The First Maxwell’s equation (Gauss’s law for electrostatics)
Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as:
∇·E = ρ/ε0
0r
∇·D = ρ
Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).
The Gauss’s law states that flux passing through any closed surface is equal to 1/ε0 times the total charge enclosed by that surface.
Integral form of Maxwell’s 1st equation

Also 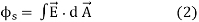
Comparing equations (1) and (2) we have

It is the integral form of Maxwell’s 1st equation.
Maxwell’s first equation in differential form
It is called the differential form of Maxwell’s 1st equation.
The value of total charge in terms of volume charge density is 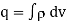 so equation (3) becomes
so equation (3) becomes
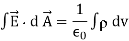
Applying divergence theorem on left hand side of above equation we have
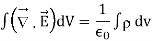

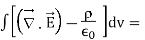
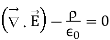
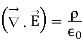
The Second Maxwell’s equation (Gauss’s law for magnetism)
The Gauss’s law for magnetism states that net flux of the magnetic field through a closed surface is zero because monopoles of a magnet do not exist.

It is the integral form of Maxwell’s second equation
Applying divergence theorem
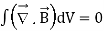
This implies that
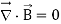
It is called differential form of Maxwell’s second equation.
We know that Gauss' Law for Electric Fields states that the divergence of the Electric Flux Density D is equal to the volume electric charge density. But the second equation, Gauss' Magnetism law states that the divergence of the Magnetic Flux Density (B) is zero.
Why? Why isn't the divergence of B equal to the magnetic charge density?
Well - it is. But it just so happens that no one has ever found magnetic charge - not in a laboratory or on the street or on the subway. And therefore, until this hypothetical magnetic charge is found, we set the right side of Gauss' Law for Magnetic Fields to zero:
∇·B = 0
Now, you may have played with magnets when you were little, and these magnetic objects attracted other magnets similar to how electric charges repel or attract like electric charges. However, there is something special about these magnets - they always have a positive and negative end. This means every magnetic object is a magnetic dipole, with a north and South Pole. No matter how many times you break the magnetic in half, it will just form more magnetic dipoles. Gauss' Law for Magnetism states that magnetic monopoles do not exist - or at least we haven't found them yet.
Maxwell’s Third equation (Faraday's Law)
Faraday figured out that a changing Magnetic Flux within a circuit (or closed loop of wire) produced an induced EMF, or voltage within the circuit. Maxwell gives his second equation from this.
Faraday's Law tells us that a magnetic field that is changing in time will give rise to a circulating E-field. This means we have two ways of generating E-fields - from Electric Charges (or flowing electric charge, current) or from a magnetic field that is changing.
∇×E = −∂B/∂t
According to Faraday’s law of electromagnetic induction

Since emf is related to electric field by the relation
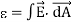
Also 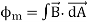
Put these values in equation (5) we have
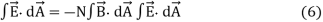
It is the integral form of Maxwell’s 3rd equation
Applying Stokes Theorem on L.H,S of equation (6) we have

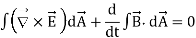

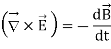 It is the differential form of Maxwell’s third equation.
It is the differential form of Maxwell’s third equation.
Maxwell’s fourth equation (Ampere's Law)
Ampere's Law tells us that a flowing electric current gives rise to a magnetic field that circles the wire. In addition to this, it also says that an Electric Field that is changing in time gives rise to a magnetic field that encircles the E-field - this is the Displacement Current term that Maxwell himself introduced.
This means there are 2 ways to generate a solenoidal (circulating) H-field - a flowing electric current or a changing Electric Field. Both give rise to the same phenomenon.
The modified form of ampere Law is given by
H.dL=(J+dD/dt)
Take integration on both sides we have
∫H.dL=∫(J+dD/dt).dS
Apply stoke’s theorem to L.H.S. Of above equation, we get
∫( ∇xH).dS=∫ H.dL
Now the above equation is written as
∫( ∇xH).dS =∫(J+dD/dt).dS
By cancelling the surface integral on both sides we have
∇xH =J+dD/dt
Which is the differential form of Maxwell’s equation.
This can also be written in the form B
The Ampere-Maxwell Law
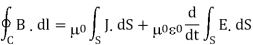
Begin with the Ampere-Maxwell law in integral form.
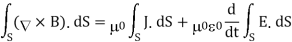
Invoke Stokes' theorem.


Set the equation to 0.
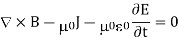
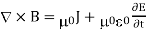
Physical significance of each equation
Physical significance of Maxwell’s Ist equation
∇·E = ρ/ε0
According to this total electric flux through any closed surface is 1/0 times the total charge enclosed by the closed surfaces, representing Gauss's law of electrostatics, As this does not depend on time, it is a steady state equation. Here for positive , divergence of electric field is positive and for negative divergence is negative. It indicates that is scalar quantity.
Physical significance of Maxwell’s 2nd equation
∇·B = 0
It represents Gauss law of magnetostatic as ∇·B = 0 resulting that isolated magnetic poles or magnetic monopoles cannot exist as they appear only in pairs and there is no source or sink for magnetic lines of forces. It is also independent of time i.e. steady state equation.
Physical significance of Maxwell’s 3rd equation
∇×E = −∂B/∂t
It shows that with time varying magnetic flux, electric field is produced in accordance with Faraday is law of electromagnetic induction. This is a time dependent equation.
Physical significance of Maxwell’s 4th equation
∇×H = J + ∂D/∂t
This is a time dependent equation which represents the modified differential form of Ampere's circuital law according to which magnetic field is produced due to combined effect of conduction current density and displacement current density.
Key Takeaways
- The First Maxwell’s equation is known as Gauss’s law for electrostatics. It is given by ∇·E = ρ/ε0 . According to this total electric flux through any closed surface is 1/0 times the total charge enclosed by the closed surfaces, representing Gauss's law of electrostatics,
- The Second Maxwell’s equation is known as Gauss’s law for magnetism. . It is given by ∇·B = 0. The Gauss’s law for magnetism states that net flux of the magnetic field through a closed surface is zero because monopoles of a magnet do not exist.
- Maxwell’s Third equation is known as Faraday's Law. It is given by ∇×E = −∂B/∂t. Faraday figured out that a changing Magnetic Flux within a circuit (or closed loop of wire) produced an induced EMF, or voltage within the circuit.
- Maxwell’s fourth equation is known as Ampere's Law. It is given by ∇×H = J + ∂D/∂t .Ampere's Law tells us that a flowing electric current gives rise to a magnetic field that circles the wire. In addition to this, it also says that an Electric Field that is changing in time gives rise to a magnetic field that encircles the E-field - this is the Displacement Current.
References:
- Introduction to Electrodynamics – D.J. Griffiths (Pearson, 4th edition, 2015)
- Foundations of Electromagnetic Theory-Ritz and Milford (Pearson) 4th Edition
- Classical Electrodynamics, J. D. Jackson (Wiley), 1998
- Electricity and Magnetism D. C. Tayal (Himalaya Publishing house), 2014
- Electricity, Magnetism and Electromagnetic Theory- S. Mahajan and Choudhury ( Tata McGraw Hill)-2012