Unit - 4
Operational Amplifiers
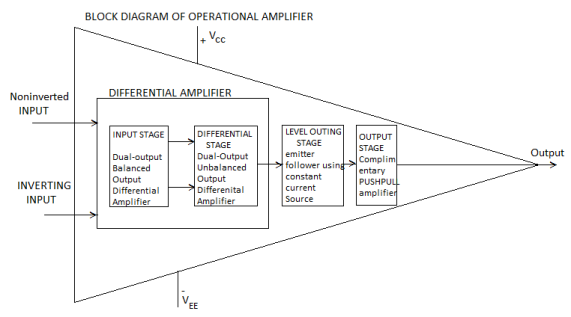
Figure 1: Block Diagram of Operational Amplifier (Op-Amp)
- The op-amp begins with a differential amplifier stage, which operates in the differential mode. Thus the inputs noted with ‘+’ & ‘- ‘.
- The positive sign is for the non-inverting input and negative is for the inverting input.
- The non-inverting input is the ac signal (or dc) applied to the differential amplifier which produces the same polarity of the signal at the output of op-amp.
- The inverting signal input is the ac signal (or dc) applied to the differential amplifier. This produces 180 degrees out of phase signal at the output.
- The inverting and non-inverting inputs are provided to the input stage which is a dual input, balanced output differential amplifier.
- The voltage gain required for the amplifier is provided in this stage along with the input resistance for the op-amp.
- The output of the initial stage is given to the intermediate stage, which is driven by the output of the input stage.
- In this stage direct coupling is used, which makes the dc voltage at the output of the intermediate stage above ground potential. Therefore, the dc level at its output must be shifted down to 0Volts with respect to the ground.
- For this, the level shifting stage is used where usually an emitter follower with the constant current source is applied.
- The level shifted signal is then given to the output stage where a push-pull amplifier increases the output voltage swing of the signal and also increases the current supplying capability of the op-amp.
IDEAL & PRACTICAL OP-AMP SPECIFICATIONS
An Operational Amplifier is basically a three-terminal device which consists of two high impedance inputs. One of the inputs is called the Inverting Input, marked with a negative or “minus” sign, ( – ). The other input is called the Non-inverting Input, marked with a positive or “plus” sign ( + ).
A third terminal represents the operational amplifiers output port which can both sink and source either a voltage or a current.
In a linear operational amplifier, the output signal is the amplification factor, known as the amplifiers gain ( A ) multiplied by the value of the input signal and depending on the nature of these input and output signals, there can be four different classifications of operational amplifier gain.
- Voltage – Voltage “in” and Voltage “out”
- Current – Current “in” and Current “out”
- Transconductance – Voltage “in” and Current “out”
- Trans resistance – Current “in” and Voltage “out”
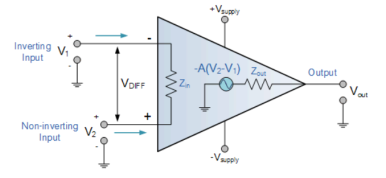
Figure 2: Operational Amplifier
Practical op-amps have zero offset voltage. The bandwidth of the practical op-amp is very small. This output can be raised to the required value by adjusting the negative feedback. The equivalent circuit is shown below.
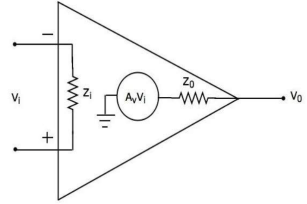
Figure 3: Practical Op-Amp
The input impedance Zi ranges to mega ohms. The output impedance Z0 is in the order of ohms and the practical op-amps have high value of open loop voltage gain AV. The value of CMRR and Slew rate should be as high as possible.
Key takeaway
- The inverting signal input is the ac signal (or dc) applied to the differential amplifier. This produces 180 degrees out of phase signal at the output.
- The inverting and non-inverting inputs are provided to the input stage which is a dual input, balanced output differential amplifier.
- For ideal Op-Amp
a) Open loop gain =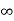 
b) Input Resistance =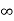 
c) Output Resistance =0
d) Offset voltage = 0
e) Bandwidth of operation =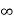 
Open-loop and Closed loop Gain
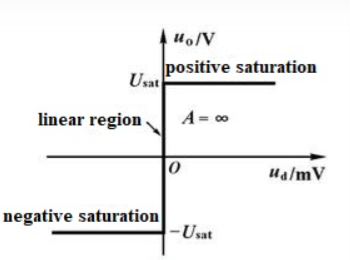
Figure 4: Transfer characteristics of ideal op-amp
Open Loop Gain (Avo)
The main function of an operational amplifier is to amplify the input signal and the more open loop gain it has the better. Open-loop gain is the gain of the op-amp without positive or negative feedback and for such an amplifier the gain will be infinite
Input impedance (ZIN)
Input impedance is the ratio of input voltage to input current and is assumed to be infinite to prevent any current flowing from the source supply into the amplifiers input circuitry ( IIN = 0 ). Real op-amps have input leakage currents from a few pico-amps to a few milli-amps.
Output impedance (ZOUT)
The output impedance of the ideal operational amplifier is assumed to be zero acting as a perfect internal voltage source with no internal resistance so that it can supply as much current as necessary to the load. This internal resistance is effectively in series with the load thereby reducing the output voltage available to the load. Real op-amps have output impedances in the 100-20kΩ range.
Bandwidth (BW)
An ideal operational amplifier has an infinite frequency response and can amplify any frequency signal from DC to the highest AC frequencies, so it is therefore assumed to have an infinite bandwidth.
With real op-amps, the bandwidth is limited by the Gain-Bandwidth product (GB), which is equal to the frequency where the amplifiers gain becomes unity.
Offset Voltage (VIO)
The amplifiers output will be zero when the voltage difference between the inverting and the non-inverting inputs is zero, the same or when both inputs are grounded. Real op-amps have some amount of output offset voltage.
Input & output offset voltages
With an input offset voltage and a differential input circuit, ideal op-amps and comparators will have an offset voltage of 0V, including error voltage.
When inputting a common-mode (same) voltage to the input pins of an op-amp or comparator, with an ideal op-amp no output voltage will be output
In case where an input offset voltage exists, a voltage will be output based on the input offset voltage. This input offset voltage, which is the differential voltage required to make the output voltage 0V, becomes the input conversion value.
The Offset voltage is normally expressed in units of mV or µV. Values closer to 0 are more ideal.
Figure 5: Op-Amp Parameters
The output offset voltage is the voltage at the output when the differential input voltage is zero.
Input & output offset currents
Bias current compensation will work if both bias currents IB+ and IB- are equal. Since the input transistor cannot be made identical. There will always be some small difference between IB+ and IB-. This difference is called the offset current
|Ios| = IB+-IB------------------------- (7)
Offset current Ios for BJT op-amp is 200nA and for FET op-amp is 10pA. Even with bias current compensation, offset current will produce an output voltage when Vi = 0.
V1 = IB + R comp
And I1 = V1 R1
KCL at node a gives
I2 = (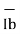 
– I1) = 
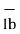- ( Ib + Rcomp/R1 )
Again V0 = I2 Rf – V1
Vo = I2 Rf - IB+ Rcomp
Vo = 1M Ω X 200nA
Vo = 200mV with Vi = 0
Input bias current:
The op-amp‘s input is differential amplifier, which may be made of BJT or FET.
In an ideal op-amp, we assumed that no current is drawn from the input terminals the base currents entering into the inverting and non-inverting terminals (IB- & IB+ respectively).
Even though both the transistors are identical, IB- and IB+ are not exactly equal due to internal imbalance between the two inputs. Manufacturers specify the input bias current IB
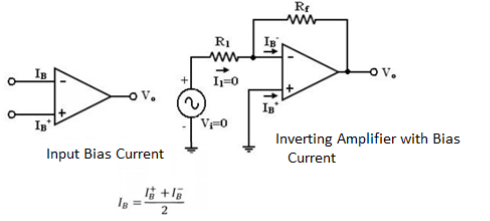
Figure 6: Input Bias Current Configuration
If input voltage Vi = 0V. The output Voltage Vo should also be (Vo = 0) but for IB = 500nA We find that the output voltage is offset by Op-amp with a 1M feedback resistor
Vo = 500nA X 1M = 500mV
The output is driven to 500mV with zero input, because of the bias currents.
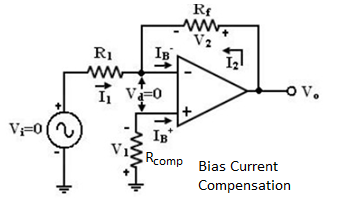
Figure 7: Input Bias Current Compensation
Current IB+ flowing through the compensating resistor Rcomp, then by KVL we get,
- V1+0+V2-Vo = 0 (or)
Vo = V2 – V1 --------- (1)
By selecting proper value of Rcomp, V2 can be cancelled with V1 and the Vo = 0. The value of Rcomp is derived as
V1 = IB+Rcomp (or)
IB+ = V1/Rcomp ------------------------ (2)
The node ‘a’ is at voltage (-V1). Because the voltage at the non-inverting input terminal is (-V1). So with Vi = 0 we get,
I1 = V1/R1 ------------------------ (3)
I2 = V2/Rf ------------------------ (4)
For compensation, Vo should equal to zero (Vo = 0, Vi = 0). i.e. from equation (3) V2 = V1. So that,
I2 = V1/Rf ——> (5)
KCL at node ‘a’ gives,
IB- = I2 + I1 =( V1/Rf ) +(V1/R1) = V1(R1+Rf)/R1Rf ------------------------ (5)
Assume IB- = IB+ and using equation (2) & (5) we get
V1 (R1+Rf)/R1Rf = V1/Rcomp
Rcomp = R1 || Rf ------------------------ (6)
i.e. to compensate for bias current, the compensating resistor, Rcomp should be equal to the parallel combination of resistor R1 and Rf.
Frequency Response
A characteristic open-loop frequency response plot is shown in figure.
At very low frequencies, the op-amp applies the maximum open-loop gain to differentiate it from the gain at higher frequencies. Gain decreases as the frequency increases, gain decreases.
There is a transition from stable gain to decreasing gain at the corner frequency. Finally the slope stabilizes. The gain decreases by 20 dB for every factor of 10 increases in input frequency.
The gain begins to decrease at such a low frequency.
This type of frequency response makes the op-amp when used in a negative-feedback configuration less likely to oscillate when used in a negative-feedback configuration.
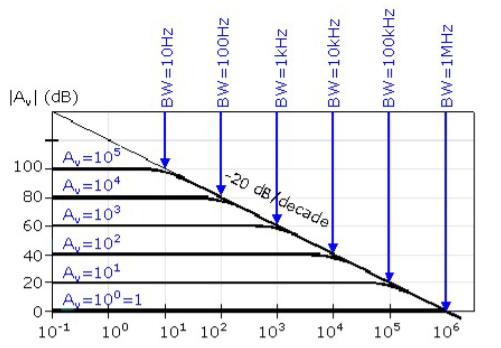
Figure 8: Frequency Response
In the above figure, take an example of voltage gain.
The vertical axis expressed in decibels (dB) and the corresponding closed loop gain noted in blue. The horizontal axis in this figure is frequency in Hertz using a logarithmic scale.
For this first order system, the bandwidth is the upper break frequency. It is also called the corner frequency. It is defined as the point at which we make the -3 dB correction from the straight line approximation.
An important characteristic of this figure is that the gain- bandwidth product (GBP) is constant. Logarithmic plot never goes to zero and the GBP must remain constant. The lowest frequency where this is true is considered the zero frequency point.
Slew Rate
The slew rate is a parameter that describes the operating speed of an op-amp. It represents the rate that can change per unit time stipulated by the output voltage.
For example, 1V/us indicates that the voltage can change by 1V in 1us. Ideal op-amps make it possible to faithfully output an output signal for any input signal. However, in reality slew rate limits do exist.
When supplying a rectangular pulse at the input with a steep rise and fall, this indicates the possible degree of change in the output voltage per unit time.
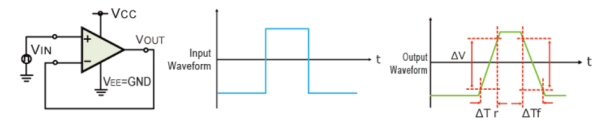
Figure 9: Voltage Follower
The rise and fall slew rates are calculated by the following equations:
SRr = ∆ V / ∆ Tr
SRf = ∆ V / ∆ Tf
Figure 10: Slew Rate Calculation
Calculate the slew rate
The output is given by
y=Asinωt
The slew rate is the slope of the tangent of the sine wave, differentiating the above equation.
Dy / Dt = Aω cosωt ωt=0
The slew rate is
SR=Aω ω=2πf
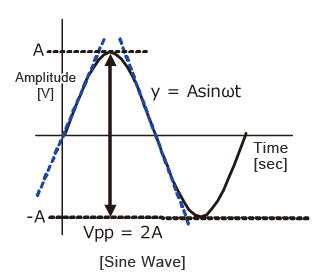
Figure 11: Sine wave amplitude
Since the amplitude of the sine wave becomes Vpp=2A (peak-to-peak), the equation can be modified as follows.
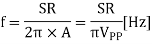
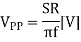
This frequency(f) is referred to as the full power bandwidth. These are conditions where the amplification factor in the op-amp has not been set, in other words the relationship of the frequency and amplitude (within the output voltage range) that can be output by the op-amp in a voltage follower circuit.
Example: Determine operating frequency for given circuit. Slew rate is 0.5V/μs.
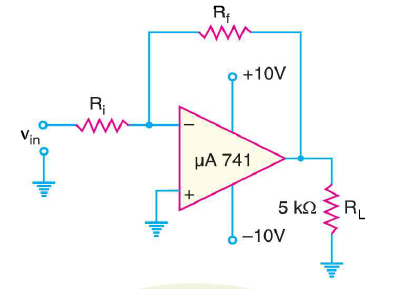
Solution:
Operating frequency for given circuit
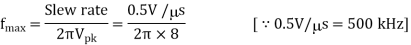
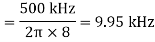
CMRR
It is the ratio of differential voltage gain Ad to the common mode voltage gain Acm.
CMRR =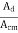 
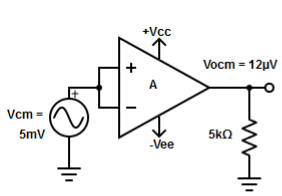
Figure 12: Common Mode Configuration
The common mode voltage gain from above figure can be
= 
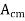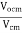
Where:
Vocm = output common mode voltage
Vcm = input common mode voltage
Acm = common mode voltage gain
In normal cases the value of Ad is large and Acm is very small making the value of CMRR very high.
Example: Differential gain of a Differential amplifier is 2000V. Common mode gain is 0.2. Calculate CMRR in dB?
Solution:
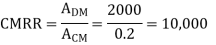
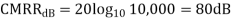
Example: Differential amplifier has differential output 1V and input 10V and output 5V with Common mode input 10mV. Calculate CMRR in dB?
Solution:
Differential gain,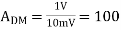 
Common-mode gain,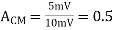 
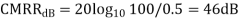
Concept of Virtual Ground
Virtual Ground simply indicates that this concept is virtual. This is different from real ground but considered as equivalent to ground.
Let us suppose, In Op-amps the term virtual ground refers to that the voltage at that particular node is almost equal to ground voltage (0V). It is not connected to ground physically.
This concept is an important and useful for Op-amp analysis and make calculations very simple.
Virtual ground in inverting Op-amp. We know that an ideal Op-amp will provide infinite voltage gain.
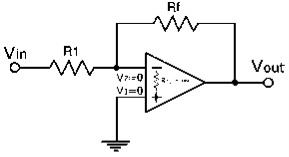
Figure 13: Virtual ground
The gain will be very high for real Op-amps. For calculation purposes it is considered as infinite.
Gain = Vo/Vin
As gain is infinite, Vin = 0
Vin = V2 – V1
Here V1 = 0
As in the above circuit V1 is grounded. Thus V2 also will be at ground potential.
V2 = 0
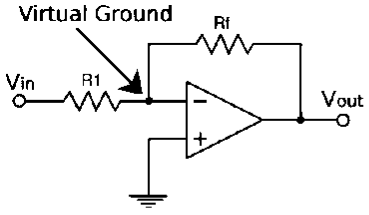
Figure 14: Virtual ground
How Virtual ground is different from real ground?
Virtual Ground | Real Ground |
Virtual Ground is a concept that concept is an important and useful for Op-amp analysis and make calculations very simple. | Real Ground is a terminal which is physically connected to ground or earth. This point acts as the reference point for the entire circuit. |
Voltage is approximately Zero | Voltage is Zero |
Not able to sink infinite current | It is an infinite current sink |
Not electrically connected to Ground | Electrically connected to Ground |
Key takeaway
- Under a certain supply voltage condition, the amplifier can only work in closed-loop (negative feedback) mode.
- Where an input offset voltage exists, a voltage will be output based on the input offset voltage. This input offset voltage, which is the differential voltage required to make the output voltage 0V, becomes the input conversion value.
- In an ideal op-amp, we assumed that no current is drawn from the input terminals the base currents entering into the inverting and non-inverting terminals. To compensate for bias current, the compensating resistor, Rcomp should be equal to the parallel combination of resistor R1 and Rf.
- Slew rate is the maximum rate of output voltage change per unit time. It is denoted by S. For getting undistorted output voltage we must have very high slew rate. It is measured in V/sec.
- The common mode voltage gain from above figure can be
= 
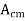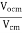
- Virtual Ground is a concept that concept is an important and useful for Op-amp analysis and make calculations very simple.
Crossing detector (8) Wein bridge oscillator
(1) Inverting Amplifier
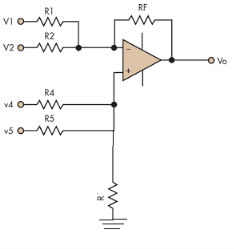
Figure 15: Summing amplifier
- In the above figure, each terminal is connected with two input sources through resistors. V1 and V2 is connected to the inverting terminal and V4 and V5 is connected to the non-inverting terminal.
- Assuming R1=R2=R4=R5=RF=R.
- Now, on applying superposition theorem, for finding output voltage due to V1 alone, keep V2=V4=V5=0V.
- Hence, now the circuit acts as an inverting amplifier.
- Therefore,
- Similarly,
- Now, for V4, voltages V1=V2=V5=0V then the circuit behaves as a non-inverting amplifier.
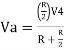
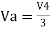
Hence,
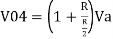
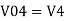
Similarly,
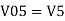
So, the resultant output voltage by all the 4 input voltages is given by,
Vo = V01 + V02 + V04 +V05
Vo = -V1 – V2 +V4 + V5
The output voltage Vo is equivalent to the sum all input voltages applied at both the terminals.
Example: In a summing amplifier, if R = 1kΩ, Va = +3V, Vb = +8V, Vc = +9V, Vd = +5V and supply voltage is ±15V. Find the output voltage Vo.
Solution:
Vo = Sum of all input voltages applied at both the terminals
Vo = Va + Vb + Vc +Vd
Vo = -3 -8 +9 +5
Vo = +3V
Example
Find the output voltage for the given circuit diagram if Rf = 5kΩ.
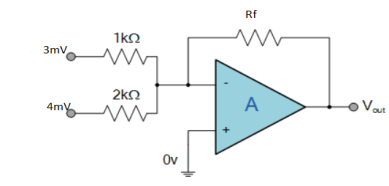
Solution:
We know,
Gain (Av) =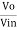
= 
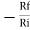
Hence,
Av1 =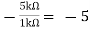 
Av2 =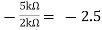 
Now, Output voltage Vo = Sum of the two amplified input signals
Vo = Av1 x V1 + Av2 x V2
Vo =(-5 x 3) + ( -2.5x 4) mV
Vo = -25mV
As the above output voltage is negative hence it is an inverting amplifier.
Example: OP-Amp is shown in figure. Calculate Rf? Closed loop voltage gain is -100V.
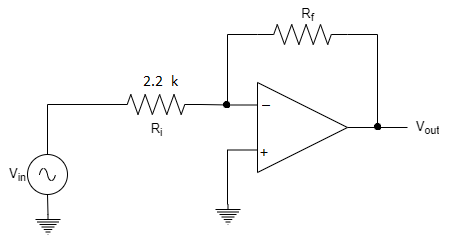
Solution:
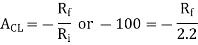
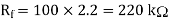
(2) Non-Inverting
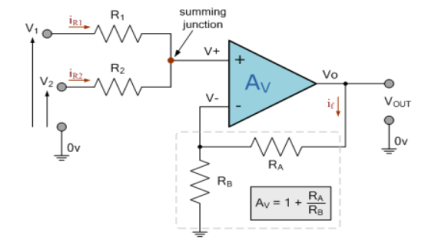
Figure 16: Non-Inverting Summing Amplifier
Applying KCL to the above circuit we have
IR1+IR2 = 0
= 
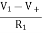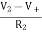= 0
When R1 = R2 =R
V+ =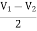 
The voltage gain for non-inverting summing amplifier is given as
AV = Vout/Vin =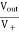 
= 1+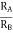
Vout= [1+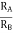
] 
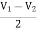
Key takeaway
AV = Vout/Vin =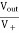 
= 1+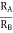
Vout= [1+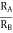
] 
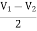
Example: Non inverting OP-Amp is shown in figure. Input Voltage 120μV.
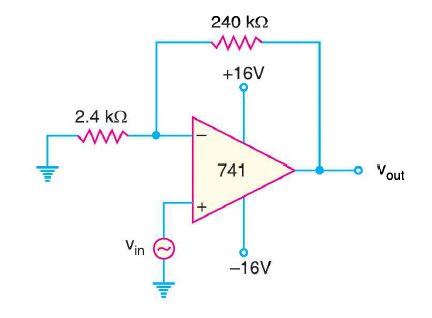
Solution:
Voltage gain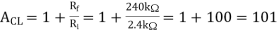 
Output voltage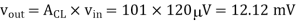 
(3) SUBTRACTOR
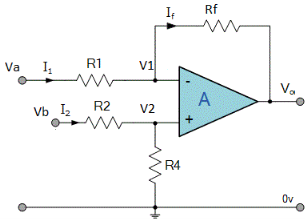
Figure 17: Difference amplifier
- Here input can be provided simultaneously at both the terminals of amplifier.
- Voltage signal Va is applied at one input terminal and another voltage signal Vb onto the other input terminal then resultant output voltage is proportional to the “Difference” between the input voltages Va and Vb.
- Vo = Vb - Va
- Now by applying superposition theorem we get,
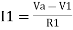
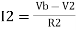
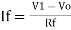
Summing point, V1 = V2 and
V2 = Vb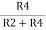
If Vb = 0 then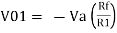 
And Va = 0 then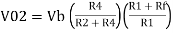 
Vo = -V01 + V02
Vo =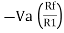 
+ 
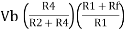
If R1 = R2 and Rf = R4 then
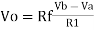
And if R1 = R2 = Rf = R4 =R then
Vo = Vb – Va
Hence, is known as a Unity Gain Differential Amplifier.
Key takeaway
The output of subtractor is
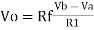
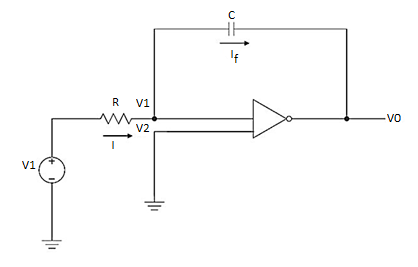
(4) Differentiator
- A differentiator is a circuit that performs differentiation operation. Hence, the output is a derivative of input.
- In an inverting amplifier, if input resistor is replaced by a capacitor then a differentiator circuit is formed.
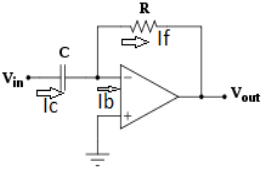
Figure 18: Differentiator
- In the above fig. On applying Kirchhoff’s law we get,
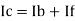
Since Ib = 0 then,
Ic ≈ If
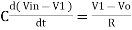
Since Gain A is very large hence, V1 = 0
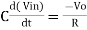
Or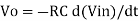 
- So, the output voltage is RC times the negative rate of change of input voltage.
- When input is a cosine wave, output is a sine wave i.e it performs the inverse function of integrator circuit.
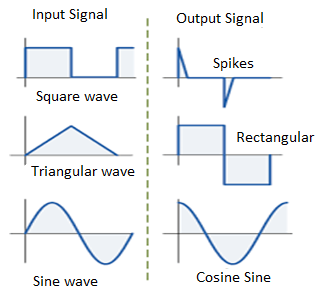
Figure 19: Input and output waveform of differentiator
Frequency response of basic differentiator circuit is given by,
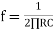( for 0 db gain)
Example: Figure shows the square wave input to a differentiator circuit. Find the output voltage if input goes from 0V to 5V is 0.1ms.
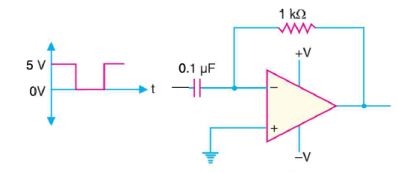
Solution:
Output Voltage
=
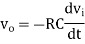
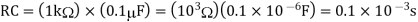
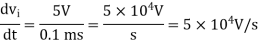
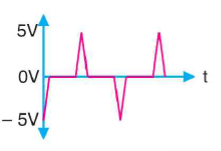
Output is shown in figure below
Key takeaway
The output voltage for differentiator is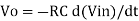 
(5) Integrator
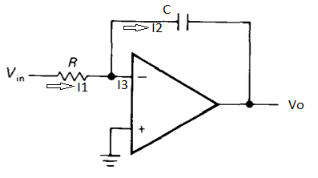
Figure 20: Integrator
- It is a circuit which provides output voltage Vo as an integral form of input voltage Vin.
- It is obtained by using an inverting amplifier and replacing its feedback resistor Rf with a capacitor C.
- Hence,
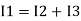
Ignoring I3 we have, I3 ≈ 0
So, I1 ≈ I2.
- We know current across the capacitor is given by,
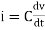
- Now by applying Kirchoffs current law,
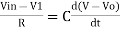
However, V = 0 because gain A is very large
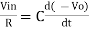
Integrating both sides we get
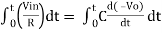
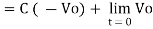
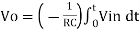+ Q
Where Q is the integration constant and is proportional to Vo at t = 0 sec.
Therefore, voltage Vo is directly proportional to Vin and inversely proportional to constant RC.
Frequency response of basic integrator circuit is given by,
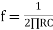( for 0 db gain)
Example-1
The integrator circuit as shown in the figure has R = 500K Ω and C=1µF. Find and plot the output voltage for the inputs as shown in the figure.
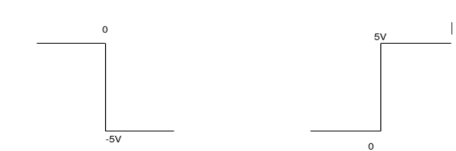
a) b)
c)vi= 2 sin 4tV d) vi= 4tV
Solution:
We know that
v0 = - 1/RC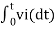 
+ v0(0)
Here R= 500K Ω and C = 1µF
1/RC = 1/ 500 x 1000 x 1 x 10-6
= 1/RC = 2
= -2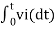 
; vi =- 5V
= -2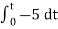 
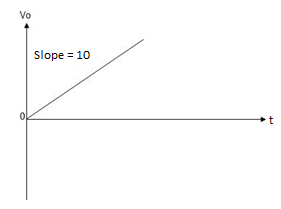
= 10t V
Which means it is a ramp voltage with positive slope.
When vi=5V
-2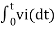 
; vi = 5V
= -2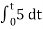 
= -10t V
Which means it is a ramp voltage with negative slope.
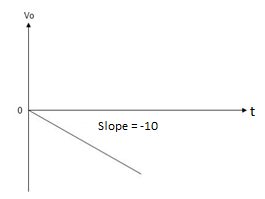
When vi= 2 sin4t V
Vo = -2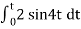 
= -4 [-cos 4t] /4 = cos 4t
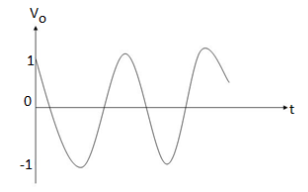
When vi=4t V
Vo =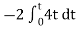 
= -8 [t2/2] = - 4V
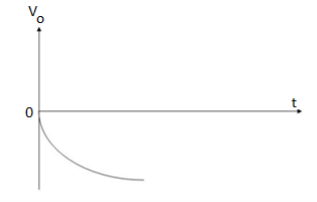
Key takeaway
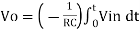+ Q
Where Q is the integration constant and is proportional to Vo at t = 0 sec.
(6) Log Amplifier
As the name says it is an amplifier which produces the output proportional to logarithmic of the applied input. The log amplifier using op-amp is shown below. The input is applied through the inverting end of op-amp. As the non-inverting end has voltage zero then by virtual ground concept the voltage at inverting terminal also becomes zero.
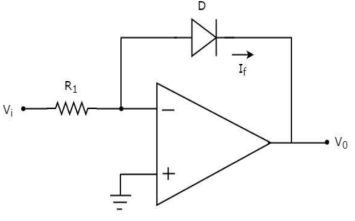
Figure 21: Log Amplifier
The equation for input voltage will be
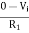+If = 0
If =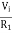 
The current flowing through diode is given as
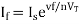
Where:
Is = Saturation Current
Vf = Voltage drop across diode in forward bias
VT = Thermal equivalent voltage
For feedback loop the KVL equation will be
0-Vf -V0 = 0
Vf = -V0
Substituting Vf in above equation of If
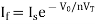
Equating both equations of If
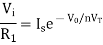
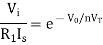
Taking natural log of both sides we get
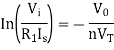
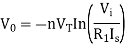
The above equations shows that the output is natural log of the applied input.
Antilog Amplifier
This device produces the output proportional to antilog of input. The inverting op-amp is used in this case as well. The figure below shows an antilog amplifier with its inverting terminal connected to the input end with diode and the non-inverting terminal is grounded.
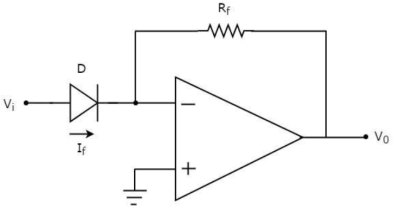
Figure 22: Antilog Amplifier
Applying KCL at input terminal we get
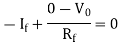
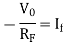
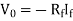
The current flowing through diode is given as
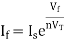
Substituting If in above voltage equation we get
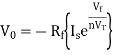
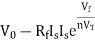
At inverting terminal applying KVL we get
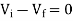
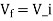
Substituting Vf in equation of V0 we get
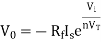
The above equations shows that the output is natural antilog of the applied input.
Key takeaways
For Log Amplifier
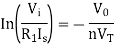
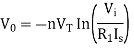
For Antilog Amplifier
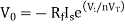
(7) Zero Crossing Detector
An op-amp detector that has the ability to detect the change from positive to negative or negative to a positive level of a sinusoidal waveform is known as a zero- crossing detector.
It is also known to be a square wave generator as the applied input signal is converted into a square wave by the zero -crossing detector.
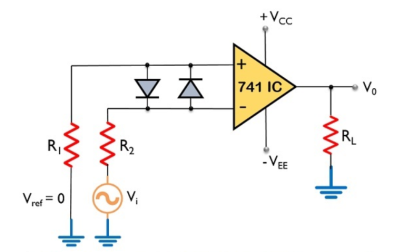
Figure 23: Zero crossing Detector
Here, the input signal Vi is provided to the inverting terminal of the op-amp while the non-inverting terminal is grounded by making use of two resistors R1 and R2.
It detects the point where the input signal crosses zero of the reference voltage level. For every crossing, the saturation level of the output signal changes from one to another.
The reference level is set at 0 and applied at the non-inverting terminal of the op-amp. The sine wave applied at the inverting terminal of the op-amp is compared with the reference level each time the phase of the wave changes either from positive to negative or negative to positive.
Firstly, when positive half of the sinusoidal signal appears at the input. Then the op-amp comparator compares the reference voltage level with the peak level of the applied signal.
Vo = Vref – Vi ---------------------------------------(1)
And we know the reference level is 0, thus
Vo = 0 – ( + Vsat) ----------------------------------------(2)
Therefore, Vo = - Vsat ---------------------------------(3)
During the negative half of the signal, thus the peak will have a negative polarity.
Again
Vo = Vref – Vi ---------------------------------------------(4)
Thus,
Vo = 0 - ( - Vsat) --------------------------------------------------(5)
So, we get
Vo = + Vsat ---------------------------------------------(6)
In this way, the zero -crossing detector detects the change in the level of the applied signal.
Zero crossing detector is also known to be a square wave generator. As the output of the window comparator is nothing but a square wave.
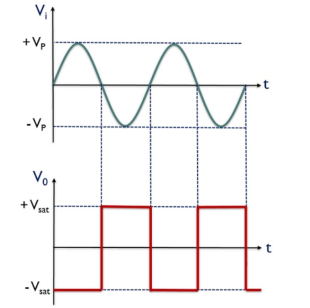
Figure 24: Input and output of zero crossing detector
V0 for the positive half of the applied signal is – Vsat,
This is the reason why we have achieved negative half of the square wave at the output when positive half of the sinusoidal signal is applied. While V0 for the negative half of the sinusoidal signal is + Vsat,
Applications:
- Phase Locked Loop
- Frequency counters and phase meters
Key takeaways
An op-amp detector that has the ability to detect the change from positive to negative or negative to a positive level of a sinusoidal waveform is known as a zero- crossing detector.
(8) Wien -Bridge Oscillator
In this, phase shift is produced by using 2 transistors. Each produces a phase shift of 180° and hence phase shift of 360° is obtained
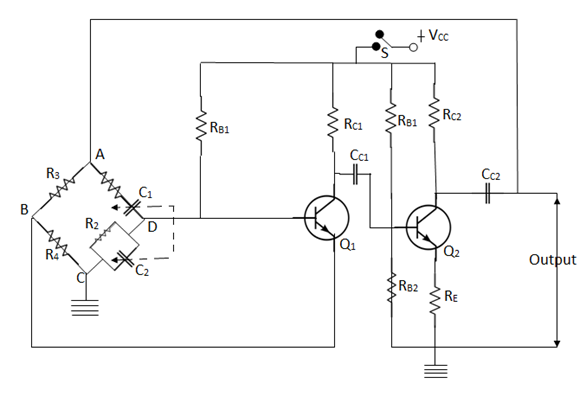
Figure 25: Wein Bridge Oscillator
It is a 2-stage amplifier with R-C bridge circuit. The bridge circuit has 4 arms each containing components R1C1 in Series, R2 C2 in parallel, R3 and R4. Q1 acts as an oscillator and amplifier whereas Q2 Serves as an inverter
When circuit is closed through switch S, the bridge circuit produces the oscillations of frequency whose expression is given by-
F=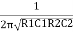 
If R1=R2=R and C1= C2 = C then
F =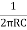 
A total phase shift of 360° is obtained at the output of the second transistor. A fraction of this output energy is fed back to the oscillatory circuit (bridge) at the upper terminal. This positive feedback is to meet with the losses in the oscillator and hence undamped oscillations are produced.
Advantages-
- It has better stability
- Output is constant
- Overall gain is high
- Frequency can be adjusted by varying C1 and C2
Disadvantages-
- Costly
- Cannot generate frequency>1MHz.
Example: In the RC network of a Wein bridge oscillator R1 = R2 = 200kΩ, determine the value of each of the capacitor to obtain a frequency of 5kHz.
Solution-
F =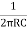 
F = 5kHz, = 5000Hz
R1= R2= 200kΩ = 200×103Ω
5000 =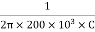 
C =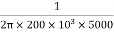 
= 159.15 pF
Expression for feedback factor (β) and frequency (f)
In order to obtain expression for β and f, we will consider only frequency sensitive arms AD and CD as shown in figure below
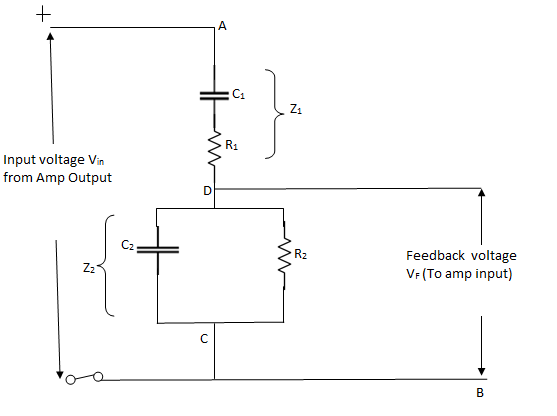
Figure 26: Wein bridge oscillator
Vin is actually the output voltage V0which comes from the amplifier output and voltage across R2C2acts as a feedback voltage VF
Feedback factor β =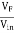 
Let impedance of arm AD be Z1 and that of DC be Z2
Therefore VF =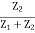 
×Vin{ using voltage divider}
β =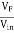 
= 
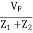………….(1)
Z1= R1 +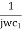 
= 
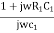…………..(2)
Z2 = R2 || Xc2=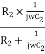 
= 
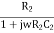………….(3)
Substituting equation (2) and (3) in (1)
β =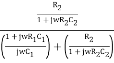 
Substituting jw = S
β =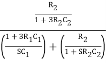 
β =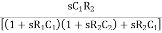 
β =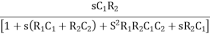 
β =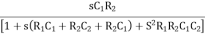 
Resubstitute jw = S, S2 = j2 w2 = -w2
β =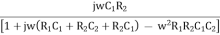 
β =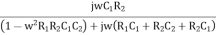 
Rationalize the above equation
β =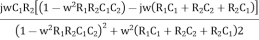 
……………(4)
The phase shift introduced by the wien bridge circuit at the desired output frequency should be 0°. For that the imaginary part of equation (4) should have a zero value.
WC1R2(1-w2R1R2C1C2) = 0
w2R1R2C1C2 = 1
= 
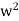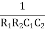
W =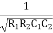 
F =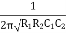 
The above equation is the expression for the oscillator frequency.
If we substitute R1 = R2 = R and C1 = C2 = C
F =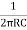 
or w =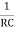 
For β, if R1 = R2 = R, C1= C2 = C
β =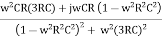 
Substituting
W =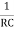 
β =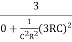 
= 
= 
Thus, at the oscillator frequency F, the value of feedback factor β is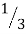 
Key takeaway
- It has better stability
- Output is constant
- Overall gain is high
- Frequency can be adjusted by varying C1 and C2
References:
- Ramakant. A. Gayakwad, “Op-Amps & Linear Integrated Circuits”, 3rd Edition, PHI
- S.Salivahanan & Bhaaskaran, “Linear Integrated Circuits”, 1st Edition, Tata McGraw Hill.
- T.R Ganesh Babu, “Linear Integrated Circuits”, 3rd Edition, SciTech Publication
- Sergio Franco, “Design with op-amp &Analog Integrated Circuits”, 3rd Edition, Tata McGraw Hill
- Concept of Electronics- D.C. Tayal (Himalay Publication)-2018
- Principle of electronics S. Chand V K Mehta and Rohit Mehta
