Unit - 4
Nuclear Physics- II
4.1.1 Radioactivity
Radioactivity is the property of certain forms of matter to spontaneously emit energy and subatomic particles. It's essentially a property of individual atomic nuclei.
An unstable nucleus will spontaneously dissolve, or decay, into a more stable structure, but only in a few precise ways, for as by generating particular particles or electromagnetic energy. Several naturally occurring elements, as well as artificially manufactured isotopes of the elements, have radioactive decay as a feature. The half-life of a radioactive element is the amount of time it takes for one-half of any given quantity of the isotope to decay. Some nuclei have half-lives of more than 1024 years, while others have half-lives of less than 1023 seconds (see below Rates of radioactive transitions). The daughter of the parent isotope, the outcome of radioactive decay, may be unstable, in which case it will decay as well. The procedure is repeated until a stable nuclide is created.
The nature of radioactive emissions
The alpha (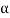 ) particle, beta (
) particle, beta ( ) particle, gamma (
) particle, gamma (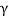 ) ray, and neutrino are the most prevalent types of spontaneous radioactive decay emissions. The nucleus of a helium-4 atom, with two positive charges 4/2He, is the alpha particle. Ions are charged atoms that have a positive charge. Two electrons outside the nucleus of a neutral helium atom balance these two charges. Negatively charged (beta minus, sign e) or positively charged (beta plus, symbol e+) beta particles exist. The beta minus [] particle is an electron that is produced in the nucleus during beta decay and has no relation to the atom's orbital electron cloud. The beta plus particle, commonly known as the positron, is the electron's antiparticle; two of these particles will mutually destroy each other when brought together. Electromagnetic radiations such as radio waves, light, and X-rays are examples of gamma rays. The neutrino and antineutrino, particles with no charge and very low mass, are also produced by beta radiation, and are denoted by v and, respectively.
) ray, and neutrino are the most prevalent types of spontaneous radioactive decay emissions. The nucleus of a helium-4 atom, with two positive charges 4/2He, is the alpha particle. Ions are charged atoms that have a positive charge. Two electrons outside the nucleus of a neutral helium atom balance these two charges. Negatively charged (beta minus, sign e) or positively charged (beta plus, symbol e+) beta particles exist. The beta minus [] particle is an electron that is produced in the nucleus during beta decay and has no relation to the atom's orbital electron cloud. The beta plus particle, commonly known as the positron, is the electron's antiparticle; two of these particles will mutually destroy each other when brought together. Electromagnetic radiations such as radio waves, light, and X-rays are examples of gamma rays. The neutrino and antineutrino, particles with no charge and very low mass, are also produced by beta radiation, and are denoted by v and, respectively.
Fission fragments, neutrons, or protons may be emitted in less common kinds of radioactivity. Fission fragments are complex nuclei with a charge Z and mass A that are usually one-third to two-thirds that of the parent nucleus. Neutrons and protons, of course, are the fundamental building components of complex nuclei, with approximately unit mass on the atomic scale and either zero or unit positive charge. The neutron can't stay in the free state for very long. It is quickly grabbed by nuclei in matter; otherwise, it decays to a proton, an electron, and an antineutrino with a half-life of 12.8 minutes in free space. The proton is the stable nucleus of ordinary hydrogen.
Types of radioactivity
Early research into natural radioactivity in uranium and thorium ores found two types of radioactivity: alpha and beta decay.
Alpha decay
An energetic helium ion (alpha particle) is released during alpha decay, leaving a daughter nucleus with an atomic number two lower than the parent and an atomic mass four lower than the parent. The decay of the abundant isotope of uranium, 238U, producing a thorium daughter plus an alpha particle (symbolised by an arrow) is an example:
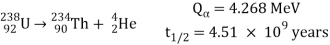
The energy released (Q) in millions of electron volts (MeV) and the half-life (t12) are given for this and following reactions. The charges, or number of protons, represented in subscript, as well as the atomic masses, displayed in superscript, are in balance on both sides of the arrow in alpha decays.
Beta-minus decay
An energetic negative electron is emitted in beta-minus decay, resulting in a daughter nucleus with one higher atomic number and the same mass number. The decay of the uranium daughter product thorium-234 into uranium is an example.
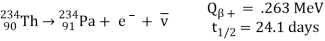
Protactinium-234:
The antineutrino is represented by v in the above process for beta decay. Here, the number of protons is increased by one in the reaction, but the total charge remains the same, because an electron, with negative charge, is also created.
4.1.2 Gamma decay
Gamma radiation, a third form of radiation, usually follows alpha or beta decay. Photons, like gamma rays, have no rest mass or charge. Without gamma emission, alpha or beta decay can simply proceed to the ground (lowest energy) state of the daughter nucleus, but it can also progress fully or partly to higher energy levels (excited states) of the daughter nucleus. Gamma emission may occur in the latter situation as the excited states change to lower energy levels of the same nucleus. (An excited nucleus can also convert to a lower energy state by ejecting an electron from the cloud surrounding it, which is an alternative to gamma emission.) Internal conversion is the ejection of an orbital electron, which results in an energetic electron and typically an X-ray as the atomic cloud fills in the ejected electron's empty orbital. The internal-conversion coefficient is the ratio of internal conversion to alternative gamma emission.)
4.1.3 Isomeric transitions
For the gamma-emission process, there is a wide range of half-life rates. Dipole transitions (see Gamma transition below), in which the gamma ray carries off one unit of angular momentum, are often quick, taking less than nanoseconds (one nanosecond is 109 second). According to the law of conservation of angular momentum, the total of the angular momenta of the radiation and the daughter nucleus must match the parent's angular momentum (spin). When the spins of the beginning and end states differ by more than one, dipole radiation is prohibited, and gamma emission must take place via a higher multipole (quadrupole, octupole, etc.) gamma transition. The excited nucleus is considered to be in a metastable, or isomeric, state (the terms for a long-lived excited state) if the gamma-emission half-life exceeds around one nanosecond, and the decay is usually classified as another type of radioactivity, an isomeric transition. The protactinium-234 nucleus of the uranium-238 decay chain is an example of isomerism:

The letter m following the mass number stands for metastable and indicates a nuclear isomer.
Beta-plus decay
New types of radioactivity, beta-plus decay, or positron emission, and electron capture, were discovered among the artificial products of nuclear reactions in the 1930s. In beta-plus decay, an energetic positron is generated and released, along with a neutrino, and the nucleus converts into a daughter with an atomic number one lower but the same mass number. Carbon-11 (Z = 6) decays to boron-11 (Z = 5), one positron, and one neutrino, for example:

4.1.4 Electron capture
Electron capture (EC) is a process in which an orbital electron is captured by the nucleus and then decays. The nucleus converts to a daughter of one lower atomic number, comparable to positron decay. It differs in that an orbital electron from the cloud is captured by the nucleus with subsequent emission of an atomic X-ray as the orbital vacancy is filled by an electron from the cloud about the nucleus. The nucleus of beryllium-7 grabbing one of its inner electrons to produce lithium-7 is an example:

A decay scheme depicts the basic characteristics of radioactive decay of a nuclear species. The degradation pathway of beryllium-7 is depicted in Figure 1. The parent and excited daughter states' half-lives, as well as their energy of 0.4774 MeV, are shown. On the level's upper left-hand side, you'll see the spins and parities for all three states. Above the vertical arrow depicting the gamma transition, the multipolarity of the gamma ray (magnetic dipole, M1, plus 0.005 percent electric quadrupole, E2) is indicated. The slanted arrows represent electron-capture decay, with labels indicating the fraction of EC decay that goes directly to ground state (89.7%) and the percentage of EC decay that goes through the excited state (12%). (10.3 percent). The boldface figures after the percentages are so-called log ft values, which are used in conjunction with beta-decay rates further down. The total energy release (QEC) is shown below. Because there are no practical ways to measure the neutrino energy associated with EC decay, the QEC must be estimated. It has been feasible to directly estimate the decay energy of a few electron-capturing nuclides by measuring a rare event known as inner bremsstrahlung (braking radiation). The neutrino and a gamma ray share the energy released in this process. The total energy released is determined by the measured distribution of gamma-ray energies. With radioactive decay, there is usually so much conventional gamma radiation that the inner bremsstrahlung is unobservable.
Spontaneous fission
Spontaneous fission is another type of radioactivity. The nucleus separates into two fragment nuclei with roughly half the mass of the parent nucleus throughout this phase. This process is only barely detectable in competition with the more prevalent alpha decay for uranium, but for some of the heaviest artificial nuclei, such as fermium-256, spontaneous fission becomes the predominant mode of radioactive decay. As the fragments are propelled away by the enormous electrical repulsion between their nuclear charges, kinetic energy releases of 150 to 200 MeV may occur. The response
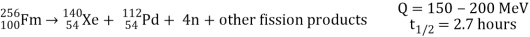
Is as follows:
Only one of many product sets is displayed. In the fission of this isotope, a few neutrons are always emitted, which is critical for chain reactions. Induced fission, the process utilised in nuclear reactors, is not to be confused with spontaneous fission. The ability of uranium-235, plutonium-239, and other isotopes to fission after absorption of a slow neutron is known as induced fission. Apart from the need for a neutron capture to start it, induced fission is quite identical to spontaneous fission in terms of total energy released, secondary neutron counts, and so on (see nuclear fission)
Proton radioactivity
Proton radioactivity was first identified in 1970 in an excited isomeric form of cobalt-53, 53mCo, of which 1.5 percent emits protons:
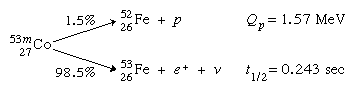
Special beta-decay processes
In addition to the aforementioned sources of radioactivity, heavy-particle emission is caused by a rare class of beta-decay processes. In these events, portion of the beta decay moves to a high excited state of the daughter nucleus, which produces a heavy particle quickly.
Beta-delayed neutron emission is one such mechanism, as demonstrated by the following reaction:44

(Emax n signifies the maximum energy detected for released neutrons, and the asterisk signifies the short-lived intermediate excited states of oxygen-17.) Following nuclear fission, there is a minor output of delayed neutron emitters, and these radio activities are notably significant in providing a reasonable response time to allow mechanically moved control rods to control nuclear fission reactors.
A number of positron emitters in the light-element area beta decay to excited states that are unstable with respect to alpha particle emission. As a result, these species produce alpha radiation with the same half-life as beta emission. Because the ground and excited states of beryllium-8 are both unstable with regard to dissociation into two alpha particles, both positron decay from boron-8 and electron decay from lithium-8 are beta-delayed alpha emission. Another example is the reaction of sodium-20 (20Na) with neon-20 (20Ne; the asterisk again indicates the short-lived intermediate state) to produce oxygen-16:
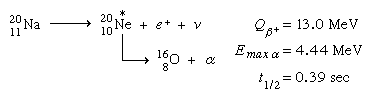
Positron decay can result in an excited nuclear state that is unable to attach a proton in a few situations. Proton radiation appears with the beta transition's half-life in these instances. In the daughter ground state, a combination of high positron-decay energy and low proton-binding energy is required. Tellurium-111 (111Te) generates antimony-111 (111Sb) and subsequently tin-110 (110Sn) in the following example:
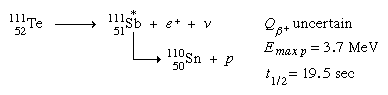
Heavy-ion radioactivity
A. Sandulescu, D.N. Poenaru, and W. Greiner published calculations in 1980 that suggested the potential of a novel type of heavy nuclei decay halfway between alpha decay and spontaneous fission. H.J. Rose and G.A. Jones discovered heavy-ion radioactivity in 1984 when they discovered a 30-MeV carbon-14 emission from radium-223. Carbon-14 decay has a ratio of around 5 1010 to alpha decay. Carbon-14 from radium-222, radium-224, and radium-226, as well as neon-24 from thorium-230, protactinium-231, and uranium-232, have all been seen. Alpha decay and spontaneous fission are examples of heavy-ion radioactivity that includes quantum-mechanical tunnelling past the potential-energy barrier. Shell effects are important in this phenomenon, and the heavy partner of carbon-14 or neon-24 in all examples recorded so far is near to doubly magical lead-208.
4.1.5 Occurrence of radioactivity
On Earth, some types of radioactivity exist naturally. Few species have half-lives comparable to the age of the elements (about 6 109 years), indicating that they did not disintegrate after forming in stars. Uranium-238, uranium-235, and thorium-232 are notable examples. There's also potassium-40, which is the body's primary source of irradiation due to its existence in potassium tissue. Vanadium-50, rubidium-87, indium-115, tellurium-123, lanthanum-138, lutetium-176, and rhenium-187 are beta emitters, while cerium-142, neodymium-144, samarium-147, gadolinium-152, dysprosium-156, hafnium-174, platinum-190, and lead-204 are alpha emitters. Aside from these about 109-year species, there are the shorter-lived daughter activities that are fed by one or more of the above species; for example, various nuclei of the elements between lead (Z = 82) and thorium (Z = 90) are fed by one or more of the above species. Species formed in the upper atmosphere by cosmic ray bombardment are another type of natural radioactivity. Carbon-14 with a 5,720-year age and 12.3-year tritium (hydrogen-3) with a 53-day age and 2,700,000-year beryllium-10 with a 2,700,000-year age are notable. Small levels of radioactivity have been discovered in meteorites as a result of cosmic ray bombardment throughout their history outside the Earth's atmospheric shield. In fresh meteorite falls, activities as short-lived as 35-day argon-37 have been measured. Since 1945, nuclear explosions have released new radio activities into the environment, including nuclear fission products as well as secondary products generated by the impact of neutrons from nuclear weapons on nearby matter.
Most of the known beta emitters in the mass range of 75–160 are included in the fission products. They are generated in various yields, peaking at around 7% per fission in the mass regions 92–102 (light peak of the fission yield vs atomic mass curve) and 134–144 (dark peak of the fission yield versus atomic mass curve) (heavy peak). There are two types of radioactivity-related delayed risks. First, fallout falling on Earth raises the overall radiation level. Until the activity has diminished to a suitably low level, protection can be provided by concrete or earth shielding. Second, depending on the half-life, nature of radiations, and chemical behaviour within the body, ingestion or inhalation of even low doses of certain radioactive species can represent a unique threat. See Radiation: Biological Impacts of Ionizing Radiation for further information on the biological effects of radiation
Nuclear reactors produce fission products as well, but they do so under controlled settings. Containment and waste-disposal procedures should keep operations contained and eliminate the likelihood of leaching into groundwater for periods longer than half-lives. If thermonuclear fusion power can be made feasible, it has a number of advantages over fission power, including not just much bigger fuel stocks (heavy hydrogen and lithium) than uranium, but also the elimination of radioactive fission product wastes. In this context, it's worth noting that radioactive decay is a major source of heat in the interiors of both the Earth and the Moon. These huge heat production sources must be factored into theories concerning the genesis and evolution of the Earth, Moon, and other planets.
Other than natural activities and fission products, desired radio activities can be created by irradiating specified target materials with reactor neutrons or using charged particle or gamma ray beams from accelerators.
4.1.6 Energetics and kinetics of radioactivity
Energy release in radioactive transitions
The fundamental question of nuclear binding energies and stabilities arises when the energy released by various radioactive transitions is considered. An isotope chart, with positions on the same horizontal row corresponding to a given proton number (Z) and those on the same vertical column corresponding to a given neutron number, is a popular way of illustrating nuclear-stability connections (N). Figure 2 depicts such a map. The region of currently known nuclei is surrounded by an irregular bold line. Because the chart may be thought of as a map of a binding energy surface, the lowest regions of which are the most stable, the area enclosed by this is commonly referred to as the valley of stability. The plentiful iron and nickel isotopes have the most closely bonded nuclei of all. The processes of alpha decay and spontaneous fission are most common near the region of the valley containing the heaviest nuclei (largest mass number A; i.e., largest number of nucleons, N + Z); both of these processes relieve the energetically unfavorable concentration of positive charge in the heavy nuclei.
The positron-emitting and electron-capturing radioactive nuclei are found along the region that borders the valley of stability on the upper left-hand side, with the energy release and decay rates increasing as the nucleus moves away from the stability line. Beta-minus decay is the primary process in the lower right-hand border region, with energy release and decay rates increasing as the nucleus moves away from the stability line.
The graph's grid lines correlate to the nucleon numbers that relate to increased stability, or "magic numbers". The circles labelled "deformed zones" demarcate areas where nuclei should have cigar shapes, but nuclei elsewhere are spherical. Outside of the dashed lines, nuclei would be unbound to neutron or proton loss and would have a very short lifetime (less than 1019 seconds).
4.1.7 Calculation and measurement of energy
It is possible to determine the energy release for unmeasured transitions using measured radioactive-energy-release (Q) values for alpha and beta decay using the method of closed energy cycles. The cycle of four nuclei serves as an illustration below:

Two alpha decays and one beta decay have energies that can be measured in this cycle. Because conservation of energy requires the total of Q values around the cycle to be zero, the unmeasured beta-decay energy for bismuth-211, Q(Bi), is easily determined. As a result, Q(Bi) + 7.59 1.43 6.75 = 0. Q(Bi) = 0.59 MeV is obtained by solving this equation. Closed energy cycles calculations may be extended from stable lead-207 all the way up the alpha and beta decay chain to its natural progenitor uranium-235 and beyond. The nuclear binding energies of a group of nuclei can be related in this way. Closed-cycle calculations based on lead-207 can only connect together nuclei with mass numbers of the general type A = 4n + 3, where n is an integer, because alpha decay decreases the mass number A by 4 and beta decay does not modify A. The 4n series, for example, has thorium-232 as a natural precursor and lead-208 as a stable end product. The 4n + 2 series, for example, uses uranium-238 as a natural precursor and produces lead-206 as the end product.
The classification of isotopes into the series described above was important in early studies on natural radioactivity since they were discovered and examined as families. Newly found radio activities were assigned symbols that corresponded to the family and order in which they occurred. Thorium-234 was designated as UX1, protactinium-234 isomers as UX2 and UZ, uranium-234 as UII, and so on. These original symbols and titles appear in more current writings on occasion, but they are primarily of historical relevance. The entire 4n + 1 series contains well-known artificial activities that decay to stable thallium-205 and is not naturally occurring.
Measurements to augment the radioactive-decay energy cycles are definitely required to further our understanding of nuclear binding energies. This can be done in part by measuring the Q values of artificial nuclear processes. The neutron-binding energies of the lead isotopes, for example, can be determined by measuring the threshold gamma-ray energy to remove a neutron (photonuclear reaction); or the energies of the incoming deuteron and outgoing proton in the reaction can be measured to provide this information.
Precision mass spectroscopy is required for further developments of nuclear-binding-energy measurements (see spectroscopy). The masses of various nuclides can be measured with remarkable precision by ionizing, accelerating, and magnetically deflecting them. A direct measurement of the energy released in the radioactive decay process is comparable to a precise measurement of the masses of atoms involved. Potassium-40, a naturally occurring but radioactive isotope, with an atomic mass of 39.964008 amu. Potassium-40 decays mostly through -emission to calcium-40, which has a mass of 39.962589. Energy is equal to mass (m) times velocity of light (c) squared, or E = mc2. The energy release (Q) and the mass difference, m, are connected by Einstein's equation, with one amu equal to 931.478 MeV as the conversion factor. Thus, in the radioactive decay Q = (39.964008 39.962589) 931.478 MeV = 1.31 MeV, the extra mass of potassium-40 over calcium-40 shows as the total energy release Q. The other isobar (same mass number, different atomic number) to argon-40 has a mass of 39.962384, which is lower than potassium-40. When the mass difference is translated to energy units, the result is a 1.5 MeV energy release, which is the energy release for EC decay to argon-40. Because the maximum energy release for positron emission is always smaller than the maximum energy release for electron capture by twice the rest mass energy of an electron (2m0c2 = 1.022 MeV), the maximum positron energy for this reaction is 1.5 1.02, or 0.48 MeV.
A detailed understanding of the alpha-particle (helium-4) atomic mass is required to correlate alpha-decay energies with nuclear mass discrepancies. The energy released is equal to the mass of the parent minus the sum of the masses of the decay products. As a result, the computation for alpha decay of plutonium-239 to uranium-235 and helium-4 is as follows:



0.00563 × 931.478
Qα = 5.24 MeV
As follows:
Extensive lists of nuclear masses have been generated by integrating radioactive-decay-energy information with nuclear-reaction Q values and precision mass spectrometry. They can be used to calculate the Q values of unmeasured reactions or decay.
The atomic masses can also be written as mass defect, indicated by the Greek letter delta (the difference between the exact mass M and the integer A, the mass number), either in energy units or atomic mass units, as an alternative to the complete mass.
4.1.8 Absolute nuclear binding energy
The absolute nuclear binding energy is the hypothetical energy release if a given nuclide were synthesized from Z separate hydrogen atoms and N (equal to A − Z) separate neutrons. The calculation for the absolute binding energy of the most stable of all nuclei, iron-56, provides an example:
26 × M(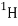 ) 26 × 1.007825 = 26.20345
) 26 × 1.007825 = 26.20345
30 × M(n) 30 × 1.008665 = 30.25995
M(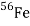 ) - 55.93493
) - 55.93493
Binding energy = 0.52847 × 931.478 =492.58 MeV
Average binding energy per nucleon of 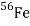 = 492.58/56 = 8.796 MeV
= 492.58/56 = 8.796 MeV
A broad study of the average binding energy per nucleon (for nuclei of all elements classified according to ascending mass) reveals a peak at iron-56, then a progressive decline on both sides to around 7 MeV at helium-4, and to roughly 7.4 MeV for the most massive nuclei known. As a result, most naturally occurring nuclei are not stable in the absolute sense. Degradation processes such as alpha decay and spontaneous fission would gain energy for nuclei heavier than iron by degrading into nuclear products closer to iron, but the rates of degradation processes such as alpha decay and spontaneous fission are only observable for the elements with the greatest mass. Nuclear energy may be obtained in a similar way by fusing most materials lighter than iron. However, unless the nuclei are exposed to temperatures greater than 107 K, the coulombic repulsion between them keeps the rates of fusion processes unobservably low. These temperatures are only reached and nuclear-fusion energy produced in the Sun's and other stars' heated cores, thermonuclear weapons, and controlled fusion plasmas.
4.1.9 Nuclear models
The liquid-drop model
With the model of a charged liquid drop, the average behaviour of the nuclear binding energy may be understood. The aggregate of nucleons in this model has the same surface tension, cohesion, and deformation properties as a liquid drop. A dominant attractive-binding-energy term proportional to the number of nucleons A is present. A surface-energy term proportional to surface area, as well as a coulombic repulsion energy proportional to the square of the number of protons and inversely related to the nuclear radius, must be deducted from this. Furthermore, there is a quantum-mechanical symmetry-energy term that favours identical amounts of protons and neutrons. Finally, there is a matching term that offers nuclei with even numbers of neutrons or protons a tiny boost in binding.
The pairing-energy term explains the extreme rarity of odd–odd nuclei that are stable against beta decay (the names odd–odd, even–even, even–odd, and odd–even relate to the evenness or oddness of proton number, Z, and neutron number, N, respectively). Deuterium, lithium-6, boron-10, and nitrogen-14 are the only examples. Other odd–odd nuclei, such as potassium-40, can be found in nature, but they are beta decay instable. Furthermore, the pairing-energy term explains why even-Z elements have more stable isotopes than odd-Z elements, as well as why element 43, technetium, and element 61, promethium, have no stable isotopes at all.
One method of calculating nuclear sizes is to use the beta-decay energy of so-called mirror nuclei. For example, the neon and fluorine nuclei, 19/10Ne9 and 19/9F10, are mirror nuclei because their respective proton and neutron counts are equal. Except for the coulombic term, which is inversely proportional to the nuclear radius, all binding-energy terms are the same in each. These calculations, combined with more direct determinations by high-energy electron scattering and energy measurements of X-rays from muonic atoms (hydrogen atoms in which the electrons have been replaced by negative muons), show that the nuclear charge is roughly uniformly distributed in a sphere with a radius of 1.2 A13 1013 centimetre. The fact that the radius is related to the mass number's cube root is significant since it means that the average density of all nuclei is roughly constant.
A close investigation of nuclear-binding energies indicates periodic deviations from the charged-liquid-drop model's smooth average behaviour. In the vicinity of particular numbers of neutrons or protons, the so-called magic numbers, an extra binding energy emerges (2, 8, 20, 28, 50, 82, and 126). 4/2He2, 16/8O8, 40/20Ca20, 48/20Ca28, and 208/82Pb126 are doubly magical in that they have both proton and neutron numbers magic. On Figure 2, these doubly magical nuclei are located at the intersections of grid lines.
The shell model
The overall trends of nuclear binding energies were given in terms of a charged-liquid-drop model in the preceding section. Nonetheless, periodic binding-energy abnormalities were seen at the magic numbers. Extra electronic stabilities at the atomic numbers of noble-gas atoms are substantially comparable to the periodic occurrence of magic numbers of extra stability. In atomic and nuclear situations, the causes for these stabilities are quite similar to the filling of particles into quantized orbitals of motion. The completion of filling an orbital shell is accompanied by an increase in stability. The shell model, as previously stated, is the nuclear model that accounts for the magic numbers. This model can account for spin zero for all even–even nuclear ground states in its simplest form; the nucleons fill pairs into orbitals with angular momenta cancelling. The nuclear spins of odd-mass nuclei close to doubly magical nuclei, such as 208/82Pb, are easily explained by the shell model. Before reaching the doubly magical configuration, the spins of 1/2 for neighbouring 207/81Tl and 207/82Pb are accounted for by filling all nucleons pairwise into the lowest energy orbits and putting the odd nucleon into the last available orbital (the Pauli exclusion principle dictates that no more than two nucleons may occupy a given orbital, and their spins must be oppositely directed); Similarly, spins of 9/2 for 209/82Pb and 209/83Bi make sense because spin-9/2 orbitals are the next available orbitals after doubly mystical lead-208. The magnetic dipole moment, which expresses the related magnetization, is well explained by the simple spherical-shell model.
The spherical-shell model's orbitals are labelled in a nomenclature similar to that of electronic orbitals in atoms. Protons and neutrons fill the orbitals 1s1/2, 1p3/2, 1p1/2, 1d5/2, and 1d3/2 in the orbital arrangement of calcium-40. In conventional spectroscopic notation, the letter signifies the orbital angular momentum, with the letters s, p, d, f, g, h, I and so on representing integer values of l ranging from zero for s (not to be confused with spins) to six for i. Because the intrinsic spin of a nucleon is 1/2, the fractional subscript yields the total angular momentum j, with values of l + 1/2 and l 1/2 permitted. For gradually higher energy values of an orbital of given l and j, the first integer is a radial quantum number with successive values 1, 2, 3, etc. A maximum of 2j + 1 nucleons can be accommodated in each orbital. For neutrons and protons, the exact arrangement of several orbitals within a shell vary slightly (see table for the orbitals comprising each shell). If l is even (s, d, g, I the orbital's parity is even (+), and if l is odd (), the orbital's parity is odd (). (p, f, h).
Shell closure number |
|
2 | 1s1/2 |
8 | 1p3/2, 1p |
20 | 1d5/2, 2s1/2, 1d3/2 |
28 | 1f7/2 |
50 | 2p3/2, 1f5/2, 2p1/2, 1g9/2 |
82 | 1g7/2, 2d5/2, 1h11/2, 2d3/2, 3s1/2 |
126 | 2f7/2, 1h9/2, 1i13/2, 3p3/2, 2f5/2, 3p1/2 |
184 (?) | 2g9/2, 1i11/2, 1j15/2, 3d5/2, 2g7/2, 4s1/2, 3d3/2 |
The beta-decay scheme of 2.2-minute thallium-209 illustrated below, in which spin and parity are specified for each state, is an example of a spherical-shell-model interpretation. The 127th neutron of the lowest accessible orbitals above the closed shell of 126 is thought to occupy the ground and lowest excited states of lead-209. It should be observed from the table's last line that
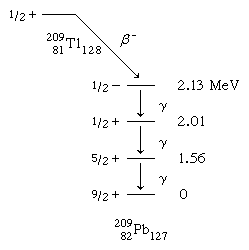
That the ground and first two excited states may be explained using the g9/2, d5/2, and s1/2 orbitals Nuclear-reaction investigations have identified low-lying states linked with the i11/2 and j15/2 orbitals, but they are not inhabited in beta decay.
The 2.13-MeV state that receives the principal beta decay isn't as straightforward to analyse as the others. It's linked to a neutron being promoted from the 3p1/2 orbital below the 126 shell closure. Above this excitation, the density (number of states per MeV) of states rapidly increases, making interpretations more difficult and uncertain.
The spherical-shell concept can be expanded beyond the doubly magical area with appropriate improvements. To begin, the assumption that nucleons move independently in orbitals must be abandoned, and a residual force, primarily short-range and attractive, must be invoked between the nucleons. A great quantity of data on binding energies, spins, magnetic moments, and the spectra of excited states can be explained and correlated around the magic areas using the spherical-shell model reinforced by residual interactions.
The collective model
The spherical-shell model has trouble explaining the significant reported electric quadrupole moments indicating cigar-shaped nuclei for nuclei further away from the doubly magical areas. The collective model, a combination of liquid-drop and shell models, has been proposed for these nuclei. (Cigar-shaped nuclei can be found in the circular sections of Figure 2.)
The nuclear shape can be deformed into a cigar shape by nucleons interacting with one another collectively. Such big spheroidal distortions are common for nuclei that aren't magical, such as 150 A 190, and 224 A (the symbol implies less than, and the number is approximate). The collective model dictates that orbitals be computed in a cigar-shaped potential and that the comparatively low-energy rotational excitations of the cigar shape's tumbling motion be taken into account in these distorted regions. In correlating and forecasting nuclear properties in distorted regions, the collective model has been quite successful. The decay of the isomer hafnium-180m through a cascade of gamma rays through the ground rotational band, seen in Figure 3, is an example of a nuclear rotational band (a succession of neighbouring states) (see below Gamma transition for explanation of M2, E1, E2, and E3).
Key takeaway:
- Nuclear radioactivity refers to the emission of the rays identified by Becquerel, while nuclear radiation refers to the rays themselves. Radioactive decay occurs when a nucleus spontaneously loses some of its mass and emits radiation. Radiation is unaffected by chemical condition.
- In 1903, Becquerel received half of the Nobel Prize in Physics for his discovery of spontaneous radioactivity, with the other half going to Pierre and Marie Curie for their investigation of the Becquerel radiation.
4.2.1 The Valley of Nuclear Stability
Protons and neutrons make up the nuclei of atoms. Electrostatic repulsion between positively charged protons causes them to repel each other. The strong nuclear force, which acts as an attracting force between nucleons, overcomes this electrostatic repulsion. Neutrons are necessary for nucleus stability. When the attractive force between nucleons exceeds the electrostatic repulsion, the nucleus becomes unstable and decays.
It describes the stability of an element's isotope. High-binding-energy nucleons are more stable. The ratio of neutrons to protons in a nucleus (N/Z) can be used to estimate an isotope's stability. Protons and neutrons are usually 1:1 in elements with atomic numbers fewer than 20. As the atomic number rises, so does the amount of neutrons. The ratio of neutrons to protons in most stable nuclei is greater than one. Only 1H and 3He are stable despite having a neutron-to-proton ratio of less than one.
Stable isotopes exist for the first 80 elements in the periodic table. Regardless of the amount of neutrons, all elements with an atomic number greater than 82 are unstable and radioactive.
4.2.2 Stability of nucleus
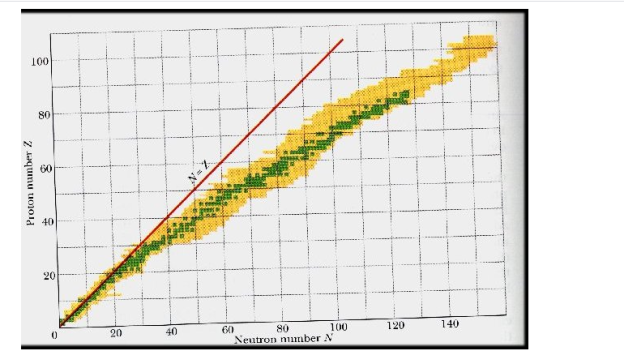
A nucleus is stable if it cannot be changed into a different configuration without the addition of external energy. Only roughly 250 nuclides are stable out of the thousands that exist. The stable isotopes fall into a narrow band when the number of neutrons vs the number of protons for stable nuclei is plotted. The band of stability is the name given to this area (also called the belt, zone, or valley of stability). The straight line in Figure 1 indicates nuclei with a protons-to-neutrons ratio of 1:1. (n:p ratio). It's worth noting that the lighter stable nuclei have an equal amount of protons and neutrons. Nitrogen-14, for example, contains seven protons and seven neutrons. Neutrons are rapidly outnumbering protons in heavier stable nuclei. For example, iron-56 contains 30 neutrons and 26 protons, resulting in a n:p ratio of 1.15, but lead-207 has 125 neutrons and 82 protons, resulting in a n:p ratio of 1.52. This is because larger nuclei have greater proton-proton repulsions, necessitating a larger number of neutrons to compensate for these electrostatic repulsions and hold the nucleus together.
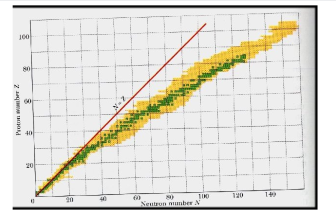
This graph depicts the known nuclides as well as those that are stable. The stable nuclides are coloured blue, whereas the unstable nuclides are coloured green. It's worth noting that all isotopes with atomic numbers greater than 83 are unstable. The solid line is the one on which n equals Z.
The nuclei on the left and right of the band of stability are unstable and produce radioactivity. They decay (transform) into other nuclei that are either within or close to the band of stability. Nuclear decay reactions transform one unstable isotope (or radioisotope) into a more stable isotope. The nature and products of this radioactive decay will be discussed in later sections of this chapter.
The relationship between the stability of a nucleus and its structure can be observed in several ways. Even-numbered protons, neutrons, or both are more likely to be stable nuclei (see Table 1). Magic numbers, or nuclei with a specific number of nucleons, are resistant to nuclear decay. In the nucleus, these numbers of protons or neutrons (2, 8, 20, 28, 50, 82, and 126) form complete shells. In concept, these are analogous to the stable electron shells observed in noble gases. Double magic nuclei, such as 42He, 168O, 4020Ca, and 20882Pb, contain magic numbers of both protons and neutrons and are extremely stable. These nuclear stability trends can be explained by using a quantum mechanical model of nuclear energy states, similar to the one used to describe electronic states previously in this textbook, although the intricacies of this model are beyond the scope of this chapter.
Number of Stable Isotopes | Proton Number | Neutron Number |
157 | Even | Even |
53 | Even | Odd |
50 | Odd | Even |
5 | Odd | Odd |
Table 1. Stable Nuclear Isotopes | ||
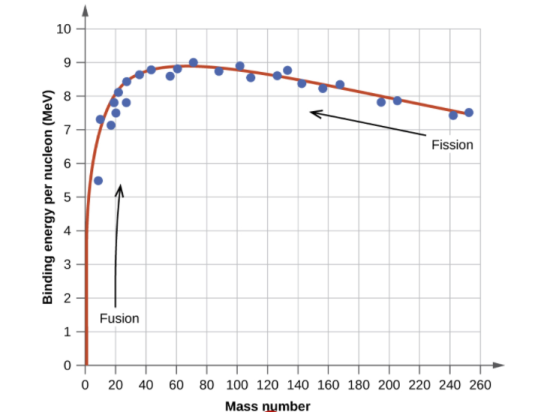
The binding energy per nucleon, or the total binding energy for the nucleus divided by the number of nucleons in the nucleus, is connected with the relative stability of a nucleus. For example, the binding energy of a 24he nucleus is 28.4 MeV, as we showed in Example 2. For a 24he nucleus, the binding energy per nucleon is 28.4MeV4nucleons=7.10MeV/nucleon. 7.10MeV/nucleon = 28.4MeV4nucleons
On the curve depicted in Figure 2, we learn how to compute the binding energy per nucleon of a nuclide in Example 3.
Protons and neutrons, together known as nucleons, make up an atomic nucleus. Despite the fact that protons resist each other, the nucleus is held together by the strong nuclear force, a short-range but extremely powerful force. The overall mass of a nucleus' constituent nucleons is smaller than that of the nucleus itself. According to Einstein's mass-energy equivalence equation, E = mc2, this "missing" mass has been turned into the binding energy that binds the nucleus together. Only a few nuclides are stable among the millions that exist. Even numbers of protons or neutrons, as well as nuclides with magic numbers of nucleons, are more likely to be stable. On a graph showing the number of protons vs the number of neutrons, these stable nuclides occupy a tight band of stability. The nuclei with mass numbers near 56 have the highest binding energy per nucleon; these are the most stable nuclei.
4.3.1 Radioactive decay law
The fundamental law governing radioactive decay.
The most essential law of radioactivity is the law of radioactive decay. When a nucleus decays by emitting an alpha particle or a beta electron, it changes, allowing for the conversion of radium into radon or tritium into helium, for example. However, the number of atoms in the radioactive substance inexorably decreases during such operations. However, the number of emissions per second decreases at the same time. The activity of a sample is determined by the decay rate, which is proportional to the number of nuclei present.
If the nucleus regains stability after having emitted a particle, the form of decay law is simple to understand: much like a currency which, every year, loses some percentage points of its ever-decreasing value. Exponential decay refers to any sort of decay of this nature, and its mathematics are widely understood. The half-life, or the length of time it takes for a given sample of a chemical to halve, is a useful measure of radioactive decay. The half-life of any substance is a property of its nucleus that does not change over time.

- The number of nuclei in a radioactive sample is halved after a specific length of time known as the 'half-life' or 'period.' The length of time it takes to divide the nuclei is independent of their age or the quantity of the sample. The size of the sample is quartered (not decreased to zero) after two half-lives, eighth after a third half-life, and so on. The half-life of a nucleus is one of the most essential aspects of a radioactive element IN2P3 because of its decay rate in relation to time.
- If the daughter nucleus (the final product of the radiation process) is radioactive, the type of decay becomes more difficult to comprehend and analyse. Nonetheless, like with any other activity, a radioactive equilibrium is eventually reached.
- A few grammes of any substance already contain millions of billions of billions of atoms; the quantity of radioactive nuclei in even the tiniest sample is unimaginably large. As a result, even for the least radioactive elements, radioactivity is always computed using large values.
Decay probability per second : λ = 0,693 /T (seconds)
Number of nuclei (masse atomique A) : N = 6,023 × 1023 m(grams) / A
Activity (becquerels) = λ N = 1,323 × 1018 m /AT(years)
m: sample mass – A : nucleons number in nucleus (atom-gram)
The activity of a mass m sample and its half-life T
Because of the value of the Avogadro number N: 6,023 followed by 23 zeros, activities calculated in becquerels have extremely high levels. The neperian logarithm of 2 is 0,693. T in years is converted to seconds by multiplying T in years by 31,6 millions, the number of seconds in a year.
IN2P3 is a three-letter acronym that stands for "
All of these radioactive changes are unpredicted and unpredictable. In other words, we can never predict when a nucleus will disintegrate or which of a group of nuclei will decay first. A Carbon-14 nucleus found in an ancient bone has the same likelihood of degrading in the same amount of time as a nucleus from a recently felled tree. To put it another way, the likelihood of a nucleus decaying radioactively is always the same. The half-life of the nucleus is inextricably related to the likelihood of decay, and both are defining aspects of any radioactive element.
4.3.2 Types of Radioactive Decay
There are three types, namely:
- Alpha
- Beta
- Gamma.
Alpha decay:
The process of an alpha particle emitting its nucleus is known as alpha decay. The alpha decay formula is as follows:
[latex]E=(m_{i}-m_{f}-m_{p})c^{2}[/latex]
- Where mi is the nucleus's initial mass and mf is the nucleus's mass after particle emission.
- The mass of the released particle is mp.
- The alpha particle, which is exceedingly stable, is taken from the nucleus of helium. It has two protons and two neutrons in its group. The alpha decay of uranium-238, for example, is depicted below.
- -[latex] -[latex] -[latex]
- The process of isotopes converting into an element of a stable nucleus is known as transmutation.
Beta Decay:
Although a beta particle is commonly referred to as an electron, it can also be referred to as a positron. If electrons are involved in the reaction, the nucleus will release neutrons one by one. As a result, the proton count rises as well. The following is a diagram of the beta decay process:
[matrix]
Pa 91234+e -10 Th 90234rightarrow Pa 91234+e -10
(latex)
Gamma Decay:
The nucleus has orbiting electrons that do have some energy, and when an electron jumps from a high energy level to a low energy level, a photon is emitted. The nucleus does the same thing: everytime it rearranges into a lower energy level, a high-energy photon known as a gamma ray is emitted.
4.3.3 Radioactive Decay Law
In nature, there are three forms of radioactive decay:
- -decay –emission of a helium nucleus (42He)
- -decay – the emission of electrons or positrons (particles with the same mass as electrons but a charge opposite that of an electron);
- -decay – photons with high energy (hundreds of keV or more) are released.

When a radioactive material undergoes α, β or γ-decay, the number of nuclei undergoing the decay, per unit time, is proportional to the total number of nuclei in the sample material. So,
If N = total number of nuclei in the sample and ΔN = number of nuclei that undergo decay in time Δt then,
ΔN/ Δt∝ N
Or, ΔN/ Δt = λN … (1)
Where λ = radioactive decay constant or disintegration constant. Now, the change in the number of nuclei in the sample is, dN = – ΔN in time Δt. Hence, the rate of change of N (in the limit Δt→ 0) is,
DN/dt = – λN
Or, dN/N = – λ dt
Now, integrating both the sides of the above equation, we get,
NN0∫ dN/N = λ tt0∫ dt … (2)
Or, ln N – ln N0 = – λ (t – t0) … (3)
Where, N0 is the number of radioactive nuclei in the sample at some arbitrary time t0 and N is the number of radioactive nuclei at any subsequent time t. Next, we set t0 = 0 and rearrange the above equation (3) to get,
Ln (N/N0) = – λt
Or, N(t) = N0e– λt … (4)
Equation (4) is the Law of Radioactive Decay.
The Decay Rate
In radioactivity calculations, the decay rate R ( = – dN/dt) is more important than the number N. The number of nuclei decaying per unit time is determined by this rate. We can compute the decay rate even if we don't know the amount of nuclei in the sample by counting the number of emissions of, or particles in 10 or 20 seconds. Let's say we take a time interval dt and calculate the decay count N (= –dN). The rate of decay is now defined as,
R = – dN/dt
Differentiating equation (4) on both sides, we get,
R = λ N0 e−λt
Or, R = R0e−λt … (5)
Where, R0 is the radioactive decay rate at the time t = 0, and R is the rate at any subsequent time t. Equation (5) is the alternative form of the Law of Radioactive Decay. Now we can rewrite equation (1) as follows,
R = λN … (6)
Where R and the number of radioactive nuclei that have not yet undergone decay must be evaluated at the same instant.
4.3.4 Half-Life and Mean Life
The total decay rate of a sample is also known as the activity of the sample. The ‘becquerel' is the SI unit for measuring activity and is defined as,
1 becquerel = 1 Bq = 1 decay per second
An older unit, the curie, is still in common use:
1 curie = 1 Ci = 3.7 × 1010 Bq (decays per second)
There are two ways to measure the time for which a radionuclide can last.
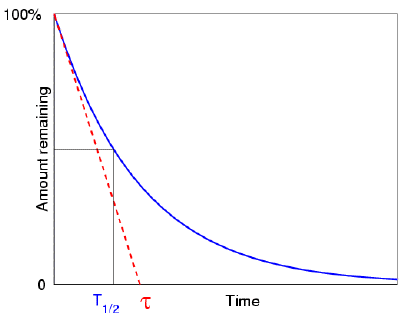
● Half-life T1/2 – the time at which both R and N are reduced to half of their initial values
● Mean life τ – the time at which both R and N have been reduced to, e-1 of their initial values.
Calculating Half-Life
Let's try to figure out what the relationship is between T1/2 and the disintegration constant. For this, let’s input the following values in equation (5),
R = (1/2)R0 and t = T1/2
So, we get T1/2 = (ln2)/ λ
Or, T1/2 = 0.693/ λ … (7)
Calculating Mean life
After that, we'll look for a relationship between the mean life and the disintegration constant. Consider the following equation (5),
● The number of nuclei which decay in the time interval: ‘t’ to ‘t + Δt’ is: R(t)Δt = (λN0e–λt Δt).
● Each of them has lived for time ‘t’.
● Hence, the total life of all these nuclei is tλN0e–λt Δt
Hence, to obtain the mean life, we integrate this expression over all the times from 0 to ∞ and divide by the total number of nuclei at t = 0 (which is N0).
τ = (λN0 0∞∫ te–λtdt)/N0
= λ0∞∫ te–λtdt
On solving this integral, we get
τ = 1/λ
Therefore, we can summarise the observations as follows:
T1/2 = (ln2)/λ = τ ln 2 … (8)
4.3.5 Radioactivity – Law of Radioactive Decay
A.H. Becquerel discovered radioactivity by accident in 1896. He was researching the fluorescence and phosphorescence of visible-light-irradiated substances. This is when he made an interesting observation. In the following section, we'll study more about the law of radioactive decay.
With visible light, he lighted certain fragments of Uranium-Potassium-Sulphate. He then wrapped these pieces in black paper and used a piece of silver to detach them from a photographic plate. He left it for a long time. When he processed the photographic plate, he discovered that it had blackened.
This meant that the compound emitted something that penetrated the silver and black paper and landed on the plate. Following investigations, it was discovered that radioactivity is a nuclear phenomenon that occurs when an unstable nucleus decays. This process is known as radioactive decay.
Radioactive Decay
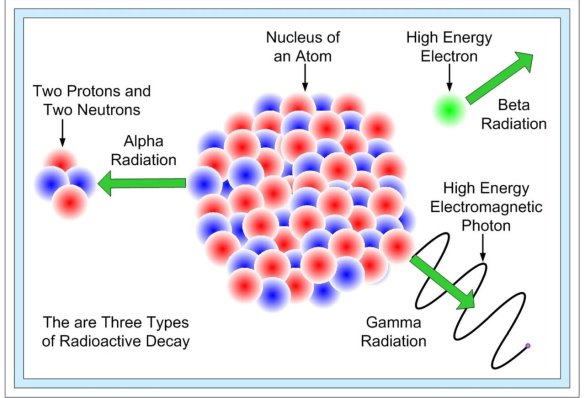
● In nature, there are three forms of radioactive decay:
● -decay –emission of a helium nucleus (42He)
● -decay – the emission of electrons or positrons (particles with the same mass as electrons but a charge opposite that of an electron);
● -decay – photons with high energy (hundreds of keV or more) are released.
4.3.6 The Decay Rate
In radioactivity calculations, the decay rate R ( = – dN/dt) is more important than the number N. The number of nuclei decaying per unit time is determined by this rate. We can compute the decay rate even if we don't know the amount of nuclei in the sample by counting the number of emissions of, or particles in 10 or 20 seconds. Let's say we take a time interval dt and calculate the decay count N (= –dN). The rate of decay is now defined as,
R = – dN/dt
Differentiating equation (4) on both sides, we get,
R = λ N0 e−λt
Or, R = R0e−λt … (5)
Where, R0 is the radioactive decay rate at the time t = 0, and R is the rate at any subsequent time t. Equation (5) is the alternative form of the Law of Radioactive Decay. Now we can rewrite equation (1) as follows,
R = λN … (6)
Where R and the number of radioactive nuclei that have not yet undergone decay must be evaluated at the same instant.
4.4.1 Half Life period
Half-Life, also known as Half-Life Period, is a phrase used in physics to describe the radioactive decay of a sample or element over a period of time. While studying nuclear physics, students will come across the term frequently.
This idea, on the other hand, is frequently used to describe a variety of decay processes, including exponential and non-exponential decay. The word is often used in medical sciences to describe the biological half-life of particular substances in the human body or in medications.
Half-Life Definition
A radioactive material's half-life is usually described as the time it takes for it to disintegrate or transition into a different substance (or one half of its atoms). Ernest Rutherford initially developed the principle in 1907. The sign Ug or t1/2 is commonly used to denote it.
If we choose a radioactive element with a one-hour half-life, it will help you understand the concept better. In this situation, half of the half would decay in an hour and the other half in another hour. The puzzle here is why the remaining material did not decompose in one hour.
Well, if the radioactive element is taken in a case where half of the atoms have decayed after one-half life, it would be proper to assume that they have a life expectancy at the average level as well-defined viz. The atoms with mean life that is much longer than their half-life. This means that the mean life equals the half-life divided by two, which is the natural algorithm. The half-life, on the other hand, is frequently defined in terms of likelihood.
Understanding The Concept Via Experiment
To understand how radioactive decay occurs, let us conduct an experiment with a large group of people, because statistical analysis will yield a reasonably obvious result.
Consider the following scenario: Nearly 1000 individuals are gathered in a hall, and each one is given a coin. The coin would represent the ability to decay, and each individual would symbolize a radioactive atom. Individuals can be requested to toss their money once every minute. If the toss result is heads, the person may be requested to leave the room (indicating atom disintegration), and if the result is tails, there is no need to do anything but wait one minute for another toss try.
You can see how, because of its importance, this topic has been addressed with zeal among students in the preceding example. As a result, the topic of radiation will be actively investigated in the coming years.
4.4.2 Half-Life Formulas
Below students will find the formulas for half-life that are used to describe the decay in substances.
- N(t) = No (½) t / t ½
- N(t) = No e-t / r
- N(t) = Noe– λt
Here we consider the following,
● N0 = the initial quantity of the substance
● N(t) = the quantity that is left over
● t1⁄2 = half-life
● τ = mean lifetime of the decaying quantity
● λ = decay constant
4.4.3 What are Half Lives and Mean Lives?
Specifying the half life or mean life of a process is a way of quantifying how fast it is occurring, when the whole process would in principle take forever to complete. The example we will talk about here is radioactive growth and decay, but examples from other fields include the recovery of a muscle after some exertion, and the filling of a cistern.
In particular then, the half-life of a radioactive element is the time required for half of it to decay (i.e. change into another element, called the "daughter" element).
So if a radioactive element has a half-life of one hour, this means that half of it will decay in one hour. After another hour, half of the remaining material will decay. But why didn't all of that remaining material decay in that second hour? Does the element somehow know that it's decaying, and alter its decay speed to suit?
Textbooks are usually content with deriving of the law of decay, and don't tend to address this question. And yet it forms a classic example of the way in which research in physics (and science in general) is carried out. Regardless of how we might expect an element to behave—where perhaps the second half might be expected to decay in the same amount of time as the first half—this simply does not happen. We must search for a theory that predicts this.
Science is often thought to proceed by our logically deducing the laws that govern the world. But it's not that simple; there are limits to what we can deduce, especially about things in which we cannot directly participate. Radioactive decay is a good example of this. We can't use a microscope to watch the events that make an element decay. The process is quite mysterious. But what we can do is make a simple theory of how decay might work, and then use that theory to make a prediction of what measurements we can expect. That's the way science proceeds: by making theories that lead to predictions. Sometimes these predictions turn out to be wrong. That's fine: it means we must tinker with the theory, perhaps discard it outright, or maybe realise that it's completely okay under certain limited circumstances. The hallmark of a good scientific theory is not what it seems to explain, but rather what it predicts. After all, a theory that says the universe just appeared yesterday, complete with life on earth, fossils and so on, in a sense "explains" everything beautifully by simply defining it to be so; but it predicts absolutely nothing. So from a scientific point of view it is not a very useful theory, because it contains nothing that allows its truth to be tested. On the other hand, while it's arguable that the theory of quantum mechanics explains anything at all, it certainly does predict a huge number of different phenomena that have been observed; and that's what makes it a very useful theory.
For radioactive decay, our theory is that the atoms decay, or change into another atom, quite spontaneously. At a basic level, we don't know why this should be; but we can only proceed step by step, and so first we begin with this simple theory. We postulate that they decay independently of whether their neighbours are decaying, and also that their tendency to decay is independent of how old they are. A given atom might decay after one microsecond, or one million years. However long it has been sitting intact makes no difference to its ability to decay right now. If the mechanism behind its decay is strong, in the sense that the atom has a large chance of decaying, then it won't last long: after all, the chance that it won't decay in some time interval is small, so the chance that it survives for any appreciable amount of time is then also small. That can be worked out by simple probability: multiplying together the probabilities that it doesn't decay for a string of those time intervals. The statistics of decaying elements, such as the mean and standard deviation of the number of atoms decaying in various time intervals, were measured soon after radioactivity was discovered; they were found to match those predicted by this idea of random decay, called Poisson statistics. Whenever anything has a small chance of happening, but there are lots of opportunities for it to happen, we get Poisson statistics.
So certainly physics has not proven, and can never prove, that its theory of atomic decay is true. The logical process is that if atoms decay randomly, then Poisson statistics will result. Experiments show that Poisson statistics do indeed result, but logically this does not mean that atoms decay randomly. Nevertheless, the way of science is that we do postulate that atoms decay randomly, until a new experiment calls this into question. But no experiment ever has. If this sounds like a reverse use of logic, then consider the same ideas for mechanics. Ideas of gravity, mass and acceleration were originally produced by Newton through the same process: because they predicted planetary orbital periods that could be verified experimentally. Because of this great success, expressions such as F = ma and F = GMm/r2 came to be canonical in physics. The logic was indeed being used in reverse; but no one was surprised when, three centuries later, one of the moon astronauts dropped a feather and a hammer together in the moon's vacuum, and found that they both fell at the same rate (although it was still beautiful and dramatic to watch!). That reverse logic had, after all, allowed him to get to the moon in the first place. So this way of conducting science works very well.
A "people" experiment to simulate radioactive decay
We may put this hypothesis of radioactive decay to the test by conducting an experiment with a large group of people; the group should be large in order to obtain good statistics. Put 1000 people in a large room and give everyone of them a coin. The coin depicts the ability of each individual to decay, and each person represents a radioactive atom. Everyone should toss their coin once every minute. If the outcome is heads, the person should exit the room immediately (which corresponds to the atom decaying). If the toss comes up tails, do nothing except wait another minute before throwing again.
So, what happens next? Because their coins landed heads up, nearly half of the people get up and walk out within one minute. After another minute, everyone will toss once more, and around half of the remaining people will leave. Of course, we don't expect everyone to depart after the second minute; around half of the group leaves every minute. Our simple random behaviour model has resulted in a half-life! This particular "element" is said to have a half-life of one minute. Of course, the laws of physics don't work in one-minute increments, so we should invite everyone to toss continually. This is acceptable, but it would create a lot of noise and make it more difficult to see what was going on.
It may be demonstrated that in a circumstance where the amount of an element halves in a constant time interval, it will also "third" in a separate constant time interval that is not difficult to calculate. In reality, we can use any integer to indicate the rate of decay. It's common to choose the halving time because it's straightforward. If a radioactive element was claimed to have a "third life" of one hour, no one would know if it meant one third had decayed or one third was remained behind after one hour. Of course, specifying the half life does not cause this issue.
Returning to our group of 1000 people who are still flipping their coin every minute, we may alter the half-life of the coin by altering the requirement to depart. Each individual, for example, throws their coin twice per minute. Only those with two heads are required to go now. In that instance, one quarter of the remaining people will depart after the first minute, and one quarter of the remaining people will depart after the second minute. The half-life has now surpassed one minute. As a result, we've made this "element" decay more slowly by reducing the chances of any of its constituent atoms decaying. Remember that anybody who seats and tosses their coin can sit for as long as they like, regardless of how many of their neighbours have left the room. They may sit for years flipping their coin, only to discover that it constantly lands tails up. Of course, the chances of this happening are slim, but it's possible. The likelihood that someone will leave is unaffected by how long they have been sitting there.
4.4.4 A "mustard seed" experiment to simulate radioactive decay
Another technique to demonstrate radioactive decay, this time with a feel more like to an actual experiment. Using a pestle, pound a couple of teaspoons of mustard seeds in a mortar. Have a microphone handy for a classroom demonstration that amplifies the click as each seed bursts. The risk that any one seed may burst is roughly independent of its neighbours and also roughly independent of time in the random crashing-together of the seeds. As a result, we hear a rush of clicks that quickly fade away, having a half-life of several seconds or longer. This is exactly what would happen if a Geiger detector was placed adjacent to a rapidly decaying element.
4.4.5 The mean life of a process
If half of the atoms in our radioactive element have decayed after one half life, we can expect some form of well-defined average life expectancy: the atoms' mean life, which is slightly greater than their half life. The half life is equal to the natural logarithm of 2 divided by the mean life (about 0.693). The time constant, which appears in the exponential term et/ associated in defining decay or growth, turns out to be exactly equal to the mean life. The term "time constant" refers to the fact that the mean life equals; the fact that the mean life equals is a nice coincidence that allows us to think about the mean life in the following, alternate way.
As previously stated, the time it takes for the remaining amount of the element to decline to a half, a third, or any fraction at all can be used to represent the speed of any decay process. One unusual choice of that number is e, and the time it takes for the remaining amount to be reduced to 1/e of the original also happens to be the decay's mean life. One of the reasons why the number e is so significant is because of this. Aside from having pleasant qualities that make the mathematics of growth and decay easier to understand, e quantifies ordinary concepts like the average life expectancy of atoms.
When we plot the amount of a radioactive element as a function of time, we see that it decreases with a typical "exponential decay curve," which helps to mathematically demonstrate the half-life concept. Here's a question for you: Assume the element did not decay exponentially (i.e. with a half-life), but rather linearly, with the rate of decay always equal to the original rate (resulting in a simple "first half in one minute, second half in the next minute—and then, all gone" scenario). How long would it take to entirely evaporate in such an idealised scenario? Assume we have 1000 atoms of a radioactive material, with 10 atoms decaying each second at the start. How long would it take to entirely evaporate if it continued to degrade at this rate (it won't, but pretend it did)? Of course, the answer is 100 seconds. It has now been discovered that this is exactly equal to the mean life of the real element. (Which means that we know straight away that the real element's half-life is 69.3 seconds.)
This way of looking at the concept of mean life also appeals to our intuition: it
According to this theory, if atoms behaved in the lovely, linear way that we humans enjoy thinking about them, the time it would take for them all to decay would be exactly equal to the mean life of the actual, real-world element. You can see how the number e is linked to basic linearity concepts, which is one of the reasons why it is such a powerful number in mathematical analysis.
The expansion of the daughter element follows the same logic. For the sake of simplicity, assume that the daughter is not radioactive. There are no daughter atoms at first, but when the parent element decays, they rise in number. Their development must finally flatten out, which takes an unlimited amount of time for the same reason that the parent element takes an unlimited amount of time to entirely decay. We ask how long it would take for the sample to be totally made up of daughter atoms if the daughter's growth maintained at its current rate (which it doesn't, remember!). This time interval turns out to be the parent's mean life once more.
4.4.6 The mean life and "probability per second"
That last application of the mean life to growth results in a language that is not always well understood by those who employ it. Assume we have a single atom of a radioactive element in front of us that is about to decay. We ask, "What is the chance that it has degraded after time t?" On average, the atom will disintegrate after one mean life. Although it may take a million times that amount of time for the atom to decay, we are confident that after two or three mean life, the atom will almost likely have decayed.
We can't actually visualise this probability as a function of time because we'd have to know when the atom will decay to do so (since then the probability equals one). Because the atom in front of us behaves exactly like the other atoms in the element, the most we can do is create a generic plot that accurately describes the entire population of decaying atoms. In that instance, we expect the likelihood to increase, eventually approaching one as t approaches infinity. Remember that this is an average prediction; each atom will undoubtedly achieve one at some point. But it's the best we can do at the moment.
The exact expression for this probability is 1 et/, which does actually tend to one as t approaches infinity. (It's the same curve as the one detailing the daughter element's growth.) What is the value of this (generic) probability when t=1: what is the likelihood that the atom will decay in one unit of time? Well, the answer is 1 e1/..., which may not convey much information! Let's ask another, relevant question, as we did before. How long would it take for the atom to decay if the chance of decaying within time t continued to increase at its initial pace (which it doesn't! ), and after how long would this probability reach one? This time interval, once again, turns out to be the mean life. However, if our linear, simplified atom decays with probability one after a time, it must decay with probability 1/ after a unit time.
With 1000 atoms and an initial rate of 10 decays per second, we calculated that the mean life was 100 seconds. So, if the likelihood of any individual atom decaying kept increasing uniformly at its starting pace, the chance of it decaying after one second would be 1/100. This is reasonable: The 10 atoms we measured to have decayed are 1/100 of the original 1000 atoms. As a result, we remark "the atom has a 1/100 per second risk of decay." Remember, this does not imply that it will have completely decayed after 100 seconds! This would only be true if the atom behaved in a straightforward, linear manner.
The fact that the atom's probability of decaying is "slowing down" is analogous to a pushed trolley starting out at 1/100 metre per second but decelerating at just the proper pace due to friction to match our atom. It would take 100 seconds to travel a metre if there was no friction and it moved at constant speed. Of course, it never fully reaches a metre distance because it is constantly slowing down; still, 1/100 m/s refers to its initial rate of distance increase. Similarly, "1/100 per second" refers to the starting rate of "decay-probability rise" for our generic atom, which represents the entire population of atoms. That decay probability will never exactly reach one in the aggregate for the entire population, but it will eventually reach one for any given atom.
Because the daughter element grows at the same rate as the parent element, the entire subject of growth may be applied to it. If it kept growing at its current rate, the sample would eventually be entirely made up of daughter atoms.
As you can see, we can manipulate these numbers to gain a sense of how an element decays or grows. But it's a lot easier to conceptualise in terms of the mean life than the half life for these more nuanced conceptions. Despite this, both the mean life and the half life give us a sense of radioactive decay, and each has its own set of applications.
4.5.1 Beta decay
A nuclear decay process in which an unstable nucleus transmutes and ejects particles to become more stable is known as beta decay. Beta decay can be divided into two types: beta minus and beta plus. A nucleon in the nucleus is changed into a new sort of nucleon in both of these decays, releasing particles in the process. Beta decay, both minus and plus, is somewhat penetrating (ie the radiation can go deep inside a solid object). Electron capture is a closely comparable mechanism in which an electron is captured in the nucleus and functions similarly to beta plus.
When a nucleus has too many neutrons, beta minus decay occurs. The electron is released from the nucleus after a neutron from the nucleus is converted into a proton and an electron. A tiny particle known as an anti-neutrino is also released to ensure that the laws of particle physics are upheld. [two] The following is a general representation of beta minus decay:
AZXN→AZ+1YN−1+e−+ν¯ZAXN→Z+1AYN−1+e−+ν¯
Where:
● AZXNZAXN is the parent nucleus
● AZ+1YN−1Z+1AYN−1 is the daughter nucleus
● e− is the released beta particle, an electron
● ν¯ is the released anti-neutrino
A nucleus with too many protons causes beta plus decay. A proton from the nucleus is turned into a neutron and a positron in this type of decay (which is simply a "positive version" of the electron). A small particle known as a neutrino is also released to guarantee that particle physics rules are followed. [two] The following is the general equation for beta positive decay:
AZXN→AZ−1YN+1+e++ν
Where:
● AZXNZAXN is the parent nucleus
● AZ−1YN+1Z−1AYN+1 is the daughter nucleus
● e+ is the released beta particle, a positron
● ν is the released neutrino
In both beta minus and beta plus decay it is the weak nuclear force that results in the changing of a nucleon into a different nucleon.
4.5.2 Applications and Importance
Beta decayed elements can be used in medical applications. RNT, often known as radiotherapy, is a cancer treatment that employs beta decay. Lutetium-177 or yttrium-90 is linked to a molecule and consumed in this method. [6] This chemical enters the body and travels to cancer cells. The radioactive atoms subsequently decay, producing beta particles and destroying cancer cells in the area.
Furthermore, the features of beta decay are used in carbon dating. The ratio of carbon-14 to carbon-12 in an object must be measured to establish the approximate age of artefacts, wood, and animal remains. [number six] Carbon-14 is produced by sunlight in the atmosphere from nitrogen-14, which plants take in during photosynthesis, therefore there is some carbon-14 in organic remnants. Animals eat plants, which absorb carbon-14 as well. When an organic organism decomposes, some of the carbon-14 is converted to nitrogen-14 (a beta decay process), and the amount of carbon-14 in the sample is decreased over time. [6] The estimated age of the item can be established by looking at the carbon-14 to carbon-12 ratio.
4.5.3 Types of beta decay
Beta decay can be divided into three categories. The “ordinary” beta decay, also known as decay or electron emission, was the first to be found. In nuclear beta decay, the symbol symbolises an electron emitted. The nuclide cobalt-60 decays in the following manner: 60Co 60Ni + neutrino.
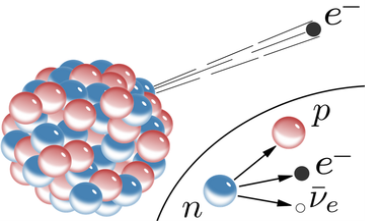
The neutrino is an unforeseen particle emitted during beta decay that is extremely important. The neutrino was not even hypothesised in theory until more than 20 years after electron emissions were discovered in beta decay. Neutrinos are so difficult to detect that it took until 1953 to gain the first direct proof of them. Neutrinos have almost no mass, no charge, and do not interact with nucleons through the strong nuclear interaction. Because they are travelling at nearly the speed of light, they have very little time to influence any nucleus they come across. This is because they don't interact through the EM force because they don't have any charge (and aren't EM waves). They do interact via the weak nuclear force, which is relatively weak and has a very short range. As a result, neutrinos can get through practically any detector and through practically any shielding. Neutrinos, on the other hand, carry energy, angular momentum (as fermions with half-integral spin), and linear momentum away from beta decay. When precise beta decay measurements were made, it became clear that the daughter nucleus and electron could not account for all of the energy, angular momentum, and linear momentum. Either they were being carried away by an unknown particle or three conservation rules were being broken. In 1930, Wolfgang Pauli proposed the existence of neutrinos in a formal paper. When he devised a detailed theory of beta decay, the Italian-born American scientist Enrico Fermi (1901–1954) gave neutrinos their name, which means "little neutral ones" (see Figure 3). The identification of the weak nuclear force as separate from the strong nuclear force, and hence responsible for beta decay, was part of Fermi's theory.
A new conservation law is also revealed by the neutrino. The electron family is one of the many different types of particles. In any process or closed system, we argue that the number of members of the electron family is constant. There are no members of the electron family present before the decay in our example of beta decay, but there is an electron and a neutrino afterward. As a result, electrons are assigned a +1 electron family number. The antineutrino of an electron in decay is given the symbol ve e, where nu is the Greek letter and the subscript e indicates that this neutrino is connected to the electron. This is an antimatter particle, as indicated by the bar. (Antimatter counterparts are almost identical to matter counterparts except that they have the opposite charge.) On Earth, antimatter is nearly absent, though it can be discovered in nuclear decay and other nuclear and particle reactions, as well as in outer space.) Because the electron is antimatter, its antineutrino e e has an electron family number of –1. Before and after the decay, the total is zero. The total electron family number is constant, according to the new conservation law, which must be followed in all circumstances. It is impossible to generate an electron without also creating an antimatter family member. In a scenario where total charge is initially zero and equal amounts of positive and negative charge must be formed in a reaction to keep the total zero, this law is equivalent to the conservation of charge.
If the decay of a nuclide AZXNZAXN is known, the decay equation is
XNYN1++ e XNYN1++ e XNYN1++ e XNYN
XNYN1++e (decay), XNYN1++e (decay), XNYN1++e (decay), XN
Y denotes a nuclide with one additional proton than X. (see Figure 4). If you know a nuclide decays, you can find the daughter nucleus by looking up Z for the parent and then figuring out which element has atomic number Z + 1. We can observe that Z = 27 for Co and Z = 28 for Ni in the decay of 60Co presented earlier. It's as though one of the parent nucleus' neutrons breaks down into a proton, electron, and neutrino. In fact, neutrons outside of nuclei do exactly that—they survive for only a few minutes on average and disintegrate in the following way:
Np++
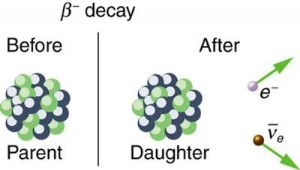
Figure: The parent nucleus produces an electron and an antineutrino during decay. The offspring nucleus has one proton and one neutron less than the parent nucleus. Neutrinos interact so weakly that they are rarely observed directly, but they play an important role in particle physics.
Because the total charge is Z before and after the decay, we can observe that charge is conserved. Because cobalt has Z = 27, the total charge before decay in 60Co decay is 27. The daughter nucleus after decay is Ni, which has Z = 28, and there is an electron, thus the total charge is 28 + (–1) or 27. Although angular momentum is preserved, it is not clearly conserved (you have to examine the spins and angular momenta of the final products in detail to verify this). Linear momentum is conserved as well, with the electron and antineutrino receiving the majority of the decay energy due to their low and zero mass, respectively. Another new conservation law is being followed in the natural world. A conserves the total amount of nucleons. There are 60 nucleons before and after the disintegration of 60Co, for example. It's worth noting that total A is conserved during decay. Also, because the total number of protons and neutrons changes, total Z and total N are not conserved in decay, as they are in decay. Given the masses of the parent and products, the energy released in decay may be estimated.
4.5.4 Decay Energy from Masses
Strategy and Concept
As in the last case, we must first calculate m, the mass difference between the parent nucleus and the decay products, using masses from Appendix A. The emitted energy is then computed using E = (m)c2 as before. The parent nucleus has the beginning mass, and the daughter nucleus and the electron generated in the decay have the final mass. The neutrino has a mass of zero or almost zero. However, since the masses given in Appendix A are for neutral atoms, the daughter nucleus has one more electron than the parent, and so the extra electron mass that corresponds to the β– is included in the atomic mass of Ni. As a result, m = m(60Co) m (60Ni).
Solution
The β− decay equation for 60Co is
6027Co33→6028Ni32+β−+¯νe2760Co33→2860Ni32+β−+ν¯e
As noticed, Δm = m(60Co ) − m(60Ni).
Entering the masses found in Appendix A gives Δm = 59.933820 u − 59.930789 u = 0.003031 u.
Thus, E = (Δm)c2 = (0.003031 u)c2.
Using 1 u=931.5 MeV/c2, we obtain E = (0.003031)(931.5 MeV/c2)(c2) = 2.82 MeV.
Discussion and Implications
The most challenging part of this example is persuading oneself that the mass of 60Ni is included in its atomic mass. There are additional ramifications as well. The decay energy is in the MeV region once more. This energy is spread across all of the decay's products. The daughter nucleus 60Ni is left in an excited state and emits photons ( rays) in multiple 60Co decays. Because the recoil kinetic energy of the daughter nucleus is low, the electron and neutrino receive the majority of the leftover energy. One final point: the decay electron is produced in the nucleus at the time of disintegration.
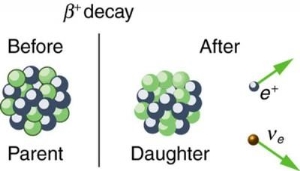
Figure. The emission of a positron that eventually finds an electron to annihilate, creating gammas in opposite directions, is known as + decay.
Beta decay in the second type is less common than beta decay in the first. It's a case of +decay. A positive electron is emitted when some nuclides decay. This is positron or antielectron decay (see Figure).
The antielectron is commonly represented by the symbol e+, although it is written as + in beta decay to show that the antielectron was emitted during nuclear decay. Antielectrons are the antimatter counterparts of electrons, and they are virtually identical to electrons in terms of mass, spin, and other properties, but they have a positive charge and an electron family number of –1. When a positron collides with an electron, the antielectron-electron pair undergoes mutual annihilation, in which all of the antielectron-electron pair's mass is transformed to pure photon energy. (The reaction e+ + e + conserves all other conserved quantities as well as the electron family number.) If a nuclide AZXNZAXN is known to have a positive decay, its +decay equation is
AZXN→YN+1+β++ve
ZAXN→YN+1+β++ve (β+ decay),
Ve is the symbol for the electron's neutrino, which has an electron family number of +1, and Y is the nuclide with one less proton than X (to conserve charge). Because the decay produces an antimatter member of the electron family (the +), a matter member of the family (here the e) must also be produced. If 22Na+ decays, for example, you may write the whole decay equation by first determining that Z = 11 for 22Na, resulting in a daughter nuclide with Z = 10, the atomic number for neon.
Thus the β+ decay equation for 22Na is
1122Na11→2210Ne12+β++ve
2211Na11→1022Ne12+β++ve
One of the protons in the parent nucleus decays into a neutron, a positron, and a neutrino in + decay. Outside of the nucleus, protons do not accomplish this, therefore the decay is due to the complexity of the nuclear force. It's worth repeating that the total number of nucleons in this and any other reaction is constant. Since atomic masses are used, you must count the number of electrons in the neutral atoms again to find the energy emitted in + decay. The daughter has one fewer electron than the father, and the decay creates one electron mass. Since we employ the masses of neutral atoms in + decay, m = m(parent) [m(daughter) + 2me].
The third type of beta decay is electron capture. A nucleus captures an electron from the inner shell and undergoes a nuclear reaction similar to + decay. Electron capture is sometimes abbreviated as EC. Although we know that electrons cannot live in the nucleus, this is a nuclear reaction that consumes the electron and only occurs spontaneously when the products have less mass than the parent plus the electron. If an AZXNZAXN nuclide is known to undergo electron capture, the electron capture equation for that nuclide is
AZXN+e−→YN+1+ve
ZAXN+e−→YN+1+ve (electron capture, or EC)
Any nuclide that can + decay can also be captured by electrons (and often does both). The same conservation laws apply to EC as they do to + decay. It's a good idea to double-check these for yourself.
Because the parent nuclide is unstable and outside the region of stability in the nuclide chart, all sorts of beta decay occur. Those nuclides with more neutrons than those in the stability region will decay to produce a daughter with fewer neutrons, bringing the daughter closer to the stability region. Similarly, nuclides with more protons than those in the stability region decay or undergo electron capture to produce a daughter with fewer protons that is closer to the stability region.
4.6.1 The Neutrino Hypothesis
The remarkable story of the neutrino
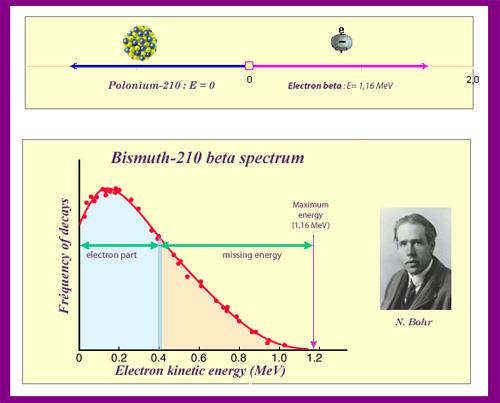
Fig. The mystery of beta electrons lost energy
Beta decay was thought to create two particles in the 1930s: the recoiling nucleus and an electron. It was expected to be a 'monokinetic' reaction, with the electron carrying away all of the available energy, similar to alpha decay. Beta decay, on the other hand, resulted in a wide range of possible and smaller energies for the electron, as shown in the diagram above. Where did all the lost energy go? Niels Bohr went so far as to question whether the law of conservation of energy was still applicable when confronted with this problem.
IN2P3 is a three-letter acronym that stands for "
The research of radioactive disintegrations had proved that alpha rays were ‘monokinetic’ - in that they always carried away the same percentage (100 percent ) of the energy available in the decay. Beta rays, on the other hand, can have a wide variety of energy levels. The energy distribution (or spectrum) of beta rays can take any value between zero and the total energy available, whereas the energy distribution (or spectrum) of alpha rays is reduced to a single value.
For physicists working in the field in 1930, this evidence was troubling. When it comes to beta decay, where did the law of conservation of energy go? The seeming lack of energy prompted Niels Bohr to propose that the most fundamental conservation law be abolished. For a physicist, this is a grave sin.
To preserve the law of conservation of energy, Swiss physicist Wolfgang Pauli proposed the creation of an electrically neutral, low mass particle (at most 1/100 the mass of the proton) that would be emitted with the beta particle. This hypothetical third body might therefore absorb any energy that was not delivered to the beta particle, resolving the most perplexing of problems. Pauli first offered this notion in a satirical letter to his colleagues Lise Meitner and Hans Geiger.
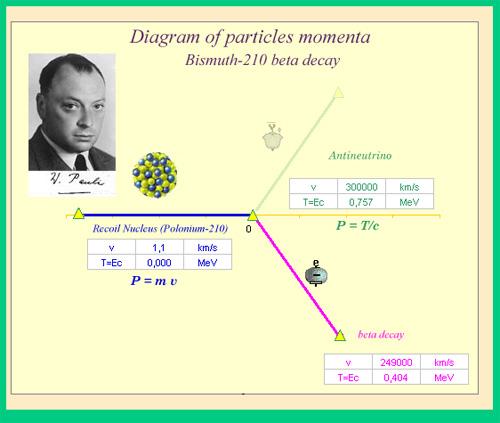
Adding a new particle to solve the problem
Wolfgang Pauli would be the one to explain the mystery of the missing energy by proposing the presence of a third particle, the neutrino, which is capable of evading detection. The image above depicts the circumstance where all three bodies have equal momenta in the case of bismuth 210 decay. The recoiling nucleus, which is 400,000 times heavier than the electron, absorbs very little energy. The leftover energy is split between the electron and the neutrino, which is depicted as a ghost particle in this illustration. The first experimental proof of a neutrino would take over a quarter-century to come to light.
IN2P3 is a three-letter acronym that stands for "
The brilliant Italian physicist Enrico Fermi was immediately convinced. He proposed the theory of beta decay based on a hypothesis that an electron-neutrino pair is spontaneously produced by a nucleus in the same way that photons can be spontaneously emitted by excited atoms, based on discussions held at the Solvay Conference in October 1933 (devoted to James Chadwick's discovery of the neutron).
According to Francis Perrin, for such a particle to exist, it must either have zero mass or be extremely light, even when compared to the electron.
Fermi's idea was the forerunner of today's 'weak interaction' hypothesis. During the first quarter of the twentieth century, Fermi's idea of a point-like interaction of four particles (for example, an initial neutron becoming a proton, an electron, and an antineutrino) was accepted as a canon, an article of faith without proof.
The neutrino remained a hypothetical particle until Reines and Cowan presented evidence for its existence in 1956.
Murray Gell Mann, an American physicist, proposed the idea of a weak force active not only in radioactive processes, but also in other processes where the impacts of various types of neutrinos may be recognised in a variety of subatomic events in 1955.
The neutrino and its antiparticle have played an important role in particle physics since its ‘discovery' by Pauli and the subsequent experimental evidence in their favour. Because neutrinos have no electrical charge, they are only affected by the weak interaction, allowing for a more detailed study of that force without the ‘background noise' produced by other nuclear or atomic interactions.
The neutrino is essential in astrophysics, in addition to its critical function in the physics of the infinitely small. It could, for example, be the key to unlocking the Universe's "hidden mass."
4.6.2 Pauli’s Idea of the Neutrino
Pauli's suggestion was an attempt to solve a difficult experimental challenge that had piqued the physics community's interest for several years. Ellis and Wooster published an experiment in 1927 that demonstrated that the electrons emitted in radioactive decay had a broad and continuous range of energy. This perplexing finding not only shattered the analogy with -decay, in which the energy of the emitted -particles was calculated for each potential -decay, but it also sparked some strange speculations. For example, Rutherford and Chadwick proposed that not all nuclei of a certain -unstable element were identical because they had various internal energies, and Bohr proposed that energy is not conserved in decay, allowing electrons to escape with a variety of energies. 13 This was hardly the only concern with nuclear research at the time. The tests in 1926 that demonstrated that nitrogen nuclei behaved according to BoseEinstein statistics revealed yet another major flaw in nuclear theory and the p-e model. According to the latter, because both protons and electrons have spin 12, nitrogen (atomic mass 14 and nuclear charge 7) should have a half-integer total spin. This suggests that nitrogen nuclei should follow Fermi-Dirac statistics if the p-e model is correct. The observed Bose-Einstein statistics, however, required that the nucleus comprised of an even number of half-integer particles, adding up to an integer total, which is required to explain these statistics. In 1929, Pauli was introduced to these challenges by Bohr, who was considering a restriction of the concept of energy conservation to solve these problems, a concept that Pauli found to be "very little satisfaction" (according to a letter to Bohr reprinted in Peierls 1986, p. 5). As Bohr and his partners continued down this route of energy nonconservation, Pauli began to consider another notion, which he first articulated in December 1930. Let us begin, like we did with Rutherford, by attempting to comprehend Pauli's perspective and models on the subject. We can next discuss how he changed Rutherford's concept to suit his own needs. Pauli, like his contemporaries, viewed radioactive decay as a reaction in which an unstable nucleus (as in the previous instance) disintegrated spontaneously into a residual nucleus, with the observed emitted - or -particle plus some -radiation (the situation afterwards). The model of this reaction preserves both energy and electric charge for -particles, but the unexplainable continuity of energies in the situation afterward has led some to believe that this continuity already existed in the situation before (Rutherford and Chadwick), or to suggest that the energy conservation constraint for this model be retracted (Bohr). This final proposal was what prompted Pauli to address the issue. We need to look at some of his objections to see why he was so opposed to Bohr's views. Bohr's notion to keep charge conservation but renounce energy conservation in -decay is challenged in a letter to Klein, a close associate of Bohr, by the following thought experiment: 13 Gauderis 2013 provides a thorough examination of this puzzle and all proposed possibilities. “Imagine a sealed chamber filled with radioactive decay. [...]... If the energy law were not applicable for -decay, the overall weight of the closed box would change as a result. This contradicts my understanding of physics! For then, even the gravitational field – which is generated [...] by the complete box (including the radioactive content) – must be expected to change, whereas the electrostatic field, [...], should remain unchanged due to charge conservation.” Jensen 2000, p. 153) (reprinted in Jensen 2000, p. 153) Pauli's main critique is that the field formalisms for gravity and electrostatics, which both rely on inverse-square laws, are built similarly and hence regarded to be of the same kind. Bohr's suggestion, by breaking this analogy, has the far-reaching consequence of undermining the physical concept of a field. Unlike most quantum theorists, who rarely dealt with gravity, 14 Pauli was a specialist in general relativity. 15 As a result, Pauli, unlike other nuclear physicists, was far more cognizant of field structures as the basic ontological ideas for physical reality. This explains why Bohr's theories bothered him so much. If Pauli was confident that conservation principles must apply in this reaction model, it occurred to him quickly that the only way to balance the disequilibrium between the before and after states was to add something to the picture. However, nothing new has been discovered in the -decay experiments thus far. As a result, he wanted to find something that was either unobservable or extremely difficult to observe. Because the law of conservation of electrical charge was already in effect, it had to be electrically neutral as well. In other words, his reaction model for the -decay process had a gap that needed to be filled by an idea or object that has these two traits. “Then I tried to connect the problem of the nucleus' spin and statistics with the other problem of the continuous-spectrum without giving up the energy conservation principle through the idea of a neutral particle,” he wrote in an autobiographical article. I wrote a letter about this in December 1930, when the heavy neutron had not yet been discovered experimentally.” (1957, p. 1316, my translation) He proposed a "desperate solution" to tackle these two problems in this letter16, namely "that there could exist electrically neutral particles in the nucleus, which I would like to term neutrons" (1957, p. 1316, my translation). This proposal was primarily an adaption of Rutherford's theory, according to Gauderis (2013). The key justifications for this thesis are, first and foremost, the fact that Pauli used the term "neutron" for this nuclear ingredient when Rutherford and his collaborators were still using the name "neutron" in papers, a fact Pauli must have known about. Second, he explains why Rutherford was unsuccessful in locating his neutron previously.
Wolfgang Pauli, an Austrian physicist, predicted in 1930 that when a beta particle is generated, another particle is emitted that is difficult to detect.
Enrico Fermi, an Italian physicist, termed it the 'neutrino,' which means "little neutral one" in Italian.
According to Pauli, the energy released in beta decay was distributed randomly between the beta particle and the neutrino. This would explain the wide variety of beta particle energies measured and the many angles at which a nucleus could recoil.
4.7.1 Pair Production and Annihilation
Photon absorption is the process in which a photon gives up some or all of its energy to a material particle. The photoelectric and Compton processes are two processes for photon absorption (contained usually within an atom in a solid). Photon absorption can be measured using an absorption coefficient, which is generally represented in m-1 or cm-1 units and determined by the equation:
The photon intensities (W/m2) at the entrance surface and at a depth x below the surface are I(0) and I(x), respectively (measured in the direction of the incident beam). As a result, the intensity within the material decays exponentially, as seen in Fig. 4-26. We can also consider x to be the material's full thickness, in which case I(x) is the photon intensity at the exit surface. The absorption coefficient can be measured by positioning radiation detectors in front and behind a sheet of material with a specified thickness x.
When the experimentally determined (mu) is plotted as a function of increasing photon frequency f (or photon energy hf), it falls continuously in the visible, ultraviolet, and x-ray regions, but eventually reaches a minimum and then begins to increase in the X-ray region; see Weidner & Sells Fig. The reason for the initial drop is that as photon energy increases, photoelectric and Compton scattering absorption processes become less likely; in other words, higher-energy radiation penetrates better.
At high photon energy, a third process called pair production occurs, in which a pair of elementary particles (a particle and its antiparticle of the same mass but opposite electrostatic charge) are created from the energy (hf) of the original photon. The two particles in this case are an electron and an antielectron (also known as a positron, with the same rest mass m0 as an electron but a charge of +e).
Pair production can be described by the following equation, which exhibits total energy (or mass-energy) conservation:
The rest energy of an electron (m0 c2) = 0.511 MeV is equal to that of the positron, hence the factor of 2 symbolises the fact that two particles with the same rest mass are generated. The kinetic energy of the electron and positron, respectively, is represented as K(-e) and K(+e).
The two particles would be generated at rest (with zero kinetic energy) if the photon energy was exactly 2m0 c2 = 1.02 MeV. This would be an example of total conversion of energy into mass. The process cannot take place if the photon energy is less than 2m0c2; in other words, the threshold energy for pair creation is 1.02 MeV. When photon energies exceed the threshold, a photon has more than enough energy to generate a particle pair, and the excess energy is manifested as kinetic energy between the two particles.
However, there is one more requirement that must be met during the pair-production process: momentum conservation. Taking this into consideration, we can deduce that pair creation cannot occur in empty space; something must absorb the initial photon's momentum (p=h/ =hf/c). (Consider the threshold case, in which particles must be generated at rest and are unable to absorb any momentum.) An atomic nucleus, which is millions of times more massive than an electron or positron, may absorb photon momentum without absorbing much energy, therefore the energy-conservation equation above remains roughly correct. As a result, when high-energy gamma rays strike a solid with a high density of atomic nuclei, pair formation occurs.
Pair annihilation is the inverse of pair formation, in which a particle and its antiparticle collide and annihilate each other, leaving the total energy of the two particles as electromagnetic radiation. The energy balance between an electron and a positron can be expressed as:
K(-e) + K(+e) = 2 hf 2m0c2 + K(-e) + K(+e)
The first term reflects both particles' rest energy, the second and third terms indicate their kinetic energies just before colliding, and the term on the right-hand side of the equation indicates the creation of two photons, each with the same frequency f and energy hf. According to the equation, hf must be at least m0c2=0.51 MeV, indicating that the photons produced correspond to -ray radiation. This process, like pair production, is usually carried out inside a solid, which provides the required electrons. Positrons are injected into the solid as a beam of particles from a particle accelerator.
The overall momentum before the collision would be close to zero if the kinetic energy of the two original particles were both tiny (m0c2). Because of momentum conservation, the momentum after annihilation must be close to zero, and the only way this can happen is if the two photons are released in opposing directions, cancelling their separate momenta. The positrons entering the solid usually have a lot of momentum, but the electrons (which were already present in the solid) are virtually at rest. The paths of the two -ray photons then intersect at the location of the pair-annihilation event, which is at an angle to each other (see Fig. 4-xx).
PET (positron emission tomography) is a medical diagnostic procedure that produces images of the inside structure of human organs based on this principle. The PET machine creates an image of the electron density within a plane (really a small slice) within the tissue by detecting the direction of passage of -ray photons that are created simultaneously (coincidence detection) and counting the number produced in different regions of space. The process can be repeated by moving the detectors (or the patient) forward to acquire three-dimensional information (a tomograph). A radioisotope is injected into the bloodstream to provide the positrons. PET is now a commercially available technique that works in conjunction with CT and MRI scanning.
The photon-electron interactions that we discussed recently are summarised schematically in Figure 4.19 (from Weidner & Sells). It's worth noting that the "particle" (electron, positron, or photon) that enters the solid is entirely annihilated in certain situations; in others (Compton and bremstrahlung effects), the particle only loses some energy.
Because lead has a larger density of electrons (and more highly charged atomic nuclei) than aluminium (which has a lower atomic number), photon absorption processes are greater (higher (mu) ; see Figs. 4-24b and 4-26), making it a good radiation-shielding material. However, because (mu) decreases as photon energy decreases (below 1 MeV), thicker sheets are required to absorb harsh (short-wavelength) x-rays or gamma rays, as opposed to soft (long-wavelength) x-rays.
There is a third way for photons to lose energy in their interactions with matter, in addition to the photoelectric effect (photon absorption) and Compton scattering (photon scattering). A photon can simply evaporate and be replaced by a matter-antimatter pair of particles in this process, known as pair creation. Because the mass of the electron and positron may be generated from the energy of the massless photon, this process provides a fantastic demonstration of how mass is not conserved. Of course, the photon must have enough energy to create the two new particles' rest masses.
This process usually takes place near a nucleus and results in the formation of an electron-positron pair. The following is a diagram of the effect:
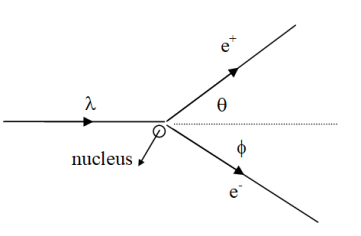
First, let’s try to imagine a simpler version of this phenomenon, with no nucleus present and the electron and positron both traveling in the same direction as the initial photon. Energy conservation would lead to:
Ephoton=Eelectron+Epositron(4.3.1)
And x-momentum conservation:
Pcphoton=pcelectron+pcpositron(4.3.2)
Using
E_{total}^2 = (pc)^2 + (mc^2)^2
However, attempting to set up and solve the conservation rules for the real pair manufacturing process will include a significant amount of algebra. Instead, we'll assume that because the nucleus is much, much more massive than the electron and positron, it can "absorb" the required amount of momentum to ensure momentum conservation without "absorbing" much kinetic energy. In a sense, we will ignore the nucleus while solving the problem, and then check to see if ignoring the nucleus was a reasonable choice once we have a solution.
As an example, consider the problem below.
When a 3.0 MeV photon collides with a lead nucleus, an electron-positron pair is formed. The electron and positron travel perpendicular to the photon's initial path of passage.
a. Assume the nucleus is at rest after the collision and calculate the kinetic energy of the electron and positron.
b. To ensure momentum conservation, determine the kinetic energy of the lead nucleus. Would this amount of kinetic energy have a significant impact on component a's outcome?
Solution
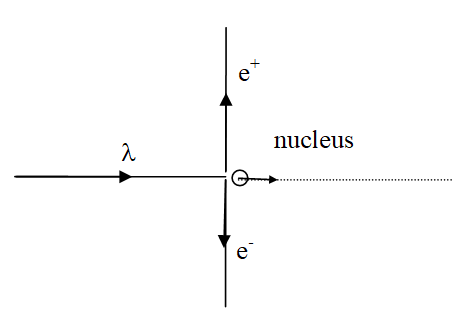
Energy conservation (ignoring the energy of the nucleus) leads to:
Ephoton=Eelectron+Epositron(4.3.7)
3=Eelectron+Epositron(4.3.8)
And yy-momentum conservation (ignoring the nucleus again):
0=−pcelectron+pcpositron(4.3.9)
Pcelectron=pcpositron(4.3.10)
Since the pair have equal momenta, they must have equal energy, so:
3=2Eeither(4.3.11)
Eeither−1.5 MeV(4.3.12)
KEeither=(1.5−0.511) MeV(4.3.13)
KEeither0.989 MeV(4.3.14)
To ensure that x-momentum is conserved,
Pcphoton=pcnucleus(4.3.15)
3 MeV=pcnucleus(4.3.16)
Using E2total=(pc)2+(mc2)2 and noting that the atomic mass of a lead atom is 207.2 u=193007 MeV207.2 yields,
Enucleus= (4.3.17)
(4.3.17)
Enucleus= (4.3.18)
(4.3.18)
then simplify using the binomial expansion,
Enucleus=193007 MeV(1+1291930072)(4.3.19)
Enucleus=193007 MeV(1+1.2×10−10)(4.3.20)
Enucleus=193007 MeV+2.33×10−5 MeV(4.3.21)
KEnucleus=2.33×10−5 MeV(4.3.22)
KEnucleus=23.3 eV(4.3.23)
As a result, the nucleus can maintain momentum conservation while stealing a minuscule fraction of the total energy available. As a result, we can ignore the nucleus when splitting the energy of the incoming photon between the electron and the positron.
4.8.1 Fission and Fusion
Introduction
The nucleus, which is the foundation of nuclear science, is made up of protons and neutrons. Understanding the process behind fission and fusion, which involves the dispersion and combination of elemental nuclei and isotopes, is an important part of nuclear research. Adding up the individual masses of each of these subatomic particles of any particular element will always give you a bigger mass than the mass of the nucleus as a whole. The concept of nuclear binding energy is missing from this finding. Nuclear binding energy is the energy required to keep the protons and neutrons of a nucleus intact, and the energy that is released during a nuclear fission or fusion is nuclear power. However, there are a few things to think about. The overall mass of an element's protons and neutrons is smaller than the mass of the nucleus as a whole. The nuclear binding energy is responsible for the mass difference. Nuclear binding energy is essentially seen as mass, and that mass becomes "missing." The nuclear energy, also known as the mass expelled from the process as neutrons, photons, or any other trajectory, is the missing mass, which is called mass defect. In a nutshell, the phrases "mass defect" and "nuclear binding energy" are synonymous.
4.8.2 Nuclear Fission and Fusion
The breaking of a heavy nucleus into two lighter nuclei is known as nuclear fission. The German scientists Otto Hahn, Lise Meitner, and Fritz Strassmann discovered fission in 1938 when they attacked a sample of uranium with neutrons in an attempt to create new elements with Z > 92. They noticed that lighter elements like barium (Z = 56) were created during the reaction and determined that these products had to come from uranium-235 fission induced by neutrons:
23592U+10n14156Ba+9236Kr+310n(1)(1)92235U+01n56141Ba+3692Kr+301n
The detection of the krypton-92 fission product backed up this theory. As explained in Section 20.2, the nucleus frequently divides asymmetrically rather than into two equal pieces, and a given nuclide's fission does not always produce the same products.
Each split nucleus releases more than one neutron in a typical nuclear fission reaction. A self-sustaining series of nuclear fission processes known as a nuclear chain reaction can ensue when these neutrons collide with and trigger fission in other adjacent nuclei (Figure). Fission of 235U, for example, releases two to three neutrons each fission event. When neutrons are absorbed by other 235U nuclei, they cause further fission events, increasing the pace of the fission reaction exponentially. A generation is a collection of events. Experiments show that a fissile isotope must have a minimum mass to sustain a nuclear chain reaction; if the mass is too low, too many neutrons escape without being collected, causing a fission reaction. The critical mass is the smallest mass that can maintain fission for an extended period of time. This amount is determined by the isotope's identity, as well as the purity of the material and the form of the mass, which correlates to the amount of surface area available from which neutrons can escape. If the mass of the fissile isotope is more than the critical mass, the resulting supercritical mass can release energy explosively under the correct conditions. The huge energy released by nuclear chain reactions is responsible for the catastrophic destruction produced by nuclear weapons like fission bombs, but it is also the foundation of the nuclear power industry.
Nuclear fusion is the reverse of nuclear fission, in which two light nuclei unite to form a heavier, more stable nucleus. The positive charge on both nuclei, as in the nuclear transmutation reactions outlined in Section 20.2, creates a large electrostatic energy barrier to fusion. This barrier can be broken if one or both particles have enough kinetic energy to overcome electrostatic repulsions, allowing the two nuclei to get near enough for fusion to happen. The concept is comparable to increasing the rate of a chemical reaction by adding heat. Fusion reactions are most exothermic for the lightest element, as demonstrated in Figure. 6.3's plot of nuclear binding energy per nucleon with atomic number. Two deuterium atoms, for example, fuse to form helium-3 in a typical fusion reaction known as deuterium–deuterium fusion (D–D fusion):
221H32He+10n(2) 221H32He+10n(2) 221H32He+10n(2) (2)
212H23He+01n
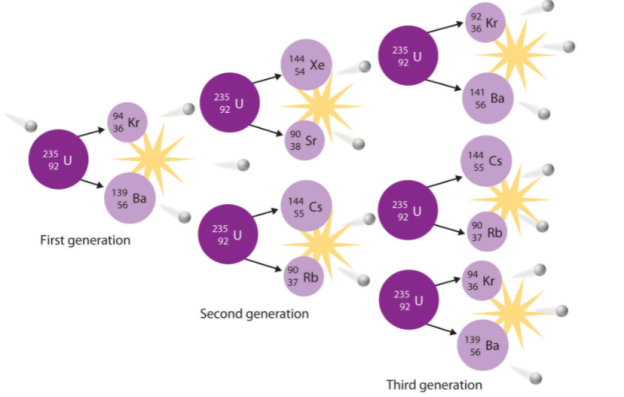
Figure: The rate of a fission process accelerates geometrically because each neutron released might promote the fission of another 235U nucleus. A generation is a collection of events.
Deuterium–tritium fusion (D–T fusion) is a reaction in which a deuterium atom and a tritium atom combine to form helium-4 (Figure 11):
12H+13H+24he+10n=12H+13H+24he+10n=12H+13H (3)
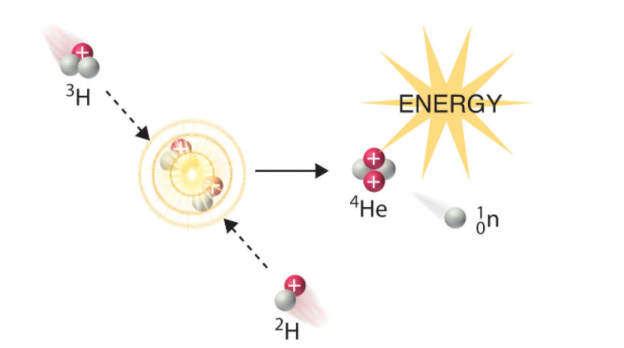
Nuclear fusion is depicted in Figure. Lighter nuclei combine to form a heavier nucleus in a nuclear fusion event. The fusion of 3H and 2H to produce 4He and a neutron produces a tremendous amount of energy, as depicted. Nuclear fusion has the potential to produce far more energy than fission, but it requires a lot of kinetic energy to overcome electrostatic repulsions between positively charged nuclei and start the fusion reaction.
However, to start these processes, a temperature similar to that of the sun's interior (about 1.5 107 K) is required. At the moment, the only way to achieve such a temperature on Earth is to detonate a fission bomb. The so-called hydrogen bomb (or H bomb) is actually a deuterium–tritium bomb (a D–T bomb), which uses a nuclear fission reaction to generate the extremely high temperatures required to ignite fusion of solid lithium deuteride (6LiD), releasing neutrons that react with 6Li to produce tritium. The deuterium-tritium process produces a large amount of energy. The tremendous amounts of energy produced by nuclear fission and fusion reactions are demonstrated in Example 21.6.3 and its accompanying exercise. Fusion processes, in fact, provide energy to all stars, including our sun.
We utilise Einstein's equation, which equates energy and mass, to compute the energy released during mass annihilation in both nuclear fission and fusion:
E=mc2(4)(4)E=mc2
With
● mm is mass (kilograms),
● cc is speed of light (meters/sec) and
● EE is energy (Joules).
Example:
Calculate the amount of energy released (in electron volts per atom and kilojoules per mole) when 235U is split into 144Cs, 90Rb, and two neutrons via neutron-induced fission:
23592U+10n→14455Cs+9037Rb+210n92235U+01n→55144Cs+3790Rb+201n
Given: balanced nuclear reaction
Asked for: energy released in electron volts per atom and kilojoules per mole
Strategy:
A Following the method used in Example 21.6.1, calculate the change in mass that accompanies the reaction. Convert this value to the change in energy in electron volts per atom.
B Calculate the change in mass per mole of 235U. Then use Equation 21.6.3 to calculate the change in energy in kilojoules per mole.
Solution
A The change in mass that accompanies the reaction is as follows:
Δm=mass products − mass reactants = mass (14455Cs+9037Rb+10n) − mass 23592 U=(143.932077 amu+89.914802 amu+1.008665 amu)−235.043930 amu=−0.188386 amu(5)(6)(7)(5)Δm=massproducts−massreactants=mass(55144Cs+3790Rb+01n)−mass 92235U(6)=(143.932077 amu+89.914802 amu+1.008665 amu)−235.043930 amu(7)=−0.188386 amu
The change in energy in electron volts per atom is as follows:
ΔE=(−0.188386 amu)(931 MeV/amu)=−175 MeVΔE=(−0.188386 amu)(931 MeV/amu)=−175 MeV
B The change in mass per mole of 23592U92235U is −0.188386 g = −1.88386 × 10−4 kg, so the change in energy in kilojoules per mole is as follows:
ΔE=(Δm)c2=(−1.88386×10−4 kg)(2.998×108 m/s)2=−1.693×1013 J/mol=−1.693×1010 kJ/mol(8)(9)(8)ΔE=(Δm)c2=(−1.88386×10−4 kg)(2.998×108 m/s)2(9)=−1.693×1013 J/mol=−1.693×1010 kJ/mol
Calculate the amount of energy (in electron volts per atom and kilojoules per mole) released when deuterium and tritium fuse to give helium-4 and a neutron:
21H+31H→42He+10n12H+13H→24He+01n
Solution
ΔE = −17.6 MeV/atom = −1.697 × 109 kJ/mol
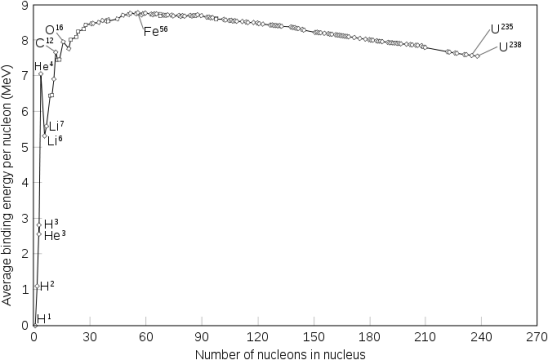
4.8.3 Fission
Fission occurs when a nucleus splits, releasing free neutrons and lighter nuclei. Heavy element fission is very exothermic, releasing roughly 200 million eV compared to coal combustion, which produces only a few eV. Because only 0.1 percent of the original nuclei are converted to energy, the quantity of energy released during nuclear fission is millions of times more efficient per mass than coal. As a result of the reaction, a daughter nucleus, energy, and particles such as neutrons are emitted. The released particles can then react with other radioactive materials, resulting in the production of daughter nuclei and more particles, and so on. Nuclear fission reactions are unique in that they can be harnessed and exploited in chain reactions. Nuclear weapons are built on this chain reaction. U235U235 is a well-known element utilised in nuclear fission that, when hit with a neutron, transforms into U236U236 which is even more unstable and splits into daughter nuclei such as Krypton-92 and Barium-141, as well as free neutrons. The fission products that occur are highly radioactive and frequently decay.
Nuclear fission occurs when the nucleus of an atom splits into nuclei of lighter atoms, releasing energy as a result of a neutron bombardment. Enrico Femi proposed the idea of nuclei splitting in 1934, believing that transuranium elements may be created by bombarding uranium with neutrons, because the loss of Beta particles would increase the atomic number. However, the properties of elements with greater atomic numbers than uranium did not coincide with the products that formed (Ra, Ac, Th, and Pa). They were instead radioisotopes of much lighter elements like Sr and Ba. The quantity of mass lost in the fission process is equal to 3.201011J3.201011J of energy.
● Consider the neutron bombardment
U92235+n10→U92236→fission products(10)
Which releases 3.20×10−11J3.20×10−11J per U235U235 atom.
How much energy would be released if 1.00g1.00g of U235U235 were to undergo fission?
Solution
(1.00gU235)×(1molU235235gU235)×(6.022×1023atomsU2351molU235)×(3.20×10−11J1atomU235)=8.20×1010J(11)
Clearly, the fission of a small amount of atoms can produce an enormous amount of energy, in the form of warmth and radiation (gamma waves). When an atom splits, each of the two new particles contains roughly half the neutrons and protons of the original nucleus, and in some cases a 2:3 ratio.
4.8.4 Critical Mass
A bomb will only explode if the chain reaction reaches its critical mass. A chain reaction reaches critical mass when it becomes self-sustaining. The reaction will not be self-sustaining if the neutrons are lost quicker than they are generated by fission. The spontaneous nuclear fission rate is the likelihood per second that an atom will spontaneously fission—that is, without any external interference. Nuclear fission is controlled in nuclear power plants by a medium such as water in the reactor. To cool the reactor and delay neutron particles, water is used as a heat transfer medium. The neutron emission and use can be controlled in this fashion. A meltdown will occur if the nuclear reaction is not regulated due to a lack of cooling water, for example.
4.8.5 Fusion
The combining of two nuclei to generate a heavier nucleus is known as nuclear fusion. Energy is released or absorbed as a result of the reaction. Fusion of nuclei with lower mass than iron produces energy, whereas fusion of nuclei with higher mass absorbs it. Iron peak is the name given to this phenomenon. Nuclear fission, on the other hand, has the opposite effect.
The energy generated from the sun and many other stars in the universe is driven by the power of the energy in a fusion process. Nuclear fusion is also used in nuclear weapons, namely the hydrogen bomb. Nuclear fusion is an energy-producing process that occurs at extremely high temperatures, such as those found in stars like the sun, when smaller nuclei are fused together to form a larger nucleus, releasing massive amounts of heat and radiation in the process. When left uncontrolled, this process can generate nearly infinite amounts of energy, and an unregulated chain can form the basis for a hydrogen bond, since hydrogen is regularly fused. This thermonuclear reaction is also fueled by the combining of deuterium atoms to generate helium atoms. Consider the following scenario:
H12+H13→He24+n01+energy(12)
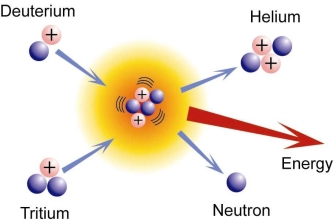
The difficulty of bringing deuterium and tritium nuclei into close contact, achieving high enough thermal energy, and thoroughly ionising gases into plasma are all issues that have yet to be thoroughly shown in a controlled fusion reaction. Plasma, which is a mixture of atomic nuclei and electrons that is required to launch a self-sustaining reaction at a temperature of more than 40,000,000 K, is an important component of nuclear fusion. Why does nuclear fusion require so much heat, even for light atoms like hydrogen? The reason for this is because the nucleus contains protons, and in order to overcome electrostatic resistance between the protons of both hydrogen atoms, both hydrogen nuclei must accelerate extremely fast and reach close enough for the nuclear force to initiate fusion. Nuclear fusion produces more energy than it takes to initiate it, hence the system's G is negative, indicating that the reaction is exothermic. The fusion of light elements is also self-sustaining because it is exothermic, as long as there is enough energy to start fusion in the first place.

4.8.6 Mass Defect
The disparity between the actual mass of an atom's nucleus and its expected mass based on the sum of its non-bound components is explained by nuclear binding energy.
Remember that the following equation connects energy (E) and mass (m):
[latex]E=mc^2[/latex]
The speed of light is denoted by c. The binding energy of nuclei is so high that it accounts for a large portion of their mass.
Because energy is withdrawn when the nucleus is formed, the actual mass is always smaller than the sum of the individual masses of the constituent protons and neutrons. The mass of this energy is subtracted from the overall mass of the original particles. The energy released when the nucleus is produced is represented by the mass defect, which is lacking in the subsequent nucleus.
Mass defect (Md) can be calculated as the difference between observed atomic mass (mo) and that expected from the combined masses of its protons (mp, each proton having a mass of 1.00728 amu) and neutrons (mn, 1.00867 amu):
[latex]M_d=(m_n+m_p)-m_o[/latex]
4.8.7 Mass–Energy Balance
The relationship between mass (m) and energy (E) is expressed in the following equation:
E=mc2(1)
Where
● cc is the speed of light (2.998×108m/s2.998×108m/s), and
The units for EE and mm are joules and kilograms, respectively.
This relationship was initially derived by Albert Einstein in 1905 as part of his special theory of relativity: a particle's mass is directly proportional to its energy. According to Equation 11, every mass has a corresponding energy, and any reaction involving a change in energy must also entail a change in mass. This means that all exothermic reactions should result in a mass loss, whereas all endothermic reactions should result in a mass increase. How can this be true, given the rule of conservation of mass? The answer to this seeming contradiction is that chemical processes do result in mass changes, but these changes are too small to be measured. All particles, as you may recall, have wavelike behaviour, but the wavelength is inversely related to the particle's mass (actually, to its momentum, the product of its mass and velocity). As a result, wavelike behaviour can only be detected in particles with extremely minuscule masses, such as electrons. The chemical equation for graphite burning to produce carbon dioxide, for example, is as follows:
C(graphite)+12O2(g)→CO2(g) ΔH∘=−393.5 kJ/mol
Combustion reactions are normally carried out under constant pressure, and the heat released or absorbed is equal to H under these conditions. The heat released or absorbed when a reaction is carried out at constant volume is equal to E. However, for the vast majority of chemical processes, E h. We can rewrite Einstein's equation as follows:
ΔE=(Δm)c2(3)
We can rearrange the equation to obtain the following relationship between the change in mass and the change in energy:
Δm=ΔEc2(4)
Because 1 J = 1 (kg•m2)/s2, the change in mass is as follows:
Δm=−393.5 kJ/mol(2.998×108 m/s)2=−3.935×105(kg⋅m2)/(s2⋅mol)(2.998×108 m/s)2=−4.38×10−12 kg/mol(5)
This corresponds to a mass change of around 3.6 1010 g/g carbon consumed, or about 100 millionths of an electron's mass per atom of carbon. In practise, the mass change is far too small to be measured experimentally and is therefore insignificant.
In comparison, a typical nuclear process involving an electron (a particle), such as the radioactive decay of 14C to 14N, results in a far bigger change in mass:
14C→14N+0−1β(6)
We can easily compute the change in mass using the empirically observed masses of subatomic particles and common isotopes listed in Table 20.1. A neutral 14C atom is converted to a positively charged 14N ion (with six, not seven, electrons) and a negatively charged particle (an electron) in this reaction, and the mass of the products is the same as that of a neutral 14N atom. The difference between the mass of a neutral 14N atom (14.003074 amu) and the mass of a 14C atom (14.003242 amu) is the entire change in mass during the reaction:
Δm=massproducts−massreactants=14.003074 amu−14.003242 amu=−0.000168 amu()
The difference in mass, which has been released as energy, corresponds to almost one-third of an electron. The change in mass for the decay of 1 mol of 14C is −0.000168 g = −1.68 × 10−4 g = −1.68 × 10−7 kg. Although a mass change of this magnitude may seem small, it is about 1000 times larger than the mass change for the combustion of graphite. The energy change is as follows:
ΔE=(Δm)c2=(−1.68×10−7 kg)(2.998×108 m/s)2=−1.51×1010(kg⋅m2)/s2=−1.51×1010 J=−1.51×107 kJ(9)(10)(9)ΔE=(Δm)c2=(−1.68×10−7 kg)(2.998×108 m/s)2(10)=−1.51×1010(kg⋅m2)/s2=−1.51×1010 J=−1.51×107 kJ
Even though 14C decay is a relatively low-energy nuclear reaction, the energy released in this nuclear reaction is more than 100,000 times larger than that generated in a normal chemical reaction.
Nuclear reactions are frequently represented in kiloelectronvolts (1 keV = 103 eV), mega electron volts (1 MeV = 106 eV), and even giga electron volts (1 GeV = 109 eV) per atom or particle since the energy changes are so significant. The change in energy that occurs as a result of a nuclear reaction can be computed using the formula 1 amu = 931 MeV. The energy released by one 14C atom decaying is therefore
(−1.68×10−4amu)(931MeVamu)=−0.156MeV=−156keV
Key takeaway:
● Nuclear energy is derived from the minor mass changes in nuclei that occur as a result of radioactive processes. Large nuclei break apart and release energy in fission; tiny nuclei unite and release energy in fusion.
● In 1932, nuclear fusion was shown in a laboratory for the first time.
● Since 1955, nuclear fusion has been a few decades away from commercialization.
● Nuclear fusion is the uniting (or fusion) of two bigger atoms, which releases a tremendous quantity of energy.
● Hydrogen is the fuel for nuclear fusion reactors, and Helium is the only by-product.
● Nuclear fission produced a million times the amount of energy produced by coal. Nuclear fusion generates 3-4 times the amount of energy as fission.
4.9.1 Generation of energy
E=mc2
In this equation, E denotes energy, mm denotes mass, and cc denotes the speed of light (31083108 metres per second), which is the constant that connects the two. Because mass is a measure of matter quantity, the importance of this equation is that matter can be turned into energy and vice versa. Let's compare this equation for converting matter and energy to some other similar conversion equations:
Inches = feet×12inches = feet×12
Or
Cents = dollars×100cents = dollars×100
When we convert matter into energy, we consider how much mass the matter has, just as any conversion formula allows you to compute the conversion of one item into another. In this situation, the conversion factor is neither 12 or 100, as in our previous instances, but another constant quantity: the speed of light squared. It's worth noting that this conversion doesn't require matter to travel at the speed of light (or the speed of light squared). The c2c2 factor is just the number that Einstein demonstrated must be used to connect mass and energy.
It's worth noting that this formula doesn't tell us how to convert mass to energy, much like the cents formula doesn't tell us where to swap coins for a dollar note. The formulas simply tell us what the corresponding numbers are if the conversion is successful. No one had any notion how to turn mass into energy in any practical sense when Einstein initially developed his formula in 1905. Einstein himself tried to dispel the notion that large-scale atomic mass to energy conversion would be possible in the near future. We regularly turn mass into energy in power plants, nuclear weapons, and high-energy physics experiments in particle accelerators nowadays as a result of advances in nuclear physics.
Because the speed of light squared (c2c2) is such a huge number, even a small amount of mass is converted into a big amount of energy. For example, converting 1 gramme of matter (about 1/28 ounce, or about 1 paperclip) to energy equivalent to burning 15,000 barrels of oil would yield the same amount of energy.
Scientists rapidly understood that the Sun's heat and light come from the conversion of mass into energy. The amount of energy radiated by the Sun could be produced by the complete conversion of nearly 4 million tonnes of matter into energy inside the Sun every second, according to Einstein's E=mc2E=mc2 equation. When compared to terrestrial objects, destroying 4 million tonnes every second may seem like a lot, but keep in mind that the Sun is a massive storehouse of matter. We will see that the Sun has more than enough mass to annihilate such massive amounts of matter while still blazing at its current rate for billions of years.
However, understanding all of this still leaves us with the question of how mass can be transformed into energy. To fully comprehend the process that occurs in the Sun, we must go further into the atom's structure.
4.9.2 Theory of relativity
Albert Einstein's two connected theories of special and general relativity are commonly referred to as the theory of relativity. In the absence of gravity, special relativity applies to all physical events. The law of gravitation and its relationship to other natural forces are explained by general relativity. It includes astronomy in the cosmological and astrophysical realms.
During the twentieth century, the idea revolutionised theoretical physics and astronomy, displacing a 200-year-old theory of mechanics developed principally by Isaac Newton. Spacetime as a single entity of space and time, simultaneity relativity, kinematic and gravitational time dilation, and length contraction were all introduced. Relativity advanced the understanding of elementary particles and their fundamental interactions, as well as ushering in the nuclear age, in the subject of physics. Cosmology and astrophysics predicted remarkable astronomical phenomena such as neutron stars, black holes, and gravitational waves based on Einstein's theory of relativity.
Relativity is a falsifiable theory in the sense that it offers predictions that can be tested in the lab. The principle of relativity, the constancy of the speed of light, and time dilation are all examples of special relativity. Since Einstein's article in 1905, the predictions of special relativity have been validated in various tests, but three experiments done between 1881 and 1938 were crucial to its validation. The Michelson–Morley experiment, the Kennedy–Thorndike experiment, and the Ives–Stilwell experiment are the three experiments in question. The Lorentz transformations were first deduced from first principles by Einstein in 1905, but these three experiments allow them to be induced from experimental evidence
Light is described as a wave that moves at a characteristic velocity according to Maxwell's equations, which are the foundation of classical electromagnetism. The present perspective is that light does not require a medium of transmission, but Maxwell and his contemporaries believed that light waves were propagated through a medium, similar to how sound travels through air and ripples travel across a pond's surface. The luminiferous aether, which is at rest in relation to the "fixed stars" and through which the Earth moves, was named after it. The measurement of first-order (v/c) effects was ruled out by Fresnel's partial ether dragging hypothesis, and though observations of second-order (v2/c2) effects were theoretically possible, Maxwell believed they were too small to be detected with then-current technology.
The Michelson–Morley experiment was set up to detect second-order effects of the "aether wind," or the movement of the aether relative to the earth. In order to accomplish this, Michelson created the Michelson interferometer. The apparatus was more than accurate enough to detect the expected effects, yet the first experiment in 1881 and the second experiment in 1887 yielded null results. Despite the sadness of not being able to identify an aether wind, the results were accepted by the scientific community. In order to save the aether paradigm, FitzGerald and Lorentz each devised an ad hoc hypothesis in which the length of material bodies varies as they move through the aether. FitzGerald–Lorentz contraction was born out of this, and their hypothesis had no theoretical foundation. The null result of the Michelson–Morley experiment indicates that the round-trip travel time for light is isotropic (independent of direction), yet this is insufficient to dismiss the aether hypothesis or support special relativity predictions.
While the Michelson–Morley experiment demonstrated that light has an isotropic velocity, it did not reveal how the magnitude of the velocity varied (if at all) in different inertial frames. The Kennedy–Thorndike experiment, initially carried out in 1932 by Roy Kennedy and Edward Thorndike, was supposed to do just that. They found no effect, concluding that "there is no influence... Until the solar system's velocity in space is little more than around half that of the earth in its orbit." That option was believed to be too fortuitous to be an acceptable explanation, thus they concluded that the round-trip duration for light is the same in all inertial reference frames based on the null result of their experiment.
Herbert Ives and G.R. Stilwell conducted the Ives–Stilwell experiment in 1938, and with improved accuracy in 1941. It was built to test Einstein's prediction of the transverse Doppler effect, which is the redshift of light from a moving source in a direction perpendicular to its velocity. The plan was to hunt for a Lorentz factor correction by comparing measured Doppler shifts to what was anticipated by classical theory. A similar adjustment was discovered, leading to the conclusion that special relativity alters the frequency of a moving atomic clock.
Those classic tests have been performed numerous times, each time with greater accuracy. Other investigations include relativistic energy and momentum increases at high speeds, experimental time dilation testing, and current Lorentz violations searches.
4.9.3 Special relativity
Special relativity is a theory of spacetime structure. It was first mentioned in Einstein's paper "On the Electrodynamics of Moving Bodies" published in 1905. (for the contributions of many other physicists see History of special relativity). Special relativity is founded on two contradicting postulates in classical mechanics:
1. For all observers in any inertial frame of reference relative to one another, the rules of physics are the same (principle of relativity).
2. Regardless of their relative mobility or the velocity of the light source, the speed of light in a vacuum is the same for all observers.
The resulting theory outperforms classical mechanics in terms of experimentation. For example, postulate 2 explains the Michelson–Morley experiment results. Furthermore, the theory has a number of unexpected and paradoxical ramifications. Here are a few examples:
If the observers are in relative motion, two events that are contemporaneous for one observer may not be simultaneous for another observer.
Time dilation refers to the fact that moving clocks tick more slowly than a "stationary" clock.
Objects are measured to be shortened in the direction that they are travelling with regard to the observer in length contraction.
The maximum speed is limited: in a vacuum, no physical item, communication, or field line can travel faster than the speed of light.
o Gravitational forces can only travel through space at the speed of light, not faster or instantly.
Equivalence of mass and energy: E = mc2, energy and mass are equivalent and interchangeable.
Some researchers use the term "relativistic mass."
[nine]
The Lorentz transformations replace the Galilean transformations of classical mechanics as the distinguishing feature of special relativity. (See Maxwell's electromagnetic equations.)
4.9.4 General relativity
Introduction to general relativity
General relativity is a gravitational theory developed by Albert Einstein between 1907 and 1915. The equivalence principle, which asserts that accelerated motion and being at rest in a gravitational field (for example, when standing on the surface of the Earth) are physically equal, was the foundation of general relativity. As a result, free fall is inertial motion: an item in free fall is falling because that is how objects move when no force is applied to them, rather than due to the force of gravity, as is the case in classical mechanics. This contradicts classical mechanics and special relativity, which state that inertially moving objects cannot accelerate with regard to one another, yet free-falling objects may. Einstein argued that spacetime is curved to overcome this problem. He developed the Einstein field equations in 1915, which relate the curvature of spacetime to the mass, energy, and momentum contained inside it.
Gravity time dilation: Clocks run slower in deeper gravitational wells, as a result of general relativity. [nine]
● Precession: In Newton's theory of gravity, orbits precess in an unexpected fashion. (This has been detected in Mercury's orbit as well as binary pulsars.)
● Light deflection occurs when light rays bend due to a gravitational field.
● Rotating masses "pull" the spacetime around them, which is known as frame-dragging.
● The cosmos is expanding metrically, and the distant reaches of it are moving away from us faster than the speed of light.
● General relativity is a gravitational theory that uses the Einstein field equations as its defining feature. The field equations' solutions are metric tensors, which determine the topology of spacetime and how inertial objects move.
4.10.1 Fission
The splitting of a nucleus is known as nuclear fission (or fissured). Controlled fission is a fact, while controlled fusion remains a distant dream. As seen in Figure 1, hundreds of nuclear fission power plants around the world attest to the fact that controlled fission is feasible and, at least in the short term, cost-effective. Following TMI and Chernobyl (and now Fukushima Daiichi), nuclear power was mostly forgotten for decades. However, mounting concerns about global warming have reintroduced nuclear power as a viable energy option. By the end of 2009, 442 reactors were operational in 30 nations, supplying 15% of global electricity. Nuclear power generates almost 75% of France's electricity, whereas the United States has 104 operational reactors that generate 20% of the country's electricity. There are none in Australia or New Zealand. China is constructing nuclear power reactors at a monthly rate of one.

Fission, on the other hand, is the polar opposite of fusion in that it only produces energy when heavy nuclei are separated. Energy is released when the products of a nuclear reaction have a higher binding energy per nucleon (BE/A) than the parent nuclei, as explained in Fusion. Figure 2 demonstrates that BE/A is higher for medium-mass nuclei than for heavy nuclei, meaning that when a heavy nucleus is split, the products have less mass per nucleon, resulting in mass destruction and energy release. Even by nuclear standards, the amount of energy released per fission reaction can be substantial. Figure 2 demonstrates that BE/A for the heaviest nuclei (A about 240) is around 7.6 MeV/nucleon, while BE/A for nuclei with A around 120 is around 8.6 MeV/nucleon. When a heavy nucleus breaks in half, around 1 MeV per nucleon is emitted, or roughly 240 MeV per fission. This is approximately 10 times the energy of a fusion reaction and approximately 100 times the energy of the average, or decay.
EXAMPLE 1. CALCULATING ENERGY RELEASED BY FISSION
Calculate the energy released in the following spontaneous fission reaction:
238U → 95Sr + 140Xe + 3n
Given the atomic masses to be m(238U) = 238.050784 u, m(95Sr) = 94.919388 u, m(140Xe) = 139.921610 u, and m(n) =1.008665 u.
Strategy
As always, the energy released is equal to the mass destroyed times c2, so we must find the difference in mass between the parent 238U and the fission products.
Solution
The products have a total mass of
Mproducts=94.919388 u+139.921610 u+3(1.008665 u)=237.866993 u
The mass lost is the mass of 238U minus mproducts, or
Δm = 238.050784 u− 237.8669933 u = 0.183791 u,
So the energy released is
E=(Δm)c2=(0.183791 u)931.5 MeV/c2uc2=171.2 MeV
Discussion
In this case, a lot of significant issues occur. The energy released was 171 MeV, which is little less than the 240 MeV previously estimated. This is due to the fact that the fission reaction produces neutrons rather than splitting the nucleus into two equal halves. The results of fission of a given nuclide, such as 238U, are not necessarily the same. Fission is a statistical process that produces a wide variety of products with varying probability. The majority of fission creates neutrons, though the number varies from fission to fission. This is a crucial aspect of fission because neutrons can produce further fission, allowing self-sustaining chain reactions to occur.
Although spontaneous fission is possible, it is rarely the most common decay mechanism for a specific nuclide. 238U, for example, can spontaneously fission but decays primarily by emission. As seen in Figure 2, neutron-induced fission is critical. Because neutrons are chargeless, they can strike a nucleus and be absorbed once they sense the nuclear force. Because the huge number of nucleons operate like atoms in a drop, a liquid drop model with surface tension and oscillation modes is used to represent big nuclei. The neutron is drawn to the nucleus and deposits energy, causing it to deform into a liquid drop. The nucleus narrows in the centre when extended far enough. The number of nucleons in contact is reduced, as is the strength of the nuclear force that holds the nucleus together. Coulomb repulsion between the two ends then fissions the nucleus, which splits into two huge pieces and a few neutrons like a water drop. Fission induced by neutrons can be written as
n + AX → FF1 + FF2 + xn,
FF1 and FF2 are the two daughter nuclei, also known as fission fragments, and x is the amount of neutrons produced. The masses of the fission fragments are usually not the same. The majority of the released energy is absorbed by the fission fragments' kinetic energy, with the remaining being absorbed by the neutrons and excited states of the fragments. Because neutrons can cause fission, a self-sustaining chain reaction can occur if more than one neutron is produced on average, or if x>1 in n + AX FF1 + FF2 + xn. Figure 3 depicts this as well. n+23592U14256Ba+9136Kr+3nn+92235U56142Ba+3691Kr+3n is an example of a typical neutron-induced fission process.
It's worth noting that the overall charge in this equation stays the same (is conserved): 56 + 36 Equals 92 + 0 Furthermore, in terms of whole numbers, the mass is constant: 1 + 235 = 142 + 91 + 3. When we consider the masses out to 6 or 7 significant places, as in the prior example, this is not the case.
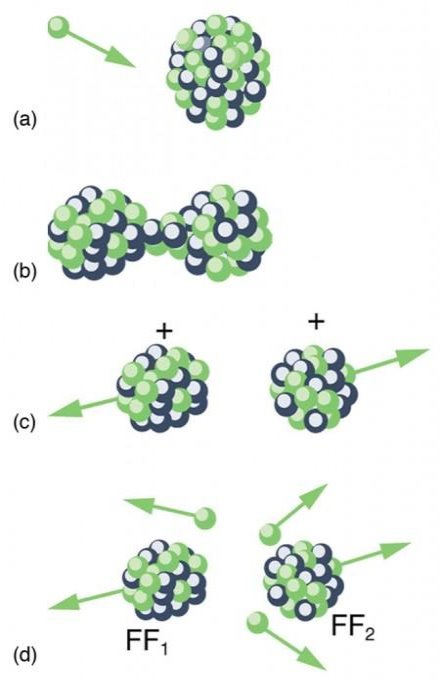
Figure shows neutron-induced fission. When a neutron is absorbed, energy is first transferred to this big nucleus. The nucleus deforms and begins to narrow in the middle, similar to a struck liquid drop. Because there are fewer nucleons in contact, the repulsive Coulomb force is able to split the nucleus in two, with some neutrons flying away as well.

Fission is not induced by every neutron produced by fission. Some neutrons escape fissionable matter, while others connect with a nucleus but do not cause it to fission. By having a big volume of fissionable material, we can increase the number of fissions caused by neutrons. The critical mass of a nuclide is the smallest amount required for self-sustaining fission. Nuclides like 239Pu produce more neutrons per fission than nuclides like 235U. Furthermore, some nuclides are more easily fissionable than others. 235U and 239Pu, in instance, are easier to fission than the far more plentiful 238U. Both of these parameters have an impact on critical mass, which is the least for 239Pu.
The nuclear force is more appealing for an even number of neutrons in a nucleus than for an odd number, which is why 235U and 239Pu are simpler to fission than 238U. Consider the following examples: 23592U14392235U143 has 143 neutrons, 23994P14594239P145 has 145 neutrons, and 23892U14692238U146 has 146 neutrons. When a neutron collides with a nucleus that has an odd number of neutrons, the nuclear force becomes more appealing since the extra neutron evens out the number. In the resultant nucleus, around 2-MeV more energy is deposited than if the number of neutrons were previously equal. This increased energy causes additional deformation, which increases the likelihood of fission. As a result, 235U and 239Pu are better fission fuels. Natural uranium contains only 0.72 percent of the isotope 235U, while 238U contains 99.27 percent and 239Pu does not. Australia possesses the world's greatest uranium resources, accounting for 28% of the total. Kazakhstan and Canada are the next two countries on the list. Only 3% of worldwide reserves are held by the United States.
The majority of fission reactors use 235U, which is purified from 238U at a cost. This is referred to as enrichment. The most frequent separation method is uranium hexafluoride (UF6) gaseous diffusion across membranes. Because 235U has a lower mass than 238U, its UF6 molecules have a greater average velocity and diffuse quicker at the same temperature. Another intriguing feature of 235U is that it absorbs very slow moving neutrons (with energies a fraction of an eV), whereas fission reactions create fast neutrons with energies in the order of a MeV. To build a self-sustaining fission reactor with 235U, the neutrons must be slowed (“thermalized”). Because neutrons clash with protons in water molecules and waste energy, water is particularly effective. Figure 4 depicts a schematic of a pressurised water reactor architecture.

Figure: A pressurised water reactor is carefully built to regulate the fission of massive amounts of 235U while creating steam using the heat produced in the fission reaction. Control rods regulate neutron flux to achieve, but not exceed, criticality. The chain reaction will stop if the reactor overheats and boils the water away, because water is required to thermalize the neutrons. In extreme conditions, this built-in safety function may be overpowered.
Neutron flux is adjusted using control rods containing nuclides that significantly absorb neutrons. Reactors with hundreds to thousands of critical masses can generate massive amounts of energy, and the chain reaction can rapidly become self-sustaining, a situation known as criticality. To avoid supercriticality, or an exponential increase in fissions, neutron flux should be carefully managed. Overheating, and even a meltdown or explosive disassembly, can be avoided by the use of control rods. The water used to thermalize neutrons, which is required to cause fission in 235U and attain criticality, acts as a negative feedback system for temperature rises. The absence of water terminates the chain reaction if the reactor overheats and boils the water to steam or if it is breached. The reactor's radioactive fission products, on the other hand, can still generate a lot of heat. Other safety elements, such as auxiliary cooling water and pumps, must be included in the case of a coolant loss accident.
One nuclide already mentioned is 239Pu, which has a 24,120-y half-life and does not exist in nature. Plutonium-239 is manufactured from 238U in reactors, and it provides an opportunity to utilize the other 99% of natural uranium as an energy source. The following reaction sequence, called breeding, produces 239Pu. Breeding begins with neutron capture by 238U :
238U + n → 239U + γ.
Uranium-239 then β– decays:
239U → 239Np + β− + ve(t1/2 = 23 min).
Neptunium-239 also β– decays:
239Np → 239Pu + β− + ve(t1/2 = 2.4 d).
The pace at which Plutonium-239 accumulates in reactor fuel is determined by the probability of neutron capture by 238U. (all reactor fuel contains more 238U than 235U). Breeder reactors are reactors that are specially designed to produce plutonium. They appear to be fundamentally riskier than traditional reactors, although it is unclear whether their risks can be made economically acceptable. The four reactors at Chernobyl, including the one that exploded, were designed to provide energy while also breeding plutonium. The design of these reactors differed greatly from that of the pressurised water reactor shown above. As a reactor fuel, Plutonium-239 has an advantage over 235U: it produces more neutrons per fission on average, and it is easier to fission with a thermal neutron. It also differs chemically from uranium, making it easier to isolate from uranium ore. This means that 239Pu has a very low critical mass, which is advantageous for nuclear weapons.
4.10.2 Fission fragment
Chronicle of the life of a fission fragment.
The most common type of nuclear fission is the splitting of a nucleus into two pieces. When first produced, the two fragments are exceedingly radioactive and unstable. Each of them will go through a sequence of transformations in order to achieve stability. The time it takes for things to return to normal can vary greatly. The voyage is similar to that of a train that must stop at various stations before arriving at its destination. The nucleus at the bottom of the stability valley is the terminal.
Consider the fission of a uranium-235 nucleus into two pieces with 140 and 94 nucleons, respectively.
Neutron + 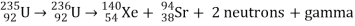
Production of two fragments with 140 and 94 nucleons.
The heaviest fragment is a radioactive xenon isotope with four more neutrons (86) than the closest stable isotope. This heavy fragment will evolve by emitting four beta electrons in a row, keeping its 140 nucleons, until it reaches a stable cerium-140 nucleus at the bottom of the stability. The cerium-140 fragment has four fewer neutrons (82) and four more protons (58) than the xenon-140 fragment.
Returning to the train analogy, the time it takes for xenon-140 to decay into cesium-140 is the time it takes for xenon-140 to decay into cesium-140: the half-life of this initial stage is 13.6 seconds, which is incredibly short. The second stage of the cesium-140 decay, with a half-life of 63 seconds, is also exceedingly brief. The third stage, baryum-140 degradation, lasts substantially longer, with a half-life of 12.7 days. Finally, the lanthanum-140 decay gives 1.67 days as the period of the last stage. The journey to the cerium-140 terminal will take roughly fifteen days in total, on the order of the longest half-life of 12.7 days.
The fragment of 140 nucleons has evolved through time.
Cerium-140 is the lightest and most stable isotope in the family of 140 nucleons (shown in blue). The mass (internal) energy difference of the nuclei in this family compared to the mass of the stable cerium-140 nucleus is depicted in the diagram, with the nuclei organised according to their increasing number of protons. On the left is a raw fission fragment, a xenon-140 nucleus. It sheds its surplus mass energy by jumping four staircases to the stable cerium-140. Each jump is accompanied by the emission of a beta electron.
IN2P3 is a three-letter acronym that stands for "
To obtain a stable zirconium-94 nucleus, the lighter strontium-94 fragment goes through a similar development.
This is a generic scenario. Raw fission fragments far from stability achieve stability by one of two mechanisms provided by Nature: neutron expulsion or beta decay. Neutron expulsion is uncommon due to its high energy cost. It may only occur early in the transformation cascade, and then become energetically banned at a later stage. Expelled neutrons are produced after the fission process and the production of primary neutrons. These delayed neutrons serve a crucial role in the management of the chain reaction in reactors, despite their small numbers.
The beta decay is mostly responsible for the return to stability. The longest half-life in the decay cascade determines the duration of this return. Transformations into stable fission products are quick for xenon-140 and strontium-94, for example. This isn't always the case, however. It can take a long time to reach the bottom of the stability valley endpoint. The final stage of cesium-137 degrading into barium-137 will take 30 years for a piece of 137 nucleons. It will take 100,000 years for a 99 nucleon fragment of technetium-99 to decay into stable ruthenium-99.
Nuclear fuel typically lasts 3 to 4 years in reactor cores. Most fission pieces, including the xenon-140 fragment, would have had enough time to shed their radioactivity over this extended stay. Others, on the other hand, are unable to achieve steadiness. These fission products, which are sluggish to reach the final stage of stability, are responsible for much of the radioactivity in reactor spent nuclear fuel.
4.11.1 Slow neutrons.
The energy of neutrons produced by fission events diminishes on the order of a few electron volts or fractions of an electron volt after a series of encounters with different nuclei. Neutrons with energy in this range are said to as 'slow,' whereas neutrons with energy that match those of the surrounding atoms are referred to as 'thermal.'
These slow neutrons enable nuclear reactors to run on natural uranium or uranium that has been lightly enriched in fissile isotope 235 as fuel. The most prevalent pressurised (PWR) and boiling water (BWR) reactors would not function without them. As a result, collisions within a medium termed a moderator must slow down the neutrons released by nuclear fission. Reactors using natural uranium fuel, which contains only 0.7% fissile uranium 235, require efficient moderators that absorb extremely few neutrons: heavy water and pure graphite are examples of such moderators.
4.11.2 Slow neutrons favour fission
Slow neutrons are neutrons that have slowed down after colliding with atomic nuclei in nuclear reactors. The kinetic energy of these particles is on the order of a few electron volts or a fraction of an electron volt(eV). The neutron is said to be thermal when its energy is equivalent to the kinetic energies of the atoms in the medium through which it travels.
It's possible that the word "slow" is a misnomer. A thermal neutron with a charge of 0,025 electron volts travels at a speed of 2 km/sec, quicker than the fastest airliner. However, compared to the speed of light, 2 km/sec is a snail's pace. The kinetic energy of the neutron is more important than its speed.

Fig. Uranium-235 fission probability
The chance of fission, also known as the fission cross-section by physicists, varies dramatically with neutron intensity. Barns are used to measure it. This fission probability is highest for a fissile nucleus like uranium-235 at kinetic energy of a few electron volts. Because the fraction of uranium-235 in most reactor fuels is only a few percent, it is necessary to compensate for this low proportion by increasing the fission probability of Uranium-235, and hence operate with a sluggish neutron flow.
IN2P3 is a three-letter acronym that stands for "
Slow neutrons allow civilian nuclear reactors to run on natural uranium or uranium that has been slightly enriched in the fissile isotope 235. The common pressurised (PWR) and boiling water (BWR) reactors could not function without slow neutrons. To accomplish this, the neutrons released by nuclear fission must collide with the atoms of a medium known as the moderator.
Only 0.7% of natural uranium includes fissile uranium 235. The use of natural uranium fuel in reactors necessitates the use of effective moderators that capture relatively few neutrons, such as heavy water or pure graphite.
When the fuel is enhanced by 3-4 percent, the moderator might be ordinary water that has been boiled or exposed to high pressure (An efficient coolant, water is also a convenient medium to evacuate the heat from the core of the reactor).
Slow neutrons enable civilian nuclear reactors to use nuclear fuel, such as natural uranium or uranium with a fissile isotope 235 enrichment. The chance of a thermal neutron of 0.025 eV fissioning a uranium-235 nucleus is 584 barns. This is a huge number when compared to the probability of a nucleus of the majority uranium-238 isitope being captured without fission, which is roughly 2 barns.
Slow neutrons do not contribute a considerable surplus of energy to the nucleus when collected. Only a few extremely fragile nuclei, named fissile for this reason, may fission: uranium-235 (the only one found in Natural), plutonium-239, and uranium-233.
Slow neutrons have the highest chance of being captured by a fissile nucleus and then triggering fission (called cross-section). The low proportion of the fuel is compensated for by the huge fission cross-section. It is thus possible to generate a chain reaction with natural or somewhat uranium fuel using a suitable moderator (0.7 percent to 5 percent isotope 235).
Everything happens as if slow neutrons notice a small fraction of uranium-235 or plutonium-239 nuclei that are significantly larger than the majority of uranium-238 nuclei that have a considerably lower chance of "sterile" capture without fission. Using a good moderator, it is then possible to get a chain reaction with the poor or somewhat enriched conditions mentioned earlier.
4.11.3 Nuclear reactor
A nuclear reactor, also known as an atomic pile, is a device that is used to start and control nuclear chain reactions or nuclear fusion processes. Nuclear reactors are used to generate electricity in nuclear power stations and for nuclear marine propulsion. Nuclear fission heat is transferred to a working fluid (water or gas), which then drives steam turbines. These either turn the shafts of electricity generators or drive the propellers of a ship. In principle, nuclear-generated steam can be used for industrial process heat or district heating. Some reactors create isotopes for medicinal and industrial purposes, while others produce weapons-grade plutonium. According to the International Atomic Energy Agency (IAEA), there are 454 nuclear power reactors and 226 nuclear research reactors in operation around the world as of early 2019.
Nuclear reactors transform the energy released by controlled nuclear fission into thermal energy for further conversion to mechanical or electrical forms, similar to how conventional thermal power plants generate electricity by harnessing the thermal energy created by burning fossil fuels.
4.11.4 Fission
Nuclear fission can occur when a big fissile atomic nucleus, such as uranium-235 or plutonium-239, receives a neutron. The heavy nucleus (the fission products) divides into two or more lighter nuclei, releasing kinetic energy, gamma radiation, and free neutrons. Other fissile atoms may absorb some of these neutrons, triggering other fission events, which release additional neutrons, and so on. A nuclear chain reaction is what this is called.
Control rods carrying neutron poisons and neutron moderators can alter the proportion of neutrons that go on to generate additional fission in such a nuclear chain reaction. If monitoring or equipment identifies harmful circumstances, most nuclear reactors feature automated and manual devices to shut off the fission reaction.
4.11.5 Heat generation
The reactor core generates heat in several ways: the kinetic energy of fission products is converted to thermal energy when these nuclei collide with nearby atoms; the reactor absorbs some of the gamma rays produced during fission and converts their energy into heat; and the reactor absorbs some of the gamma rays produced during fission and converts their energy into heat.
The radioactive decay of fission products and materials that have been activated by neutron absorption produces heat. Even after the reactor is turned off, the decay heat source will continue to exist.
A kilogram of uranium-235 (U-235) transformed through nuclear processes releases around three million times the energy of a kilograms of coal burned conventionally (7.2 1013 joules per kilograms of uranium-235 versus 2.4 107 joules per kilograms of coal).
4.11.6 Cooling
A nuclear reactor coolant — typically water, but occasionally a gas, a liquid metal (such as liquid sodium or lead), or molten salt — is pumped past the reactor core to absorb the heat it generates. The heat is transferred away from the reactor and used to produce steam. Like the pressurized water reactor, most reactor systems have a cooling system that is physically separated from the water that will be boiled to produce pressure steam for the turbines. However, in some reactors, such as the boiling water reactor, the water for the steam turbines is boiled directly by the reactor core.
4.11.7 Reactivity control
The quantity of neutrons capable of inducing further fission events can be controlled to influence the rate of fission reactions within a reactor core. To alter the reactor's power output, nuclear reactors commonly use a variety of neutron control technologies. Some of these approaches are based on the physics of radioactive decay and are simply accounted for during reactor operation, while others are built-in mechanisms with a specific goal in mind.
The control rods are the quickest way to modify the levels of fission-inducing neutrons in a reactor. Neutron poisons are used to make control rods, which absorb neutrons. When a control rod is put further into the reactor, it absorbs more neutrons than the substance it replaces, which is usually the moderator. As a result of this activity, there are fewer neutrons available for fission, lowering the reactor's power output. Extraction of the control rod, on the other hand, will result in an increase in the rate of fission events and a boost in power.
Neutron populations in a reactor are also affected by the physics of radioactive decay. Delay neutron emission by a number of neutron-rich fission isotopes is one of these processes. The delayed neutrons make up roughly 0.65% of all neutrons produced in fission, with the rest (dubbed "quick neutrons") released immediately after fission. Because the half-lives for the fission products that create delayed neutrons varies from milliseconds to several minutes, it takes a long time to determine when a reactor hits the critical point. Keeping the reactor in the chain reactivity zone, where delayed neutrons are required to achieve a critical mass state, allows mechanical devices or human operators to control a chain reaction in "real time"; otherwise, the time between criticality and nuclear meltdown as a result of an exponential power surge from a normal nuclear chain reaction would be too short to allow for a chain reaction to be controlled in "real time." The prompt critical point is the final step, where delayed neutrons are no longer required to maintain criticality. The bare criticality is known as zero dollars, the immediate critical point is one dollar, and other stages in the process are interpolated in cents, according to a scale for representing criticality in numerical form.
The coolant in certain reactors also serves as a neutron moderator. By causing the fast neutrons created by fission to lose energy and become thermal neutrons, a moderator increases the reactor's power. Thermal neutrons are more likely to produce fission than fast neutrons. Temperature fluctuations can impact the density of the coolant/moderator and thus modify power output if the coolant is a moderator. A cooler at a higher temperature would be less dense and hence less useful as a moderator.
In other reactors, the coolant, like the control rods, functions as a poison by absorbing neutrons. The power output of these reactors can be boosted by boiling the coolant, making it a less dense poison. In most nuclear reactors, automatic and manual procedures are in place to scram the reactor in the event of an emergency shutdown. If unsafe conditions are detected or anticipated, these systems inject massive volumes of poison (typically boron in the form of boric acid) into the reactor to stop the fission reaction.
The iodine pit, also known as xenon poisoning, is a process that affects most types of reactors. In the fission process, the common fission product Xenon-135 acts as a neutron poison, absorbing neutrons and so tending to shut down the reactor. The accumulation of xenon-135 can be managed by keeping power levels high enough to eliminate it as quickly as it is created by neutron absorption. Fission also produces iodine-135, which decays to fresh xenon-135, with a half-life of 6.57 hours. When the reactor is turned down, iodine-135 continues to decay to xenon-135, making restarting the reactor more difficult for a day or two until the xenon-135 decays to cesium-135, which has a half-life of 9.2 hours and is not nearly as deadly as xenon-135. The "iodine pit" is the name for this transitory state. The reactor can be restarted if it has enough excess reactivity capacity. The reactor experiences a "xenon burn off (power) transient" within a few hours when the additional xenon-135 is transmuted to xenon-136, which is substantially less of a neutron poison. To replace the neutron absorption of the lost xenon-135, more control rods must be inserted. A major stage in the Chernobyl tragedy was the failure to correctly follow such a protocol.
Nuclear reactors used in nuclear marine propulsion (particularly nuclear submarines) are frequently unable to operate at full power around the clock, as is the case with land-based power reactors, and must also have a lengthy core life without refueling. As a result, several designs use highly enriched uranium in the fuel rods but include burnable neutron poison. This enables the reactor to be built with an excess of fissionable material that is made relatively safe early in the fuel burn cycle by the presence of neutron-absorbing material, which is later replaced by normally produced long-lived neutron poisons (far longer-lived than xenon-135) that gradually accumulate over the fuel load's operating life.
Key takeaway:
● A cooling system that creates steam removes the heat produced by a nuclear reaction from the reactor core. The steam powers a turbine, which in turn powers a generator, which generates electricity. Fission can occur when a fissile atomic nucleus absorbs a neutron.
● Nuclear reactors work on the principle of nuclear fission, which is the splitting of a heavy atomic nucleus into two smaller fragments.
● This process releases a significant quantity of energy, which is used to fuel nuclear power plants.
4.12.1 Fusion reactions in stars
Stars' principal energy source and the process for the nucleosynthesis of light elements are fusion processes. Hans Bethe discovered in the late 1930s that the fusion of hydrogen nuclei to generate deuterium is exoergic (i.e., there is a net release of energy) and leads to the synthesis of helium when combined with subsequent nuclear processes. Helium production is the primary source of energy emitted by ordinary stars like the Sun, whose burning-core plasma has a temperature of less than 15,000,000 K. However, because the gas that forms a star often contains certain heavier elements, like as carbon (C) and nitrogen (N), nuclear interactions between protons and these nuclei are vital to consider. The proton-proton cycle is the reaction chain between protons that eventually leads to helium. When protons also cause carbon and nitrogen to burn, the CN cycle must be taken into account; and when oxygen (O) is added, the CNO bi-cycle must also be taken into account. (For further information, see the carbon cycle.)
In a hydrogen-only star, the proton-proton nuclear fusion cycle begins with the reaction H + H D + + + v; Q = 1.44 MeV, where the Q-value assumes positron annihilation by an electron. Although deuterium can combine with other deuterium nuclei, the D/H ratio is kept low, typically 1018, due to the abundance of hydrogen. As a result, the following phase is H + D 3He +; Q = 5.49 MeV, where shows that some of the energy output is carried away by gamma rays. The last stage in the chain, the burning of the helium-3 isotope, produces ordinary helium and hydrogen: 3He + 3He 4He + 2(H); Q = 12.86 MeV.
Because its reaction rate with hydrogen is minimal, helium-3 burns mostly by reactions with itself at equilibrium, while burning with deuterium is minimal due to the low deuterium concentration. If the temperature is greater than roughly 10,000,000 K, reactions with helium-3 can result in the creation of still-heavier elements such as beryllium-7, beryllium-8, lithium-7, and boron-8.
The stages of star evolution are the outcome of long-term compositional changes. A star's size, on the other hand, is determined by a balance between the pressure produced by hot plasma and the gravitational pull exerted by the mass of the star. The burning core's energy is carried to the star's surface, where it is radiated at a useful temperature. The effective temperature of the Sun's surface is around 6,000 K, and the Sun emits substantial amounts of visible and infrared radiation.
4.12.2 Inertial confinement fusion (ICF)
By creating pressures as high as 1017 pascals (1012 atmospheres) for periods as short as a nanosecond (109 second), a fuel mass is compressed fast to densities 1,000 to 10,000 times greater than normal. The implosion speed nears 3 105 metres per second near the end of this time span. The energy in converging shock waves is sufficient to heat the very centre of the fuel to temperatures high enough to initiate fusion reactions at maximum compression of the fuel, which is now in a cold plasma state (greater than an equivalent energy of about 4,400 eV). Before this hot plasma ball disassembles, energy will be created through fusion reactions if the bulk of this highly compressed fuel material is large enough. Much more energy can be released under ideal conditions than is required to compress and shock heat the fuel to thermonuclear burning temperatures.
The physical processes in ICF, such as collapse, compression heating, and the initiation of nuclear fusion, are similar to those in thermonuclear weapons and star formation. The scenario in star formation differs in one respect: a collapsed star begins to expand again due to heat from exoergic nuclear fusion processes, whereas a collapsed star is caused by gravity. The gravitational pull associated with the massive mass of the star eventually stops the expansion, bringing the size and temperature of the star to a state of equilibrium. The fuel in a thermonuclear bomb or ICF, on the other hand, totally disassembles. However, in the ideal ICF situation, this does not happen until around 30% of the fusion fuel has consumed.
The technology and methods for high-energy, short-time-pulse drivers, which are required to collapse the fusion fuel, have advanced significantly over the decades. A high-power laser is the most frequent driver, though particle accelerators capable of creating high-energy ion beams are also utilised. Experiments are presently being conducted with lasers that produce more than 100,000 joules in pulses of around one nanosecond, and the power available in brief bursts reaches 1014 watts.
Two lasers are operational, each capable of delivering up to 5,000,000 joules in equally brief bursts and generating a power output on the fusion targets of more than 5 1014 watts. The Laser Mega Joule in Bordeaux, France, is one such facility. The National Ignition Facility, located at the Lawrence Livermore National Laboratory in Livermore, California, is the other.
4.12.3 Muon-catalyzed fusion
The requirement to contain very high-temperature plasmas in classic nuclear fusion systems has led some researchers to look into alternatives that would allow fusion reactants to approach each other more closely at much lower temperatures. One approach includes replacing the electrons that normally surround the nucleus of a fuel atom with muons (). Muons are negatively charged subatomic particles that are comparable to electrons except that their mass is about 200 times that of an electron and that they are unstable, with a half-life of roughly 2.2 106 seconds. In reality, when muons were injected into liquid and gas mixes of deuterium and tritium at cryogenic temperatures, fusion was detected.
The technique of achieving fusion reactions by forcing a deuteron (deuterium nucleus, D+), a triton (tritium nucleus, T+), and a muon to produce a muonic molecule is known as muon-catalyzed fusion. The rate of fusion processes after the formation of a muonic molecule is around 3 108 seconds. A muonic molecule's production, on the other hand, is complicated, involving a succession of atomic, molecular, and nuclear processes.
When a muon enters a mixture of deuterium and tritium, it is initially grabbed by one of the two hydrogen isotopes present, generating either atomic D+- or T+-, and the atom is now in an excited state. Through a cascade collision process, the excited atom relaxes to its ground state, with the muon being transferred from a deuteron to a triton or vice versa. More importantly, the formation of a muonic molecule (D+—T+) is conceivable. Although a considerably uncommon reaction, once a muonic molecule forms, fusion occurs practically instantly, freeing the muon in the mixture for capture by a deuterium or tritium nucleus and allowing the process to continue. The muon functions as a trigger for fusion processes inside the mixture in this way. The ability to induce enough fusion reactions before the muon decays is essential for practical energy production.
The challenges of muon-catalyzed fusion are numerous, including producing muons (at an energy cost of around five billion electron volts per muon) and injecting them into the deuterium-tritium mixture instantly. Within the half-life of a muon, around 300 D-T fusion reactions must occur in order to produce more energy than is necessary to start the process.
4.12.4 Cold fusion and bubble fusion
There are two controversial fusion experiments worth mentioning. Martin Fleischmann of the University of Utah and Stanley Pons of the University of Southampton in England claimed in 1989 that they had successfully created fusion reactions at virtually room temperature. Electrolytic cells holding heavy water (deuterium oxide, D2O) and palladium rods that absorbed the deuterium from the heavy water comprised their system. Attempts to provide a theoretical explanation for the data, as well as worldwide efforts to replicate the purported cold fusion, were unsuccessful.
During acoustic cavitation experiments with chilled deuterated (bombarded with deuterium) acetone in 2002, Rusi Taleyar khan and colleagues at Purdue University in Lafayette, Indiana, claimed to have observed a statistically significant increase in nuclear emissions of products of fusion reactions (neutrons and tritium). Their setup was inspired by the well-known phenomena of sonoluminescence. A gas bubble is burst with high-pressure sound waves in sonoluminescence. Conditions of high density and temperature are obtained at the end of the implosion process, and for a short time following, resulting in light emission. The researchers claimed to have created densities and temperatures sufficient to cause fusion reactions just before the bubbles split up by starting with larger, millimetre-sized cavitations (bubbles) that had been deuterated in the acetone liquid. Most attempts to reproduce these outcomes, including cold fusion, have failed.
4.12.5 Stellar energy generation on the main sequence
We designate an object a star once fusion processes commence in the middle of a cloud of gas. A star's core fuses hydrogen into helium during the majority of its existence. During this phase, the star is either hot and luminous, if it is massive, or cool and dark, if it is a lightweight, on the HR diagram's main sequence.
Let's take a look at the nuclear reactions which provide energy during the hydrogen-burning phase of its life.
Nuclear Reactions on the main sequence
As long as stars are on the main sequence, they turn hydrogen nuclei into helium. The output helium has a smaller mass than the input hydrogens.
Mass of 1 proton p = 1.67358 x 10^(-27) kg
Mass of 4 protons 4p = 6.6943 x 10^(-27) kg
Mass of helium nucleus He = 6.6466 x 10^(-27) kg
--------------------------------------------------------------
Difference 4p - He = 0.0477 x 10^(-27) kg
The "missing" mass appears as energy, according to Einstein's famous equation E = mc^2. So, the net result of building one new helium atom is the release of
8 8
E = 0.0477 x 10^(-27) kg * (3 x 10 m/s) * (3 x 10 m/s)
= 4.3 x 10^(-12) Joules
It may be a small amount of energy per event, but at the core of a star, a LOT of reactions happen per second.
A simultaneous collision of four protons appears to be the most easy approach to create a helium nucleus:
Unfortunately, the chances of four protons travelling in the same direction and colliding at the same time are extremely slim. Furthermore, because each proton has a positive charge, even if four protons moved in the same direction, their mutual electric repulsion would prevent them from fusing.
So, how does hydrogen become helium? It turns out that there are two different reactions that can lead to the same outcome.
The p-
It occurs in low-mass stars like our Sun and only involves hydrogen and helium isotopes.
The CNO cycle
Requires heavier elements (Carbon, Oxygen, Nitrogen) to act as catalyts; it dominates energy production in high-mass stars.
The p-p chain
The p-p chain is the main energy source in the Sun and stars which are less massive. It involves three steps:
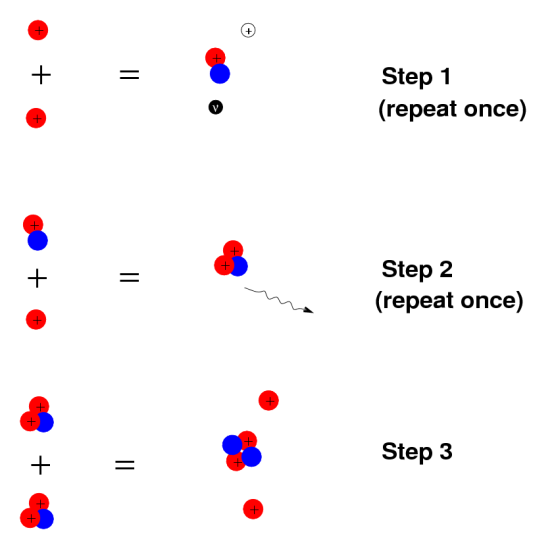
Only the first stage necessitates the fusion of bare protons. Neutrons (shown as blue circles) are used in all subsequent phases to help overcome the electric repulsion. It's worth noting that the first and second processes must be repeated twice to generate the two helium-3 nuclei that will fuse in the final phase. This fundamental technique has various variations, but the one illustrated is the most frequent.
The p-p chain can only work if the temperatures in a star's core are high enough to force particles to collide violently. Around 10 million Kelvin is the key value. The quantity of energy generated by the chain is proportional to its temperature: higher temperatures result in more violent collisions, which lead to fusion more frequently. The rate of energy production is about.
Rate of energy production = (something) * T
The CNO cycle
The CNO cycle is the main energy source in stars more massive than the Sun. It involves many steps, and the assistance of "heavy" nuclei:
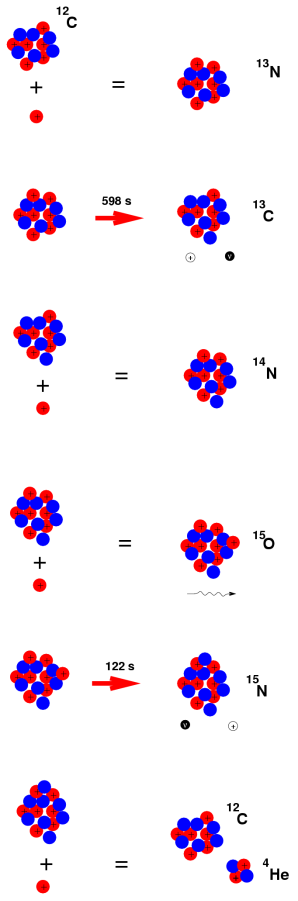
Only the main branches of the p-p chain are represented in the diagram above.
If the cloud from which a star forms contains only pure hydrogen, or hydrogen and helium, then the CNO cycle cannot take place: there won't be any Carbon, Nitrogen, or Oxygen atoms in the core. There were no "heavy" components in the initial generation of stars that formed after the Big Bang, so they couldn't have generated energy in this way.
The CNO cycle requires significantly greater temperatures than the p-p chain; below around 16 million Kelvin, it produces relatively little energy. The Sun's centre temperature, at 15 million Kelvin, is just below this essential number. Only stars with masses greater than our Sun may achieve such core temperatures.
The CNO cycle is extremely temperature sensitive once it begins to run. It can be written as the rate at which it creates energy.
20
Rate of energy production = (something) * T
Q: If the temperature at the center of a star
Rises by 10 percent, how much more energy
Is generated by the CNO cycle?
To sum it up, if you where a star falls on the HR diagram, then you know what sort of nuclear reactions are taking place deep within its interior:

4.12.6 A stellar thermostat
Both the p-p chain and the CNO cycle operate as stellar thermostats because they are so sensitive to temperature variations. Changes in the pace of energy generation can lead the gas layers above the core to expand outwards or contract inwards, depending on the rate of energy generation. However, the high temperatures required for fusion reactions are produced by the gravitational pressure of these overlying layers of gas. As a result, there is a delicate balance that tends to return to its original state.
Energy pushing OUT balances gravity pulling IN at Equilibrium Temp.
If the temperature in the centre of the building lowers,
o Energy production declines..
As a result, the amount of gas pushing outwards lowers...
As a result, gravity pulls the outer layers inwards.
It appears bleak... But as the outer layers press the core within, the situation improves.
o The centre temperature returns to its original level...
As a result, fusion rates rise...
As a result, more energy is created...
As a result, the gas pressure pushing outwards rises...
o resulting in the outer layers returning to their previous position
You can demonstrate that if the central temperature raises slightly for some reason, a similar set of activities will cause the core to expand slightly, causing the temperature to decrease back to its original amount.
In short, a stable equilibrium is achieved when the energy released by fusion events pushes outwards and the gravitational force pulls gas inside. A star will keep a nearly constant central temperature as long as it has hydrogen in its core to fuse, which means it will generate an approximately constant quantity of energy, which means it will shine with a nearly constant luminosity. During its long phase of hydrogen burning, its location on the HR diagram (based on luminosity and photosphere temperature) won't vary significantly.
4.12.7 Nuclear Fusion
Stars are largely comprised of hydrogen and helium, which are packed so densely in a star's core that the pressure is high enough to trigger nuclear fusion events. The nuclei of two atoms unite to form a new atom in a nuclear fusion reaction. Two hydrogen atoms fuse to form a helium atom most typically in the centre of a star. Although it takes a lot of energy to initiate a nuclear fusion process, once it is up and running, it produces vast amounts of energy (Figure below).

A thermonuclear bomb is a controlled fusion process that releases massive amounts of energy.
The energy released by fusion events in the centre of a star pushes outward to counteract gravity's inward pull. This energy travels outward through the star's layers until it reaches the star's outer surface. The star's outer layer burns brightly, emitting energy as electromagnetic radiation such as visible light, heat, ultraviolet light, and radio waves into space (Figure below).
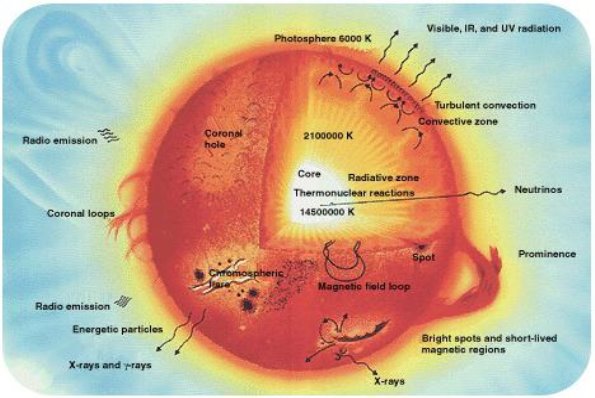
Fig. A diagram of a star like the Sun.
Subatomic particles are accelerated in particle accelerators until they have about the same amount of energy as the centre of a star (Figure below). New particles are formed when these particles meet head-on. The nuclear fusion that occurs in the centres of stars is simulated by this mechanism. The procedure also mimics the conditions that permitted the first helium atom to form from the collision of two hydrogen atoms in the universe's early minutes.
Key takeaway:
● The creation of helium is the principal source of energy emitted by typical stars, such as the Sun, where the burning-core plasma has a temperature of less than 15,000,000 K. Fusion processes are the principal energy source of stars and the mechanism for the nucleosynthesis of the light elements.
References:
1.Quantum Mechanics: Theory and Applications, A.K.Ghatakand S. Lokanathan,(Macmillan)-2004
2. Introduction to Quantum Theory, David Park (Dover Publications)-1974
3. Theory and Problems of Modern Physics, Schaum‘s outline,R.Gautreau and W.Savin- (Tata McGraw-Hill) 2nd Edition
4. Physics for scientists and engineer with Modern Physics-Jewell and Serway -(CENGAGE Learnings) 2010.
5. Modern Physics of Atoms and Molecules Bransden and Joachim (PearsonIndia)-2003
Unit - 4
Nuclear Physics- II
4.1.1 Radioactivity
Radioactivity is the property of certain forms of matter to spontaneously emit energy and subatomic particles. It's essentially a property of individual atomic nuclei.
An unstable nucleus will spontaneously dissolve, or decay, into a more stable structure, but only in a few precise ways, for as by generating particular particles or electromagnetic energy. Several naturally occurring elements, as well as artificially manufactured isotopes of the elements, have radioactive decay as a feature. The half-life of a radioactive element is the amount of time it takes for one-half of any given quantity of the isotope to decay. Some nuclei have half-lives of more than 1024 years, while others have half-lives of less than 1023 seconds (see below Rates of radioactive transitions). The daughter of the parent isotope, the outcome of radioactive decay, may be unstable, in which case it will decay as well. The procedure is repeated until a stable nuclide is created.
The nature of radioactive emissions
The alpha (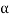 ) particle, beta (
) particle, beta (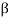 ) particle, gamma (
) particle, gamma (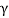 ) ray, and neutrino are the most prevalent types of spontaneous radioactive decay emissions. The nucleus of a helium-4 atom, with two positive charges 4/2He, is the alpha particle. Ions are charged atoms that have a positive charge. Two electrons outside the nucleus of a neutral helium atom balance these two charges. Negatively charged (beta minus, sign e) or positively charged (beta plus, symbol e+) beta particles exist. The beta minus [] particle is an electron that is produced in the nucleus during beta decay and has no relation to the atom's orbital electron cloud. The beta plus particle, commonly known as the positron, is the electron's antiparticle; two of these particles will mutually destroy each other when brought together. Electromagnetic radiations such as radio waves, light, and X-rays are examples of gamma rays. The neutrino and antineutrino, particles with no charge and very low mass, are also produced by beta radiation, and are denoted by v and, respectively.
) ray, and neutrino are the most prevalent types of spontaneous radioactive decay emissions. The nucleus of a helium-4 atom, with two positive charges 4/2He, is the alpha particle. Ions are charged atoms that have a positive charge. Two electrons outside the nucleus of a neutral helium atom balance these two charges. Negatively charged (beta minus, sign e) or positively charged (beta plus, symbol e+) beta particles exist. The beta minus [] particle is an electron that is produced in the nucleus during beta decay and has no relation to the atom's orbital electron cloud. The beta plus particle, commonly known as the positron, is the electron's antiparticle; two of these particles will mutually destroy each other when brought together. Electromagnetic radiations such as radio waves, light, and X-rays are examples of gamma rays. The neutrino and antineutrino, particles with no charge and very low mass, are also produced by beta radiation, and are denoted by v and, respectively.
Fission fragments, neutrons, or protons may be emitted in less common kinds of radioactivity. Fission fragments are complex nuclei with a charge Z and mass A that are usually one-third to two-thirds that of the parent nucleus. Neutrons and protons, of course, are the fundamental building components of complex nuclei, with approximately unit mass on the atomic scale and either zero or unit positive charge. The neutron can't stay in the free state for very long. It is quickly grabbed by nuclei in matter; otherwise, it decays to a proton, an electron, and an antineutrino with a half-life of 12.8 minutes in free space. The proton is the stable nucleus of ordinary hydrogen.
Types of radioactivity
Early research into natural radioactivity in uranium and thorium ores found two types of radioactivity: alpha and beta decay.
Alpha decay
An energetic helium ion (alpha particle) is released during alpha decay, leaving a daughter nucleus with an atomic number two lower than the parent and an atomic mass four lower than the parent. The decay of the abundant isotope of uranium, 238U, producing a thorium daughter plus an alpha particle (symbolised by an arrow) is an example:
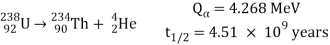
The energy released (Q) in millions of electron volts (MeV) and the half-life (t12) are given for this and following reactions. The charges, or number of protons, represented in subscript, as well as the atomic masses, displayed in superscript, are in balance on both sides of the arrow in alpha decays.
Beta-minus decay
An energetic negative electron is emitted in beta-minus decay, resulting in a daughter nucleus with one higher atomic number and the same mass number. The decay of the uranium daughter product thorium-234 into uranium is an example.
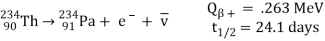
Protactinium-234:
The antineutrino is represented by v in the above process for beta decay. Here, the number of protons is increased by one in the reaction, but the total charge remains the same, because an electron, with negative charge, is also created.
4.1.2 Gamma decay
Gamma radiation, a third form of radiation, usually follows alpha or beta decay. Photons, like gamma rays, have no rest mass or charge. Without gamma emission, alpha or beta decay can simply proceed to the ground (lowest energy) state of the daughter nucleus, but it can also progress fully or partly to higher energy levels (excited states) of the daughter nucleus. Gamma emission may occur in the latter situation as the excited states change to lower energy levels of the same nucleus. (An excited nucleus can also convert to a lower energy state by ejecting an electron from the cloud surrounding it, which is an alternative to gamma emission.) Internal conversion is the ejection of an orbital electron, which results in an energetic electron and typically an X-ray as the atomic cloud fills in the ejected electron's empty orbital. The internal-conversion coefficient is the ratio of internal conversion to alternative gamma emission.)
4.1.3 Isomeric transitions
For the gamma-emission process, there is a wide range of half-life rates. Dipole transitions (see Gamma transition below), in which the gamma ray carries off one unit of angular momentum, are often quick, taking less than nanoseconds (one nanosecond is 109 second). According to the law of conservation of angular momentum, the total of the angular momenta of the radiation and the daughter nucleus must match the parent's angular momentum (spin). When the spins of the beginning and end states differ by more than one, dipole radiation is prohibited, and gamma emission must take place via a higher multipole (quadrupole, octupole, etc.) gamma transition. The excited nucleus is considered to be in a metastable, or isomeric, state (the terms for a long-lived excited state) if the gamma-emission half-life exceeds around one nanosecond, and the decay is usually classified as another type of radioactivity, an isomeric transition. The protactinium-234 nucleus of the uranium-238 decay chain is an example of isomerism:

The letter m following the mass number stands for metastable and indicates a nuclear isomer.
Beta-plus decay
New types of radioactivity, beta-plus decay, or positron emission, and electron capture, were discovered among the artificial products of nuclear reactions in the 1930s. In beta-plus decay, an energetic positron is generated and released, along with a neutrino, and the nucleus converts into a daughter with an atomic number one lower but the same mass number. Carbon-11 (Z = 6) decays to boron-11 (Z = 5), one positron, and one neutrino, for example:

4.1.4 Electron capture
Electron capture (EC) is a process in which an orbital electron is captured by the nucleus and then decays. The nucleus converts to a daughter of one lower atomic number, comparable to positron decay. It differs in that an orbital electron from the cloud is captured by the nucleus with subsequent emission of an atomic X-ray as the orbital vacancy is filled by an electron from the cloud about the nucleus. The nucleus of beryllium-7 grabbing one of its inner electrons to produce lithium-7 is an example:

A decay scheme depicts the basic characteristics of radioactive decay of a nuclear species. The degradation pathway of beryllium-7 is depicted in Figure 1. The parent and excited daughter states' half-lives, as well as their energy of 0.4774 MeV, are shown. On the level's upper left-hand side, you'll see the spins and parities for all three states. Above the vertical arrow depicting the gamma transition, the multipolarity of the gamma ray (magnetic dipole, M1, plus 0.005 percent electric quadrupole, E2) is indicated. The slanted arrows represent electron-capture decay, with labels indicating the fraction of EC decay that goes directly to ground state (89.7%) and the percentage of EC decay that goes through the excited state (12%). (10.3 percent). The boldface figures after the percentages are so-called log ft values, which are used in conjunction with beta-decay rates further down. The total energy release (QEC) is shown below. Because there are no practical ways to measure the neutrino energy associated with EC decay, the QEC must be estimated. It has been feasible to directly estimate the decay energy of a few electron-capturing nuclides by measuring a rare event known as inner bremsstrahlung (braking radiation). The neutrino and a gamma ray share the energy released in this process. The total energy released is determined by the measured distribution of gamma-ray energies. With radioactive decay, there is usually so much conventional gamma radiation that the inner bremsstrahlung is unobservable.
Spontaneous fission
Spontaneous fission is another type of radioactivity. The nucleus separates into two fragment nuclei with roughly half the mass of the parent nucleus throughout this phase. This process is only barely detectable in competition with the more prevalent alpha decay for uranium, but for some of the heaviest artificial nuclei, such as fermium-256, spontaneous fission becomes the predominant mode of radioactive decay. As the fragments are propelled away by the enormous electrical repulsion between their nuclear charges, kinetic energy releases of 150 to 200 MeV may occur. The response
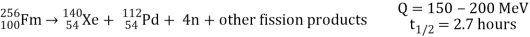
Is as follows:
Only one of many product sets is displayed. In the fission of this isotope, a few neutrons are always emitted, which is critical for chain reactions. Induced fission, the process utilised in nuclear reactors, is not to be confused with spontaneous fission. The ability of uranium-235, plutonium-239, and other isotopes to fission after absorption of a slow neutron is known as induced fission. Apart from the need for a neutron capture to start it, induced fission is quite identical to spontaneous fission in terms of total energy released, secondary neutron counts, and so on (see nuclear fission)
Proton radioactivity
Proton radioactivity was first identified in 1970 in an excited isomeric form of cobalt-53, 53mCo, of which 1.5 percent emits protons:
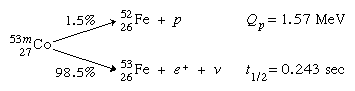
Special beta-decay processes
In addition to the aforementioned sources of radioactivity, heavy-particle emission is caused by a rare class of beta-decay processes. In these events, portion of the beta decay moves to a high excited state of the daughter nucleus, which produces a heavy particle quickly.
Beta-delayed neutron emission is one such mechanism, as demonstrated by the following reaction:44
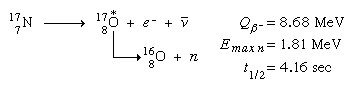
(Emax n signifies the maximum energy detected for released neutrons, and the asterisk signifies the short-lived intermediate excited states of oxygen-17.) Following nuclear fission, there is a minor output of delayed neutron emitters, and these radio activities are notably significant in providing a reasonable response time to allow mechanically moved control rods to control nuclear fission reactors.
A number of positron emitters in the light-element area beta decay to excited states that are unstable with respect to alpha particle emission. As a result, these species produce alpha radiation with the same half-life as beta emission. Because the ground and excited states of beryllium-8 are both unstable with regard to dissociation into two alpha particles, both positron decay from boron-8 and electron decay from lithium-8 are beta-delayed alpha emission. Another example is the reaction of sodium-20 (20Na) with neon-20 (20Ne; the asterisk again indicates the short-lived intermediate state) to produce oxygen-16:
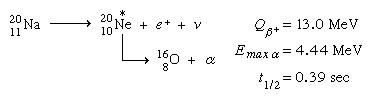
Positron decay can result in an excited nuclear state that is unable to attach a proton in a few situations. Proton radiation appears with the beta transition's half-life in these instances. In the daughter ground state, a combination of high positron-decay energy and low proton-binding energy is required. Tellurium-111 (111Te) generates antimony-111 (111Sb) and subsequently tin-110 (110Sn) in the following example:
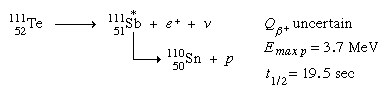
Heavy-ion radioactivity
A. Sandulescu, D.N. Poenaru, and W. Greiner published calculations in 1980 that suggested the potential of a novel type of heavy nuclei decay halfway between alpha decay and spontaneous fission. H.J. Rose and G.A. Jones discovered heavy-ion radioactivity in 1984 when they discovered a 30-MeV carbon-14 emission from radium-223. Carbon-14 decay has a ratio of around 5 1010 to alpha decay. Carbon-14 from radium-222, radium-224, and radium-226, as well as neon-24 from thorium-230, protactinium-231, and uranium-232, have all been seen. Alpha decay and spontaneous fission are examples of heavy-ion radioactivity that includes quantum-mechanical tunnelling past the potential-energy barrier. Shell effects are important in this phenomenon, and the heavy partner of carbon-14 or neon-24 in all examples recorded so far is near to doubly magical lead-208.
4.1.5 Occurrence of radioactivity
On Earth, some types of radioactivity exist naturally. Few species have half-lives comparable to the age of the elements (about 6 109 years), indicating that they did not disintegrate after forming in stars. Uranium-238, uranium-235, and thorium-232 are notable examples. There's also potassium-40, which is the body's primary source of irradiation due to its existence in potassium tissue. Vanadium-50, rubidium-87, indium-115, tellurium-123, lanthanum-138, lutetium-176, and rhenium-187 are beta emitters, while cerium-142, neodymium-144, samarium-147, gadolinium-152, dysprosium-156, hafnium-174, platinum-190, and lead-204 are alpha emitters. Aside from these about 109-year species, there are the shorter-lived daughter activities that are fed by one or more of the above species; for example, various nuclei of the elements between lead (Z = 82) and thorium (Z = 90) are fed by one or more of the above species. Species formed in the upper atmosphere by cosmic ray bombardment are another type of natural radioactivity. Carbon-14 with a 5,720-year age and 12.3-year tritium (hydrogen-3) with a 53-day age and 2,700,000-year beryllium-10 with a 2,700,000-year age are notable. Small levels of radioactivity have been discovered in meteorites as a result of cosmic ray bombardment throughout their history outside the Earth's atmospheric shield. In fresh meteorite falls, activities as short-lived as 35-day argon-37 have been measured. Since 1945, nuclear explosions have released new radio activities into the environment, including nuclear fission products as well as secondary products generated by the impact of neutrons from nuclear weapons on nearby matter.
Most of the known beta emitters in the mass range of 75–160 are included in the fission products. They are generated in various yields, peaking at around 7% per fission in the mass regions 92–102 (light peak of the fission yield vs atomic mass curve) and 134–144 (dark peak of the fission yield versus atomic mass curve) (heavy peak). There are two types of radioactivity-related delayed risks. First, fallout falling on Earth raises the overall radiation level. Until the activity has diminished to a suitably low level, protection can be provided by concrete or earth shielding. Second, depending on the half-life, nature of radiations, and chemical behaviour within the body, ingestion or inhalation of even low doses of certain radioactive species can represent a unique threat. See Radiation: Biological Impacts of Ionizing Radiation for further information on the biological effects of radiation
Nuclear reactors produce fission products as well, but they do so under controlled settings. Containment and waste-disposal procedures should keep operations contained and eliminate the likelihood of leaching into groundwater for periods longer than half-lives. If thermonuclear fusion power can be made feasible, it has a number of advantages over fission power, including not just much bigger fuel stocks (heavy hydrogen and lithium) than uranium, but also the elimination of radioactive fission product wastes. In this context, it's worth noting that radioactive decay is a major source of heat in the interiors of both the Earth and the Moon. These huge heat production sources must be factored into theories concerning the genesis and evolution of the Earth, Moon, and other planets.
Other than natural activities and fission products, desired radio activities can be created by irradiating specified target materials with reactor neutrons or using charged particle or gamma ray beams from accelerators.
4.1.6 Energetics and kinetics of radioactivity
Energy release in radioactive transitions
The fundamental question of nuclear binding energies and stabilities arises when the energy released by various radioactive transitions is considered. An isotope chart, with positions on the same horizontal row corresponding to a given proton number (Z) and those on the same vertical column corresponding to a given neutron number, is a popular way of illustrating nuclear-stability connections (N). Figure 2 depicts such a map. The region of currently known nuclei is surrounded by an irregular bold line. Because the chart may be thought of as a map of a binding energy surface, the lowest regions of which are the most stable, the area enclosed by this is commonly referred to as the valley of stability. The plentiful iron and nickel isotopes have the most closely bonded nuclei of all. The processes of alpha decay and spontaneous fission are most common near the region of the valley containing the heaviest nuclei (largest mass number A; i.e., largest number of nucleons, N + Z); both of these processes relieve the energetically unfavorable concentration of positive charge in the heavy nuclei.
The positron-emitting and electron-capturing radioactive nuclei are found along the region that borders the valley of stability on the upper left-hand side, with the energy release and decay rates increasing as the nucleus moves away from the stability line. Beta-minus decay is the primary process in the lower right-hand border region, with energy release and decay rates increasing as the nucleus moves away from the stability line.
The graph's grid lines correlate to the nucleon numbers that relate to increased stability, or "magic numbers". The circles labelled "deformed zones" demarcate areas where nuclei should have cigar shapes, but nuclei elsewhere are spherical. Outside of the dashed lines, nuclei would be unbound to neutron or proton loss and would have a very short lifetime (less than 1019 seconds).
4.1.7 Calculation and measurement of energy
It is possible to determine the energy release for unmeasured transitions using measured radioactive-energy-release (Q) values for alpha and beta decay using the method of closed energy cycles. The cycle of four nuclei serves as an illustration below:
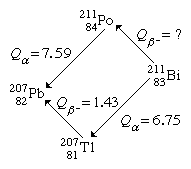
Two alpha decays and one beta decay have energies that can be measured in this cycle. Because conservation of energy requires the total of Q values around the cycle to be zero, the unmeasured beta-decay energy for bismuth-211, Q(Bi), is easily determined. As a result, Q(Bi) + 7.59 1.43 6.75 = 0. Q(Bi) = 0.59 MeV is obtained by solving this equation. Closed energy cycles calculations may be extended from stable lead-207 all the way up the alpha and beta decay chain to its natural progenitor uranium-235 and beyond. The nuclear binding energies of a group of nuclei can be related in this way. Closed-cycle calculations based on lead-207 can only connect together nuclei with mass numbers of the general type A = 4n + 3, where n is an integer, because alpha decay decreases the mass number A by 4 and beta decay does not modify A. The 4n series, for example, has thorium-232 as a natural precursor and lead-208 as a stable end product. The 4n + 2 series, for example, uses uranium-238 as a natural precursor and produces lead-206 as the end product.
The classification of isotopes into the series described above was important in early studies on natural radioactivity since they were discovered and examined as families. Newly found radio activities were assigned symbols that corresponded to the family and order in which they occurred. Thorium-234 was designated as UX1, protactinium-234 isomers as UX2 and UZ, uranium-234 as UII, and so on. These original symbols and titles appear in more current writings on occasion, but they are primarily of historical relevance. The entire 4n + 1 series contains well-known artificial activities that decay to stable thallium-205 and is not naturally occurring.
Measurements to augment the radioactive-decay energy cycles are definitely required to further our understanding of nuclear binding energies. This can be done in part by measuring the Q values of artificial nuclear processes. The neutron-binding energies of the lead isotopes, for example, can be determined by measuring the threshold gamma-ray energy to remove a neutron (photonuclear reaction); or the energies of the incoming deuteron and outgoing proton in the reaction can be measured to provide this information.
Precision mass spectroscopy is required for further developments of nuclear-binding-energy measurements (see spectroscopy). The masses of various nuclides can be measured with remarkable precision by ionizing, accelerating, and magnetically deflecting them. A direct measurement of the energy released in the radioactive decay process is comparable to a precise measurement of the masses of atoms involved. Potassium-40, a naturally occurring but radioactive isotope, with an atomic mass of 39.964008 amu. Potassium-40 decays mostly through -emission to calcium-40, which has a mass of 39.962589. Energy is equal to mass (m) times velocity of light (c) squared, or E = mc2. The energy release (Q) and the mass difference, m, are connected by Einstein's equation, with one amu equal to 931.478 MeV as the conversion factor. Thus, in the radioactive decay Q = (39.964008 39.962589) 931.478 MeV = 1.31 MeV, the extra mass of potassium-40 over calcium-40 shows as the total energy release Q. The other isobar (same mass number, different atomic number) to argon-40 has a mass of 39.962384, which is lower than potassium-40. When the mass difference is translated to energy units, the result is a 1.5 MeV energy release, which is the energy release for EC decay to argon-40. Because the maximum energy release for positron emission is always smaller than the maximum energy release for electron capture by twice the rest mass energy of an electron (2m0c2 = 1.022 MeV), the maximum positron energy for this reaction is 1.5 1.02, or 0.48 MeV.
A detailed understanding of the alpha-particle (helium-4) atomic mass is required to correlate alpha-decay energies with nuclear mass discrepancies. The energy released is equal to the mass of the parent minus the sum of the masses of the decay products. As a result, the computation for alpha decay of plutonium-239 to uranium-235 and helium-4 is as follows:



0.00563 × 931.478
Qα = 5.24 MeV
As follows:
Extensive lists of nuclear masses have been generated by integrating radioactive-decay-energy information with nuclear-reaction Q values and precision mass spectrometry. They can be used to calculate the Q values of unmeasured reactions or decay.
The atomic masses can also be written as mass defect, indicated by the Greek letter delta (the difference between the exact mass M and the integer A, the mass number), either in energy units or atomic mass units, as an alternative to the complete mass.
4.1.8 Absolute nuclear binding energy
The absolute nuclear binding energy is the hypothetical energy release if a given nuclide were synthesized from Z separate hydrogen atoms and N (equal to A − Z) separate neutrons. The calculation for the absolute binding energy of the most stable of all nuclei, iron-56, provides an example:
26 × M( ) 26 × 1.007825 = 26.20345
) 26 × 1.007825 = 26.20345
30 × M(n) 30 × 1.008665 = 30.25995
M( ) - 55.93493
) - 55.93493
Binding energy = 0.52847 × 931.478 =492.58 MeV
Average binding energy per nucleon of  = 492.58/56 = 8.796 MeV
= 492.58/56 = 8.796 MeV
A broad study of the average binding energy per nucleon (for nuclei of all elements classified according to ascending mass) reveals a peak at iron-56, then a progressive decline on both sides to around 7 MeV at helium-4, and to roughly 7.4 MeV for the most massive nuclei known. As a result, most naturally occurring nuclei are not stable in the absolute sense. Degradation processes such as alpha decay and spontaneous fission would gain energy for nuclei heavier than iron by degrading into nuclear products closer to iron, but the rates of degradation processes such as alpha decay and spontaneous fission are only observable for the elements with the greatest mass. Nuclear energy may be obtained in a similar way by fusing most materials lighter than iron. However, unless the nuclei are exposed to temperatures greater than 107 K, the coulombic repulsion between them keeps the rates of fusion processes unobservably low. These temperatures are only reached and nuclear-fusion energy produced in the Sun's and other stars' heated cores, thermonuclear weapons, and controlled fusion plasmas.
4.1.9 Nuclear models
The liquid-drop model
With the model of a charged liquid drop, the average behaviour of the nuclear binding energy may be understood. The aggregate of nucleons in this model has the same surface tension, cohesion, and deformation properties as a liquid drop. A dominant attractive-binding-energy term proportional to the number of nucleons A is present. A surface-energy term proportional to surface area, as well as a coulombic repulsion energy proportional to the square of the number of protons and inversely related to the nuclear radius, must be deducted from this. Furthermore, there is a quantum-mechanical symmetry-energy term that favours identical amounts of protons and neutrons. Finally, there is a matching term that offers nuclei with even numbers of neutrons or protons a tiny boost in binding.
The pairing-energy term explains the extreme rarity of odd–odd nuclei that are stable against beta decay (the names odd–odd, even–even, even–odd, and odd–even relate to the evenness or oddness of proton number, Z, and neutron number, N, respectively). Deuterium, lithium-6, boron-10, and nitrogen-14 are the only examples. Other odd–odd nuclei, such as potassium-40, can be found in nature, but they are beta decay instable. Furthermore, the pairing-energy term explains why even-Z elements have more stable isotopes than odd-Z elements, as well as why element 43, technetium, and element 61, promethium, have no stable isotopes at all.
One method of calculating nuclear sizes is to use the beta-decay energy of so-called mirror nuclei. For example, the neon and fluorine nuclei, 19/10Ne9 and 19/9F10, are mirror nuclei because their respective proton and neutron counts are equal. Except for the coulombic term, which is inversely proportional to the nuclear radius, all binding-energy terms are the same in each. These calculations, combined with more direct determinations by high-energy electron scattering and energy measurements of X-rays from muonic atoms (hydrogen atoms in which the electrons have been replaced by negative muons), show that the nuclear charge is roughly uniformly distributed in a sphere with a radius of 1.2 A13 1013 centimetre. The fact that the radius is related to the mass number's cube root is significant since it means that the average density of all nuclei is roughly constant.
A close investigation of nuclear-binding energies indicates periodic deviations from the charged-liquid-drop model's smooth average behaviour. In the vicinity of particular numbers of neutrons or protons, the so-called magic numbers, an extra binding energy emerges (2, 8, 20, 28, 50, 82, and 126). 4/2He2, 16/8O8, 40/20Ca20, 48/20Ca28, and 208/82Pb126 are doubly magical in that they have both proton and neutron numbers magic. On Figure 2, these doubly magical nuclei are located at the intersections of grid lines.
The shell model
The overall trends of nuclear binding energies were given in terms of a charged-liquid-drop model in the preceding section. Nonetheless, periodic binding-energy abnormalities were seen at the magic numbers. Extra electronic stabilities at the atomic numbers of noble-gas atoms are substantially comparable to the periodic occurrence of magic numbers of extra stability. In atomic and nuclear situations, the causes for these stabilities are quite similar to the filling of particles into quantized orbitals of motion. The completion of filling an orbital shell is accompanied by an increase in stability. The shell model, as previously stated, is the nuclear model that accounts for the magic numbers. This model can account for spin zero for all even–even nuclear ground states in its simplest form; the nucleons fill pairs into orbitals with angular momenta cancelling. The nuclear spins of odd-mass nuclei close to doubly magical nuclei, such as 208/82Pb, are easily explained by the shell model. Before reaching the doubly magical configuration, the spins of 1/2 for neighbouring 207/81Tl and 207/82Pb are accounted for by filling all nucleons pairwise into the lowest energy orbits and putting the odd nucleon into the last available orbital (the Pauli exclusion principle dictates that no more than two nucleons may occupy a given orbital, and their spins must be oppositely directed); Similarly, spins of 9/2 for 209/82Pb and 209/83Bi make sense because spin-9/2 orbitals are the next available orbitals after doubly mystical lead-208. The magnetic dipole moment, which expresses the related magnetization, is well explained by the simple spherical-shell model.
The spherical-shell model's orbitals are labelled in a nomenclature similar to that of electronic orbitals in atoms. Protons and neutrons fill the orbitals 1s1/2, 1p3/2, 1p1/2, 1d5/2, and 1d3/2 in the orbital arrangement of calcium-40. In conventional spectroscopic notation, the letter signifies the orbital angular momentum, with the letters s, p, d, f, g, h, I and so on representing integer values of l ranging from zero for s (not to be confused with spins) to six for i. Because the intrinsic spin of a nucleon is 1/2, the fractional subscript yields the total angular momentum j, with values of l + 1/2 and l 1/2 permitted. For gradually higher energy values of an orbital of given l and j, the first integer is a radial quantum number with successive values 1, 2, 3, etc. A maximum of 2j + 1 nucleons can be accommodated in each orbital. For neutrons and protons, the exact arrangement of several orbitals within a shell vary slightly (see table for the orbitals comprising each shell). If l is even (s, d, g, I the orbital's parity is even (+), and if l is odd (), the orbital's parity is odd (). (p, f, h).
Shell closure number |
|
2 | 1s1/2 |
8 | 1p3/2, 1p |
20 | 1d5/2, 2s1/2, 1d3/2 |
28 | 1f7/2 |
50 | 2p3/2, 1f5/2, 2p1/2, 1g9/2 |
82 | 1g7/2, 2d5/2, 1h11/2, 2d3/2, 3s1/2 |
126 | 2f7/2, 1h9/2, 1i13/2, 3p3/2, 2f5/2, 3p1/2 |
184 (?) | 2g9/2, 1i11/2, 1j15/2, 3d5/2, 2g7/2, 4s1/2, 3d3/2 |
The beta-decay scheme of 2.2-minute thallium-209 illustrated below, in which spin and parity are specified for each state, is an example of a spherical-shell-model interpretation. The 127th neutron of the lowest accessible orbitals above the closed shell of 126 is thought to occupy the ground and lowest excited states of lead-209. It should be observed from the table's last line that
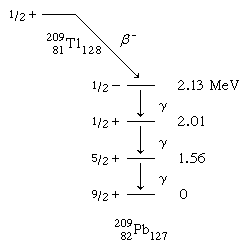
That the ground and first two excited states may be explained using the g9/2, d5/2, and s1/2 orbitals Nuclear-reaction investigations have identified low-lying states linked with the i11/2 and j15/2 orbitals, but they are not inhabited in beta decay.
The 2.13-MeV state that receives the principal beta decay isn't as straightforward to analyse as the others. It's linked to a neutron being promoted from the 3p1/2 orbital below the 126 shell closure. Above this excitation, the density (number of states per MeV) of states rapidly increases, making interpretations more difficult and uncertain.
The spherical-shell concept can be expanded beyond the doubly magical area with appropriate improvements. To begin, the assumption that nucleons move independently in orbitals must be abandoned, and a residual force, primarily short-range and attractive, must be invoked between the nucleons. A great quantity of data on binding energies, spins, magnetic moments, and the spectra of excited states can be explained and correlated around the magic areas using the spherical-shell model reinforced by residual interactions.
The collective model
The spherical-shell model has trouble explaining the significant reported electric quadrupole moments indicating cigar-shaped nuclei for nuclei further away from the doubly magical areas. The collective model, a combination of liquid-drop and shell models, has been proposed for these nuclei. (Cigar-shaped nuclei can be found in the circular sections of Figure 2.)
The nuclear shape can be deformed into a cigar shape by nucleons interacting with one another collectively. Such big spheroidal distortions are common for nuclei that aren't magical, such as 150 A 190, and 224 A (the symbol implies less than, and the number is approximate). The collective model dictates that orbitals be computed in a cigar-shaped potential and that the comparatively low-energy rotational excitations of the cigar shape's tumbling motion be taken into account in these distorted regions. In correlating and forecasting nuclear properties in distorted regions, the collective model has been quite successful. The decay of the isomer hafnium-180m through a cascade of gamma rays through the ground rotational band, seen in Figure 3, is an example of a nuclear rotational band (a succession of neighbouring states) (see below Gamma transition for explanation of M2, E1, E2, and E3).
Key takeaway:
- Nuclear radioactivity refers to the emission of the rays identified by Becquerel, while nuclear radiation refers to the rays themselves. Radioactive decay occurs when a nucleus spontaneously loses some of its mass and emits radiation. Radiation is unaffected by chemical condition.
- In 1903, Becquerel received half of the Nobel Prize in Physics for his discovery of spontaneous radioactivity, with the other half going to Pierre and Marie Curie for their investigation of the Becquerel radiation.
4.2.1 The Valley of Nuclear Stability

Protons and neutrons make up the nuclei of atoms. Electrostatic repulsion between positively charged protons causes them to repel each other. The strong nuclear force, which acts as an attracting force between nucleons, overcomes this electrostatic repulsion. Neutrons are necessary for nucleus stability. When the attractive force between nucleons exceeds the electrostatic repulsion, the nucleus becomes unstable and decays.
It describes the stability of an element's isotope. High-binding-energy nucleons are more stable. The ratio of neutrons to protons in a nucleus (N/Z) can be used to estimate an isotope's stability. Protons and neutrons are usually 1:1 in elements with atomic numbers fewer than 20. As the atomic number rises, so does the amount of neutrons. The ratio of neutrons to protons in most stable nuclei is greater than one. Only 1H and 3He are stable despite having a neutron-to-proton ratio of less than one.
Stable isotopes exist for the first 80 elements in the periodic table. Regardless of the amount of neutrons, all elements with an atomic number greater than 82 are unstable and radioactive.
4.2.2 Stability of nucleus
A nucleus is stable if it cannot be changed into a different configuration without the addition of external energy. Only roughly 250 nuclides are stable out of the thousands that exist. The stable isotopes fall into a narrow band when the number of neutrons vs the number of protons for stable nuclei is plotted. The band of stability is the name given to this area (also called the belt, zone, or valley of stability). The straight line in Figure 1 indicates nuclei with a protons-to-neutrons ratio of 1:1. (n:p ratio). It's worth noting that the lighter stable nuclei have an equal amount of protons and neutrons. Nitrogen-14, for example, contains seven protons and seven neutrons. Neutrons are rapidly outnumbering protons in heavier stable nuclei. For example, iron-56 contains 30 neutrons and 26 protons, resulting in a n:p ratio of 1.15, but lead-207 has 125 neutrons and 82 protons, resulting in a n:p ratio of 1.52. This is because larger nuclei have greater proton-proton repulsions, necessitating a larger number of neutrons to compensate for these electrostatic repulsions and hold the nucleus together.
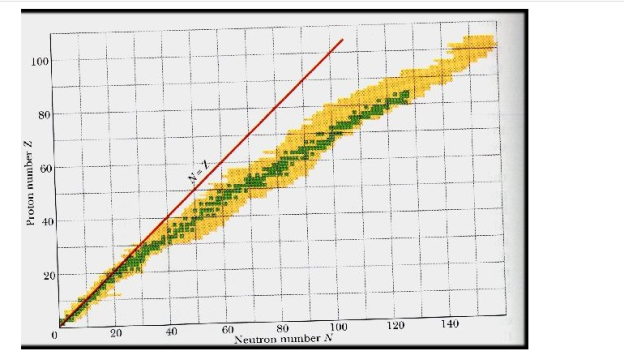
This graph depicts the known nuclides as well as those that are stable. The stable nuclides are coloured blue, whereas the unstable nuclides are coloured green. It's worth noting that all isotopes with atomic numbers greater than 83 are unstable. The solid line is the one on which n equals Z.
The nuclei on the left and right of the band of stability are unstable and produce radioactivity. They decay (transform) into other nuclei that are either within or close to the band of stability. Nuclear decay reactions transform one unstable isotope (or radioisotope) into a more stable isotope. The nature and products of this radioactive decay will be discussed in later sections of this chapter.
The relationship between the stability of a nucleus and its structure can be observed in several ways. Even-numbered protons, neutrons, or both are more likely to be stable nuclei (see Table 1). Magic numbers, or nuclei with a specific number of nucleons, are resistant to nuclear decay. In the nucleus, these numbers of protons or neutrons (2, 8, 20, 28, 50, 82, and 126) form complete shells. In concept, these are analogous to the stable electron shells observed in noble gases. Double magic nuclei, such as 42He, 168O, 4020Ca, and 20882Pb, contain magic numbers of both protons and neutrons and are extremely stable. These nuclear stability trends can be explained by using a quantum mechanical model of nuclear energy states, similar to the one used to describe electronic states previously in this textbook, although the intricacies of this model are beyond the scope of this chapter.
Number of Stable Isotopes | Proton Number | Neutron Number |
157 | Even | Even |
53 | Even | Odd |
50 | Odd | Even |
5 | Odd | Odd |
Table 1. Stable Nuclear Isotopes | ||
The binding energy per nucleon, or the total binding energy for the nucleus divided by the number of nucleons in the nucleus, is connected with the relative stability of a nucleus. For example, the binding energy of a 24he nucleus is 28.4 MeV, as we showed in Example 2. For a 24he nucleus, the binding energy per nucleon is 28.4MeV4nucleons=7.10MeV/nucleon. 7.10MeV/nucleon = 28.4MeV4nucleons
On the curve depicted in Figure 2, we learn how to compute the binding energy per nucleon of a nuclide in Example 3.
Protons and neutrons, together known as nucleons, make up an atomic nucleus. Despite the fact that protons resist each other, the nucleus is held together by the strong nuclear force, a short-range but extremely powerful force. The overall mass of a nucleus' constituent nucleons is smaller than that of the nucleus itself. According to Einstein's mass-energy equivalence equation, E = mc2, this "missing" mass has been turned into the binding energy that binds the nucleus together. Only a few nuclides are stable among the millions that exist. Even numbers of protons or neutrons, as well as nuclides with magic numbers of nucleons, are more likely to be stable. On a graph showing the number of protons vs the number of neutrons, these stable nuclides occupy a tight band of stability. The nuclei with mass numbers near 56 have the highest binding energy per nucleon; these are the most stable nuclei.
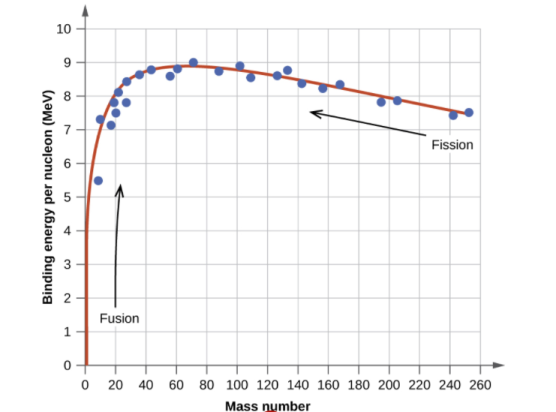
4.3.1 Radioactive decay law
The fundamental law governing radioactive decay.
The most essential law of radioactivity is the law of radioactive decay. When a nucleus decays by emitting an alpha particle or a beta electron, it changes, allowing for the conversion of radium into radon or tritium into helium, for example. However, the number of atoms in the radioactive substance inexorably decreases during such operations. However, the number of emissions per second decreases at the same time. The activity of a sample is determined by the decay rate, which is proportional to the number of nuclei present.
If the nucleus regains stability after having emitted a particle, the form of decay law is simple to understand: much like a currency which, every year, loses some percentage points of its ever-decreasing value. Exponential decay refers to any sort of decay of this nature, and its mathematics are widely understood. The half-life, or the length of time it takes for a given sample of a chemical to halve, is a useful measure of radioactive decay. The half-life of any substance is a property of its nucleus that does not change over time.
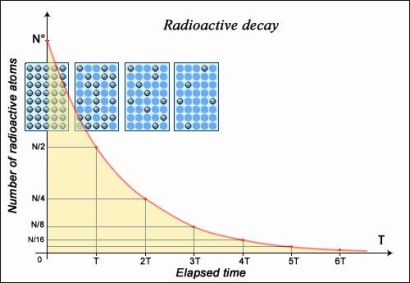
- The number of nuclei in a radioactive sample is halved after a specific length of time known as the 'half-life' or 'period.' The length of time it takes to divide the nuclei is independent of their age or the quantity of the sample. The size of the sample is quartered (not decreased to zero) after two half-lives, eighth after a third half-life, and so on. The half-life of a nucleus is one of the most essential aspects of a radioactive element IN2P3 because of its decay rate in relation to time.
- If the daughter nucleus (the final product of the radiation process) is radioactive, the type of decay becomes more difficult to comprehend and analyse. Nonetheless, like with any other activity, a radioactive equilibrium is eventually reached.
- A few grammes of any substance already contain millions of billions of billions of atoms; the quantity of radioactive nuclei in even the tiniest sample is unimaginably large. As a result, even for the least radioactive elements, radioactivity is always computed using large values.
Decay probability per second : λ = 0,693 /T (seconds)
Number of nuclei (masse atomique A) : N = 6,023 × 1023 m(grams) / A
Activity (becquerels) = λ N = 1,323 × 1018 m /AT(years)
m: sample mass – A : nucleons number in nucleus (atom-gram)
The activity of a mass m sample and its half-life T
Because of the value of the Avogadro number N: 6,023 followed by 23 zeros, activities calculated in becquerels have extremely high levels. The neperian logarithm of 2 is 0,693. T in years is converted to seconds by multiplying T in years by 31,6 millions, the number of seconds in a year.
IN2P3 is a three-letter acronym that stands for "
All of these radioactive changes are unpredicted and unpredictable. In other words, we can never predict when a nucleus will disintegrate or which of a group of nuclei will decay first. A Carbon-14 nucleus found in an ancient bone has the same likelihood of degrading in the same amount of time as a nucleus from a recently felled tree. To put it another way, the likelihood of a nucleus decaying radioactively is always the same. The half-life of the nucleus is inextricably related to the likelihood of decay, and both are defining aspects of any radioactive element.
4.3.2 Types of Radioactive Decay
There are three types, namely:
- Alpha
- Beta
- Gamma.
Alpha decay:
The process of an alpha particle emitting its nucleus is known as alpha decay. The alpha decay formula is as follows:
[latex]E=(m_{i}-m_{f}-m_{p})c^{2}[/latex]
- Where mi is the nucleus's initial mass and mf is the nucleus's mass after particle emission.
- The mass of the released particle is mp.
- The alpha particle, which is exceedingly stable, is taken from the nucleus of helium. It has two protons and two neutrons in its group. The alpha decay of uranium-238, for example, is depicted below.
- -[latex] -[latex] -[latex]
- The process of isotopes converting into an element of a stable nucleus is known as transmutation.
Beta Decay:
Although a beta particle is commonly referred to as an electron, it can also be referred to as a positron. If electrons are involved in the reaction, the nucleus will release neutrons one by one. As a result, the proton count rises as well. The following is a diagram of the beta decay process:
[matrix]
Pa 91234+e -10 Th 90234rightarrow Pa 91234+e -10
(latex)
Gamma Decay:
The nucleus has orbiting electrons that do have some energy, and when an electron jumps from a high energy level to a low energy level, a photon is emitted. The nucleus does the same thing: everytime it rearranges into a lower energy level, a high-energy photon known as a gamma ray is emitted.
4.3.3 Radioactive Decay Law
In nature, there are three forms of radioactive decay:
- -decay –emission of a helium nucleus (42He)
- -decay – the emission of electrons or positrons (particles with the same mass as electrons but a charge opposite that of an electron);
- -decay – photons with high energy (hundreds of keV or more) are released.
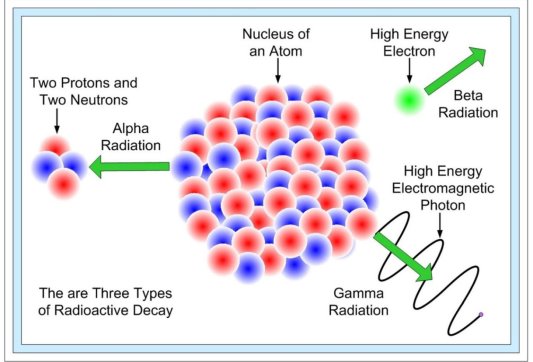
When a radioactive material undergoes α, β or γ-decay, the number of nuclei undergoing the decay, per unit time, is proportional to the total number of nuclei in the sample material. So,
If N = total number of nuclei in the sample and ΔN = number of nuclei that undergo decay in time Δt then,
ΔN/ Δt∝ N
Or, ΔN/ Δt = λN … (1)
Where λ = radioactive decay constant or disintegration constant. Now, the change in the number of nuclei in the sample is, dN = – ΔN in time Δt. Hence, the rate of change of N (in the limit Δt→ 0) is,
DN/dt = – λN
Or, dN/N = – λ dt
Now, integrating both the sides of the above equation, we get,
NN0∫ dN/N = λ tt0∫ dt … (2)
Or, ln N – ln N0 = – λ (t – t0) … (3)
Where, N0 is the number of radioactive nuclei in the sample at some arbitrary time t0 and N is the number of radioactive nuclei at any subsequent time t. Next, we set t0 = 0 and rearrange the above equation (3) to get,
Ln (N/N0) = – λt
Or, N(t) = N0e– λt … (4)
Equation (4) is the Law of Radioactive Decay.
The Decay Rate
In radioactivity calculations, the decay rate R ( = – dN/dt) is more important than the number N. The number of nuclei decaying per unit time is determined by this rate. We can compute the decay rate even if we don't know the amount of nuclei in the sample by counting the number of emissions of, or particles in 10 or 20 seconds. Let's say we take a time interval dt and calculate the decay count N (= –dN). The rate of decay is now defined as,
R = – dN/dt
Differentiating equation (4) on both sides, we get,
R = λ N0 e−λt
Or, R = R0e−λt … (5)
Where, R0 is the radioactive decay rate at the time t = 0, and R is the rate at any subsequent time t. Equation (5) is the alternative form of the Law of Radioactive Decay. Now we can rewrite equation (1) as follows,
R = λN … (6)
Where R and the number of radioactive nuclei that have not yet undergone decay must be evaluated at the same instant.
4.3.4 Half-Life and Mean Life
The total decay rate of a sample is also known as the activity of the sample. The ‘becquerel' is the SI unit for measuring activity and is defined as,
1 becquerel = 1 Bq = 1 decay per second
An older unit, the curie, is still in common use:
1 curie = 1 Ci = 3.7 × 1010 Bq (decays per second)
There are two ways to measure the time for which a radionuclide can last.
● Half-life T1/2 – the time at which both R and N are reduced to half of their initial values
● Mean life τ – the time at which both R and N have been reduced to, e-1 of their initial values.
Calculating Half-Life
Let's try to figure out what the relationship is between T1/2 and the disintegration constant. For this, let’s input the following values in equation (5),
R = (1/2)R0 and t = T1/2
So, we get T1/2 = (ln2)/ λ
Or, T1/2 = 0.693/ λ … (7)
Calculating Mean life
After that, we'll look for a relationship between the mean life and the disintegration constant. Consider the following equation (5),
● The number of nuclei which decay in the time interval: ‘t’ to ‘t + Δt’ is: R(t)Δt = (λN0e–λt Δt).
● Each of them has lived for time ‘t’.
● Hence, the total life of all these nuclei is tλN0e–λt Δt
Hence, to obtain the mean life, we integrate this expression over all the times from 0 to ∞ and divide by the total number of nuclei at t = 0 (which is N0).
τ = (λN0 0∞∫ te–λtdt)/N0
= λ0∞∫ te–λtdt
On solving this integral, we get
τ = 1/λ
Therefore, we can summarise the observations as follows:
T1/2 = (ln2)/λ = τ ln 2 … (8)
4.3.5 Radioactivity – Law of Radioactive Decay
A.H. Becquerel discovered radioactivity by accident in 1896. He was researching the fluorescence and phosphorescence of visible-light-irradiated substances. This is when he made an interesting observation. In the following section, we'll study more about the law of radioactive decay.
With visible light, he lighted certain fragments of Uranium-Potassium-Sulphate. He then wrapped these pieces in black paper and used a piece of silver to detach them from a photographic plate. He left it for a long time. When he processed the photographic plate, he discovered that it had blackened.
This meant that the compound emitted something that penetrated the silver and black paper and landed on the plate. Following investigations, it was discovered that radioactivity is a nuclear phenomenon that occurs when an unstable nucleus decays. This process is known as radioactive decay.
Radioactive Decay
● In nature, there are three forms of radioactive decay:
● -decay –emission of a helium nucleus (42He)
● -decay – the emission of electrons or positrons (particles with the same mass as electrons but a charge opposite that of an electron);
● -decay – photons with high energy (hundreds of keV or more) are released.
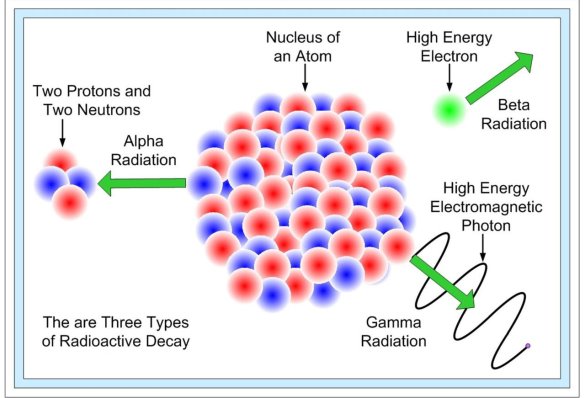
4.3.6 The Decay Rate
In radioactivity calculations, the decay rate R ( = – dN/dt) is more important than the number N. The number of nuclei decaying per unit time is determined by this rate. We can compute the decay rate even if we don't know the amount of nuclei in the sample by counting the number of emissions of, or particles in 10 or 20 seconds. Let's say we take a time interval dt and calculate the decay count N (= –dN). The rate of decay is now defined as,
R = – dN/dt
Differentiating equation (4) on both sides, we get,
R = λ N0 e−λt
Or, R = R0e−λt … (5)
Where, R0 is the radioactive decay rate at the time t = 0, and R is the rate at any subsequent time t. Equation (5) is the alternative form of the Law of Radioactive Decay. Now we can rewrite equation (1) as follows,
R = λN … (6)
Where R and the number of radioactive nuclei that have not yet undergone decay must be evaluated at the same instant.
4.4.1 Half Life period
Half-Life, also known as Half-Life Period, is a phrase used in physics to describe the radioactive decay of a sample or element over a period of time. While studying nuclear physics, students will come across the term frequently.
This idea, on the other hand, is frequently used to describe a variety of decay processes, including exponential and non-exponential decay. The word is often used in medical sciences to describe the biological half-life of particular substances in the human body or in medications.
Half-Life Definition
A radioactive material's half-life is usually described as the time it takes for it to disintegrate or transition into a different substance (or one half of its atoms). Ernest Rutherford initially developed the principle in 1907. The sign Ug or t1/2 is commonly used to denote it.
If we choose a radioactive element with a one-hour half-life, it will help you understand the concept better. In this situation, half of the half would decay in an hour and the other half in another hour. The puzzle here is why the remaining material did not decompose in one hour.
Well, if the radioactive element is taken in a case where half of the atoms have decayed after one-half life, it would be proper to assume that they have a life expectancy at the average level as well-defined viz. The atoms with mean life that is much longer than their half-life. This means that the mean life equals the half-life divided by two, which is the natural algorithm. The half-life, on the other hand, is frequently defined in terms of likelihood.
Understanding The Concept Via Experiment
To understand how radioactive decay occurs, let us conduct an experiment with a large group of people, because statistical analysis will yield a reasonably obvious result.
Consider the following scenario: Nearly 1000 individuals are gathered in a hall, and each one is given a coin. The coin would represent the ability to decay, and each individual would symbolize a radioactive atom. Individuals can be requested to toss their money once every minute. If the toss result is heads, the person may be requested to leave the room (indicating atom disintegration), and if the result is tails, there is no need to do anything but wait one minute for another toss try.
You can see how, because of its importance, this topic has been addressed with zeal among students in the preceding example. As a result, the topic of radiation will be actively investigated in the coming years.
4.4.2 Half-Life Formulas
Below students will find the formulas for half-life that are used to describe the decay in substances.
- N(t) = No (½) t / t ½
- N(t) = No e-t / r
- N(t) = Noe– λt
Here we consider the following,
● N0 = the initial quantity of the substance
● N(t) = the quantity that is left over
● t1⁄2 = half-life
● τ = mean lifetime of the decaying quantity
● λ = decay constant
4.4.3 What are Half Lives and Mean Lives?
Specifying the half life or mean life of a process is a way of quantifying how fast it is occurring, when the whole process would in principle take forever to complete. The example we will talk about here is radioactive growth and decay, but examples from other fields include the recovery of a muscle after some exertion, and the filling of a cistern.
In particular then, the half-life of a radioactive element is the time required for half of it to decay (i.e. change into another element, called the "daughter" element).
So if a radioactive element has a half-life of one hour, this means that half of it will decay in one hour. After another hour, half of the remaining material will decay. But why didn't all of that remaining material decay in that second hour? Does the element somehow know that it's decaying, and alter its decay speed to suit?
Textbooks are usually content with deriving of the law of decay, and don't tend to address this question. And yet it forms a classic example of the way in which research in physics (and science in general) is carried out. Regardless of how we might expect an element to behave—where perhaps the second half might be expected to decay in the same amount of time as the first half—this simply does not happen. We must search for a theory that predicts this.
Science is often thought to proceed by our logically deducing the laws that govern the world. But it's not that simple; there are limits to what we can deduce, especially about things in which we cannot directly participate. Radioactive decay is a good example of this. We can't use a microscope to watch the events that make an element decay. The process is quite mysterious. But what we can do is make a simple theory of how decay might work, and then use that theory to make a prediction of what measurements we can expect. That's the way science proceeds: by making theories that lead to predictions. Sometimes these predictions turn out to be wrong. That's fine: it means we must tinker with the theory, perhaps discard it outright, or maybe realise that it's completely okay under certain limited circumstances. The hallmark of a good scientific theory is not what it seems to explain, but rather what it predicts. After all, a theory that says the universe just appeared yesterday, complete with life on earth, fossils and so on, in a sense "explains" everything beautifully by simply defining it to be so; but it predicts absolutely nothing. So from a scientific point of view it is not a very useful theory, because it contains nothing that allows its truth to be tested. On the other hand, while it's arguable that the theory of quantum mechanics explains anything at all, it certainly does predict a huge number of different phenomena that have been observed; and that's what makes it a very useful theory.
For radioactive decay, our theory is that the atoms decay, or change into another atom, quite spontaneously. At a basic level, we don't know why this should be; but we can only proceed step by step, and so first we begin with this simple theory. We postulate that they decay independently of whether their neighbours are decaying, and also that their tendency to decay is independent of how old they are. A given atom might decay after one microsecond, or one million years. However long it has been sitting intact makes no difference to its ability to decay right now. If the mechanism behind its decay is strong, in the sense that the atom has a large chance of decaying, then it won't last long: after all, the chance that it won't decay in some time interval is small, so the chance that it survives for any appreciable amount of time is then also small. That can be worked out by simple probability: multiplying together the probabilities that it doesn't decay for a string of those time intervals. The statistics of decaying elements, such as the mean and standard deviation of the number of atoms decaying in various time intervals, were measured soon after radioactivity was discovered; they were found to match those predicted by this idea of random decay, called Poisson statistics. Whenever anything has a small chance of happening, but there are lots of opportunities for it to happen, we get Poisson statistics.
So certainly physics has not proven, and can never prove, that its theory of atomic decay is true. The logical process is that if atoms decay randomly, then Poisson statistics will result. Experiments show that Poisson statistics do indeed result, but logically this does not mean that atoms decay randomly. Nevertheless, the way of science is that we do postulate that atoms decay randomly, until a new experiment calls this into question. But no experiment ever has. If this sounds like a reverse use of logic, then consider the same ideas for mechanics. Ideas of gravity, mass and acceleration were originally produced by Newton through the same process: because they predicted planetary orbital periods that could be verified experimentally. Because of this great success, expressions such as F = ma and F = GMm/r2 came to be canonical in physics. The logic was indeed being used in reverse; but no one was surprised when, three centuries later, one of the moon astronauts dropped a feather and a hammer together in the moon's vacuum, and found that they both fell at the same rate (although it was still beautiful and dramatic to watch!). That reverse logic had, after all, allowed him to get to the moon in the first place. So this way of conducting science works very well.
A "people" experiment to simulate radioactive decay
We may put this hypothesis of radioactive decay to the test by conducting an experiment with a large group of people; the group should be large in order to obtain good statistics. Put 1000 people in a large room and give everyone of them a coin. The coin depicts the ability of each individual to decay, and each person represents a radioactive atom. Everyone should toss their coin once every minute. If the outcome is heads, the person should exit the room immediately (which corresponds to the atom decaying). If the toss comes up tails, do nothing except wait another minute before throwing again.
So, what happens next? Because their coins landed heads up, nearly half of the people get up and walk out within one minute. After another minute, everyone will toss once more, and around half of the remaining people will leave. Of course, we don't expect everyone to depart after the second minute; around half of the group leaves every minute. Our simple random behaviour model has resulted in a half-life! This particular "element" is said to have a half-life of one minute. Of course, the laws of physics don't work in one-minute increments, so we should invite everyone to toss continually. This is acceptable, but it would create a lot of noise and make it more difficult to see what was going on.
It may be demonstrated that in a circumstance where the amount of an element halves in a constant time interval, it will also "third" in a separate constant time interval that is not difficult to calculate. In reality, we can use any integer to indicate the rate of decay. It's common to choose the halving time because it's straightforward. If a radioactive element was claimed to have a "third life" of one hour, no one would know if it meant one third had decayed or one third was remained behind after one hour. Of course, specifying the half life does not cause this issue.
Returning to our group of 1000 people who are still flipping their coin every minute, we may alter the half-life of the coin by altering the requirement to depart. Each individual, for example, throws their coin twice per minute. Only those with two heads are required to go now. In that instance, one quarter of the remaining people will depart after the first minute, and one quarter of the remaining people will depart after the second minute. The half-life has now surpassed one minute. As a result, we've made this "element" decay more slowly by reducing the chances of any of its constituent atoms decaying. Remember that anybody who seats and tosses their coin can sit for as long as they like, regardless of how many of their neighbours have left the room. They may sit for years flipping their coin, only to discover that it constantly lands tails up. Of course, the chances of this happening are slim, but it's possible. The likelihood that someone will leave is unaffected by how long they have been sitting there.
4.4.4 A "mustard seed" experiment to simulate radioactive decay
Another technique to demonstrate radioactive decay, this time with a feel more like to an actual experiment. Using a pestle, pound a couple of teaspoons of mustard seeds in a mortar. Have a microphone handy for a classroom demonstration that amplifies the click as each seed bursts. The risk that any one seed may burst is roughly independent of its neighbours and also roughly independent of time in the random crashing-together of the seeds. As a result, we hear a rush of clicks that quickly fade away, having a half-life of several seconds or longer. This is exactly what would happen if a Geiger detector was placed adjacent to a rapidly decaying element.
4.4.5 The mean life of a process
If half of the atoms in our radioactive element have decayed after one half life, we can expect some form of well-defined average life expectancy: the atoms' mean life, which is slightly greater than their half life. The half life is equal to the natural logarithm of 2 divided by the mean life (about 0.693). The time constant, which appears in the exponential term et/ associated in defining decay or growth, turns out to be exactly equal to the mean life. The term "time constant" refers to the fact that the mean life equals; the fact that the mean life equals is a nice coincidence that allows us to think about the mean life in the following, alternate way.
As previously stated, the time it takes for the remaining amount of the element to decline to a half, a third, or any fraction at all can be used to represent the speed of any decay process. One unusual choice of that number is e, and the time it takes for the remaining amount to be reduced to 1/e of the original also happens to be the decay's mean life. One of the reasons why the number e is so significant is because of this. Aside from having pleasant qualities that make the mathematics of growth and decay easier to understand, e quantifies ordinary concepts like the average life expectancy of atoms.
When we plot the amount of a radioactive element as a function of time, we see that it decreases with a typical "exponential decay curve," which helps to mathematically demonstrate the half-life concept. Here's a question for you: Assume the element did not decay exponentially (i.e. with a half-life), but rather linearly, with the rate of decay always equal to the original rate (resulting in a simple "first half in one minute, second half in the next minute—and then, all gone" scenario). How long would it take to entirely evaporate in such an idealised scenario? Assume we have 1000 atoms of a radioactive material, with 10 atoms decaying each second at the start. How long would it take to entirely evaporate if it continued to degrade at this rate (it won't, but pretend it did)? Of course, the answer is 100 seconds. It has now been discovered that this is exactly equal to the mean life of the real element. (Which means that we know straight away that the real element's half-life is 69.3 seconds.)
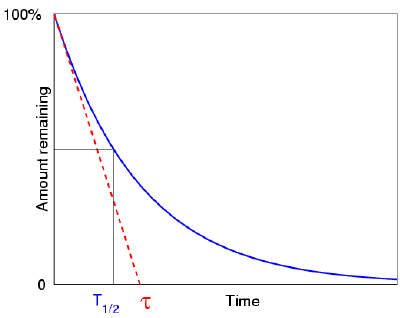
This way of looking at the concept of mean life also appeals to our intuition: it
According to this theory, if atoms behaved in the lovely, linear way that we humans enjoy thinking about them, the time it would take for them all to decay would be exactly equal to the mean life of the actual, real-world element. You can see how the number e is linked to basic linearity concepts, which is one of the reasons why it is such a powerful number in mathematical analysis.
The expansion of the daughter element follows the same logic. For the sake of simplicity, assume that the daughter is not radioactive. There are no daughter atoms at first, but when the parent element decays, they rise in number. Their development must finally flatten out, which takes an unlimited amount of time for the same reason that the parent element takes an unlimited amount of time to entirely decay. We ask how long it would take for the sample to be totally made up of daughter atoms if the daughter's growth maintained at its current rate (which it doesn't, remember!). This time interval turns out to be the parent's mean life once more.
4.4.6 The mean life and "probability per second"
That last application of the mean life to growth results in a language that is not always well understood by those who employ it. Assume we have a single atom of a radioactive element in front of us that is about to decay. We ask, "What is the chance that it has degraded after time t?" On average, the atom will disintegrate after one mean life. Although it may take a million times that amount of time for the atom to decay, we are confident that after two or three mean life, the atom will almost likely have decayed.
We can't actually visualise this probability as a function of time because we'd have to know when the atom will decay to do so (since then the probability equals one). Because the atom in front of us behaves exactly like the other atoms in the element, the most we can do is create a generic plot that accurately describes the entire population of decaying atoms. In that instance, we expect the likelihood to increase, eventually approaching one as t approaches infinity. Remember that this is an average prediction; each atom will undoubtedly achieve one at some point. But it's the best we can do at the moment.
The exact expression for this probability is 1 et/, which does actually tend to one as t approaches infinity. (It's the same curve as the one detailing the daughter element's growth.) What is the value of this (generic) probability when t=1: what is the likelihood that the atom will decay in one unit of time? Well, the answer is 1 e1/..., which may not convey much information! Let's ask another, relevant question, as we did before. How long would it take for the atom to decay if the chance of decaying within time t continued to increase at its initial pace (which it doesn't! ), and after how long would this probability reach one? This time interval, once again, turns out to be the mean life. However, if our linear, simplified atom decays with probability one after a time, it must decay with probability 1/ after a unit time.
With 1000 atoms and an initial rate of 10 decays per second, we calculated that the mean life was 100 seconds. So, if the likelihood of any individual atom decaying kept increasing uniformly at its starting pace, the chance of it decaying after one second would be 1/100. This is reasonable: The 10 atoms we measured to have decayed are 1/100 of the original 1000 atoms. As a result, we remark "the atom has a 1/100 per second risk of decay." Remember, this does not imply that it will have completely decayed after 100 seconds! This would only be true if the atom behaved in a straightforward, linear manner.
The fact that the atom's probability of decaying is "slowing down" is analogous to a pushed trolley starting out at 1/100 metre per second but decelerating at just the proper pace due to friction to match our atom. It would take 100 seconds to travel a metre if there was no friction and it moved at constant speed. Of course, it never fully reaches a metre distance because it is constantly slowing down; still, 1/100 m/s refers to its initial rate of distance increase. Similarly, "1/100 per second" refers to the starting rate of "decay-probability rise" for our generic atom, which represents the entire population of atoms. That decay probability will never exactly reach one in the aggregate for the entire population, but it will eventually reach one for any given atom.
Because the daughter element grows at the same rate as the parent element, the entire subject of growth may be applied to it. If it kept growing at its current rate, the sample would eventually be entirely made up of daughter atoms.
As you can see, we can manipulate these numbers to gain a sense of how an element decays or grows. But it's a lot easier to conceptualise in terms of the mean life than the half life for these more nuanced conceptions. Despite this, both the mean life and the half life give us a sense of radioactive decay, and each has its own set of applications.
4.5.1 Beta decay
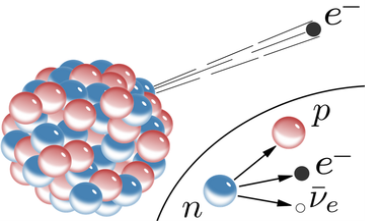
A nuclear decay process in which an unstable nucleus transmutes and ejects particles to become more stable is known as beta decay. Beta decay can be divided into two types: beta minus and beta plus. A nucleon in the nucleus is changed into a new sort of nucleon in both of these decays, releasing particles in the process. Beta decay, both minus and plus, is somewhat penetrating (ie the radiation can go deep inside a solid object). Electron capture is a closely comparable mechanism in which an electron is captured in the nucleus and functions similarly to beta plus.
When a nucleus has too many neutrons, beta minus decay occurs. The electron is released from the nucleus after a neutron from the nucleus is converted into a proton and an electron. A tiny particle known as an anti-neutrino is also released to ensure that the laws of particle physics are upheld. [two] The following is a general representation of beta minus decay:
AZXN→AZ+1YN−1+e−+ν¯ZAXN→Z+1AYN−1+e−+ν¯
Where:
● AZXNZAXN is the parent nucleus
● AZ+1YN−1Z+1AYN−1 is the daughter nucleus
● e− is the released beta particle, an electron
● ν¯ is the released anti-neutrino
A nucleus with too many protons causes beta plus decay. A proton from the nucleus is turned into a neutron and a positron in this type of decay (which is simply a "positive version" of the electron). A small particle known as a neutrino is also released to guarantee that particle physics rules are followed. [two] The following is the general equation for beta positive decay:
AZXN→AZ−1YN+1+e++ν
Where:
● AZXNZAXN is the parent nucleus
● AZ−1YN+1Z−1AYN+1 is the daughter nucleus
● e+ is the released beta particle, a positron
● ν is the released neutrino
In both beta minus and beta plus decay it is the weak nuclear force that results in the changing of a nucleon into a different nucleon.
4.5.2 Applications and Importance
Beta decayed elements can be used in medical applications. RNT, often known as radiotherapy, is a cancer treatment that employs beta decay. Lutetium-177 or yttrium-90 is linked to a molecule and consumed in this method. [6] This chemical enters the body and travels to cancer cells. The radioactive atoms subsequently decay, producing beta particles and destroying cancer cells in the area.
Furthermore, the features of beta decay are used in carbon dating. The ratio of carbon-14 to carbon-12 in an object must be measured to establish the approximate age of artefacts, wood, and animal remains. [number six] Carbon-14 is produced by sunlight in the atmosphere from nitrogen-14, which plants take in during photosynthesis, therefore there is some carbon-14 in organic remnants. Animals eat plants, which absorb carbon-14 as well. When an organic organism decomposes, some of the carbon-14 is converted to nitrogen-14 (a beta decay process), and the amount of carbon-14 in the sample is decreased over time. [6] The estimated age of the item can be established by looking at the carbon-14 to carbon-12 ratio.
4.5.3 Types of beta decay
Beta decay can be divided into three categories. The “ordinary” beta decay, also known as decay or electron emission, was the first to be found. In nuclear beta decay, the symbol symbolises an electron emitted. The nuclide cobalt-60 decays in the following manner: 60Co 60Ni + neutrino.
The neutrino is an unforeseen particle emitted during beta decay that is extremely important. The neutrino was not even hypothesised in theory until more than 20 years after electron emissions were discovered in beta decay. Neutrinos are so difficult to detect that it took until 1953 to gain the first direct proof of them. Neutrinos have almost no mass, no charge, and do not interact with nucleons through the strong nuclear interaction. Because they are travelling at nearly the speed of light, they have very little time to influence any nucleus they come across. This is because they don't interact through the EM force because they don't have any charge (and aren't EM waves). They do interact via the weak nuclear force, which is relatively weak and has a very short range. As a result, neutrinos can get through practically any detector and through practically any shielding. Neutrinos, on the other hand, carry energy, angular momentum (as fermions with half-integral spin), and linear momentum away from beta decay. When precise beta decay measurements were made, it became clear that the daughter nucleus and electron could not account for all of the energy, angular momentum, and linear momentum. Either they were being carried away by an unknown particle or three conservation rules were being broken. In 1930, Wolfgang Pauli proposed the existence of neutrinos in a formal paper. When he devised a detailed theory of beta decay, the Italian-born American scientist Enrico Fermi (1901–1954) gave neutrinos their name, which means "little neutral ones" (see Figure 3). The identification of the weak nuclear force as separate from the strong nuclear force, and hence responsible for beta decay, was part of Fermi's theory.
A new conservation law is also revealed by the neutrino. The electron family is one of the many different types of particles. In any process or closed system, we argue that the number of members of the electron family is constant. There are no members of the electron family present before the decay in our example of beta decay, but there is an electron and a neutrino afterward. As a result, electrons are assigned a +1 electron family number. The antineutrino of an electron in decay is given the symbol ve e, where nu is the Greek letter and the subscript e indicates that this neutrino is connected to the electron. This is an antimatter particle, as indicated by the bar. (Antimatter counterparts are almost identical to matter counterparts except that they have the opposite charge.) On Earth, antimatter is nearly absent, though it can be discovered in nuclear decay and other nuclear and particle reactions, as well as in outer space.) Because the electron is antimatter, its antineutrino e e has an electron family number of –1. Before and after the decay, the total is zero. The total electron family number is constant, according to the new conservation law, which must be followed in all circumstances. It is impossible to generate an electron without also creating an antimatter family member. In a scenario where total charge is initially zero and equal amounts of positive and negative charge must be formed in a reaction to keep the total zero, this law is equivalent to the conservation of charge.
If the decay of a nuclide AZXNZAXN is known, the decay equation is
XNYN1++ e XNYN1++ e XNYN1++ e XNYN
XNYN1++e (decay), XNYN1++e (decay), XNYN1++e (decay), XN
Y denotes a nuclide with one additional proton than X. (see Figure 4). If you know a nuclide decays, you can find the daughter nucleus by looking up Z for the parent and then figuring out which element has atomic number Z + 1. We can observe that Z = 27 for Co and Z = 28 for Ni in the decay of 60Co presented earlier. It's as though one of the parent nucleus' neutrons breaks down into a proton, electron, and neutrino. In fact, neutrons outside of nuclei do exactly that—they survive for only a few minutes on average and disintegrate in the following way:
Np++
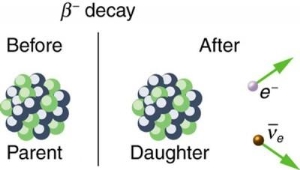
Figure: The parent nucleus produces an electron and an antineutrino during decay. The offspring nucleus has one proton and one neutron less than the parent nucleus. Neutrinos interact so weakly that they are rarely observed directly, but they play an important role in particle physics.
Because the total charge is Z before and after the decay, we can observe that charge is conserved. Because cobalt has Z = 27, the total charge before decay in 60Co decay is 27. The daughter nucleus after decay is Ni, which has Z = 28, and there is an electron, thus the total charge is 28 + (–1) or 27. Although angular momentum is preserved, it is not clearly conserved (you have to examine the spins and angular momenta of the final products in detail to verify this). Linear momentum is conserved as well, with the electron and antineutrino receiving the majority of the decay energy due to their low and zero mass, respectively. Another new conservation law is being followed in the natural world. A conserves the total amount of nucleons. There are 60 nucleons before and after the disintegration of 60Co, for example. It's worth noting that total A is conserved during decay. Also, because the total number of protons and neutrons changes, total Z and total N are not conserved in decay, as they are in decay. Given the masses of the parent and products, the energy released in decay may be estimated.
4.5.4 Decay Energy from Masses
Strategy and Concept
As in the last case, we must first calculate m, the mass difference between the parent nucleus and the decay products, using masses from Appendix A. The emitted energy is then computed using E = (m)c2 as before. The parent nucleus has the beginning mass, and the daughter nucleus and the electron generated in the decay have the final mass. The neutrino has a mass of zero or almost zero. However, since the masses given in Appendix A are for neutral atoms, the daughter nucleus has one more electron than the parent, and so the extra electron mass that corresponds to the β– is included in the atomic mass of Ni. As a result, m = m(60Co) m (60Ni).
Solution
The β− decay equation for 60Co is
6027Co33→6028Ni32+β−+¯νe2760Co33→2860Ni32+β−+ν¯e
As noticed, Δm = m(60Co ) − m(60Ni).
Entering the masses found in Appendix A gives Δm = 59.933820 u − 59.930789 u = 0.003031 u.
Thus, E = (Δm)c2 = (0.003031 u)c2.
Using 1 u=931.5 MeV/c2, we obtain E = (0.003031)(931.5 MeV/c2)(c2) = 2.82 MeV.
Discussion and Implications
The most challenging part of this example is persuading oneself that the mass of 60Ni is included in its atomic mass. There are additional ramifications as well. The decay energy is in the MeV region once more. This energy is spread across all of the decay's products. The daughter nucleus 60Ni is left in an excited state and emits photons ( rays) in multiple 60Co decays. Because the recoil kinetic energy of the daughter nucleus is low, the electron and neutrino receive the majority of the leftover energy. One final point: the decay electron is produced in the nucleus at the time of disintegration.
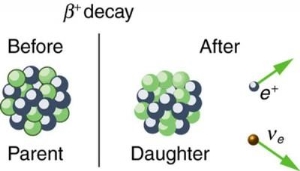
Figure. The emission of a positron that eventually finds an electron to annihilate, creating gammas in opposite directions, is known as + decay.
Beta decay in the second type is less common than beta decay in the first. It's a case of +decay. A positive electron is emitted when some nuclides decay. This is positron or antielectron decay (see Figure).
The antielectron is commonly represented by the symbol e+, although it is written as + in beta decay to show that the antielectron was emitted during nuclear decay. Antielectrons are the antimatter counterparts of electrons, and they are virtually identical to electrons in terms of mass, spin, and other properties, but they have a positive charge and an electron family number of –1. When a positron collides with an electron, the antielectron-electron pair undergoes mutual annihilation, in which all of the antielectron-electron pair's mass is transformed to pure photon energy. (The reaction e+ + e + conserves all other conserved quantities as well as the electron family number.) If a nuclide AZXNZAXN is known to have a positive decay, its +decay equation is
AZXN→YN+1+β++ve
ZAXN→YN+1+β++ve (β+ decay),
Ve is the symbol for the electron's neutrino, which has an electron family number of +1, and Y is the nuclide with one less proton than X (to conserve charge). Because the decay produces an antimatter member of the electron family (the +), a matter member of the family (here the e) must also be produced. If 22Na+ decays, for example, you may write the whole decay equation by first determining that Z = 11 for 22Na, resulting in a daughter nuclide with Z = 10, the atomic number for neon.
Thus the β+ decay equation for 22Na is
1122Na11→2210Ne12+β++ve
2211Na11→1022Ne12+β++ve
One of the protons in the parent nucleus decays into a neutron, a positron, and a neutrino in + decay. Outside of the nucleus, protons do not accomplish this, therefore the decay is due to the complexity of the nuclear force. It's worth repeating that the total number of nucleons in this and any other reaction is constant. Since atomic masses are used, you must count the number of electrons in the neutral atoms again to find the energy emitted in + decay. The daughter has one fewer electron than the father, and the decay creates one electron mass. Since we employ the masses of neutral atoms in + decay, m = m(parent) [m(daughter) + 2me].
The third type of beta decay is electron capture. A nucleus captures an electron from the inner shell and undergoes a nuclear reaction similar to + decay. Electron capture is sometimes abbreviated as EC. Although we know that electrons cannot live in the nucleus, this is a nuclear reaction that consumes the electron and only occurs spontaneously when the products have less mass than the parent plus the electron. If an AZXNZAXN nuclide is known to undergo electron capture, the electron capture equation for that nuclide is
AZXN+e−→YN+1+ve
ZAXN+e−→YN+1+ve (electron capture, or EC)
Any nuclide that can + decay can also be captured by electrons (and often does both). The same conservation laws apply to EC as they do to + decay. It's a good idea to double-check these for yourself.
Because the parent nuclide is unstable and outside the region of stability in the nuclide chart, all sorts of beta decay occur. Those nuclides with more neutrons than those in the stability region will decay to produce a daughter with fewer neutrons, bringing the daughter closer to the stability region. Similarly, nuclides with more protons than those in the stability region decay or undergo electron capture to produce a daughter with fewer protons that is closer to the stability region.
4.6.1 The Neutrino Hypothesis
The remarkable story of the neutrino
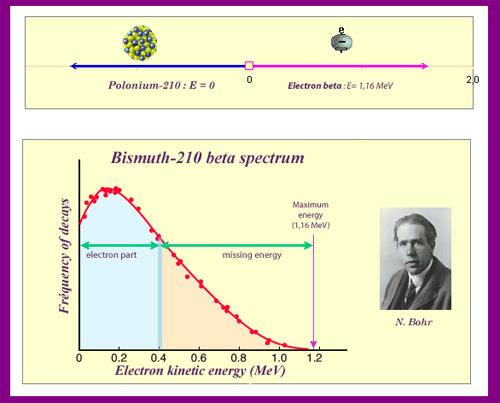
Fig. The mystery of beta electrons lost energy
Beta decay was thought to create two particles in the 1930s: the recoiling nucleus and an electron. It was expected to be a 'monokinetic' reaction, with the electron carrying away all of the available energy, similar to alpha decay. Beta decay, on the other hand, resulted in a wide range of possible and smaller energies for the electron, as shown in the diagram above. Where did all the lost energy go? Niels Bohr went so far as to question whether the law of conservation of energy was still applicable when confronted with this problem.
IN2P3 is a three-letter acronym that stands for "
The research of radioactive disintegrations had proved that alpha rays were ‘monokinetic’ - in that they always carried away the same percentage (100 percent ) of the energy available in the decay. Beta rays, on the other hand, can have a wide variety of energy levels. The energy distribution (or spectrum) of beta rays can take any value between zero and the total energy available, whereas the energy distribution (or spectrum) of alpha rays is reduced to a single value.
For physicists working in the field in 1930, this evidence was troubling. When it comes to beta decay, where did the law of conservation of energy go? The seeming lack of energy prompted Niels Bohr to propose that the most fundamental conservation law be abolished. For a physicist, this is a grave sin.
To preserve the law of conservation of energy, Swiss physicist Wolfgang Pauli proposed the creation of an electrically neutral, low mass particle (at most 1/100 the mass of the proton) that would be emitted with the beta particle. This hypothetical third body might therefore absorb any energy that was not delivered to the beta particle, resolving the most perplexing of problems. Pauli first offered this notion in a satirical letter to his colleagues Lise Meitner and Hans Geiger.

Adding a new particle to solve the problem
Wolfgang Pauli would be the one to explain the mystery of the missing energy by proposing the presence of a third particle, the neutrino, which is capable of evading detection. The image above depicts the circumstance where all three bodies have equal momenta in the case of bismuth 210 decay. The recoiling nucleus, which is 400,000 times heavier than the electron, absorbs very little energy. The leftover energy is split between the electron and the neutrino, which is depicted as a ghost particle in this illustration. The first experimental proof of a neutrino would take over a quarter-century to come to light.
IN2P3 is a three-letter acronym that stands for "
The brilliant Italian physicist Enrico Fermi was immediately convinced. He proposed the theory of beta decay based on a hypothesis that an electron-neutrino pair is spontaneously produced by a nucleus in the same way that photons can be spontaneously emitted by excited atoms, based on discussions held at the Solvay Conference in October 1933 (devoted to James Chadwick's discovery of the neutron).
According to Francis Perrin, for such a particle to exist, it must either have zero mass or be extremely light, even when compared to the electron.
Fermi's idea was the forerunner of today's 'weak interaction' hypothesis. During the first quarter of the twentieth century, Fermi's idea of a point-like interaction of four particles (for example, an initial neutron becoming a proton, an electron, and an antineutrino) was accepted as a canon, an article of faith without proof.
The neutrino remained a hypothetical particle until Reines and Cowan presented evidence for its existence in 1956.
Murray Gell Mann, an American physicist, proposed the idea of a weak force active not only in radioactive processes, but also in other processes where the impacts of various types of neutrinos may be recognised in a variety of subatomic events in 1955.
The neutrino and its antiparticle have played an important role in particle physics since its ‘discovery' by Pauli and the subsequent experimental evidence in their favour. Because neutrinos have no electrical charge, they are only affected by the weak interaction, allowing for a more detailed study of that force without the ‘background noise' produced by other nuclear or atomic interactions.
The neutrino is essential in astrophysics, in addition to its critical function in the physics of the infinitely small. It could, for example, be the key to unlocking the Universe's "hidden mass."
4.6.2 Pauli’s Idea of the Neutrino
Pauli's suggestion was an attempt to solve a difficult experimental challenge that had piqued the physics community's interest for several years. Ellis and Wooster published an experiment in 1927 that demonstrated that the electrons emitted in radioactive decay had a broad and continuous range of energy. This perplexing finding not only shattered the analogy with -decay, in which the energy of the emitted -particles was calculated for each potential -decay, but it also sparked some strange speculations. For example, Rutherford and Chadwick proposed that not all nuclei of a certain -unstable element were identical because they had various internal energies, and Bohr proposed that energy is not conserved in decay, allowing electrons to escape with a variety of energies. 13 This was hardly the only concern with nuclear research at the time. The tests in 1926 that demonstrated that nitrogen nuclei behaved according to BoseEinstein statistics revealed yet another major flaw in nuclear theory and the p-e model. According to the latter, because both protons and electrons have spin 12, nitrogen (atomic mass 14 and nuclear charge 7) should have a half-integer total spin. This suggests that nitrogen nuclei should follow Fermi-Dirac statistics if the p-e model is correct. The observed Bose-Einstein statistics, however, required that the nucleus comprised of an even number of half-integer particles, adding up to an integer total, which is required to explain these statistics. In 1929, Pauli was introduced to these challenges by Bohr, who was considering a restriction of the concept of energy conservation to solve these problems, a concept that Pauli found to be "very little satisfaction" (according to a letter to Bohr reprinted in Peierls 1986, p. 5). As Bohr and his partners continued down this route of energy nonconservation, Pauli began to consider another notion, which he first articulated in December 1930. Let us begin, like we did with Rutherford, by attempting to comprehend Pauli's perspective and models on the subject. We can next discuss how he changed Rutherford's concept to suit his own needs. Pauli, like his contemporaries, viewed radioactive decay as a reaction in which an unstable nucleus (as in the previous instance) disintegrated spontaneously into a residual nucleus, with the observed emitted - or -particle plus some -radiation (the situation afterwards). The model of this reaction preserves both energy and electric charge for -particles, but the unexplainable continuity of energies in the situation afterward has led some to believe that this continuity already existed in the situation before (Rutherford and Chadwick), or to suggest that the energy conservation constraint for this model be retracted (Bohr). This final proposal was what prompted Pauli to address the issue. We need to look at some of his objections to see why he was so opposed to Bohr's views. Bohr's notion to keep charge conservation but renounce energy conservation in -decay is challenged in a letter to Klein, a close associate of Bohr, by the following thought experiment: 13 Gauderis 2013 provides a thorough examination of this puzzle and all proposed possibilities. “Imagine a sealed chamber filled with radioactive decay. [...]... If the energy law were not applicable for -decay, the overall weight of the closed box would change as a result. This contradicts my understanding of physics! For then, even the gravitational field – which is generated [...] by the complete box (including the radioactive content) – must be expected to change, whereas the electrostatic field, [...], should remain unchanged due to charge conservation.” Jensen 2000, p. 153) (reprinted in Jensen 2000, p. 153) Pauli's main critique is that the field formalisms for gravity and electrostatics, which both rely on inverse-square laws, are built similarly and hence regarded to be of the same kind. Bohr's suggestion, by breaking this analogy, has the far-reaching consequence of undermining the physical concept of a field. Unlike most quantum theorists, who rarely dealt with gravity, 14 Pauli was a specialist in general relativity. 15 As a result, Pauli, unlike other nuclear physicists, was far more cognizant of field structures as the basic ontological ideas for physical reality. This explains why Bohr's theories bothered him so much. If Pauli was confident that conservation principles must apply in this reaction model, it occurred to him quickly that the only way to balance the disequilibrium between the before and after states was to add something to the picture. However, nothing new has been discovered in the -decay experiments thus far. As a result, he wanted to find something that was either unobservable or extremely difficult to observe. Because the law of conservation of electrical charge was already in effect, it had to be electrically neutral as well. In other words, his reaction model for the -decay process had a gap that needed to be filled by an idea or object that has these two traits. “Then I tried to connect the problem of the nucleus' spin and statistics with the other problem of the continuous-spectrum without giving up the energy conservation principle through the idea of a neutral particle,” he wrote in an autobiographical article. I wrote a letter about this in December 1930, when the heavy neutron had not yet been discovered experimentally.” (1957, p. 1316, my translation) He proposed a "desperate solution" to tackle these two problems in this letter16, namely "that there could exist electrically neutral particles in the nucleus, which I would like to term neutrons" (1957, p. 1316, my translation). This proposal was primarily an adaption of Rutherford's theory, according to Gauderis (2013). The key justifications for this thesis are, first and foremost, the fact that Pauli used the term "neutron" for this nuclear ingredient when Rutherford and his collaborators were still using the name "neutron" in papers, a fact Pauli must have known about. Second, he explains why Rutherford was unsuccessful in locating his neutron previously.
Wolfgang Pauli, an Austrian physicist, predicted in 1930 that when a beta particle is generated, another particle is emitted that is difficult to detect.
Enrico Fermi, an Italian physicist, termed it the 'neutrino,' which means "little neutral one" in Italian.
According to Pauli, the energy released in beta decay was distributed randomly between the beta particle and the neutrino. This would explain the wide variety of beta particle energies measured and the many angles at which a nucleus could recoil.
4.7.1 Pair Production and Annihilation
Photon absorption is the process in which a photon gives up some or all of its energy to a material particle. The photoelectric and Compton processes are two processes for photon absorption (contained usually within an atom in a solid). Photon absorption can be measured using an absorption coefficient, which is generally represented in m-1 or cm-1 units and determined by the equation:
The photon intensities (W/m2) at the entrance surface and at a depth x below the surface are I(0) and I(x), respectively (measured in the direction of the incident beam). As a result, the intensity within the material decays exponentially, as seen in Fig. 4-26. We can also consider x to be the material's full thickness, in which case I(x) is the photon intensity at the exit surface. The absorption coefficient can be measured by positioning radiation detectors in front and behind a sheet of material with a specified thickness x.
When the experimentally determined (mu) is plotted as a function of increasing photon frequency f (or photon energy hf), it falls continuously in the visible, ultraviolet, and x-ray regions, but eventually reaches a minimum and then begins to increase in the X-ray region; see Weidner & Sells Fig. The reason for the initial drop is that as photon energy increases, photoelectric and Compton scattering absorption processes become less likely; in other words, higher-energy radiation penetrates better.
At high photon energy, a third process called pair production occurs, in which a pair of elementary particles (a particle and its antiparticle of the same mass but opposite electrostatic charge) are created from the energy (hf) of the original photon. The two particles in this case are an electron and an antielectron (also known as a positron, with the same rest mass m0 as an electron but a charge of +e).
Pair production can be described by the following equation, which exhibits total energy (or mass-energy) conservation:
The rest energy of an electron (m0 c2) = 0.511 MeV is equal to that of the positron, hence the factor of 2 symbolises the fact that two particles with the same rest mass are generated. The kinetic energy of the electron and positron, respectively, is represented as K(-e) and K(+e).
The two particles would be generated at rest (with zero kinetic energy) if the photon energy was exactly 2m0 c2 = 1.02 MeV. This would be an example of total conversion of energy into mass. The process cannot take place if the photon energy is less than 2m0c2; in other words, the threshold energy for pair creation is 1.02 MeV. When photon energies exceed the threshold, a photon has more than enough energy to generate a particle pair, and the excess energy is manifested as kinetic energy between the two particles.
However, there is one more requirement that must be met during the pair-production process: momentum conservation. Taking this into consideration, we can deduce that pair creation cannot occur in empty space; something must absorb the initial photon's momentum (p=h/ =hf/c). (Consider the threshold case, in which particles must be generated at rest and are unable to absorb any momentum.) An atomic nucleus, which is millions of times more massive than an electron or positron, may absorb photon momentum without absorbing much energy, therefore the energy-conservation equation above remains roughly correct. As a result, when high-energy gamma rays strike a solid with a high density of atomic nuclei, pair formation occurs.
Pair annihilation is the inverse of pair formation, in which a particle and its antiparticle collide and annihilate each other, leaving the total energy of the two particles as electromagnetic radiation. The energy balance between an electron and a positron can be expressed as:
K(-e) + K(+e) = 2 hf 2m0c2 + K(-e) + K(+e)
The first term reflects both particles' rest energy, the second and third terms indicate their kinetic energies just before colliding, and the term on the right-hand side of the equation indicates the creation of two photons, each with the same frequency f and energy hf. According to the equation, hf must be at least m0c2=0.51 MeV, indicating that the photons produced correspond to -ray radiation. This process, like pair production, is usually carried out inside a solid, which provides the required electrons. Positrons are injected into the solid as a beam of particles from a particle accelerator.
The overall momentum before the collision would be close to zero if the kinetic energy of the two original particles were both tiny (m0c2). Because of momentum conservation, the momentum after annihilation must be close to zero, and the only way this can happen is if the two photons are released in opposing directions, cancelling their separate momenta. The positrons entering the solid usually have a lot of momentum, but the electrons (which were already present in the solid) are virtually at rest. The paths of the two -ray photons then intersect at the location of the pair-annihilation event, which is at an angle to each other (see Fig. 4-xx).
PET (positron emission tomography) is a medical diagnostic procedure that produces images of the inside structure of human organs based on this principle. The PET machine creates an image of the electron density within a plane (really a small slice) within the tissue by detecting the direction of passage of -ray photons that are created simultaneously (coincidence detection) and counting the number produced in different regions of space. The process can be repeated by moving the detectors (or the patient) forward to acquire three-dimensional information (a tomograph). A radioisotope is injected into the bloodstream to provide the positrons. PET is now a commercially available technique that works in conjunction with CT and MRI scanning.
The photon-electron interactions that we discussed recently are summarised schematically in Figure 4.19 (from Weidner & Sells). It's worth noting that the "particle" (electron, positron, or photon) that enters the solid is entirely annihilated in certain situations; in others (Compton and bremstrahlung effects), the particle only loses some energy.
Because lead has a larger density of electrons (and more highly charged atomic nuclei) than aluminium (which has a lower atomic number), photon absorption processes are greater (higher (mu) ; see Figs. 4-24b and 4-26), making it a good radiation-shielding material. However, because (mu) decreases as photon energy decreases (below 1 MeV), thicker sheets are required to absorb harsh (short-wavelength) x-rays or gamma rays, as opposed to soft (long-wavelength) x-rays.
There is a third way for photons to lose energy in their interactions with matter, in addition to the photoelectric effect (photon absorption) and Compton scattering (photon scattering). A photon can simply evaporate and be replaced by a matter-antimatter pair of particles in this process, known as pair creation. Because the mass of the electron and positron may be generated from the energy of the massless photon, this process provides a fantastic demonstration of how mass is not conserved. Of course, the photon must have enough energy to create the two new particles' rest masses.
This process usually takes place near a nucleus and results in the formation of an electron-positron pair. The following is a diagram of the effect:
First, let’s try to imagine a simpler version of this phenomenon, with no nucleus present and the electron and positron both traveling in the same direction as the initial photon. Energy conservation would lead to:
Ephoton=Eelectron+Epositron(4.3.1)
And x-momentum conservation:
Pcphoton=pcelectron+pcpositron(4.3.2)
Using
E_{total}^2 = (pc)^2 + (mc^2)^2
However, attempting to set up and solve the conservation rules for the real pair manufacturing process will include a significant amount of algebra. Instead, we'll assume that because the nucleus is much, much more massive than the electron and positron, it can "absorb" the required amount of momentum to ensure momentum conservation without "absorbing" much kinetic energy. In a sense, we will ignore the nucleus while solving the problem, and then check to see if ignoring the nucleus was a reasonable choice once we have a solution.
As an example, consider the problem below.
When a 3.0 MeV photon collides with a lead nucleus, an electron-positron pair is formed. The electron and positron travel perpendicular to the photon's initial path of passage.
a. Assume the nucleus is at rest after the collision and calculate the kinetic energy of the electron and positron.
b. To ensure momentum conservation, determine the kinetic energy of the lead nucleus. Would this amount of kinetic energy have a significant impact on component a's outcome?
Solution
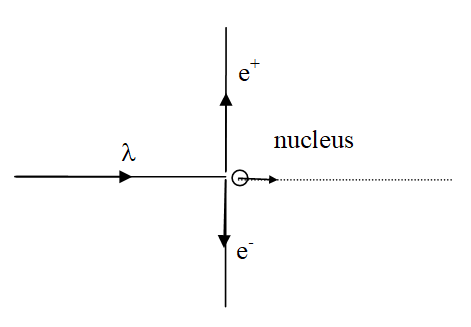
Energy conservation (ignoring the energy of the nucleus) leads to:
Ephoton=Eelectron+Epositron(4.3.7)
3=Eelectron+Epositron(4.3.8)
And yy-momentum conservation (ignoring the nucleus again):
0=−pcelectron+pcpositron(4.3.9)
Pcelectron=pcpositron(4.3.10)
Since the pair have equal momenta, they must have equal energy, so:
3=2Eeither(4.3.11)
Eeither−1.5 MeV(4.3.12)
KEeither=(1.5−0.511) MeV(4.3.13)
KEeither0.989 MeV(4.3.14)
To ensure that x-momentum is conserved,
Pcphoton=pcnucleus(4.3.15)
3 MeV=pcnucleus(4.3.16)
Using E2total=(pc)2+(mc2)2 and noting that the atomic mass of a lead atom is 207.2 u=193007 MeV207.2 yields,
Enucleus= (4.3.17)
(4.3.17)
Enucleus= (4.3.18)
(4.3.18)
then simplify using the binomial expansion,
Enucleus=193007 MeV(1+1291930072)(4.3.19)
Enucleus=193007 MeV(1+1.2×10−10)(4.3.20)
Enucleus=193007 MeV+2.33×10−5 MeV(4.3.21)
KEnucleus=2.33×10−5 MeV(4.3.22)
KEnucleus=23.3 eV(4.3.23)
As a result, the nucleus can maintain momentum conservation while stealing a minuscule fraction of the total energy available. As a result, we can ignore the nucleus when splitting the energy of the incoming photon between the electron and the positron.
4.8.1 Fission and Fusion
Introduction
The nucleus, which is the foundation of nuclear science, is made up of protons and neutrons. Understanding the process behind fission and fusion, which involves the dispersion and combination of elemental nuclei and isotopes, is an important part of nuclear research. Adding up the individual masses of each of these subatomic particles of any particular element will always give you a bigger mass than the mass of the nucleus as a whole. The concept of nuclear binding energy is missing from this finding. Nuclear binding energy is the energy required to keep the protons and neutrons of a nucleus intact, and the energy that is released during a nuclear fission or fusion is nuclear power. However, there are a few things to think about. The overall mass of an element's protons and neutrons is smaller than the mass of the nucleus as a whole. The nuclear binding energy is responsible for the mass difference. Nuclear binding energy is essentially seen as mass, and that mass becomes "missing." The nuclear energy, also known as the mass expelled from the process as neutrons, photons, or any other trajectory, is the missing mass, which is called mass defect. In a nutshell, the phrases "mass defect" and "nuclear binding energy" are synonymous.
4.8.2 Nuclear Fission and Fusion
The breaking of a heavy nucleus into two lighter nuclei is known as nuclear fission. The German scientists Otto Hahn, Lise Meitner, and Fritz Strassmann discovered fission in 1938 when they attacked a sample of uranium with neutrons in an attempt to create new elements with Z > 92. They noticed that lighter elements like barium (Z = 56) were created during the reaction and determined that these products had to come from uranium-235 fission induced by neutrons:
23592U+10n14156Ba+9236Kr+310n(1)(1)92235U+01n56141Ba+3692Kr+301n
The detection of the krypton-92 fission product backed up this theory. As explained in Section 20.2, the nucleus frequently divides asymmetrically rather than into two equal pieces, and a given nuclide's fission does not always produce the same products.
Each split nucleus releases more than one neutron in a typical nuclear fission reaction. A self-sustaining series of nuclear fission processes known as a nuclear chain reaction can ensue when these neutrons collide with and trigger fission in other adjacent nuclei (Figure). Fission of 235U, for example, releases two to three neutrons each fission event. When neutrons are absorbed by other 235U nuclei, they cause further fission events, increasing the pace of the fission reaction exponentially. A generation is a collection of events. Experiments show that a fissile isotope must have a minimum mass to sustain a nuclear chain reaction; if the mass is too low, too many neutrons escape without being collected, causing a fission reaction. The critical mass is the smallest mass that can maintain fission for an extended period of time. This amount is determined by the isotope's identity, as well as the purity of the material and the form of the mass, which correlates to the amount of surface area available from which neutrons can escape. If the mass of the fissile isotope is more than the critical mass, the resulting supercritical mass can release energy explosively under the correct conditions. The huge energy released by nuclear chain reactions is responsible for the catastrophic destruction produced by nuclear weapons like fission bombs, but it is also the foundation of the nuclear power industry.
Nuclear fusion is the reverse of nuclear fission, in which two light nuclei unite to form a heavier, more stable nucleus. The positive charge on both nuclei, as in the nuclear transmutation reactions outlined in Section 20.2, creates a large electrostatic energy barrier to fusion. This barrier can be broken if one or both particles have enough kinetic energy to overcome electrostatic repulsions, allowing the two nuclei to get near enough for fusion to happen. The concept is comparable to increasing the rate of a chemical reaction by adding heat. Fusion reactions are most exothermic for the lightest element, as demonstrated in Figure. 6.3's plot of nuclear binding energy per nucleon with atomic number. Two deuterium atoms, for example, fuse to form helium-3 in a typical fusion reaction known as deuterium–deuterium fusion (D–D fusion):
221H32He+10n(2) 221H32He+10n(2) 221H32He+10n(2) (2)
212H23He+01n
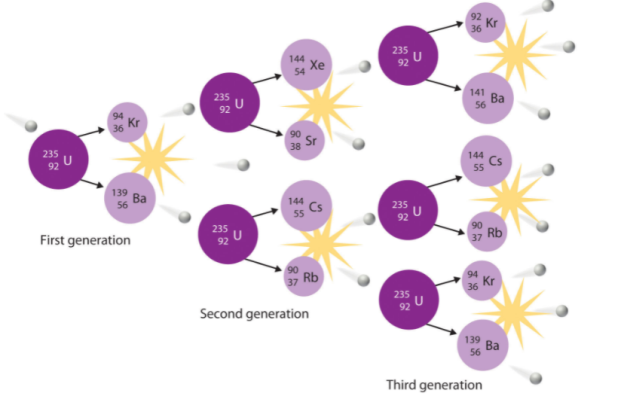
Figure: The rate of a fission process accelerates geometrically because each neutron released might promote the fission of another 235U nucleus. A generation is a collection of events.
Deuterium–tritium fusion (D–T fusion) is a reaction in which a deuterium atom and a tritium atom combine to form helium-4 (Figure 11):
12H+13H+24he+10n=12H+13H+24he+10n=12H+13H (3)

Nuclear fusion is depicted in Figure. Lighter nuclei combine to form a heavier nucleus in a nuclear fusion event. The fusion of 3H and 2H to produce 4He and a neutron produces a tremendous amount of energy, as depicted. Nuclear fusion has the potential to produce far more energy than fission, but it requires a lot of kinetic energy to overcome electrostatic repulsions between positively charged nuclei and start the fusion reaction.
However, to start these processes, a temperature similar to that of the sun's interior (about 1.5 107 K) is required. At the moment, the only way to achieve such a temperature on Earth is to detonate a fission bomb. The so-called hydrogen bomb (or H bomb) is actually a deuterium–tritium bomb (a D–T bomb), which uses a nuclear fission reaction to generate the extremely high temperatures required to ignite fusion of solid lithium deuteride (6LiD), releasing neutrons that react with 6Li to produce tritium. The deuterium-tritium process produces a large amount of energy. The tremendous amounts of energy produced by nuclear fission and fusion reactions are demonstrated in Example 21.6.3 and its accompanying exercise. Fusion processes, in fact, provide energy to all stars, including our sun.
We utilise Einstein's equation, which equates energy and mass, to compute the energy released during mass annihilation in both nuclear fission and fusion:
E=mc2(4)(4)E=mc2
With
● mm is mass (kilograms),
● cc is speed of light (meters/sec) and
● EE is energy (Joules).
Example:
Calculate the amount of energy released (in electron volts per atom and kilojoules per mole) when 235U is split into 144Cs, 90Rb, and two neutrons via neutron-induced fission:
23592U+10n→14455Cs+9037Rb+210n92235U+01n→55144Cs+3790Rb+201n
Given: balanced nuclear reaction
Asked for: energy released in electron volts per atom and kilojoules per mole
Strategy:
A Following the method used in Example 21.6.1, calculate the change in mass that accompanies the reaction. Convert this value to the change in energy in electron volts per atom.
B Calculate the change in mass per mole of 235U. Then use Equation 21.6.3 to calculate the change in energy in kilojoules per mole.
Solution
A The change in mass that accompanies the reaction is as follows:
Δm=mass products − mass reactants = mass (14455Cs+9037Rb+10n) − mass 23592 U=(143.932077 amu+89.914802 amu+1.008665 amu)−235.043930 amu=−0.188386 amu(5)(6)(7)(5)Δm=massproducts−massreactants=mass(55144Cs+3790Rb+01n)−mass 92235U(6)=(143.932077 amu+89.914802 amu+1.008665 amu)−235.043930 amu(7)=−0.188386 amu
The change in energy in electron volts per atom is as follows:
ΔE=(−0.188386 amu)(931 MeV/amu)=−175 MeVΔE=(−0.188386 amu)(931 MeV/amu)=−175 MeV
B The change in mass per mole of 23592U92235U is −0.188386 g = −1.88386 × 10−4 kg, so the change in energy in kilojoules per mole is as follows:
ΔE=(Δm)c2=(−1.88386×10−4 kg)(2.998×108 m/s)2=−1.693×1013 J/mol=−1.693×1010 kJ/mol(8)(9)(8)ΔE=(Δm)c2=(−1.88386×10−4 kg)(2.998×108 m/s)2(9)=−1.693×1013 J/mol=−1.693×1010 kJ/mol
Calculate the amount of energy (in electron volts per atom and kilojoules per mole) released when deuterium and tritium fuse to give helium-4 and a neutron:
21H+31H→42He+10n12H+13H→24He+01n
Solution
ΔE = −17.6 MeV/atom = −1.697 × 109 kJ/mol
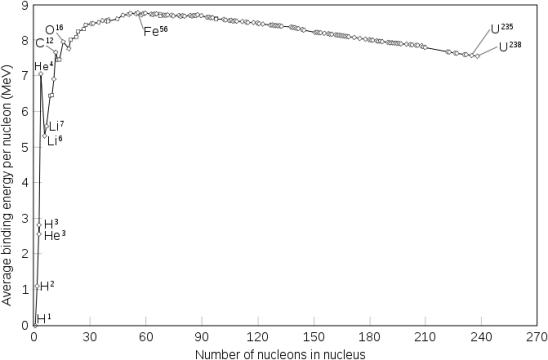
4.8.3 Fission
Fission occurs when a nucleus splits, releasing free neutrons and lighter nuclei. Heavy element fission is very exothermic, releasing roughly 200 million eV compared to coal combustion, which produces only a few eV. Because only 0.1 percent of the original nuclei are converted to energy, the quantity of energy released during nuclear fission is millions of times more efficient per mass than coal. As a result of the reaction, a daughter nucleus, energy, and particles such as neutrons are emitted. The released particles can then react with other radioactive materials, resulting in the production of daughter nuclei and more particles, and so on. Nuclear fission reactions are unique in that they can be harnessed and exploited in chain reactions. Nuclear weapons are built on this chain reaction. U235U235 is a well-known element utilised in nuclear fission that, when hit with a neutron, transforms into U236U236 which is even more unstable and splits into daughter nuclei such as Krypton-92 and Barium-141, as well as free neutrons. The fission products that occur are highly radioactive and frequently decay.
Nuclear fission occurs when the nucleus of an atom splits into nuclei of lighter atoms, releasing energy as a result of a neutron bombardment. Enrico Femi proposed the idea of nuclei splitting in 1934, believing that transuranium elements may be created by bombarding uranium with neutrons, because the loss of Beta particles would increase the atomic number. However, the properties of elements with greater atomic numbers than uranium did not coincide with the products that formed (Ra, Ac, Th, and Pa). They were instead radioisotopes of much lighter elements like Sr and Ba. The quantity of mass lost in the fission process is equal to 3.201011J3.201011J of energy.
● Consider the neutron bombardment
U92235+n10→U92236→fission products(10)
Which releases 3.20×10−11J3.20×10−11J per U235U235 atom.
How much energy would be released if 1.00g1.00g of U235U235 were to undergo fission?
Solution
(1.00gU235)×(1molU235235gU235)×(6.022×1023atomsU2351molU235)×(3.20×10−11J1atomU235)=8.20×1010J(11)
Clearly, the fission of a small amount of atoms can produce an enormous amount of energy, in the form of warmth and radiation (gamma waves). When an atom splits, each of the two new particles contains roughly half the neutrons and protons of the original nucleus, and in some cases a 2:3 ratio.
4.8.4 Critical Mass
A bomb will only explode if the chain reaction reaches its critical mass. A chain reaction reaches critical mass when it becomes self-sustaining. The reaction will not be self-sustaining if the neutrons are lost quicker than they are generated by fission. The spontaneous nuclear fission rate is the likelihood per second that an atom will spontaneously fission—that is, without any external interference. Nuclear fission is controlled in nuclear power plants by a medium such as water in the reactor. To cool the reactor and delay neutron particles, water is used as a heat transfer medium. The neutron emission and use can be controlled in this fashion. A meltdown will occur if the nuclear reaction is not regulated due to a lack of cooling water, for example.
4.8.5 Fusion
The combining of two nuclei to generate a heavier nucleus is known as nuclear fusion. Energy is released or absorbed as a result of the reaction. Fusion of nuclei with lower mass than iron produces energy, whereas fusion of nuclei with higher mass absorbs it. Iron peak is the name given to this phenomenon. Nuclear fission, on the other hand, has the opposite effect.
The energy generated from the sun and many other stars in the universe is driven by the power of the energy in a fusion process. Nuclear fusion is also used in nuclear weapons, namely the hydrogen bomb. Nuclear fusion is an energy-producing process that occurs at extremely high temperatures, such as those found in stars like the sun, when smaller nuclei are fused together to form a larger nucleus, releasing massive amounts of heat and radiation in the process. When left uncontrolled, this process can generate nearly infinite amounts of energy, and an unregulated chain can form the basis for a hydrogen bond, since hydrogen is regularly fused. This thermonuclear reaction is also fueled by the combining of deuterium atoms to generate helium atoms. Consider the following scenario:
H12+H13→He24+n01+energy(12)
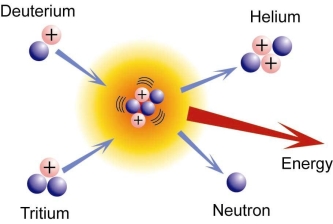
The difficulty of bringing deuterium and tritium nuclei into close contact, achieving high enough thermal energy, and thoroughly ionising gases into plasma are all issues that have yet to be thoroughly shown in a controlled fusion reaction. Plasma, which is a mixture of atomic nuclei and electrons that is required to launch a self-sustaining reaction at a temperature of more than 40,000,000 K, is an important component of nuclear fusion. Why does nuclear fusion require so much heat, even for light atoms like hydrogen? The reason for this is because the nucleus contains protons, and in order to overcome electrostatic resistance between the protons of both hydrogen atoms, both hydrogen nuclei must accelerate extremely fast and reach close enough for the nuclear force to initiate fusion. Nuclear fusion produces more energy than it takes to initiate it, hence the system's G is negative, indicating that the reaction is exothermic. The fusion of light elements is also self-sustaining because it is exothermic, as long as there is enough energy to start fusion in the first place.

4.8.6 Mass Defect
The disparity between the actual mass of an atom's nucleus and its expected mass based on the sum of its non-bound components is explained by nuclear binding energy.
Remember that the following equation connects energy (E) and mass (m):
[latex]E=mc^2[/latex]
The speed of light is denoted by c. The binding energy of nuclei is so high that it accounts for a large portion of their mass.
Because energy is withdrawn when the nucleus is formed, the actual mass is always smaller than the sum of the individual masses of the constituent protons and neutrons. The mass of this energy is subtracted from the overall mass of the original particles. The energy released when the nucleus is produced is represented by the mass defect, which is lacking in the subsequent nucleus.
Mass defect (Md) can be calculated as the difference between observed atomic mass (mo) and that expected from the combined masses of its protons (mp, each proton having a mass of 1.00728 amu) and neutrons (mn, 1.00867 amu):
[latex]M_d=(m_n+m_p)-m_o[/latex]
4.8.7 Mass–Energy Balance
The relationship between mass (m) and energy (E) is expressed in the following equation:
E=mc2(1)
Where
● cc is the speed of light (2.998×108m/s2.998×108m/s), and
The units for EE and mm are joules and kilograms, respectively.
This relationship was initially derived by Albert Einstein in 1905 as part of his special theory of relativity: a particle's mass is directly proportional to its energy. According to Equation 11, every mass has a corresponding energy, and any reaction involving a change in energy must also entail a change in mass. This means that all exothermic reactions should result in a mass loss, whereas all endothermic reactions should result in a mass increase. How can this be true, given the rule of conservation of mass? The answer to this seeming contradiction is that chemical processes do result in mass changes, but these changes are too small to be measured. All particles, as you may recall, have wavelike behaviour, but the wavelength is inversely related to the particle's mass (actually, to its momentum, the product of its mass and velocity). As a result, wavelike behaviour can only be detected in particles with extremely minuscule masses, such as electrons. The chemical equation for graphite burning to produce carbon dioxide, for example, is as follows:
C(graphite)+12O2(g)→CO2(g) ΔH∘=−393.5 kJ/mol
Combustion reactions are normally carried out under constant pressure, and the heat released or absorbed is equal to H under these conditions. The heat released or absorbed when a reaction is carried out at constant volume is equal to E. However, for the vast majority of chemical processes, E h. We can rewrite Einstein's equation as follows:
ΔE=(Δm)c2(3)
We can rearrange the equation to obtain the following relationship between the change in mass and the change in energy:
Δm=ΔEc2(4)
Because 1 J = 1 (kg•m2)/s2, the change in mass is as follows:
Δm=−393.5 kJ/mol(2.998×108 m/s)2=−3.935×105(kg⋅m2)/(s2⋅mol)(2.998×108 m/s)2=−4.38×10−12 kg/mol(5)
This corresponds to a mass change of around 3.6 1010 g/g carbon consumed, or about 100 millionths of an electron's mass per atom of carbon. In practise, the mass change is far too small to be measured experimentally and is therefore insignificant.
In comparison, a typical nuclear process involving an electron (a particle), such as the radioactive decay of 14C to 14N, results in a far bigger change in mass:
14C→14N+0−1β(6)
We can easily compute the change in mass using the empirically observed masses of subatomic particles and common isotopes listed in Table 20.1. A neutral 14C atom is converted to a positively charged 14N ion (with six, not seven, electrons) and a negatively charged particle (an electron) in this reaction, and the mass of the products is the same as that of a neutral 14N atom. The difference between the mass of a neutral 14N atom (14.003074 amu) and the mass of a 14C atom (14.003242 amu) is the entire change in mass during the reaction:
Δm=massproducts−massreactants=14.003074 amu−14.003242 amu=−0.000168 amu()
The difference in mass, which has been released as energy, corresponds to almost one-third of an electron. The change in mass for the decay of 1 mol of 14C is −0.000168 g = −1.68 × 10−4 g = −1.68 × 10−7 kg. Although a mass change of this magnitude may seem small, it is about 1000 times larger than the mass change for the combustion of graphite. The energy change is as follows:
ΔE=(Δm)c2=(−1.68×10−7 kg)(2.998×108 m/s)2=−1.51×1010(kg⋅m2)/s2=−1.51×1010 J=−1.51×107 kJ(9)(10)(9)ΔE=(Δm)c2=(−1.68×10−7 kg)(2.998×108 m/s)2(10)=−1.51×1010(kg⋅m2)/s2=−1.51×1010 J=−1.51×107 kJ
Even though 14C decay is a relatively low-energy nuclear reaction, the energy released in this nuclear reaction is more than 100,000 times larger than that generated in a normal chemical reaction.
Nuclear reactions are frequently represented in kiloelectronvolts (1 keV = 103 eV), mega electron volts (1 MeV = 106 eV), and even giga electron volts (1 GeV = 109 eV) per atom or particle since the energy changes are so significant. The change in energy that occurs as a result of a nuclear reaction can be computed using the formula 1 amu = 931 MeV. The energy released by one 14C atom decaying is therefore
(−1.68×10−4amu)(931MeVamu)=−0.156MeV=−156keV
Key takeaway:
● Nuclear energy is derived from the minor mass changes in nuclei that occur as a result of radioactive processes. Large nuclei break apart and release energy in fission; tiny nuclei unite and release energy in fusion.
● In 1932, nuclear fusion was shown in a laboratory for the first time.
● Since 1955, nuclear fusion has been a few decades away from commercialization.
● Nuclear fusion is the uniting (or fusion) of two bigger atoms, which releases a tremendous quantity of energy.
● Hydrogen is the fuel for nuclear fusion reactors, and Helium is the only by-product.
● Nuclear fission produced a million times the amount of energy produced by coal. Nuclear fusion generates 3-4 times the amount of energy as fission.
4.9.1 Generation of energy
E=mc2
In this equation, E denotes energy, mm denotes mass, and cc denotes the speed of light (31083108 metres per second), which is the constant that connects the two. Because mass is a measure of matter quantity, the importance of this equation is that matter can be turned into energy and vice versa. Let's compare this equation for converting matter and energy to some other similar conversion equations:
Inches = feet×12inches = feet×12
Or
Cents = dollars×100cents = dollars×100
When we convert matter into energy, we consider how much mass the matter has, just as any conversion formula allows you to compute the conversion of one item into another. In this situation, the conversion factor is neither 12 or 100, as in our previous instances, but another constant quantity: the speed of light squared. It's worth noting that this conversion doesn't require matter to travel at the speed of light (or the speed of light squared). The c2c2 factor is just the number that Einstein demonstrated must be used to connect mass and energy.
It's worth noting that this formula doesn't tell us how to convert mass to energy, much like the cents formula doesn't tell us where to swap coins for a dollar note. The formulas simply tell us what the corresponding numbers are if the conversion is successful. No one had any notion how to turn mass into energy in any practical sense when Einstein initially developed his formula in 1905. Einstein himself tried to dispel the notion that large-scale atomic mass to energy conversion would be possible in the near future. We regularly turn mass into energy in power plants, nuclear weapons, and high-energy physics experiments in particle accelerators nowadays as a result of advances in nuclear physics.
Because the speed of light squared (c2c2) is such a huge number, even a small amount of mass is converted into a big amount of energy. For example, converting 1 gramme of matter (about 1/28 ounce, or about 1 paperclip) to energy equivalent to burning 15,000 barrels of oil would yield the same amount of energy.
Scientists rapidly understood that the Sun's heat and light come from the conversion of mass into energy. The amount of energy radiated by the Sun could be produced by the complete conversion of nearly 4 million tonnes of matter into energy inside the Sun every second, according to Einstein's E=mc2E=mc2 equation. When compared to terrestrial objects, destroying 4 million tonnes every second may seem like a lot, but keep in mind that the Sun is a massive storehouse of matter. We will see that the Sun has more than enough mass to annihilate such massive amounts of matter while still blazing at its current rate for billions of years.
However, understanding all of this still leaves us with the question of how mass can be transformed into energy. To fully comprehend the process that occurs in the Sun, we must go further into the atom's structure.
4.9.2 Theory of relativity
Albert Einstein's two connected theories of special and general relativity are commonly referred to as the theory of relativity. In the absence of gravity, special relativity applies to all physical events. The law of gravitation and its relationship to other natural forces are explained by general relativity. It includes astronomy in the cosmological and astrophysical realms.
During the twentieth century, the idea revolutionised theoretical physics and astronomy, displacing a 200-year-old theory of mechanics developed principally by Isaac Newton. Spacetime as a single entity of space and time, simultaneity relativity, kinematic and gravitational time dilation, and length contraction were all introduced. Relativity advanced the understanding of elementary particles and their fundamental interactions, as well as ushering in the nuclear age, in the subject of physics. Cosmology and astrophysics predicted remarkable astronomical phenomena such as neutron stars, black holes, and gravitational waves based on Einstein's theory of relativity.
Relativity is a falsifiable theory in the sense that it offers predictions that can be tested in the lab. The principle of relativity, the constancy of the speed of light, and time dilation are all examples of special relativity. Since Einstein's article in 1905, the predictions of special relativity have been validated in various tests, but three experiments done between 1881 and 1938 were crucial to its validation. The Michelson–Morley experiment, the Kennedy–Thorndike experiment, and the Ives–Stilwell experiment are the three experiments in question. The Lorentz transformations were first deduced from first principles by Einstein in 1905, but these three experiments allow them to be induced from experimental evidence
Light is described as a wave that moves at a characteristic velocity according to Maxwell's equations, which are the foundation of classical electromagnetism. The present perspective is that light does not require a medium of transmission, but Maxwell and his contemporaries believed that light waves were propagated through a medium, similar to how sound travels through air and ripples travel across a pond's surface. The luminiferous aether, which is at rest in relation to the "fixed stars" and through which the Earth moves, was named after it. The measurement of first-order (v/c) effects was ruled out by Fresnel's partial ether dragging hypothesis, and though observations of second-order (v2/c2) effects were theoretically possible, Maxwell believed they were too small to be detected with then-current technology.
The Michelson–Morley experiment was set up to detect second-order effects of the "aether wind," or the movement of the aether relative to the earth. In order to accomplish this, Michelson created the Michelson interferometer. The apparatus was more than accurate enough to detect the expected effects, yet the first experiment in 1881 and the second experiment in 1887 yielded null results. Despite the sadness of not being able to identify an aether wind, the results were accepted by the scientific community. In order to save the aether paradigm, FitzGerald and Lorentz each devised an ad hoc hypothesis in which the length of material bodies varies as they move through the aether. FitzGerald–Lorentz contraction was born out of this, and their hypothesis had no theoretical foundation. The null result of the Michelson–Morley experiment indicates that the round-trip travel time for light is isotropic (independent of direction), yet this is insufficient to dismiss the aether hypothesis or support special relativity predictions.
While the Michelson–Morley experiment demonstrated that light has an isotropic velocity, it did not reveal how the magnitude of the velocity varied (if at all) in different inertial frames. The Kennedy–Thorndike experiment, initially carried out in 1932 by Roy Kennedy and Edward Thorndike, was supposed to do just that. They found no effect, concluding that "there is no influence... Until the solar system's velocity in space is little more than around half that of the earth in its orbit." That option was believed to be too fortuitous to be an acceptable explanation, thus they concluded that the round-trip duration for light is the same in all inertial reference frames based on the null result of their experiment.
Herbert Ives and G.R. Stilwell conducted the Ives–Stilwell experiment in 1938, and with improved accuracy in 1941. It was built to test Einstein's prediction of the transverse Doppler effect, which is the redshift of light from a moving source in a direction perpendicular to its velocity. The plan was to hunt for a Lorentz factor correction by comparing measured Doppler shifts to what was anticipated by classical theory. A similar adjustment was discovered, leading to the conclusion that special relativity alters the frequency of a moving atomic clock.
Those classic tests have been performed numerous times, each time with greater accuracy. Other investigations include relativistic energy and momentum increases at high speeds, experimental time dilation testing, and current Lorentz violations searches.
4.9.3 Special relativity
Special relativity is a theory of spacetime structure. It was first mentioned in Einstein's paper "On the Electrodynamics of Moving Bodies" published in 1905. (for the contributions of many other physicists see History of special relativity). Special relativity is founded on two contradicting postulates in classical mechanics:
1. For all observers in any inertial frame of reference relative to one another, the rules of physics are the same (principle of relativity).
2. Regardless of their relative mobility or the velocity of the light source, the speed of light in a vacuum is the same for all observers.
The resulting theory outperforms classical mechanics in terms of experimentation. For example, postulate 2 explains the Michelson–Morley experiment results. Furthermore, the theory has a number of unexpected and paradoxical ramifications. Here are a few examples:
If the observers are in relative motion, two events that are contemporaneous for one observer may not be simultaneous for another observer.
Time dilation refers to the fact that moving clocks tick more slowly than a "stationary" clock.
Objects are measured to be shortened in the direction that they are travelling with regard to the observer in length contraction.
The maximum speed is limited: in a vacuum, no physical item, communication, or field line can travel faster than the speed of light.
o Gravitational forces can only travel through space at the speed of light, not faster or instantly.
Equivalence of mass and energy: E = mc2, energy and mass are equivalent and interchangeable.
Some researchers use the term "relativistic mass."
[nine]
The Lorentz transformations replace the Galilean transformations of classical mechanics as the distinguishing feature of special relativity. (See Maxwell's electromagnetic equations.)
4.9.4 General relativity
Introduction to general relativity
General relativity is a gravitational theory developed by Albert Einstein between 1907 and 1915. The equivalence principle, which asserts that accelerated motion and being at rest in a gravitational field (for example, when standing on the surface of the Earth) are physically equal, was the foundation of general relativity. As a result, free fall is inertial motion: an item in free fall is falling because that is how objects move when no force is applied to them, rather than due to the force of gravity, as is the case in classical mechanics. This contradicts classical mechanics and special relativity, which state that inertially moving objects cannot accelerate with regard to one another, yet free-falling objects may. Einstein argued that spacetime is curved to overcome this problem. He developed the Einstein field equations in 1915, which relate the curvature of spacetime to the mass, energy, and momentum contained inside it.
Gravity time dilation: Clocks run slower in deeper gravitational wells, as a result of general relativity. [nine]
● Precession: In Newton's theory of gravity, orbits precess in an unexpected fashion. (This has been detected in Mercury's orbit as well as binary pulsars.)
● Light deflection occurs when light rays bend due to a gravitational field.
● Rotating masses "pull" the spacetime around them, which is known as frame-dragging.
● The cosmos is expanding metrically, and the distant reaches of it are moving away from us faster than the speed of light.
● General relativity is a gravitational theory that uses the Einstein field equations as its defining feature. The field equations' solutions are metric tensors, which determine the topology of spacetime and how inertial objects move.
4.10.1 Fission
The splitting of a nucleus is known as nuclear fission (or fissured). Controlled fission is a fact, while controlled fusion remains a distant dream. As seen in Figure 1, hundreds of nuclear fission power plants around the world attest to the fact that controlled fission is feasible and, at least in the short term, cost-effective. Following TMI and Chernobyl (and now Fukushima Daiichi), nuclear power was mostly forgotten for decades. However, mounting concerns about global warming have reintroduced nuclear power as a viable energy option. By the end of 2009, 442 reactors were operational in 30 nations, supplying 15% of global electricity. Nuclear power generates almost 75% of France's electricity, whereas the United States has 104 operational reactors that generate 20% of the country's electricity. There are none in Australia or New Zealand. China is constructing nuclear power reactors at a monthly rate of one.

Fission, on the other hand, is the polar opposite of fusion in that it only produces energy when heavy nuclei are separated. Energy is released when the products of a nuclear reaction have a higher binding energy per nucleon (BE/A) than the parent nuclei, as explained in Fusion. Figure 2 demonstrates that BE/A is higher for medium-mass nuclei than for heavy nuclei, meaning that when a heavy nucleus is split, the products have less mass per nucleon, resulting in mass destruction and energy release. Even by nuclear standards, the amount of energy released per fission reaction can be substantial. Figure 2 demonstrates that BE/A for the heaviest nuclei (A about 240) is around 7.6 MeV/nucleon, while BE/A for nuclei with A around 120 is around 8.6 MeV/nucleon. When a heavy nucleus breaks in half, around 1 MeV per nucleon is emitted, or roughly 240 MeV per fission. This is approximately 10 times the energy of a fusion reaction and approximately 100 times the energy of the average, or decay.
EXAMPLE 1. CALCULATING ENERGY RELEASED BY FISSION
Calculate the energy released in the following spontaneous fission reaction:
238U → 95Sr + 140Xe + 3n
Given the atomic masses to be m(238U) = 238.050784 u, m(95Sr) = 94.919388 u, m(140Xe) = 139.921610 u, and m(n) =1.008665 u.
Strategy
As always, the energy released is equal to the mass destroyed times c2, so we must find the difference in mass between the parent 238U and the fission products.
Solution
The products have a total mass of
Mproducts=94.919388 u+139.921610 u+3(1.008665 u)=237.866993 u
The mass lost is the mass of 238U minus mproducts, or
Δm = 238.050784 u− 237.8669933 u = 0.183791 u,
So the energy released is
E=(Δm)c2=(0.183791 u)931.5 MeV/c2uc2=171.2 MeV
Discussion
In this case, a lot of significant issues occur. The energy released was 171 MeV, which is little less than the 240 MeV previously estimated. This is due to the fact that the fission reaction produces neutrons rather than splitting the nucleus into two equal halves. The results of fission of a given nuclide, such as 238U, are not necessarily the same. Fission is a statistical process that produces a wide variety of products with varying probability. The majority of fission creates neutrons, though the number varies from fission to fission. This is a crucial aspect of fission because neutrons can produce further fission, allowing self-sustaining chain reactions to occur.
Although spontaneous fission is possible, it is rarely the most common decay mechanism for a specific nuclide. 238U, for example, can spontaneously fission but decays primarily by emission. As seen in Figure 2, neutron-induced fission is critical. Because neutrons are chargeless, they can strike a nucleus and be absorbed once they sense the nuclear force. Because the huge number of nucleons operate like atoms in a drop, a liquid drop model with surface tension and oscillation modes is used to represent big nuclei. The neutron is drawn to the nucleus and deposits energy, causing it to deform into a liquid drop. The nucleus narrows in the centre when extended far enough. The number of nucleons in contact is reduced, as is the strength of the nuclear force that holds the nucleus together. Coulomb repulsion between the two ends then fissions the nucleus, which splits into two huge pieces and a few neutrons like a water drop. Fission induced by neutrons can be written as
n + AX → FF1 + FF2 + xn,
FF1 and FF2 are the two daughter nuclei, also known as fission fragments, and x is the amount of neutrons produced. The masses of the fission fragments are usually not the same. The majority of the released energy is absorbed by the fission fragments' kinetic energy, with the remaining being absorbed by the neutrons and excited states of the fragments. Because neutrons can cause fission, a self-sustaining chain reaction can occur if more than one neutron is produced on average, or if x>1 in n + AX FF1 + FF2 + xn. Figure 3 depicts this as well. n+23592U14256Ba+9136Kr+3nn+92235U56142Ba+3691Kr+3n is an example of a typical neutron-induced fission process.
It's worth noting that the overall charge in this equation stays the same (is conserved): 56 + 36 Equals 92 + 0 Furthermore, in terms of whole numbers, the mass is constant: 1 + 235 = 142 + 91 + 3. When we consider the masses out to 6 or 7 significant places, as in the prior example, this is not the case.
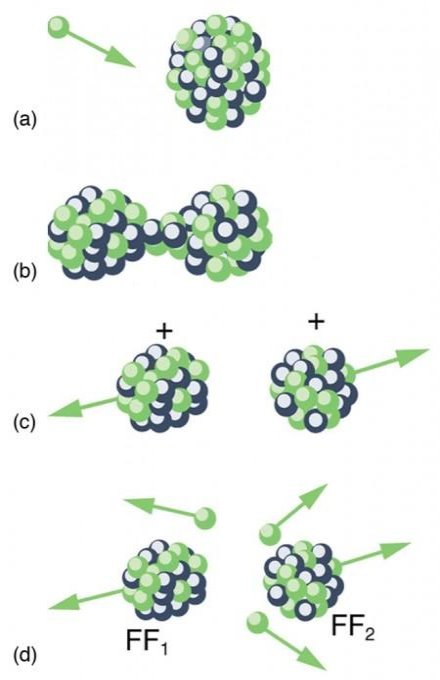
Figure shows neutron-induced fission. When a neutron is absorbed, energy is first transferred to this big nucleus. The nucleus deforms and begins to narrow in the middle, similar to a struck liquid drop. Because there are fewer nucleons in contact, the repulsive Coulomb force is able to split the nucleus in two, with some neutrons flying away as well.
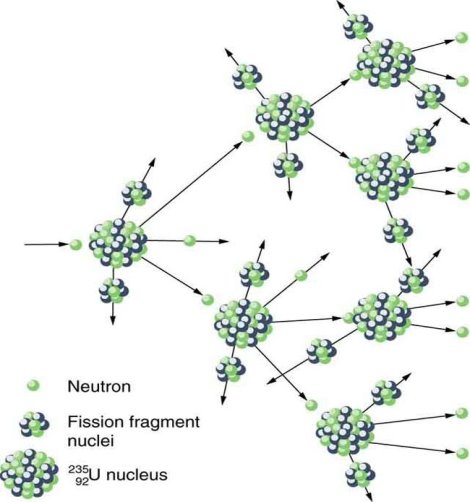
Fission is not induced by every neutron produced by fission. Some neutrons escape fissionable matter, while others connect with a nucleus but do not cause it to fission. By having a big volume of fissionable material, we can increase the number of fissions caused by neutrons. The critical mass of a nuclide is the smallest amount required for self-sustaining fission. Nuclides like 239Pu produce more neutrons per fission than nuclides like 235U. Furthermore, some nuclides are more easily fissionable than others. 235U and 239Pu, in instance, are easier to fission than the far more plentiful 238U. Both of these parameters have an impact on critical mass, which is the least for 239Pu.
The nuclear force is more appealing for an even number of neutrons in a nucleus than for an odd number, which is why 235U and 239Pu are simpler to fission than 238U. Consider the following examples: 23592U14392235U143 has 143 neutrons, 23994P14594239P145 has 145 neutrons, and 23892U14692238U146 has 146 neutrons. When a neutron collides with a nucleus that has an odd number of neutrons, the nuclear force becomes more appealing since the extra neutron evens out the number. In the resultant nucleus, around 2-MeV more energy is deposited than if the number of neutrons were previously equal. This increased energy causes additional deformation, which increases the likelihood of fission. As a result, 235U and 239Pu are better fission fuels. Natural uranium contains only 0.72 percent of the isotope 235U, while 238U contains 99.27 percent and 239Pu does not. Australia possesses the world's greatest uranium resources, accounting for 28% of the total. Kazakhstan and Canada are the next two countries on the list. Only 3% of worldwide reserves are held by the United States.
The majority of fission reactors use 235U, which is purified from 238U at a cost. This is referred to as enrichment. The most frequent separation method is uranium hexafluoride (UF6) gaseous diffusion across membranes. Because 235U has a lower mass than 238U, its UF6 molecules have a greater average velocity and diffuse quicker at the same temperature. Another intriguing feature of 235U is that it absorbs very slow moving neutrons (with energies a fraction of an eV), whereas fission reactions create fast neutrons with energies in the order of a MeV. To build a self-sustaining fission reactor with 235U, the neutrons must be slowed (“thermalized”). Because neutrons clash with protons in water molecules and waste energy, water is particularly effective. Figure 4 depicts a schematic of a pressurised water reactor architecture.
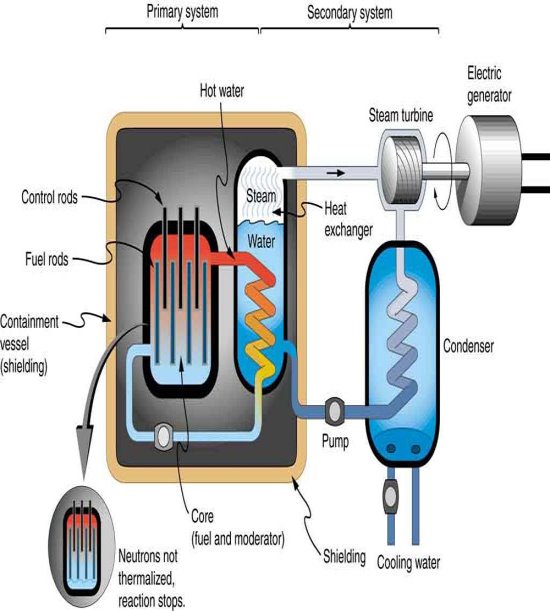
Figure: A pressurised water reactor is carefully built to regulate the fission of massive amounts of 235U while creating steam using the heat produced in the fission reaction. Control rods regulate neutron flux to achieve, but not exceed, criticality. The chain reaction will stop if the reactor overheats and boils the water away, because water is required to thermalize the neutrons. In extreme conditions, this built-in safety function may be overpowered.
Neutron flux is adjusted using control rods containing nuclides that significantly absorb neutrons. Reactors with hundreds to thousands of critical masses can generate massive amounts of energy, and the chain reaction can rapidly become self-sustaining, a situation known as criticality. To avoid supercriticality, or an exponential increase in fissions, neutron flux should be carefully managed. Overheating, and even a meltdown or explosive disassembly, can be avoided by the use of control rods. The water used to thermalize neutrons, which is required to cause fission in 235U and attain criticality, acts as a negative feedback system for temperature rises. The absence of water terminates the chain reaction if the reactor overheats and boils the water to steam or if it is breached. The reactor's radioactive fission products, on the other hand, can still generate a lot of heat. Other safety elements, such as auxiliary cooling water and pumps, must be included in the case of a coolant loss accident.
One nuclide already mentioned is 239Pu, which has a 24,120-y half-life and does not exist in nature. Plutonium-239 is manufactured from 238U in reactors, and it provides an opportunity to utilize the other 99% of natural uranium as an energy source. The following reaction sequence, called breeding, produces 239Pu. Breeding begins with neutron capture by 238U :
238U + n → 239U + γ.
Uranium-239 then β– decays:
239U → 239Np + β− + ve(t1/2 = 23 min).
Neptunium-239 also β– decays:
239Np → 239Pu + β− + ve(t1/2 = 2.4 d).
The pace at which Plutonium-239 accumulates in reactor fuel is determined by the probability of neutron capture by 238U. (all reactor fuel contains more 238U than 235U). Breeder reactors are reactors that are specially designed to produce plutonium. They appear to be fundamentally riskier than traditional reactors, although it is unclear whether their risks can be made economically acceptable. The four reactors at Chernobyl, including the one that exploded, were designed to provide energy while also breeding plutonium. The design of these reactors differed greatly from that of the pressurised water reactor shown above. As a reactor fuel, Plutonium-239 has an advantage over 235U: it produces more neutrons per fission on average, and it is easier to fission with a thermal neutron. It also differs chemically from uranium, making it easier to isolate from uranium ore. This means that 239Pu has a very low critical mass, which is advantageous for nuclear weapons.
4.10.2 Fission fragment
Chronicle of the life of a fission fragment.
The most common type of nuclear fission is the splitting of a nucleus into two pieces. When first produced, the two fragments are exceedingly radioactive and unstable. Each of them will go through a sequence of transformations in order to achieve stability. The time it takes for things to return to normal can vary greatly. The voyage is similar to that of a train that must stop at various stations before arriving at its destination. The nucleus at the bottom of the stability valley is the terminal.
Consider the fission of a uranium-235 nucleus into two pieces with 140 and 94 nucleons, respectively.
Neutron + 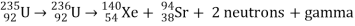
Production of two fragments with 140 and 94 nucleons.
The heaviest fragment is a radioactive xenon isotope with four more neutrons (86) than the closest stable isotope. This heavy fragment will evolve by emitting four beta electrons in a row, keeping its 140 nucleons, until it reaches a stable cerium-140 nucleus at the bottom of the stability. The cerium-140 fragment has four fewer neutrons (82) and four more protons (58) than the xenon-140 fragment.
Returning to the train analogy, the time it takes for xenon-140 to decay into cesium-140 is the time it takes for xenon-140 to decay into cesium-140: the half-life of this initial stage is 13.6 seconds, which is incredibly short. The second stage of the cesium-140 decay, with a half-life of 63 seconds, is also exceedingly brief. The third stage, baryum-140 degradation, lasts substantially longer, with a half-life of 12.7 days. Finally, the lanthanum-140 decay gives 1.67 days as the period of the last stage. The journey to the cerium-140 terminal will take roughly fifteen days in total, on the order of the longest half-life of 12.7 days.
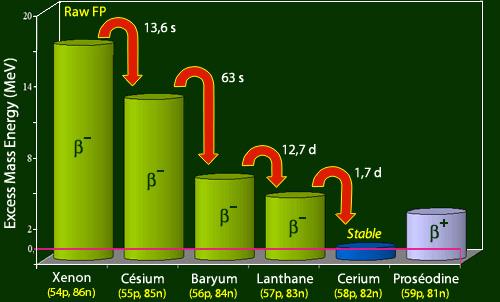
The fragment of 140 nucleons has evolved through time.
Cerium-140 is the lightest and most stable isotope in the family of 140 nucleons (shown in blue). The mass (internal) energy difference of the nuclei in this family compared to the mass of the stable cerium-140 nucleus is depicted in the diagram, with the nuclei organised according to their increasing number of protons. On the left is a raw fission fragment, a xenon-140 nucleus. It sheds its surplus mass energy by jumping four staircases to the stable cerium-140. Each jump is accompanied by the emission of a beta electron.
IN2P3 is a three-letter acronym that stands for "
To obtain a stable zirconium-94 nucleus, the lighter strontium-94 fragment goes through a similar development.
This is a generic scenario. Raw fission fragments far from stability achieve stability by one of two mechanisms provided by Nature: neutron expulsion or beta decay. Neutron expulsion is uncommon due to its high energy cost. It may only occur early in the transformation cascade, and then become energetically banned at a later stage. Expelled neutrons are produced after the fission process and the production of primary neutrons. These delayed neutrons serve a crucial role in the management of the chain reaction in reactors, despite their small numbers.
The beta decay is mostly responsible for the return to stability. The longest half-life in the decay cascade determines the duration of this return. Transformations into stable fission products are quick for xenon-140 and strontium-94, for example. This isn't always the case, however. It can take a long time to reach the bottom of the stability valley endpoint. The final stage of cesium-137 degrading into barium-137 will take 30 years for a piece of 137 nucleons. It will take 100,000 years for a 99 nucleon fragment of technetium-99 to decay into stable ruthenium-99.
Nuclear fuel typically lasts 3 to 4 years in reactor cores. Most fission pieces, including the xenon-140 fragment, would have had enough time to shed their radioactivity over this extended stay. Others, on the other hand, are unable to achieve steadiness. These fission products, which are sluggish to reach the final stage of stability, are responsible for much of the radioactivity in reactor spent nuclear fuel.
4.11.1 Slow neutrons.
The energy of neutrons produced by fission events diminishes on the order of a few electron volts or fractions of an electron volt after a series of encounters with different nuclei. Neutrons with energy in this range are said to as 'slow,' whereas neutrons with energy that match those of the surrounding atoms are referred to as 'thermal.'
These slow neutrons enable nuclear reactors to run on natural uranium or uranium that has been lightly enriched in fissile isotope 235 as fuel. The most prevalent pressurised (PWR) and boiling water (BWR) reactors would not function without them. As a result, collisions within a medium termed a moderator must slow down the neutrons released by nuclear fission. Reactors using natural uranium fuel, which contains only 0.7% fissile uranium 235, require efficient moderators that absorb extremely few neutrons: heavy water and pure graphite are examples of such moderators.
4.11.2 Slow neutrons favour fission
Slow neutrons are neutrons that have slowed down after colliding with atomic nuclei in nuclear reactors. The kinetic energy of these particles is on the order of a few electron volts or a fraction of an electron volt(eV). The neutron is said to be thermal when its energy is equivalent to the kinetic energies of the atoms in the medium through which it travels.
It's possible that the word "slow" is a misnomer. A thermal neutron with a charge of 0,025 electron volts travels at a speed of 2 km/sec, quicker than the fastest airliner. However, compared to the speed of light, 2 km/sec is a snail's pace. The kinetic energy of the neutron is more important than its speed.
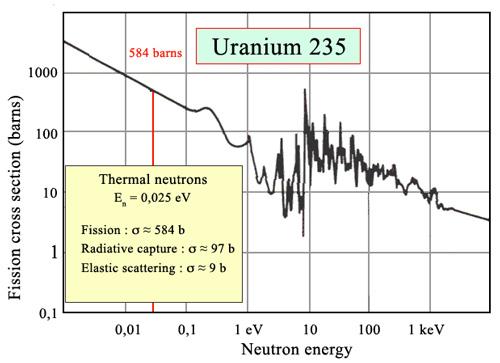
Fig. Uranium-235 fission probability
The chance of fission, also known as the fission cross-section by physicists, varies dramatically with neutron intensity. Barns are used to measure it. This fission probability is highest for a fissile nucleus like uranium-235 at kinetic energy of a few electron volts. Because the fraction of uranium-235 in most reactor fuels is only a few percent, it is necessary to compensate for this low proportion by increasing the fission probability of Uranium-235, and hence operate with a sluggish neutron flow.
IN2P3 is a three-letter acronym that stands for "
Slow neutrons allow civilian nuclear reactors to run on natural uranium or uranium that has been slightly enriched in the fissile isotope 235. The common pressurised (PWR) and boiling water (BWR) reactors could not function without slow neutrons. To accomplish this, the neutrons released by nuclear fission must collide with the atoms of a medium known as the moderator.
Only 0.7% of natural uranium includes fissile uranium 235. The use of natural uranium fuel in reactors necessitates the use of effective moderators that capture relatively few neutrons, such as heavy water or pure graphite.
When the fuel is enhanced by 3-4 percent, the moderator might be ordinary water that has been boiled or exposed to high pressure (An efficient coolant, water is also a convenient medium to evacuate the heat from the core of the reactor).
Slow neutrons enable civilian nuclear reactors to use nuclear fuel, such as natural uranium or uranium with a fissile isotope 235 enrichment. The chance of a thermal neutron of 0.025 eV fissioning a uranium-235 nucleus is 584 barns. This is a huge number when compared to the probability of a nucleus of the majority uranium-238 isitope being captured without fission, which is roughly 2 barns.
Slow neutrons do not contribute a considerable surplus of energy to the nucleus when collected. Only a few extremely fragile nuclei, named fissile for this reason, may fission: uranium-235 (the only one found in Natural), plutonium-239, and uranium-233.
Slow neutrons have the highest chance of being captured by a fissile nucleus and then triggering fission (called cross-section). The low proportion of the fuel is compensated for by the huge fission cross-section. It is thus possible to generate a chain reaction with natural or somewhat uranium fuel using a suitable moderator (0.7 percent to 5 percent isotope 235).
Everything happens as if slow neutrons notice a small fraction of uranium-235 or plutonium-239 nuclei that are significantly larger than the majority of uranium-238 nuclei that have a considerably lower chance of "sterile" capture without fission. Using a good moderator, it is then possible to get a chain reaction with the poor or somewhat enriched conditions mentioned earlier.
4.11.3 Nuclear reactor
A nuclear reactor, also known as an atomic pile, is a device that is used to start and control nuclear chain reactions or nuclear fusion processes. Nuclear reactors are used to generate electricity in nuclear power stations and for nuclear marine propulsion. Nuclear fission heat is transferred to a working fluid (water or gas), which then drives steam turbines. These either turn the shafts of electricity generators or drive the propellers of a ship. In principle, nuclear-generated steam can be used for industrial process heat or district heating. Some reactors create isotopes for medicinal and industrial purposes, while others produce weapons-grade plutonium. According to the International Atomic Energy Agency (IAEA), there are 454 nuclear power reactors and 226 nuclear research reactors in operation around the world as of early 2019.
Nuclear reactors transform the energy released by controlled nuclear fission into thermal energy for further conversion to mechanical or electrical forms, similar to how conventional thermal power plants generate electricity by harnessing the thermal energy created by burning fossil fuels.
4.11.4 Fission
Nuclear fission can occur when a big fissile atomic nucleus, such as uranium-235 or plutonium-239, receives a neutron. The heavy nucleus (the fission products) divides into two or more lighter nuclei, releasing kinetic energy, gamma radiation, and free neutrons. Other fissile atoms may absorb some of these neutrons, triggering other fission events, which release additional neutrons, and so on. A nuclear chain reaction is what this is called.
Control rods carrying neutron poisons and neutron moderators can alter the proportion of neutrons that go on to generate additional fission in such a nuclear chain reaction. If monitoring or equipment identifies harmful circumstances, most nuclear reactors feature automated and manual devices to shut off the fission reaction.
4.11.5 Heat generation
The reactor core generates heat in several ways: the kinetic energy of fission products is converted to thermal energy when these nuclei collide with nearby atoms; the reactor absorbs some of the gamma rays produced during fission and converts their energy into heat; and the reactor absorbs some of the gamma rays produced during fission and converts their energy into heat.
The radioactive decay of fission products and materials that have been activated by neutron absorption produces heat. Even after the reactor is turned off, the decay heat source will continue to exist.
A kilogram of uranium-235 (U-235) transformed through nuclear processes releases around three million times the energy of a kilograms of coal burned conventionally (7.2 1013 joules per kilograms of uranium-235 versus 2.4 107 joules per kilograms of coal).
4.11.6 Cooling
A nuclear reactor coolant — typically water, but occasionally a gas, a liquid metal (such as liquid sodium or lead), or molten salt — is pumped past the reactor core to absorb the heat it generates. The heat is transferred away from the reactor and used to produce steam. Like the pressurized water reactor, most reactor systems have a cooling system that is physically separated from the water that will be boiled to produce pressure steam for the turbines. However, in some reactors, such as the boiling water reactor, the water for the steam turbines is boiled directly by the reactor core.
4.11.7 Reactivity control
The quantity of neutrons capable of inducing further fission events can be controlled to influence the rate of fission reactions within a reactor core. To alter the reactor's power output, nuclear reactors commonly use a variety of neutron control technologies. Some of these approaches are based on the physics of radioactive decay and are simply accounted for during reactor operation, while others are built-in mechanisms with a specific goal in mind.
The control rods are the quickest way to modify the levels of fission-inducing neutrons in a reactor. Neutron poisons are used to make control rods, which absorb neutrons. When a control rod is put further into the reactor, it absorbs more neutrons than the substance it replaces, which is usually the moderator. As a result of this activity, there are fewer neutrons available for fission, lowering the reactor's power output. Extraction of the control rod, on the other hand, will result in an increase in the rate of fission events and a boost in power.
Neutron populations in a reactor are also affected by the physics of radioactive decay. Delay neutron emission by a number of neutron-rich fission isotopes is one of these processes. The delayed neutrons make up roughly 0.65% of all neutrons produced in fission, with the rest (dubbed "quick neutrons") released immediately after fission. Because the half-lives for the fission products that create delayed neutrons varies from milliseconds to several minutes, it takes a long time to determine when a reactor hits the critical point. Keeping the reactor in the chain reactivity zone, where delayed neutrons are required to achieve a critical mass state, allows mechanical devices or human operators to control a chain reaction in "real time"; otherwise, the time between criticality and nuclear meltdown as a result of an exponential power surge from a normal nuclear chain reaction would be too short to allow for a chain reaction to be controlled in "real time." The prompt critical point is the final step, where delayed neutrons are no longer required to maintain criticality. The bare criticality is known as zero dollars, the immediate critical point is one dollar, and other stages in the process are interpolated in cents, according to a scale for representing criticality in numerical form.
The coolant in certain reactors also serves as a neutron moderator. By causing the fast neutrons created by fission to lose energy and become thermal neutrons, a moderator increases the reactor's power. Thermal neutrons are more likely to produce fission than fast neutrons. Temperature fluctuations can impact the density of the coolant/moderator and thus modify power output if the coolant is a moderator. A cooler at a higher temperature would be less dense and hence less useful as a moderator.
In other reactors, the coolant, like the control rods, functions as a poison by absorbing neutrons. The power output of these reactors can be boosted by boiling the coolant, making it a less dense poison. In most nuclear reactors, automatic and manual procedures are in place to scram the reactor in the event of an emergency shutdown. If unsafe conditions are detected or anticipated, these systems inject massive volumes of poison (typically boron in the form of boric acid) into the reactor to stop the fission reaction.
The iodine pit, also known as xenon poisoning, is a process that affects most types of reactors. In the fission process, the common fission product Xenon-135 acts as a neutron poison, absorbing neutrons and so tending to shut down the reactor. The accumulation of xenon-135 can be managed by keeping power levels high enough to eliminate it as quickly as it is created by neutron absorption. Fission also produces iodine-135, which decays to fresh xenon-135, with a half-life of 6.57 hours. When the reactor is turned down, iodine-135 continues to decay to xenon-135, making restarting the reactor more difficult for a day or two until the xenon-135 decays to cesium-135, which has a half-life of 9.2 hours and is not nearly as deadly as xenon-135. The "iodine pit" is the name for this transitory state. The reactor can be restarted if it has enough excess reactivity capacity. The reactor experiences a "xenon burn off (power) transient" within a few hours when the additional xenon-135 is transmuted to xenon-136, which is substantially less of a neutron poison. To replace the neutron absorption of the lost xenon-135, more control rods must be inserted. A major stage in the Chernobyl tragedy was the failure to correctly follow such a protocol.
Nuclear reactors used in nuclear marine propulsion (particularly nuclear submarines) are frequently unable to operate at full power around the clock, as is the case with land-based power reactors, and must also have a lengthy core life without refueling. As a result, several designs use highly enriched uranium in the fuel rods but include burnable neutron poison. This enables the reactor to be built with an excess of fissionable material that is made relatively safe early in the fuel burn cycle by the presence of neutron-absorbing material, which is later replaced by normally produced long-lived neutron poisons (far longer-lived than xenon-135) that gradually accumulate over the fuel load's operating life.
Key takeaway:
● A cooling system that creates steam removes the heat produced by a nuclear reaction from the reactor core. The steam powers a turbine, which in turn powers a generator, which generates electricity. Fission can occur when a fissile atomic nucleus absorbs a neutron.
● Nuclear reactors work on the principle of nuclear fission, which is the splitting of a heavy atomic nucleus into two smaller fragments.
● This process releases a significant quantity of energy, which is used to fuel nuclear power plants.
4.12.1 Fusion reactions in stars
Stars' principal energy source and the process for the nucleosynthesis of light elements are fusion processes. Hans Bethe discovered in the late 1930s that the fusion of hydrogen nuclei to generate deuterium is exoergic (i.e., there is a net release of energy) and leads to the synthesis of helium when combined with subsequent nuclear processes. Helium production is the primary source of energy emitted by ordinary stars like the Sun, whose burning-core plasma has a temperature of less than 15,000,000 K. However, because the gas that forms a star often contains certain heavier elements, like as carbon (C) and nitrogen (N), nuclear interactions between protons and these nuclei are vital to consider. The proton-proton cycle is the reaction chain between protons that eventually leads to helium. When protons also cause carbon and nitrogen to burn, the CN cycle must be taken into account; and when oxygen (O) is added, the CNO bi-cycle must also be taken into account. (For further information, see the carbon cycle.)
In a hydrogen-only star, the proton-proton nuclear fusion cycle begins with the reaction H + H D + + + v; Q = 1.44 MeV, where the Q-value assumes positron annihilation by an electron. Although deuterium can combine with other deuterium nuclei, the D/H ratio is kept low, typically 1018, due to the abundance of hydrogen. As a result, the following phase is H + D 3He +; Q = 5.49 MeV, where shows that some of the energy output is carried away by gamma rays. The last stage in the chain, the burning of the helium-3 isotope, produces ordinary helium and hydrogen: 3He + 3He 4He + 2(H); Q = 12.86 MeV.
Because its reaction rate with hydrogen is minimal, helium-3 burns mostly by reactions with itself at equilibrium, while burning with deuterium is minimal due to the low deuterium concentration. If the temperature is greater than roughly 10,000,000 K, reactions with helium-3 can result in the creation of still-heavier elements such as beryllium-7, beryllium-8, lithium-7, and boron-8.
The stages of star evolution are the outcome of long-term compositional changes. A star's size, on the other hand, is determined by a balance between the pressure produced by hot plasma and the gravitational pull exerted by the mass of the star. The burning core's energy is carried to the star's surface, where it is radiated at a useful temperature. The effective temperature of the Sun's surface is around 6,000 K, and the Sun emits substantial amounts of visible and infrared radiation.
4.12.2 Inertial confinement fusion (ICF)
By creating pressures as high as 1017 pascals (1012 atmospheres) for periods as short as a nanosecond (109 second), a fuel mass is compressed fast to densities 1,000 to 10,000 times greater than normal. The implosion speed nears 3 105 metres per second near the end of this time span. The energy in converging shock waves is sufficient to heat the very centre of the fuel to temperatures high enough to initiate fusion reactions at maximum compression of the fuel, which is now in a cold plasma state (greater than an equivalent energy of about 4,400 eV). Before this hot plasma ball disassembles, energy will be created through fusion reactions if the bulk of this highly compressed fuel material is large enough. Much more energy can be released under ideal conditions than is required to compress and shock heat the fuel to thermonuclear burning temperatures.
The physical processes in ICF, such as collapse, compression heating, and the initiation of nuclear fusion, are similar to those in thermonuclear weapons and star formation. The scenario in star formation differs in one respect: a collapsed star begins to expand again due to heat from exoergic nuclear fusion processes, whereas a collapsed star is caused by gravity. The gravitational pull associated with the massive mass of the star eventually stops the expansion, bringing the size and temperature of the star to a state of equilibrium. The fuel in a thermonuclear bomb or ICF, on the other hand, totally disassembles. However, in the ideal ICF situation, this does not happen until around 30% of the fusion fuel has consumed.
The technology and methods for high-energy, short-time-pulse drivers, which are required to collapse the fusion fuel, have advanced significantly over the decades. A high-power laser is the most frequent driver, though particle accelerators capable of creating high-energy ion beams are also utilised. Experiments are presently being conducted with lasers that produce more than 100,000 joules in pulses of around one nanosecond, and the power available in brief bursts reaches 1014 watts.
Two lasers are operational, each capable of delivering up to 5,000,000 joules in equally brief bursts and generating a power output on the fusion targets of more than 5 1014 watts. The Laser Mega Joule in Bordeaux, France, is one such facility. The National Ignition Facility, located at the Lawrence Livermore National Laboratory in Livermore, California, is the other.
4.12.3 Muon-catalyzed fusion
The requirement to contain very high-temperature plasmas in classic nuclear fusion systems has led some researchers to look into alternatives that would allow fusion reactants to approach each other more closely at much lower temperatures. One approach includes replacing the electrons that normally surround the nucleus of a fuel atom with muons (). Muons are negatively charged subatomic particles that are comparable to electrons except that their mass is about 200 times that of an electron and that they are unstable, with a half-life of roughly 2.2 106 seconds. In reality, when muons were injected into liquid and gas mixes of deuterium and tritium at cryogenic temperatures, fusion was detected.
The technique of achieving fusion reactions by forcing a deuteron (deuterium nucleus, D+), a triton (tritium nucleus, T+), and a muon to produce a muonic molecule is known as muon-catalyzed fusion. The rate of fusion processes after the formation of a muonic molecule is around 3 108 seconds. A muonic molecule's production, on the other hand, is complicated, involving a succession of atomic, molecular, and nuclear processes.
When a muon enters a mixture of deuterium and tritium, it is initially grabbed by one of the two hydrogen isotopes present, generating either atomic D+- or T+-, and the atom is now in an excited state. Through a cascade collision process, the excited atom relaxes to its ground state, with the muon being transferred from a deuteron to a triton or vice versa. More importantly, the formation of a muonic molecule (D+—T+) is conceivable. Although a considerably uncommon reaction, once a muonic molecule forms, fusion occurs practically instantly, freeing the muon in the mixture for capture by a deuterium or tritium nucleus and allowing the process to continue. The muon functions as a trigger for fusion processes inside the mixture in this way. The ability to induce enough fusion reactions before the muon decays is essential for practical energy production.
The challenges of muon-catalyzed fusion are numerous, including producing muons (at an energy cost of around five billion electron volts per muon) and injecting them into the deuterium-tritium mixture instantly. Within the half-life of a muon, around 300 D-T fusion reactions must occur in order to produce more energy than is necessary to start the process.
4.12.4 Cold fusion and bubble fusion
There are two controversial fusion experiments worth mentioning. Martin Fleischmann of the University of Utah and Stanley Pons of the University of Southampton in England claimed in 1989 that they had successfully created fusion reactions at virtually room temperature. Electrolytic cells holding heavy water (deuterium oxide, D2O) and palladium rods that absorbed the deuterium from the heavy water comprised their system. Attempts to provide a theoretical explanation for the data, as well as worldwide efforts to replicate the purported cold fusion, were unsuccessful.
During acoustic cavitation experiments with chilled deuterated (bombarded with deuterium) acetone in 2002, Rusi Taleyar khan and colleagues at Purdue University in Lafayette, Indiana, claimed to have observed a statistically significant increase in nuclear emissions of products of fusion reactions (neutrons and tritium). Their setup was inspired by the well-known phenomena of sonoluminescence. A gas bubble is burst with high-pressure sound waves in sonoluminescence. Conditions of high density and temperature are obtained at the end of the implosion process, and for a short time following, resulting in light emission. The researchers claimed to have created densities and temperatures sufficient to cause fusion reactions just before the bubbles split up by starting with larger, millimetre-sized cavitations (bubbles) that had been deuterated in the acetone liquid. Most attempts to reproduce these outcomes, including cold fusion, have failed.
4.12.5 Stellar energy generation on the main sequence
We designate an object a star once fusion processes commence in the middle of a cloud of gas. A star's core fuses hydrogen into helium during the majority of its existence. During this phase, the star is either hot and luminous, if it is massive, or cool and dark, if it is a lightweight, on the HR diagram's main sequence.

Let's take a look at the nuclear reactions which provide energy during the hydrogen-burning phase of its life.
Nuclear Reactions on the main sequence
As long as stars are on the main sequence, they turn hydrogen nuclei into helium. The output helium has a smaller mass than the input hydrogens.
Mass of 1 proton p = 1.67358 x 10^(-27) kg
Mass of 4 protons 4p = 6.6943 x 10^(-27) kg
Mass of helium nucleus He = 6.6466 x 10^(-27) kg
--------------------------------------------------------------
Difference 4p - He = 0.0477 x 10^(-27) kg
The "missing" mass appears as energy, according to Einstein's famous equation E = mc^2. So, the net result of building one new helium atom is the release of
8 8
E = 0.0477 x 10^(-27) kg * (3 x 10 m/s) * (3 x 10 m/s)
= 4.3 x 10^(-12) Joules
It may be a small amount of energy per event, but at the core of a star, a LOT of reactions happen per second.
A simultaneous collision of four protons appears to be the most easy approach to create a helium nucleus:
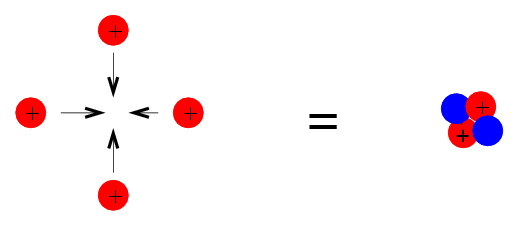
Unfortunately, the chances of four protons travelling in the same direction and colliding at the same time are extremely slim. Furthermore, because each proton has a positive charge, even if four protons moved in the same direction, their mutual electric repulsion would prevent them from fusing.
So, how does hydrogen become helium? It turns out that there are two different reactions that can lead to the same outcome.
The p-
It occurs in low-mass stars like our Sun and only involves hydrogen and helium isotopes.
The CNO cycle
Requires heavier elements (Carbon, Oxygen, Nitrogen) to act as catalyts; it dominates energy production in high-mass stars.
The p-p chain
The p-p chain is the main energy source in the Sun and stars which are less massive. It involves three steps:
Only the first stage necessitates the fusion of bare protons. Neutrons (shown as blue circles) are used in all subsequent phases to help overcome the electric repulsion. It's worth noting that the first and second processes must be repeated twice to generate the two helium-3 nuclei that will fuse in the final phase. This fundamental technique has various variations, but the one illustrated is the most frequent.
The p-p chain can only work if the temperatures in a star's core are high enough to force particles to collide violently. Around 10 million Kelvin is the key value. The quantity of energy generated by the chain is proportional to its temperature: higher temperatures result in more violent collisions, which lead to fusion more frequently. The rate of energy production is about.
Rate of energy production = (something) * T
The CNO cycle
The CNO cycle is the main energy source in stars more massive than the Sun. It involves many steps, and the assistance of "heavy" nuclei:
Only the main branches of the p-p chain are represented in the diagram above.
If the cloud from which a star forms contains only pure hydrogen, or hydrogen and helium, then the CNO cycle cannot take place: there won't be any Carbon, Nitrogen, or Oxygen atoms in the core. There were no "heavy" components in the initial generation of stars that formed after the Big Bang, so they couldn't have generated energy in this way.
The CNO cycle requires significantly greater temperatures than the p-p chain; below around 16 million Kelvin, it produces relatively little energy. The Sun's centre temperature, at 15 million Kelvin, is just below this essential number. Only stars with masses greater than our Sun may achieve such core temperatures.
The CNO cycle is extremely temperature sensitive once it begins to run. It can be written as the rate at which it creates energy.
20
Rate of energy production = (something) * T
Q: If the temperature at the center of a star
Rises by 10 percent, how much more energy
Is generated by the CNO cycle?
To sum it up, if you where a star falls on the HR diagram, then you know what sort of nuclear reactions are taking place deep within its interior:
4.12.6 A stellar thermostat
Both the p-p chain and the CNO cycle operate as stellar thermostats because they are so sensitive to temperature variations. Changes in the pace of energy generation can lead the gas layers above the core to expand outwards or contract inwards, depending on the rate of energy generation. However, the high temperatures required for fusion reactions are produced by the gravitational pressure of these overlying layers of gas. As a result, there is a delicate balance that tends to return to its original state.
Energy pushing OUT balances gravity pulling IN at Equilibrium Temp.
If the temperature in the centre of the building lowers,
o Energy production declines..
As a result, the amount of gas pushing outwards lowers...
As a result, gravity pulls the outer layers inwards.
It appears bleak... But as the outer layers press the core within, the situation improves.
o The centre temperature returns to its original level...
As a result, fusion rates rise...
As a result, more energy is created...
As a result, the gas pressure pushing outwards rises...
o resulting in the outer layers returning to their previous position
You can demonstrate that if the central temperature raises slightly for some reason, a similar set of activities will cause the core to expand slightly, causing the temperature to decrease back to its original amount.
In short, a stable equilibrium is achieved when the energy released by fusion events pushes outwards and the gravitational force pulls gas inside. A star will keep a nearly constant central temperature as long as it has hydrogen in its core to fuse, which means it will generate an approximately constant quantity of energy, which means it will shine with a nearly constant luminosity. During its long phase of hydrogen burning, its location on the HR diagram (based on luminosity and photosphere temperature) won't vary significantly.
4.12.7 Nuclear Fusion
Stars are largely comprised of hydrogen and helium, which are packed so densely in a star's core that the pressure is high enough to trigger nuclear fusion events. The nuclei of two atoms unite to form a new atom in a nuclear fusion reaction. Two hydrogen atoms fuse to form a helium atom most typically in the centre of a star. Although it takes a lot of energy to initiate a nuclear fusion process, once it is up and running, it produces vast amounts of energy (Figure below).

A thermonuclear bomb is a controlled fusion process that releases massive amounts of energy.
The energy released by fusion events in the centre of a star pushes outward to counteract gravity's inward pull. This energy travels outward through the star's layers until it reaches the star's outer surface. The star's outer layer burns brightly, emitting energy as electromagnetic radiation such as visible light, heat, ultraviolet light, and radio waves into space (Figure below).
Fig. A diagram of a star like the Sun.
Subatomic particles are accelerated in particle accelerators until they have about the same amount of energy as the centre of a star (Figure below). New particles are formed when these particles meet head-on. The nuclear fusion that occurs in the centres of stars is simulated by this mechanism. The procedure also mimics the conditions that permitted the first helium atom to form from the collision of two hydrogen atoms in the universe's early minutes.
Key takeaway:
● The creation of helium is the principal source of energy emitted by typical stars, such as the Sun, where the burning-core plasma has a temperature of less than 15,000,000 K. Fusion processes are the principal energy source of stars and the mechanism for the nucleosynthesis of the light elements.
References:
1.Quantum Mechanics: Theory and Applications, A.K.Ghatakand S. Lokanathan,(Macmillan)-2004
2. Introduction to Quantum Theory, David Park (Dover Publications)-1974
3. Theory and Problems of Modern Physics, Schaum‘s outline,R.Gautreau and W.Savin- (Tata McGraw-Hill) 2nd Edition
4. Physics for scientists and engineer with Modern Physics-Jewell and Serway -(CENGAGE Learnings) 2010.
5. Modern Physics of Atoms and Molecules Bransden and Joachim (PearsonIndia)-2003