Unit - 1
Complex Analysis
1.1.1 Complex number in mathematics:
Definition
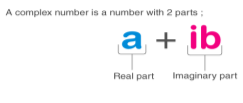
A complex number is a number that is made up of both real and imaginary numbers. The complex number is in the form of a+ib, where a = real number and ib = imaginary number. In addition, a,b are real values, and I = -1.
Hence, a complex number is a simple representation of addition of two numbers, i.e., real number and an imaginary number. One side is entirely genuine, while the other is entirely imagined.
What are Real Numbers?
Real numbers are any numbers that exist in a number system, such as positive, negative, zero, integer, rational, irrational, fractions, and so on. Re is the symbol for it (). 12, -45, 0, 1/7, 2.8, 5, and other real numbers are examples.
What are Imaginary Numbers?
Imaginary numbers are numbers that are not real. We get a negative return when we square an imaginary number. Im is the symbol for it (). For example, the numbers -2, -7, and 11 are all fictional.
To answer the equation x2+1 = 0, complex numbers were introduced. The equation's roots are of the form x = -1, and there are no true roots. As a result of the addition of complex numbers, we now have imaginary roots.
The symbol I which stands for Iota, is used to represent -1. (Imaginary number).
Notation
A complex number is defined as an equation of the form z= a+ib, where a and b are real numbers. Re z = a denotes the real part, while Im z = ib denotes the imaginary part.
Z = a + i b
Examples
To tell the difference between a real and an imaginary number, look at the table below.
Complex Number | Real Number | Imaginary Number |
-1+2i | -1 | 2i |
7-9i | 7 | -9i |
-6i | 0 | -6i (Purely Imaginary) |
6 | 6 | 0i (Purely Real) |
Is 0 a complex Number?
0 is a real number, as we all know. Real numbers are also included in the category of complex numbers. As a result, 0 is a complex number and can be written as 0+0i.
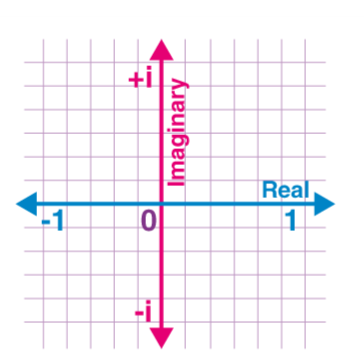
Graphical representation
Examine the axes in the graph below to see how complex numbers are represented. The x-axis represents the real part, while the y-axis represents the imaginary part.
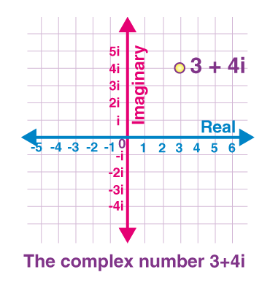
Let's have a look at an example. If we need to draw a graph of the complex number 3 + 4i, we can use the following formula.
Absolute Value
A real number's absolute value is the number itself. Modulus, i.e. |x|, represents the absolute value of x. As a result, the modulus of any value is always positive, as follows:
|3| = 3
|-3| = 3
Finding the modulus of complex numbers now requires a different approach.
Let's pretend that z = x+iy is a complicated number. After that, mod of z will be:
|z| = √(x2+y2)
When we apply the Pythagorean theorem in a complex plane, we get this expression. As a result, the mod of a complex number, z, is extended from 0 to z, while the mod of real numbers, x and y, are respectively extended from 0 to x and 0 to y. These numbers now form a right triangle, with 0 as the acute angle's vertex. Using Pythagoras' theorem as a guide,
|z|2 = |x|2+|y|2
|z|2 = x2 + y2
|z| = √(x2+y2)
Algebraic Operations on Complex Numbers
There are four different types of algebraic operations that can be performed on complex numbers, as listed below. More information about these algebraic operations, as well as solved examples, can be found in the linked article. The four operations on complex numbers are as follows:
- Addition
- Subtraction
- Multiplication
- Division
Roots of Complex Numbers
When we solve a quadratic equation of the form ax2 +bx+c = 0, we can discover the roots of the equations in three ways:
- Two Distinct Real Roots
- Similar Root
- No Real roots (Complex Roots)
Complex Number Formulas
Combine comparable phrases while executing complicated number arithmetic operations like addition and subtraction. It means that you should add real numbers to real numbers and imaginary numbers to imaginary numbers.
- Addition
(a + ib) + (c + id) = (a + c) + i(b + d)
- Subtraction
(a + ib) – (c + id) = (a – c) + i(b – d)
- Multiplication
When two complex integers are multiplied by each other, the technique should be identical to that of binomial multiplication. It denotes the application of the FOIL method (Distributive multiplication procedure).
(a + ib). (c + id) = (ac – bd) + i(ad + bc)
- Division
The FOIL Method can be used to divide two complex numbers by multiplying the numerator and denominator by the denominator's conjugate value and then applying the FOIL Method.
(a + ib) / (c + id) = (ac+bd)/ (c2 + d2) + i(bc – ad) / (c2 + d2)
Power of Iota (i)
It can take the following values depending on the power of I
i4k+1 = i.i4k+2 = -1 i4k+3 = -i.i4k = 1
Where k might have a positive or negative integral value (positive or negative).
Similarly, we may determine the values for the negative power of I as follows:
i-1 = 1 / i
We get the following by multiplying and dividing the above term with I
i-1 = 1 / i × i/i × i-1 = i / i2 = i / -1 = -i / -1 = -i
Note: √-1 × √-1 = √(-1 × -1) = √1 = 1 contradicts to the fact that i2 = -1.
As a result, a b is not equivalent to ab for an imaginary number.
Identities
Let us see some of the identities.
- (z1 + z2)2 = (z1)2 + (z2)2 + 2 z1 × z2
- (z1 – z2)2 = (z1)2 + (z2)2 – 2 z1 × z2
- (z1)2 – (z2)2 = (z1 + z2)(z1 – z2)
- (z1 + z2)3 = (z1)3 + 3(z1)2 z2 +3(z2)2 z1 + (z2)3
- (z1 – z2)3 = (z1)3 – 3(z1)2 z2 +3(z2)2 z1 – (z2)3
Properties
The properties of complex numbers are listed below:
1. A real number is obtained by adding two conjugate complex numbers.
2. A real number can be obtained by multiplying two conjugate complex numbers.
3.If x and y are real numbers and x+yi = 0, then x and y must be equal.
4. If p, q, r, and s are real numbers, and p+qi = r+si, p = r, and q=s.
5. The commutative law of addition and multiplication applies to complex numbers.
z1 + z2 = z1 + z2
z1 x z2 = z2 x z1 x z2 x z1 x z2
6. The associative law of addition and multiplication applies to complex numbers.
z1 + (z2+z3) = (z1+z2) + (z2+z3)
(z1.z2).z3 = (z1.z2).z3 = (z1.z2).z3 = (z1.z2).
(3.z2)
7. The distributive law applies to complex numbers.
z1.z2 + z1.z3 = z1.(z2+z3)
8. If the sum of two complex numbers is real, and the product of two complex numbers is also real, these numbers are conjugate.
9. If two complex numbers are given, say z1 and z2, then |z1+z2| = |z1|+|z2|.
10. The result of multiplying two complex numbers and their conjugate value should be another complex number with a positive value.
Modulus and Conjugate
Let z = a+ib be a complex number.
The Modulus of z is represented by |z|.
Mathematically, |z|=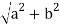
The conjugate of “z” is denoted by z¯.
Mathematically, z¯= a – ib
Argand Plane and Polar Form
The Argand(or complex) plane, like the XY plane, is a rectangular coordinate system in which the complex number a+ib is represented by a point with coordinates a and b.
The real and complex components are calculated in terms of r and, where r is the vector's length and r is the angle formed with the real axis. Check out this page for a full explanation of the argand plane and polar representation of complex numbers, along with solved examples.
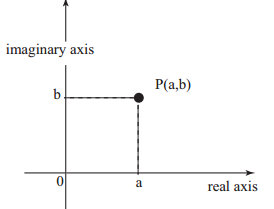
A point P(a,b) on a xy plane can represent the complex number z=a+ib. The actual part is represented by the x-axis, while the imaginary part is represented by the y-axis.
The Argand Plane, often known as the Complex Plane, is a type of graphic.
Points to Note
(1) The module of z is the length OP and is denoted by|z|
|z|=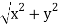
OP=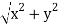
(2) The X-axis represents pure real numbers, whereas the y-axis represents pure imaginary numbers.
(3) The Line OP makes an angle θθ with the positive direction of x-axis in anti-clockwise sense is called the argument or amplitude of z
It is provided byθ=tan−1
(4) A complex number's argument is not unique because if is the value of argument, then 2nπ+θ (n=0, ±±1, ±±2, ....) The argument of a complex number is not unique because if is the value of argument, then
(5) The principal value of the amplitude or principal argument is the unique value of such that =.
(6) The main argument of a complex number can be found by following the steps below.
Step 1) for z=a+ib , find the acute angle value of θ=tan−1| |
|
Step 2) Look for the values of a ,b
If (a,b) lies in First quadrant then Argument=θ
If (a,b) lies in second quadrant then Argument =π−θ
If (a,b) lies in third quadrant then Argument =−π+θ
If (a,b) lies in Fourth quadrant then Argument =−θ
(7) The complex number's conjugate rotates symmetrically along the x-axis
(8) Every real number can be expressed as a complex number with no imaginary component. As though it were a +i(0) As a result, we can consider real numbers to be a subset of a larger set of complex numbers.
1.1.2 Geometry of complex number
Representation of Z modulus on Argand Plane
Argand plane consists of real axis (x – axis) and imaginary axis (y – axis).
|Z| = √(α – 0)2 + (β – 0)2
= √(α )2 + (β)2
= √Re (z )2 + Img (z)2
|z| = | α + iβ| = √(α )2 + (β)2
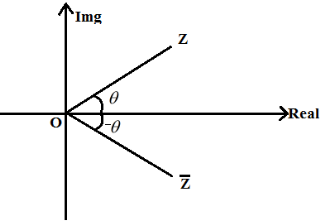
Conjugate of Complex Numbers on argand plane
A complex number's conjugate is a number with the same real portion and the opposite sign of the imaginary portion but identical magnitude.
The complex number Z = + I will be used.
The conjugate of a particular complex number will be represented as the mirror image of Z = + I along the real axis.

Z = α + iβ (complex number)
 (Conjugate of complex number)
(Conjugate of complex number)
Distance between Two Points in Complex Plane
In the argand plane, if two complex integers Z1 and Z2 are labelled as P and Q, respectively, the distance between P and Q is given as.
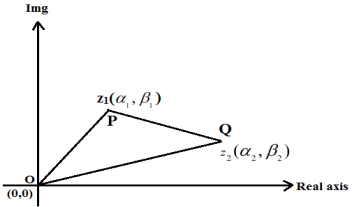
PQ = |z2 – z1| = |(α2 – α1) + i(β2 – β1)| = √( α2 – α1)2 + (β2 – β1)2
For example, Find the distance of a point P, Z = (3 + 4i) from origin.
Solution:
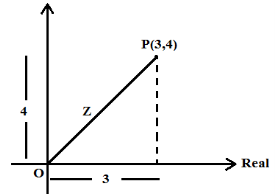
|Z| = |3 + 4i|
= √ 32 + 42 = 5 units
Polar form of complex number
Both rectangular and polar coordinates can be used to represent complex values. We'll look at the polar form of any complex number here.
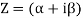

Z = α + iβ, |z| = r
OM = r cos θ = α
ON = r sin θ = β
Hence, Z = α + iβ
= (OM) + i (ON)
= r cos θ + i r sin θ = r( cos θ + i sin θ) r = 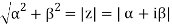
Where ‘' stands for complex number argument.
θ = arg (z)
For a complex number's conjugate
Arg (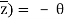
Algebra of Complex Numbers
Let's look at the many algebras for complex numbers. We mostly deal with complicated number addition, subtraction, multiplication, and division.
Product of two complex number
Let P and Q represent complex number
Z1=(α1+iβ1) and
Z2=(α2+iβ2) in argand plane
θ1=arg(z1),
θ2=arg(z2) (given)
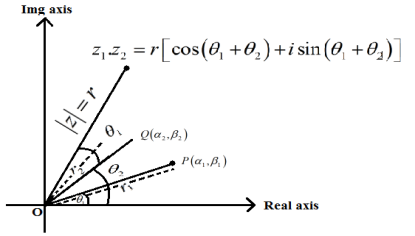
Now, on multiplying Z1 Z2 = Z
Z = ( α1 + i β1) ( α2 + i β2) = r1 ( cos θ1 + i sin θ1). r2 ( cos θ2 + i sin θ2)=
r1r2[ cos(θ1 + θ2) + i sin (θ1 + θ2)]
Let say r1. r2 = r
Z = r( cos(θ1 + θ2) + i sin (θ1 + θ2))
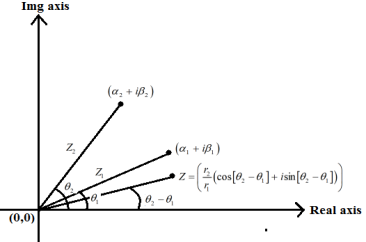
Two complex numbers are divided.
Let Z1 = α1 + i β1 = r1 (cos θ1 + i sin θ1)
Z2 = α2 + i β2 = r2 (cos θ2 + i sin θ2)
Where, θ1 = arg (Z1)
θ2 = arg (Z2)
Z now stands for a complicated number.
Z = Z2/Z1 = Z2Z1-1
Z = Z2 Z1-1 = Z2  / |Z|2
/ |Z|2
= r2/r1 (cos(θ2 – θ1) + i sin (θ2 – θ1))
Note:
1. When two complex numbers are multiplied, their argument is added.
θ=θ1+θ2
2. The argument of two complex numbers is subtracted when they are divided.
θ=θ1−θ2
Equation of Straight Line Passing through Two Complex Points
The equation of a straight line going through two points (x1, y1) and (x2, y2) has been examined in Algebra.
y – y1 = y2 – y1/ x2 – x1 (x – x1)
In complex numbers
A straight-line equation passes through two points. A(Z1) and B(Z2) are two variables that can be expressed as
Z – Z1 = Z2 – Z1/ 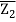 -
-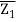 (
(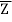 -
-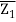 )
)
Z – Z1/ Z2 – Z1 = 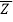 -
-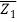 /
/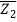 -
-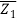
Where Z stands for Z's conjugate.
Or
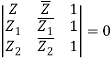
Section Formula in Complex Numbers
The three points on a line are A(Z1), B(Z2), and C(Z).
If C splits line AB in the ratio m:n (internally), then
AC/BC = m/n
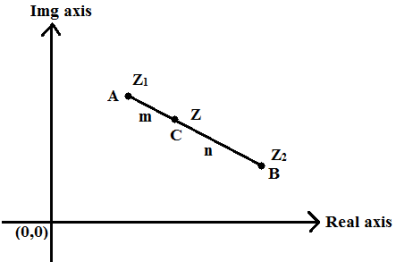
Then, Z = mZ2 + nZ1/ m+n
Co-linearity condition
Let A(Z1), B(Z2), and C(Z3) be the three points Z1, Z2, and Z3 (Z3).
As a result, collinearity will be a condition.
|AB| + |BC| = |AC|
Or,
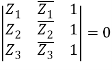
Equation of circle in Complex Plane
The complex number Z0 is represented by a circle whose centre is the complex number Z0. And let the radius be ‘r'.
The circle's equation will be
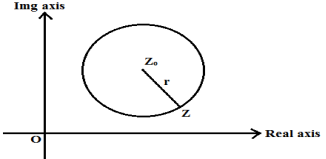
|Z – Z0| = r
If Z1 and Z2 are the circle's diametric end points, the equation is
( Z – Z1)(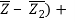 ( Z – Z2)(
( Z – Z2)(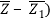 = 0
= 0
NUMERICALS
- Perform the indicated operation and write your answer in standard form.
(4 – 5i)(12 + 11i)
Ans:
We know how to multiply two polynomials and so we also know how to multiply two complex numbers. All we need to do is “foil” the two complex numbers to get,
(4 – 5i)(12 +11i) = 48 + 44i – 60i – 55i2 = 48 – 16i – 55i2
All we need to do to finish the problem is to recall that i2=−1. Upon using this fact we can finish the problem.
|(4 – 5i)(12 + 11i) = 48 – 16i – 55 (-1) = 103 – 16i
- Perform the indicated operation and write your answer in standard form.
7 – i/ 2 + 10i
Ans:
Because standard form does not allow for ii’s to be in the denominator we’ll need to multiply the numerator and denominator by the conjugate of the denominator, which is 2−10i.
Multiplying by the conjugate gives,
7 – i/ 2 + 10i 2- 10i/2-10i = (7 – i)(2 – 10i)/(2 + 10i)(2 – 10i)
Now all we need to do is do the multiplication in the numerator and denominator and put the result in standard form.
7 – i/2+10i = 14 – 72i + 10i2/ 4 – 100i2 = 4 – 72i/ 104 = 4/104 – 72/104 i = 1/26 – 9/13 i
1.2.1 Euler’s Formula Explained: Introduction, Interpretation and Examples:
Euler's formula is the theorem that asserts, in a word, that
eix = cos x + i sin x
- The number x is a genuine number. The natural logarithm's base is e. The imaginary unit (i.e., the square root of 1) is denoted by the letter i.
- The essential link between trigonometric and exponential functions is established by Euler's formula. It can be viewed of as a technique of linking two representations of the same unit complex number in the complex plane from a geometric standpoint.
- Let's look at some of the main values in Euler's formula and see how they relate to trigonometric/unit circle points:
- We have e0=cos0+isin0 for x=0, which provides 1=1. So far, so good: we know that a 0 degree angle on the trigonometric circle equals a 1 degree angle on the real axis, and that's what we get here. We have ei=cos1+isin1 for x=1. This implies that ei is the exact point on the unit circle with a 1 radian angle. We have ei2=cos2+isin2=i for x=2. This finding is important in a number of physics calculations. We have ei=cos+isin for x=, which suggests that ei=1. This result is the same as the well-known Euler's identity. We have ei(2 )=cos2+isin2 for x=2, which means that ei(2 )=1, the same as for x=0.
- The following is a rewrite of Euler's formula that will help you comprehend it better:
- (ei)x=sinx+icosx
- The unit complex number with angle x can be thought of as the right-hand equation.
- The 1-radian unit complex number increased to x can be thought of as the left-hand expression.
- Euler's formula can be interpreted as two distinct ways of running around the unit circle to arrive at the same place, because increasing a unit complex number to a power can be thought of as repeated multiplications (i.e., adding up angles in this example).
1.2.2 Derivations
There are at least three techniques to prove Euler's formula. The first derivation is based on power series, in which the exponential, sine, and cosine functions are expanded as power series to determine whether or not the formula holds.
The second derivation of Euler's formula is based on calculus, which treats both sides of the equation as functions and differentiates them accordingly. This leads to the discovery of a common attribute that can be used to demonstrate that both functions are equivalent.
Another way to derive Euler's formula is to utilise polar coordinates in the complex plane, which can then be used to find the values of r and.
Derivation 1: Power Series
The use of power series is one of the more intuitive derivations of Euler's formula. It entails expanding the exponential, sine, and cosine power series to arrive at the conclusion that the equivalence holds.
As a precaution, this method presupposes that the sinz, cosz, and ez power series expansions are perfectly convergent everywhere (e.g., that they hold for all complex numbers z). It does, however, have the advantage of demonstrating that Euler's formula holds for all complex numbers z.
The power series expansion of ez for a complex variable z is
ez = 1 + z/ 1! + z2/2! + z3/3! + z4/4! + . . .
Let's pretend that z is ix (where x is an arbitrary complex number). I am raised to greater powers as z is raised to greater abilities. The first eight powers of I are as follows:
i0 = 1 i4 = i2 . i2 = 1
i1 = i i5 = i . i4 =i
i2 = 1 (by the definition of i) i6 = i . i5 = -1
i3 = i . i2 = - i i7 = i . i6 = -i
(Notice how the powers of I are cyclical: 1, I 1, i. We'll be putting these abilities to good use soon.)
When z=ix, the expansion of ez is as follows:
eix = 1 + ix + (ix)2/2! + (ix)3/3! + (ix)4/4! + . . .
We get the following results when we extract the powers of I
eix = 1 + ix - (ix)2/2! - (ix)3/3! + (ix)4/4! + (ix)5/5! - (ix)6/6! - (ix)7/7! + (ix)8/8! +. . .
We can rearrange the terms of ez's power series expansion without changing its value because it is totally convergent. The result of combining the real and imaginary terms is
eix = (1 - x2/2! + x4/4! - x6/6! + x8/8! - . . .) + i (x – x3/3! + x5/5! – x7/7! +. . .)
Let's take a detour and look at the sine and cosine power series. The cos x power series is
Cos x = 1 - x2/2! + x4/4! - x6/6! + x8/8! - . . .
And for sinx, it is
Sin x = x – x3/3! + x5/5! – x7/7! +. . .
To put it another way, the last equation we had was exact.
eix = cos x + i sin x
This is the Euler's formula statement we were seeking for.
Derivation 2: Calculus
Consider both eix and cosx+isinx as functions of x before differentiating them to locate a common attribute between them.
However, in order for this to happen, one must suppose that the functions ez, cosx, and sinx are defined and differentiable for all real and complex values x and z. It is also possible to establish that Euler's formula holds for all complex numbers by assuming that these functions are differentiable for all complex numbers.
First, let f1(x) and f2(x) be eix and cosx+isinx,
:correspondingly The chain rule is then used to differentiate f1 and the result is
f’1 (x) = i eix = i f1(x)
Differentiating f2 produces the following results:
f’2 (x) = - sin x + i cos x = i f2 (x)
In other words, the differential equation f′(x)=if is satisfied by both functions (x). Consider the function f 1/f 2, which is well-defined for all x (since f2(x)=cosx+isinx corresponds to never-zero points on the unit circle). After that, applying the quotient rule to this function yields:
(f1/f2)’ (x) = f’1(x)f2(x) – f1(x)f’2(x)/ [ f2(x)]2
= if1(x) f2(x) – f1(x) i f2(x)/ [ f2(x)]2
= 0
Because the derivative is 0 in this case, the function f 1/f 2 must have been a constant to begin with. What is this constant's value? Let's see what happens if we put x=0 into the function:
In other words, we must have that for all x: which becomes the renowned formula we've been looking for after moving cosx+isinx to the right.
Derivation 3: Polar Coordinates
Another clever proof of Euler's formula is to treat exponentials like numbers, or more precisely, as complex numbers in polar coordinates.
We already know that all non-zero complex numbers have a unique way of being expressed in polar coordinates. In specifically, any non-zero number of the type eix (with real x) can be represented as:
eix = r(cos θ + i sin θ)
Where r is its radius (with r>0) and is its primary angle from the positive real axis (say, 02). Except for the fact that r and are functions of x, we make no assumptions about their values (which may or may not contain x as variable). They'll be determined as the proof progresses.
(However, we do know that for x=0, the left-hand side is 1, implying that r and meet the r(0)=1 and (0)=0 beginning conditions, respectively.)
For what it's worth, let's start by separating the two sides of the equation. Differentiating the left side of the equation with respect to x provides ieix, according to the definition of exponential. The equation becomes: after differentiating the right side of the equation.
Ieix = dr/dx (cos θ + i sin θ) + r( - sin θ + i cos θ) d θ/dx
We're seeking for a statement that is unique in terms of the letters r and. To get rid of eix, we replace it with r(cos+isin) and get:
Ir(cos θ + i sin θ) = (cos θ + i sin θ) dr/dx + r(- sin θ + i cos θ) d θ/dx
The I on the left-hand side is then distributed, yielding:
r(i cos θ – sin θ) = ( cos θ + i sin θ) dr/dx + r ( - sin θ + i cos θ) d θ/dx
When the imagined and actual components are added together, we get:
Ir cos θ = i sin θ dr/dx + i r cos θ d θ/dx
And
-r sin θ = cos θ dr/dx – r sin θ d θ/dx
The variables dr/dx and d/dx are the variables in this system of two equations and two unknowns. In only a few steps, we'll be able to solve it. First, we get: by assigning to dr/dx and d/dx:
r cos θ = ( sin θ)α + (r cos θ)β (I)
-rsin θ = (cos θ) α – ( r sin θ) β (II)
Second, we get (I) by cos and (II) by sin by multiplying (I) by cos and (II) by sin.:
r cos2 θ = ( sin θ cos θ)α + (r cos2 θ)β (III)
-rsin2 θ = (sin θ cos θ) α – ( r sin2 θ) β (IV)
The goal of these operations is to eliminate by doing (III) – (IV), which results in:
r( cos2 θ + sin2 θ) = r( cos 2 θ + sin2 θ) β
Because cos2+sin2=1, a more straightforward equation emerges:
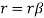
And because r>0 for any x, this means that — which we specified to be d/dx — is equal to 1.
Substituting this result back into (I) and (II) and cancelling the result, we get:
0=(sinθ)α
0=(cosθ)α
This indicates that — which we have determined to be the case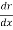 —0 must be present.
—0 must be present.
We may deduce that r must be a constant from the fact that dr/dx=0. Similarly, we can derive that =x+C for some constant C from the fact that d/dx=1.
However, we must have r=1 because r meets the beginning condition r(0)=1. Similarly, we must have C=0 since meets the beginning condition (0)=0. That is, x Now that we know what r and are, we can insert them into the original equation to get:
eix = r( cos θ + i sin θ)
= cos x + i sin x
Which, as one might anticipate, is the exact formulation of Euler's formula for real numbers x.
Applications
Euler's formula, as one of the most important equations in mathematics, has a plethora of interesting applications in a variety of fields. These include, for example:
- The famous Euler's identity The exponential form of complex numbers Trigonometric and hyperbolic functions with different meanings
- Exponential and logarithmic functions are generalised to complex numbers.
- De Moivre's theorem alternate proofs and trigonometric additive identities
- Euler's Personality
- Euler's identity is frequently regarded as mathematics' most beautiful equation. It's written like this:
- Ei+1=0
- Where five of the most essential constants in mathematics are highlighted. These are the following:
- The identity of addition 0
- The unity number one
- The Pi constant (circumference to diameter ratio) is a mathematical constant.
- e is the natural logarithm's base.
- The fictitious unit I
Integers, irrational numbers, and imaginary numbers are among the three types of numbers represented. Addition, multiplication, and exponentiation are three basic mathematical operations that are also illustrated.
Starting with Euler's formula eix=cosx+isinx, we set x= and transmit the succeeding 1 to the left-hand side to obtain Euler's identity. The intermediate forme iπ=−1is common in the context of trigonometric unit circle in the complex plane: it corresponds to the point on the unit circle whose angle with respect to the positive real axis is π.
Exponential Form for Complex Numbers
We already know that a complex number z may be written in Cartesian coordinates as x+iy, where x and y are the real and imaginary parts of z, respectively.
In fact, the identical complex number may be written in polar coordinates as r(cos+isin), where r is the magnitude of the distance to the origin and is the angle with respect to the positive real axis.
But it doesn't stop there: every complex number can now be written as a complex exponential using Euler's formula:
z=r(cosθ+isinθ)=reiθ
Where the numbers r and are the same as previously.
To go from (x,y) to (r,θ),
We employ formulae.
r = 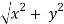
θ = a tan2(y, x)
(where 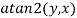 is the two-argument arc tangent
is the two-argument arc tangent
Function with atan2(y,x)=arctan( ) whenever x>0.)
) whenever x>0.)
To go from (r,) to (x,y), we utilise the following formulas: rcosy=rsin x=rcosy=rsin In the same manner that rectangular coordinates make addition simple, the exponential form of complex numbers makes multiplying complex numbers considerably easier. For example, if we have two complex numbers z1=r1ei1 and z2=r2ei2, we can multiply them as follows:
z1z2 = r1eiθ1 . r2eiθ2
= r1 . r2ei(θ1+θ2)
In the same vein, the same two numbers can be divided as follows:
z1/z2 = r1eiθ1/ r2eiθ2
= r1 ./r2ei(θ1-θ2)
The identical division would have required multiplying by the complex conjugate in the numerator and denominator if we had used the rectangular x+iy notation instead. The situation would have been the same if the polar coordinates had been used (save perhaps worse).
Multiplying two complex numbers is actually the same as multiplying magnitudes and adding angles, while dividing two complex numbers is really the same as dividing magnitudes and subtracting angles.
Alternative Key Function Definitions
Euler's formula can also be used to define essential functions like the complex exponential function, trigonometric functions like sine, cosine, and tangent, as well as their hyperbolic analogues. It can also be used to figure out how some of these functions relate to one another.
Exponential Function (Complex)
To begin, remember Euler's formula, which asserts that
eix = cos x + i sin x
The exponential function is only defined up to the imaginary numbers if the formula is assumed to hold exclusively for real x. However, by using a simple method, we may extend the exponential function to encompass all complex numbers:
ez = ex+ iy ( = ex eiy) = dy = ex(cos y + i sin y)
In other words, the complex number x+iy's exponential is just the complex number with magnitude ex and angle y. This means that the complex exponential effectively transfers vertical lines to circles. Here's an example of what I'm talking about:
Trigonometric Functions are a type of trigonometric function that is used
We may utilise Euler's formula to get a similar equation for the opposite anglex, in addition to increasing the domain of exponential functions:
e-ix = cos x – i sin x
This equation, along with Euler's formula, create a system of equations from which the sine and cosine functions can be isolated.
The cosines cancel out when the eix equation is subtracted from the eix equation, and after dividing by 2i, we get the complex exponential form of the sine function:
Sin x = eix – e-ix/2i
Similarly, the sines cancel out when the two equations are added together, and after dividing by two, we get the complex exponential form of the cosine function:
Cos x = eix + e-ix/2
To be sure, here's a movie that goes over the same derivations in greater depth.
On the other hand, the tangent function is defined to be sin x / cos x, so in terms of complex exponentials, it becomes:
Tan x = eix – e-ix/ i (eix + e-ix)
If we can show that Euler's formula holds for all complex numbers (as we did in the power series demonstration), then the same can be said for these three formulas. When it comes to computing derivatives and integrals, their presence allows us to flexibly move between trigonometric functions and complex exponentials.
De Moivre's theorem establishes a formula for computing complex number powers. Consider what occurs when we multiply a complex number by itself to obtain some idea for de Moivre's theorem.
Remember that any complex number z=a+ib can be expressed as with the polar form.
Then squaring the complex number z gives
z2 =(r( cos θ + i sin θ))2
= r2( cos θ + i sin θ)2
= r2( cos θ cos θ + i sin θ cos θ + i sin θ cos θ + i2 sin θ sin θ)
= r2((cos θ cos θ – sin θ sin θ) + i(sin θ cos θ + sin θ cos θ))
= r2(cos 2 θ + i sin 2 θ)
This demonstrates that squaring a complex integer squares the absolute value and multiplies the argument by two. For n3, de Moivre's theorem shows that to increase a complex number to the nth power, the absolute value must be raised to the nth power, and the argument must be multiplied by n.
1.3.1 Proof:
We'll use induction to illustrate our point.
zn = (r( cos (θ) + i sin (θ)n
= rn ( cos (θ) + i sin(θ))n
We have
Let's focus on the second part: ( cos (θ) + i sin(θ))n
For n=1, we have
( cos (θ) + i sin(θ))1 = cos ( 1. θ) + i sin( 1. θ)
Which is true.
We can suppose that n=k follows the same formula, thus we obtain
(cos (θ) + i sin (θ))k = cos ( k θ) + i sin (k θ)
For n=k+1, we expect to have
(cos (θ) + i sin (θ))k+1 = cos ((k+1) θ) + i sin ((k+1) θ)
We get
(cos θ + i sin θ)k+1 = (cos θ + i sin θ)k(cos θ + i sin θ)1
= (cos (k θ) + i sin (k θ))(cos( 1. θ) + i sin (1. θ )) (We assume this to be true for x = k)
= cos ( k θ) cos (θ) + cos (kθ) i sin(θ) + i sin (k θ) cos (θ) + i2 sin(k θ)sin(θ) (We have i2 = - 1)
= cos(k θ)cos(θ) – sin(k θ)sin(θ) + i (cos (k θ)sin(θ) + sin(k θ) cos(θ))
= cos(k θ + θ) + i sin(k θ + θ) (deducted from the trigonometry rules)
= cos((k+1) θ) + i sin((k+1) θ)
Thus, for n=k+1, we have (cos (θ) + i sin (θ ))k+1 = cos((k+1) θ ) + i sin((k+1) θ )(cos (θ ) + i sin θ(θ ))k+1 as expected.
As the theorem is true for n=1 and n=k+1, it is true for all n≥1.
NUMERICALS:
1) (sin 𝛑/6 + i cos 𝛑/6)18
ANS:
We have, sin 𝛑 /6 + i cos 𝛑 /6 = i(cos 𝛑 /6 – i sin 𝛑 /6)
Raising to the power 18 on both sides gives,
(sin 𝛑 /6 + i cos 𝛑 /6)18 = (i)18(cos 𝛑 /6 – sin 𝛑 /6)18
= (-1)( cos 18 𝛑 /6 – i sin 18 𝛑 /6)
= -(cos 3 - i sin 3 𝛑 ) = 1 + 0i
Therefore, (sin 𝛑 /6 + i cos 𝛑 /6)18=1
2) Simplify ((1+cos 2 𝛉 + i sin 2𝛉 )/(1+cos 2 𝛉 – i sin2 𝛉 ))3θ
ANS:
Let z = cos 2𝛉 + i sin 𝛉
As |z| = |z|2 = z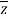 = 1 , we get
= 1 , we get 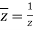 = cos 2 𝛉 – i sin 2 𝛉
= cos 2 𝛉 – i sin 2 𝛉
Therefore, (1+cos 2𝛉 + i sin 2𝛉 )/(1+cos 2𝛉 – i sin 2𝛉 ) = 1+z/ 1+ 1/z = (1+z)z/z+1 = z
Therefore, ((1+cos 2 𝛉 + i sin 2 𝛉 )/(1+cos 2 𝛉 – i sin2 𝛉 ))3θ = z3θ = ( cos 2θ + i sin 2 θ)3θ
= cos 60 θ + i sin 60 θ
3) (1+ i)18
ANS:
Let 1+ i = r (cosθ + i sinθ ) . Then, we get
r =  ; α = tan-1(1/1) = π/4
; α = tan-1(1/1) = π/4
θ = α = π/4 ( 1+i lies in the first Quadrant)
Therefore 1+i = √2 (cos π/4 + i sin π/4)
Raising to power 18 on both sides,
(1+i)18 = [√2 (cos π/4 + i sin π/4)]18 = √218 (cos π/4 + i sin π/4)18
By de Moivre’s heorem,
(1+i)18 = 29( cos 18π/4 + i sin 18 π/4)
= 29 ( cos(4 π + π/2) + i sin(4 π + π/2)) = 29(cos π/2 + i sin π/2)
(1+i)18 = 29 (i) = 512 i
Let z be a complex number that is not zero. Then in C, there are exactly k many kth roots of z.
Assume that w is a complex number. We want to identify all z such that zn=w, or the nth roots of w.
There are n different nth roots, which can be discovered in the following order:
1. Write z and w in polar form as z=rei,w=sei. Zn=w then becomes:
(reiθ)n = rneinθ = seiϕ
We need to solve for r and θ.
2. Solve the following two equations:
rn=s
einθ=eiϕ
The solutions to rn=s are given by r=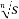 .
.
The solutions to einθ=eiϕ are given by
nθ = ϕ + 2 πl, for l = 0, 1, 2, . . ., n - 1
Or
θ = ϕ/n + 2/n πl, for l = 0, 1, 2, . . . , n -1
Using the solutions r,θ to the equations given in construct the nth roots of the form z=reiθ.
1.5.1 Logarithm functions
Because a complex number can be expressed as an exponential function, reiP , A logarithm is nearly instantaneous. We get it. ln reiP = ln r + ln eiP = ln r + iP , This is the natural logarithm's primary value. The angle PP, on the other hand, is not unique, as it can vary by multiples of two. As a result, the formula for a complex number's natural logarithm is ln reiP = ln r + iP + 2kπi
We can find the natural logarithm of I for example. Its main benefit is
Ln i = ln (1 eiπ/2) = π/2 i
The natural logarithm of negative one is another fascinating example. Its main benefit is ln(-1) = ln(1 eiπ ) = πi. (And you thought you couldn't handle negative logarithms!) You can, but the results aren't accurate.)
Other base logarithms can be found using the change-of-base formula.
Log4 e = ln e/ ln i = 1/ πi/2 = -2i/π
Complex bases). For example,
1.5.2 Trigonometric Functions
We can quickly obtain some formulas for the sine and cosine functions in terms of complex exponentials thanks to the formula. These formulas are frequently used as trigonometric function definitions for complex numbers.
Cos x = eix + e-ix/2 sin x = eix - e-ix/2i
Substituting the quantity ix in place of the variable x, we can produce formulas for pure imaginary numbers. It's worth noting that the outcomes are linked to hyperbolic functions.
Cos ix = ex + e-x/2 = cosh x, sin ix = e-x - ex/2 = i sinh x
The sine and cosine of complex numbers can then be calculated using the formulas for the sine and cosine of the sum of two angles.
Cos(a + bi) = cos a cosh b – i sin a sinh b
Sin(a + bi) = sin a cosh b + i cos a sinh b
Consider the cosine of I as an example.
Cos i = cos 0 cosh 1 – i sin 0 sinh 1 = cosh 1 = e1 + e-1/2 ≈ 1.5431
1.5.3 Hyperbolic Functions
The results for hyperbolic functions are virtually instantaneous when using the connection between hyperbolic and trigonometric functions.
Cosh(a + bi) = cosh a cos b – i sinh a sin b
Sinh(a + bi) = sinh a cos b + i cosh a sin b
As an example, consider the hyperbolic cosine of i. We get
Cosh i = cosh 0 cos 1 + i sinh 0 sin 1 = cos 1 ≈ 0.5403
1.5.4 Inverse Trigonometric Functions
Since cos x = eix + e-ix/2 , we can find the inverse by replacing the function with the variable y, swapping x and y, then solving for y. After the variable switch, we'll go on to the next step.
Have x = eiy+ e-iy/2 . Both sides are multiplied by 2eiy provides the formula 0 = e2iy – 2xeiy +1. The quadratic formula can be used to solve this.
eiy = 2x ± √4x2 – 4 /2. After simplifying, we can take the natural logarithm of both sides and divide by i. The end result is as follows: cos-1x = - i ln [ x ± i √ 1 – x2]
(A factor of ii typically appears as the coefficient of the square root so that the similarities between the inverse cosine and inverse sine formulas are more apparent.)
The inverse sine formula is discovered to be by using similar arguments.
Sin-1x = - i ln [i x ± i√ 1 – x2]
The inverse tangent formula is as follows:
Tan-1 x = i/2 ln i+x/i - x
Consider the inverse cosine of ii as an example. Using the plus sign in the formula, we will find only one of its numerous values. We get cos-1 i = - i ln [ i + i √ 1 – i2] = - i ln [(1+√2)i]Then we use the logarithm formula to continue:
-i ln [(1+√2)i] = - i ln [(1+√2)eix/2] = - i [ ln (1 + √2) + πi/2]
This can be simplified, and we get
- i [ ln (1 + √2) + πi/2] = π/2 – i ln ( 1 + √2) ≈ 1.57 – 0.88i
1.5.5 Inverse Hyperbolic Functions
The formulas are the same as those derived for inverse hyperbolic functions previously:
Cosh-1 x = ln[ x ± √x2 – 1]
Sinh-1 x = ln[ x ± √x2 + 1]
For example, using the plus sign in the formula, one of the values of the inverse hyperbolic cosine of ii is: cosh-1 x = ln[ i ± √i2 – 1] = ln [(1+ √2)i]
Then using the logarithm formula, we get:
Ln [(1+ √2)i] = ln (1+ √2) + πi/2 ≈ 0.88 + 1.57i
1.6.1 Cauchy-Riemann Equations:
Let
f(x, y) ≡ u(x, y) + iv(x, y)
Where
z ≡ x+ iy
So
Dz = dx + i dy
After that, the total derivative of with respect to is
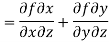
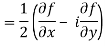
In the context of and, (5) becomes
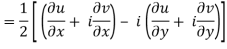
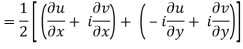
Along the x-axis, or real axis,
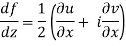
Along the y-axis, or imaginary axis,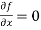 , so
, so
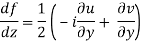
If f is complex differentiable, then the value of the derivative must be the same for a given dz, regardless of how it is oriented as a result, (8) must equal (9), implying that
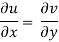
And
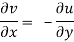
The Cauchy-Riemann equations are what they're called.
They are the causes of the disorders.
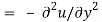
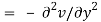
Where  is the complex conjugate.
is the complex conjugate.
If z = r eiθ, then the Cauchy-Riemann equations become
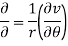
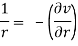
(Abramowitz and Stegun 1972, p. 17).
In two dimensions, if and satisfy the Cauchy-Riemann equations, they also satisfy Laplace's equation.
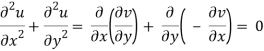
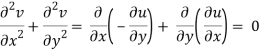
Solutions that fulfil the Cauchy-Riemann equations and Laplace's equation can be found by picking an arbitrary. This fact is utilised to solve physical problems involving scalar potentials, such as fluid flow and electrostatics, using conformal mappings.
1.6.2 A necessary condition for a complex function to be analytic:
Let
f(x, y) = u(x, y) + iv(x, y)
To be a complicated function Since then, x = (z + 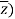 /2 and y = (z -
/2 and y = (z - 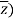 /2i
/2i
By replacing x and y for x and y, we get
f(z , 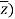 = u(x, y) + iv(x, y)
= u(x, y) + iv(x, y)
a required condition for f(z, 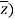 It is to be analytic.
It is to be analytic. 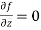
As a result, one of the required conditions for being analytic is that f depends solely on z. Condition (1) is equal to condition (2) in terms of the real and imaginary portions u,v of f.
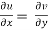 (2)
(2)
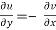 (3)
(3)
Equations (2, 3) are known as the Cauchy-Riemann equations. They are a necessary condition for f = u + iv to be analytic.
NUMERICAL:
Use the Cauchy-Riemann equations to show that f(z)= is not differentiable.
is not differentiable.
SOLUTION:
f(x + iy) = x – iy, so u(x, y) = x, v(x, y) = - y
Taking partial derivatives
ux = 1, uy = 0, vx = 0, vy = - 1
Since ux≠vy the Cauchy-Riemann equations are not satisfied and therefore ff is not differentiable.
1.7.1 What is Analytic Function
The enlarged Taylor series can be represented as follows. Analytic Function is defined as an indefinitely differential function over a variable named x.
T(x) = 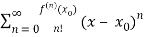
This explains the extended Taylor overvalue Xo; this function is analytic for the value x in its domain, but there is another value in the domain that converges the series to one point.
1.7.2 Examples:
Rational functions
The rational functions are the most basic complex analytic functions. These are the features.
R(z) = P(z)/Q(z),(1)
Where
P(z) = amzm + am−1zm−1 + ··· + a1z + a0
AndQ(z) = bnzn + bn−1zn−1 + ··· + b1z + b0
Are polynomials with complex coefficients
am, am−1, ..., a1, a0,bn, bn−1, ..., b1, b0,
And we assume that am 6 = 0 and bn 6 = 0. We also suppose that P and Q have no factors in common. At every point of C S, where S is the finite set of points within C where the denominator Q(z) vanishes, the function R(z) is differentiable. The degree of the rational function R is the sum of the two degrees, the degree of the numerator and the degree of the denominator (z).
The product and the sum of two rational functions are both rational functions. Indeed, the space of rational functions fulfils the field axioms with these addition and multiplication operations, and we call this field by C. (X). This is a good example of a field that can be added to the Q, R, and C fields.
We can factor polynomials using the Fundamental Theorem of Algebra.
P(z) and Q(z) ,
P(z) = am(z −z1)p1(z −z2)p2 ···(z −zr)pr
AndQ(z) = bn(z −ζ1)q1(z −ζ2)q2 ···(z −ζs)qs,
The first of two significant canonical forms for a rational function is: where the exponents denote the multiplicities of the roots, and thus gives us:
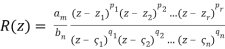 (2)
(2)
The numerator's zeros z1,...,zr are known as the rational function's zeros, whereas the denominator's zeros 1,...,s are known as the denominator's poles. The multiplicity of a zero or pole as a root of either the numerator or the denominator determines its order. Order one poles are believed to be simple. A rational function R(z) is said to be appropriate if
m = degP(z) ≤ n = degQ(z),
And strictly proper if m < n. If R(z) is not strictly proper, we can divide by the denominator to obtain
R(z) = P1(z) + R1(z),
The remainder R1(z) is a strictly valid rational function, and P1(z) is a polynomial.
Theorem. R(z) has a partial fraction decomposition if the rational function R(z) = P(z)/Q(z) is rigorously proper, that is, if degP degQ.
R(z) = 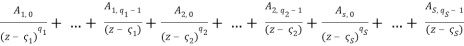 (3)
(3)
What you should concentrate on is calculating a rational function's partial fraction decomposition. If all of r's poles are simple, that is, if all of the denominator's roots have multiplicity one, (3) simplifies to
R(z) = 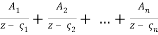 .(4)
.(4)
The coefficients in the partial fraction expansion can be found using the formula in this simpler situation.
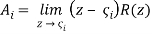 (5)
(5)
Linear fractional transformations
The linear fractional transformations or Mobius transformations, the rational functions of degree one, are of central importance among the rational functions:
w = T(z) = 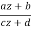 ,(8)
,(8)
Where ad bc 6=0 and a, b, c, and d are complex numbers. We may show that any linear fractional transformation T has an inverse by solving for z as a function of w.
z = T-1(w) = 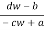 ,
,
As though checking with a calculator As a result, linear fractional transformations are always one-to-one and represented as C-to-C maps. Indeed, they are the only complex analytic functions from C to themselves that have complex analytic inverses.
Furthermore, the composition of two linear fractional transformations is simply verified to be another linear fractional transformation. Composition transforms the space of linear fractional transformations into a group, as algebraists term it.
The linear fractional transformation becomes a complex linear transformation when c = 0 and d = 1.
z 7→w = T(z) = az + b.
The following are examples of sophisticated linear transformations:
Translationsz 7→w = T(z) = z + b,
Rotationsz →7 w = T(z) = eiθz,
And expansions and contractionsz →7 w = T(z) = ρz,
Where and are real numbers, both of which are nonzero. When a = d = 0 and b = c = 1, the linear fractional transformation reduces to an inversion
w = T(z) = 1/z
T is a reflection in the circle in this case.
z ↦ 1/z reiθ ↦ 1/r eiθ
Followed by conjugation.
The following Proposition can be used to figure out what qualities a linear fractional transformation has. Linear fractional transformations will become increasingly important as the course progresses, and will be studied in more detail in 122B; see §7.3 of [4] or Chapter 7, § 5 of [3].
Proposition. Any fractional linear transformation is made up of complex linear maps and inversions. b. Any fractional linear transformation transforms circles and lines back to circles and lines. c. There is a unique linear fractional transformation T such that given any three independent points z1, z2, and z3 of C,
T(z1) = 0,T(z2) = 1andT(z3) = ∞.(9)
Illustration of a proof of a: If we make the replacements, the transformation (8) remains unaltered.
a 7→λa,b →7 λb,c →7 λc,d →7 λd,
When 6 equals 0 As a result, we can assume that ad bc = 1 without losing generality. Furthermore, we may safely conclude that c 6= 0 because the transformation is clearly linear when c = 0. The map can then be factored.
z’ = T(z) = az +b/cz + d
Into a four-transformation composite
z1 = z + d/c, z2 = c2z1, z3 = - 1/z2 , z’ = z3 + a/c(10)
To see this, consider the following:

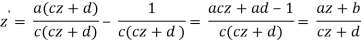
The Proposition is proven because each of the transformations in (10) is either complex linear or an inversion.
A rough sketch of b's proof is as follows: Complex linear transformations take circles and lines to circles and lines, so we need only check that inversions take circles and lines to circles and lines. A circle's equation, on the other hand, can be represented as
A(x2 + y2) + Re[(C −iD)(x + iy)] + B = 0,
For some choice of real constants A, B, C and D. We can rewrite this as
Azz¯+ Re[(C −iD)z] + B = 0. If we replace z by 1/w, this becomes

Or
A + Re[(C −iD)w¯] + Bww¯ = 0,
Which is once again the equation for a circle.
Sketch of proof of c: If none of the three points is infinity, the linear fractional transformation satisfying (9) is
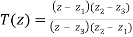 (11)
(11)
One needs to adjust this formula appropriately when one of the three points is ∞.
Exponential and trigonometric functions
The complex exponential function was formerly defined in terms of real-valued functions as
w = exp(z) = ez = ex(cosy + isiny),(12)
And used identities from trigonometry to show that
Ez1+z2 = ez1ez2,
As well as to show that the exponential function is periodic of period 2πi:
Exp(z + 2πki) = exp(z),for k ∈Z.(13)
Moreover, writing
ez = u(x,y) + iv(x,y), where u(x,y) = ex cosy and v(x,y) = ex siny and using the Cauchy-Riemann equations, we find that
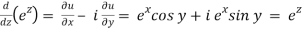 .(14)
.(14)
Although the exponential function exp is certainly quite well-behaved on C, it does not extend to a well-behaved function on the extended complex plane C∪{∞}. Neither

As a result, one might state that exp(z) has a "essential singularity" at. Indeed, when w is in any neighbourhood N(0;) of 0, one may show that e1/w takes on every nonzero complex integer an unlimited number of times.
We'd like to define a function that is the inverse of exp on C0, but the periodicity prevents us from doing so. Indeed, if w = ez, (12) is the sole conclusion.
w = reiθ= r(cosθ+ isinθ) = ex(cosy + I siny),
So y is one of the many possible values of the angular coordinate θ, all of these values differing by integer multiples of 2π. Thus we write
x = Log(r) = Log(|w|),y = θ= arg(w),
Where arg is the multiple-valued function which gives the various possible angular coordinates θ of w, and
z = x + iy = Log(|w|) + I arg(w).
In this way, we are led to define the multiple-valued function log by
Log(w) = Log(|w|) + I arg(w),
Where Log(|w|) is the usual natural logarithm of the nonzero real number |w|. It follows from (13) that the various values of the multiple-valued function log differ by integer multiples of 2π.
Dangerous curve: A multiple-valued function is not the same as a true function as studied in the rest of mathematics. For a given argument choice, a valid function can only assume one value. Nonetheless, the concept of a multiple-valued function is widely utilised in complex variable theory since it is extremely valuable. In more advanced complex variable treatments, multiple-valued functions on open subsets of the complex plane are replaced with true single-valued functions defined on "Riemann surfaces" over the open subsets (see [2]).
We may erase the uncertainty in the logarithm by replacing it, as we saw earlier.
C−{0} by the smaller domain
D = C−{x + iy ∈C : x ≤ 0},(15)
And choosing a branch of the multiple-valued function log that is single-valued in D. We do this by first letting Arg(w) be the value of the angular coordinate θ which lies in the interval (−π,π] and then define
Log : D −→C byLog(w) = Log(|w|) = I Arg(w).
Choosing a branch does give us a genuine single-valued complex analytic logarithm function, and as we saw when discussing the Cauchy-Riemann equations,
d/dw Log(w) = 1/w
However, this destroys some of the nice properties one might hope for the logarithm; for example, although
Log(z1z2) = log(z1) + log(z2),
Where equality means that the values taken by the multiple-valued functions on the two sides are the same, it is not true that
Log(z1z2) = Log(z1) + Log(z2)
In general.
One of the most useful applications of the multiple-valued logarithm function is in defining arbitrary powers of a complex number. The definition is motivated by the fact that zn = exp (n log(z)), when n ∈N.
Definition. If z ∈C−{0} and α∈C, we define zα by zα= exp(αlog(z)).
Trigonometric functions. As previously stated, we can represent the trigonometric functions cosine and sine in terms of exponentials using Euler's identity.

As a result, the relationship between exponential and trigonometric functions is simplified. All of the normal properties of trigonometric functions can be determined using these equations. For example, (14) demonstrates that

As a result of the definition of derivative, if f(z) = sinz, then
1 = cos (0) = f’ (0) = 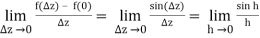
When h is considered to be real, this limit is recognised from first-year calculus.
We may also use the logarithm to find the inverses of trigonometric functions. If this is the case,
z = sin w = 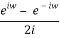
We can get the result by multiplying by eiw.
2iew z = eiw)2 or eiw)2 – 2izeiw – 1 = 0
As a result of the quadratic formula, it follows that
eiw = iz ±p1 −z2,
And we find that
w = arc sin (z) = i 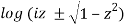 ,(17)
,(17)
Of course, this is a multi-valued function. The inverse of the cosine is also a multi-valued function.
w = arc cos(z) = π/2 – arc sin(z) = π/2 – i 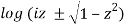
We must choose a branch of the square root as well as a branch of the logarithm to choose a specific branch of the inverse trigonometric functions. It follows from (17) that for any such branch
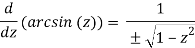
It's worth noting that a single-valued branch of the derivative of the inverse of the sine can be defined over in Example 3.
D = C− (R− [−1,1]),
We'll see later how this allows us to create a single-valued inverse of the sine across the same D region.
Similarly, the inverses of the hyperbolic cosine can be found; therefore, if
z = cosh w = 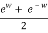
We can get the result by multiplying by ew.
2ewz = (ew)2 + 1or(ew)2− 2zew + 1 = 0.
The quadratic formula gets this result this time.
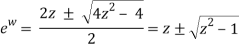
As a result, we discover that
w = 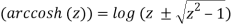
This time, differentiation produces
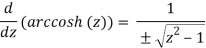
Example 4 shows a derivative with a single-valued branch over the domain C [1,1].
Steady-state temperature distributions
The real and imaginary components of the complex logarithm are currently used to determine the steady-state temperature distribution in numerous planar regions.
But first, we must show that a solution to the Laplace equation represents steady-state temperature. We assume that a material with homogeneous characteristics exists in area U of the (x,y)plane. When the temperature is given on the boundary, we want to find the steady-state temperature within the region.
Let u(x,y) denote the temperature at the given location (x,y). The heat flow at (x,y) should then be V(x,y), where
v(x, y) = - (k ∇ u)(x, y) = - k 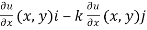 ,(18)
,(18)
Where is a positive constant referred to as the material's thermal conductivity.
We agree to meet at a certain time.
V(x,y) = M(x,y)i + N(x,y)j.
The divergence theorem states that if D is an area within U with a smooth border, then
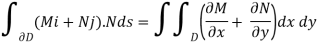
N is the normal to D outward-pointing unit, and s is the arc-length parameter along D. Remember that the left-hand line integral is calculated using a unit-speed parametrization: [a,b] D with (a) = (b).
The rate at which heat flows outward through D can be deduced from this line integral. As a result, the line integral must vanish if no heat is created or destroyed within D.
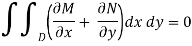
This double integral must vanish for every option of D U if no heat is created or destroyed anywhere within U, and this can only happen if
∇ . V = 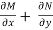 =0on U.
=0on U.
We infer that the temperature u must meet Laplace's equation in the specific case where V is supplied by (18).
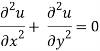
Alternatively, to put it another way, u has to be a harmonic function. (For a more leisurely discussion, see section 2.6 of [4].)
We have a wonderful application of complex analytic functions since harmonic functions are the real components of complex analytic functions: The steady-state temperature distribution in a homogeneous medium can be represented by their real parts.
1.8.1 Singularity:
A singularity is a point when an equation, surface, or other object blows up or degenerates. Singularities are also referred to as singular points.
Singularities play a crucial role in complex analysis, as they define the range of conceivable behaviours for analytic functions. Complex singularities are spots in a function's domain where the function fails to be analytic. Poles, essential singularities, logarithmic singularities, and detachable singularities are all types of isolated singularities. Natural boundaries or branch cuttings can produce non isolated singularities.
Consider the ordinary differential equation of second order.
y’’ + P(x) y’ + Q(x)y = 0
If and stay finite at, then is referred to be an ordinary point. When either or diverges as, the result is referred to as a unique point. Singular points are further divided into the following categories:
1. If either or diverges as but remains finite as, is referred to as a normal singular point (or nonessential singularity).
2. If diverges faster than and approaches infinity as, or diverges faster than and goes to infinity as, then is referred to as an irregular singularity (or essential singularity).
A point of such that the Laurent series of has for and is referred to as a pole of order.
Essential singularities are infinite-order poles. A pole of order is a singularity of for which the function is non-singular but is singular for, 1,...,.
A logarithmic singularity is an analytic function singularity with a primary -dependent term of order, etc.
Singularities that may be assigned a complex number in such a way that it becomes analytic are known as removable singularities. For example, the function has a detachable singularity at 0 since it is equal to 0 everywhere except 0. Singularities that can be removed are not poles.
The function, for example, exhibits two singularities: poles at and a nonisolated singularity at 0.
1.8.2 Poles
Poles refer to isolated singularities. So, we suppose f(z) is analytic on 0<|z−z0|<r and has Laurent series
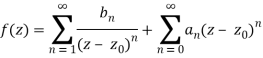
(8.9.1)
The terminology can be perplexing. Assume I inform you that on the punctured disc 0|zz0|r, f is defined and analytic. Then we suppose f has a singularity at z0 a priori. However, if there is no unique component after computing the Laurent series, we can extend the definition of ff to the entire disc, effectively eradicating the singularity.
The word essential singularity can be explained as follows. (zz0)kf(z) is analytic (has a detachable singularity) at z0 if f(z) has a pole of order k at z0. As a result, f(z) isn't substantially more difficult to work with than an analytic function. If z0 is an important singularity, however, no algebraic method will convert f(z) to an analytic function at z0.
1.8.3 Branch Point
The complex argument of an analytic function can be transferred from a single point in the domain to numerous points in the range at a branch point in the complex plane. Consider the behaviour of the point when it is subjected to the power function.
f(z) = za (1)
For complex non-integer a, i.e., a ∈ ℂ with a∉ℤ. Writing z = eiθ and taking θ from 0 to 2π gives
f(∈ = e0 = 1
f(∈ = e2πia
Despite the fact that at and correspond to the same place in the domain, their values are different.
Algebraic branch points of order are branch points whose neighbourhood of values wraps around the range a finite number of times as varies from 0 to correspond to the point under functions of the kind. A logarithmic branch point is a branch point that occurs at the point beneath the function and whose neighbourhood of values revolves around an infinite number of times. Logarithmic branch points and logarithmic singularities are the same thing.
Branch points are another name for pinch points.
It's worth noting that branch cuts' endpoints aren't always branch points.
A branch cut is a curve in the complex plane in which an analytic multivalued function is discontinuous (having ends that may be open, closed, or half-open). Branch cuts are frequently represented as lines or line segments for ease of use. Cut lines (Arfken 1985, p. 397), slits (Kahan 1987), and branch lines are all terms used to describe branch cuts (including ones with curves).
Take, for example, the function that converts each complex number to a well-defined number. Its inverse function, on the other hand, transfers the value to, for example. While such functions can have a single primary value (in this case, the main square root is positive), the choices cannot be made continuously across the complex plane. Instead, discontinuity lines must be drawn. The implementation of so-called branch cuts is the most prevalent method for coping with these discontinuities. Branch cuts are not unique in general; instead, they are chosen by convention to provide easy analytic features (Kahan 1987). Some functions have a relatively simple branch cut structure, while others have exceedingly intricate branch cuts.
Riemann surfaces are a multivalued function representation alternative to branch cuts.
Singularities known as branch points exist in addition to branch cuts. It should be emphasised, however, that branch cut endpoints are not always branch points.
The single-valued trigonometric, hyperbolic, integer power, and exponential functions do not have branch cuts. Their multivalued inverses, on the other hand, necessitate branch cuts. The graphs and table below show the branch cut structure of the Wolfram Language's inverse trigonometric, inverse hyperbolic, no integer power, and logarithmic functions.
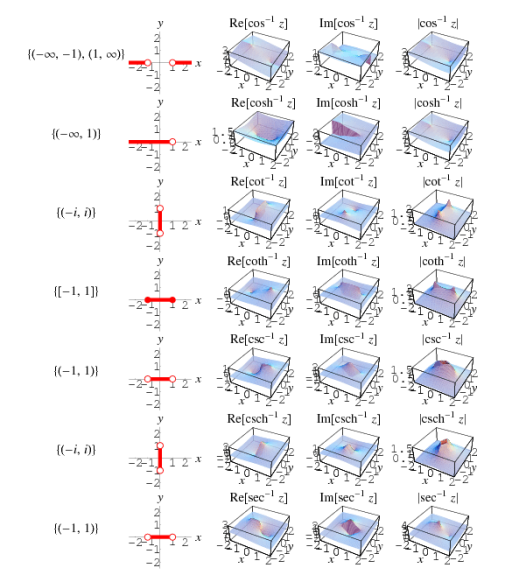
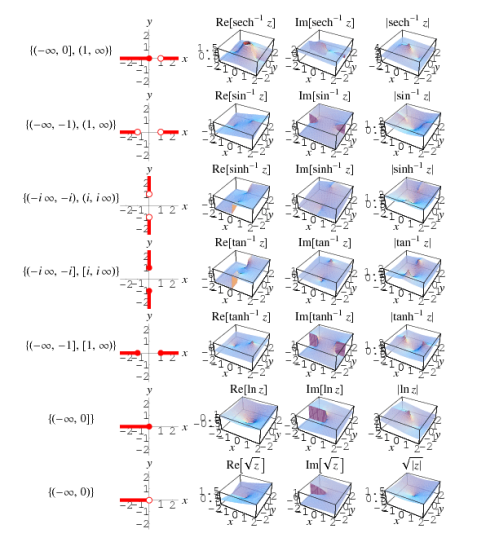
Function name | Function | Branch cut(s) |
Inverse cosecant | Csc-1 z | (-1, 1) |
Inverse cosine | Cos -1 z | (-∞, -1) and ( 1, ∞) |
Inverse cotangent | Cot -1 z | (-i, i) |
Inverse hyperbolic cosecant | Csch-1 | (-i, i) |
Inverse hyperbolic cosine | Cosh -1 | (-∞, 1) |
Inverse hyperbolic cotangent | Coth-1 | [-1, 1] |
Inverse hyperbolic secant | Sech-1 | (-∞, 0] and (1, ∞] |
Inverse hyperbolic sine | Sinh-1 | (-i∞, -i) and (i, i∞) |
Inverse hyperbolic tangent | Tanh-1 | (-∞, -1] and [1, ∞) |
Inverse secant | Sec-1z | (-1, 1) |
Inverse sine | Sin-1z | (-∞, -1) and (1, ∞) |
Inverse tangent | Tan-1 z | (-1∞, -i] and [i, i∞) |
Natural logarithm | Ln z | (-∞, 0] |
Power | zn, n ∉ ℤ | (-∞, 0) for R[n] ≤ 0 ; (-∞, 0] for R[n] > 0 |
Square root | √z | (-∞, 0) |
1.10.1 Cauchy’s Inequality:
A special case of Hölder's sum inequality with p = q= 2,

In two-dimensions, it becomes
(a2 + b2)(c2 + d2) ≥ (ac + bd)2
It can be proven by writing
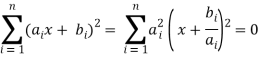
If 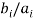 is a constant c, then x = -c. If it is not a constant, then all terms cannot simultaneously vanish for real x, so the solution is complex and can be found using the quadratic equation
is a constant c, then x = -c. If it is not a constant, then all terms cannot simultaneously vanish for real x, so the solution is complex and can be found using the quadratic equation
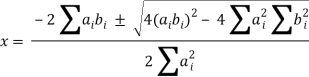
In order for this to be complex, it must be true that
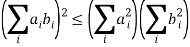
With equality when bi/ai is a constant. The vector derivation is much simpler,
(a . b)2 = a2 b2 cos2 θ ≤ a2 b2
Where
a2 = a . a = 
And similarly for b.
1.10.2 Cauchy's integral formula:
Cauchy's integral formula, named after Augustin-Louis Cauchy, is a key statement in complex analysis in mathematics. It reflects the fact that the values on the disk's boundary entirely determine a holomorphic function defined on the disc, and it gives integral formulas for all derivatives of a holomorphic function. Cauchy's formula demonstrates that "differentiation is comparable to integration" in complex analysis: complex differentiation, like integration, performs well within uniform boundaries, a result that does not hold in real analysis.
Assume that U is an open subset of the complex plane C, and that D is a closed disc.
D = { z : |z – z0| ≤ r}
Is entirely confined within U. Let f : U C be a holomorphic function, and let be the counter clockwise-oriented circle that forms D's boundary. Then, for each an in D's interior,
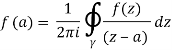
This statement is proved using the Cauchy integral theorem, which, like that theorem, just needs that f is complex differentiable. Since 1/(z-a) can be expanded as a power series in the variable 𝑎:
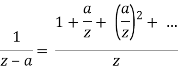
— it follows that holomorphic functions are analytic, i.e. they can be expanded as convergent power series. In particular f is actually infinitely differentiable, with
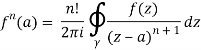
Cauchy's differentiation formula is another name for this formula.
The previous theorem can be generalised. Any closed rectifiable curve in U with winding number one around a can be substituted for the circle. Furthermore, as with the Cauchy integral theorem, all that is required is for f to be holomorphic in the open region circumscribed by the path and continuous on its closure.
It's worth noting that not every continuous border function may be used to generate a function inside the boundary that fits the provided boundary function. For example, in the Cauchy integral formula, we get zero for all locations inside the circle if we use the function f (z) = 1/z, which is specified for |z| = 1. In reality, providing simply the real component of a holomorphic function's border is sufficient to define the function up to an imaginary constant – there is only one imaginary component on the border that corresponds to the given real portion, up to the addition of a constant. The holomorphic function can be constructed from the real component on the boundary using a Möbius transformation and the Stieltjes inversion formula. The function f (z) = I iz, for example, has a real portion Re f (z) = Im z. This can be expressed as i/z iz/2 on the unit circle. The function inside the circle is constructed using the Möbius transformation and the Stieltjes formula. We find the function iz since the i/z term has no effect. This provides us the right real part on the border, as well as the matching imaginary component, but it is off by a constant, namely i.
NUMERICALS:
1)
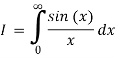
This integral is not absolutely convergent, but it is conditionally convergent. Formally, of course, we mean
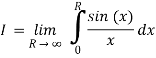
First note that sin(x)/x is even, so
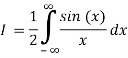
Next, to avoid the problem that sin(z) goes to infinity in both the upper and lower half-planes we replace the integrand by
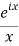
We’ve changed the problem to computing
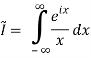
The problems with this integral are caused by the pole at 0. The biggest problem is that the integral doesn’t converge! The other problem is that when we try to use our usual strategy of choosing a closed contour we can’t use one that includes z=0 on the real axis. This is our motivation for defining principal value. We will come back to this example below.
1.11.1 Simply connected definition
A simply connected domain is a path-connected domain in which every simple closed curve can be constantly shrunk into a point while remaining in the domain.

For two-dimensional regions, a simply connected domain is one without holes in it.

The concept of simply connected is more subtle in three-dimensional spaces. A domain that is simply connected has no gaps running through it. However, a domain with just a hole in the middle (like a ball whose center is hollow) is still simply connected, as we can continuously shrink any closed curve to a point by going around the hole and remaining in the domain. A ball with a hole bored all the way through it, or a spool with a hollow centre axis, on the other hand, cannot be simply linked. While remaining in the domain, a closed curve that travelled around the hole could not be shortened to a point. Because there is no way for the curve to avoid the hole, it is locked around it.
1.11.2 Multiply-connected domain
n a path-connected space
In a domain D, there are closed pathways that are not homotopic to zero, or whose basic group is not trivial. This means that in D, there are closed pathways that cannot be continuously deformed to a point while remaining inside D, or that a multiply-connected domain exists. D is a domain that isn't related in any way.
The number of (homologically) independent one-dimensional cycles, or the one-dimensional Betti number p1 of D, is the order of connectedness of a planar domain D in R2 or C=C1 (or in the compactification of these spaces, R 2 or C). If the number k of linked components of a plane domain D, regarded as a domain in the compactified space R 2 or C, is finite, then p1=k; otherwise, p1=. DD is a simply-connected domain when p1=1, and a finitely-connected domain when p1p1 (other terminology include doubly-connected domain, triply-connected domain, and so on). When p1=, DD is an indefinitely connected domain (k-connected domain). Homeomorphism exists between all plane finitely linked domains with the same order of connectivity, k. It is always feasible to produce a simply-connected domain DD by deleting all sites of k1 cuts, that is, Jordan arcs joining pairs of linked components of the boundary, from such a domain D. About planar multiply-connected domains' conformal types.
Domain topological types in Rn, n3, or Cm, m2 are significantly more varied and cannot be described by a single number. When the fundamental group is trivial but a higher-dimensional homology group is not trivial, the phrase "multiply-connected domain" (with various provisos) is occasionally used.
1.12.1 Laurent Series
If is analytic in the annular area between and on the concentric circles, and is centred at and of radii, then there exists a unique series expansion in terms of positive and negative powers of. (z-a),

Where
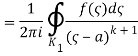
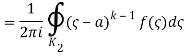
(Korn and Korn 1968, pp. 197-198).
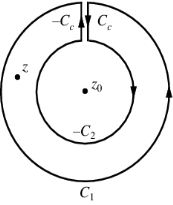
Let's say there are two circular shapes and, one having a radius that is larger than that of the other. Allow to be at the intersection of and, and between and. Create a cut line between and and integrate it around the path so that the plus and minus contributions cancel each other out, as shown above. The integral formula of Cauchy is as follows:
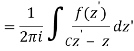
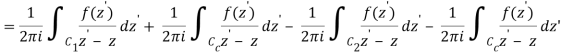
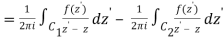
Now, because the cut line's contributions in opposite directions cancel each other out,
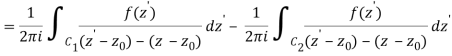
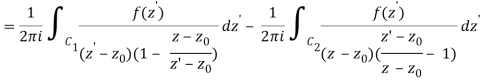
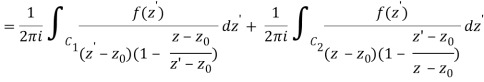
For the first integral’ – z0| > |z – z0|. For the second, |z’ – z0| < |z – z0| Now use the Taylor series (valid for |t|<1)
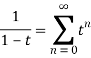
To obtain
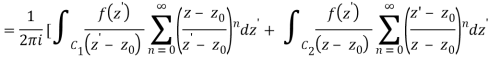
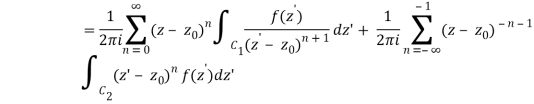
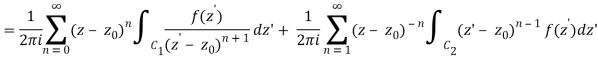
Where the second term has been re-indexed. Re-indexing again,
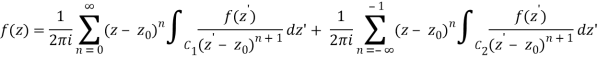
Since the integrands, including the function f(z), are analytic in the annular region defined by C1 and C2, the integrals are independent of the path of integration in that region. If we replace paths of integration C1 and C2 by a circle C of radius r with r1 ≤ r ≤ r2, then
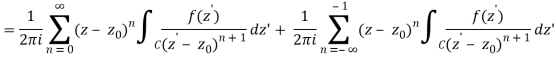

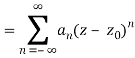
Any path that lies in the annular region and encircles once in the positive (counter clockwise) direction can be used as an integration path.
As a result, the complex residues are defined by
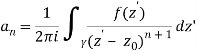
It's worth noting that the annular region can be enlarged by increasing and reducing until singularities lie near outside or just inside. If there are no singularities inside, then all of the terms in () are equal to zero, and the Laurent series of () is reduced to a Taylor series with coefficients.
1.12.2 Taylor series:
For Real Functions
Let a∈R and f(x) be and infinitely differentiable function on an interval I containing a. The Taylor series of f around an in one dimension is thus given by
f(x) = f(a) + f’ (a) (x – a) + f’’(a)/2! (x –a)2 + f(3)(a)/3! (x – a)3 + ...
Which can be written in the most compact form:
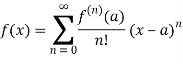 Recall that, in real analysis, Taylor’s theorem gives an approximation of a k-times differentiable function around a given point by a k-th order Taylor polynomial.
Recall that, in real analysis, Taylor’s theorem gives an approximation of a k-times differentiable function around a given point by a k-th order Taylor polynomial.
The best linear approximation for f(x) is, for example,
f(x) ≈ f(a) + f’(a) (x – a)
This linear approximation matches the slope of f at a by fitting f(x) with a line through x=a.
We can improve the approximation by including more terms in the expansion. The best quadratic approximation, for example, is
f(x) ≈ f(a) + f’(a)(x – a) + ½ f’’ (a) (x – a)2
The partial sums of the Taylor series for a given function are displayed in the applet below. To see more terms from the series, move the slider. Change the function or drag the point a.
For Complex Functions
Assume that a function f is analytic throughout a disc |zz0|R with radius R0 and a centre at z0z0. Then there's f(z), which is a power series representation.
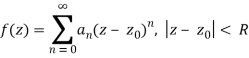
Where
an = 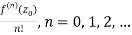
When z is in the indicated open disc, series (1) converges to f(z).
A radius of convergence exists for any complex power series (1). A complex power series (1) has a circle of convergence, which is the circle centred at z0 of maximum radius R>0 for which (1) converges at every point within the circle |zz0|=R|, similar to the concept of an interval of convergence for real power series. A power series converges absolutely for all z within its circle of convergence, that is, for all z satisfying |zz0|R, and diverges for all z satisfying |zz0|>R. The radius of convergence can be: 1. R=0 (in which case (1) converges only at its centre z=z0), 2. R=1 (in which case (1) converges only at its centre z=z0), 3. R=2 (in which case
(1) converges only at
2. RR is either a finite positive number (in which case (1) converges at all interior points of the circle |zz0|=R) or a finite negative number (in which case (1) converges at all interior points of the circle |zz0|=R).
3. R= (in which case (1) for every z converges).
The ratio test of convergence can be used to calculate the radius of convergence. Consider the following scenario:



Dynamic Exploration
Explore Taylor series representations and their radius of convergence, which is dependent on the value of z0, using the applet below.
A phase portrait of a complex function is shown on the left side of the applet below. The function's approximation through its Taylor polynomials at the blue base point z0 may be seen on the right side. Modify the complex function, the base point z0, the polynomial order (vertical slider), and the zoom (horizontal slider).
Maclaurin series
A Taylor series with centre z0=0
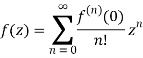
Is referred to as Maclaurin series.
Some important Maclaurin series are:
1/(1 – z) = 
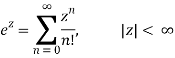

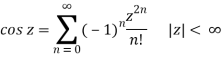
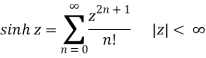
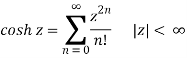
NUMERICALS:
1) Find the Laurent series for
f(z) = z+1/z
Around z0=0. Give the region where it is valid.
ANSWER:
|f(z) = 1 + 1/z
This is a Laurent series, valid on the infinite region 0<|z|<∞.
z = 0 for f(z) = 1/z(z-1)
2) Find the Laurent series around in each of the following regions:
The region A1:0<|z|<1
The region A2:1<|z|<∞.
Solution:
For (i)
f(z) = - 1/z . 1/ 1 – z = - 1/z ( 1+ z + z2 + . . .) = - 1/z – 1 –z –z2 - ...
For (ii): Since the usual geometric series for 1/(1−z) does not converge on A2 we need a different form,
f(z) = 1/z . 1/ z(1 – 1/z) = 1/z2 ( 1 + 1/z + 1/z2 + . . .)
Since |1/z|<1 on A2 our use of the geometric series is justified.
3) Expand f(z)=z8e3z in a Taylor series around z=0.
Solution
Let w=3z. So,
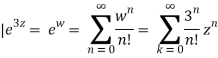
Thus,
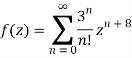
1.13.1 Cauchy Residue Theorem
This is a major theorem in complex analysis, and it will allow us to make our earlier ad hoc technique to computing integrals on contours that surround singularities more systematic.
Except for a few isolated singularities, suppose f(z) is analytic in the region A. Assume C is a simple closed curve in A that passes through none of ff's singularities and is oriented counter clockwise. After that,
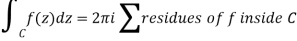
Proof
The following figures are used to prove the point. Although they only depict a curve with two singularities, the generalisation to any number of singularities is simple. In the next sections, we will use the term pole to refer to an isolated singularity, such as a finite order pole or an essential singularity (‘infinite order pole').
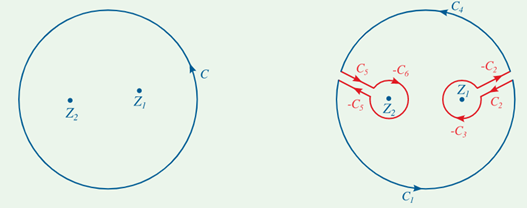
The curve C is shown on the left, encircling two of f's poles, z1 and z2. The same curve is seen on the right, but with several cuts and little circles added. It is chosen so that no f poles are contained within it, and the little circles surrounding each of the poles are so small that no additional poles are contained inside them. The curve on the right hand is
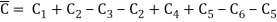
C=C1+C4C=C1+C4C=C1+C4C=C1+C4C=C1+C4C=C1+C4C=C Because there are no poles within CC, we obtain, according to Cauchy's theorem,
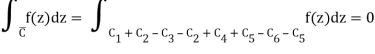 When C2 and C5, which are both added and subtracted, are removed, the result is
When C2 and C5, which are both added and subtracted, are removed, the result is
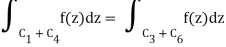
If
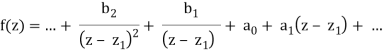
If f's Laurent expansion around z1 is true,
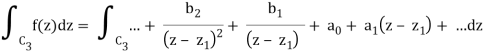
= 2 πib1
= 2πi Res(f, z1)
Likewise
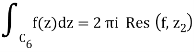
Equation 9.5.4 is formed using these residues and the fact that C=C1+C4
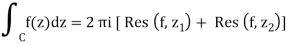
For the situation of two poles, this demonstrates the residue theorem. As previously stated, generalising to any number of poles is simple.
1.14.1 Application of definite integral:
Functions, differentiation, and integration are only a few examples of calculating procedures. Integrals are used in a variety of domains, including mathematics, science, and engineering. In most cases, integral formulas are used to calculate area. So, let us begin with a brief introduction to integrals based on the mathematics subject in order to determine areas under simple curves, areas bounded by a curve and a line, and areas between two curves, as well as the application of integrals in mathematical disciplines and the solved problem.
Integral Definition
An integral is a function whose derivative is another function. Integration is mostly used to compute the volumes of three-dimensional objects and to calculate the areas of two-dimensional regions. As a result, determining the integral of a function with respect to x entails determining the area of the curve with respect to the X-axis. Because it is the opposite of differentiation, the integral is also known as anti-derivative.
1.14.2 Application of Integrals
Integrals have a wide range of applications, some of which are listed below:
In Maths
- Identifying the centre of mass (Centroid) of a curved-sided area Identifying the region between two curves
- To determine the area beneath a curve
- The average of a curve's values
In Physics
Integrals are used to compute a vehicle's centre of gravity, mass, and moment of inertia.
- Satellites' mass and momentum
- A tower's mass and momentum
- The centre of mass is a term used to describe the centre of mass of an object.
- The velocity of a spacecraft when it is launched into orbit.
- The path taken by a satellite as it is sent into orbit.
References:
1. Mathematical Physics and Special Relativity–M.Das, P.K. Jena and B.K. Dash (Srikrishna Prakashan)-2009
2. Mathematical Physics–H. K. Das, Dr. Rama Verma (S. Chand Publishing) 2011
3. Complex Variable: Schaum’s Outlines Series M. Spiegel (2nd Edition, Mc- Graw Hill Education)-2004
4. Complex variables and applications J.W.Brown and R.V.Churchill 7th Edition 2003
5. Mathematical Physics, Satya Prakash (Sultan Chand)-2014
Unit - 1
Complex Analysis
1.1.1 Complex number in mathematics:
Definition
A complex number is a number that is made up of both real and imaginary numbers. The complex number is in the form of a+ib, where a = real number and ib = imaginary number. In addition, a,b are real values, and I = -1.
Hence, a complex number is a simple representation of addition of two numbers, i.e., real number and an imaginary number. One side is entirely genuine, while the other is entirely imagined.
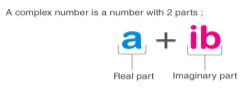
What are Real Numbers?
Real numbers are any numbers that exist in a number system, such as positive, negative, zero, integer, rational, irrational, fractions, and so on. Re is the symbol for it (). 12, -45, 0, 1/7, 2.8, 5, and other real numbers are examples.
What are Imaginary Numbers?
Imaginary numbers are numbers that are not real. We get a negative return when we square an imaginary number. Im is the symbol for it (). For example, the numbers -2, -7, and 11 are all fictional.
To answer the equation x2+1 = 0, complex numbers were introduced. The equation's roots are of the form x = -1, and there are no true roots. As a result of the addition of complex numbers, we now have imaginary roots.
The symbol I which stands for Iota, is used to represent -1. (Imaginary number).
Notation
A complex number is defined as an equation of the form z= a+ib, where a and b are real numbers. Re z = a denotes the real part, while Im z = ib denotes the imaginary part.
Z = a + i b
Examples
To tell the difference between a real and an imaginary number, look at the table below.
Complex Number | Real Number | Imaginary Number |
-1+2i | -1 | 2i |
7-9i | 7 | -9i |
-6i | 0 | -6i (Purely Imaginary) |
6 | 6 | 0i (Purely Real) |
Is 0 a complex Number?
0 is a real number, as we all know. Real numbers are also included in the category of complex numbers. As a result, 0 is a complex number and can be written as 0+0i.
Graphical representation
Examine the axes in the graph below to see how complex numbers are represented. The x-axis represents the real part, while the y-axis represents the imaginary part.
Let's have a look at an example. If we need to draw a graph of the complex number 3 + 4i, we can use the following formula.
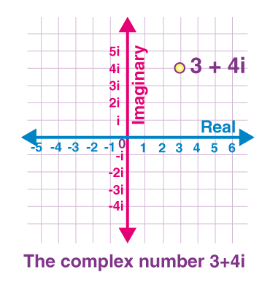
Absolute Value
A real number's absolute value is the number itself. Modulus, i.e. |x|, represents the absolute value of x. As a result, the modulus of any value is always positive, as follows:
|3| = 3
|-3| = 3
Finding the modulus of complex numbers now requires a different approach.
Let's pretend that z = x+iy is a complicated number. After that, mod of z will be:
|z| = √(x2+y2)
When we apply the Pythagorean theorem in a complex plane, we get this expression. As a result, the mod of a complex number, z, is extended from 0 to z, while the mod of real numbers, x and y, are respectively extended from 0 to x and 0 to y. These numbers now form a right triangle, with 0 as the acute angle's vertex. Using Pythagoras' theorem as a guide,
|z|2 = |x|2+|y|2
|z|2 = x2 + y2
|z| = √(x2+y2)
Algebraic Operations on Complex Numbers
There are four different types of algebraic operations that can be performed on complex numbers, as listed below. More information about these algebraic operations, as well as solved examples, can be found in the linked article. The four operations on complex numbers are as follows:
- Addition
- Subtraction
- Multiplication
- Division
Roots of Complex Numbers
When we solve a quadratic equation of the form ax2 +bx+c = 0, we can discover the roots of the equations in three ways:
- Two Distinct Real Roots
- Similar Root
- No Real roots (Complex Roots)
Complex Number Formulas
Combine comparable phrases while executing complicated number arithmetic operations like addition and subtraction. It means that you should add real numbers to real numbers and imaginary numbers to imaginary numbers.
- Addition
(a + ib) + (c + id) = (a + c) + i(b + d)
- Subtraction
(a + ib) – (c + id) = (a – c) + i(b – d)
- Multiplication
When two complex integers are multiplied by each other, the technique should be identical to that of binomial multiplication. It denotes the application of the FOIL method (Distributive multiplication procedure).
(a + ib). (c + id) = (ac – bd) + i(ad + bc)
- Division
The FOIL Method can be used to divide two complex numbers by multiplying the numerator and denominator by the denominator's conjugate value and then applying the FOIL Method.
(a + ib) / (c + id) = (ac+bd)/ (c2 + d2) + i(bc – ad) / (c2 + d2)
Power of Iota (i)
It can take the following values depending on the power of I
i4k+1 = i.i4k+2 = -1 i4k+3 = -i.i4k = 1
Where k might have a positive or negative integral value (positive or negative).
Similarly, we may determine the values for the negative power of I as follows:
i-1 = 1 / i
We get the following by multiplying and dividing the above term with I
i-1 = 1 / i × i/i × i-1 = i / i2 = i / -1 = -i / -1 = -i
Note: √-1 × √-1 = √(-1 × -1) = √1 = 1 contradicts to the fact that i2 = -1.
As a result, a b is not equivalent to ab for an imaginary number.
Identities
Let us see some of the identities.
- (z1 + z2)2 = (z1)2 + (z2)2 + 2 z1 × z2
- (z1 – z2)2 = (z1)2 + (z2)2 – 2 z1 × z2
- (z1)2 – (z2)2 = (z1 + z2)(z1 – z2)
- (z1 + z2)3 = (z1)3 + 3(z1)2 z2 +3(z2)2 z1 + (z2)3
- (z1 – z2)3 = (z1)3 – 3(z1)2 z2 +3(z2)2 z1 – (z2)3
Properties
The properties of complex numbers are listed below:
1. A real number is obtained by adding two conjugate complex numbers.
2. A real number can be obtained by multiplying two conjugate complex numbers.
3.If x and y are real numbers and x+yi = 0, then x and y must be equal.
4. If p, q, r, and s are real numbers, and p+qi = r+si, p = r, and q=s.
5. The commutative law of addition and multiplication applies to complex numbers.
z1 + z2 = z1 + z2
z1 x z2 = z2 x z1 x z2 x z1 x z2
6. The associative law of addition and multiplication applies to complex numbers.
z1 + (z2+z3) = (z1+z2) + (z2+z3)
(z1.z2).z3 = (z1.z2).z3 = (z1.z2).z3 = (z1.z2).
(3.z2)
7. The distributive law applies to complex numbers.
z1.z2 + z1.z3 = z1.(z2+z3)
8. If the sum of two complex numbers is real, and the product of two complex numbers is also real, these numbers are conjugate.
9. If two complex numbers are given, say z1 and z2, then |z1+z2| = |z1|+|z2|.
10. The result of multiplying two complex numbers and their conjugate value should be another complex number with a positive value.
Modulus and Conjugate
Let z = a+ib be a complex number.
The Modulus of z is represented by |z|.
Mathematically, |z|=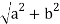
The conjugate of “z” is denoted by z¯.
Mathematically, z¯= a – ib
Argand Plane and Polar Form
The Argand(or complex) plane, like the XY plane, is a rectangular coordinate system in which the complex number a+ib is represented by a point with coordinates a and b.
The real and complex components are calculated in terms of r and, where r is the vector's length and r is the angle formed with the real axis. Check out this page for a full explanation of the argand plane and polar representation of complex numbers, along with solved examples.
A point P(a,b) on a xy plane can represent the complex number z=a+ib. The actual part is represented by the x-axis, while the imaginary part is represented by the y-axis.
The Argand Plane, often known as the Complex Plane, is a type of graphic.
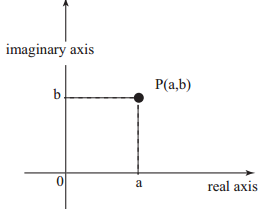
Points to Note
(1) The module of z is the length OP and is denoted by|z|
|z|=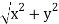
OP=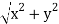
(2) The X-axis represents pure real numbers, whereas the y-axis represents pure imaginary numbers.
(3) The Line OP makes an angle θθ with the positive direction of x-axis in anti-clockwise sense is called the argument or amplitude of z
It is provided byθ=tan−1
(4) A complex number's argument is not unique because if is the value of argument, then 2nπ+θ (n=0, ±±1, ±±2, ....) The argument of a complex number is not unique because if is the value of argument, then
(5) The principal value of the amplitude or principal argument is the unique value of such that =.
(6) The main argument of a complex number can be found by following the steps below.
Step 1) for z=a+ib , find the acute angle value of θ=tan−1| |
|
Step 2) Look for the values of a ,b
If (a,b) lies in First quadrant then Argument=θ
If (a,b) lies in second quadrant then Argument =π−θ
If (a,b) lies in third quadrant then Argument =−π+θ
If (a,b) lies in Fourth quadrant then Argument =−θ
(7) The complex number's conjugate rotates symmetrically along the x-axis
(8) Every real number can be expressed as a complex number with no imaginary component. As though it were a +i(0) As a result, we can consider real numbers to be a subset of a larger set of complex numbers.
1.1.2 Geometry of complex number
Representation of Z modulus on Argand Plane
Argand plane consists of real axis (x – axis) and imaginary axis (y – axis).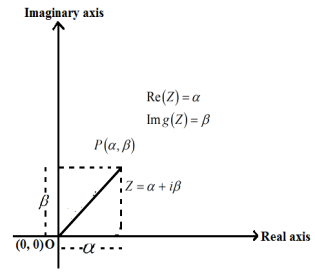
|Z| = √(α – 0)2 + (β – 0)2
= √(α )2 + (β)2
= √Re (z )2 + Img (z)2
|z| = | α + iβ| = √(α )2 + (β)2
Conjugate of Complex Numbers on argand plane
A complex number's conjugate is a number with the same real portion and the opposite sign of the imaginary portion but identical magnitude.
The complex number Z = + I will be used.
The conjugate of a particular complex number will be represented as the mirror image of Z = + I along the real axis.
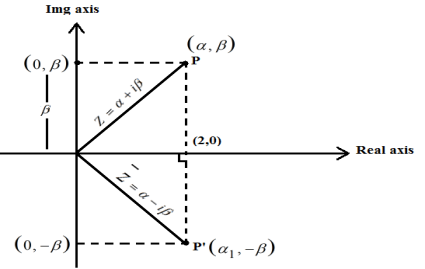
Z = α + iβ (complex number)
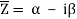 (Conjugate of complex number)
(Conjugate of complex number)
Distance between Two Points in Complex Plane
In the argand plane, if two complex integers Z1 and Z2 are labelled as P and Q, respectively, the distance between P and Q is given as.
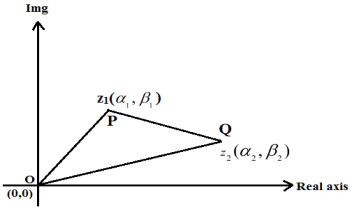
PQ = |z2 – z1| = |(α2 – α1) + i(β2 – β1)| = √( α2 – α1)2 + (β2 – β1)2
For example, Find the distance of a point P, Z = (3 + 4i) from origin.
Solution:
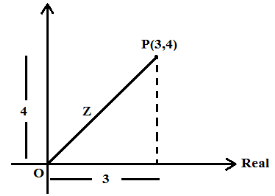
|Z| = |3 + 4i|
= √ 32 + 42 = 5 units
Polar form of complex number
Both rectangular and polar coordinates can be used to represent complex values. We'll look at the polar form of any complex number here.
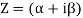
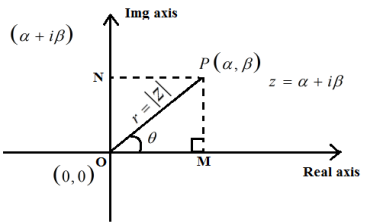
Z = α + iβ, |z| = r
OM = r cos θ = α
ON = r sin θ = β
Hence, Z = α + iβ
= (OM) + i (ON)
= r cos θ + i r sin θ = r( cos θ + i sin θ) r = 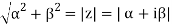
Where ‘' stands for complex number argument.
θ = arg (z)
For a complex number's conjugate
Arg (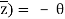
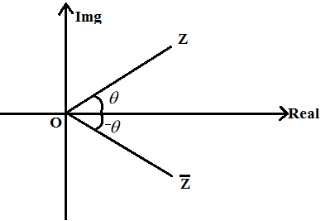
Algebra of Complex Numbers
Let's look at the many algebras for complex numbers. We mostly deal with complicated number addition, subtraction, multiplication, and division.
Product of two complex number
Let P and Q represent complex number
Z1=(α1+iβ1) and
Z2=(α2+iβ2) in argand plane
θ1=arg(z1),
θ2=arg(z2) (given)
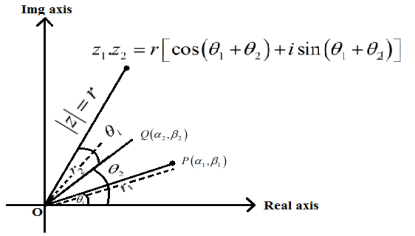
Now, on multiplying Z1 Z2 = Z
Z = ( α1 + i β1) ( α2 + i β2) = r1 ( cos θ1 + i sin θ1). r2 ( cos θ2 + i sin θ2)=
r1r2[ cos(θ1 + θ2) + i sin (θ1 + θ2)]
Let say r1. r2 = r
Z = r( cos(θ1 + θ2) + i sin (θ1 + θ2))
Two complex numbers are divided.
Let Z1 = α1 + i β1 = r1 (cos θ1 + i sin θ1)
Z2 = α2 + i β2 = r2 (cos θ2 + i sin θ2)
Where, θ1 = arg (Z1)
θ2 = arg (Z2)
Z now stands for a complicated number.
Z = Z2/Z1 = Z2Z1-1
Z = Z2 Z1-1 = Z2 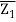 / |Z|2
/ |Z|2
= r2/r1 (cos(θ2 – θ1) + i sin (θ2 – θ1))

Note:
1. When two complex numbers are multiplied, their argument is added.
θ=θ1+θ2
2. The argument of two complex numbers is subtracted when they are divided.
θ=θ1−θ2
Equation of Straight Line Passing through Two Complex Points
The equation of a straight line going through two points (x1, y1) and (x2, y2) has been examined in Algebra.
y – y1 = y2 – y1/ x2 – x1 (x – x1)
In complex numbers
A straight-line equation passes through two points. A(Z1) and B(Z2) are two variables that can be expressed as
Z – Z1 = Z2 – Z1/ 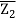 -
-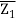 (
(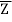 -
-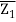 )
)
Z – Z1/ Z2 – Z1 = 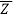 -
-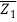 /
/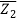 -
-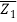
Where Z stands for Z's conjugate.
Or
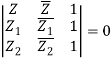
Section Formula in Complex Numbers
The three points on a line are A(Z1), B(Z2), and C(Z).
If C splits line AB in the ratio m:n (internally), then
AC/BC = m/n
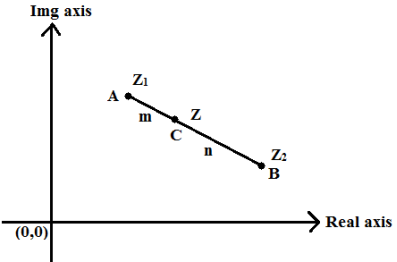
Then, Z = mZ2 + nZ1/ m+n
Co-linearity condition
Let A(Z1), B(Z2), and C(Z3) be the three points Z1, Z2, and Z3 (Z3).
As a result, collinearity will be a condition.
|AB| + |BC| = |AC|
Or,
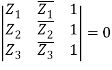
Equation of circle in Complex Plane
The complex number Z0 is represented by a circle whose centre is the complex number Z0. And let the radius be ‘r'.
The circle's equation will be
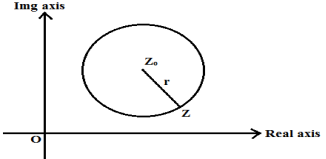
|Z – Z0| = r
If Z1 and Z2 are the circle's diametric end points, the equation is
( Z – Z1)(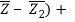 ( Z – Z2)(
( Z – Z2)(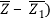 = 0
= 0
NUMERICALS
- Perform the indicated operation and write your answer in standard form.
(4 – 5i)(12 + 11i)
Ans:
We know how to multiply two polynomials and so we also know how to multiply two complex numbers. All we need to do is “foil” the two complex numbers to get,
(4 – 5i)(12 +11i) = 48 + 44i – 60i – 55i2 = 48 – 16i – 55i2
All we need to do to finish the problem is to recall that i2=−1. Upon using this fact we can finish the problem.
|(4 – 5i)(12 + 11i) = 48 – 16i – 55 (-1) = 103 – 16i
- Perform the indicated operation and write your answer in standard form.
7 – i/ 2 + 10i
Ans:
Because standard form does not allow for ii’s to be in the denominator we’ll need to multiply the numerator and denominator by the conjugate of the denominator, which is 2−10i.
Multiplying by the conjugate gives,
7 – i/ 2 + 10i 2- 10i/2-10i = (7 – i)(2 – 10i)/(2 + 10i)(2 – 10i)
Now all we need to do is do the multiplication in the numerator and denominator and put the result in standard form.
7 – i/2+10i = 14 – 72i + 10i2/ 4 – 100i2 = 4 – 72i/ 104 = 4/104 – 72/104 i = 1/26 – 9/13 i
1.2.1 Euler’s Formula Explained: Introduction, Interpretation and Examples:
Euler's formula is the theorem that asserts, in a word, that
eix = cos x + i sin x
- The number x is a genuine number. The natural logarithm's base is e. The imaginary unit (i.e., the square root of 1) is denoted by the letter i.
- The essential link between trigonometric and exponential functions is established by Euler's formula. It can be viewed of as a technique of linking two representations of the same unit complex number in the complex plane from a geometric standpoint.
- Let's look at some of the main values in Euler's formula and see how they relate to trigonometric/unit circle points:
- We have e0=cos0+isin0 for x=0, which provides 1=1. So far, so good: we know that a 0 degree angle on the trigonometric circle equals a 1 degree angle on the real axis, and that's what we get here. We have ei=cos1+isin1 for x=1. This implies that ei is the exact point on the unit circle with a 1 radian angle. We have ei2=cos2+isin2=i for x=2. This finding is important in a number of physics calculations. We have ei=cos+isin for x=, which suggests that ei=1. This result is the same as the well-known Euler's identity. We have ei(2 )=cos2+isin2 for x=2, which means that ei(2 )=1, the same as for x=0.
- The following is a rewrite of Euler's formula that will help you comprehend it better:
- (ei)x=sinx+icosx
- The unit complex number with angle x can be thought of as the right-hand equation.
- The 1-radian unit complex number increased to x can be thought of as the left-hand expression.
- Euler's formula can be interpreted as two distinct ways of running around the unit circle to arrive at the same place, because increasing a unit complex number to a power can be thought of as repeated multiplications (i.e., adding up angles in this example).
1.2.2 Derivations
There are at least three techniques to prove Euler's formula. The first derivation is based on power series, in which the exponential, sine, and cosine functions are expanded as power series to determine whether or not the formula holds.
The second derivation of Euler's formula is based on calculus, which treats both sides of the equation as functions and differentiates them accordingly. This leads to the discovery of a common attribute that can be used to demonstrate that both functions are equivalent.
Another way to derive Euler's formula is to utilise polar coordinates in the complex plane, which can then be used to find the values of r and.
Derivation 1: Power Series
The use of power series is one of the more intuitive derivations of Euler's formula. It entails expanding the exponential, sine, and cosine power series to arrive at the conclusion that the equivalence holds.
As a precaution, this method presupposes that the sinz, cosz, and ez power series expansions are perfectly convergent everywhere (e.g., that they hold for all complex numbers z). It does, however, have the advantage of demonstrating that Euler's formula holds for all complex numbers z.
The power series expansion of ez for a complex variable z is
ez = 1 + z/ 1! + z2/2! + z3/3! + z4/4! + . . .
Let's pretend that z is ix (where x is an arbitrary complex number). I am raised to greater powers as z is raised to greater abilities. The first eight powers of I are as follows:
i0 = 1 i4 = i2 . i2 = 1
i1 = i i5 = i . i4 =i
i2 = 1 (by the definition of i) i6 = i . i5 = -1
i3 = i . i2 = - i i7 = i . i6 = -i
(Notice how the powers of I are cyclical: 1, I 1, i. We'll be putting these abilities to good use soon.)
When z=ix, the expansion of ez is as follows:
eix = 1 + ix + (ix)2/2! + (ix)3/3! + (ix)4/4! + . . .
We get the following results when we extract the powers of I
eix = 1 + ix - (ix)2/2! - (ix)3/3! + (ix)4/4! + (ix)5/5! - (ix)6/6! - (ix)7/7! + (ix)8/8! +. . .
We can rearrange the terms of ez's power series expansion without changing its value because it is totally convergent. The result of combining the real and imaginary terms is
eix = (1 - x2/2! + x4/4! - x6/6! + x8/8! - . . .) + i (x – x3/3! + x5/5! – x7/7! +. . .)
Let's take a detour and look at the sine and cosine power series. The cos x power series is
Cos x = 1 - x2/2! + x4/4! - x6/6! + x8/8! - . . .
And for sinx, it is
Sin x = x – x3/3! + x5/5! – x7/7! +. . .
To put it another way, the last equation we had was exact.
eix = cos x + i sin x
This is the Euler's formula statement we were seeking for.
Derivation 2: Calculus
Consider both eix and cosx+isinx as functions of x before differentiating them to locate a common attribute between them.
However, in order for this to happen, one must suppose that the functions ez, cosx, and sinx are defined and differentiable for all real and complex values x and z. It is also possible to establish that Euler's formula holds for all complex numbers by assuming that these functions are differentiable for all complex numbers.
First, let f1(x) and f2(x) be eix and cosx+isinx,
:correspondingly The chain rule is then used to differentiate f1 and the result is
f’1 (x) = i eix = i f1(x)
Differentiating f2 produces the following results:
f’2 (x) = - sin x + i cos x = i f2 (x)
In other words, the differential equation f′(x)=if is satisfied by both functions (x). Consider the function f 1/f 2, which is well-defined for all x (since f2(x)=cosx+isinx corresponds to never-zero points on the unit circle). After that, applying the quotient rule to this function yields:
(f1/f2)’ (x) = f’1(x)f2(x) – f1(x)f’2(x)/ [ f2(x)]2
= if1(x) f2(x) – f1(x) i f2(x)/ [ f2(x)]2
= 0
Because the derivative is 0 in this case, the function f 1/f 2 must have been a constant to begin with. What is this constant's value? Let's see what happens if we put x=0 into the function:
In other words, we must have that for all x: which becomes the renowned formula we've been looking for after moving cosx+isinx to the right.
Derivation 3: Polar Coordinates
Another clever proof of Euler's formula is to treat exponentials like numbers, or more precisely, as complex numbers in polar coordinates.
We already know that all non-zero complex numbers have a unique way of being expressed in polar coordinates. In specifically, any non-zero number of the type eix (with real x) can be represented as:
eix = r(cos θ + i sin θ)
Where r is its radius (with r>0) and is its primary angle from the positive real axis (say, 02). Except for the fact that r and are functions of x, we make no assumptions about their values (which may or may not contain x as variable). They'll be determined as the proof progresses.
(However, we do know that for x=0, the left-hand side is 1, implying that r and meet the r(0)=1 and (0)=0 beginning conditions, respectively.)
For what it's worth, let's start by separating the two sides of the equation. Differentiating the left side of the equation with respect to x provides ieix, according to the definition of exponential. The equation becomes: after differentiating the right side of the equation.
Ieix = dr/dx (cos θ + i sin θ) + r( - sin θ + i cos θ) d θ/dx
We're seeking for a statement that is unique in terms of the letters r and. To get rid of eix, we replace it with r(cos+isin) and get:
Ir(cos θ + i sin θ) = (cos θ + i sin θ) dr/dx + r(- sin θ + i cos θ) d θ/dx
The I on the left-hand side is then distributed, yielding:
r(i cos θ – sin θ) = ( cos θ + i sin θ) dr/dx + r ( - sin θ + i cos θ) d θ/dx
When the imagined and actual components are added together, we get:
Ir cos θ = i sin θ dr/dx + i r cos θ d θ/dx
And
-r sin θ = cos θ dr/dx – r sin θ d θ/dx
The variables dr/dx and d/dx are the variables in this system of two equations and two unknowns. In only a few steps, we'll be able to solve it. First, we get: by assigning to dr/dx and d/dx:
r cos θ = ( sin θ)α + (r cos θ)β (I)
-rsin θ = (cos θ) α – ( r sin θ) β (II)
Second, we get (I) by cos and (II) by sin by multiplying (I) by cos and (II) by sin.:
r cos2 θ = ( sin θ cos θ)α + (r cos2 θ)β (III)
-rsin2 θ = (sin θ cos θ) α – ( r sin2 θ) β (IV)
The goal of these operations is to eliminate by doing (III) – (IV), which results in:
r( cos2 θ + sin2 θ) = r( cos 2 θ + sin2 θ) β
Because cos2+sin2=1, a more straightforward equation emerges:
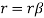
And because r>0 for any x, this means that — which we specified to be d/dx — is equal to 1.
Substituting this result back into (I) and (II) and cancelling the result, we get:
0=(sinθ)α
0=(cosθ)α
This indicates that — which we have determined to be the case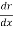 —0 must be present.
—0 must be present.
We may deduce that r must be a constant from the fact that dr/dx=0. Similarly, we can derive that =x+C for some constant C from the fact that d/dx=1.
However, we must have r=1 because r meets the beginning condition r(0)=1. Similarly, we must have C=0 since meets the beginning condition (0)=0. That is, x Now that we know what r and are, we can insert them into the original equation to get:
eix = r( cos θ + i sin θ)
= cos x + i sin x
Which, as one might anticipate, is the exact formulation of Euler's formula for real numbers x.
Applications
Euler's formula, as one of the most important equations in mathematics, has a plethora of interesting applications in a variety of fields. These include, for example:
- The famous Euler's identity The exponential form of complex numbers Trigonometric and hyperbolic functions with different meanings
- Exponential and logarithmic functions are generalised to complex numbers.
- De Moivre's theorem alternate proofs and trigonometric additive identities
- Euler's Personality
- Euler's identity is frequently regarded as mathematics' most beautiful equation. It's written like this:
- Ei+1=0
- Where five of the most essential constants in mathematics are highlighted. These are the following:
- The identity of addition 0
- The unity number one
- The Pi constant (circumference to diameter ratio) is a mathematical constant.
- e is the natural logarithm's base.
- The fictitious unit I
Integers, irrational numbers, and imaginary numbers are among the three types of numbers represented. Addition, multiplication, and exponentiation are three basic mathematical operations that are also illustrated.
Starting with Euler's formula eix=cosx+isinx, we set x= and transmit the succeeding 1 to the left-hand side to obtain Euler's identity. The intermediate forme iπ=−1is common in the context of trigonometric unit circle in the complex plane: it corresponds to the point on the unit circle whose angle with respect to the positive real axis is π.
Exponential Form for Complex Numbers
We already know that a complex number z may be written in Cartesian coordinates as x+iy, where x and y are the real and imaginary parts of z, respectively.
In fact, the identical complex number may be written in polar coordinates as r(cos+isin), where r is the magnitude of the distance to the origin and is the angle with respect to the positive real axis.
But it doesn't stop there: every complex number can now be written as a complex exponential using Euler's formula:
z=r(cosθ+isinθ)=reiθ
Where the numbers r and are the same as previously.
To go from (x,y) to (r,θ),
We employ formulae.
r = 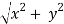
θ = a tan2(y, x)
(where 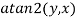 is the two-argument arc tangent
is the two-argument arc tangent
Function with atan2(y,x)=arctan(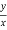 ) whenever x>0.)
) whenever x>0.)
To go from (r,) to (x,y), we utilise the following formulas: rcosy=rsin x=rcosy=rsin In the same manner that rectangular coordinates make addition simple, the exponential form of complex numbers makes multiplying complex numbers considerably easier. For example, if we have two complex numbers z1=r1ei1 and z2=r2ei2, we can multiply them as follows:
z1z2 = r1eiθ1 . r2eiθ2
= r1 . r2ei(θ1+θ2)
In the same vein, the same two numbers can be divided as follows:
z1/z2 = r1eiθ1/ r2eiθ2
= r1 ./r2ei(θ1-θ2)
The identical division would have required multiplying by the complex conjugate in the numerator and denominator if we had used the rectangular x+iy notation instead. The situation would have been the same if the polar coordinates had been used (save perhaps worse).
Multiplying two complex numbers is actually the same as multiplying magnitudes and adding angles, while dividing two complex numbers is really the same as dividing magnitudes and subtracting angles.
Alternative Key Function Definitions
Euler's formula can also be used to define essential functions like the complex exponential function, trigonometric functions like sine, cosine, and tangent, as well as their hyperbolic analogues. It can also be used to figure out how some of these functions relate to one another.
Exponential Function (Complex)
To begin, remember Euler's formula, which asserts that
eix = cos x + i sin x
The exponential function is only defined up to the imaginary numbers if the formula is assumed to hold exclusively for real x. However, by using a simple method, we may extend the exponential function to encompass all complex numbers:
ez = ex+ iy ( = ex eiy) = dy = ex(cos y + i sin y)
In other words, the complex number x+iy's exponential is just the complex number with magnitude ex and angle y. This means that the complex exponential effectively transfers vertical lines to circles. Here's an example of what I'm talking about:
Trigonometric Functions are a type of trigonometric function that is used
We may utilise Euler's formula to get a similar equation for the opposite anglex, in addition to increasing the domain of exponential functions:
e-ix = cos x – i sin x
This equation, along with Euler's formula, create a system of equations from which the sine and cosine functions can be isolated.
The cosines cancel out when the eix equation is subtracted from the eix equation, and after dividing by 2i, we get the complex exponential form of the sine function:
Sin x = eix – e-ix/2i
Similarly, the sines cancel out when the two equations are added together, and after dividing by two, we get the complex exponential form of the cosine function:
Cos x = eix + e-ix/2
To be sure, here's a movie that goes over the same derivations in greater depth.
On the other hand, the tangent function is defined to be sin x / cos x, so in terms of complex exponentials, it becomes:
Tan x = eix – e-ix/ i (eix + e-ix)
If we can show that Euler's formula holds for all complex numbers (as we did in the power series demonstration), then the same can be said for these three formulas. When it comes to computing derivatives and integrals, their presence allows us to flexibly move between trigonometric functions and complex exponentials.
De Moivre's theorem establishes a formula for computing complex number powers. Consider what occurs when we multiply a complex number by itself to obtain some idea for de Moivre's theorem.
Remember that any complex number z=a+ib can be expressed as with the polar form.
Then squaring the complex number z gives
z2 =(r( cos θ + i sin θ))2
= r2( cos θ + i sin θ)2
= r2( cos θ cos θ + i sin θ cos θ + i sin θ cos θ + i2 sin θ sin θ)
= r2((cos θ cos θ – sin θ sin θ) + i(sin θ cos θ + sin θ cos θ))
= r2(cos 2 θ + i sin 2 θ)
This demonstrates that squaring a complex integer squares the absolute value and multiplies the argument by two. For n3, de Moivre's theorem shows that to increase a complex number to the nth power, the absolute value must be raised to the nth power, and the argument must be multiplied by n.
1.3.1 Proof:
We'll use induction to illustrate our point.
zn = (r( cos (θ) + i sin (θ)n
= rn ( cos (θ) + i sin(θ))n
We have
Let's focus on the second part: ( cos (θ) + i sin(θ))n
For n=1, we have
( cos (θ) + i sin(θ))1 = cos ( 1. θ) + i sin( 1. θ)
Which is true.
We can suppose that n=k follows the same formula, thus we obtain
(cos (θ) + i sin (θ))k = cos ( k θ) + i sin (k θ)
For n=k+1, we expect to have
(cos (θ) + i sin (θ))k+1 = cos ((k+1) θ) + i sin ((k+1) θ)
We get
(cos θ + i sin θ)k+1 = (cos θ + i sin θ)k(cos θ + i sin θ)1
= (cos (k θ) + i sin (k θ))(cos( 1. θ) + i sin (1. θ )) (We assume this to be true for x = k)
= cos ( k θ) cos (θ) + cos (kθ) i sin(θ) + i sin (k θ) cos (θ) + i2 sin(k θ)sin(θ) (We have i2 = - 1)
= cos(k θ)cos(θ) – sin(k θ)sin(θ) + i (cos (k θ)sin(θ) + sin(k θ) cos(θ))
= cos(k θ + θ) + i sin(k θ + θ) (deducted from the trigonometry rules)
= cos((k+1) θ) + i sin((k+1) θ)
Thus, for n=k+1, we have (cos (θ) + i sin (θ ))k+1 = cos((k+1) θ ) + i sin((k+1) θ )(cos (θ ) + i sin θ(θ ))k+1 as expected.
As the theorem is true for n=1 and n=k+1, it is true for all n≥1.
NUMERICALS:
1) (sin 𝛑/6 + i cos 𝛑/6)18
ANS:
We have, sin 𝛑 /6 + i cos 𝛑 /6 = i(cos 𝛑 /6 – i sin 𝛑 /6)
Raising to the power 18 on both sides gives,
(sin 𝛑 /6 + i cos 𝛑 /6)18 = (i)18(cos 𝛑 /6 – sin 𝛑 /6)18
= (-1)( cos 18 𝛑 /6 – i sin 18 𝛑 /6)
= -(cos 3 - i sin 3 𝛑 ) = 1 + 0i
Therefore, (sin 𝛑 /6 + i cos 𝛑 /6)18=1
2) Simplify ((1+cos 2 𝛉 + i sin 2𝛉 )/(1+cos 2 𝛉 – i sin2 𝛉 ))3θ
ANS:
Let z = cos 2𝛉 + i sin 𝛉
As |z| = |z|2 = z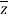 = 1 , we get
= 1 , we get 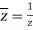 = cos 2 𝛉 – i sin 2 𝛉
= cos 2 𝛉 – i sin 2 𝛉
Therefore, (1+cos 2𝛉 + i sin 2𝛉 )/(1+cos 2𝛉 – i sin 2𝛉 ) = 1+z/ 1+ 1/z = (1+z)z/z+1 = z
Therefore, ((1+cos 2 𝛉 + i sin 2 𝛉 )/(1+cos 2 𝛉 – i sin2 𝛉 ))3θ = z3θ = ( cos 2θ + i sin 2 θ)3θ
= cos 60 θ + i sin 60 θ
3) (1+ i)18
ANS:
Let 1+ i = r (cosθ + i sinθ ) . Then, we get
r = 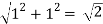 ; α = tan-1(1/1) = π/4
; α = tan-1(1/1) = π/4
θ = α = π/4 ( 1+i lies in the first Quadrant)
Therefore 1+i = √2 (cos π/4 + i sin π/4)
Raising to power 18 on both sides,
(1+i)18 = [√2 (cos π/4 + i sin π/4)]18 = √218 (cos π/4 + i sin π/4)18
By de Moivre’s heorem,
(1+i)18 = 29( cos 18π/4 + i sin 18 π/4)
= 29 ( cos(4 π + π/2) + i sin(4 π + π/2)) = 29(cos π/2 + i sin π/2)
(1+i)18 = 29 (i) = 512 i
Let z be a complex number that is not zero. Then in C, there are exactly k many kth roots of z.
Assume that w is a complex number. We want to identify all z such that zn=w, or the nth roots of w.
There are n different nth roots, which can be discovered in the following order:
1. Write z and w in polar form as z=rei,w=sei. Zn=w then becomes:
(reiθ)n = rneinθ = seiϕ
We need to solve for r and θ.
2. Solve the following two equations:
rn=s
einθ=eiϕ
The solutions to rn=s are given by r= .
.
The solutions to einθ=eiϕ are given by
nθ = ϕ + 2 πl, for l = 0, 1, 2, . . ., n - 1
Or
θ = ϕ/n + 2/n πl, for l = 0, 1, 2, . . . , n -1
Using the solutions r,θ to the equations given in construct the nth roots of the form z=reiθ.
1.5.1 Logarithm functions
Because a complex number can be expressed as an exponential function, reiP , A logarithm is nearly instantaneous. We get it. ln reiP = ln r + ln eiP = ln r + iP , This is the natural logarithm's primary value. The angle PP, on the other hand, is not unique, as it can vary by multiples of two. As a result, the formula for a complex number's natural logarithm is ln reiP = ln r + iP + 2kπi
We can find the natural logarithm of I for example. Its main benefit is
Ln i = ln (1 eiπ/2) = π/2 i
The natural logarithm of negative one is another fascinating example. Its main benefit is ln(-1) = ln(1 eiπ ) = πi. (And you thought you couldn't handle negative logarithms!) You can, but the results aren't accurate.)
Other base logarithms can be found using the change-of-base formula.
Log4 e = ln e/ ln i = 1/ πi/2 = -2i/π
Complex bases). For example,
1.5.2 Trigonometric Functions
We can quickly obtain some formulas for the sine and cosine functions in terms of complex exponentials thanks to the formula. These formulas are frequently used as trigonometric function definitions for complex numbers.
Cos x = eix + e-ix/2 sin x = eix - e-ix/2i
Substituting the quantity ix in place of the variable x, we can produce formulas for pure imaginary numbers. It's worth noting that the outcomes are linked to hyperbolic functions.
Cos ix = ex + e-x/2 = cosh x, sin ix = e-x - ex/2 = i sinh x
The sine and cosine of complex numbers can then be calculated using the formulas for the sine and cosine of the sum of two angles.
Cos(a + bi) = cos a cosh b – i sin a sinh b
Sin(a + bi) = sin a cosh b + i cos a sinh b
Consider the cosine of I as an example.
Cos i = cos 0 cosh 1 – i sin 0 sinh 1 = cosh 1 = e1 + e-1/2 ≈ 1.5431
1.5.3 Hyperbolic Functions
The results for hyperbolic functions are virtually instantaneous when using the connection between hyperbolic and trigonometric functions.
Cosh(a + bi) = cosh a cos b – i sinh a sin b
Sinh(a + bi) = sinh a cos b + i cosh a sin b
As an example, consider the hyperbolic cosine of i. We get
Cosh i = cosh 0 cos 1 + i sinh 0 sin 1 = cos 1 ≈ 0.5403
1.5.4 Inverse Trigonometric Functions
Since cos x = eix + e-ix/2 , we can find the inverse by replacing the function with the variable y, swapping x and y, then solving for y. After the variable switch, we'll go on to the next step.
Have x = eiy+ e-iy/2 . Both sides are multiplied by 2eiy provides the formula 0 = e2iy – 2xeiy +1. The quadratic formula can be used to solve this.
eiy = 2x ± √4x2 – 4 /2. After simplifying, we can take the natural logarithm of both sides and divide by i. The end result is as follows: cos-1x = - i ln [ x ± i √ 1 – x2]
(A factor of ii typically appears as the coefficient of the square root so that the similarities between the inverse cosine and inverse sine formulas are more apparent.)
The inverse sine formula is discovered to be by using similar arguments.
Sin-1x = - i ln [i x ± i√ 1 – x2]
The inverse tangent formula is as follows:
Tan-1 x = i/2 ln i+x/i - x
Consider the inverse cosine of ii as an example. Using the plus sign in the formula, we will find only one of its numerous values. We get cos-1 i = - i ln [ i + i √ 1 – i2] = - i ln [(1+√2)i]Then we use the logarithm formula to continue:
-i ln [(1+√2)i] = - i ln [(1+√2)eix/2] = - i [ ln (1 + √2) + πi/2]
This can be simplified, and we get
- i [ ln (1 + √2) + πi/2] = π/2 – i ln ( 1 + √2) ≈ 1.57 – 0.88i
1.5.5 Inverse Hyperbolic Functions
The formulas are the same as those derived for inverse hyperbolic functions previously:
Cosh-1 x = ln[ x ± √x2 – 1]
Sinh-1 x = ln[ x ± √x2 + 1]
For example, using the plus sign in the formula, one of the values of the inverse hyperbolic cosine of ii is: cosh-1 x = ln[ i ± √i2 – 1] = ln [(1+ √2)i]
Then using the logarithm formula, we get:
Ln [(1+ √2)i] = ln (1+ √2) + πi/2 ≈ 0.88 + 1.57i
1.6.1 Cauchy-Riemann Equations:
Let
f(x, y) ≡ u(x, y) + iv(x, y)
Where
z ≡ x+ iy
So
Dz = dx + i dy
After that, the total derivative of with respect to is
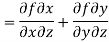

In the context of and, (5) becomes
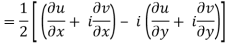
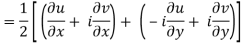
Along the x-axis, or real axis,
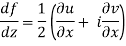
Along the y-axis, or imaginary axis, , so
, so

If f is complex differentiable, then the value of the derivative must be the same for a given dz, regardless of how it is oriented as a result, (8) must equal (9), implying that

And
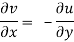
The Cauchy-Riemann equations are what they're called.
They are the causes of the disorders.
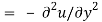
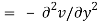
Where  is the complex conjugate.
is the complex conjugate.
If z = r eiθ, then the Cauchy-Riemann equations become
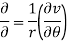
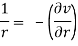
(Abramowitz and Stegun 1972, p. 17).
In two dimensions, if and satisfy the Cauchy-Riemann equations, they also satisfy Laplace's equation.
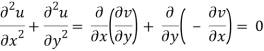
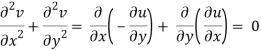
Solutions that fulfil the Cauchy-Riemann equations and Laplace's equation can be found by picking an arbitrary. This fact is utilised to solve physical problems involving scalar potentials, such as fluid flow and electrostatics, using conformal mappings.
1.6.2 A necessary condition for a complex function to be analytic:
Let
f(x, y) = u(x, y) + iv(x, y)
To be a complicated function Since then, x = (z + 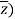 /2 and y = (z -
/2 and y = (z - 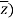 /2i
/2i
By replacing x and y for x and y, we get
f(z , 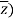 = u(x, y) + iv(x, y)
= u(x, y) + iv(x, y)
a required condition for f(z, 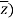 It is to be analytic.
It is to be analytic. 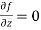
As a result, one of the required conditions for being analytic is that f depends solely on z. Condition (1) is equal to condition (2) in terms of the real and imaginary portions u,v of f.
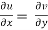 (2)
(2)
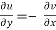 (3)
(3)
Equations (2, 3) are known as the Cauchy-Riemann equations. They are a necessary condition for f = u + iv to be analytic.
NUMERICAL:
Use the Cauchy-Riemann equations to show that f(z)=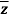 is not differentiable.
is not differentiable.
SOLUTION:
f(x + iy) = x – iy, so u(x, y) = x, v(x, y) = - y
Taking partial derivatives
ux = 1, uy = 0, vx = 0, vy = - 1
Since ux≠vy the Cauchy-Riemann equations are not satisfied and therefore ff is not differentiable.
1.7.1 What is Analytic Function
The enlarged Taylor series can be represented as follows. Analytic Function is defined as an indefinitely differential function over a variable named x.
T(x) = 
This explains the extended Taylor overvalue Xo; this function is analytic for the value x in its domain, but there is another value in the domain that converges the series to one point.
1.7.2 Examples:
Rational functions
The rational functions are the most basic complex analytic functions. These are the features.
R(z) = P(z)/Q(z),(1)
Where
P(z) = amzm + am−1zm−1 + ··· + a1z + a0
AndQ(z) = bnzn + bn−1zn−1 + ··· + b1z + b0
Are polynomials with complex coefficients
am, am−1, ..., a1, a0,bn, bn−1, ..., b1, b0,
And we assume that am 6 = 0 and bn 6 = 0. We also suppose that P and Q have no factors in common. At every point of C S, where S is the finite set of points within C where the denominator Q(z) vanishes, the function R(z) is differentiable. The degree of the rational function R is the sum of the two degrees, the degree of the numerator and the degree of the denominator (z).
The product and the sum of two rational functions are both rational functions. Indeed, the space of rational functions fulfils the field axioms with these addition and multiplication operations, and we call this field by C. (X). This is a good example of a field that can be added to the Q, R, and C fields.
We can factor polynomials using the Fundamental Theorem of Algebra.
P(z) and Q(z) ,
P(z) = am(z −z1)p1(z −z2)p2 ···(z −zr)pr
AndQ(z) = bn(z −ζ1)q1(z −ζ2)q2 ···(z −ζs)qs,
The first of two significant canonical forms for a rational function is: where the exponents denote the multiplicities of the roots, and thus gives us:
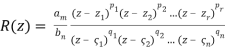 (2)
(2)
The numerator's zeros z1,...,zr are known as the rational function's zeros, whereas the denominator's zeros 1,...,s are known as the denominator's poles. The multiplicity of a zero or pole as a root of either the numerator or the denominator determines its order. Order one poles are believed to be simple. A rational function R(z) is said to be appropriate if
m = degP(z) ≤ n = degQ(z),
And strictly proper if m < n. If R(z) is not strictly proper, we can divide by the denominator to obtain
R(z) = P1(z) + R1(z),
The remainder R1(z) is a strictly valid rational function, and P1(z) is a polynomial.
Theorem. R(z) has a partial fraction decomposition if the rational function R(z) = P(z)/Q(z) is rigorously proper, that is, if degP degQ.
R(z) = 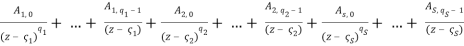 (3)
(3)
What you should concentrate on is calculating a rational function's partial fraction decomposition. If all of r's poles are simple, that is, if all of the denominator's roots have multiplicity one, (3) simplifies to
R(z) = 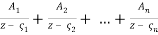 .(4)
.(4)
The coefficients in the partial fraction expansion can be found using the formula in this simpler situation.
 (5)
(5)
Linear fractional transformations
The linear fractional transformations or Mobius transformations, the rational functions of degree one, are of central importance among the rational functions:
w = T(z) = 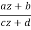 ,(8)
,(8)
Where ad bc 6=0 and a, b, c, and d are complex numbers. We may show that any linear fractional transformation T has an inverse by solving for z as a function of w.
z = T-1(w) = 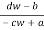 ,
,
As though checking with a calculator As a result, linear fractional transformations are always one-to-one and represented as C-to-C maps. Indeed, they are the only complex analytic functions from C to themselves that have complex analytic inverses.
Furthermore, the composition of two linear fractional transformations is simply verified to be another linear fractional transformation. Composition transforms the space of linear fractional transformations into a group, as algebraists term it.
The linear fractional transformation becomes a complex linear transformation when c = 0 and d = 1.
z 7→w = T(z) = az + b.
The following are examples of sophisticated linear transformations:
Translationsz 7→w = T(z) = z + b,
Rotationsz →7 w = T(z) = eiθz,
And expansions and contractionsz →7 w = T(z) = ρz,
Where and are real numbers, both of which are nonzero. When a = d = 0 and b = c = 1, the linear fractional transformation reduces to an inversion
w = T(z) = 1/z
T is a reflection in the circle in this case.
z ↦ 1/z reiθ ↦ 1/r eiθ
Followed by conjugation.
The following Proposition can be used to figure out what qualities a linear fractional transformation has. Linear fractional transformations will become increasingly important as the course progresses, and will be studied in more detail in 122B; see §7.3 of [4] or Chapter 7, § 5 of [3].
Proposition. Any fractional linear transformation is made up of complex linear maps and inversions. b. Any fractional linear transformation transforms circles and lines back to circles and lines. c. There is a unique linear fractional transformation T such that given any three independent points z1, z2, and z3 of C,
T(z1) = 0,T(z2) = 1andT(z3) = ∞.(9)
Illustration of a proof of a: If we make the replacements, the transformation (8) remains unaltered.
a 7→λa,b →7 λb,c →7 λc,d →7 λd,
When 6 equals 0 As a result, we can assume that ad bc = 1 without losing generality. Furthermore, we may safely conclude that c 6= 0 because the transformation is clearly linear when c = 0. The map can then be factored.
z’ = T(z) = az +b/cz + d
Into a four-transformation composite
z1 = z + d/c, z2 = c2z1, z3 = - 1/z2 , z’ = z3 + a/c(10)
To see this, consider the following:
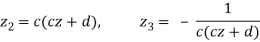
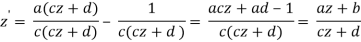
The Proposition is proven because each of the transformations in (10) is either complex linear or an inversion.
A rough sketch of b's proof is as follows: Complex linear transformations take circles and lines to circles and lines, so we need only check that inversions take circles and lines to circles and lines. A circle's equation, on the other hand, can be represented as
A(x2 + y2) + Re[(C −iD)(x + iy)] + B = 0,
For some choice of real constants A, B, C and D. We can rewrite this as
Azz¯+ Re[(C −iD)z] + B = 0. If we replace z by 1/w, this becomes
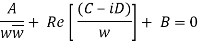
Or
A + Re[(C −iD)w¯] + Bww¯ = 0,
Which is once again the equation for a circle.
Sketch of proof of c: If none of the three points is infinity, the linear fractional transformation satisfying (9) is
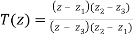 (11)
(11)
One needs to adjust this formula appropriately when one of the three points is ∞.
Exponential and trigonometric functions
The complex exponential function was formerly defined in terms of real-valued functions as
w = exp(z) = ez = ex(cosy + isiny),(12)
And used identities from trigonometry to show that
Ez1+z2 = ez1ez2,
As well as to show that the exponential function is periodic of period 2πi:
Exp(z + 2πki) = exp(z),for k ∈Z.(13)
Moreover, writing
ez = u(x,y) + iv(x,y), where u(x,y) = ex cosy and v(x,y) = ex siny and using the Cauchy-Riemann equations, we find that
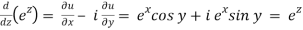 .(14)
.(14)
Although the exponential function exp is certainly quite well-behaved on C, it does not extend to a well-behaved function on the extended complex plane C∪{∞}. Neither

As a result, one might state that exp(z) has a "essential singularity" at. Indeed, when w is in any neighbourhood N(0;) of 0, one may show that e1/w takes on every nonzero complex integer an unlimited number of times.
We'd like to define a function that is the inverse of exp on C0, but the periodicity prevents us from doing so. Indeed, if w = ez, (12) is the sole conclusion.
w = reiθ= r(cosθ+ isinθ) = ex(cosy + I siny),
So y is one of the many possible values of the angular coordinate θ, all of these values differing by integer multiples of 2π. Thus we write
x = Log(r) = Log(|w|),y = θ= arg(w),
Where arg is the multiple-valued function which gives the various possible angular coordinates θ of w, and
z = x + iy = Log(|w|) + I arg(w).
In this way, we are led to define the multiple-valued function log by
Log(w) = Log(|w|) + I arg(w),
Where Log(|w|) is the usual natural logarithm of the nonzero real number |w|. It follows from (13) that the various values of the multiple-valued function log differ by integer multiples of 2π.
Dangerous curve: A multiple-valued function is not the same as a true function as studied in the rest of mathematics. For a given argument choice, a valid function can only assume one value. Nonetheless, the concept of a multiple-valued function is widely utilised in complex variable theory since it is extremely valuable. In more advanced complex variable treatments, multiple-valued functions on open subsets of the complex plane are replaced with true single-valued functions defined on "Riemann surfaces" over the open subsets (see [2]).
We may erase the uncertainty in the logarithm by replacing it, as we saw earlier.
C−{0} by the smaller domain
D = C−{x + iy ∈C : x ≤ 0},(15)
And choosing a branch of the multiple-valued function log that is single-valued in D. We do this by first letting Arg(w) be the value of the angular coordinate θ which lies in the interval (−π,π] and then define
Log : D −→C byLog(w) = Log(|w|) = I Arg(w).
Choosing a branch does give us a genuine single-valued complex analytic logarithm function, and as we saw when discussing the Cauchy-Riemann equations,
d/dw Log(w) = 1/w
However, this destroys some of the nice properties one might hope for the logarithm; for example, although
Log(z1z2) = log(z1) + log(z2),
Where equality means that the values taken by the multiple-valued functions on the two sides are the same, it is not true that
Log(z1z2) = Log(z1) + Log(z2)
In general.
One of the most useful applications of the multiple-valued logarithm function is in defining arbitrary powers of a complex number. The definition is motivated by the fact that zn = exp (n log(z)), when n ∈N.
Definition. If z ∈C−{0} and α∈C, we define zα by zα= exp(αlog(z)).
Trigonometric functions. As previously stated, we can represent the trigonometric functions cosine and sine in terms of exponentials using Euler's identity.

As a result, the relationship between exponential and trigonometric functions is simplified. All of the normal properties of trigonometric functions can be determined using these equations. For example, (14) demonstrates that

As a result of the definition of derivative, if f(z) = sinz, then
1 = cos (0) = f’ (0) = 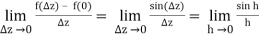
When h is considered to be real, this limit is recognised from first-year calculus.
We may also use the logarithm to find the inverses of trigonometric functions. If this is the case,
z = sin w = 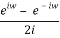
We can get the result by multiplying by eiw.
2iew z = eiw)2 or eiw)2 – 2izeiw – 1 = 0
As a result of the quadratic formula, it follows that
eiw = iz ±p1 −z2,
And we find that
w = arc sin (z) = i 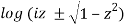 ,(17)
,(17)
Of course, this is a multi-valued function. The inverse of the cosine is also a multi-valued function.
w = arc cos(z) = π/2 – arc sin(z) = π/2 – i 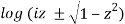
We must choose a branch of the square root as well as a branch of the logarithm to choose a specific branch of the inverse trigonometric functions. It follows from (17) that for any such branch

It's worth noting that a single-valued branch of the derivative of the inverse of the sine can be defined over in Example 3.
D = C− (R− [−1,1]),
We'll see later how this allows us to create a single-valued inverse of the sine across the same D region.
Similarly, the inverses of the hyperbolic cosine can be found; therefore, if
z = cosh w = 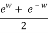
We can get the result by multiplying by ew.
2ewz = (ew)2 + 1or(ew)2− 2zew + 1 = 0.
The quadratic formula gets this result this time.
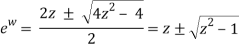
As a result, we discover that
w = 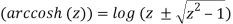
This time, differentiation produces

Example 4 shows a derivative with a single-valued branch over the domain C [1,1].
Steady-state temperature distributions
The real and imaginary components of the complex logarithm are currently used to determine the steady-state temperature distribution in numerous planar regions.
But first, we must show that a solution to the Laplace equation represents steady-state temperature. We assume that a material with homogeneous characteristics exists in area U of the (x,y)plane. When the temperature is given on the boundary, we want to find the steady-state temperature within the region.
Let u(x,y) denote the temperature at the given location (x,y). The heat flow at (x,y) should then be V(x,y), where
v(x, y) = - (k ∇ u)(x, y) = - k 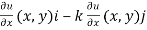 ,(18)
,(18)
Where is a positive constant referred to as the material's thermal conductivity.
We agree to meet at a certain time.
V(x,y) = M(x,y)i + N(x,y)j.
The divergence theorem states that if D is an area within U with a smooth border, then
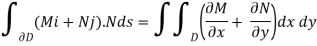
N is the normal to D outward-pointing unit, and s is the arc-length parameter along D. Remember that the left-hand line integral is calculated using a unit-speed parametrization: [a,b] D with (a) = (b).
The rate at which heat flows outward through D can be deduced from this line integral. As a result, the line integral must vanish if no heat is created or destroyed within D.
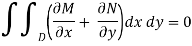
This double integral must vanish for every option of D U if no heat is created or destroyed anywhere within U, and this can only happen if
∇ . V = 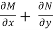 =0on U.
=0on U.
We infer that the temperature u must meet Laplace's equation in the specific case where V is supplied by (18).
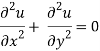
Alternatively, to put it another way, u has to be a harmonic function. (For a more leisurely discussion, see section 2.6 of [4].)
We have a wonderful application of complex analytic functions since harmonic functions are the real components of complex analytic functions: The steady-state temperature distribution in a homogeneous medium can be represented by their real parts.
1.8.1 Singularity:
A singularity is a point when an equation, surface, or other object blows up or degenerates. Singularities are also referred to as singular points.
Singularities play a crucial role in complex analysis, as they define the range of conceivable behaviours for analytic functions. Complex singularities are spots in a function's domain where the function fails to be analytic. Poles, essential singularities, logarithmic singularities, and detachable singularities are all types of isolated singularities. Natural boundaries or branch cuttings can produce non isolated singularities.
Consider the ordinary differential equation of second order.
y’’ + P(x) y’ + Q(x)y = 0
If and stay finite at, then is referred to be an ordinary point. When either or diverges as, the result is referred to as a unique point. Singular points are further divided into the following categories:
1. If either or diverges as but remains finite as, is referred to as a normal singular point (or nonessential singularity).
2. If diverges faster than and approaches infinity as, or diverges faster than and goes to infinity as, then is referred to as an irregular singularity (or essential singularity).
A point of such that the Laurent series of has for and is referred to as a pole of order.
Essential singularities are infinite-order poles. A pole of order is a singularity of for which the function is non-singular but is singular for, 1,...,.
A logarithmic singularity is an analytic function singularity with a primary -dependent term of order, etc.
Singularities that may be assigned a complex number in such a way that it becomes analytic are known as removable singularities. For example, the function has a detachable singularity at 0 since it is equal to 0 everywhere except 0. Singularities that can be removed are not poles.
The function, for example, exhibits two singularities: poles at and a nonisolated singularity at 0.
1.8.2 Poles
Poles refer to isolated singularities. So, we suppose f(z) is analytic on 0<|z−z0|<r and has Laurent series
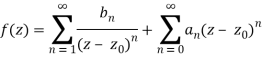
(8.9.1)
The terminology can be perplexing. Assume I inform you that on the punctured disc 0|zz0|r, f is defined and analytic. Then we suppose f has a singularity at z0 a priori. However, if there is no unique component after computing the Laurent series, we can extend the definition of ff to the entire disc, effectively eradicating the singularity.
The word essential singularity can be explained as follows. (zz0)kf(z) is analytic (has a detachable singularity) at z0 if f(z) has a pole of order k at z0. As a result, f(z) isn't substantially more difficult to work with than an analytic function. If z0 is an important singularity, however, no algebraic method will convert f(z) to an analytic function at z0.
1.8.3 Branch Point
The complex argument of an analytic function can be transferred from a single point in the domain to numerous points in the range at a branch point in the complex plane. Consider the behaviour of the point when it is subjected to the power function.
f(z) = za (1)
For complex non-integer a, i.e., a ∈ ℂ with a∉ℤ. Writing z = eiθ and taking θ from 0 to 2π gives
f(∈ = e0 = 1
f(∈ = e2πia
Despite the fact that at and correspond to the same place in the domain, their values are different.
Algebraic branch points of order are branch points whose neighbourhood of values wraps around the range a finite number of times as varies from 0 to correspond to the point under functions of the kind. A logarithmic branch point is a branch point that occurs at the point beneath the function and whose neighbourhood of values revolves around an infinite number of times. Logarithmic branch points and logarithmic singularities are the same thing.
Branch points are another name for pinch points.
It's worth noting that branch cuts' endpoints aren't always branch points.
A branch cut is a curve in the complex plane in which an analytic multivalued function is discontinuous (having ends that may be open, closed, or half-open). Branch cuts are frequently represented as lines or line segments for ease of use. Cut lines (Arfken 1985, p. 397), slits (Kahan 1987), and branch lines are all terms used to describe branch cuts (including ones with curves).
Take, for example, the function that converts each complex number to a well-defined number. Its inverse function, on the other hand, transfers the value to, for example. While such functions can have a single primary value (in this case, the main square root is positive), the choices cannot be made continuously across the complex plane. Instead, discontinuity lines must be drawn. The implementation of so-called branch cuts is the most prevalent method for coping with these discontinuities. Branch cuts are not unique in general; instead, they are chosen by convention to provide easy analytic features (Kahan 1987). Some functions have a relatively simple branch cut structure, while others have exceedingly intricate branch cuts.
Riemann surfaces are a multivalued function representation alternative to branch cuts.
Singularities known as branch points exist in addition to branch cuts. It should be emphasised, however, that branch cut endpoints are not always branch points.
The single-valued trigonometric, hyperbolic, integer power, and exponential functions do not have branch cuts. Their multivalued inverses, on the other hand, necessitate branch cuts. The graphs and table below show the branch cut structure of the Wolfram Language's inverse trigonometric, inverse hyperbolic, no integer power, and logarithmic functions.
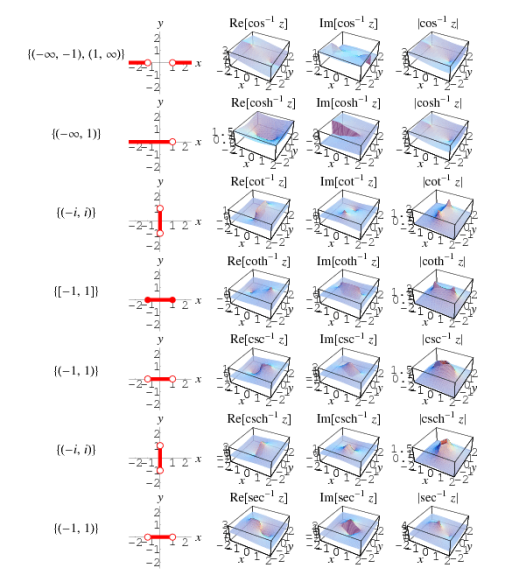
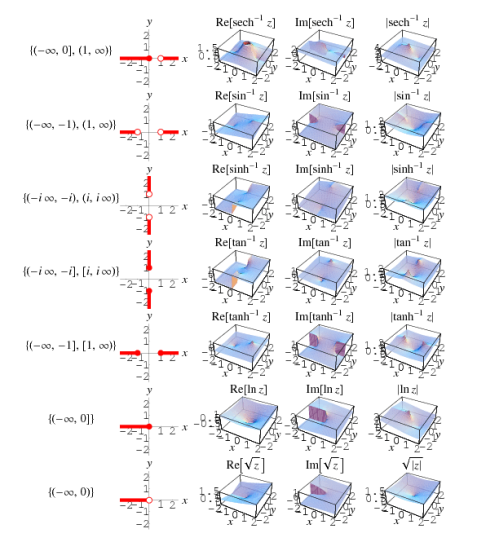
Function name | Function | Branch cut(s) |
Inverse cosecant | Csc-1 z | (-1, 1) |
Inverse cosine | Cos -1 z | (-∞, -1) and ( 1, ∞) |
Inverse cotangent | Cot -1 z | (-i, i) |
Inverse hyperbolic cosecant | Csch-1 | (-i, i) |
Inverse hyperbolic cosine | Cosh -1 | (-∞, 1) |
Inverse hyperbolic cotangent | Coth-1 | [-1, 1] |
Inverse hyperbolic secant | Sech-1 | (-∞, 0] and (1, ∞] |
Inverse hyperbolic sine | Sinh-1 | (-i∞, -i) and (i, i∞) |
Inverse hyperbolic tangent | Tanh-1 | (-∞, -1] and [1, ∞) |
Inverse secant | Sec-1z | (-1, 1) |
Inverse sine | Sin-1z | (-∞, -1) and (1, ∞) |
Inverse tangent | Tan-1 z | (-1∞, -i] and [i, i∞) |
Natural logarithm | Ln z | (-∞, 0] |
Power | zn, n ∉ ℤ | (-∞, 0) for R[n] ≤ 0 ; (-∞, 0] for R[n] > 0 |
Square root | √z | (-∞, 0) |
1.10.1 Cauchy’s Inequality:
A special case of Hölder's sum inequality with p = q= 2,
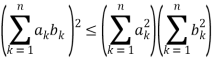
In two-dimensions, it becomes
(a2 + b2)(c2 + d2) ≥ (ac + bd)2
It can be proven by writing
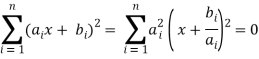
If  is a constant c, then x = -c. If it is not a constant, then all terms cannot simultaneously vanish for real x, so the solution is complex and can be found using the quadratic equation
is a constant c, then x = -c. If it is not a constant, then all terms cannot simultaneously vanish for real x, so the solution is complex and can be found using the quadratic equation

In order for this to be complex, it must be true that
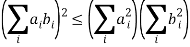
With equality when bi/ai is a constant. The vector derivation is much simpler,
(a . b)2 = a2 b2 cos2 θ ≤ a2 b2
Where
a2 = a . a = 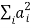
And similarly for b.
1.10.2 Cauchy's integral formula:
Cauchy's integral formula, named after Augustin-Louis Cauchy, is a key statement in complex analysis in mathematics. It reflects the fact that the values on the disk's boundary entirely determine a holomorphic function defined on the disc, and it gives integral formulas for all derivatives of a holomorphic function. Cauchy's formula demonstrates that "differentiation is comparable to integration" in complex analysis: complex differentiation, like integration, performs well within uniform boundaries, a result that does not hold in real analysis.
Assume that U is an open subset of the complex plane C, and that D is a closed disc.
D = { z : |z – z0| ≤ r}
Is entirely confined within U. Let f : U C be a holomorphic function, and let be the counter clockwise-oriented circle that forms D's boundary. Then, for each an in D's interior,
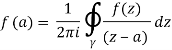
This statement is proved using the Cauchy integral theorem, which, like that theorem, just needs that f is complex differentiable. Since 1/(z-a) can be expanded as a power series in the variable 𝑎:
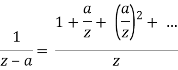
— it follows that holomorphic functions are analytic, i.e. they can be expanded as convergent power series. In particular f is actually infinitely differentiable, with

Cauchy's differentiation formula is another name for this formula.
The previous theorem can be generalised. Any closed rectifiable curve in U with winding number one around a can be substituted for the circle. Furthermore, as with the Cauchy integral theorem, all that is required is for f to be holomorphic in the open region circumscribed by the path and continuous on its closure.
It's worth noting that not every continuous border function may be used to generate a function inside the boundary that fits the provided boundary function. For example, in the Cauchy integral formula, we get zero for all locations inside the circle if we use the function f (z) = 1/z, which is specified for |z| = 1. In reality, providing simply the real component of a holomorphic function's border is sufficient to define the function up to an imaginary constant – there is only one imaginary component on the border that corresponds to the given real portion, up to the addition of a constant. The holomorphic function can be constructed from the real component on the boundary using a Möbius transformation and the Stieltjes inversion formula. The function f (z) = I iz, for example, has a real portion Re f (z) = Im z. This can be expressed as i/z iz/2 on the unit circle. The function inside the circle is constructed using the Möbius transformation and the Stieltjes formula. We find the function iz since the i/z term has no effect. This provides us the right real part on the border, as well as the matching imaginary component, but it is off by a constant, namely i.
NUMERICALS:
1)
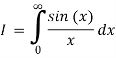
This integral is not absolutely convergent, but it is conditionally convergent. Formally, of course, we mean
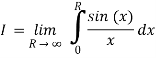
First note that sin(x)/x is even, so

Next, to avoid the problem that sin(z) goes to infinity in both the upper and lower half-planes we replace the integrand by
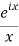
We’ve changed the problem to computing
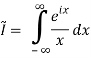
The problems with this integral are caused by the pole at 0. The biggest problem is that the integral doesn’t converge! The other problem is that when we try to use our usual strategy of choosing a closed contour we can’t use one that includes z=0 on the real axis. This is our motivation for defining principal value. We will come back to this example below.
1.11.1 Simply connected definition
A simply connected domain is a path-connected domain in which every simple closed curve can be constantly shrunk into a point while remaining in the domain.

For two-dimensional regions, a simply connected domain is one without holes in it.
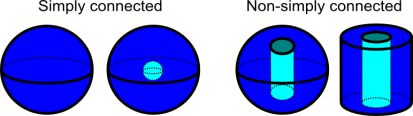
The concept of simply connected is more subtle in three-dimensional spaces. A domain that is simply connected has no gaps running through it. However, a domain with just a hole in the middle (like a ball whose center is hollow) is still simply connected, as we can continuously shrink any closed curve to a point by going around the hole and remaining in the domain. A ball with a hole bored all the way through it, or a spool with a hollow centre axis, on the other hand, cannot be simply linked. While remaining in the domain, a closed curve that travelled around the hole could not be shortened to a point. Because there is no way for the curve to avoid the hole, it is locked around it.
1.11.2 Multiply-connected domain
n a path-connected space
In a domain D, there are closed pathways that are not homotopic to zero, or whose basic group is not trivial. This means that in D, there are closed pathways that cannot be continuously deformed to a point while remaining inside D, or that a multiply-connected domain exists. D is a domain that isn't related in any way.
The number of (homologically) independent one-dimensional cycles, or the one-dimensional Betti number p1 of D, is the order of connectedness of a planar domain D in R2 or C=C1 (or in the compactification of these spaces, R 2 or C). If the number k of linked components of a plane domain D, regarded as a domain in the compactified space R 2 or C, is finite, then p1=k; otherwise, p1=. DD is a simply-connected domain when p1=1, and a finitely-connected domain when p1p1 (other terminology include doubly-connected domain, triply-connected domain, and so on). When p1=, DD is an indefinitely connected domain (k-connected domain). Homeomorphism exists between all plane finitely linked domains with the same order of connectivity, k. It is always feasible to produce a simply-connected domain DD by deleting all sites of k1 cuts, that is, Jordan arcs joining pairs of linked components of the boundary, from such a domain D. About planar multiply-connected domains' conformal types.
Domain topological types in Rn, n3, or Cm, m2 are significantly more varied and cannot be described by a single number. When the fundamental group is trivial but a higher-dimensional homology group is not trivial, the phrase "multiply-connected domain" (with various provisos) is occasionally used.
1.12.1 Laurent Series
If is analytic in the annular area between and on the concentric circles, and is centred at and of radii, then there exists a unique series expansion in terms of positive and negative powers of. (z-a),
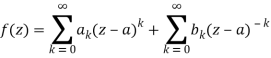
Where
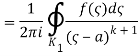
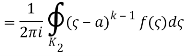
(Korn and Korn 1968, pp. 197-198).
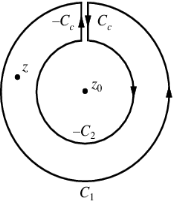
Let's say there are two circular shapes and, one having a radius that is larger than that of the other. Allow to be at the intersection of and, and between and. Create a cut line between and and integrate it around the path so that the plus and minus contributions cancel each other out, as shown above. The integral formula of Cauchy is as follows:
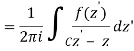
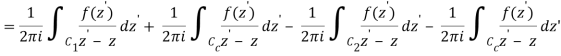
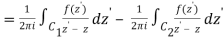
Now, because the cut line's contributions in opposite directions cancel each other out,
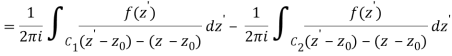
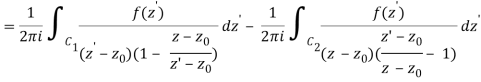
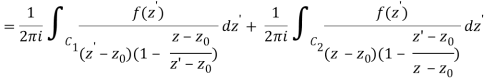
For the first integral’ – z0| > |z – z0|. For the second, |z’ – z0| < |z – z0| Now use the Taylor series (valid for |t|<1)

To obtain

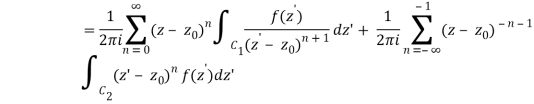
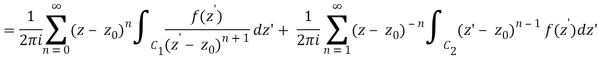
Where the second term has been re-indexed. Re-indexing again,

Since the integrands, including the function f(z), are analytic in the annular region defined by C1 and C2, the integrals are independent of the path of integration in that region. If we replace paths of integration C1 and C2 by a circle C of radius r with r1 ≤ r ≤ r2, then
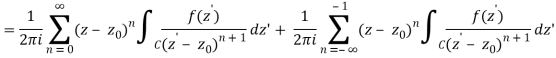
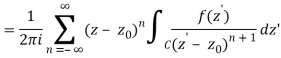
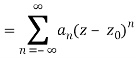
Any path that lies in the annular region and encircles once in the positive (counter clockwise) direction can be used as an integration path.
As a result, the complex residues are defined by
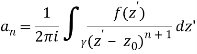
It's worth noting that the annular region can be enlarged by increasing and reducing until singularities lie near outside or just inside. If there are no singularities inside, then all of the terms in () are equal to zero, and the Laurent series of () is reduced to a Taylor series with coefficients.
1.12.2 Taylor series:
For Real Functions
Let a∈R and f(x) be and infinitely differentiable function on an interval I containing a. The Taylor series of f around an in one dimension is thus given by
f(x) = f(a) + f’ (a) (x – a) + f’’(a)/2! (x –a)2 + f(3)(a)/3! (x – a)3 + ...
Which can be written in the most compact form:
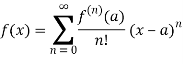 Recall that, in real analysis, Taylor’s theorem gives an approximation of a k-times differentiable function around a given point by a k-th order Taylor polynomial.
Recall that, in real analysis, Taylor’s theorem gives an approximation of a k-times differentiable function around a given point by a k-th order Taylor polynomial.
The best linear approximation for f(x) is, for example,
f(x) ≈ f(a) + f’(a) (x – a)
This linear approximation matches the slope of f at a by fitting f(x) with a line through x=a.
We can improve the approximation by including more terms in the expansion. The best quadratic approximation, for example, is
f(x) ≈ f(a) + f’(a)(x – a) + ½ f’’ (a) (x – a)2
The partial sums of the Taylor series for a given function are displayed in the applet below. To see more terms from the series, move the slider. Change the function or drag the point a.
For Complex Functions
Assume that a function f is analytic throughout a disc |zz0|R with radius R0 and a centre at z0z0. Then there's f(z), which is a power series representation.
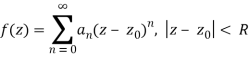
Where
an = 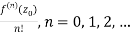
When z is in the indicated open disc, series (1) converges to f(z).
A radius of convergence exists for any complex power series (1). A complex power series (1) has a circle of convergence, which is the circle centred at z0 of maximum radius R>0 for which (1) converges at every point within the circle |zz0|=R|, similar to the concept of an interval of convergence for real power series. A power series converges absolutely for all z within its circle of convergence, that is, for all z satisfying |zz0|R, and diverges for all z satisfying |zz0|>R. The radius of convergence can be: 1. R=0 (in which case (1) converges only at its centre z=z0), 2. R=1 (in which case (1) converges only at its centre z=z0), 3. R=2 (in which case
(1) converges only at
2. RR is either a finite positive number (in which case (1) converges at all interior points of the circle |zz0|=R) or a finite negative number (in which case (1) converges at all interior points of the circle |zz0|=R).
3. R= (in which case (1) for every z converges).
The ratio test of convergence can be used to calculate the radius of convergence. Consider the following scenario:



Dynamic Exploration
Explore Taylor series representations and their radius of convergence, which is dependent on the value of z0, using the applet below.
A phase portrait of a complex function is shown on the left side of the applet below. The function's approximation through its Taylor polynomials at the blue base point z0 may be seen on the right side. Modify the complex function, the base point z0, the polynomial order (vertical slider), and the zoom (horizontal slider).
Maclaurin series
A Taylor series with centre z0=0
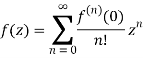
Is referred to as Maclaurin series.
Some important Maclaurin series are:
1/(1 – z) = 

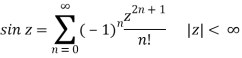
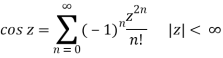
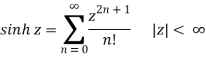
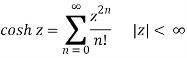
NUMERICALS:
1) Find the Laurent series for
f(z) = z+1/z
Around z0=0. Give the region where it is valid.
ANSWER:
|f(z) = 1 + 1/z
This is a Laurent series, valid on the infinite region 0<|z|<∞.
z = 0 for f(z) = 1/z(z-1)
2) Find the Laurent series around in each of the following regions:
The region A1:0<|z|<1
The region A2:1<|z|<∞.
Solution:
For (i)
f(z) = - 1/z . 1/ 1 – z = - 1/z ( 1+ z + z2 + . . .) = - 1/z – 1 –z –z2 - ...
For (ii): Since the usual geometric series for 1/(1−z) does not converge on A2 we need a different form,
f(z) = 1/z . 1/ z(1 – 1/z) = 1/z2 ( 1 + 1/z + 1/z2 + . . .)
Since |1/z|<1 on A2 our use of the geometric series is justified.
3) Expand f(z)=z8e3z in a Taylor series around z=0.
Solution
Let w=3z. So,
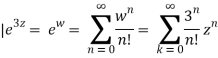
Thus,

1.13.1 Cauchy Residue Theorem
This is a major theorem in complex analysis, and it will allow us to make our earlier ad hoc technique to computing integrals on contours that surround singularities more systematic.
Except for a few isolated singularities, suppose f(z) is analytic in the region A. Assume C is a simple closed curve in A that passes through none of ff's singularities and is oriented counter clockwise. After that,
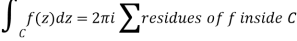
Proof
The following figures are used to prove the point. Although they only depict a curve with two singularities, the generalisation to any number of singularities is simple. In the next sections, we will use the term pole to refer to an isolated singularity, such as a finite order pole or an essential singularity (‘infinite order pole').
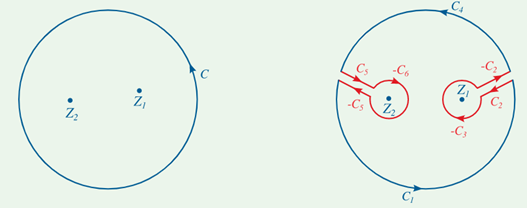
The curve C is shown on the left, encircling two of f's poles, z1 and z2. The same curve is seen on the right, but with several cuts and little circles added. It is chosen so that no f poles are contained within it, and the little circles surrounding each of the poles are so small that no additional poles are contained inside them. The curve on the right hand is
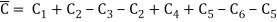
C=C1+C4C=C1+C4C=C1+C4C=C1+C4C=C1+C4C=C1+C4C=C Because there are no poles within CC, we obtain, according to Cauchy's theorem,
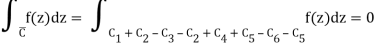 When C2 and C5, which are both added and subtracted, are removed, the result is
When C2 and C5, which are both added and subtracted, are removed, the result is
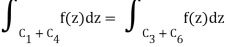
If
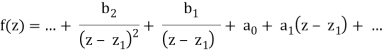
If f's Laurent expansion around z1 is true,
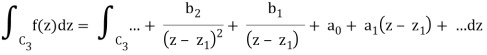
= 2 πib1
= 2πi Res(f, z1)
Likewise
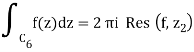
Equation 9.5.4 is formed using these residues and the fact that C=C1+C4
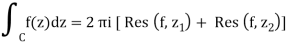
For the situation of two poles, this demonstrates the residue theorem. As previously stated, generalising to any number of poles is simple.
1.14.1 Application of definite integral:
Functions, differentiation, and integration are only a few examples of calculating procedures. Integrals are used in a variety of domains, including mathematics, science, and engineering. In most cases, integral formulas are used to calculate area. So, let us begin with a brief introduction to integrals based on the mathematics subject in order to determine areas under simple curves, areas bounded by a curve and a line, and areas between two curves, as well as the application of integrals in mathematical disciplines and the solved problem.
Integral Definition
An integral is a function whose derivative is another function. Integration is mostly used to compute the volumes of three-dimensional objects and to calculate the areas of two-dimensional regions. As a result, determining the integral of a function with respect to x entails determining the area of the curve with respect to the X-axis. Because it is the opposite of differentiation, the integral is also known as anti-derivative.
1.14.2 Application of Integrals
Integrals have a wide range of applications, some of which are listed below:
In Maths
- Identifying the centre of mass (Centroid) of a curved-sided area Identifying the region between two curves
- To determine the area beneath a curve
- The average of a curve's values
In Physics
Integrals are used to compute a vehicle's centre of gravity, mass, and moment of inertia.
- Satellites' mass and momentum
- A tower's mass and momentum
- The centre of mass is a term used to describe the centre of mass of an object.
- The velocity of a spacecraft when it is launched into orbit.
- The path taken by a satellite as it is sent into orbit.
References:
1. Mathematical Physics and Special Relativity–M.Das, P.K. Jena and B.K. Dash (Srikrishna Prakashan)-2009
2. Mathematical Physics–H. K. Das, Dr. Rama Verma (S. Chand Publishing) 2011
3. Complex Variable: Schaum’s Outlines Series M. Spiegel (2nd Edition, Mc- Graw Hill Education)-2004
4. Complex variables and applications J.W.Brown and R.V.Churchill 7th Edition 2003
5. Mathematical Physics, Satya Prakash (Sultan Chand)-2014