Unit - 2
Integral Transforms-I
2.1.1 The Fourier Integral Theorem
So far, we've looked at expressing functions in terms of their Fourier series, notably 2-periodic functions. Naturally, not all functions are 2-periodic, thus it may be impossible to express a function defined on all of R using a Fourier series. The next best option is to represent these functions as integrals. Fortunately, under the right circumstances, a function fL(R) can be written as an integral, as stated by the Fourier Integral Theorem
Theorem 1 (The Fourier Integral Theorem): If f ∈ L(R) and if there exists an x ∈ R and a δ>0 such that either:
1) f is of bounded variation on [x−δ, x+δ].
2) f(x+) and f(x−) both exist, and
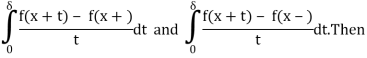
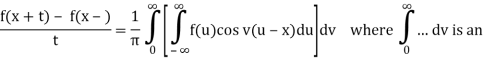
Riemann integral that isn't right.
Before we look at any examples of the Fourier integral theorem, we'll demonstrate the following two equalities for even and off functions that satisfy the theorem:
Theorem 2: If f∈L(R) satisfies either of the conditions of the Fourier integral theorem then:
a) If f is an even function then
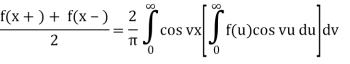
b) If f is an odd function then
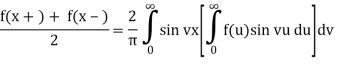
Proof of a) Suppose that f ∈ L(R) satisfies either of the conditions of the Fourier integral theorem. Then:
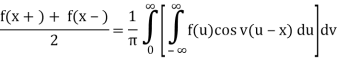
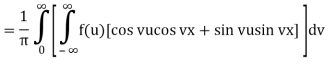
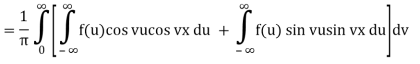
Because f is an even function of u and sin vu is an odd function of u, f(u)sin vu is also an odd function of u, and so on.
Interval
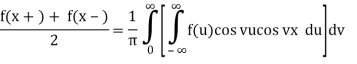
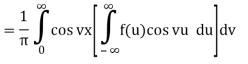
Because f is an even function of u and cos vu is an even function of u, f(u)cos vu is an even function of u, and so on for the symmetric functions.
Interval so:
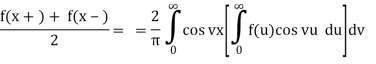
Proof of b) Assume that fL(R) fulfils one of the Fourier integral theorem's requirements. Then there's the following:
Because f is an odd function of u and cos vu is an even function of u, we get f(u)cos vu, and similarly, since sin vu is an odd function of u, we get f(u)sin vu. As in
(a) above, the evidence is as follows:
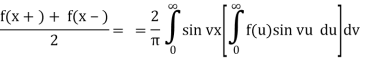
2.2.1 Fourier transform
The Fourier Transform comes into play here. The notion that every non-linear function can be represented as a sum of (infinite) sine waves is used in this method. This is depicted in the underlying picture, where a step function is approximated by a slew of sine waves.
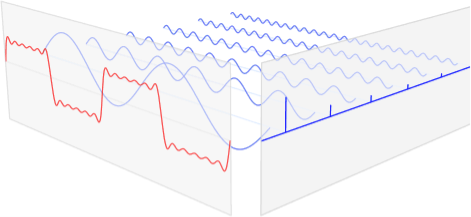
Fig. Step function simulated with sine waves
A Fourier Transform deconstructs a temporal signal and returns information on the frequency of all sine waves required to reproduce that signal. The Discrete Fourier Transform (DFT) is defined as follows for sequences of equally spaced values:
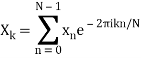
Where:
- N is the total number of samples.
- n denotes the current sample.
- Xn is the signal's value at time n.
- k is the frequency of the current (0 Hz to N-1 Hz)
- Xk denotes the DFT result (amplitude and phase)
It's worth noting that a dot product is defined as follows:
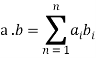
A DFT algorithm can thus be as written as:
Import numpy as np
DefDFT(x):
Compute the discrete Fourier Transform of the 1D array x
:param x: (array)
N =x.size
n =np.arange(N)
k =n.reshape((N, 1))
e =np.exp(-2j*np.pi* k * n / N)
Return np.dot(e, x)
However, running this code on our time signal, which contains around 10,000 data, takes more than 10 seconds!
Iiftyhr56gyuzlhskssaasdfhkqqweaeqwertip77aszxmnbbvcxxz
Fortunately, some brilliant people (Cooley and Tukey) devised the Fast Fourier Transform (FFT) technique, which recursively divides the DFT into smaller DFTs, greatly reducing the required computing time. The FFT scales O(N log(N), whereas the normal DFT scales O(N2).
2.2.2 Fourier Series Example
Example: Determine the fourier series of the function f(x) = 1 – x2 in the interval [-1, 1].
Solution:
Given,
f(x) = 1 – x2; [-1, 1]
We know that, the fourier series of the function f(x) in the interval [-L, L], i.e. -L ≤ x ≤ L is written as:
f(x) = A0 +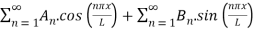 
Here,
A0 =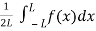 
An =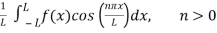 
Bn =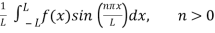 
Now, by applying he formula for f(x) in the interval [-1, 1]:
f(x) =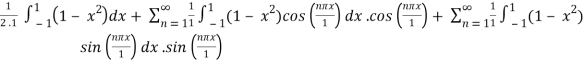 
By simplifying the definite integrals,
= 
= 
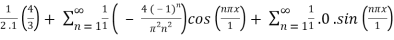
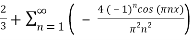
2.3.1 Fourier Transform—Cosine
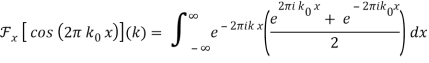
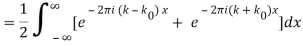
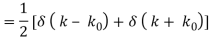
Where δ(x) is the delta function.
2.3.2 Fourier Transform—Gaussian
The Fourier transform of a Gaussian function f(x) ≡ e-ax2 is given by
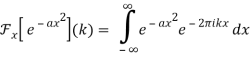
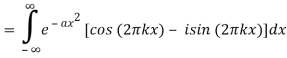
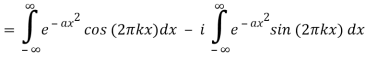
Integration across a symmetrical range yield 0 since the second integrand is odd. Abramowitz and Stegun (1972, p. 302, equation 7.4.6) give the value of the first integral, so
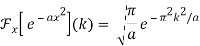
As a result, a Gaussian becomes another Gaussian.
2.3.3 Find the Fourier transform of finite wave train
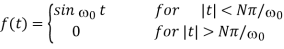
A function f(t) represents a sine wave of time
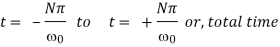
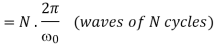
Since f(t) is odd, we use fourier sine transform,
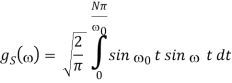
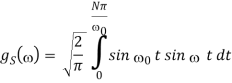
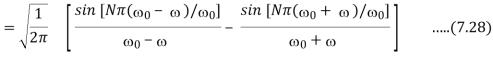
2.3.4 Travelling wave
When something in the physical world changes, information about that change spreads outwards in all directions, away from the source. The information travels in the form of a wave as it travels. Waves carry sound to our ears, light to our eyes, and electromagnetic radiation to our cell phones. The waves formed on the surface of the water when a stone is dropped into a lake are a nice visual example of wave propagation. We'll learn more about travelling waves in this article.
2.3.5 Describing a Wave
A wave is a disturbance in a medium that travels while transferring momentum and energy without causing the medium to move. A travelling wave is a wave that travels through the medium between its greatest and minimum amplitude levels. Consider the disturbance generated when we jump on a trampoline to better understand a wave. When we jump on a trampoline, the downward force we exert at one location on the trampoline causes the material adjacent to it to go downward as well.
When the produced disturbance spreads outward, the spot where our feet originally impacted the trampoline recovers and moves outward due to the trampoline's tension force, which also moves the adjoining materials outward. As the trampoline's surface area is covered, the up and down motion gradually spreads out. This disruption takes the form of a wave.
Here are a few key considerations to keep in mind about the wave:
The crests and troughs of a wave are the high and low points of the wave, respectively.
The maximum distance of the wave's disturbance from the mid-point to either the top of the crest or the bottom of a trough is known as amplitude, while the distance between two consecutive crests or troughs is known as wavelength and is represented by
A time period is the length of time between full vibrations.
A frequency is the number of vibrations a wave experiences in one second.
The following is the link between time period and frequency:
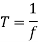
The equation for a wave's speed can be found here.
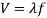
Different Types of Waves
Waves come in a variety of shapes and sizes, each with its own set of features. These qualities aid in the classification of wave types. One approach to distinguish travelling waves is the orientation of particle motion in relation to the direction of wave propagation. The following are the several forms of waves, which are classified based on particle motion:
● Pulse Waves – A pulse wave is a wave that goes through the transmission medium with only one disruption or peak.
● Continuous Waves – A continuous wave is a waveform with the same amplitude and frequency all the time.
● Transverse Waves – The velocity of a particle in a transverse wave is perpendicular to the wave's propagation direction.
● Longitudinal Waves – Longitudinal waves are those in which the particle's motion is in the same direction as the wave's propagation.
Despite their differences, they all have one thing in common: energy transfer. E=1/2 KA2 is the energy of an object in simple harmonic motion. We can deduce from this equation that a wave's energy is proportional to the square of its amplitude, i.e. E/A2. This link between energy and amplitude is crucial in determining the extent of damage that earthquake shock waves can do. Because the waves are spread out across a larger area, they become weaker as they spread out.
Constructive and Destructive Interference
Interference is a phenomenon in which two waves superimpose to generate a new wave of lower, larger, or equal amplitude. The interaction of waves that are associated with one other, either because of the same frequency or because they come from the same source, causes constructive and destructive interference. Interference effects can be seen in a variety of waves, including gravity and light waves.
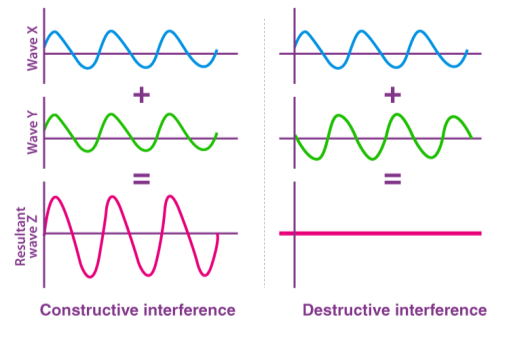
When two or more propagating waves of the same kind collide at the same site, the resulting amplitude is equal to the vector sum of the individual waves' amplitudes, according to the principle of superposition of waves. The resultant amplitude is the total of the individual amplitudes when the crest of one wave meets the crest of another wave of the same frequency at the same place. Constructive interference is the term for this form of interference. When a wave's crest collides with a wave's trough, the resulting amplitude equals the difference between the separate amplitudes, which is known as destructive interference.
NUMERICALS:
1) find the transform of
f(t) = e-at u(t)
Whereas a>0. By definition we have
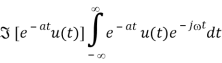
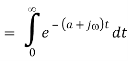
OR
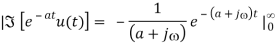
The upper limit is given by
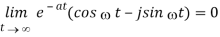
Since the expression in parentheses is bounded while the exponential goes to zero. Thus we have
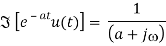
Or
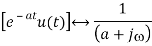
2) x(t) = u(t – 2)
ANS:
X(s) =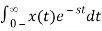 
= 
= 
= 
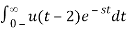
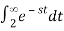
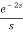
3) x(t) = e-2t u(t + 1)
ANS:
X(s) =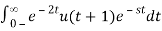 
= 
= 
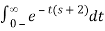
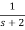
2.4.1 Dirac's delta function and the Fourier transform
We use a limiting approach to define the Dirac delta function, which is not a function in the traditional sense (mathematicians term it a distribution).
δ(x) = lim Λ fΛ(x)
Where fΛ(x) is an ordinary function depending on the parameter Λ. The requirement on δ(x) is
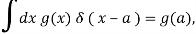
Where the point x=a is included in the integration range. The function g is referred to as a 'test' function because it is expected to behave 'nicely,' with no singularities and approaching 0 at infinity. It follows from the basic property (76) that
xδ(x) = 0
This is significant when dividing: It is not necessary to conclude that f(x)g(x)=h(x) from f(x)g(x)=h(x) (x). Instead, C is an arbitrary constant, as can be seen by multiplying both sides by g(x) and using.
We get the special result by putting g=1 in (76). To satisfy (76), the quantity can only have support at x=0, and it must be infinite at this point to yield a finite integral. As a result, the ordinary function must grow increasingly peaked around x=0 and larger and larger for rising.
A limiting function is exemplified by the following example.
fΛ (x) = sin Λ x / π x
This function has the value Λ/π for x=0, and the width of its first peak is π/ Λ 0. For larger values of x it oscillates rapidly. To show that f Λ approaches a delta function for , we notice that (take y = Λ x)
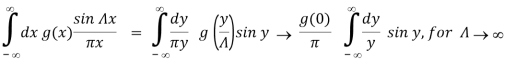The last y-integral has been performed in eqs. (3-10) and (3-11) in the book and is equal to 
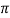. The property (76) is seen to be satisfied (with the arbitrary point a taken to be 0). Therefore
δ(x) =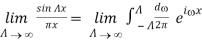 
There are numerous alternative ways to represent the delta function, but the one provided by (80) is particularly useful, as shown in the example below.
Let's say we have a function f(x) and we want to create a new function.
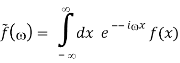
The methods below can be used to flip this relationship.
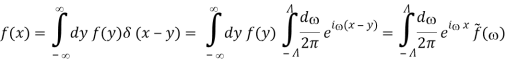
Where we used eqs. (76) and (80). We then get the pair of equations in the limit
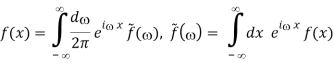
Thus, eq. (82) is a one-line derivation of Mathews and Walker's eqs. (4-16). This demonstrates the delta function's immense power.
It's worth noting that, thanks to eq. (80), the delta function has the following formal integral representation:
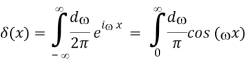
This could also be obtained by taking f(x) = δ(x) in (83). The limits of the integral should really be understood as beeing between -Λ and Λ, but in calculations one can often use this integral with Λ already taken to infinity.
As a further illustration of the delta function, let us return to the Fourier series discussed in the former section. Taking into account that S(θ) = f(θ) (assuming f to be continuous), we see that eq. (69) requires
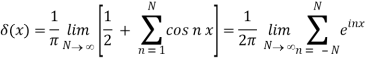
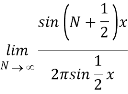
We utilised eq. In the last step (70). This delta function form is identical to the one shown in eq. (80) and in (84). In particular, we may formalise eq. (85) as
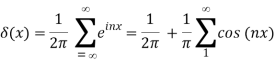
Which is a discrete version of (84).
To show (85) directly we study how it acts in an integral,
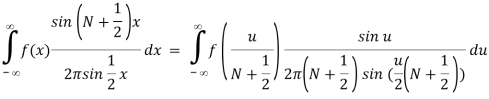
f(0)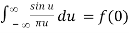 
For N . The final expression is the same as what we would have gotten if we had used (80). As a result, when the integral sign is used, the two representations (80) and (85) end up being the same.
The Dirac delta distribution (1.16) is historically and commonly replaced by the Dirac delta (or Dirac delta function) in physics and engineering applications (x). This is an operator with the following characteristics:
δ(x)=0,
x∈ℝ, x≠0,
And
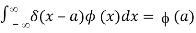
If specific requirements on the function are met (x). The left-hand side of the above can be read mathematically as a generalised integral in the sense that
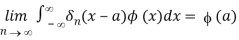
n(x), n=1,2,.... For an appropriately chosen series of functions A delta sequence is what we name it, and we write it symbolically as
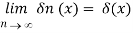
An example of a delta sequence is provided by
δn (x – a) =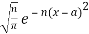 
In this case
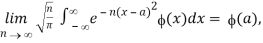
For all functions ϕ(x) that are continuous when x∈(-∞,∞), and for each a,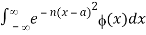 
converges absolutely for all sufficiently large values of n. The last condition is satisfied, for example, when (x) = O(
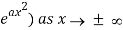, where α is a real constant.
More generally, assume ϕ(x) is piecewise continuous (§1.4(ii)) when x∈[-c,c] for any finite positive real value of c, and for each a,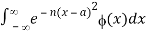 
converges absolutely for all sufficiently large values of n. Then
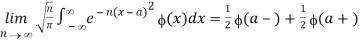
2.4.2 Integral Representations
Formal interchange of the order of integration in the Fourier integral formula.
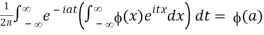
Yields
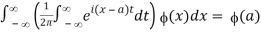
The inner integral does not converge. However, for n=1,2,…,
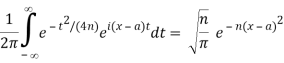
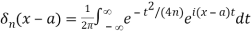
Provided that ϕ(x) is continuous when x∈(-∞,∞), and for each a,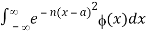 
converges absolutely for all sufficiently large values of n (as in the case. Then comparison of the two yields the formal integral representation
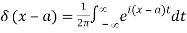
2.4.3 Properties of the Delta Function
The following features can be easily verified from the definition as a Gaussian wave packet limit:
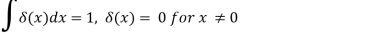
δ(x) = δ(-x) , δ(ax) = 1/|a| δ(x)
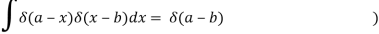
NUMERICALS:
1) Solve the following IVP.
y’’ + 2y’ – 15y = 6 δ (t – 9) , y(0) = -5 y’(0) = 7
ANS:
First take the Laplace transform of everything in the differential equation and apply the initial conditions.
s2 Y(s) – sy(0) – y’(0) + 2(sY (s) – y(0)) – 15Y (s) = 6 e-9s (s2 + 2s – 15) Y(s) + 5s + 3 = 6e-9s
Now solve for Y(s).
Y(s) = 6e-9s/(s+5)(s – 3) - 5s+3/(s+5)(s – 3)
= 6e-9s F(s) – G(s)
We’ll leave it to you to verify the partial fractions and their inverse transforms are,
F(s) = 1/ (s+5)(s -3) =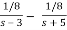 
f(t) = 1/8 e3t – 1/8 e-5t
G(s) = 5s + 3/(s + 5)(s – 3) =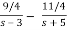 
g(t) = 9/4 e3t + 11/4 e-5t
The solution is then,
Y(s) = 6e-9s F(s) – G(s)
y(t) = 6u9 (t) f(t – 9) – g(t)
Where, f(t) and g(t) are defined above.
2) Solve the following IVP.
2y’’ + 10y = 3u12(t) – 5 δ( t – 4) , y(0) = - 1 y’(0) = - 2
ANS:
Take the Laplace transform of everything in the differential equation and apply the initial conditions.
2( s2Y(s) – sy(0) – y’(0)) + 10Y (s) = 3e-12s/s – 5e-4s
(2s2 + 10) Y(s) +2s + 4 = 3e-12s/s – 5e-4s
Now solve for Y(s).
Y(s) = 3e-12s/s(2s2 + 10) – 5e-4s/2s2 + 10 – 2s+4/2s2+10
= 3e-12s F(s) – 5e-4sG(s) – H(s)
We’ll need to partial fraction the first function. The remaining two will just need a little work and they’ll be ready. I’ll leave the details to you to check.
F(s) = 1/s(2s2 + 10) = 1/10 1/s – 1/10 s/s2 + 5
f(t) = 1/10 – 1/10 cos ( √5 t)
|g(t) = 1/2√5 sin(√5 t)
h(t) = cos(√5 t) + 2/ √5 sin (√5 t)
The solution is then,
Y(s) = 3e-12sF(s) – 5e-4sG(s) – H(s)
y(t) = 3u12(t) f(t – 12) – 5u4 (t) g(t – 4) – h(t)
Where, f(t), g(t) and h(t) are defined above.
2.5.1 Derivatives
The Fourier transform of a derivative, in 3D:
F[i f(x)] =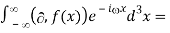 
=[f(x)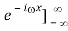
- 
= - 
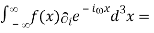
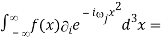
= -(-ii)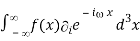 
= ii F[f(x)]
An alternative derivation is to start from:
f(x) = F-1[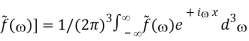
And differentiate both sides:
if(x) =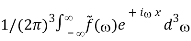 
if(x) =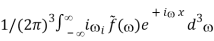 
From which:
F[i f(x)] = ii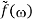
= 
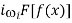
2.5.2 Properties of Fourier Transform
The Fourier transform's properties are listed below. The above-mentioned properties of the Fourier expansion of periodic functions are special cases of the features given here. We'll go over the following points in detail
f[x(t)] = X(j) and F[y(t)] = Y(j). Assume
- Linearity
F[ax (t) + by(t)] = aF[x(t)] + bF[y(t)]
- Time shift
F[x(t ± t0)] = X(j)e±jt0
Proof: Let t’ = t ± t0, i.e., t = t’ ∓ t0, we have
F[x(t ± t0)]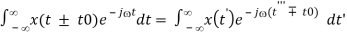 
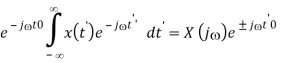
- Frequency shift
F-1 [ X(j ± 0)] = x(t) e∓ j 0’
Proof: Let ’ = ± 0 , i.e., = ’ ∓ 0
, we have
F-1[X (j( ± 0 1/2π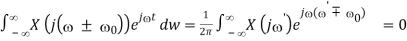 
e∓ j 0t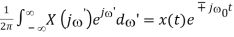 
- Time reversal
F[x(-t)] = X(-)
Proof:
F[x(-t)] =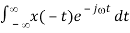 
Replacing t by –t’, we get
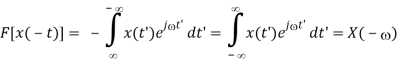
- Even and Odd Signals and Spectra
If the signal x(t) is an even (or odd) function of time, its spectrum X(j) is an even (or odd) function of frequency:
If x(t) = x(-t) then X(j) = X(-j)
And
If x(t) = - x(-t) then X(j) = - X(-j)
Proof: If x(t) = x(-t) is even, then according to the time reversal property, we have
X(j) = F[x(t)] = F[x(-t)] = X(-)
i.e., the spectrum X(j) = X(-) is also even. Similarly, if x(t) = -x(-t) is odd, we have
X(j) = F[x(t)] = F[ - x( - t)] = - X(-)
i.e., the spectrum X(j) = - X(-) is also odd.
- Time and frequency scaling
F[x(at)] = 1/a X(/a) or F[ax(at)] = X(/a)
Proof: Let u = at, i.e., t = u/a, where a > 0 is a scaling factor, we have
F[x(at)] =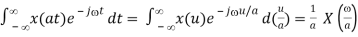 
Note that when a<1, time function x(at) is stretched, and X(j/a) is compressed; when a>1, x(at) is compressed and X(j/a) is stretched. This is a general feature of Fourier transform, i.e., compressing one of the x(t) and X(j) will stretch the other and vice versa. In particular, when a0, x(at) is stretched to approach a constant, and X(j/a)/a is compressed with its value increased to approach an impulse; on the other hand, when a, ax(at) is compressed with its value increased to approach an impulse and X(j/a) is stretched to approach a constant.
- Complex Conjugation
If F[x(t)] = X(j), then F[x* (t)] = X*(-j)
Proof: Taking the complex conjugate of the inverse Fourier transform, we get
x*(t) = [ 1/2π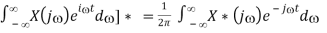 
Replacing by -’ we get the desired result:
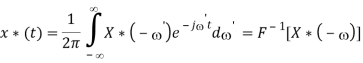
We further consider two special cases:
- If x(t) = x*(t) is real, then
F[x(t)] = X(j) = Xr (j) + jXi(j)
F[x*(t)] = X*(-) = Xr (-) – jXi(-)
i.e., the real part of the spectrum is even (with respect to frequency ), and the imaginary part is odd:
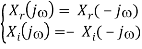
- If x(t) = - x*(t) is imaginary, then
F[x(t)] = X(j) = Xr(j) + jXi(j)
F[-x*(t)] = - X*(-j) = - Xr(-j) + jXi(-j)
- In other words, the imaginary component of the spectrum is even, whereas the real part is odd:
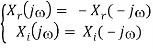
If the time signal x(t) is one of the four combinations shown in the table (real even, real odd, imaginary even, and imaginary odd), then its spectrum X(j) is given in the corresponding table entry:
| If x(t) is real | If x(t) is imaginary |
| Xr even, Xi odd | Xr odd, Xi even |
If x(t) is Even |
|
|
Xr and Xi even | Xi = 0, X = Xr even | Xr = 0, X = Xi even |
If x(t) is Odd |
|
|
Xr and Xi odd | Xr = 0, X = Xi odd | Xi = 0, X = Xr odd |
It's worth noting that if a real or imaginary element of the table must be both even and odd at the same time, it must be zero.
These characteristics are enumerated below:
| x(t) = xr(t) + j xi(t) | X(j) = Xr(j) + j Xi(j) |
1 | Real x(t) = xr(t) | Even Xr(j), odd Xi(j) |
2 | Real and even x(-t) = xr(t) | Real and even Xr(j) |
3 | Real and odd x(-t) = - xr(t) | Imaginary and odd Xi(j) |
4 | Imaginary x(t) = xi(t) | Odd Xr(j), even Xi(j) |
5 | Imaginary and even x(-t) = xi(t) | Imaginary and even Xi(j) |
6 | Imaginary and odd x(-t) =- xi(t) | Real and odd Xi(j) |
The first three elements above imply that the spectrum of the even part of a real signal is real and even, and the spectrum of the odd half of the signal is imaginary and odd, because any signal can be described as the sum of its even and odd components.
- Symmetry (or Duality)
If F[x(t)] = X(j), then F[X(t)] = 2π x(-j)
Or in a more symmetric form:
If F[x(t)] = X(f), then F[X(t)] = x(-f)
Proof: As F[x(t)] = X(j), we have
x(t) = F-1[X(j)] = 1/2π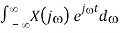 
Letting t’ = - t, we get
x(-t’) = 1/2π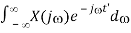 
Interchanging t’ and we get:
2πx(-) =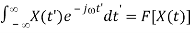 
Or
x(-f) = =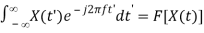 
In particular, if the signal is even:
x(t) = x(-t)
Then we have
If F[x(t)] = X(f), then F[X(t)] = x(f)
An even square wave's spectrum, for example, is a sinc function, while a sinc function's spectrum is an even square wave.
Multiplication theorem
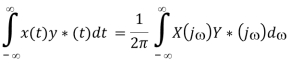
Proof:
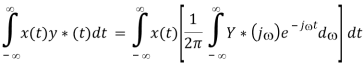
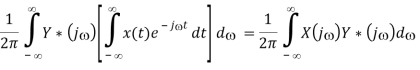
Parseval's equation
In the special case when y(t) = x(t), the above becomes the Parseval's equation (Antoine Parseval 1799):
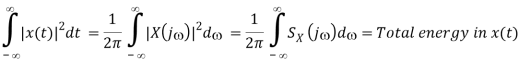
Where
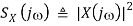
Is the energy density function representing how the signal's energy is distributed along the frequency axes. The total energy contained in the signal is obtained by integrating S(j) over the entire frequency axes.
The Parseval's equation implies that the signal's energy or information is reserved, i.e., the signal can be represented in either the time or frequency domain without losing or gaining energy.
Correlation
The cross-correlation of two real signals x(t) and y(t) is defined as
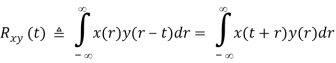
Specially, when x(t) = y(t), the above becomes the auto-correlation of signal x(t)
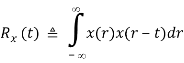
Assuming F[x(t)] = X(j), we have F[x(t-r)] = X(j) e-jr and according to multiplication theorem, Rx(r) can be written as
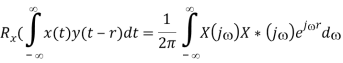
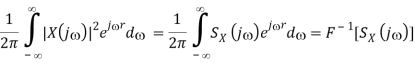
i.e.,
F[Rx(t)] = SX(j)
That is, the auto-correlation and the energy density function of a signal x(t) are a Fourier transform pair.
Convolution Theorems
Convolution in the time domain corresponds to multiplication in the frequency domain, and vice versa, according to the convolution theorem:
F[x(t) * y(t)] = X(j) Y(j) (a)
F[x(t) y(t)] = X(j) * Y(j) (b)
Proof of (a):
F[x(t) * y(t)]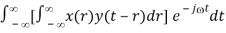 
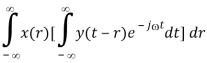
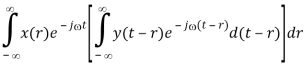
X(j) Y(j)
Proof of (b):
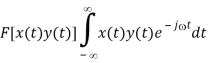
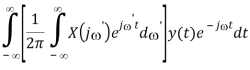
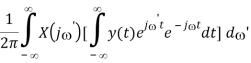
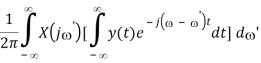
Time Derivative
F[ d/dt x(t)] = j X(j)
Proof: Differentiating the inverse Fourier transform X(j) with respect to t we get:
d/dt x( t d/dt [ 1/2π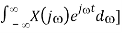 
= 1/2π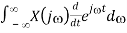 
1/2π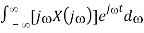 
= F-1 [j X (j)]
Repeating this process we get
F[dn/dtn x(t) ] = (j)n X(j)
Time Integration
Consider the Fourier transforms of the two signals below:
u(t) =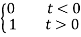 
sgn(t) = 
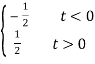= u(t) – ½
d u(t)/dt = δ(t), d sgn(t)/dt = d/dt [ u(t) – ½ ] = δ(t)
According to the time derivative property above
X(j) = F[x(t)] = 1/j F [ d/dt x(t)]
We get
F[u(t)] = 1/j F[d/dt x(t)] = 1/j F[δ(t)] = 1/j
And
F[sgn(t)] = 1/j F[d/dt sgnt)] = 1/j F[δ(t)] = 1/j
Why do the two different functions have the same transform?
In general, any two function f(t) and g(t) = f(t) + c with a constant difference c have the same derivative d f(t)/dt, and therefore they have the same transform according the above method. This problem is obviously caused by the fact that the constant difference c is lost in the derivative operation. To recover this constant difference in time domain, a delta function needs to be added in frequency domain. Specifically, as function sgn(t) does not have DC component, its transform does not contain a delta:
F[sgn(t)] = 1/j
To find the transform of u(t), consider
u(t) = sgn(t) + ½
And
F[u(t)] = F[sgn(t)] + F[1/2] = 1/j + πδ()
The added impulse term πδ() directly reflects the constant c = ½ in time domain.
Now we show that the Fourier transform of a time integration is
F[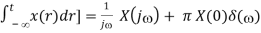
Proof:
First consider the convolution of x(t) and u(t):
x(t) * u(t) =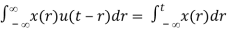 
Due to the convolution theorem, we have
F[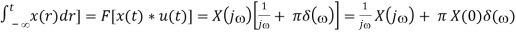
Frequency Derivative
F[t x(t)] = j d/d X(j)
Proof: We differentiate the Fourier transform of x(t) with respect to to get
d/d X (j) d/d [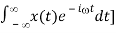 
= 
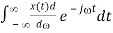
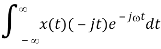
i.e.,
F[-jtx(t)] = d/d X (j)
Multiplying both sides by j, we get
j d/d X(j) =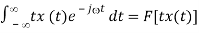 
Repeating this process we get
F[tn x(t)] = jn dn/dn X(j)
The Fourier transform of the generalized function 1/x is given by
Fx(-PV 1/πx) (k) = 1/π PV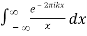 
= PV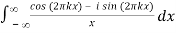 
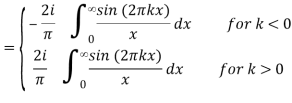
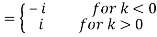
Where PV denotes the Cauchy principal value. Equation (4) can also be written as the single equation
Fx (-PV 1/πx)(k) = i[1 – 2H (-k)]
Where H(x) is the Heaviside step function. The integrals follow from the identity
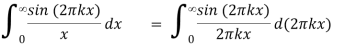
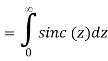
= ½ π
NUMERICALS:
1) We have
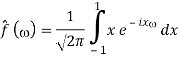
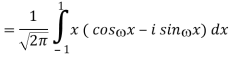
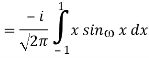
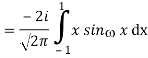
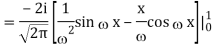
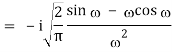
2) Use integration by parts to evaluate the integrals
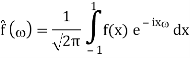
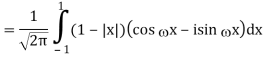
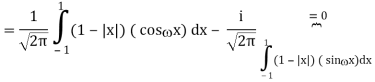
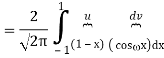
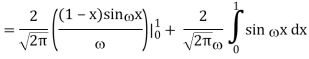
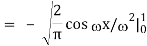
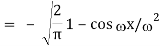
Key takeaway:
- But, in the Fourier transform, when we multiply our signal (whether in the time or frequency domain) by an imaginary/complex exponential function, what does the term 'j' stand for? j*j = -1, or j, is a complex number with unit magnitude and zero real portion.
- In the field of audio and acoustics measurement, the "Fast Fourier Transform" (FFT) is a significant measurement method. It breaks down a signal into its various spectral components and hence offers frequency information.
- The Fourier Transform is a useful image processing method for breaking down an image into sine and cosine components.
- Image analysis, picture filtering, image reconstruction, and image compression are among applications that use the Fourier Transform.
- A complex-valued function of frequency, whose magnitude (absolute value) denotes the amount of that frequency present in the original function, is the Fourier transform of a function of time.
References:
1. Mathematical Physics and Special Relativity–M.Das, P.K. Jena and B.K. Dash (Srikrishna Prakashan)-2009
2. Mathematical Physics–H. K. Das, Dr. Rama Verma (S. Chand Publishing) 2011
3. Complex Variable: Schaum’s Outlines Series M. Spiegel (2nd Edition, Mc- Graw Hill Education)-2004
4. Complex variables and applications J.W.Brown and R.V.Churchill 7th Edition 2003
5. Mathematical Physics, Satya Prakash (Sultan Chand)-2014
Unit - 2
Integral Transforms-I
2.1.1 The Fourier Integral Theorem
So far, we've looked at expressing functions in terms of their Fourier series, notably 2-periodic functions. Naturally, not all functions are 2-periodic, thus it may be impossible to express a function defined on all of R using a Fourier series. The next best option is to represent these functions as integrals. Fortunately, under the right circumstances, a function fL(R) can be written as an integral, as stated by the Fourier Integral Theorem
Theorem 1 (The Fourier Integral Theorem): If f ∈ L(R) and if there exists an x ∈ R and a δ>0 such that either:
1) f is of bounded variation on [x−δ, x+δ].
2) f(x+) and f(x−) both exist, and
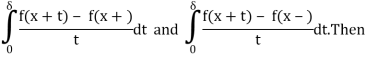
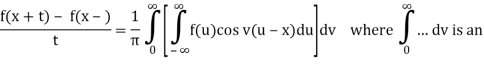
Riemann integral that isn't right.
Before we look at any examples of the Fourier integral theorem, we'll demonstrate the following two equalities for even and off functions that satisfy the theorem:
Theorem 2: If f∈L(R) satisfies either of the conditions of the Fourier integral theorem then:
a) If f is an even function then
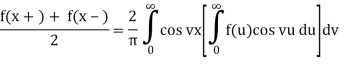
b) If f is an odd function then
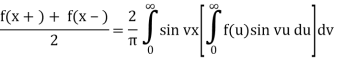
Proof of a) Suppose that f ∈ L(R) satisfies either of the conditions of the Fourier integral theorem. Then:
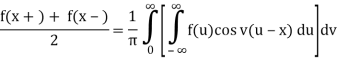
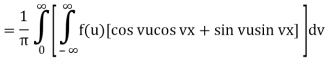
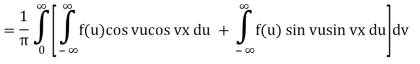
Because f is an even function of u and sin vu is an odd function of u, f(u)sin vu is also an odd function of u, and so on.
Interval
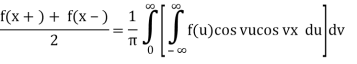
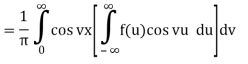
Because f is an even function of u and cos vu is an even function of u, f(u)cos vu is an even function of u, and so on for the symmetric functions.
Interval so:
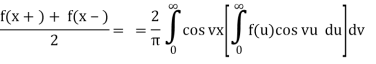
Proof of b) Assume that fL(R) fulfils one of the Fourier integral theorem's requirements. Then there's the following:
Because f is an odd function of u and cos vu is an even function of u, we get f(u)cos vu, and similarly, since sin vu is an odd function of u, we get f(u)sin vu. As in
(a) above, the evidence is as follows:
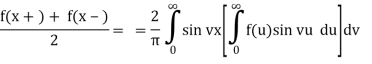
2.2.1 Fourier transform
The Fourier Transform comes into play here. The notion that every non-linear function can be represented as a sum of (infinite) sine waves is used in this method. This is depicted in the underlying picture, where a step function is approximated by a slew of sine waves.
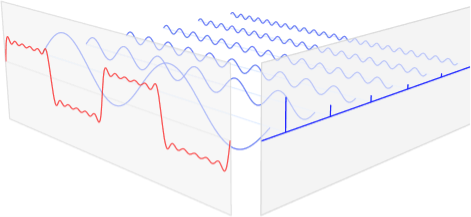
Fig. Step function simulated with sine waves
A Fourier Transform deconstructs a temporal signal and returns information on the frequency of all sine waves required to reproduce that signal. The Discrete Fourier Transform (DFT) is defined as follows for sequences of equally spaced values:
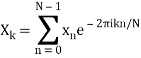
Where:
- N is the total number of samples.
- n denotes the current sample.
- Xn is the signal's value at time n.
- k is the frequency of the current (0 Hz to N-1 Hz)
- Xk denotes the DFT result (amplitude and phase)
It's worth noting that a dot product is defined as follows:
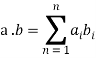
A DFT algorithm can thus be as written as:
Import numpy as np
DefDFT(x):
Compute the discrete Fourier Transform of the 1D array x
:param x: (array)
N =x.size
n =np.arange(N)
k =n.reshape((N, 1))
e =np.exp(-2j*np.pi* k * n / N)
Return np.dot(e, x)
However, running this code on our time signal, which contains around 10,000 data, takes more than 10 seconds!
Iiftyhr56gyuzlhskssaasdfhkqqweaeqwertip77aszxmnbbvcxxz
Fortunately, some brilliant people (Cooley and Tukey) devised the Fast Fourier Transform (FFT) technique, which recursively divides the DFT into smaller DFTs, greatly reducing the required computing time. The FFT scales O(N log(N), whereas the normal DFT scales O(N2).
2.2.2 Fourier Series Example
Example: Determine the fourier series of the function f(x) = 1 – x2 in the interval [-1, 1].
Solution:
Given,
f(x) = 1 – x2; [-1, 1]
We know that, the fourier series of the function f(x) in the interval [-L, L], i.e. -L ≤ x ≤ L is written as:
f(x) = A0 +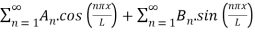 
Here,
A0 =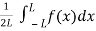 
An =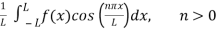 
Bn =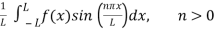 
Now, by applying he formula for f(x) in the interval [-1, 1]:
f(x) =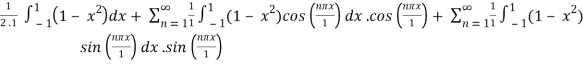 
By simplifying the definite integrals,
= 
= 
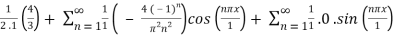
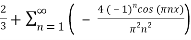
2.3.1 Fourier Transform—Cosine
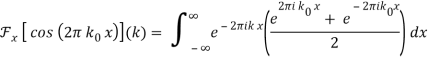
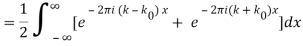
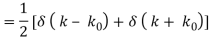
Where δ(x) is the delta function.
2.3.2 Fourier Transform—Gaussian
The Fourier transform of a Gaussian function f(x) ≡ e-ax2 is given by
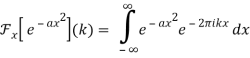
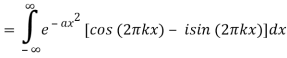
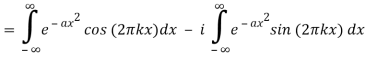
Integration across a symmetrical range yield 0 since the second integrand is odd. Abramowitz and Stegun (1972, p. 302, equation 7.4.6) give the value of the first integral, so
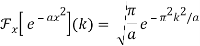
As a result, a Gaussian becomes another Gaussian.
2.3.3 Find the Fourier transform of finite wave train
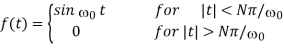
A function f(t) represents a sine wave of time
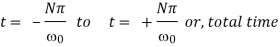
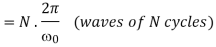
Since f(t) is odd, we use fourier sine transform,
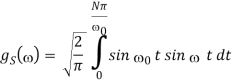
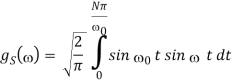
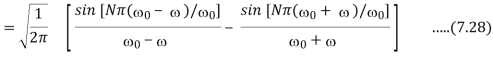
2.3.4 Travelling wave
When something in the physical world changes, information about that change spreads outwards in all directions, away from the source. The information travels in the form of a wave as it travels. Waves carry sound to our ears, light to our eyes, and electromagnetic radiation to our cell phones. The waves formed on the surface of the water when a stone is dropped into a lake are a nice visual example of wave propagation. We'll learn more about travelling waves in this article.
2.3.5 Describing a Wave
A wave is a disturbance in a medium that travels while transferring momentum and energy without causing the medium to move. A travelling wave is a wave that travels through the medium between its greatest and minimum amplitude levels. Consider the disturbance generated when we jump on a trampoline to better understand a wave. When we jump on a trampoline, the downward force we exert at one location on the trampoline causes the material adjacent to it to go downward as well.
When the produced disturbance spreads outward, the spot where our feet originally impacted the trampoline recovers and moves outward due to the trampoline's tension force, which also moves the adjoining materials outward. As the trampoline's surface area is covered, the up and down motion gradually spreads out. This disruption takes the form of a wave.
Here are a few key considerations to keep in mind about the wave:
The crests and troughs of a wave are the high and low points of the wave, respectively.
The maximum distance of the wave's disturbance from the mid-point to either the top of the crest or the bottom of a trough is known as amplitude, while the distance between two consecutive crests or troughs is known as wavelength and is represented by
A time period is the length of time between full vibrations.
A frequency is the number of vibrations a wave experiences in one second.
The following is the link between time period and frequency:
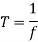
The equation for a wave's speed can be found here.
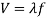
Different Types of Waves
Waves come in a variety of shapes and sizes, each with its own set of features. These qualities aid in the classification of wave types. One approach to distinguish travelling waves is the orientation of particle motion in relation to the direction of wave propagation. The following are the several forms of waves, which are classified based on particle motion:
● Pulse Waves – A pulse wave is a wave that goes through the transmission medium with only one disruption or peak.
● Continuous Waves – A continuous wave is a waveform with the same amplitude and frequency all the time.
● Transverse Waves – The velocity of a particle in a transverse wave is perpendicular to the wave's propagation direction.
● Longitudinal Waves – Longitudinal waves are those in which the particle's motion is in the same direction as the wave's propagation.
Despite their differences, they all have one thing in common: energy transfer. E=1/2 KA2 is the energy of an object in simple harmonic motion. We can deduce from this equation that a wave's energy is proportional to the square of its amplitude, i.e. E/A2. This link between energy and amplitude is crucial in determining the extent of damage that earthquake shock waves can do. Because the waves are spread out across a larger area, they become weaker as they spread out.
Constructive and Destructive Interference
Interference is a phenomenon in which two waves superimpose to generate a new wave of lower, larger, or equal amplitude. The interaction of waves that are associated with one other, either because of the same frequency or because they come from the same source, causes constructive and destructive interference. Interference effects can be seen in a variety of waves, including gravity and light waves.
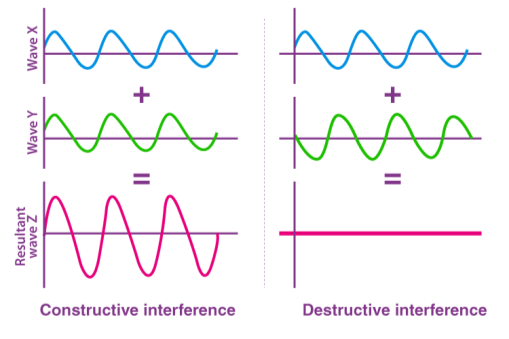
When two or more propagating waves of the same kind collide at the same site, the resulting amplitude is equal to the vector sum of the individual waves' amplitudes, according to the principle of superposition of waves. The resultant amplitude is the total of the individual amplitudes when the crest of one wave meets the crest of another wave of the same frequency at the same place. Constructive interference is the term for this form of interference. When a wave's crest collides with a wave's trough, the resulting amplitude equals the difference between the separate amplitudes, which is known as destructive interference.
NUMERICALS:
1) find the transform of
f(t) = e-at u(t)
Whereas a>0. By definition we have
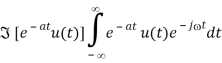
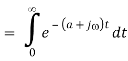
OR
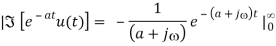
The upper limit is given by
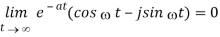
Since the expression in parentheses is bounded while the exponential goes to zero. Thus we have
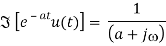
Or
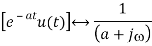
2) x(t) = u(t – 2)
ANS:
X(s) =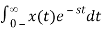 
= 
= 
= 
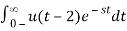
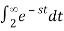
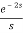
3) x(t) = e-2t u(t + 1)
ANS:
X(s) =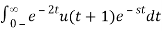 
= 
= 
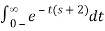
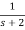
2.4.1 Dirac's delta function and the Fourier transform
We use a limiting approach to define the Dirac delta function, which is not a function in the traditional sense (mathematicians term it a distribution).
δ(x) = lim Λ fΛ(x)
Where fΛ(x) is an ordinary function depending on the parameter Λ. The requirement on δ(x) is
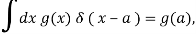
Where the point x=a is included in the integration range. The function g is referred to as a 'test' function because it is expected to behave 'nicely,' with no singularities and approaching 0 at infinity. It follows from the basic property (76) that
xδ(x) = 0
This is significant when dividing: It is not necessary to conclude that f(x)g(x)=h(x) from f(x)g(x)=h(x) (x). Instead, C is an arbitrary constant, as can be seen by multiplying both sides by g(x) and using.
We get the special result by putting g=1 in (76). To satisfy (76), the quantity can only have support at x=0, and it must be infinite at this point to yield a finite integral. As a result, the ordinary function must grow increasingly peaked around x=0 and larger and larger for rising.
A limiting function is exemplified by the following example.
fΛ (x) = sin Λ x / π x
This function has the value Λ/π for x=0, and the width of its first peak is π/ Λ 0. For larger values of x it oscillates rapidly. To show that f Λ approaches a delta function for , we notice that (take y = Λ x)
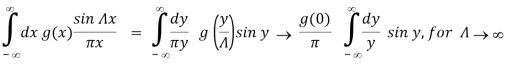The last y-integral has been performed in eqs. (3-10) and (3-11) in the book and is equal to 
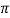. The property (76) is seen to be satisfied (with the arbitrary point a taken to be 0). Therefore
δ(x) =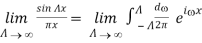 
There are numerous alternative ways to represent the delta function, but the one provided by (80) is particularly useful, as shown in the example below.
Let's say we have a function f(x) and we want to create a new function.
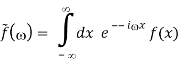
The methods below can be used to flip this relationship.
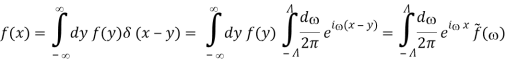
Where we used eqs. (76) and (80). We then get the pair of equations in the limit
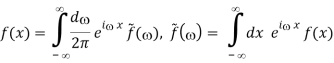
Thus, eq. (82) is a one-line derivation of Mathews and Walker's eqs. (4-16). This demonstrates the delta function's immense power.
It's worth noting that, thanks to eq. (80), the delta function has the following formal integral representation:
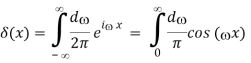
This could also be obtained by taking f(x) = δ(x) in (83). The limits of the integral should really be understood as beeing between -Λ and Λ, but in calculations one can often use this integral with Λ already taken to infinity.
As a further illustration of the delta function, let us return to the Fourier series discussed in the former section. Taking into account that S(θ) = f(θ) (assuming f to be continuous), we see that eq. (69) requires
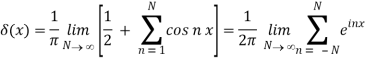
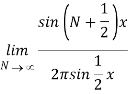
We utilised eq. In the last step (70). This delta function form is identical to the one shown in eq. (80) and in (84). In particular, we may formalise eq. (85) as
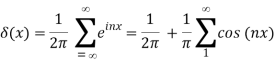
Which is a discrete version of (84).
To show (85) directly we study how it acts in an integral,
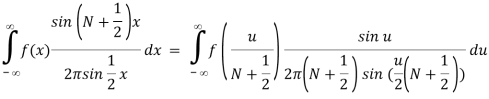
f(0)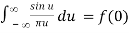 
For N . The final expression is the same as what we would have gotten if we had used (80). As a result, when the integral sign is used, the two representations (80) and (85) end up being the same.
The Dirac delta distribution (1.16) is historically and commonly replaced by the Dirac delta (or Dirac delta function) in physics and engineering applications (x). This is an operator with the following characteristics:
δ(x)=0,
x∈ℝ, x≠0,
And
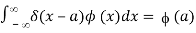
If specific requirements on the function are met (x). The left-hand side of the above can be read mathematically as a generalised integral in the sense that
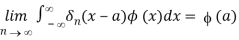
n(x), n=1,2,.... For an appropriately chosen series of functions A delta sequence is what we name it, and we write it symbolically as
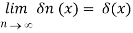
An example of a delta sequence is provided by
δn (x – a) =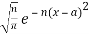 
In this case
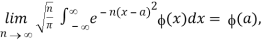
For all functions ϕ(x) that are continuous when x∈(-∞,∞), and for each a,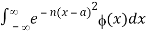 
converges absolutely for all sufficiently large values of n. The last condition is satisfied, for example, when (x) = O(
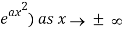, where α is a real constant.
More generally, assume ϕ(x) is piecewise continuous (§1.4(ii)) when x∈[-c,c] for any finite positive real value of c, and for each a,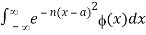 
converges absolutely for all sufficiently large values of n. Then
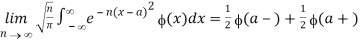
2.4.2 Integral Representations
Formal interchange of the order of integration in the Fourier integral formula.
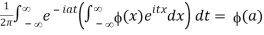
Yields
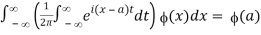
The inner integral does not converge. However, for n=1,2,…,
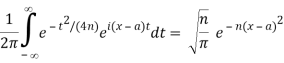
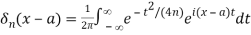
Provided that ϕ(x) is continuous when x∈(-∞,∞), and for each a,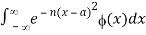 
converges absolutely for all sufficiently large values of n (as in the case. Then comparison of the two yields the formal integral representation
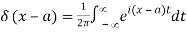
2.4.3 Properties of the Delta Function
The following features can be easily verified from the definition as a Gaussian wave packet limit:
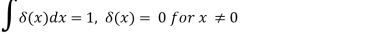
δ(x) = δ(-x) , δ(ax) = 1/|a| δ(x)
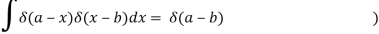
NUMERICALS:
1) Solve the following IVP.
y’’ + 2y’ – 15y = 6 δ (t – 9) , y(0) = -5 y’(0) = 7
ANS:
First take the Laplace transform of everything in the differential equation and apply the initial conditions.
s2 Y(s) – sy(0) – y’(0) + 2(sY (s) – y(0)) – 15Y (s) = 6 e-9s (s2 + 2s – 15) Y(s) + 5s + 3 = 6e-9s
Now solve for Y(s).
Y(s) = 6e-9s/(s+5)(s – 3) - 5s+3/(s+5)(s – 3)
= 6e-9s F(s) – G(s)
We’ll leave it to you to verify the partial fractions and their inverse transforms are,
F(s) = 1/ (s+5)(s -3) =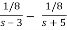 
f(t) = 1/8 e3t – 1/8 e-5t
G(s) = 5s + 3/(s + 5)(s – 3) =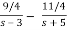 
g(t) = 9/4 e3t + 11/4 e-5t
The solution is then,
Y(s) = 6e-9s F(s) – G(s)
y(t) = 6u9 (t) f(t – 9) – g(t)
Where, f(t) and g(t) are defined above.
2) Solve the following IVP.
2y’’ + 10y = 3u12(t) – 5 δ( t – 4) , y(0) = - 1 y’(0) = - 2
ANS:
Take the Laplace transform of everything in the differential equation and apply the initial conditions.
2( s2Y(s) – sy(0) – y’(0)) + 10Y (s) = 3e-12s/s – 5e-4s
(2s2 + 10) Y(s) +2s + 4 = 3e-12s/s – 5e-4s
Now solve for Y(s).
Y(s) = 3e-12s/s(2s2 + 10) – 5e-4s/2s2 + 10 – 2s+4/2s2+10
= 3e-12s F(s) – 5e-4sG(s) – H(s)
We’ll need to partial fraction the first function. The remaining two will just need a little work and they’ll be ready. I’ll leave the details to you to check.
F(s) = 1/s(2s2 + 10) = 1/10 1/s – 1/10 s/s2 + 5
f(t) = 1/10 – 1/10 cos ( √5 t)
|g(t) = 1/2√5 sin(√5 t)
h(t) = cos(√5 t) + 2/ √5 sin (√5 t)
The solution is then,
Y(s) = 3e-12sF(s) – 5e-4sG(s) – H(s)
y(t) = 3u12(t) f(t – 12) – 5u4 (t) g(t – 4) – h(t)
Where, f(t), g(t) and h(t) are defined above.
2.5.1 Derivatives
The Fourier transform of a derivative, in 3D:
F[i f(x)] =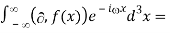 
=[f(x)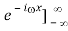
- 
= - 
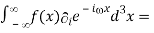
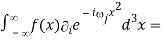
= -(-ii)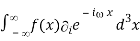 
= ii F[f(x)]
An alternative derivation is to start from:
f(x) = F-1[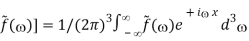
And differentiate both sides:
if(x) =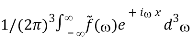 
if(x) =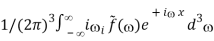 
From which:
F[i f(x)] = ii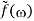
= 
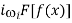
2.5.2 Properties of Fourier Transform
The Fourier transform's properties are listed below. The above-mentioned properties of the Fourier expansion of periodic functions are special cases of the features given here. We'll go over the following points in detail
f[x(t)] = X(j) and F[y(t)] = Y(j). Assume
- Linearity
F[ax (t) + by(t)] = aF[x(t)] + bF[y(t)]
- Time shift
F[x(t ± t0)] = X(j)e±jt0
Proof: Let t’ = t ± t0, i.e., t = t’ ∓ t0, we have
F[x(t ± t0)]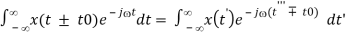 
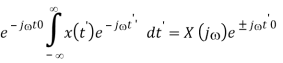
- Frequency shift
F-1 [ X(j ± 0)] = x(t) e∓ j 0’
Proof: Let ’ = ± 0 , i.e., = ’ ∓ 0
, we have
F-1[X (j( ± 0 1/2π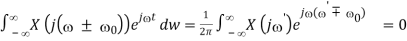 
e∓ j 0t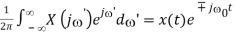 
- Time reversal
F[x(-t)] = X(-)
Proof:
F[x(-t)] =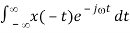 
Replacing t by –t’, we get
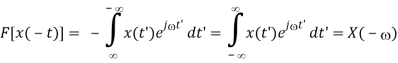
- Even and Odd Signals and Spectra
If the signal x(t) is an even (or odd) function of time, its spectrum X(j) is an even (or odd) function of frequency:
If x(t) = x(-t) then X(j) = X(-j)
And
If x(t) = - x(-t) then X(j) = - X(-j)
Proof: If x(t) = x(-t) is even, then according to the time reversal property, we have
X(j) = F[x(t)] = F[x(-t)] = X(-)
i.e., the spectrum X(j) = X(-) is also even. Similarly, if x(t) = -x(-t) is odd, we have
X(j) = F[x(t)] = F[ - x( - t)] = - X(-)
i.e., the spectrum X(j) = - X(-) is also odd.
- Time and frequency scaling
F[x(at)] = 1/a X(/a) or F[ax(at)] = X(/a)
Proof: Let u = at, i.e., t = u/a, where a > 0 is a scaling factor, we have
F[x(at)] =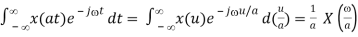 
Note that when a<1, time function x(at) is stretched, and X(j/a) is compressed; when a>1, x(at) is compressed and X(j/a) is stretched. This is a general feature of Fourier transform, i.e., compressing one of the x(t) and X(j) will stretch the other and vice versa. In particular, when a0, x(at) is stretched to approach a constant, and X(j/a)/a is compressed with its value increased to approach an impulse; on the other hand, when a, ax(at) is compressed with its value increased to approach an impulse and X(j/a) is stretched to approach a constant.
- Complex Conjugation
If F[x(t)] = X(j), then F[x* (t)] = X*(-j)
Proof: Taking the complex conjugate of the inverse Fourier transform, we get
x*(t) = [ 1/2π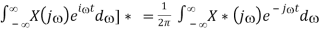 
Replacing by -’ we get the desired result:
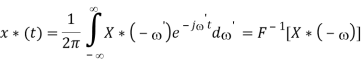
We further consider two special cases:
- If x(t) = x*(t) is real, then
F[x(t)] = X(j) = Xr (j) + jXi(j)
F[x*(t)] = X*(-) = Xr (-) – jXi(-)
i.e., the real part of the spectrum is even (with respect to frequency ), and the imaginary part is odd:
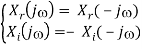
- If x(t) = - x*(t) is imaginary, then
F[x(t)] = X(j) = Xr(j) + jXi(j)
F[-x*(t)] = - X*(-j) = - Xr(-j) + jXi(-j)
- In other words, the imaginary component of the spectrum is even, whereas the real part is odd:
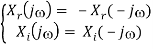
If the time signal x(t) is one of the four combinations shown in the table (real even, real odd, imaginary even, and imaginary odd), then its spectrum X(j) is given in the corresponding table entry:
| If x(t) is real | If x(t) is imaginary |
| Xr even, Xi odd | Xr odd, Xi even |
If x(t) is Even |
|
|
Xr and Xi even | Xi = 0, X = Xr even | Xr = 0, X = Xi even |
If x(t) is Odd |
|
|
Xr and Xi odd | Xr = 0, X = Xi odd | Xi = 0, X = Xr odd |
It's worth noting that if a real or imaginary element of the table must be both even and odd at the same time, it must be zero.
These characteristics are enumerated below:
| x(t) = xr(t) + j xi(t) | X(j) = Xr(j) + j Xi(j) |
1 | Real x(t) = xr(t) | Even Xr(j), odd Xi(j) |
2 | Real and even x(-t) = xr(t) | Real and even Xr(j) |
3 | Real and odd x(-t) = - xr(t) | Imaginary and odd Xi(j) |
4 | Imaginary x(t) = xi(t) | Odd Xr(j), even Xi(j) |
5 | Imaginary and even x(-t) = xi(t) | Imaginary and even Xi(j) |
6 | Imaginary and odd x(-t) =- xi(t) | Real and odd Xi(j) |
The first three elements above imply that the spectrum of the even part of a real signal is real and even, and the spectrum of the odd half of the signal is imaginary and odd, because any signal can be described as the sum of its even and odd components.
- Symmetry (or Duality)
If F[x(t)] = X(j), then F[X(t)] = 2π x(-j)
Or in a more symmetric form:
If F[x(t)] = X(f), then F[X(t)] = x(-f)
Proof: As F[x(t)] = X(j), we have
x(t) = F-1[X(j)] = 1/2π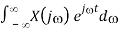 
Letting t’ = - t, we get
x(-t’) = 1/2π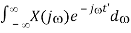 
Interchanging t’ and we get:
2πx(-) =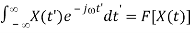 
Or
x(-f) = =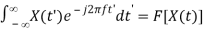 
In particular, if the signal is even:
x(t) = x(-t)
Then we have
If F[x(t)] = X(f), then F[X(t)] = x(f)
An even square wave's spectrum, for example, is a sinc function, while a sinc function's spectrum is an even square wave.
Multiplication theorem
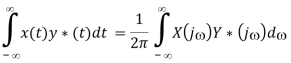
Proof:
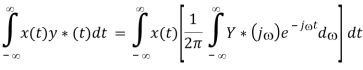
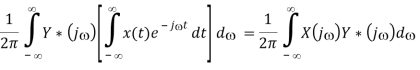
Parseval's equation
In the special case when y(t) = x(t), the above becomes the Parseval's equation (Antoine Parseval 1799):
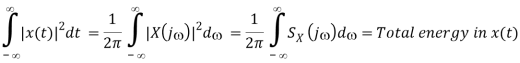
Where
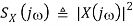
Is the energy density function representing how the signal's energy is distributed along the frequency axes. The total energy contained in the signal is obtained by integrating S(j) over the entire frequency axes.
The Parseval's equation implies that the signal's energy or information is reserved, i.e., the signal can be represented in either the time or frequency domain without losing or gaining energy.
Correlation
The cross-correlation of two real signals x(t) and y(t) is defined as
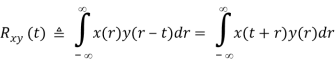
Specially, when x(t) = y(t), the above becomes the auto-correlation of signal x(t)
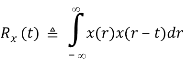
Assuming F[x(t)] = X(j), we have F[x(t-r)] = X(j) e-jr and according to multiplication theorem, Rx(r) can be written as
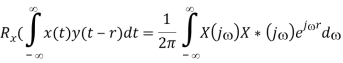
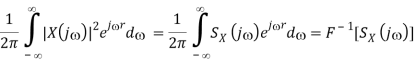
i.e.,
F[Rx(t)] = SX(j)
That is, the auto-correlation and the energy density function of a signal x(t) are a Fourier transform pair.
Convolution Theorems
Convolution in the time domain corresponds to multiplication in the frequency domain, and vice versa, according to the convolution theorem:
F[x(t) * y(t)] = X(j) Y(j) (a)
F[x(t) y(t)] = X(j) * Y(j) (b)
Proof of (a):
F[x(t) * y(t)]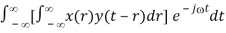 
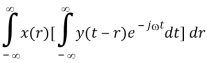
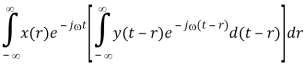
X(j) Y(j)
Proof of (b):
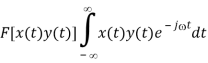
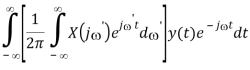
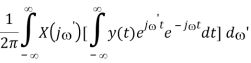
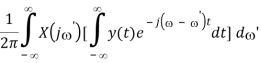
Time Derivative
F[ d/dt x(t)] = j X(j)
Proof: Differentiating the inverse Fourier transform X(j) with respect to t we get:
d/dt x( t d/dt [ 1/2π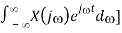 
= 1/2π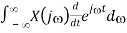 
1/2π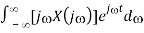 
= F-1 [j X (j)]
Repeating this process we get
F[dn/dtn x(t) ] = (j)n X(j)
Time Integration
Consider the Fourier transforms of the two signals below:
u(t) =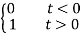 
sgn(t) = 
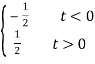= u(t) – ½
d u(t)/dt = δ(t), d sgn(t)/dt = d/dt [ u(t) – ½ ] = δ(t)
According to the time derivative property above
X(j) = F[x(t)] = 1/j F [ d/dt x(t)]
We get
F[u(t)] = 1/j F[d/dt x(t)] = 1/j F[δ(t)] = 1/j
And
F[sgn(t)] = 1/j F[d/dt sgnt)] = 1/j F[δ(t)] = 1/j
Why do the two different functions have the same transform?
In general, any two function f(t) and g(t) = f(t) + c with a constant difference c have the same derivative d f(t)/dt, and therefore they have the same transform according the above method. This problem is obviously caused by the fact that the constant difference c is lost in the derivative operation. To recover this constant difference in time domain, a delta function needs to be added in frequency domain. Specifically, as function sgn(t) does not have DC component, its transform does not contain a delta:
F[sgn(t)] = 1/j
To find the transform of u(t), consider
u(t) = sgn(t) + ½
And
F[u(t)] = F[sgn(t)] + F[1/2] = 1/j + πδ()
The added impulse term πδ() directly reflects the constant c = ½ in time domain.
Now we show that the Fourier transform of a time integration is
F[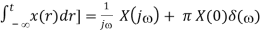
Proof:
First consider the convolution of x(t) and u(t):
x(t) * u(t) =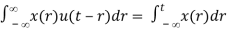 
Due to the convolution theorem, we have
F[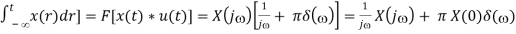
Frequency Derivative
F[t x(t)] = j d/d X(j)
Proof: We differentiate the Fourier transform of x(t) with respect to to get
d/d X (j) d/d [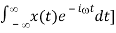 
= 
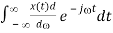
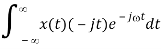
i.e.,
F[-jtx(t)] = d/d X (j)
Multiplying both sides by j, we get
j d/d X(j) =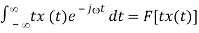 
Repeating this process we get
F[tn x(t)] = jn dn/dn X(j)
The Fourier transform of the generalized function 1/x is given by
Fx(-PV 1/πx) (k) = 1/π PV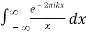 
= PV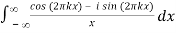 
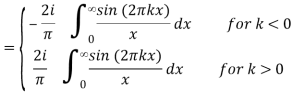
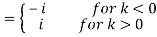
Where PV denotes the Cauchy principal value. Equation (4) can also be written as the single equation
Fx (-PV 1/πx)(k) = i[1 – 2H (-k)]
Where H(x) is the Heaviside step function. The integrals follow from the identity
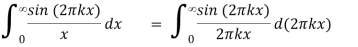
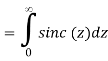
= ½ π
NUMERICALS:
1) We have
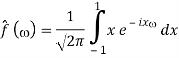
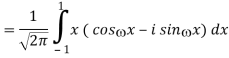
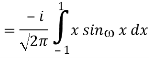
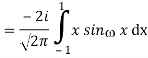
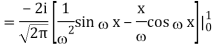
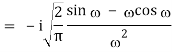
2) Use integration by parts to evaluate the integrals
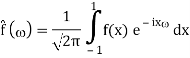
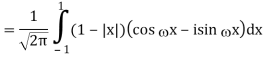
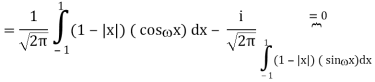
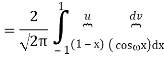
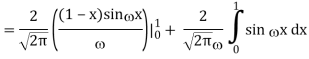
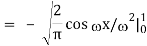
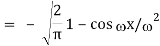
Key takeaway:
- But, in the Fourier transform, when we multiply our signal (whether in the time or frequency domain) by an imaginary/complex exponential function, what does the term 'j' stand for? j*j = -1, or j, is a complex number with unit magnitude and zero real portion.
- In the field of audio and acoustics measurement, the "Fast Fourier Transform" (FFT) is a significant measurement method. It breaks down a signal into its various spectral components and hence offers frequency information.
- The Fourier Transform is a useful image processing method for breaking down an image into sine and cosine components.
- Image analysis, picture filtering, image reconstruction, and image compression are among applications that use the Fourier Transform.
- A complex-valued function of frequency, whose magnitude (absolute value) denotes the amount of that frequency present in the original function, is the Fourier transform of a function of time.
References:
1. Mathematical Physics and Special Relativity–M.Das, P.K. Jena and B.K. Dash (Srikrishna Prakashan)-2009
2. Mathematical Physics–H. K. Das, Dr. Rama Verma (S. Chand Publishing) 2011
3. Complex Variable: Schaum’s Outlines Series M. Spiegel (2nd Edition, Mc- Graw Hill Education)-2004
4. Complex variables and applications J.W.Brown and R.V.Churchill 7th Edition 2003
5. Mathematical Physics, Satya Prakash (Sultan Chand)-2014
