Unit – 4
Laplace Transforms
4.1.1 Introduction
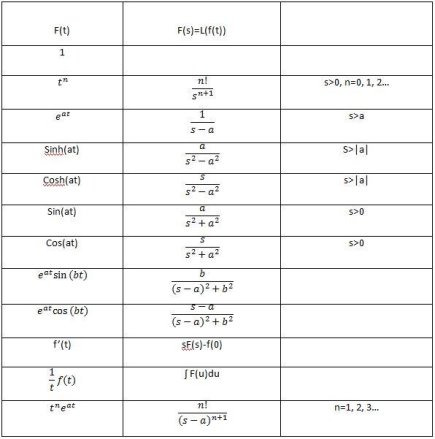
The Laplace integral and how it is used to solve differential equations were reviewed in the previous two parts of the course. Let's review the Laplace integral over f(t):
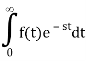
Then we talked about the Laplace transform's Region of Convergence (ROC). The output convergence or divergence is solely determined by the values of s. As a result, the range of s values that converge the output signal is known as the ROC area.
The Laplace Transform, as previously stated, translates integral and differential equations into simple algebraic equations. Let's look at the Laplace integral for a simple function and analyse the results.
4.1.2 Definition
If a function repeats the same values after a certain interval or period, it is said to be periodic. Periodicity can be seen in a variety of phenomena such as oscillations and waves. If f(t+T)=f, a function is periodic mathematically (t)
T can be any constant as long as it is greater than zero. The condition given above must hold for any value of t. The period is abbreviated as T.
If a function's graph has translational symmetry, it is called periodic geometrically. Trigonometric functions such as sine and cosine are the most known examples of periodic functions. They have a two-radian period. The triangle wave is another outstanding example of periodic functions. It is defined as follows:
f(t+2)=f f(t+2)=f f(t+2)= (t)
With the help of a hypothesis that we will address later in this article, we can demonstrate Laplace transform of practically all periodic functions for any value of t. Aperiodic refers to a function that does not repeat its values over a set period of time.
4.1.3 Proposition
We propose a method for computing the Laplace transform of periodic functions. It states that if f is a periodic function with period T and f 1 is one period of the function, the Laplace transform of the function may be written as:
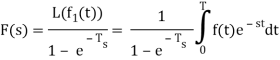
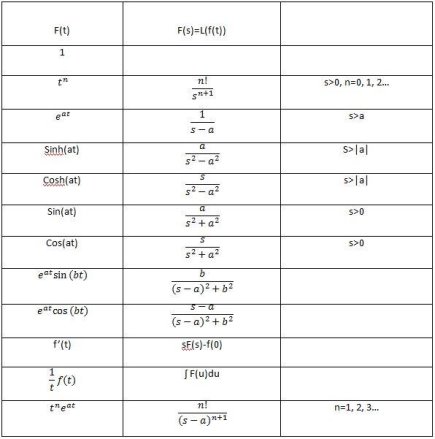
4.1.4 Laplace Transform of Some Important Elementary Functions
To use the Laplace transform on a periodic function, we must first change the domain from time to Laplace. To find the Laplace transform, we must first evaluate the integral. Let's have a look at the Laplace transform of several important elementary functions.
The Unit Step Function:
We know how to write the unit step function:
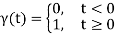
It's depicted graphically as:
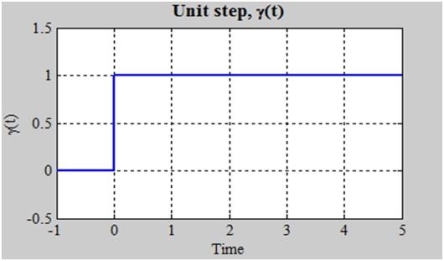
The definition of step is sometimes altered so that the bottom inequality becomes a strict inequality (t>0), leaving (0) undefined. There is also a discontinuity at t=0, but we have drawn a vertical line to make it easier to grasp and to demonstrate that the blue line represents a single function.
We'll now use the definition to obtain the Laplace transform.
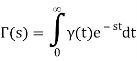
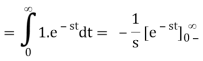
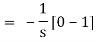
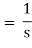 Thus,
Thus,
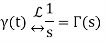
The Unit Impulse Function:
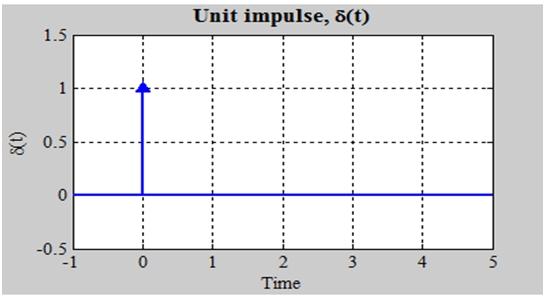
To give you a quick overview of the impulse function, it exists everywhere except at t=0, when it is infinitely huge. One is the impulse function area. On a graph, it can be represented by an arrow with a height equal to its area.
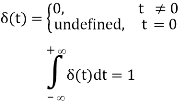
Now we'll use the following formula to find the Laplace transform:

We'll apply the impulse property, which states that the impulse is 0 everywhere except at t=0, when the upper limit of the integral is 0+.
 We can argue that e-st is constant from t=0– to t=0+ because it is continuous at t=0. We can now place the value of e-st at t=0.
We can argue that e-st is constant from t=0– to t=0+ because it is continuous at t=0. We can now place the value of e-st at t=0.
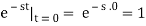
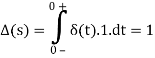
 By this derivation, we get to know that Laplace transform is just one of unit impulse. This shows that the impulse is very easy to deal with in Laplace domain unlike in time domain. Unit impulse will be significant in what we do.
By this derivation, we get to know that Laplace transform is just one of unit impulse. This shows that the impulse is very easy to deal with in Laplace domain unlike in time domain. Unit impulse will be significant in what we do.
The Exponential Function:
For t>0, we are considering exponential.
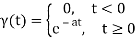
Or
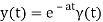
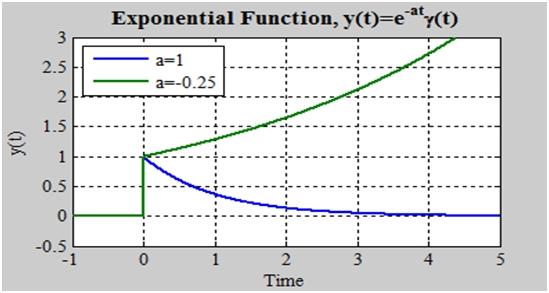
If the function is 0 for t>0, it is considered exponential. We can express the function in pieces, as in the first form, or as exponential multiplied by b unit step, as in the second definition. We normally choose the second ne since it is more efficient. Because all functions for t>0 are zero, multiplication with (t) will not show exact (t) and will be implicit on a frequent basis.
If a0 is zero, the function will fall to zero, but if a>0, the function will freely rise. We mostly look at falling to zero exponentials, and they're common in systems.
We'll use the following formula to find the Laplace transform:
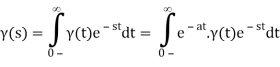 We can remove it from the integral since we know that for all positive t (t) is one.
We can remove it from the integral since we know that for all positive t (t) is one.
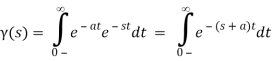
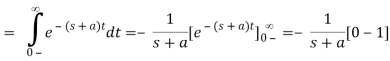
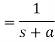
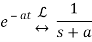
In the last equation, you can see that (t) is implicit. We get a step function if a=1 and L(s) =1/s.
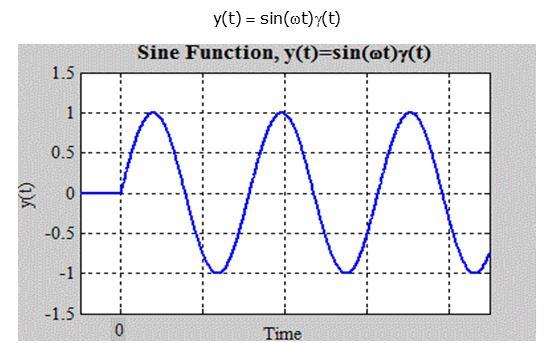
The Sine Function:
y(t) =sin(t)γ(t)
We'll use definition again to determine the Laplace transform:
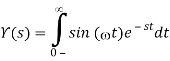
We can take Euler’s identity for sine:
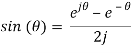 Thus,
Thus,
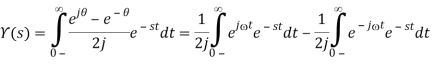 We've already done this integral in the exponential function before.
We've already done this integral in the exponential function before.
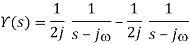
Taking common denominator
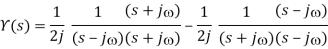
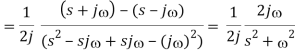
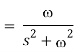
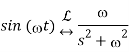
Laplace Transform of Some Other Elementary Functions
Some of the Laplace transformation properties are:
If f1 (t) ⟷ F1 (s) and [note: ⟷ implies Laplace Transform]
f2 (t) ⟷ F2 (s), then
Linearity Property | A f1(t) + B f2(t) ⟷ A F1(s) + B F2(s) |
Frequency Shifting Property | es0t f(t)) ⟷ F(s – s0) |
Integration | t∫0 f(λ) dλ⟷ 1⁄s F(s) |
Multiplication by Time | T f(t) ⟷ (−d F(s)⁄ds) |
Complex Shift Property | f(t) e−at ⟷ F(s + a) |
Time Reversal Property | f (-t) ⟷ F(-s) |
Time Scaling Property | f (t⁄a) ⟷ a F(as) |
Change of Scale Property
If ℒ{f(t)} = F(s), and ℒ{f(at)} = 1/a F(s/a)
Proof of Change of Scale Property
ℒ{f(at)} = 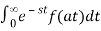
Let
z = at
t = z/a
Dt = dz/a
When t=0,z=0
When t=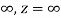
ℒ{f(at)} = 
ℒ{f(at)} = 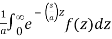
Hence,
ℒ{f(at)} = 1/a F (s/a)
NUMERICALS:
1) Find the Laplace transform of f(t)=cos4t using the change of scale property.
ANSWER:
ℒ{f(at)} = 1/a F(s/a)
ℒ(cos t) = s/ s2 + 1
Thus,
ℒ(cos 4t) = ¼ 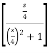
ℒ(cos 4t) = ¼ 
ℒ(cos 4t) = ¼ 
ℒ(cos 4t) = ¼ 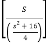
ℒ(cos 4t) = ¼ 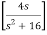
ℒ(cos 4t) = 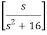
2) Given that
ℒ(sin t/t) = arctan (1/s) , find ℒ(sin 3t/t)
ANSWER:
ℒ{f(at)} = 1/a F (s/a)
ℒ(sin 3t/t) = 3ℒ(sin 3t/3t), thus, a = 3
ℒ(sin 3t/t) = 3[ 1/3 arctan (1/s/3)]
ℒ(sin 3t/t) = arctan (3/s) answer
4.4.1 First Shifting Property
If ℒ{f(t)} = F (s) , when s>a then,
ℒ{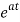 f(t)} = F (s-a)
f(t)} = F (s-a)
In other words, the transform substitution sa for s equates to the original function being multiplied by eat.
Proof of First Shifting Property
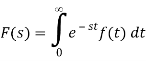
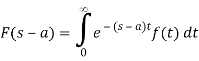

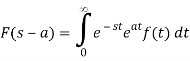
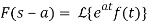
IF
f(t) continuous t≥ 0, f(t) limited such as |f(t)| ≤ Me-kt
f’(t) piecewise continuous for t ≥ 0,
Okay, nothing is completely free. At the very least, we must demand that our function f(t) be continuous anywhere we want to work with it. This isn't to say that it needs to be between; in fact, there aren't many engineering problems that must be handled for an infinite range of time or space; instead, we're usually concerned in addressing difficulties for a very narrow "DEFINITION RANGE."
This would be something like the length of a bridge - who cares if the bridge body oscillates kilometres away where the bridge no longer exists?
Furthermore, we need our function to be constrained by an exponential function (which can be enormous but never infinite).
We also need it (f') to be piecewise continuous because we'll be working with f's derivative. This is sufficient in and of itself.
Okay, and if all of these conditions are met, then....
THEN
ℒ(f’) = s . ℒ(f) – f(0) (s > k) (“k” is the exponent from our limitation)
See what I mean? That's why it's so thrilling!
By Laplace converting the original function f(x), multiplying it with "s," and subtracting the function value of f (the f from the "t"-space! at t=0), we may derive the Laplace transform of the derivative of our function (this is just a number)
In the "s"-space, instead of a derivative, we have a simple product. Isn't it cool?
So, the Laplace transform of f’ is given as ℒ(f’) = s . ℒ(f) – f(0) (s>k)
It should come as no surprise that the transforms for the second, third, and higher derivatives appear to be comparable (after all, it should be useful for something):
ADDITIONALLY: Second Derivative:
ℒ(f’’)= s2 . ℒ(f) – s . f(0) – f’(0)
Third . . .
ℒ(f’’) = s3 . ℒ(f) – s2 . f(0) – s . f’(0) – f’’(0)
Etc.
AND, IN GENERAL:
ℒ(f(π)) = sπ ℒ(f) - sπ-1 . f(0) - sπ – 2 f’(0) - . . . – f(π-1)(0)
(all the time assuming all the derivatives are piecewise continuous….)
Let’s verbalize this: In order to find the Laplace transform of the nth derivative of a function f(t) – this would be f(π) (t) - we have to do the following:
Find the transform for f(t) and multiply it with 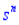
Then, subsequently subtract
- The zero’st derivative of f(t) in the t-space at t=0 (this would be f(0)), multiplied with sπ-1
- The first derivative of f(t) in the t-space at t=0, multiplied with sπ-2
a.s.o., until
The (n-1)th derivative of f(t) in the t-space at t=0, multiplied with 1.
1st Example: f(t) = t2 What is ℒ (t2)???
All right, in this first example we will use this nice characteristics of the derivative of the Laplace transform to find transform for the function f(t) = t2. Why is doing something like this important – there are tables of Laplace transforms all over the place, aren’t they?
The answer is a resounding "maybe." Maybe you're lucky and there are tables available. And maybe you'll get lucky and locate the function you're looking for in those tables. However, you may need to employ strategies like the ones below to find a new Laplace transform......
Anyway, we are trying to find the transform to f(t) = t2 now:
We easily determine the derivative of our function and it’s value at zero:
Solution:
With f(t) = t2
f(0) = 02 = 0 . f’(0) = 2.0 = 0
Then we calculate the second derivative of f, f ":
And f’’(t) = 2 L(2) = 2 . L . (1) =2 1/s = 2/s
It turns out to be equal "2" (or, equal to the constant function y=2).
But we know the transform of "2" already!!!! It is 2/3!
Now use, that ℒ(f’’) = s2 . ℒ(f) – s . f(0) – f’(0)
Let’s add all the information together now:
ℒ(f’’) = ℒ(2) = 2/s = s2 ℒ(f) ℒ(f) = ℒ(t2) = 2/s2
And, after a minimum of algebra, we now know the transform to t2: It is 2/s3.
Let's look for a couple more transformations: for example, the cosine function
2nd Example: Find ℒ{cos( . t)}
Solution:
Again, we first determine the derivatives of f(t) = cos(t)
f(t) = cos(t) f’(t) = - sin(t) and f’’(t) = - 2 cos(t)
And f(0) = 1 . f’(0) = 0
We also need the values of f and f’ at t=0 …..
Now we can use that f’’ = - 2 f ℒ(f’’) = - 2 ℒ(f)
Before we go any further, we'll take use of the fact that the cosine function nearly duplicates itself after two differentiations! This must also work for the cosine's transform, since the Laplace transform is linear!
So, on the one hand, we obtained the transform of the second derivative (left side) by our theorem.
s2 . ℒ(f) – s = - 2 ℒ(f)
And the differentiation (right side) transform of the identical second derivative solutions instantly to:
⇔ ℒ(f) = ℒ(cos (t)) = s/s2 + 24444
⇔ ℒ(f) = ℒ(cos(t)) = s/s2 + 2
As you can see, coming up with these "tricks" sometimes requires some intuition. However, after a while, you will begin to look for "patterns" on your own. Things like a function replicating itself after one or two differentiation steps, for example.
Another one is as follows: locating the transformation for sin2x:
Example 3:
Find ℒ(sin2 t)
Solution:
This time: 1st derivative!
For this function we only require the 1st derivative. Plus we will utilize an identity for trigonometric functions: That sin(2a) = 2 sin(a) cos(a). Because 2 sin(t) cos(t)is exactly what we get if we differentiate sin2 x (chain rule…). Therefore,
f’(t) = 2 sin t cos t = sin 2t
And
f(0) = 0
ℒ{f’(t)} = ℒ{ sin 2t} = 2/s2+4 = s ℒ{sin2t} = s ℒ{f(t)}
And again we are able use our identity of the derivative to our benefit! sin (2t) is easy for us to look up from a table, and the rest is – again – simple algebra….
ℒ(sin2 t) = 2/s(s2 + 4)
And we can go even further, let's try to find ℒ(tsin(t))!
Example 4:
Find ℒ(t sin (t))
Solution: Use the second derivative!
But, let's look at the derivatives of f(t) = t sin(t) first:
f’(t) = sin (t) +at cos (t) (chain and product rule)
f’’(t) = cos(t) + cos(t) - 2 t sin (t) = 2 cos(t) = 2 f(t)
(again, chain and product rule)
And f(0) = 0, f’(0) = 0
Because f(0) = 0 . Sin(0)
f’(t) = sint + t cos(t) (chain and product rule)
f’’(t) = cos (t) + cos (t) - 2 t sin(t) = 2 cos (t) - 2 f(t)
And (again, chain and product rule)
Now look at this: the second derivative of f equals to 2 cos (t) - 2 f(t). And since the transform works linear we get the following expression for ℒ(f’’):
And again, on one side:
ℒ(f’’) = ℒ(2 cos (t) - 2 f(t))
= 2 ℒ ( cos (t)) - 2 ℒ(f)
= 2 s/s2 + 2 - 2 ℒ(f)
On the other side ℒ (f’’) = s2 ℒ (f)
But again we can apply our theorem
Add 1 and 1 together and we obtain:
(s2 + 2) ℒ(f) = 2s/s2 + 2
ℒ(f) = ℒ(t sin(t)) = 2s/(s2 + 2)2
Therefore,
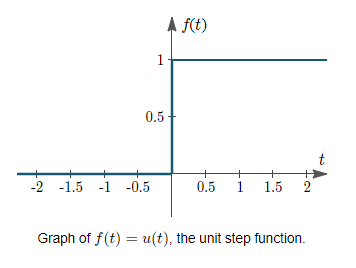
Definition: The unit step function, u(t), is defined as

That is, u is a function of time t, and when time is negative (before we flip the switch), u has value zero, and when time is positive, u has value one (from when we flip the switch).
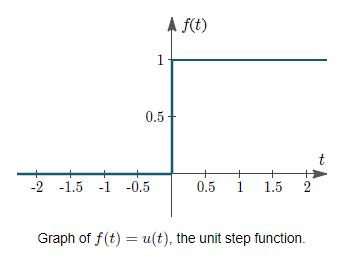
Value at t = 0?
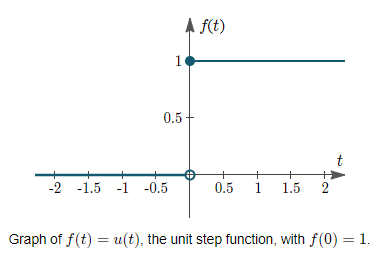
The unit step function is specified as having value 1 at t = 0 in various textbooks, as follows:
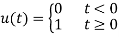
On our graph, we might indicate the discontinuity as follows:
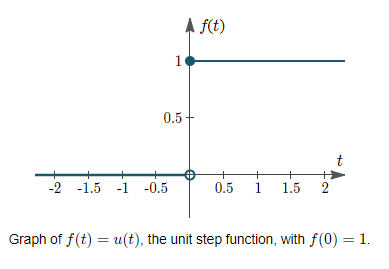
Also, sometimes you'll see the value given as f(0)=0.5.
Example:
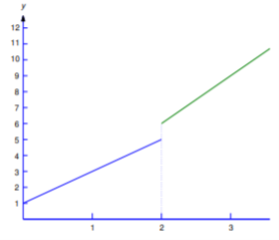
Use the table of Laplace transforms to find the Laplace transform of
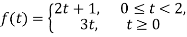 (8.4.1)
(8.4.1)
Solution
Since the formula for f changes at t=2, we write
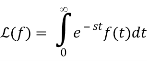
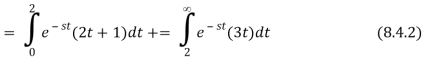
We add and subtract to link the first term to a Laplace transform.
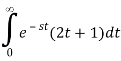
In Equation 8.4.2 to obtain
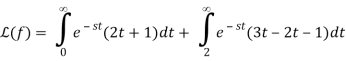
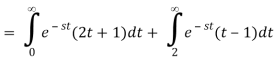
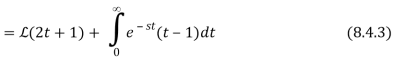
We alter variable x=t2 and rewrite the integral as to relate the final integral to a Laplace transform.
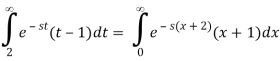
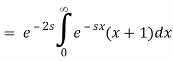
Because the symbol for the integration variable has no effect on the value of a definite integral, we can now substitute t for x and write
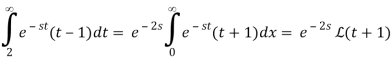
This and Equation 8.4.3 imply that
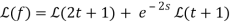
We may now find it using the table of Laplace transforms.

The Dirac Delta function can be defined in a variety of ways. The Dirac Delta function has three primary properties that we must be aware of.
These are the following:
- δ(t – a) = 0, t ≠ a
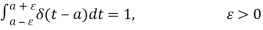

The Dirac Delta function is sometimes assumed to have a "infinite" value when t=a. So, the Dirac Delta function is a function that is zero everywhere except one point, at which point it is either undefined or has a "infinite" value.
It's worth noting that the integrals in the second and third properties are valid for any interval having t=a as long as it's not one of the endpoints. Limits are mentioned here since they are required to prove the properties, and they are also stated in the properties. We shall, however, take advantage of the fact that they are true if we are integrating over a time interval with t=a.
This is a peculiar function. Except for one point, it is zero everywhere, but the integral of any interval encompassing that one point is 1. The Dirac Delta function is not a real function in the sense that we understand it. Instead, it's an example of what's known as a generalised function or distribution.
Despite its oddity, this "function" does an excellent job at simulating unexpected shocks or enormous forces in a system.
We'll need the Dirac Delta function's transform before we can solve an IVP. To get this, we can use the third property mentioned above.
ℒ{δ(t – a)} = 
The second and third qualities are frequently presented with infinity and negative infinity limits, though they are applicable for any interval in which t=a is in the interior.
We can now solve an IVP involving a Dirac Delta function using this.
So, with the exception of the new function, these work in the same way that all of the previous problems have. It's also worth noting that the exponential was introduced into the transform via the Dirac Delta function, but it doesn't matter where it came from once it's there. In other words, when we used inverse transforms, we got a Heaviside function back.
Before moving on to the following part, it's worth noting that the Heaviside function and the Dirac Delta function are related. Begin with the integral below.
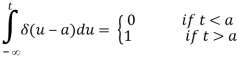
However, this is exactly how the Heaviside function is defined. As a result,

Now, if we recollect the Calculus Fundamental Theorem, we get,
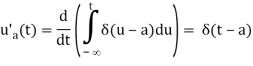
The Dirac Delta function is the derivative of the Heaviside function.
4.8.1 Laplace Transform of Periodic Function
If function f(t) is:
Periodic with period p > 0, so that f(t + p) = f(t), and
f1(t) is one period (i.e. one cycle) of the function, written using Unit Step functions,
Then
ℒ{f(t)} = ℒ{f1 (t)} e-sp
The Laplace Transform of the periodic function f(t) with period p, equals the Laplace Transform of one cycle of the function, divided by (1−e−sp).
Examples
Find the Laplace transforms of the periodic functions shown below:
(a)

From the graph, we see that the first period is given by:
f1(t) = t . [u(t) – u(t – 1)]
And that the period is p=2.
ℒ{f1(t)}
=ℒ{t . [(u(t) – u(t – 1)]}
= ℒ {t . u(t)} - ℒ{ t . u(t – 1)}
Now
t . u(t – 1) = ( t – 1) . u(t – 1) + u(t – 1)
So
ℒ{t . u(t)} - ℒ{t . u(t – 1)}
= ℒ{t . u(t)} - ℒ{(t-1) . u(t-1) + u(t-1)}
= ℒ{t . u(t)} - ℒ{(t – 1) . u(t – 1)} - ℒ{u(t-1)}
= 1/s2 – e-s/s2 – e-s/s
= 1 – e-s – se-s/s2
Hence, the Laplace transform of the periodic function, f(t) is given by:
ℒ{f(t)} = (1 – e-s – se-s/s2) 1/1-e-2s
= 1-e-s – se-s/s2(1 – e-2s)
NUMERICALS:
1) Let f(x) be a function and “k” be a positive real number such that:
f(x+k) + f(x) = 0 for all x ∈ R
Prove that f(x) is periodic. Also determine its period.
Solution:
The given equation can be re-written as:
f(x+k) = - f(x) for all x ∈ R
Here, our objective is to convert RHS of the equation as f(x). For this, we need to substitute "x" such that RHS function acquires RHS function form. Replacing “x” by “x+k”, we have:
f(x+2k) = -f(x+k) for all x∈R
Combining two equations,
f(x+2k) = - 1X – f(x) = f(x) for all x∈R
It means that f(x) is a periodic function and its period is “2k”
2) What is the period of function:
f(x) = 3+2 sin {(πx+2)/3}
Solution:
Rearranging, we have:
f(x) = 3+2 sin (π/3 x + 2/3)
The period of sine function is “2π”. Comparing with function form "af(bx+c)+d, magnitude of b i.e. |b| is π/3. Hence, period of the given function is:
T’ = T/ |b| = 2π/ π/3 = 6
If we have a table of transforms in front of us, like we did in the last section, finding the Laplace transform of a function is not difficult. Now we'd like to turn around and go the other way.
We'll be given a transform, F(s), and we'll have to figure out what function (or functions) we had before. As you can see, this is a more difficult and time-consuming operation than taking transforms. We indicate we're looking for the Inverse Laplace Transform of F(s) in these circumstances and use the notation below.
f(t) = ℒ-1 {F(s)}
We have the same fact to help us with the inverse transform as we have with Laplace transforms.
So we reverse the individual transforms, add or subtract the results back up, and then reverse the inverse transforms.
Let's look at a handful of straightforward inverse transforms.
So, looking at the denominator is definitely the best way to get the transform. If there are multiple options, utilise the numerator to choose the best one. If necessary, adjust the numerator to get it into the shape required for the inverse transform. Finally, reverse the transform.
Let's try some slightly more difficult issues. These are a little more difficult than the previous ones.
To get the inverse transform, the latter section of this example required partial fractions. When we return to differential equations and begin solving them with Laplace transforms, you will immediately see that partial fractions are a way of life in these situations. To some extent, almost every situation will necessitate partial fractions.
It's worth noting that the final element of this example might have been completed in the same way as the first two. We would have received hyperbolic functions if we had. We could have written the result in the form we got from the way we worked our problem if we remembered the definition of hyperbolic functions. Most students, on the other hand, have a better understanding of exponentials than hyperbolic functions, thus it's usually easier to just use partial fractions and express the result in terms of exponentials. It may take a little longer, but the result will be a more appealing (and simpler to work with) version of the response.
Be aware that in my class, if the denominator can be factored using integer coefficients, it must be factored.
So, let me remind you how to decompose partial fractions correctly. The first step is to factor as much as feasible in the denominator. Then we'll utilise the following table to find a term or terms for each term in the denominator for our partial fraction decomposition.

It's worth noting that the first and third cases are, respectively, special instances of the second and fourth situations.
So, let's go through a couple more examples to refresh your memory on how to work with partial fractions.
4.10.1 Differential Equations
The Laplace Transform can make solving problems with differential equations much easier.
Solving a first order differential equation
Consider the differential equation given by:
y(t) + 2y(t) = f(t)
y(0-) = - 2
f(t) = γ(t) – γ(t-1) (i.e., a 1 second pulse, 1 unit high)
Find y(t).
Aside: Origin of the First Order Differential Equation
The differential equation with input f(t) and output y(t)
y(t) + 2y(t) = f(t)
Can represent many different systems. Two examples are given below, one for a mechanical system and one for an electrical system.
Mechanical System
Input = force = φ(t). Output = velocity of mass. b=2, m=1.
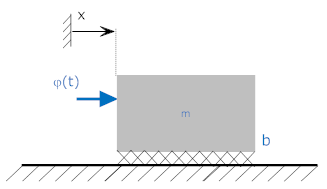
Free Body Diagram
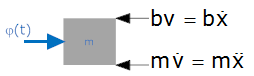
Mv + bv = (t)
v+2v = (t)
You can see that this is equivalent to the original equation (with output v(t) and input φ(t)).
Electrical System
Input = current = ia(t). Output = voltage across elements. R=½, C=1.

ic(t) + iR(t) = ia(t)
Ce0 + 1/R e0 = ia(t)
e0 + 2e0 = ia(t)
This is equivalent to the original equation (with output eo(t) and input ia(t)).
Solution:
There are four steps to the solution:
Take the differential equation's Laplace Transform. As needed, we employ the derivative property (and in this case we also need the time delay property)
y(t) 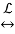 sY(s) – y(0-)
sY(s) – y(0-)
y(t)  Y(s)
Y(s)
f(t) 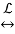 F(s) = 1/s – e-s 1/s
F(s) = 1/s – e-s 1/s
SY(s) - y(0-) + 2Y(s) = F(s) = 1/s – e-s1/s
So
y(t) + 2y(t) = γ(t) – γ(t-1)  sY(s) - y(0-) + 2Y(s) = 1/s – e-s 1/s
sY(s) - y(0-) + 2Y(s) = 1/s – e-s 1/s
Put initial conditions into the resulting equation
SY(s) - y(0-) + 2Y(s) = 1/s – e-s 1/s
Solve for Y(s)
Y(s) = 1/s(s+2) – e-s 1/s(s+2) – 2 1/(s+2)
Get result from the Laplace Transform tables. (look up the terms individually)
1/s(s+2)  ½ (1 – e-2t)
½ (1 – e-2t)
1/s(s+2)e-s 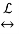 ½ (1 – e-2(t-1))γ(t-1)
½ (1 – e-2(t-1))γ(t-1)
1/(s+2)  e-2t
e-2t
y(t) = ½ (1 – e-2t) – ½ (1 – e-2(t-1))γ(t-1) - 2 e-2t
In this scenario, all terms are in the table, and the time delay attribute must be used. If the terms aren't in the table, we'll need to use the Inverse Laplace Transform procedures. For t0, note that the function is automatically zero. By multiplying by the unit step, we may make this explicit:
y(t) = ½ (1 – e-2t) γ(t) - ½ (1 – e-2(t-1))γ(t-1) - 2 e-2t γ(t)
Find the equation of motion of an object exhibiting simple harmonic motion with a resistive force. In physics, the equation of an object undergoing simple harmonic motion with no resistance is given by m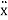 + m2x = 0 where is the angular frequency of oscillation, and the number of dots specifies the number of derivatives (Newton's notation for derivatives). Of course, in real life, there will always be some form of resistance. In this example, the resistive force is assumed to be proportional to velocity F = - m β
+ m2x = 0 where is the angular frequency of oscillation, and the number of dots specifies the number of derivatives (Newton's notation for derivatives). Of course, in real life, there will always be some form of resistance. In this example, the resistive force is assumed to be proportional to velocity F = - m β 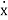 , where β is a constant. Our initial conditions are a displacement of 1 from equilibrium at rest. By using Newton's second law, we can write the differential equation in the following manner. Notice that the presence of mass 𝑚 in each of the terms means that our solution must eventually be independent of 𝑚.
, where β is a constant. Our initial conditions are a displacement of 1 from equilibrium at rest. By using Newton's second law, we can write the differential equation in the following manner. Notice that the presence of mass 𝑚 in each of the terms means that our solution must eventually be independent of 𝑚.
- m
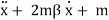 2x = 0, x(0) = 1,
2x = 0, x(0) = 1, 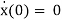
 2x = 0
2x = 0
Take the Laplace transform of both sides, and solve for 𝑿(s).
- s2X – s + 2βsX - 2β + 2X = 0
- X(s) = (s+2β)/s2 + 2βs + 2
Rewrite the denominator by completing the square
The goal is to get a solution that will allow us to look at a table of Laplace transforms and study the function in physical space. Of course, to compensate for the extra 2 term, we must deduct it from the total so that we are "adding 0."
X = s + 2β/ (s+ β)2 + 2 – β2
Write out the solution in physical space. From the numerator, it is obvious that this is going to be a sum of a cosine and sine term. From the (s+β)2 in the denominator, it is obvious that both of these terms will be multiplied by an exponential term (in fact, an exponential decay term e-βt. In order to see the two contributions more clearly, we can rewrite the numerator as (s+β)+β
x(t) = e-βt cos ( √2 – β2t) + β/ √2 – β2t e-βt sin ( √2 – β2t)
This example has demonstrated that the Laplace transform method can be used to solve homogeneous differential equations with initial conditions without requiring the use of derivatives to solve the resulting system of equations. However, it's a good idea to double-check your solution by using the conventional ansatz method to solve the differential equation.
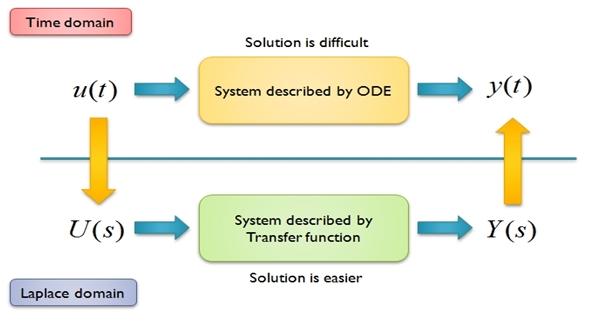
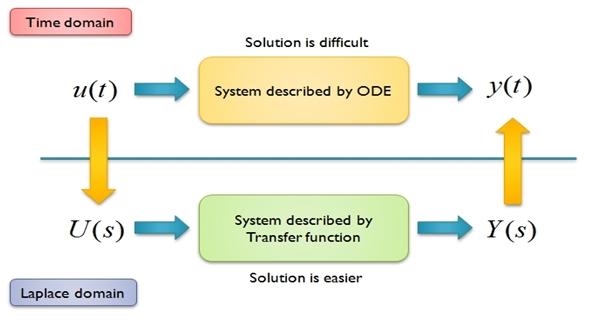
The Laplace Transform is a powerful tool that is very useful in Electrical Engineering. The transform allows equations in the "time domain" to be transformed into an equivalent equation in the Complex S Domain. The laplace transform is an integral transform, although the reader does not need to have a knowledge of integral calculus because all results will be provided. This page will discuss the Laplace transform as being simply a tool for solving and manipulating ordinary differential equations.
Laplace transformations of circuit elements are similar to phasor representations, but they are not the same. Laplace transformations are more general than phasors, and can be easier to use in some instances. Also, do not confuse the term "Complex S Domain" with the complex power ideas that we have been talking about earlier. Complex power uses the variable , while the Laplace transform uses the variable s. The Laplace variable s has nothing to do with power.
The transform is named after the mathematician Pierre Simon Laplace (1749-1827). The transform itself did not become popular until Oliver Heaviside, a famous electrical engineer, began using a variation of it to solve electrical circuits.
Laplace Domain
The Laplace domain, also known as the "Complex s Domain," is the domain into which a time-domain equation is transformed via the Laplace transform. s is a complex variable with real and imaginary components:
s = σ + j
The Laplace domain graphs the real part (σ) as the horizontal axis, and the imaginary part (ω) as the vertical axis. The real and imaginary parts of s can be considered as independent quantities.
The similarity of this notation with the notation used in Fourier transform theory is no coincidence; for σ=0, the Laplace transform is the same as the Fourier transform if the signal is causal.
Key takeaway:
- For an LTI system, a Laplace transform is a generalisation of a Fourier transform to complex eigenvalues. In LTI systems or systems with harmonic time-dependence in particular parameters, Laplace transforms make stability analysis simple.
- A differential equation is transformed into an algebraic equation using the Laplace transform.
- A function's Laplace transform is defined as:
F(s) = ℒ(f(t)) = 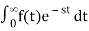
- The Laplace transform is invertible, meaning that ℒ(f(t)) = F(s) implies ℒ -1(F(s)) = f(t). This is how we invert the Laplace transform, since the inverse Laplace transform formula is very difficult to work with and not well-defined in many cases.
- We always look up the Laplace transform of a function from a transform table when solving ODEs. Tables are also used to find inverse transformations.
- We take the transform of both sides according to our Laplace transform theorems, algebraically rearrange to solve for F(s), and take the inverse transform to discover f to solve a linear ODE using Laplace transform (t)
References:
1. Mathematical Physics and Special Relativity–M.Das, P.K. Jena and B.K. Dash (Srikrishna Prakashan)-2009
2. Mathematical Physics–H. K. Das, Dr. Rama Verma (S. Chand Publishing) 2011
3. Complex Variable: Schaum’s Outlines Series M. Spiegel (2nd Edition, Mc- Graw Hill Education)-2004
4. Complex variables and applications J.W.Brown and R.V.Churchill 7th Edition 2003
5. Mathematical Physics, Satya Prakash (Sultan Chand)-2014
Unit – 4
Laplace Transforms
4.1.1 Introduction
The Laplace integral and how it is used to solve differential equations were reviewed in the previous two parts of the course. Let's review the Laplace integral over f(t):
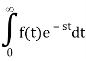
Then we talked about the Laplace transform's Region of Convergence (ROC). The output convergence or divergence is solely determined by the values of s. As a result, the range of s values that converge the output signal is known as the ROC area.
The Laplace Transform, as previously stated, translates integral and differential equations into simple algebraic equations. Let's look at the Laplace integral for a simple function and analyse the results.
4.1.2 Definition
If a function repeats the same values after a certain interval or period, it is said to be periodic. Periodicity can be seen in a variety of phenomena such as oscillations and waves. If f(t+T)=f, a function is periodic mathematically (t)
T can be any constant as long as it is greater than zero. The condition given above must hold for any value of t. The period is abbreviated as T.
If a function's graph has translational symmetry, it is called periodic geometrically. Trigonometric functions such as sine and cosine are the most known examples of periodic functions. They have a two-radian period. The triangle wave is another outstanding example of periodic functions. It is defined as follows:
f(t+2)=f f(t+2)=f f(t+2)= (t)
With the help of a hypothesis that we will address later in this article, we can demonstrate Laplace transform of practically all periodic functions for any value of t. Aperiodic refers to a function that does not repeat its values over a set period of time.
4.1.3 Proposition
We propose a method for computing the Laplace transform of periodic functions. It states that if f is a periodic function with period T and f 1 is one period of the function, the Laplace transform of the function may be written as:

4.1.4 Laplace Transform of Some Important Elementary Functions
To use the Laplace transform on a periodic function, we must first change the domain from time to Laplace. To find the Laplace transform, we must first evaluate the integral. Let's have a look at the Laplace transform of several important elementary functions.
The Unit Step Function:
We know how to write the unit step function:
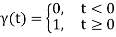
It's depicted graphically as:
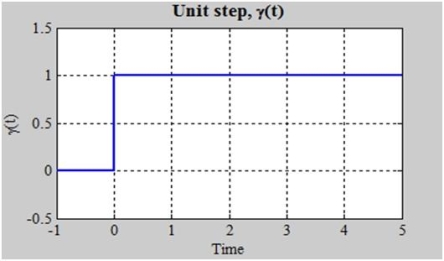
The definition of step is sometimes altered so that the bottom inequality becomes a strict inequality (t>0), leaving (0) undefined. There is also a discontinuity at t=0, but we have drawn a vertical line to make it easier to grasp and to demonstrate that the blue line represents a single function.
We'll now use the definition to obtain the Laplace transform.
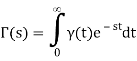
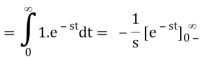
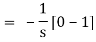
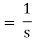 Thus,
Thus,
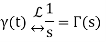
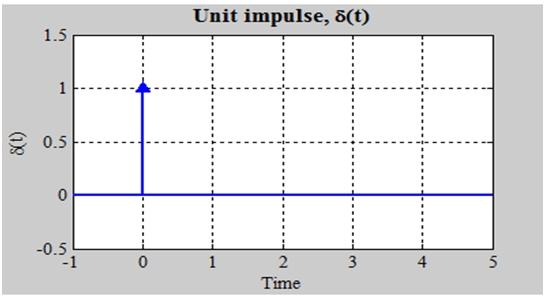
The Unit Impulse Function:
To give you a quick overview of the impulse function, it exists everywhere except at t=0, when it is infinitely huge. One is the impulse function area. On a graph, it can be represented by an arrow with a height equal to its area.
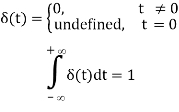
Now we'll use the following formula to find the Laplace transform:
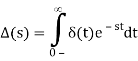
We'll apply the impulse property, which states that the impulse is 0 everywhere except at t=0, when the upper limit of the integral is 0+.
 We can argue that e-st is constant from t=0– to t=0+ because it is continuous at t=0. We can now place the value of e-st at t=0.
We can argue that e-st is constant from t=0– to t=0+ because it is continuous at t=0. We can now place the value of e-st at t=0.
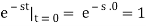
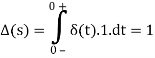
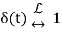 By this derivation, we get to know that Laplace transform is just one of unit impulse. This shows that the impulse is very easy to deal with in Laplace domain unlike in time domain. Unit impulse will be significant in what we do.
By this derivation, we get to know that Laplace transform is just one of unit impulse. This shows that the impulse is very easy to deal with in Laplace domain unlike in time domain. Unit impulse will be significant in what we do.
The Exponential Function:
For t>0, we are considering exponential.
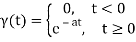
Or
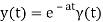
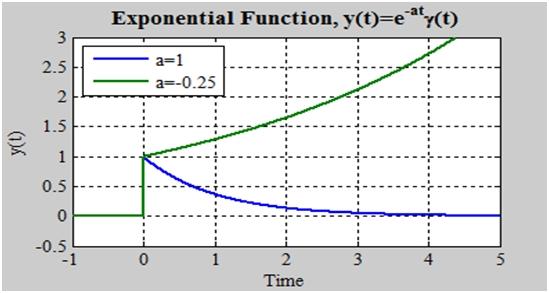
If the function is 0 for t>0, it is considered exponential. We can express the function in pieces, as in the first form, or as exponential multiplied by b unit step, as in the second definition. We normally choose the second ne since it is more efficient. Because all functions for t>0 are zero, multiplication with (t) will not show exact (t) and will be implicit on a frequent basis.
If a0 is zero, the function will fall to zero, but if a>0, the function will freely rise. We mostly look at falling to zero exponentials, and they're common in systems.
We'll use the following formula to find the Laplace transform:
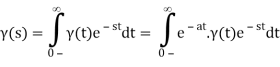 We can remove it from the integral since we know that for all positive t (t) is one.
We can remove it from the integral since we know that for all positive t (t) is one.
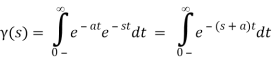
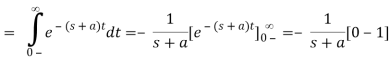
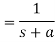
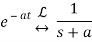
In the last equation, you can see that (t) is implicit. We get a step function if a=1 and L(s) =1/s.
The Sine Function:
y(t) =sin(t)γ(t)

We'll use definition again to determine the Laplace transform:
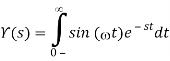
We can take Euler’s identity for sine:
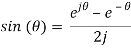 Thus,
Thus,
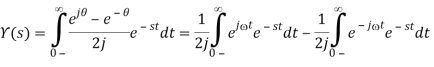 We've already done this integral in the exponential function before.
We've already done this integral in the exponential function before.
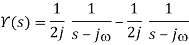
Taking common denominator
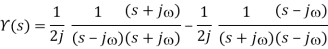
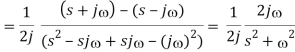
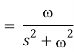
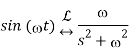
Laplace Transform of Some Other Elementary Functions
Some of the Laplace transformation properties are:
If f1 (t) ⟷ F1 (s) and [note: ⟷ implies Laplace Transform]
f2 (t) ⟷ F2 (s), then
Linearity Property | A f1(t) + B f2(t) ⟷ A F1(s) + B F2(s) |
Frequency Shifting Property | es0t f(t)) ⟷ F(s – s0) |
Integration | t∫0 f(λ) dλ⟷ 1⁄s F(s) |
Multiplication by Time | T f(t) ⟷ (−d F(s)⁄ds) |
Complex Shift Property | f(t) e−at ⟷ F(s + a) |
Time Reversal Property | f (-t) ⟷ F(-s) |
Time Scaling Property | f (t⁄a) ⟷ a F(as) |
Change of Scale Property
If ℒ{f(t)} = F(s), and ℒ{f(at)} = 1/a F(s/a)
Proof of Change of Scale Property
ℒ{f(at)} = 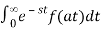
Let
z = at
t = z/a
Dt = dz/a
When t=0,z=0
When t=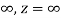
ℒ{f(at)} = 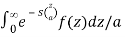
ℒ{f(at)} = 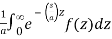
Hence,
ℒ{f(at)} = 1/a F (s/a)
NUMERICALS:
1) Find the Laplace transform of f(t)=cos4t using the change of scale property.
ANSWER:
ℒ{f(at)} = 1/a F(s/a)
ℒ(cos t) = s/ s2 + 1
Thus,
ℒ(cos 4t) = ¼ 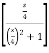
ℒ(cos 4t) = ¼ 
ℒ(cos 4t) = ¼ 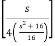
ℒ(cos 4t) = ¼ 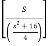
ℒ(cos 4t) = ¼ 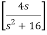
ℒ(cos 4t) = 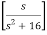
2) Given that
ℒ(sin t/t) = arctan (1/s) , find ℒ(sin 3t/t)
ANSWER:
ℒ{f(at)} = 1/a F (s/a)
ℒ(sin 3t/t) = 3ℒ(sin 3t/3t), thus, a = 3
ℒ(sin 3t/t) = 3[ 1/3 arctan (1/s/3)]
ℒ(sin 3t/t) = arctan (3/s) answer
4.4.1 First Shifting Property
If ℒ{f(t)} = F (s) , when s>a then,
ℒ{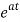 f(t)} = F (s-a)
f(t)} = F (s-a)
In other words, the transform substitution sa for s equates to the original function being multiplied by eat.
Proof of First Shifting Property
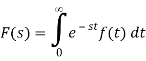
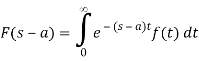
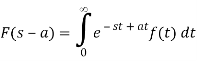
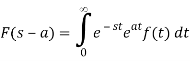
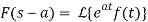
IF
f(t) continuous t≥ 0, f(t) limited such as |f(t)| ≤ Me-kt
f’(t) piecewise continuous for t ≥ 0,
Okay, nothing is completely free. At the very least, we must demand that our function f(t) be continuous anywhere we want to work with it. This isn't to say that it needs to be between; in fact, there aren't many engineering problems that must be handled for an infinite range of time or space; instead, we're usually concerned in addressing difficulties for a very narrow "DEFINITION RANGE."
This would be something like the length of a bridge - who cares if the bridge body oscillates kilometres away where the bridge no longer exists?
Furthermore, we need our function to be constrained by an exponential function (which can be enormous but never infinite).
We also need it (f') to be piecewise continuous because we'll be working with f's derivative. This is sufficient in and of itself.
Okay, and if all of these conditions are met, then....
THEN
ℒ(f’) = s . ℒ(f) – f(0) (s > k) (“k” is the exponent from our limitation)
See what I mean? That's why it's so thrilling!
By Laplace converting the original function f(x), multiplying it with "s," and subtracting the function value of f (the f from the "t"-space! at t=0), we may derive the Laplace transform of the derivative of our function (this is just a number)
In the "s"-space, instead of a derivative, we have a simple product. Isn't it cool?
So, the Laplace transform of f’ is given as ℒ(f’) = s . ℒ(f) – f(0) (s>k)
It should come as no surprise that the transforms for the second, third, and higher derivatives appear to be comparable (after all, it should be useful for something):
ADDITIONALLY: Second Derivative:
ℒ(f’’)= s2 . ℒ(f) – s . f(0) – f’(0)
Third . . .
ℒ(f’’) = s3 . ℒ(f) – s2 . f(0) – s . f’(0) – f’’(0)
Etc.
AND, IN GENERAL:
ℒ(f(π)) = sπ ℒ(f) - sπ-1 . f(0) - sπ – 2 f’(0) - . . . – f(π-1)(0)
(all the time assuming all the derivatives are piecewise continuous….)
Let’s verbalize this: In order to find the Laplace transform of the nth derivative of a function f(t) – this would be f(π) (t) - we have to do the following:
Find the transform for f(t) and multiply it with 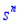
Then, subsequently subtract
- The zero’st derivative of f(t) in the t-space at t=0 (this would be f(0)), multiplied with sπ-1
- The first derivative of f(t) in the t-space at t=0, multiplied with sπ-2
a.s.o., until
The (n-1)th derivative of f(t) in the t-space at t=0, multiplied with 1.
1st Example: f(t) = t2 What is ℒ (t2)???
All right, in this first example we will use this nice characteristics of the derivative of the Laplace transform to find transform for the function f(t) = t2. Why is doing something like this important – there are tables of Laplace transforms all over the place, aren’t they?
The answer is a resounding "maybe." Maybe you're lucky and there are tables available. And maybe you'll get lucky and locate the function you're looking for in those tables. However, you may need to employ strategies like the ones below to find a new Laplace transform......
Anyway, we are trying to find the transform to f(t) = t2 now:
We easily determine the derivative of our function and it’s value at zero:
Solution:
With f(t) = t2
f(0) = 02 = 0 . f’(0) = 2.0 = 0
Then we calculate the second derivative of f, f ":
And f’’(t) = 2 L(2) = 2 . L . (1) =2 1/s = 2/s
It turns out to be equal "2" (or, equal to the constant function y=2).
But we know the transform of "2" already!!!! It is 2/3!
Now use, that ℒ(f’’) = s2 . ℒ(f) – s . f(0) – f’(0)
Let’s add all the information together now:
ℒ(f’’) = ℒ(2) = 2/s = s2 ℒ(f) ℒ(f) = ℒ(t2) = 2/s2
And, after a minimum of algebra, we now know the transform to t2: It is 2/s3.
Let's look for a couple more transformations: for example, the cosine function
2nd Example: Find ℒ{cos( . t)}
Solution:
Again, we first determine the derivatives of f(t) = cos(t)
f(t) = cos(t) f’(t) = - sin(t) and f’’(t) = - 2 cos(t)
And f(0) = 1 . f’(0) = 0
We also need the values of f and f’ at t=0 …..
Now we can use that f’’ = - 2 f ℒ(f’’) = - 2 ℒ(f)
Before we go any further, we'll take use of the fact that the cosine function nearly duplicates itself after two differentiations! This must also work for the cosine's transform, since the Laplace transform is linear!
So, on the one hand, we obtained the transform of the second derivative (left side) by our theorem.
s2 . ℒ(f) – s = - 2 ℒ(f)
And the differentiation (right side) transform of the identical second derivative solutions instantly to:
⇔ ℒ(f) = ℒ(cos (t)) = s/s2 + 24444
⇔ ℒ(f) = ℒ(cos(t)) = s/s2 + 2
As you can see, coming up with these "tricks" sometimes requires some intuition. However, after a while, you will begin to look for "patterns" on your own. Things like a function replicating itself after one or two differentiation steps, for example.
Another one is as follows: locating the transformation for sin2x:
Example 3:
Find ℒ(sin2 t)
Solution:
This time: 1st derivative!
For this function we only require the 1st derivative. Plus we will utilize an identity for trigonometric functions: That sin(2a) = 2 sin(a) cos(a). Because 2 sin(t) cos(t)is exactly what we get if we differentiate sin2 x (chain rule…). Therefore,
f’(t) = 2 sin t cos t = sin 2t
And
f(0) = 0
ℒ{f’(t)} = ℒ{ sin 2t} = 2/s2+4 = s ℒ{sin2t} = s ℒ{f(t)}
And again we are able use our identity of the derivative to our benefit! sin (2t) is easy for us to look up from a table, and the rest is – again – simple algebra….
ℒ(sin2 t) = 2/s(s2 + 4)
And we can go even further, let's try to find ℒ(tsin(t))!
Example 4:
Find ℒ(t sin (t))
Solution: Use the second derivative!
But, let's look at the derivatives of f(t) = t sin(t) first:
f’(t) = sin (t) +at cos (t) (chain and product rule)
f’’(t) = cos(t) + cos(t) - 2 t sin (t) = 2 cos(t) = 2 f(t)
(again, chain and product rule)
And f(0) = 0, f’(0) = 0
Because f(0) = 0 . Sin(0)
f’(t) = sint + t cos(t) (chain and product rule)
f’’(t) = cos (t) + cos (t) - 2 t sin(t) = 2 cos (t) - 2 f(t)
And (again, chain and product rule)
Now look at this: the second derivative of f equals to 2 cos (t) - 2 f(t). And since the transform works linear we get the following expression for ℒ(f’’):
And again, on one side:
ℒ(f’’) = ℒ(2 cos (t) - 2 f(t))
= 2 ℒ ( cos (t)) - 2 ℒ(f)
= 2 s/s2 + 2 - 2 ℒ(f)
On the other side ℒ (f’’) = s2 ℒ (f)
But again we can apply our theorem
Add 1 and 1 together and we obtain:
(s2 + 2) ℒ(f) = 2s/s2 + 2
ℒ(f) = ℒ(t sin(t)) = 2s/(s2 + 2)2
Therefore,
Definition: The unit step function, u(t), is defined as

That is, u is a function of time t, and when time is negative (before we flip the switch), u has value zero, and when time is positive, u has value one (from when we flip the switch).
Value at t = 0?
The unit step function is specified as having value 1 at t = 0 in various textbooks, as follows:
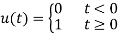
On our graph, we might indicate the discontinuity as follows:
Also, sometimes you'll see the value given as f(0)=0.5.
Example:
Use the table of Laplace transforms to find the Laplace transform of
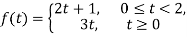 (8.4.1)
(8.4.1)
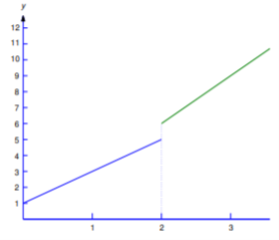
Solution
Since the formula for f changes at t=2, we write
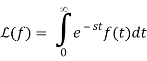
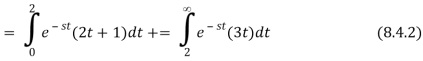
We add and subtract to link the first term to a Laplace transform.
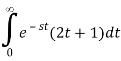
In Equation 8.4.2 to obtain
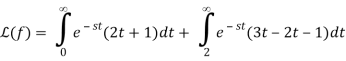
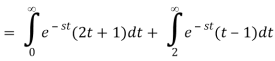
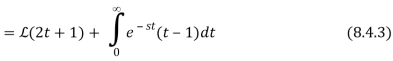
We alter variable x=t2 and rewrite the integral as to relate the final integral to a Laplace transform.
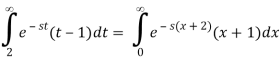
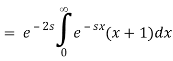
Because the symbol for the integration variable has no effect on the value of a definite integral, we can now substitute t for x and write
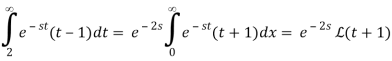
This and Equation 8.4.3 imply that

We may now find it using the table of Laplace transforms.
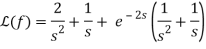
The Dirac Delta function can be defined in a variety of ways. The Dirac Delta function has three primary properties that we must be aware of.
These are the following:
- δ(t – a) = 0, t ≠ a
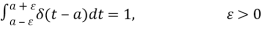
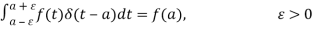
The Dirac Delta function is sometimes assumed to have a "infinite" value when t=a. So, the Dirac Delta function is a function that is zero everywhere except one point, at which point it is either undefined or has a "infinite" value.
It's worth noting that the integrals in the second and third properties are valid for any interval having t=a as long as it's not one of the endpoints. Limits are mentioned here since they are required to prove the properties, and they are also stated in the properties. We shall, however, take advantage of the fact that they are true if we are integrating over a time interval with t=a.
This is a peculiar function. Except for one point, it is zero everywhere, but the integral of any interval encompassing that one point is 1. The Dirac Delta function is not a real function in the sense that we understand it. Instead, it's an example of what's known as a generalised function or distribution.
Despite its oddity, this "function" does an excellent job at simulating unexpected shocks or enormous forces in a system.
We'll need the Dirac Delta function's transform before we can solve an IVP. To get this, we can use the third property mentioned above.
ℒ{δ(t – a)} = 
The second and third qualities are frequently presented with infinity and negative infinity limits, though they are applicable for any interval in which t=a is in the interior.
We can now solve an IVP involving a Dirac Delta function using this.
So, with the exception of the new function, these work in the same way that all of the previous problems have. It's also worth noting that the exponential was introduced into the transform via the Dirac Delta function, but it doesn't matter where it came from once it's there. In other words, when we used inverse transforms, we got a Heaviside function back.
Before moving on to the following part, it's worth noting that the Heaviside function and the Dirac Delta function are related. Begin with the integral below.

However, this is exactly how the Heaviside function is defined. As a result,
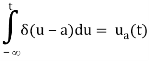
Now, if we recollect the Calculus Fundamental Theorem, we get,
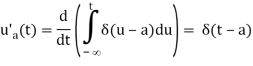
The Dirac Delta function is the derivative of the Heaviside function.
4.8.1 Laplace Transform of Periodic Function
If function f(t) is:
Periodic with period p > 0, so that f(t + p) = f(t), and
f1(t) is one period (i.e. one cycle) of the function, written using Unit Step functions,
Then
ℒ{f(t)} = ℒ{f1 (t)} e-sp
The Laplace Transform of the periodic function f(t) with period p, equals the Laplace Transform of one cycle of the function, divided by (1−e−sp).
Examples
Find the Laplace transforms of the periodic functions shown below:
(a)
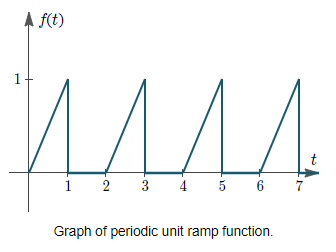
From the graph, we see that the first period is given by:
f1(t) = t . [u(t) – u(t – 1)]
And that the period is p=2.
ℒ{f1(t)}
=ℒ{t . [(u(t) – u(t – 1)]}
= ℒ {t . u(t)} - ℒ{ t . u(t – 1)}
Now
t . u(t – 1) = ( t – 1) . u(t – 1) + u(t – 1)
So
ℒ{t . u(t)} - ℒ{t . u(t – 1)}
= ℒ{t . u(t)} - ℒ{(t-1) . u(t-1) + u(t-1)}
= ℒ{t . u(t)} - ℒ{(t – 1) . u(t – 1)} - ℒ{u(t-1)}
= 1/s2 – e-s/s2 – e-s/s
= 1 – e-s – se-s/s2
Hence, the Laplace transform of the periodic function, f(t) is given by:
ℒ{f(t)} = (1 – e-s – se-s/s2) 1/1-e-2s
= 1-e-s – se-s/s2(1 – e-2s)
NUMERICALS:
1) Let f(x) be a function and “k” be a positive real number such that:
f(x+k) + f(x) = 0 for all x ∈ R
Prove that f(x) is periodic. Also determine its period.
Solution:
The given equation can be re-written as:
f(x+k) = - f(x) for all x ∈ R
Here, our objective is to convert RHS of the equation as f(x). For this, we need to substitute "x" such that RHS function acquires RHS function form. Replacing “x” by “x+k”, we have:
f(x+2k) = -f(x+k) for all x∈R
Combining two equations,
f(x+2k) = - 1X – f(x) = f(x) for all x∈R
It means that f(x) is a periodic function and its period is “2k”
2) What is the period of function:
f(x) = 3+2 sin {(πx+2)/3}
Solution:
Rearranging, we have:
f(x) = 3+2 sin (π/3 x + 2/3)
The period of sine function is “2π”. Comparing with function form "af(bx+c)+d, magnitude of b i.e. |b| is π/3. Hence, period of the given function is:
T’ = T/ |b| = 2π/ π/3 = 6
If we have a table of transforms in front of us, like we did in the last section, finding the Laplace transform of a function is not difficult. Now we'd like to turn around and go the other way.
We'll be given a transform, F(s), and we'll have to figure out what function (or functions) we had before. As you can see, this is a more difficult and time-consuming operation than taking transforms. We indicate we're looking for the Inverse Laplace Transform of F(s) in these circumstances and use the notation below.
f(t) = ℒ-1 {F(s)}
We have the same fact to help us with the inverse transform as we have with Laplace transforms.
So we reverse the individual transforms, add or subtract the results back up, and then reverse the inverse transforms.
Let's look at a handful of straightforward inverse transforms.
So, looking at the denominator is definitely the best way to get the transform. If there are multiple options, utilise the numerator to choose the best one. If necessary, adjust the numerator to get it into the shape required for the inverse transform. Finally, reverse the transform.
Let's try some slightly more difficult issues. These are a little more difficult than the previous ones.
To get the inverse transform, the latter section of this example required partial fractions. When we return to differential equations and begin solving them with Laplace transforms, you will immediately see that partial fractions are a way of life in these situations. To some extent, almost every situation will necessitate partial fractions.
It's worth noting that the final element of this example might have been completed in the same way as the first two. We would have received hyperbolic functions if we had. We could have written the result in the form we got from the way we worked our problem if we remembered the definition of hyperbolic functions. Most students, on the other hand, have a better understanding of exponentials than hyperbolic functions, thus it's usually easier to just use partial fractions and express the result in terms of exponentials. It may take a little longer, but the result will be a more appealing (and simpler to work with) version of the response.
Be aware that in my class, if the denominator can be factored using integer coefficients, it must be factored.
So, let me remind you how to decompose partial fractions correctly. The first step is to factor as much as feasible in the denominator. Then we'll utilise the following table to find a term or terms for each term in the denominator for our partial fraction decomposition.

It's worth noting that the first and third cases are, respectively, special instances of the second and fourth situations.
So, let's go through a couple more examples to refresh your memory on how to work with partial fractions.
4.10.1 Differential Equations
The Laplace Transform can make solving problems with differential equations much easier.
Solving a first order differential equation
Consider the differential equation given by:
y(t) + 2y(t) = f(t)
y(0-) = - 2
f(t) = γ(t) – γ(t-1) (i.e., a 1 second pulse, 1 unit high)
Find y(t).
Aside: Origin of the First Order Differential Equation
The differential equation with input f(t) and output y(t)
y(t) + 2y(t) = f(t)
Can represent many different systems. Two examples are given below, one for a mechanical system and one for an electrical system.
Mechanical System
Input = force = φ(t). Output = velocity of mass. b=2, m=1.
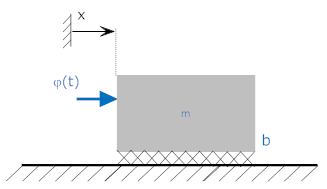
Free Body Diagram
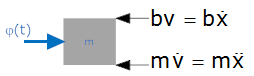
Mv + bv = (t)
v+2v = (t)
You can see that this is equivalent to the original equation (with output v(t) and input φ(t)).
Electrical System
Input = current = ia(t). Output = voltage across elements. R=½, C=1.

ic(t) + iR(t) = ia(t)
Ce0 + 1/R e0 = ia(t)
e0 + 2e0 = ia(t)
This is equivalent to the original equation (with output eo(t) and input ia(t)).
Solution:
There are four steps to the solution:
Take the differential equation's Laplace Transform. As needed, we employ the derivative property (and in this case we also need the time delay property)
y(t)  sY(s) – y(0-)
sY(s) – y(0-)
y(t) 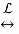 Y(s)
Y(s)
f(t) 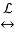 F(s) = 1/s – e-s 1/s
F(s) = 1/s – e-s 1/s
SY(s) - y(0-) + 2Y(s) = F(s) = 1/s – e-s1/s
So
y(t) + 2y(t) = γ(t) – γ(t-1) 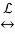 sY(s) - y(0-) + 2Y(s) = 1/s – e-s 1/s
sY(s) - y(0-) + 2Y(s) = 1/s – e-s 1/s
Put initial conditions into the resulting equation
SY(s) - y(0-) + 2Y(s) = 1/s – e-s 1/s
Solve for Y(s)
Y(s) = 1/s(s+2) – e-s 1/s(s+2) – 2 1/(s+2)
Get result from the Laplace Transform tables. (look up the terms individually)
1/s(s+2) 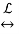 ½ (1 – e-2t)
½ (1 – e-2t)
1/s(s+2)e-s  ½ (1 – e-2(t-1))γ(t-1)
½ (1 – e-2(t-1))γ(t-1)
1/(s+2) 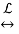 e-2t
e-2t
y(t) = ½ (1 – e-2t) – ½ (1 – e-2(t-1))γ(t-1) - 2 e-2t
In this scenario, all terms are in the table, and the time delay attribute must be used. If the terms aren't in the table, we'll need to use the Inverse Laplace Transform procedures. For t0, note that the function is automatically zero. By multiplying by the unit step, we may make this explicit:
y(t) = ½ (1 – e-2t) γ(t) - ½ (1 – e-2(t-1))γ(t-1) - 2 e-2t γ(t)
Find the equation of motion of an object exhibiting simple harmonic motion with a resistive force. In physics, the equation of an object undergoing simple harmonic motion with no resistance is given by m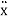 + m2x = 0 where is the angular frequency of oscillation, and the number of dots specifies the number of derivatives (Newton's notation for derivatives). Of course, in real life, there will always be some form of resistance. In this example, the resistive force is assumed to be proportional to velocity F = - m β
+ m2x = 0 where is the angular frequency of oscillation, and the number of dots specifies the number of derivatives (Newton's notation for derivatives). Of course, in real life, there will always be some form of resistance. In this example, the resistive force is assumed to be proportional to velocity F = - m β 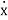 , where β is a constant. Our initial conditions are a displacement of 1 from equilibrium at rest. By using Newton's second law, we can write the differential equation in the following manner. Notice that the presence of mass 𝑚 in each of the terms means that our solution must eventually be independent of 𝑚.
, where β is a constant. Our initial conditions are a displacement of 1 from equilibrium at rest. By using Newton's second law, we can write the differential equation in the following manner. Notice that the presence of mass 𝑚 in each of the terms means that our solution must eventually be independent of 𝑚.
- m
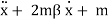 2x = 0, x(0) = 1,
2x = 0, x(0) = 1, 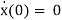
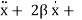 2x = 0
2x = 0
Take the Laplace transform of both sides, and solve for 𝑿(s).
- s2X – s + 2βsX - 2β + 2X = 0
- X(s) = (s+2β)/s2 + 2βs + 2
Rewrite the denominator by completing the square
The goal is to get a solution that will allow us to look at a table of Laplace transforms and study the function in physical space. Of course, to compensate for the extra 2 term, we must deduct it from the total so that we are "adding 0."
X = s + 2β/ (s+ β)2 + 2 – β2
Write out the solution in physical space. From the numerator, it is obvious that this is going to be a sum of a cosine and sine term. From the (s+β)2 in the denominator, it is obvious that both of these terms will be multiplied by an exponential term (in fact, an exponential decay term e-βt. In order to see the two contributions more clearly, we can rewrite the numerator as (s+β)+β
x(t) = e-βt cos ( √2 – β2t) + β/ √2 – β2t e-βt sin ( √2 – β2t)
This example has demonstrated that the Laplace transform method can be used to solve homogeneous differential equations with initial conditions without requiring the use of derivatives to solve the resulting system of equations. However, it's a good idea to double-check your solution by using the conventional ansatz method to solve the differential equation.
The Laplace Transform is a powerful tool that is very useful in Electrical Engineering. The transform allows equations in the "time domain" to be transformed into an equivalent equation in the Complex S Domain. The laplace transform is an integral transform, although the reader does not need to have a knowledge of integral calculus because all results will be provided. This page will discuss the Laplace transform as being simply a tool for solving and manipulating ordinary differential equations.
Laplace transformations of circuit elements are similar to phasor representations, but they are not the same. Laplace transformations are more general than phasors, and can be easier to use in some instances. Also, do not confuse the term "Complex S Domain" with the complex power ideas that we have been talking about earlier. Complex power uses the variable , while the Laplace transform uses the variable s. The Laplace variable s has nothing to do with power.
The transform is named after the mathematician Pierre Simon Laplace (1749-1827). The transform itself did not become popular until Oliver Heaviside, a famous electrical engineer, began using a variation of it to solve electrical circuits.
Laplace Domain
The Laplace domain, also known as the "Complex s Domain," is the domain into which a time-domain equation is transformed via the Laplace transform. s is a complex variable with real and imaginary components:
s = σ + j
The Laplace domain graphs the real part (σ) as the horizontal axis, and the imaginary part (ω) as the vertical axis. The real and imaginary parts of s can be considered as independent quantities.
The similarity of this notation with the notation used in Fourier transform theory is no coincidence; for σ=0, the Laplace transform is the same as the Fourier transform if the signal is causal.
Key takeaway:
- For an LTI system, a Laplace transform is a generalisation of a Fourier transform to complex eigenvalues. In LTI systems or systems with harmonic time-dependence in particular parameters, Laplace transforms make stability analysis simple.
- A differential equation is transformed into an algebraic equation using the Laplace transform.
- A function's Laplace transform is defined as:
F(s) = ℒ(f(t)) = 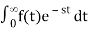
- The Laplace transform is invertible, meaning that ℒ(f(t)) = F(s) implies ℒ -1(F(s)) = f(t). This is how we invert the Laplace transform, since the inverse Laplace transform formula is very difficult to work with and not well-defined in many cases.
- We always look up the Laplace transform of a function from a transform table when solving ODEs. Tables are also used to find inverse transformations.
- We take the transform of both sides according to our Laplace transform theorems, algebraically rearrange to solve for F(s), and take the inverse transform to discover f to solve a linear ODE using Laplace transform (t)
References:
1. Mathematical Physics and Special Relativity–M.Das, P.K. Jena and B.K. Dash (Srikrishna Prakashan)-2009
2. Mathematical Physics–H. K. Das, Dr. Rama Verma (S. Chand Publishing) 2011
3. Complex Variable: Schaum’s Outlines Series M. Spiegel (2nd Edition, Mc- Graw Hill Education)-2004
4. Complex variables and applications J.W.Brown and R.V.Churchill 7th Edition 2003
5. Mathematical Physics, Satya Prakash (Sultan Chand)-2014