Unit - 2
EM Wave Propagation in Unbounded Media
2.1.1 Electromagnetic Waves
Waves are ubiquitous in nature, transferring energy or information from one point to another. The wave is made up of two components: space and time. Electromagnetic waves are an exotic type of wave whose existence is confirmed by professor Heinrich Hertz, but they were anticipated by Maxwell himself before.
These waves can travel in a vacuum or via no medium at all. These are distinct from mechanical waves, such as sound waves, which can travel or transmit energy across a material medium.
Electromagnetic waves, unlike mechanical waves, may pass into vacuum. Visible light waves, radio waves, radar beams, and television transmissions are all examples of EM waves. The subject of electromagnetic waves is a combination of electric and magnetic fields.
2.1.2 Uniform Plane Wave and Wave Equation
The fundamental concept of uniform plane wave provides a basic understanding of electromagnetic wave propagation in a material. The uniform plane wave is the simplest solution to Maxwell's equation for time variable fields in an unbound, homogeneous medium, and it is a key idea in electro magnetics.
Although there is no such thing as an unbound, homogeneous medium in practice, the fundamental concept of uniform plane wave is extremely valuable in understanding electromagnetic waves. In addition, in many practical situations, the uniform plane wave solution is highly beneficial and appropriate. The solution closely resembles the uniform wave solution in some circumstances where the media have physical dimensions substantially bigger than the wavelength.
Consider an unbounded, homogeneous, isotropic medium devoid of any electric or magnetic sources. The medium permeability and permittivity are then constant throughout the medium. There are no free costs in the medium because it is a source-free medium. The Maxwell equations are as follows:
∇. D‾= 0
∇ . B̅ = 0
∇ × E̅ = − ∂B̅/ ∂t
∇ × H̅ = J̅ + ∂D̅/ ∂t
From constitutive relations,
B̅ = µ H̅
D̅ = є E̅
J̅ = σ E̅
Due to the homogenous and non-time changing medium, the permeability and permittivity are constant as a function of time and space. As a result, the Maxwell equations become,
∇ . B ̅ = ∇. (µ H ̅) = µ ∇. H ̅ = 0
∇. H ̅ = 0 ………. (1)
∇ . D ̅ = ∇. (є E ̅) = є ∇. E ̅ = 0
∇. E ̅ = 0 ………. (2)
∇ × E ̅ = − ∂ (µ H) / ∂t
∇ × E ̅ = − µ ∂ H ̅ / ∂t ………. (3)
∇ × H ̅ = ∂ (є E ̅) / ∂t
∇ × H ̅ = σ E ̅ + є ∂ E ̅ / ∂t ………. (4)
In above, ∇ signifies differentiation in terms of space, whereas /t implies differentiation in terms of time. We can deduce from the above 3 and 4 equations that the magnetic field's time derivative is connected to the space derivative of the electric field, and that the electric field's time derivative is connected to the space derivative of the electric field.
Thus, a time-varying magnetic field cannot exist without a corresponding electric and magnetic field, as shown by these two equations. To produce time-varying fields, both magnetic and electric fields must exist simultaneously.
We can't acquire solely magnetic or only electric time varying fields for such time varying fields. However, time invariant fields such as electrostatic and magnetostatic fields can exist independently of one another.
Taking the curl of equation 3 and 4, we get
∇ × ∇ × E ̅ = − µ ∇ × ∂ H ̅ / ∂t
∇ × ∇ × H ̅ = ∇ × (σ E ̅) + ∇ (є ∂ E ̅ / ∂t)
Both ∇ and ∂ / ∂t are independent of each other hence the operators can be interchanged as
∇ × ∇ ×E ̅ = − µ × ∂ (∇ ×H ̅) / ∂t
∇ × ∇ × H ̅ = σ (∇ × E ̅) + є × ∂ (∇ × E ̅) / ∂t
Substituting the (∇ × H) and (∇ × E) values from 3 and 4 equations, we get
∇ × ∇ × E ̅ = − µ × ∂ / ∂t (σ E ̅ + є ∂ E ̅ / ∂t)
∇ × ∇ × E ̅ = − µ σ × ∂ E ̅/ ∂t − µ є (∂2 E ̅ / ∂t2)
Similarly
∇ × ∇ × H ̅ = σ (− µ ∂ H ̅ / ∂t) + є × ∂ / ∂t (− µ ∂ H ̅ / ∂t)
= − µ σ (∂ H ̅ / ∂t) − µ є (∂2 H ̅ / ∂t2)
Using the vector identity ∇ × ∇ × A = ∇ (∇. A) − ∇2 A, where A is the any arbitrary vector, then the above equations can be written as
∇ (∇. E ̅) − ∇2E ̅ = − µ × ∂ / ∂t (σ E ̅ + є ∂ E ̅ / ∂t)
∇ (∇.H ̅) − ∇2 H ̅ = − µ σ × ∂ E ̅/ ∂t − µ є (∂2 E ̅ / ∂t2)
But equations 1 and 2, (∇. E ̅) = 0 and (∇.H ̅) = 0 then
− ∇2 E ̅ = − µ σ × ∂ E ̅/ ∂t − µ є (∂2 E ̅ / ∂t2)
∇2 E ̅ = µ σ × ∂ E ̅/ ∂t + µ є (∂2 E ̅ / ∂t2) …… (5)
This is the wave equation for the electric field E ̅ for a medium. And similarly
−∇2 H ̅ = − µ σ (∂ H ̅ / ∂t) − µ є (∂2 H ̅ / ∂t2)
∇2 H ̅ = µ σ (∂ H ̅ / ∂t) + µ є (∂2 H ̅ / ∂t2) …… (6)
This is the magnetic field wave equation for a medium.
The wave equations are the five and six equations listed above, and their solutions reflect the wave phenomena in three dimensions. Finally, we get to the conclusion that time-varying fields must exist in the form of a wave in a homogenous, unbounded medium.
Furthermore, both electric and magnetic fields must exist simultaneously. An electromagnetic wave is the name given to this phenomena.
But for free space, J = 0, σ = 0, є = єo and µ = µo. Substituting these values in 5 and 6 equations we get
∇2 E ̅ = µo єo (∂2 E ̅ / ∂t2)
∇2 H ̅ = µo єo (∂2 H ̅ / ∂t2)
EM waves are travelling in the direction of Z plane, hence both vectors E ̅ and H ̅ are independent of x and y. Thus, the vectors E ̅ and H ̅ are the function of z and t. Therefore, the above equations become
∂2 E ̅ / ∂z2= µo єo (∂2 E ̅ / ∂t2)
By rearranging the terms, we get
∂2 E ̅ / ∂t2= (1/µo єo) (∂2E ̅ / ∂z2)
According to the results in physics,
Velocity of the light v = (1/√ (µo єo)) = 3 × 108 m/s
v2 = (1/µ є)
Substituting in the above equation we get
∂2E ̅ / ∂t2= v2 (∂2 E ̅ / ∂z2)
Similarly, ∂2H ̅ = v2 (∂2H ̅ / ∂t2)
2.1.3 Plane wave propagation
Electrical properties such as permeability, permittivity, and conductivity characterize electromagnetic waves in a medium. Electrical and magnetic fields that are perpendicular to each other as well as to the propagation direction are connected with EM waves.
In general, the propagation direction should be along the Z axis. In free space, the propagation velocity of all EM waves is equal to the speed of light, which is 3 108 m/s. The magnetic and electric field vectors form a plane, and the propagation direction is normal to that plane. Furthermore, because the phase of these fields is independent of the x and y axes, no phase variation exists over planar surfaces orthogonal to the propagation direction.
Plane waves are waves that are uniform in size and direction in the planes of a certain orientation. In the xy-plane, the magnitudes of EM wave fields (electric and magnetic fields) remain constant, and the surface of constant phase forms a plane parallel to the xy-plane, hence these waves are called plane waves.
The oscillating electrical field produces a magnetic flux, which then oscillates to form the electric field, according to Maxwell's curl equations. This interaction between these two fields causes the energy to be stored, and hence the power to be carried.
Amplitude, phase, and frequency are crucial qualities of waves that allow them to transmit information from source to destination.
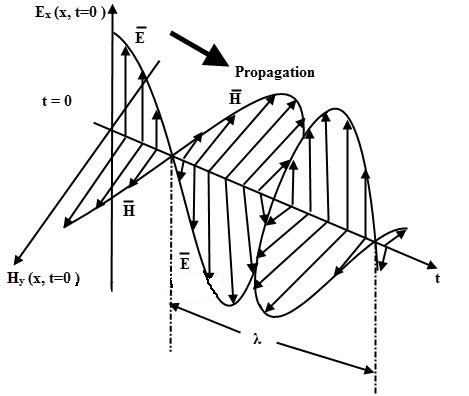
Uniform plane waves, in particular, are EM waves in which the electric field is a function of x and time t and is independent of the y and z axes.
These waves are TEM waves (Transverse EM waves) in which the E and H fields are in temporal phase and have constant magnitudes. The E and H fields transmit their energy in the direction of propagation.
The transverse nature of electromagnetic waves
The electric and magnetic field vectors of an electromagnetic wave are perpendicular to each other and to the wave's propagation direction at the same time. Transverse nature is the name given to this type of electromagnetic wave.
In the direction of wave propagation, both the electric and magnetic fields are perpendicular to each other, according to Maxwell. He imagined a positive x-axis electromagnetic wave propagating. The electric and magnetic fields propagate sinusoidally with the x-axis and are independent of the y and z-axes when a rectangular parallelepiped is placed parallel to the three co-ordinate axes.
A rectangular parallelepiped in a positive direction is depicted in the figure.
Because there is no charge inside the rectangular parallelepiped, the total electric flow across it must be zero. Gauss' law is the name given to this law.
∮E→.ds→=0
Have you ever held one end of a rope in your hand while anchoring the other? By shifting your hands in a different direction, you can make a transverse wave.
The electric field remains constant at various positions along the x-axis, indicating that it is static in nature. Because static fields are known to travel as waves, EX = 0.
Because the electric field is perpendicular to the wave propagation path, the component of the electric field along the propagation direction is zero.
This is also true for a magnetic field, because the magnetic field is perpendicular to the wave propagation direction. This demonstrates the electromagnetic wave's transverse nature with respect to wave propagation direction.
2.3.1 What is Dielectric Constant?
Thermoelectricity A constant defines the influence of an insulating material or a dielectric on an electric field in the region where the substance is located. The dielectric constant of a substance, also known as relative permittivity, shows its capacity to polarize a substance when exposed to an electric field. It demonstrates how easily a substance can become polarized when exposed to an electric field. The dielectric constant is frequently combined with the permittivity constant because the impacts of dielectric qualities are not restricted to the usage of that substance in a capacitor. The dielectric constant is one of the most important properties of a substance that impacts how electric fields propagate. It is a dimensionless measure since it is a relative measure of the ratio of two identical quantities.
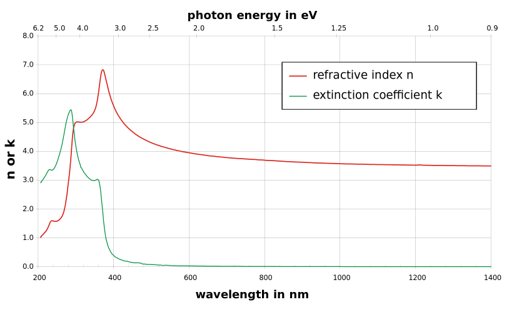
2.3.2 What is Refractive Index?
Most materials' optical properties may be described by a single number termed the "refractive Index," which is applied to solids, liquids, and gases. The refractive index is a measurement of how light propagates through a substance in basic terms. It's the ratio of light speed in a vacuum to light speed in a medium. It's also a dimensionless number that governs how much light rays bend when they pass through one medium and into another. Despite being one of science's oldest topics of interest, the study of optics remains a key part of physics and engineering. Willebrord Snell, a Dutch mathematician, was the first to think of it, formulating the principle of refraction, or the bending of light paths as it passes from one medium to another, in 1621.
Where c is the speed of light in vacuum and v is the speed of light in a medium, the refractive index (n) = c/v.
2.3.3 Difference Between Dielectric Constant and Refractive Index
Over the last few years, technology has surpassed human aspirations and continues to amaze in many fields of study. Recent advancements in microelectronics have resulted in a significant increase in the demand for low and high dielectric constant materials. Low and high dielectric constant materials show to be one of the key components of Internet devices that perform operations such as storage, transport, and communication, as the Internet spreads across all industrial sectors. Low-dielectric-constant materials are especially important in high-frequency or high-power applications, such as ULSI interlayer-dielectric applications and microelectronic packaging. On the other hand, materials with a high dielectric constant have a lot of potential for producing DRAM capacitors. Before we go any further, let's review some fundamentals, such as what is a material's dielectric constant and how it relates to or differs from its refractive index.
2.4.1 Wave Impedance and Phase
The ratio between the transverse components of the electric and magnetic fields supported by an EM planewave is known as wave impedance. The impedance of the downward propagating EM planewave seen in Fig. 48 is given by:
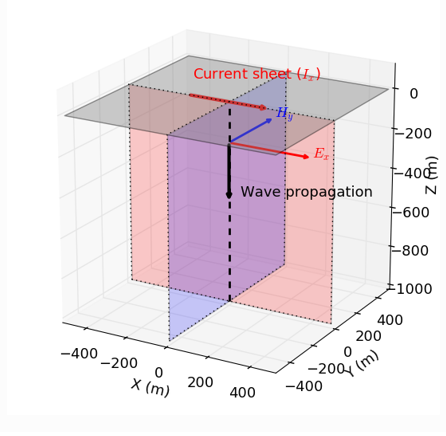
Fig. Geometry of an EM planewave propagating downwards.
Zxy=−ExHy=ωμk
Where μ is the complex wavenumber, and k is the magnetic permeability. The wave impedance is dependent on the frequency and physical parameters of the medium, as shown in the previous equation. A single wave impedance can thus be used to define EM waves travelling in any direction in a homogeneous isotropic material. Waves propagating in distinct directions are characterized by varying impedances if the physical parameters are anisotropic (direction dependent).
2.4.2 Phase
The phase difference between the electric and magnetic fields provided by a planewave can be calculated using wave impedance. Figure shows the phase difference between the electric and magnetic fields:
ϕZxy=tan−1(Im [Zxy]Re [Zxy])
Where 0≤ϕxy≤π/4. According the above expression, the electric field lags the magnetic field.
2.4.3 Approximations
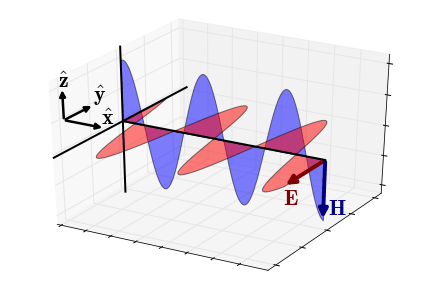
Fig. Electric and magnetic fields of an EM wave propagating in the x-direction (quasi-static regime).
2.4.4 Quasi-Static Approximation
In the quasi-static regime (ϵω≪σϵω≪σ), the wavenumber becomes −iωμσ√−iωμσ and the impedance simplifies to:
Zxy=ωμ−iωμσ√=iωμσ√
The phase of the impedance is given by:
ϕZxy=tan−1(Im [Zxy]Re [Zxy]) =π4
In this case, the electric field lags the magnetic field by π/4 radians.
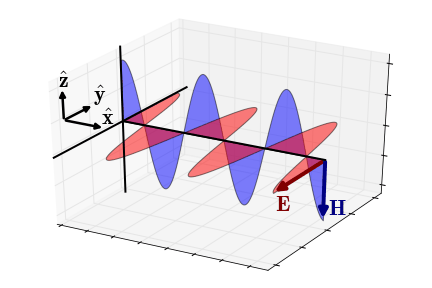
Fig. Electric and magnetic fields of an EM wave propagating in the x-direction (wave regime).
2.4.5 Wave Regime Approximation
In the wave regime (ϵω≫σϵω≫σ), the wavenumber simplifies to ωμe√ and the impedance simplifies to:
Zxy=ωμωμ√=μϵ√
Where the phase is equal to:
ϕZxy=tan−1(Im [Zxy]Re [Zxy]) =0
2.5.1 Wave Propagation in Conducting Media
In the limit 
, The response of a dielectric material to an electromagnetic wave differs significantly depending on whether the lowest resonant frequency is zero or non-zero. When it comes to insulators, the lowest resonant frequency is not zero. The low frequency refractive index is primarily real in this scenario, and it is also bigger than unity. In a conducting medium, on the other hand, some fraction, 
, of the electrons are free,'' in the sense of having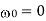 
. In this situation, the low frequency dielectric constant takes the form
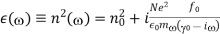
Where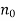 
is the contribution to the refractive index from all of the other resonances, and 
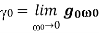. Consider the Ampère-Maxwell equation,
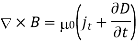
Here,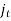 
is the true current: that is, the current carried by free, as opposed to bound, charges. Let us assume that the medium in question obeys Ohm's law, 
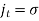, and has a “normal” dielectric constant 
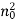. Here, 
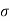is the conductivity. Assuming an 
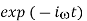time dependence of all field quantities, the previous equation yields
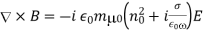
Assume, however, that we do not apply Ohm's law explicitly and instead assign all of the medium's properties to the dielectric constant. The effective dielectric constant of the medium in this situation is equal to the term in round brackets on the right-hand side of the previous equation:
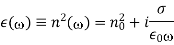
When this term is compared to Equation, the conductivity is expressed as follows:
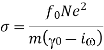
Thus, at low frequencies, conductors possess predominately real conductivities (i.e., the current remains in phase with the electric field). However, at higher frequencies, the conductivity becomes complex. At such frequencies, there is little meaningful distinction between a conductor and an insulator, because the conductivity'' contribution to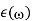 
appears as a resonant amplitude, just like the other contributions. For a good conductor, such as copper, the conductivity remains predominately real for all frequencies up to, and including, those in the microwave region of the electromagnetic spectrum.
The conventional way in which to represent the complex refractive index of a conducting medium (in the low frequency limit) is to write it in terms of a real “normal” dielectric constant,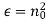
, and a real conductivity, 
. Thus, from Equation,
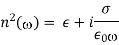
For a poor conductor (i.e.,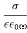
<<1), we find that
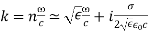
In this limit,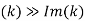 
, and the attenuation of the wave, which is governed by
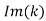, is independent of the frequency. Thus, for a poor conductor, the wave acts like a wave propagating through a conventional dielectric of dielectric constant, except that it attenuates gradually over a distance of very many wavelengths. For a good conductor (i.e., 
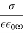>>1), we obtain
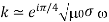
It follows from Equation that
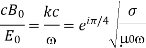
Thus, the phase of the magnetic field lags that of the electric field by π/4 radians. Moreover, the magnitude of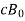 
is much larger than that of 
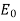(because 
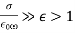). As a result, wave energy is virtually exclusively magnetic in nature. Clearly, the properties of an electromagnetic wave travelling through a good conductor differ significantly from those of a wave travelling through a standard dielectric. For a wave propagating in the 
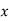-direction, the amplitudes of the electric and magnetic fields attenuate like 
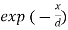, where
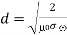
The depth of the skin is referred to as the skin depth. An electromagnetic wave incident on a conducting material will obviously only penetrate a few skin deep into that material.
When current flows, it is the time interval between two successive collisions of electrons in a conductor.
The following graph shows the link between relaxation time (T) and drift velocity (Vd).
Where
vd = drift velocity
e = charge of electron
E = field
m = mass of electron
T = Relaxation time
So, the expression for relaxation time (T) is
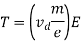
Let L = Length of the conductor
A = Area of the conductor
n = current density
Then current flowing through the conductor is
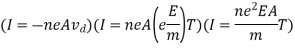
Field E can be expressed as
E = V/L
Then current flowing through the conductor becomes
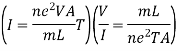
From ohm’s law
V = IR
R = V/I
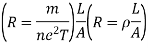
2.7.1 Skin depth
The distance a wave must travel before its amplitude decays by a factor of 1/e is known as skin depth. The reciprocal of the decay constant is skin depth. β. Thus:
δ=1β=1ω(μϵ2[(1+σ2ϵ2ω2)1/2−1])1/2
The skin depth varies depending on the frequency and physical qualities of the media. The skin depth can be thought of as a very sophisticated function in general. In the quasi-static and wave regimes, however, approximations exist.
On this high-voltage cable, why are there two conductors? Depth of the skin!!!
More information about skin depth and how it affects microwave circuits may be found here:
Skin depth is a key issue in microwave engineering, but it also has an impact on lower frequencies, like 60 cycle AC power. In microwave engineering, the skin depth equation is as important as Newton's law (F=mA) in physics.
This is one of the most comprehensive treatments on skin depth effects available anywhere, and it includes the IEEE's whole searchable microwave paper collection. We know because we conducted the investigation! We've included a download with this article that calculates equivalent RF sheet resistance for metals with up to three layers. This email address is being protected from spambots if you are a thin film vendor and would like to sponsor this amazing page and beat your competitors to the punch. To view it, you must have JavaScript enabled.
By the way, for this talk and the download, we utilize the metric system. What is the reason for this? Because the English system lacks widely used bulk resistivity units. If you wish to convert microns to micro-inches exactly for skin depths and thin film thicknesses, divide microns by 0.0254. When it comes to plating, one micron is around 40 micro-inches, which is close enough.
2.7.2 Skin depth – what is it?
Skin depth is a frequency-dependent measure of how far electrical conduction occurs in a conductor. At DC (0 Hz), the entire conductor, regardless of thickness, is utilized. According to Ohm's law, the DC resistance per unit length reduces by half when the cross-sectional area of a wire is doubled. The effect of conductor thickness on conductance at RF frequencies is nonlinear (actually, a negative exponential.) The amount of conductance you can accomplish is limited, and increasing the thickness of precious metals to lessen losses is not an option. If you don't know what you're doing, RF can be a waste of money.
One typical misunderstanding concerning skin depth is which conductor surface carries the RF current. The EM wave propagates (almost) always (mostly*) on the surface closest to the media. The RF currents are largest in the lower surface of the microstrip line, as shown in the cross-section below. In a microstrip multi-metal stack-up, the initial metal is the most significant for conductivity. Please keep in mind that for waveguide, the converse is true: it doesn't matter what you underplate with; what matters is the surface plating.
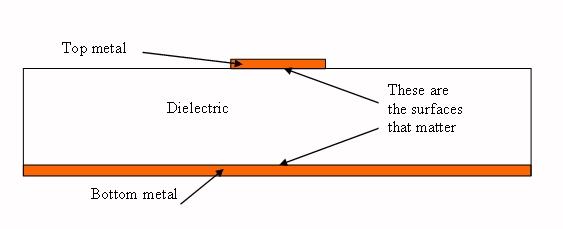
* There are some fields toward the top of the microstrip line, but they are much weaker. In April 2009, we propose analyzing this and creating a page on the subject. This page on microstrip loss can help you understand the concept.
2.7.3 Skin depth equation
The well-known equation is for skin depth given below. Note that skin depth
(δ) is a function of only three variables, frequency (f), resistivity (ρ), and relative permeability (μR).
Skin Depth=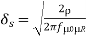
Where
=bulk resistivity(ohm-meters)
f=frequency (Hertz)
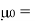Permeability constant (Henries/meter)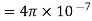
relative Permeability (usually 
1)
Bulk resistivity is a measurement of a material's resistance. Bulk conductivity is the inverse of bulk conductivity.
Because the skin depth reduces with frequency, conductors can get thinner at higher frequencies with little effect on circuit loss. Despite the fact that metallization’s sheet resistance always increases with frequency, the RF loss per wavelength can actually decrease. For millimeter wave applications, 150 microinches of gold on alumina thin-films can be reduced to half that thickness to save money without sacrificing performance. A Q-band branch line coupler will have fewer dB loss than one intended for L-band.
2.8.1 Electron conductivity of a thermally ionized gas in an electric field
It is generally understood that the proportion of current carriers in a thermally ionized gas varies, but that electrons contribute the most to the gas's conductivity since their mobility is vastly greater than that of other current-carrying particles. As a result, we'll solely be concerned with electron conductivity. When a gas is under high pressure with a weak electric field, the same notions used by Drude in the theory of metallic conduction are frequently used to estimate its electrical conductivity using classical methods. Cowling and Chapman improved the Drude-Lorentz formula for electrical conductivity by adding a coefficient to account for the rate at which particle interaction forces decrease with distance. When compared to the Drude-Lorentz formula, this coefficient takes the value 0.532 instead of 0.500 for electron Coulomb interaction.
Because the electron drift velocity in the field is vanishingly small compared to the mean velocity of random motion at high pressures and low electric field strengths, it is logical to assume that the electron free time is independent of the drift velocity, and this supposition leads to the conclusion that Ohm's law applies to gases at high pressure in very weak fields.
However, we must keep in mind that, even under the aforementioned conditions, the conclusion about the validity of Ohm's law is simply an approximation, which becomes less accurate as the gas pressure and field strength decrease.
Drude's approach is used to measure the conductivity of the gas in the following, with the addition that the drift velocity of these particles in the field is taken into account when computing the electron free time.
The plasma frequency,
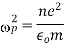
In plasma physics, is the most fundamental time-scale. Clearly, each species has a different plasma frequency. The comparatively rapid electron frequency, on the other hand, is by far the most relevant, and text-book references to "the plasma frequency" generally refer to the electron plasma frequency.
It is easily seen that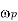 
corresponds to the typical electrostatic oscillation frequency of a given species in response to a small charge separation. For instance, consider a one-dimensional situation in which a slab consisting entirely of one charge species is displaced from its quasi-neutral position by an infinitesimal distance 
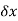. The resulting charge density which develops on the leading face of the slab is 
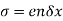. An equal and opposite charge density develops on the opposite face. The 
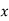-directed electric field generated inside the slab is of magnitude 
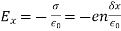. Thus, Newton's law applied to an individual particle inside the slab yields
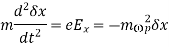
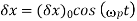
Note that plasma oscillations will only be observed if the plasma system is studied over time periods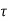 
longer than the plasma period 
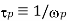, and if external actions change the system at a rate no faster than 
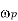. In the opposite case, one is clearly studying something other than plasma physics (e.g., nuclear reactions), and the system cannot not usefully be considered to be a plasma. Likewise, observations over length-scales 
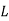shorter than the distance 
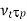traveled by a typical plasma particle during a plasma period will also not detect plasma behaviour. In this case, particles will exit the system before completing a plasma oscillation. This distance, which is the spatial equivalent to 
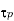, is called the Debye length, and takes the form
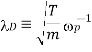Note that
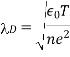is unaffected by bulk and, as a result, is generally comparable among species.
Clearly, our idealized system can only be regarded a plasma if the following conditions are met.
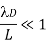
And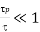 
Here, 
and 
represent the typical time-scale and length-scale of the process under investigation.
It's worth noting that, despite the traditional condition (9), plasma physics can take into account structures on the Debye scale. The Debye sheath, or boundary layer that surrounds a plasma confined by a material surface, is the most prominent example of this.
Refractive Index (Index of Refraction)
The ratio of the speed of light in a vacuum to the speed of light in a second medium of larger density is used to determine the Refractive Index (Index of Refraction). In descriptive prose and mathematical formulae, the refractive index variable is most usually represented by the letter n or n'.
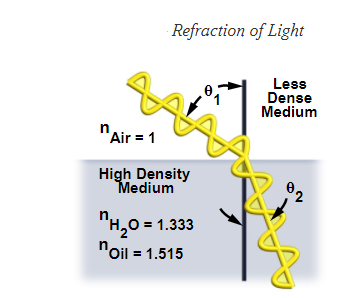
As presented in the figure above, a wavefront incident upon a plane surface separating two media is refracted upon entering the second medium if the incident wave is oblique to the surface. The incident angle (θ (1)) is related to the refraction angle (θ (2)) by the simple relationship known as Snell's law:
n1 × sin(θ1) = n2 × sin(θ2)
The refractive indices of materials 1 and 2 are represented by n, and the angles of light flowing through these materials with respect to the normal are represented by. This equation can be used to draw numerous key conclusions. The angle of refraction is always greater than the angle of incidence when n (1) is bigger than n (2). The angle of refraction is always less than the angle of incidence when n (2) is bigger than n (1). The light passes through without refraction when the two refractive indices are equivalent (n (1) = n (2)).
In optical microscopy, the refractive index is a key factor in determining numerical aperture, which is a measurement of an objective's light-gathering and resolving capacity. The imaging medium for microscopy is usually air, but to improve resolution, high-magnification objectives frequently use oil or a similar liquid between the objective front lens and the specimen. The following is the numerical aperture equation:
NA (numerical aperture) = n × sin(θ)
Where n is the refractive index of the imaging medium and θ is the angular aperture of the objective. It is obvious from the equation that increasing the refractive index by replacing the imaging medium from air (refractive index = 1.000) with a low-dispersion oil (refractive index = 1.515) dramatically increases the numerical aperture.
The link between the incident angles and the ratio of the velocities of light in the two mediums was initially defined by Snell's law. The refractive index, often known as the index of refraction, is the ratio of light's velocity (c) in free space (for all practical purposes, air or a vacuum) to its velocity in a certain medium:
n = c/η
The more the deflection (or refraction) of a light beam entering or leaving a material as its refractive index rises, the more light is deflected (or refracted). The frequency of light travelling through a material affects its refractive index (to some extent), with the highest frequencies having the highest values of n. For example, the refractive index of violet light is about 1% higher than that of red light in common glass. When a heterogeneous light beam containing many frequencies enters or exits the medium, each wavelength experiences a slightly varying degree of refraction as a result of this phenomenon. The chromatic aberration in microscope objectives is caused by this process, which is known as dispersion.
Radio Wave Propagation Through the Ionosphere
The Earth's ionosphere, to a first approximation, is made up of an unmagnetized, horizontally stratified, partially ionized gas. For an electromagnetic plasma wave, the dispersion relation is [see Eq.].
Where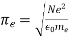 
Here,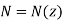 
is the density of free electrons in the ionosphere, and 
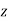is a coordinate which measures height above the surface of the Earth. (N.B., the curvature of the Earth is neglected in the following analysis.)
Now,
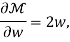
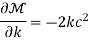
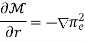
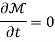
Thus, the ray equations, yield
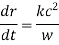
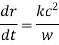
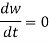
Note that the frequency of a radio pulse does not change as it propagates through the ionosphere, provided that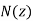 
does not vary in time. It is clear, from Eqs., and the fact that 
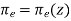, that a radio pulse which starts off at ground level propagating in the 
plane, say, will continue to propagate in this plane.
For pulse propagation in the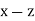 
plane, we have
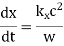
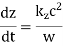
The dispersion relation (661) yields
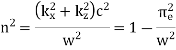
Where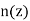 
is the refractive index.
We assume th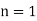at 
at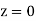 
, which is equivalent to the reasonable assumption that the atmosphere is non-ionized at ground level. It follows from Eq. (672) that
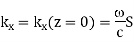
Where S is the sine of the angle of incidence of the pulse, with respect to the vertical axis, at ground level. Equation’s yield
The plus sign relates to the upward trajectory of the pulse, whereas the minus sign refers to the downward trajectory, according to Eq. Finally, Eqs. Produce the pulse motion equations:
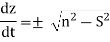
The pulse attains its maximum altitude,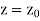 
, when
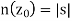
The pulse's total distance travelled (i.e., the distance from its launch point to the point where it intersects the Earth's surface for the second time) is
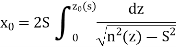
In the limit in which the radio pulse is launched vertically (i.e.,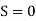 
) into the ionosphere, the turning point condition (678) reduces to that characteristic of a cutoff (i.e., 
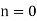). The WKB turning point described in Eq. (678) is a generalization of the conventional turning point, which occurs when 
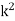changes sign. Here, 
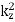changes sign, whilst 
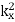and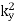 
are constrained by symmetry (i.e., 
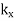is constant, and 
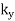is zero).
The equation of motion of the pulse can also be written
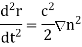
It follows that the trajectory of the pulse is the same as that of a particle moving in the gravitational potential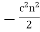 
. Thus, if
decreases linearly with increasing height above the ground [which is the case if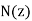 
increases linearly with 
] then the trajectory of the pulse is a parabola.
References:
1. Classical Electrodynamics by J.D. Jackson (Willey)-2007
2. Foundation of electromagnetic theory: Ritz and Milford (Pearson)-2008
3. Electricity and Magnetism: D C Tayal (Himalaya Publication)-2014
4. Optics: A.K. Ghatak (McGraw Hill Education)- 2017
5. Electricity and Magnetism: Chattopadhyaya, Rakhit (New Central)-2018
