UNIT 3

Digital Fundamentals

3.1   Binary Numbers, Decimal-to-Binary & Binary-to-Decimal Conversion

• It uses two digits 0 and 1.
• It is also called as base 2 number system.
• Here, each position in any binary number represents a power of the base (2). Example: 23
• The last position represents a y power of the base (2). Example: 2y where y represents the last position.

Example

Binary Number: 101112

Calculating the Decimal Equivalent of binary number −

Note: 101112 is normally written as 10111.

Binary Number − 111102 = Decimal Number − 3010

3.2 Binary Addition, Subtraction, Multiplication and Division

It is an essential part of all the digital calculations.

Binary Addition

• It is a basis for binary subtraction, multiplication, division.
• There are four rules which are as follows:

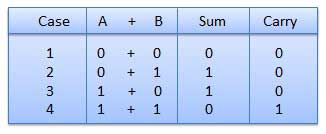
Fig.1 Rules of Binary addition

In fourth step, a sum (1 + 1 = 10) i.e. 0 is written in the given column and a carry of 1 over to the next column is done.

For Example −

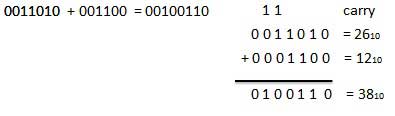
Fig.2 Binary addition

Binary Subtraction

Subtraction and Borrow, these are the two words that will be used very frequently for binary subtraction. There rules of binary subtraction are:

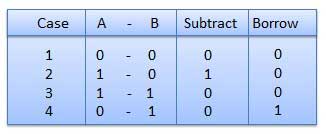
Fig.3 Rules of Binary Subtraction

For Example

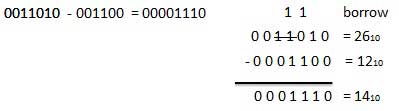
Fig.4 Binary subtraction

Binary Multiplication

• It is similar to decimal multiplication.
• It is also simpler than decimal multiplication as only 0s and 1s are involved.
• There are four rules of binary multiplication which are:

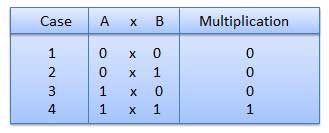
Fig.5 Rules of Binary Multiplication (Ref. 1)

For Example

Fig.6 Binary Multiplication

Binary Division

• It is similar to decimal division.
• It is also called as the long division procedure.

For Example

Fig.7 Binary Division

Binary system complements

• Complements are used in order to simplify the subtraction operation and the logical manipulations can be done.
• For each radix-r system there are two types of complements:

• The binary system has radix r = 2.
• Therefore, the two types of complements for the binary system are known as 1's complement and 2's complement.

1's complement

• Here, a number is obtained by changing all 1's to 0's and all 0's to 1's.
• This is called as 1's complement.
• For Example :

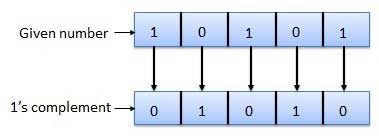
Fig.8: 1's complement

2's complement

• It is obtained by adding 1 to the Least Significant Bit (LSB) of 1's complement of the number.
• Hence, 2's complement = 1's complement + 1
• For Example:

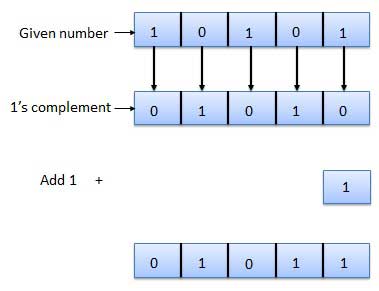
Fig.9: 2's complement

Octal Number System

• It consists of eight digits 0, 1,2,3,4,5,6,7.
• It is also named as base 8 number system.
• Here each position represents a power of the base (8). Example: 82

• The last position represents a y power of the base (8). Example: 8y where y represents the last position .

Example

Octal Number − 125758

Calculating Decimal Equivalent −

Note: 125758 is normally written as 12575 in octal.

Octal Addition

The octal addition table is as follows:

Fig.10: Octal addition table

• To use the above table, simply follow the example:
• Add 68and 58.
• Locate 6 in the A column then locate the 5 in the B column.
• The point in 'sum' area where these two columns intersect is the 'sum' of two numbers.

68 + 58 = 138.

For Example :

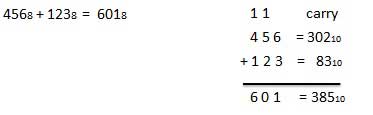
Fig.11: Octal addition  (Ref. 1)

Octal Subtraction

• It follows the same rules as the subtraction of numbers in any other system.
• The only difference is in borrowed number.
• In the decimal system, we borrow a group of 1010.
• In the binary system, we borrow a group of 210.
• But in the octal system we borrow a group of 810.

For Example

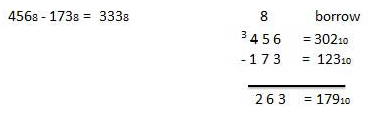
Fig.12: Octal subtraction  (Ref. 1)

3.3 Hexadecimal Number Systems

• It uses 10 digits starting from 0,1,2,3,4,5,6,7,8,9 and 6 letters A,B,C,D,E,F.
• These letters represents numbers as A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
• It is also known as base 16 number system.
• Here each position represents a power of the base (16). Example 161.
• The last position represents a y power of the base (16). Example: 16y where y represents the last position .

Example −

Hexadecimal Number: 19FDA16

Calculating Decimal Equivalent −

Note − 19FDA16 is normally written as 19FDA in hexa decimal.

3.4 Logic Gates

The basic gates are namely AND gate, OR gate  & NOT gate.

AND gate

It is a digital circuit that consists of two or more inputs and a single output which is the logical AND of all those inputs. It is represented with the symbol ‘.’.

The following is the truth table of 2-input AND gate.

Here A, B are the inputs and Y is the output of two input AND gate.

If both inputs are ‘1’, then only the output, Y is ‘1’. For remaining combinations of inputs, the output, Y is ‘0’.

The figure below shows the symbol of an AND gate, which is having two inputs A, B and one output, Y.

Fig. : AND gate (ref. 1)

Timing Diagram:

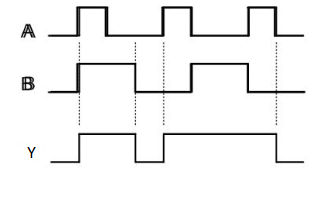
OR gate

It is a digital circuit which has two or more inputs and a single output which is the logical OR of all those inputs. It is represented with the symbol ‘+’.

The truth table of 2-input OR gate is:

Here A, B are the inputs and Y is the output of two input OR gate.

When both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.

The figure below shows the symbol of an OR gate, which is having two inputs A, B and one output, Y.

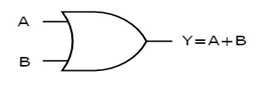
Fig. : OR gate (ref. 1)

Timing Diagram:

NOT gate

It is a digital circuit that has one input and one output. Here the output is the logical inversion of input. Hence, it is also called as an inverter.

The truth table of NOT gate is:

Here A and Y are the corresponding input and output of NOT gate. When A is ‘0’, then, Y is ‘1’. Similarly, when, A is ‘1’, then, Y is ‘0’.

The figure below shows the symbol of NOT gate, which has one input, A and one output, Y.

Fig. : NOT gate (ref. 1)

Timing Diagram:

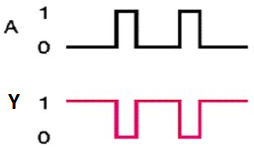
Universal gates

      NAND & NOR gates are known as universal gates.

      We can implement any Boolean function by using NAND gates and NOR gates alone.

NAND gate

It is a digital circuit which has two or more inputs and single output and it is the inversion of logical AND gate.

The truth table of 2-input NAND gate is:

Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, then the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just the inverse of AND operation.

The image shows the symbol of NAND gate:

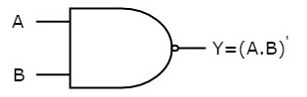
Fig.: NAND gate (ref. 1)

NAND gate works same as AND gate followed by an inverter.

Timing Diagram:

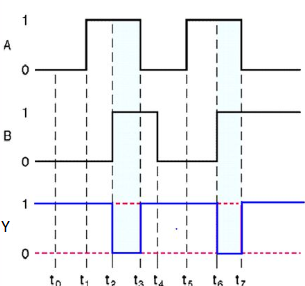
NOR gate

It is a digital circuit that has two or more inputs and a single output which is the inversion of logical OR of all inputs.

The truth table of 2-input NOR gate is:

Here A and B are the two inputs and Y is the output. If both inputs are ‘0’, then the output is ‘1’. If any one of the input is ‘1’, then the output is ‘0’. This is exactly opposite to two input OR gate operation.

The symbol of NOR gate is:

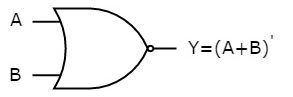
                                                           Fig.: NOR gate (ref. 1)

NOR gate works exactly same as that of OR gate followed by an inverter.

Timing Diagram:

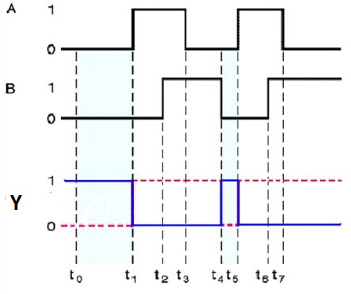
Special Gates

Ex-OR gate

It stands for Exclusive-OR gate. Its function varies when the inputs have even number of ones.

The truth table of 2-input Ex-OR gate is:

Here A, B are the inputs and Y is the output of two input Ex-OR gate. The output (Y) is zero instead of one when both the inputs are one.

Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.

The symbol of Ex-OR gate is as follows:

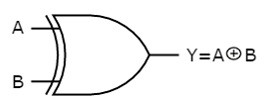
Fig.: XOR gate (ref. 1)

It is similar to that of OR gate with an exception for few combination(s) of inputs. Hence, the output is also known as an odd function.

Timing Diagram:

Ex-NOR gate

It stands for Exclusive-NOR gate. Its function is same as that of NOR gate except when the inputs having even number of ones.

The truth table of 2-input Ex-NOR gate is:

Here A, B are the inputs and Y is the output. It is same as Ex-NOR gate with the only modification in the fourth row. The output is 1 instead of 0, when both the inputs are one.

Hence the output of Ex-NOR gate is ‘1’, when both inputs are same and 0, when both the inputs are different.

The symbol of Ex-NOR gate is:

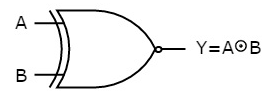
Fig.: XNOR gate (ref. 1)

It is similar to NOR gate except for few combination(s) of inputs. Here the output is ‘1’, when even number of 1 is present at the inputs. Hence is also called as an even function.

Timing Diagram:

3.5 Boolean Algebra

• It deals with binary numbers & variables.
• Therefore, also known as Binary Algebra or logical Algebra.
• A mathematician named as George Boole had developed this algebra in 1854.
• The variables that are used in this algebra are known as Boolean variables.
• Considering the range of voltages as logic ‘High’ is represented with ‘1’ and logic ‘Low’ is represented with ‘0’.

Postulates and Basic Laws of Boolean Algebra

Here, the Boolean postulates and basic laws that are used are given underneath.

Boolean Postulates

• Considering the binary numbers 0 and 1, boolean variable (x) and its complement (x’).
• They known as literal.
• The possible logical OR operations are:

x + 0 = x

x + 1 = 1

x + x = x

x + x’ = 1

• Similarly, the possible logical AND operations are:

x.1 = x

x.0 = 0

x.x = x

x.x’ = 0

• These are the simple Boolean postulates and verification can be done by substituting the Boolean variable with ‘0’ or ‘1’.

3.6 De Morgan’s Theorems, Laws of Boolean Algebra

De Morgan’s Theorems

• It is useful in finding the complement of Boolean function.
• It states that “The complement of logical OR of at least two Boolean variables is equal to the logical AND of each complemented variable”.
• It can be represented using 2 Boolean variables x and y as

(x + y)’ = x’.y’

• The dual of the above Boolean function is

(x.y)’ = x’ + y’

• Therefore, the complement of logical AND of the two Boolean variables is equivalent to the logical OR of each complemented variable.
• Similarly, DeMorgan’s theorem can be applied for more than 2 Boolean variables also.

Simplification of Boolean Functions

Numerical

• Simplify the Boolean function,

f = p’qr + pq’r + pqr’ + pqr

Method 1

Given

f = p’qr + pq’r + pqr’ +pqr.

In first and second term r is common and in third and fourth terms pq is common.

So, taking out the common terms by using Distributive law we get,

⇒ f = (p’q + pq’)r + pq(r’ + r)

The terms present in first parenthesis can be simplified by using Ex-OR operation.

The terms present in second parenthesis is equal to ‘1’ using Boolean postulate we get

⇒ f = (p ⊕q)r + pq(1)

The first term can’t be simplified further.

But, the second term is equal to pq using Boolean postulate.

⇒ f = (p ⊕q)r + pq

Therefore, the simplified Boolean function is f = (p⊕q)r + pq

Method 2

Given f = p’qr + pq’r + pqr’ + pqr.

Using the Boolean postulate, x + x = x.

Hence we can write the last term pqr two more times.

⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr

Now using the Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms we get.

⇒ f = qr(p’ + p) + pr(q’ + q) + pq(r’ + r)

Using Boolean postulate, x + x’ = 1 and x.1 = x for further simplification .

⇒ f = qr(1) + pr(1) + pq(1)

⇒ f = qr + pr + pq

⇒ f = pq + qr + pr

Therefore, the simplified Boolean function is f = pq + qr + pr.

Hence we got two different Boolean functions after simplification of the given Boolean function. Functionally, these two functions are same. As per requirement, we can choose one of them.

Numerical

Find the complement of the Boolean function,

f = p’q + pq’.

Solution:

Using DeMorgan’s theorem, (x + y)’ = x’.y’ we get

⇒ f’ = (p’q)’.(pq’)’

Then by second law, (x.y)’ = x’ + y’ we get

⇒ f’ = {(p’)’ + q’}.{p’ + (q’)’}

Then by using, (x’)’=x  we get

⇒ f’ = {p + q’}.{p’ + q}

⇒ f’ = pp’ + pq + p’q’ + qq’

Using x.x’=0 we get

⇒ f = 0 + pq + p’q’ + 0

⇒ f = pq + p’q’

Therefore, the complement of Boolean function, p’q + pq’ is pq + p’q’.

Laws of Boolean Algebra

• The three basic laws of Boolean Algebra are:

• Commutative law
• Associative law
• Distributive law

Commutative Law

• The logical operation carried between two Boolean variables when gives the same result irrespective of the order the two variables, then that operation is said to be Commutative. The logical OR & logical AND operations between x & y are shown below

x + y = y + x

x.y = y.x

• The symbol ‘+’ and ‘.’ indicates logical OR operation and logical AND operation.
• Commutative law holds good for logical OR & logical AND operations.

Associative Law

• If a logical OR operation of any two Boolean variables is performed first and then the same operation is performed with the remaining variable providing the same result, then that operation is said to be Associative. The logical OR & logical AND operations of x, y & z are:

x + (y + z) = (x + y) + z

x.(y.z) = (x.y).z

• Associative law holds good for logical OR & logical AND operations.

Distributive Law

• If a logical OR operation of any two Boolean variables is performed first and then AND operation is performed with the remaining variable, then that logical operation is said to be Distributive. The distribution of logical OR & logical AND operations between variables x, y & z are :

x.(y + z) = x.y + x.z

x + (y.z) = (x + y).(x + z)

• Distributive law holds good for logical OR and logical AND operations.
• These are the Basic laws of Boolean algebra and we can verify them by substituting the Boolean variables with ‘0’ or ‘1’.

3.7 Flip flops

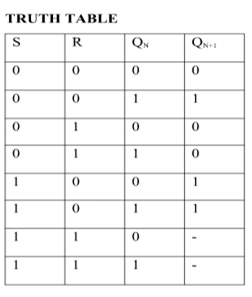
SR Flip Flop

JK Flip Flop

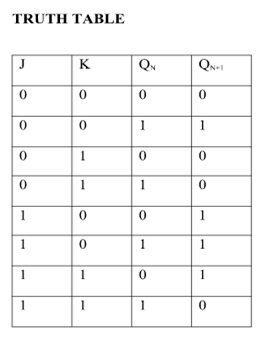
Race Around Condition In JK Flip-flop –

• For J-K flip-flop, if J=K=1, and if clk=1 for a long period of time, then output Q will toggle as long as CLK remains high which makes the output unstable or uncertain.
• This problem is known as race around condition in J-K flip-flop.
• This problem can be avoided by ensuring that the clock input is at logic “1” only for a very short time.
• Hence the concept of Master Slave JK flip flop was introduced.

Master Slave JK flip flop –
It is basically a combination of two JK flip-flops connected together in series.

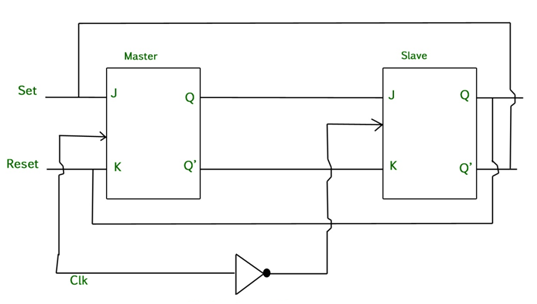
Fig.  Master Slave Flip flop

Working of a master slave flip flop –

1. When the clock pulse goes high, the slave is isolated; J and K inputs can affect the state of the system. The slave flip-flop is isolated when the CP goes low. When the CP goes back to 0, information is transmitted from the master flip-flop to the slave flip-flop and output is obtained.
2. The master flip flop is positive level triggered and the slave flip flop is negative level triggered, hence the master responds prior to the slave.
3. If J=0 and K=1, Q’ = 1 then the master goes to the K input of the slave and the clock forces the slave to reset therefore the slave copies the master.
4. If J=1 and K=0, Q = 1 then the master goes to the J input of the slave and the Negative transition of the clock sets the slave and thus copy the master.
5. If J=1 and K=1, the master toggles on the positive transition and the slave toggles on the negative transition of the clock.
6. If J=0 and K=0, the flip flop becomes disabled and Q remains unchanged.

Timing Diagram of a Master flip flop –

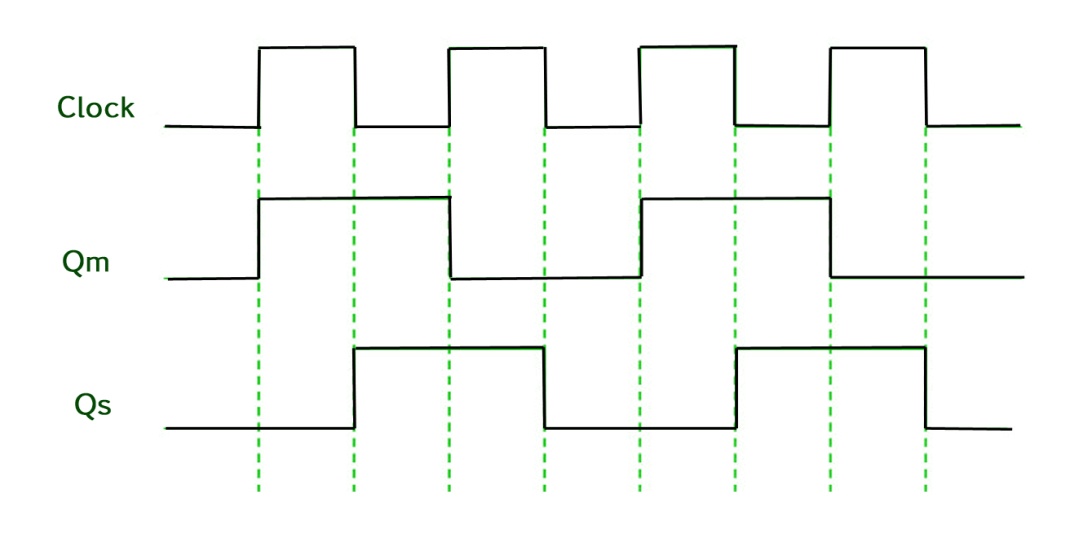
1. When the CP = 1 then the output of master is high and remains high till  CP = 0 because the state is stored.
2. Now the output of master becomes low when the clock CP = 1 and remains low until the clock becomes high again.
3. Thus toggling takes place for a clock cycle.
4. When the CP = 1 then the master is operational but not the slave.
5. When the clock is low, the slave becomes operational and remains high until the clock again becomes low.
6. Toggling takes place during the whole process since the output changes once in a cycle.
7. This makes the Master-Slave J-K flip flop a Synchronous device which passes data with the clock signal.

D Flip Flop

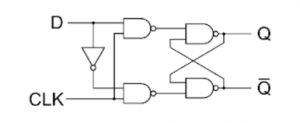
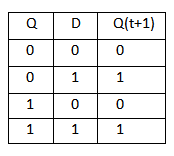
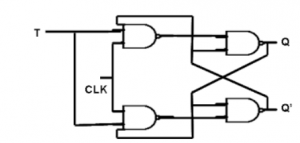
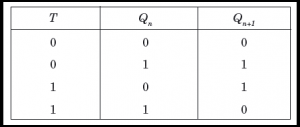
T Flip Flop

3.8 Shift Registers

• Flip flops are used to store one bit of binary data (1or 0).
• If we need to store multiple bits of data, we use multiple flip flops.
• N flip flops are connected to store n bits of data.
• A Register is a device which stores such information. It is a group of flip flops connected in series which is used to store multiple bits of data.
• The information stored in these registers can be transferred with the help of shift registers.
• This register is a group of flip flops used to store multiple bits of data.
• The bits stored in these registers can be moved in/out of the registers by applying clock pulses.
• The registers which shift the bits towards left are called “Shift left registers”.
  The registers which shift the bits towards right are called “Shift right registers”.

Shift registers are of 4 types and they are:

1. Serial In Serial Out register
2. Serial In parallel Out register
3. Parallel In Serial Out register
4. Parallel In parallel Out register

Serial-In Serial-Out Shift Register (SISO) –

• It allows serial input i.e. one bit after another and produces a serial output is known as Serial-In Serial-Out shift register.
• Since it has one output, the data leaves the register one bit at a time in a serial pattern, hence known as Serial-In Serial-Out Shift Register.
• The logic circuit is given underneath.
• The circuit comprises of four D flip-flops which are connected serially.
• All these flip-flops are synchronous in nature

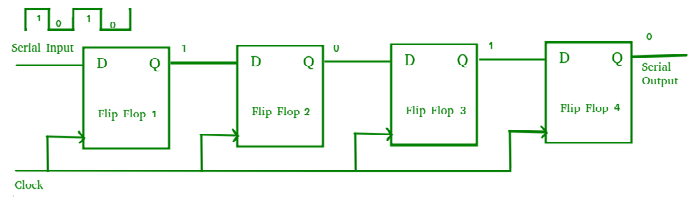
Fig. 6 SISO

Serial-In Parallel-Out shift Register (SIPO) –

• It allows serial input through a single data line and produces a parallel output.
• The logic circuit is given underneath .
• The circuit consists of four D flip-flops which are connected synchronously.
• The clear (CLR) signal is also connected to all the 4 flip flops in order to RESET them.
• The output of the first flip flop is sent to the input of the next and so on.

Fig. 7 SIPO

• They are used in communication lines because the main use of the SIPO register is to convert serial data into parallel data.

Parallel-In Serial-Out Shift Register (PISO) –

• It allows parallel input data and produces a serial output.
• The logic circuit is given underneath.
• The circuit comprises of four D flip-flops which are connected synchronously.
• The clock is connected to all the flip flops but the input data is connected to each flip flop individually through a multiplexer .
• The output of the previous flip flop and parallel data input are connected to the input of the MUX and the output of MUX is connected to the next flip flop.

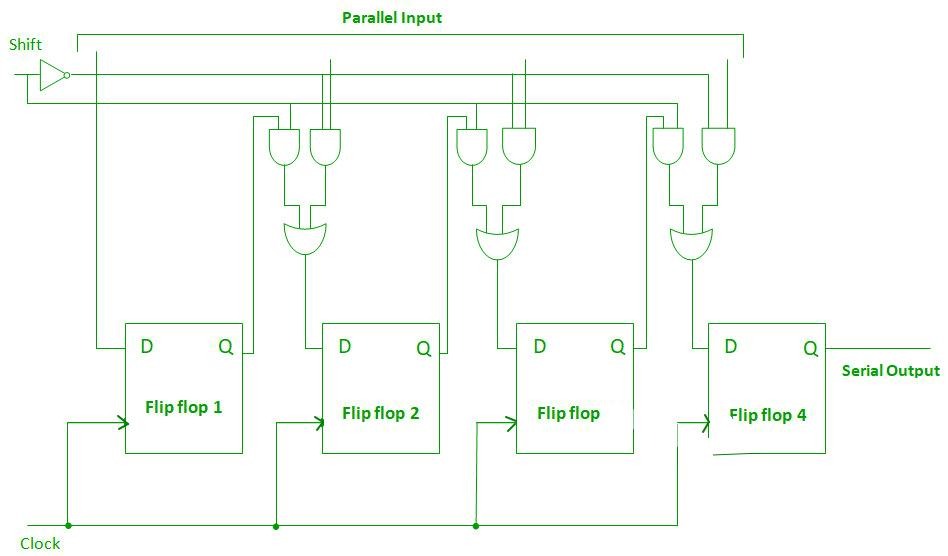
Fig. 8 PISO

• It used to convert parallel data to serial data.

Parallel-In Parallel-Out Shift Register (PIPO) –

• It allows parallel input data and produces a parallel output.
• The logic circuit is given underneath.
• The circuit comprises of four D flip-flops which are connected in a synchronous manner.
• The clear (CLR) and clock signals are connected to all flip flops.
• In this, there are no interconnections between flip-flops as no serial shifting of the data is required.
• Data is provided separately as input for each flip flop and the output is also collected individually from each flip flop.

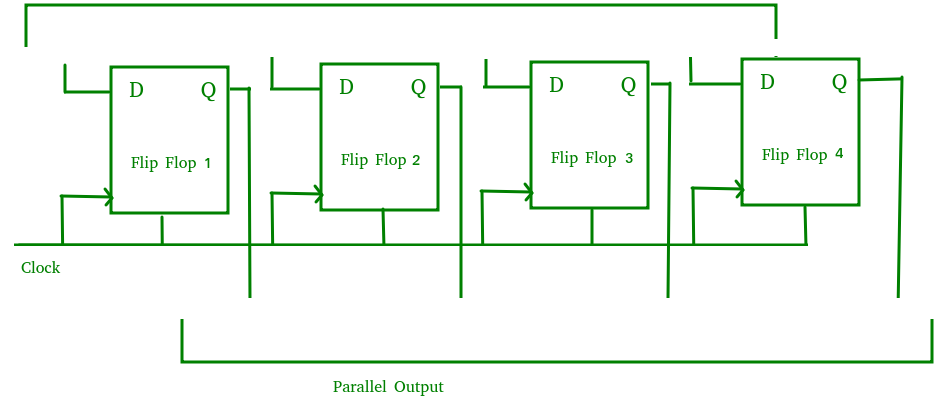
Fig. 9 PIPO

It is used as a temporary storage device and it acts as a delay element too

References:

• Basic Electrical Engineering” by C L Wadhwa.
• “ Basic Electrical Engineering” by Mehta V K and Mehta Rohit.
• “ Basic Electrical Engineering” by Nagrath, I and Kothari.