Unit 3
Development Of Algorithms
To express the running time complexity of algorithm three asymptotic notations are available. Asymptotic notations are also called as asymptotic bounds. Notations are used to relate the growth of complex function with the simple function. Asymptotic notations have domain of natural numbers. These notations are as follows
1. Big-oh notation : Big-oh notations can be express by using ‘o’ symbol. This notation indicates the maximum number of steps required to solve the problem. This notation expresses the worst case growth of an algorithm. Consider the following diagram in which there are two functions f(x) and g(x). f(x) is more complex than the function g(x).
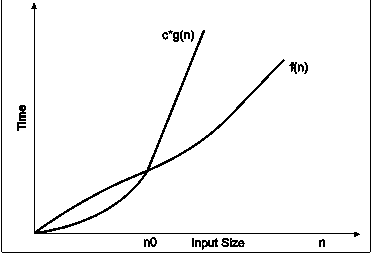
Fig. 3.7
In the above diagram out of two function f(n) and g(n), more complex function is f(n), so need to relate its growth as compare to simple function g(n). More specifically we need one constant function c(n) which bound function f(n) at some point n0. Beyond the point ‘n0’ function c*g(n) is always greater than f(n).
Now f(n)=Og(n)if there is some constant ‘c’ and some initial value ‘n0’. Such that f(n)<=c*g(n) for all n>n0
In the above expression ‘n’ represents the input size
f(n) represents the time that algorithm will take
f(n) and g(n) are non-negative functions.
Consider the following example
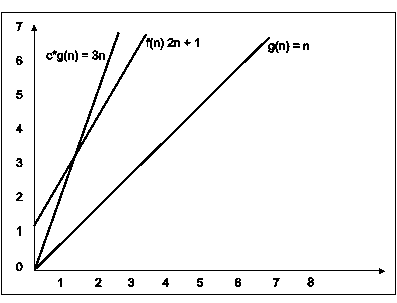
Fig. 3.8
In the above example g(n) is ‘’n’ and f(n) is ‘2n+1’ and value of constant is 3. The point where c*g(n) and f(n) intersect is ‘’n0’. Beyond ‘n0’ c*g(n) is always greater than f(n) for constant ‘3’. We can write the conclusion as follows
f(n)=O g(n) for constant ‘c’ =3 and ‘n0’=1
Such that f(n)<=c*g(n) for all n>n0
2. Big-omega notation : Big-omega notations can be express by using ‘Ω’ symbol. This notation indicates the minimum number of steps required to solve the problem. This notation expresses the best case growth of an algorithm. Consider the following diagram in which there are two functions f(n) and g(n). f(n) is more complex than the function g(n).
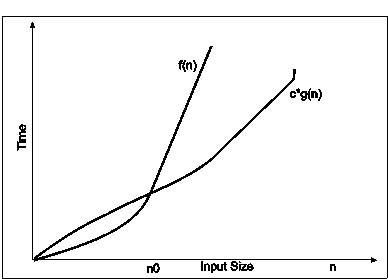
Fig. 3.9
In the above diagram out of two function f(n) and g(n), more complex function is f(n), so need to relate its growth as compare to simple function g(n). More specifically we need one constant function c(n) which bound function f(n) at some point n0. Beyond the point ‘n0’ function c*g(n) is always smaller than f(n).
Now f(n)=Ωg(n)if there is some constant ‘c’ and some initial value ‘n0’. Such that c*g(n) <= f(n)for all n>n0
In the above expression ‘n’ represents the input size
f(n) represents the time that algorithm will take
f(n) and g(n) are non-negative functions.
Consider the following example
In the above example g(n) is ‘2n’ and f(n) is ‘2n-2’ and value of constant is 0.5. The point where c*g(n) and f(n) intersect is ‘’n0’. Beyond ‘n0’ c*g(n) is always smaller than f(n) for constant ‘0.5’. We can write the conclusion as follows
f(n) = Ω g(n) for constant ‘c’ =0.5 and ‘n0’=2
Such that c*g(n)<= f(n) for all n>n0
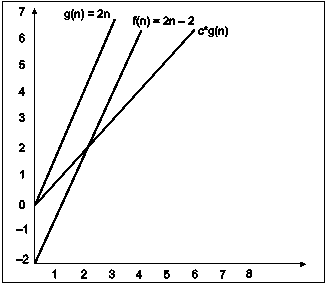
Fig. 3.10
Big-theta notation : Big-theta notations can be express by using ‘Ɵ’ symbol. This notation indicates the exact number of steps required to solve the problem. This notation expresses the average case growth of an algorithm. Consider the following diagram in which there are two functions f(n) and g(n). f(n) is more complex than the function g(n).
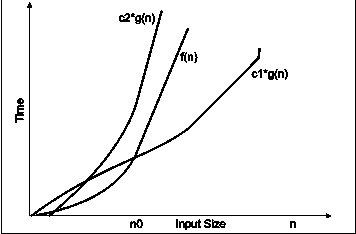
Fig. 3.11
In the above diagram out of two function f(n) and g(n), more complex function is f(n), so need to relate its growth as compare to simple function g(n). More specifically we need one constant function c1 and c2 which bound function f(n) at some point n0. Beyond the point ‘n0’ function c1*g(n) is always smaller than f(n) and c2*g(n) is always greater than f(n).
Now f(n) = g(n) if there is some constant ‘c1 and c2’ and some initial value ‘n0’. Such that c1*g(n) <= f(n)<=c2*g(n)for all n>n0
In the above expression ‘n’ represents the input size
f(n) represents the time that algorithm will take
f(n) and g(n) are non-negative functions.
f(n) = g(n) if and only if f(n)=O g(n) and f(n)=Ω g(n)
Consider the following example
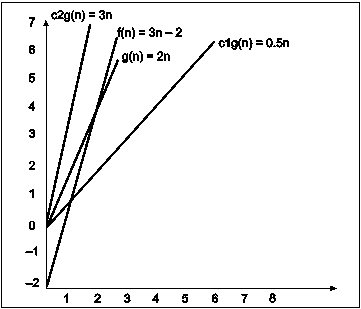
Fig. 3.12
In the above example g(n) is ‘2n’ and f(n) is ‘3n-2’ and value of constant c1 is 0.5 and c2 is 2. The point where c*g(n) and f(n) intersect is ‘’n0’. Beyond ‘n0’ c1*g(n) is always smaller than f(n) for constant ‘0.5’ and c2*g(n) is always greater than f(n) for constant ‘2’. We can write the conclusion as follows
f(n)=Ω g(n) for constant ‘c1’ =0.5 , ‘c2’ = 2 and ‘n0’=2
Such that c1*g(n)<= f(n)<=c2*g(n) for all n>n0
Stack
Stack is a list of elements in which insertion and deletion of elements can be done only at one end called as top of stack.
To construct a stack we insert element from top of stack.
The operation of inserting an element to stack is called as push and the operation of deleting an element from a stack is called as pop.
Imagine stacking a set of books on top of each other, we can push a new book on top of the stack, and we can pop the book that is currently on the top of the stack.
We cannot add to or remove the book from middle of the stack.
Book can only be added to the top and the only book that can be taken out of the stack is the most recently added one; Thus stack is a "Last In First Out" (LIFO) data structure.

ADT of Stack
An ADT is a collection of data and associated operations for manipulating that data. Stack ADT contains following data members and member functions.
Data members: 1. Top: Index of top of stack.
2. A[size]: Array to hold elements of stack:
Member Functions:
Operations on stack | Significance |
Stack()
| Constructor to create an empty stack |
~stack()
| Destructor to destroy an existing stack
|
IsEmpty() | Determines whether the stack is empty. It returns true if stack is empty, and false otherwise
|
IsFull()
| Determines whether the stack is full. It returns true if stack is full, and false otherwise
|
Push()
| Add an element to the top of the stack. PRECONDITION: Stack cannot be full.
|
Pop()
| Remove the element that is on the top of stack. PRECONDITION: Stack cannot be empty.
|
Peek()
| Function to return the element on top of stack without modifying the stack. PRECONDITION: Stack cannot be empty.
|
Stackcount() | Function to return total number of elements currently in stack. |
Operations on Stack
There are three fundamental operations on stack.
Push: Insert element to the stack
Pop: Delete element from stack
Peek: Returns element at the top of stack
We will see these operations with respect to an example.
Here we assume stack size is 3.
Initially stack is empty. If pop operation is called on empty stack then stack underflow occurs.
----- (empty stack)
Push element ‘7’ to the stack. Then stack becomes
| 7 | <-- top
-----
Push element ‘2’ to the stack. So new top of stack is 2.
| 2 | <-- top
| 7 |
-----
Push element ‘10’ to the stack. Now top of stack becomes 10.
|10 | <-- top
| 2 |
| 7 |
-----
Now the stack becomes full as we are assuming stack size is 3. If we insert one more element onto stack then stack overflow occurs.
Pop element from stack. Element 10 is popped out. Hence new top is 2.
| 2 | <-- top
| 7 |
-----
Since Stack is LIFO data structure element inserted most recently will be popped out first.
Pop element 2 from stack. Hence new top is 7.
| 7 | <-- top
-----
Pop element 7 from stack. Now stack becomes empty.
----- (empty stack)
Array Implementation of Stack
Array implementation of stack is efficient if we know maximum size of stack.
Our stack must be able to store any type of data i.e.int, char, float or any other primitive data type.
Stack which is used to hold integer values must be able to hold float and character values.
For this we will not explicitly recode specific version of stack for each data type.
C++ provides this feature through class templates. Thus we implement stack ADT in C++ using class templates.
When we create class template, it can perform operations on any type of data.
The compiler will automatically generate correct type of object, depending on the type we specify when object is created.
Thus a stack ADT can be written as follows.
First we create node structure template.
Template<class TYPE>
Struct Node
{
Type value;
};
Template<class TYPE> // class template
Class stack
{
Private:
Node<TYPE> *P; // pointer to structure
Int count; // total no. Of elements present in stack
Int max; // total no. Of elements allowed in stack
Int top; // index of top of stack
Public:
Stack(int size=100); // constructor to create a stack
~stack(); // destructor to destroy stack
Bool push(TYPE in); // function to insert element in stack
Bool pop(TYPE &out); // function to delete element in stack
Bool peek(TYPE& out); //return top element of stack
Bool isempty(); //check if stack is empty
Bool isfull(); //check if stack is full
Int stackcount();// returns no. Of elements currently in stack
};
Now we will see algorithms for these operations on stack in detail.
Create stack: stack()
Stack is created using constructor.
Steps
| Algorithm: stack(int size) | Description |
1 | Template<class TYPE> Stack<TYPE>::stack(int size) {
| Design constructor which takes stack size as an argument |
2 | Max=size;
| Assign size to max. Value of size can be passed or default size of 100 is assumed. |
3 | P=new Node<TYPE>[max]; | Allocate memory to P
|
4 | If(!P) { Cout<<”Memory overflow”; Abort(); }
| Check if memory is available. If memory is not available, abort and print “memory overflow “. |
5 | Count=0; Top=-1; }
| Initially stack is empty. So count is 0 and stack top is -1.
|
2. Insert element in Stack: push()
Steps
| Algorithm: bool push(TYPE in)
| Description |
1 | Template<class TYPE> Bool stack<TYPE>::push(TYPE in) {
| Design function push which inserts element ‘in’ to stack |
2 | If(count>=max) Return false | Compare current total no. Of elements with maximum stack size. If stack is full then return false to indicate element cannot be inserted. |
3 | P[top].value=in
| If stack is not full copy data to top of stack
|
4 | Count++; Top++; Return true } | Increment count and top. Return true to indicate element is successfully inserted in stack. |
3.Remove element from stack: pop()
Steps
| Algorithm: bool pop(TYPE& out) | Description |
1 | Template<class TYPE> Bool stack<TYPE>::pop(TYPE& out) {
| Design function pop which deletes element on the top of stack. Out is a reference variable to receive element to be popped out. |
2 | Bool flag; If(count==0) Flag=false; | If stack is empty then set flag to false |
3 | Else { Out=P[top].value;
| If stack has elements, copy element at top of stack to variable out. |
4 | Top--; Count--; Flag=true; }
| Decrement count and top. Set flag to true to indicate pop is successful. |
5 | Return flag; } | Return flag |
4.Find top of stack(tos):peek
Steps
| Algorithm: bool peek(TYPE& out) | Description |
1 | Template<class TYPE> Bool stack<TYPE>::peek(TYPE& out) {
| Design function peek which returns element on the top of stack without modifying stack. Out is a reference variable to receive element at the top of stack. |
2 | Bool flag; If(count==0) Flag=false; | If stack is empty then set flag to false |
3 | Else { Out=P[top].value;
| If stack has elements, copy element at top of stack to variable out. |
4 | Flag=true; }
| Set flag to true. |
5 | Return flag; } | Return flag |
5.Check if the stack is empty: isEmpty()
Steps
| Algorithm: bool isEmpty() | Description |
1 | Template<class TYPE> Bool stack<TYPE>::isEmpty() {
| Design function isEmpty() which returns true if stack is empty and false otherwise. |
2 | Bool flag; If(count==0) Flag=true; | If stack is empty then set flag to true |
3 | Else Flag=false;
| If stack has elements set flag to false. |
4 | Return flag; } | Return flag |
6. Check if the stack is full: isFull()
Steps
| Algorithm: bool isFull() | Description |
1 | Template<class TYPE> Bool stack<TYPE>::isFull() {
| Design function isFull() which returns true if stack is full and false otherwise. |
2 | Bool flag; If(count==max) Flag=true; | Compare count with maximum number of elements allocated for a stack. If they are equal set flag to true. |
3 | Else Flag=false;
| If count is not equal to max set flag to false. |
4 | Return flag; } | Return flag |
7.Find total number of elements in stack: stackcount()
Steps
| Algorithm: int stackcount() | Description |
1 | Template<class TYPE> Int stack<TYPE>::stackcount() {
| Design function stackcount() which returns total number of elements present in stack. |
2 | Return count; } | ‘count’ specifies total number of elements present in stack so return count |
Destroy stack:~stack()
Stack is destroyed using destructor.
Steps
| Algorithm: ~stack() | Description |
1 | Template<class TYPE> Stack<TYPE>::~stack() {
| Design destructor to destroy stack |
2 | Delete[] P P=NULL; Count=0; Max=0; Top=-1; } | Release memory of P. Set variables count,max to 0 and top to -1. |
Program in C++ to perform various operations on stack .
#include<iostream.h>
# define int MAX 100
Template< class TYPE > //class template
Class Stack {
Int count; //number of elements present in stack
TYPE A[Max]; // Array of size MAX
TYPE out;
Int top; // index of top of stack
Public:
Stack(int MAX);
~Stack();
Bool push(TYPE);
TYPE pop();
Bool isEmpty();
Bool isFull();
Int stackcount();
Void display();
};
Template< class TYPE > //constructor to create stack
Stack< TYPE >::Stack(int MAX)
{
Count=0;
Top = -1;
}
Template< class TYPE > //destructor to remove stack
Stack< TYPE >::~Stack()
{ delete[] A;
Count=0;
MAX=0;
Top=-1;
}
Template< class TYPE>// function to push elements in stack
Void Stack< TYPE >::push(TYPE in)
{
If(count>=MAX)
Cout<<”stack overflow”
Count++;
Top++;
A[ top ] = in; //copy data to top of stack
}
Template< class TYPE > // Function to pop elements from stack
TYPE Stack< TYPE >::pop()
{ return A[ top-- ];
Count--;
}
Template< class TYPE> //Function to check if stack is full
Int Stack< TYPE>::isFull()
{
Return (count == Max);
}
Template< class TYPE> //Function to check if stack is empty
Int Stack< TYPE>::isEmpty()
{
Return (count == 0);
}
Template< class TYPE>
Int Stack< TYPE>::stackcount()
{
Return count;
}
Template< class TYPE> //Function to display stack elements
Void Stack<TYPE>::display()
{
If(top<0)
Cout<<”stack empty”;
For(int i=top;i>=0;i--)
Cout<<A[i]<<” ”;
}
Void main()
{
Int choice,data;
Stack<int> S; //create stack of integers
While(1)
{
Cout<<”Enter choice for operation”;
Cout<<”\t 1.PUSH”<<endl;
Cout<<”\t 2.POP”<<endl;
Cout<<”\t 3.ISFULL”<<endl;
Cout<<”\t 4.ISEMPTY”<<endl;
Cout<<”\t 5.Stackcount”<<endl;
Cout<<”\t 6.Display”<<endl;
Cin>>choice;
Switch(choice)
{
Case 1:
Cout<<”Enter element to be pushed”;
Cin>>data
S.push(data);
Break;
Case 2:
Out=S.pop();
Cout<<”Popped element is”<<out;
Break;
Case 3:
Int flag=S.isFull();
If(flag=1)
Cout<<”stack is full”;
Else
Cout<<”stack is not full”;
Break;
Case 4:
Int flag=S.isEmpty();
If(flag=1)
Cout<<”stack is empty”;
Else
Cout<<”stack is not empty”;
Break;
Case 5:int c=S.stackcount();
Cout<<”Stack count is”<<c;
Break;
Case 6: S.display();
Break;
} //end of switch
} //end of while
} //end of program
Applications of Stack – Well form-ness of Parenthesis, Infix to Postfix Conversion and Postfix Evaluation
Applications of Stacks
Applications of stacks are as follows.
- Reversing data
- Parsing
- Expression evaluation
- Expression conversion
- Reversing data
Data reversing is a technique of reordering data elements so that first element becomes last, second element becomes last but one and so on. Consider array A
10 | 5 | 2 | 4 | 9 |
A=
Fig. Original Array
After reversing array becomes
A=
9 | 4 | 2 | 5 | 10 |
Algorithm to reverse list of integers is as follows.
Steps
| Algorithm(Reverse) | Description |
1 | Create Stack | Create an empty stack |
2 | Read number | Accept integer from user |
3
3.1 3.2 | Loop(!fullstack(stack)) { Push(stack.number) Read number } | Accept integers from user to fill the stack till it is not full. |
4
4.1 4.2 | Loop(!emptystack(stack)) { Pop(stack.out) Print(out) } | Pop elements from stack till stack is not empty. Print popped element to user. |
Another application of reversing data is conversion of decimal number to binary number. Algorithm for conversion of decimal to binary number is as follows.
Steps
| Algorithm(DecimaltoBinary) | Description |
1 | Create Stack | Create an empty stack |
2 | Read decimal number | Accept decimal number from user |
3
3.1 3.2 3.3
3.3.1 | Loop(number>0) { d=number%2 Flag=push(stack.d) If(flag==false) { Print stack overflow } Number=number/2 } | Convert the number to binary and push to stack. When stack becomes full print “stack overflow.” |
4
4.1 4.2 | Loop(!emptystack(stack)) { Pop(stack.d) Print(d) } | Pop elements from stack till stack is not empty. Print popped element to user |
***Program to convert decimal number to binary number****
#include <iostream>
#include <stdio.h>
#include <conio.h>
Using namespace std;
Struct Node
{
Int value;
Node *next;
}*top = NULL, *P = NULL, *temp = NULL;
Int x;
Void push(int P)
{
Temp = new Node;
Temp->value = P;
Temp->next = NULL;
If (top == NULL)
{
Top = temp;
}
Else
{
Temp->next = top;
Top = temp;
}
}
Int pop()
{
If (top == NULL)
{
Cout<<"underflow\n";
}
Else
{
P = top;
Top = top->next;
x = P->value;
Delete(P);
Return(x);
}
}
Void main()
{
Int num, a;
Cout<<"enter the decimal number\n";
Cin>>num;
While (num > 0)
{
a = num % 2;
Num = num / 2;
Push(a);
}
P = top;
Cout<<"resultant binary no:";
While(1)
{
If (top != NULL)
Cout<<pop()<<"\t";
Else
Break;
}
Getch();
}
Parsing
Parsing breaks data into independent parts for processing.
For example a program parsing is breaking program into independent parts like keywords, identifiers, tokens and operators if any.
While writing any algebraic expression all of the parentheses should be properly paired. Unmatched parentheses in an algebraic expression pop errors such as missing of opening and closing parentheses.
We can use stacks for parsing so that all of the parentheses are paired properly.
Algorithm for parsing using stack is as follows.
Steps
| Algorithm(Parsing) | Description |
1
1.1 1.2
1.2.1 1.3
1.3.1
1.3.1.1
1.3.1.2 | While(1) { Read character If(character is an opening parenthesis) { Push(stack.character) Else { If(character is an closing parenthesis) { If(emptystack) Print(“Closing parenthesis not matched”) Else Pop(stack.token) } } } }
|
Accept character from user If character is an opening parenthesis then push character in stack
If character is an closing parenthesis and if stack is empty then Closing parenthesis not matched If character is an closing parenthesis and if stack is not empty then pop its matching opening parenthesis from stack |
2 | If(!emptystack(stack)) Print(“opening parenthesis not matched”); | If stack is not empty then opening parentheses not matched. |
Expression Evaluation
An expression can be represented in one of the following forms.
Infix: Infix expression has operator between operands. Eg. A + B
Prefix: Prefix expression has operator before operands. Eg. + A B
Postfix: Postfix expression has operator after operands. Eg. A B +
Evaluation of an Infix Expression:
Infix expressions are always evaluated from left to right. While evaluating it we must take care of operator precedence.
Following table shows priority of operators in C++.
Operators
|
Unary minus(-),! |
*,/,% |
+,- |
<,<=,>=,> |
==,!= |
&& |
|| |
Highest Priority
LeastPriority
Priority of operators in C++
According to above table – and ! have highest priority and logical OR has least priority. If an expression consists of operators with same priority(*,/,%)then evaluation is performed from left to right. If expression consists of parentheses then they are given top priority. Innermost parentheses are evaluated first.
Eg. Evaluate following infix expression
A / B – C + D * E. Given A=4,B=2,C=1,D=5,E=6
Considering above rules infix expression becomes.
((A / B) – C) + (D * E) Putting values in it
((4/2)-1)+(5*6)
(2-1)+(5*6)
1+30
31(Output)
Evaluation of prefix expression
Prefix expression has operator before operands. Prefix expression is always evaluated from right to left.
Eg. + 1 * 2 3
Evaluating from right to left, first operator we come across is ‘*’.so evaluate 2*3.so now expression becomes
+1 6
Again start evaluating from right to left. Next operator is +.
Add 1 and 6. So final output is 7.
Evaluation of prefix expression using Stack
Steps for Evaluation of prefix expression using Stack are as follows.
Accept prefix expression from user
Scan the expression from right to left
If token is an operand then push it in a stack.
If token is an operator then pop corresponding operands and perform operation.
Push result in stack.
Move to next token
Repeat steps 3 to 6 till the end of prefix expression.
Eg. -*+5 3 1 6
Prefix Input |
Stack |
Operand 1 |
Operand 2 |
Output |
Description |
-* 5 3 + 1 6
|
| - | - | - | Initially stack is empty. Evaluate expression from right to left. |
-* 5 3 + 1
|
| - | - | - | First token is an operand hence push operand 6 in stack |
-* 5 3 +
|
| - | - | - | Next token is again operand hence push operand 1 in stack |
-* 5 3 |
|
1 |
6 |
7 |
Next token is operator +, hence pop 1 and 6 and perform addition. Result is 7 .Push it in to stack
|
-* 5 |
| - | - | - | Next token is 3. Push it into stack.
|
-*
|
| - | - | - | Next token is 5. Push it into stack.
|
- |
| 5 | 3 | 15 | Next token is operator *, hence pop 5 and 3 and perform multiplication. Result is 15 .Push it in to stack
|
|
| 15 | 7 | 8 | Next token is operator -, hence pop 15 and 7 and perform subtraction. Result is 8 .Push it in to stack
|
Eg. 2: Evaluate the following prefix expression using stack for A= 16, B= 2, C=3, D=10, and E=4.Prefix Expression is
-+/A^BC*DE*AC DEC2007
Prefix Input |
Stack |
Op 1 |
Op 2 |
Output |
Description |
-+/A^BC*DE*AC |
| - | - | - | Initially stack is empty. Evaluate expression from right to left. |
-+/A^BC*DE*A
|
| - | - | - | First token is an operand C hence push operand 3 in stack
|
-+/A^BC*DE* |
| - | - | - | Next token is an operand A hence push operand 16 in stack |
-+/A^BC*DE |
|
16 |
3 |
48 |
Next token is operator *, hence pop 3 and 16 and perform multipliaction. Result is 48 .Push it in to stack
|
-+/A^BC*D |
| - | - | - | Next token is E. Push it into stack.
|
-+/A^BC* |
| - | - | - | Next token is D. Push it into stack.
|
-+/A^BC |
| 10 | 4 | 40 | Next token is operator *, hence pop 4 and 10 and perform multiplication. Result is 40 .Push it in to stack
|
-+/A^B |
| - | - | - |
Next token is C. Push it into stack
|
-+/A^ |
| - | - | - |
Next token is B. Push it into stack
|
-+/A
|
| 2 | 3 | 8 | Next token is operator ^, hence pop 2 and 3 and perform ^. Result is 8 .Push it into stack.
|
-+/
|
| - | - | - | Next token is A. Push it into stack
|
-+ |
| 16 | 8 | 2 | Next token is operator /, hence pop 16 and 8 and perform /. Result of 16/8 is 2 .Push it into stack.
|
- |
| 2 | 40 | 42 | Next token is operator +, hence pop 40 and 2 and perform +. Result of 40+2 is 42 .Push it into stack. |
|
|
42 |
48 |
-6 |
Next token is operator -, hence pop 42 and 48 and perform - . Result of 42-48 is -6 .Push it into stack. |
Hence final result is -6.
*****program for prefix expression evaluation.***
#include <iostream.h>
#include <conio.h>
#include <stdio.h>
#include <math.h>
#include <string.h>
template <class TYPE> //class template
class stack
{
private:
TYPE *a;
int top,max;
public:
stack()
{
max = 50;
a = new TYPE[max];
top = 0;
}
stack(int n)
{
max = n + 1;
a = new TYPE[max];
top= 0;
}
~stack()
{
delete a;
}
friend void push(stack &,TYPE); // member functions for stack
friend TYPE pop(stack &);
friend int isEmpty(stack);
};
template <class TYPE>
void push(stack <TYPE> &s, TYPE x)
{
if(s.top != s.max)
{
s.top++;
s.a[s.top] = x;
}
else
cout << "\nStack Overflow.";
}
template <class TYPE>
TYPE pop(stack <TYPE> &s)
{
TYPE temp;
if(s.top != 0)
{
temp = s.a[s.top];
s.top--;
return temp;
}
else
{
temp = -999;
return temp;
}
}
template <class TYPE>
int isEmpty(stack <TYPE> s)
{
if(s.top == 0)
return 1;
else
return 0;
}
int main()
{
char prefix[30],b[2];
int i = 0;
float e;
cout << "Enter a Prefix Expression,\n";
prefix[i - 1] ='\0';
while(prefix[i-1] != '\n')
prefix[i++] = getchar(); // prefix expression
stack <float> O(50); //call constructor to create stack
float value,operand1,operand2;
int j = i - 2,pos,k;
while(j >= 0)
{
pos = 0;
if(prefix[j] >= '0' && prefix[j] <= '9')
{
b[0] = prefix[j]; // Save Prefix[j] to b
i = j - 1;
k = 1;
if(prefix[j-1] != ' ') //Check for next character, If not Space
{
while(prefix[i] != ' ') //While space is not found
{
b[k++] = prefix[i--]; //Save Prefix[i] to b
pos++; //Increase Position
}
pos += 2;//At Last Increase Position by 2 to Skip Space
}
else //If a Single Character
pos = 2; //Skip Space
b[k] = '\0'; //End String temp
strrev(b);
x = atof(b); //Convert string b to float and store to x
push(O,x); //Push to stack
}
else if(prefix[j] == '+' || prefix[j] == '-' || prefix[j] == '*' || prefix[j] == '/' || prefix[j] == '^' ) // check for operators
{
operand1 = pop(O);
if(operand1 == -999)
break;
if(prefix[j] == '+' || prefix[j] == '-' || prefix[j] == '*' || prefix[j] == '/' || prefix[j] == '^')
{
operand2 = pop(O);
if(operand2 == -999)
break;
}
if(prefix[j] == '+')
value = operand1 + operand2;
if(prefix[j] == '-')
value = operand1 - operand2;
if(prefix[j] == '*')
value = operand1 * operand2;
if(prefix[j] == '/')
{
if(operand2 != 0)
value = operand1 / float(operand2); //Cast one operand to float
else
{
cout << "\nError ! Cannot Divide by Zero";
getch();
return 0;
}
}
if(prefix[j] == '^')
value = pow(operand1,operand2);
push(O,value);
pos = 2;
}
else
{
cout << "\nError : Illegal Character";
getch();
return 0;
}
j -= pos;
}
float output = pop(O);
if(output == -999 || !isEmpty(O)) //If Underflow Condition or stack is not empty,
{
cout << "\nError : The Given Prefix Expression is Not Valid.";
getch();
return 0;
}
else
cout << "\nOutput = " << Output;
getch();
return 0;
}
Evaluation of Postfix expression
Postfix expression has operator after operands. Postfix expression is evaluated from left to right.
Eg.6 4 2 * +
Evaluating from left to right first operator we come across is ‘*’.so evaluate 4*2.so now expression becomes
6 8 +. Again start evaluating from left to right. Next operator is +. Add 6 and 8. So final output is 14.
Evaluation of postfix expression using Stack
Steps for Evaluation of postfix expression using Stack are as follows.
Accept postfix expression from user
Scan the expression from left to right
If token is an operand then push it in a stack.
If token is an operator then pop corresponding operands and perform operation.
Store result in stack.
Move to next token
Repeat steps 3 to 6 till the end of postfix expression.
Eg. : 623+-382/+*2^3+
Postfix Input
| Stack | Op1 | Op2 | Output | Description |
623+-382/+*2^3+
|
| - | - | - | Initially stack is empty. Evaluate expression from left to right. |
23+-382/+*2^3+
|
| - | - | - | First token is an operand 6. Push it into stack. |
3+-382/+*2^3+
|
| - | - | - | Next token is an operand 2. Push it into stack.
|
+-382/+*2^3+ |
| - | - | - | Next token is an operand 3. Push it into stack.
|
-382/+*2^3+
|
| 2 | 3 | 5 | Next token is operator +, hence pop 2 and 3 and perform +. Result of 2+3 is 5 .Push it into stack. |
382/+*2^3+
|
| 6 | 5 | 1 | Next token is operator -, hence pop 5 and 6 and perform -. Result of 6-5 is 1 .Push it into stack.
|
82/+*2^3+
|
| - | - | - | Next token is an operand 3. Push it into stack.
|
2/+*2^3+
|
| - | - | - | Next token is an operand 8. Push it into stack.
|
/+*2^3+
|
| - | - | - |
Next token is an operand 2. Push it into stack.
|
+*2^3+
|
| 8 | 2 | 4 | Next token is operator /, hence pop 2 and 8 and perform /. Result of 8/2 is 4 .Push it into stack.
|
*2^3+
|
| 3 | 4 | 7 | Next token is operator +, hence pop 4 and 3 and perform +. Result of 3+4 is 7 .Push it into stack.
|
2^3+
|
| 1 | 7 | 7 | Next token is operator *, hence pop 7 and 1 and perform *. Result of 1*7 is 7 .Push it into stack.
|
^3+ |
| - | - | - | Next token is an operand 2. Push it into stack.
|
3+
|
| 7 | 2 | 49 | Next token is operator ^, hence pop 2 and 7 and perform ^. Result of 7^2 is 49 .Push it into stack.
|
+ |
| - | - | - | Next token is an operand 3. Push it into stack.
|
|
|
49
|
3 |
52 | Next token is operator +, hence pop 3 and 49 and perform +. Result of 49+3 is 52 .Push it into stack.
|
Hence final result is 52.
Eg.2: Evaluate the following postfix expression and show stack after every step in tabular form. Given A= 5, B= 6, C=2, D=12, and E=4.POSTfix Expression is
ABC+*DE\- MAY2007
Postfix Input
| Stack | Op1 | Op2 | Output | Description |
ABC+*DE\- |
| - | - | - | Initially stack is Empty. Evaluate expression from left to right. |
BC+*DE\- |
| - | - | - | First token is an operand A i.e.5. Push it into stack.
|
C+*DE\- |
| - | - | - | Next token is an operand B i.e.6. Push it into stack.
|
+*DE\-
|
| - | - | - | Next token is an operand C i.e.2. Push it into stack.
|
*DE\-
|
| 6 | 2 | 8 | Next token is operator +, hence pop 2 and 6 and perform +. Result of 6+2 is 8 .Push it into stack.
|
DE\- |
| 5 | 8 | 40 | Next token is operator *, hence pop 8 and 5 and perform *. Result of 8*5 is 40 .Push it into stack.
|
E\-
|
| - | - | - | Next token is an operand D i.e.12. Push it into stack.
|
\-
|
| - | - | - | Next token is an operand E i.e.4. Push it into stack.
|
- |
| 12 | 4 | 3 | Next token is operator \, hence pop 4 and 12 and perform \. Result of 12\4 is 3 .Push it into stack.
|
|
| 40 | 3 | 37 | Next token is operator -, hence pop 3 and 40 and perform -. Result of 40-3 is 37 .Push it into stack.
|
Hence final output is 37.
*******Program to evaluate Postfix expression********
#include <iostream.h>
#include <stdlib.h>
#include <math.h>
#include <ctype.h>
# define int MAX = 50 ;
Class stack
{
Private :
Int A[MAX] ;
Int top, y ;
Char *s ;
Public :
Stack( ) ;
Void exprn ( char *str ) ;
Void push ( int x ) ;
Int pop( ) ;
Void calculate( ) ;
Void display( ) ;
} ;
Stack :: stack( )
{
Top = -1 ;
}
Void stack :: exprn ( char *str )
{
s = str ;
}
Void stack :: push ( int x )
{
If ( top == MAX - 1 )
Cout << endl << "Stack is full" ;
Else
{
Top++ ;
A[top] = x ;
}
}
Int stack :: pop( )
{
If ( top == -1 )
{
Cout << endl << "Stack is empty" ;
Return NULL ;
}
Int data = A[top] ;
Top-- ;
Return data ;
}
Void stack :: calculate( )
{
Int n1, n2, n3 ;
While ( *s )
{
If ( *s == ' ' || *s == '\t' )
{
s++ ;
Continue ;
}
If ( isdigit ( *s ) )
{
y = *s - '0' ;
Push ( y ) ;
}
Else
{
n1 = pop( ) ;
n2 = pop( ) ;
Switch ( *s )
{
Case '+' :
n3 = n2 + n1 ;
Break ;
Case '-' :
n3 = n2 - n1 ;
Break ;
Case '/' :
n3 = n2 / n1 ;
Break ;
Case '*' :
n3 = n2 * n1 ;
Break ;
Case '%' :
n3 = n2 % n1 ;
Break ;
Case '^' :
n3 = pow ( n2 , n1 ) ;
Break ;
Default :
Cout << "Unknown operator" ;
Exit ( 1 ) ;
}
Push ( n3 ) ;
}
s++ ;
}
}
Void stack :: display( )
{
y = pop ( ) ;
Cout << "Result is: " << y ;
}
Void main( )
{
Char C[MAX] ;
Cout << "\nEnter postfix expression to be evaluated : " ;
Cin.getline ( C, MAX ) ;
Stack o ;
o.exprn ( C ) ;
o.calculate( ) ;
o.display( ) ;
}
Expression conversion
Expression conversion is of following types
Infix to Postfix
Infix to Prefix
Postfix to Infix
Postfix to prefix
Prefix to Infix
Prefix to Postfix
Infix to Postfix
Manual Transformation
Infix expression can be manually converted to postfix in following steps.
Fully parenthesize the infix expression considering operator precedence. There should be one set of parentheses for each operator.
Evaluate innermost expression first. Replace right parenthesis with corresponding operator.
Remove left parentheses.
Eg. X+Y/Z
Step 1: (X+(Y/Z))
Step 2: (X+(YZ/)
(X(YZ/+
Step 3: XYZ/+
Stack Transformation
Infix expression can be converted to postfix using stack in following steps.
Initialize an empty stack.
While not to end of infix expression
Scan the expression from left to right.
Get the input token in the infix expression.
If the token is
A left parenthesis then push it onto the stack
A right parenthesis then Pop and display stack elements until a left parenthesis is encountered.
Note: Do not display parenthesis. Parenthesis has least priority in stack but highest priority when in input expression.
An operator: If the stack is empty or input token has higher priority than the top stack, push onto the stack. Otherwise, pop and display the top stack element. Repeat the comparison of input token with the new top stack element.
An operand: Just display it.
When end of infix expression is reached, pop and display stack elements until the stack is empty.
Eg1. 4+5*9/1
Infix | Stack | Postfix | Description |
4+5*9/1 |
|
| Initially stack is empty. Scan expression from left to right. |
+5*9/1 |
| 4
| First token is an operand 4 so add to postfix expression. |
5*9/1 |
| 4 | Next token is operator + and stack is empty so push it into stack |
*9/1
|
| 45 | Next token is an operand 5 so add to postfix expression.
|
9/1
|
| 45 | Next token is operator *.Compare * with +. * has higher precedence over + so push it to stack. |
/1 |
| 459 | Next token is an operand 9 so add to postfix expression.
|
1 |
| 459* | Next token is operator /.Compare / with *. * has higher precedence over / so pop it from stack and push /.
|
|
| 459*1 | Next token is an operand 1 so add to postfix expression. |
|
| 459*1/+ | Pop remaining tokens from stack and add to postfix expression |
Hence Postfix expression is 459*1/+
Eg.2 Convert (2+4)*(5-6)/((1-2)*(9+2)) to Postfix expression.
Infix | Stack | Postfix |
(2+4)*(5-6)/((1-2)*(9+2)) |
|
|
2+4)*(5-6)/((1-2)*(9+2)) | ( |
|
+4)*(5-6)/((1-2)*(9+2)) | ( | 2 |
)*(5-6)/((1-2)*(9+2)) | (+ | 24 |
*(5-6)/((1-2)*(9+2)) |
| 24+ |
(5-6)/((1-2)*(9+2)) | * | 24+ |
5-6)/((1-2)*(9+2)) | *( | 24+ |
-6)/((1-2)*(9+2)) | *( | 24+5 |
6)/((1-2)*(9+2)) | *(- | 24+5 |
)/((1-2)*(9+2)) | *(- | 24+56 |
/((1-2)*(9+2)) | * | 24+56- |
((1-2)*(9+2)) | / | 24+56-* |
(1-2)*(9+2)) | /( | 24+56-* |
1-2)*(9+2)) | /(( | 24+56-* |
-2)*(9+2)) | /(( | 24+56-*1 |
2)*(9+2)) | /((- | 24+56-*1 |
)*(9+2)) | /((- | 24+56-*12 |
*(9+2)) | /( | 24+56-*12- |
(9+2)) | /(* | 24+56-*12- |
9+2)) | /(*( | 24+56-*12- |
+2)) | /(*( | 24+56-*12-9 |
2)) | /(*(+ | 24+56-*12-9 |
)) | /(*(+ | 24+56-*12-92 |
) | /(* | 24+56-*12-92+ |
| / | 24+56-*12-92+* |
|
| 24+56-*12-92+*/ |
Eg.3:Convert the following arithmetic expression into postfix
A+(B*C-(D/E-F)*G)*H MAY 2007
Infix | Stack | Postfix |
A+(B*C-(D/E-F)*G)*H
|
|
|
+(B*C-(D/E-F)*G)*H |
| A |
(B*C-(D/E-F)*G)*H | + | A |
B*C-(D/E-F)*G)*H | +( | A |
*C-(D/E-F)*G)*H | +( | AB |
C-(D/E-F)*G)*H | +(* | AB |
-(D/E-F)*G)*H | +(* | ABC |
(D/E-F)*G)*H | +(- | ABC* |
D/E-F)*G)*H | +(-( | ABC* |
/E-F)*G)*H | +(-( | ABC*D |
E-F)*G)*H | +(-(/ | ABC*D |
-F)*G)*H | +(-(/ | ABC*DE |
F)*G)*H | +(-(- | ABC*DE/ |
)*G)*H | +(-(- | ABC*DE/F |
*G)*H | +(- | ABC*DE/F- |
G)*H | +(-* | ABC*DE/F- |
)*H | +(-* | ABC*DE/F-G |
*H | + | ABC*DE/F-G*- |
H | +* | ABC*DE/F-G*-H |
| +* | ABC*DE/F-G*-H |
|
| ABC*DE/F-G*-H*+ |
EG. Convert the following expression into postfix.
(A+B)*D+E/(F+A*D)+C
A*(B+C)/D-G MAY 2008
1. (A+B)*D+E/(F+A*D)+C
Infix | Stack | Postfix |
(A+B)*D+E/(F+A*D)+C
|
|
|
A+B)*D+E/(F+A*D)+C | ( |
|
+B)*D+E/(F+A*D)+C | ( | A |
B)*D+E/(F+A*D)+C | (+ | A |
)*D+E/(F+A*D)+C | (+ | AB |
*D+E/(F+A*D)+C |
| AB+ |
D+E/(F+A*D)+C | * | AB+ |
+E/(F+A*D)+C | * | AB+D |
E/(F+A*D)+C | + | AB+D* |
/(F+A*D)+C | + | AB+D*E |
(F+A*D)+C | +/ | AB+D*E |
F+A*D)+C | +/( | AB+D*E |
+A*D)+C | +/( | AB+D*EF |
A*D)+C | +/(+ | AB+D*EF |
*D)+C | +/(+ | AB+D*EFA |
D)+C | +/(+* | AB+D*EFA |
)+C | +/(+* | AB+D*EFAD |
+C | +/ | AB+D*EFAD*+ |
C | + | AB+D*EFAD*+/+ |
| + | AB+D*EFAD*+/+C |
|
| AB+D*EFAD*+/+C+ |
2. A*(B+C)/D-G
Infix | Stack | Postfix |
A*(B+C)/D-G |
|
|
*(B+C)/D-G |
| A |
(B+C)/D-G | * | A |
B+C)/D-G | *( | A |
+C)/D-G | *( | AB |
C)/D-G | *(+ | AB |
)/D-G | *(+ | ABC |
/D-G | * | ABC+ |
D-G | / | ABC+* |
-G | / | ABC+*D |
G | - | ABC+*D/ |
| - | ABC+*D/G |
|
| ABC+*D/G- |
Hence postfix expression is ABC+*D/G-
*********PROGRAM FOR INFIX TO POSTFIX****************
#include <iostream.h>
#include <string.h>
#include <ctype.h>
#define int MAX = 50 ;
Class stack
{
Private :
Char S[MAX], A[MAX] ;
Char *s, *t ;
Int top ;
Public :
Stack( ) ;
Void exprn ( char *str ) ;
Void push ( char c ) ;
Char pop( ) ;
Void convert( ) ;
Int priority ( char c ) ;
Void display( ) ;
} ;
Stack :: stack( )
{
Top = -1 ;
Strcpy ( S, "" ) ;
Strcpy ( A, "" ) ;
t = S ;
s = "" ;
}
Void stack :: exprn ( char *str )
{
s = str ;
}
Void stack :: push ( char c )
{
If ( top == MAX )
Cout << "\nStack is full\n" ;
Else
{
Top++ ;
A[top] = c ;
}
}
Char stack :: pop( )
{
If ( top == -1 )
{
Cout << "\nStack is empty\n" ;
Return -1 ;
}
Else
{
Char x = A[top] ;
Top-- ;
Return x ;
}
}
Void stack :: convert( )
{
While ( *s )
{
If ( *s == ' ' || *s == '\t' )
{
s++ ;
Continue ;
}
If ( isdigit ( *s ) || isalpha ( *s ) )
{
While ( isdigit ( *s ) || isalpha ( *s ) )
{
*t = *s ;
s++ ;
t++ ;
}
}
If ( *s == '(' )
{
Push ( *s ) ;
s++ ;
}
Char opr ;
If ( *s == '*' || *s == '+' || *s == '/' || *s == '%' || *s == '-' || *s == '^' )
{
If ( top != -1 )
{
Opr = pop( ) ;
While ( priority ( opr ) >= priority ( *s ) )
{
*t = opr ;
t++ ;
Opr = pop( ) ;
}
Push ( opr ) ;
Push ( *s ) ;
}
Else
Push ( *s ) ;
s++ ;
}
If ( *s == ')' )
{
Opr = pop( ) ;
While ( ( opr ) != '(' )
{
*t = opr ;
t++ ;
Opr = pop( ) ;
}
s++ ;
}
}
While ( top != -1 )
{
Char opr = pop( ) ;
*t = opr ;
t++ ;
}
*t = '\0' ;
}
Int stack :: priority ( char c )
{
If ( c == '^' )
Return 3 ;
If ( c == '*' || c == '/' || c == '%' )
Return 2 ;
Else
{
If ( c == '+' || c == '-' )
Return 1 ;
Else
Return 0 ;
}
}
Void stack :: display( )
{
Cout << S ;
}
Void main( )
{
Char Y[MAX] ;
Stack O ;
Cout << "\nEnter an expression in infix form: " ;
Cin.getline ( Y, MAX ) ;
O.exprn ( Y ) ;
O.convert( ) ;
Cout << "\nThe postfix expression is: " ;
O.display( ) ;
}
Infix to Prefix
Manual Transformation
Infix expression can be manually converted to prefix in following steps.
Fully parenthesize the infix expression considering operator precedence. There should be one set of parentheses per operator.
Evaluate innermost expression first. Replace left parenthesis with corresponding operator.
Remove right parentheses.
Eg. X+Y/Z
Step 1 :(X+(Y/Z))
Step 2:(X+/YZ))
+X/YZ))
Step 3 :+X/YZ
Stack Transformation
Infix expression can be converted to prefix using stack in following steps.
Reverse the given infix expression.
Convert every opening bracket( into closing bracket ) and vice versa.
Convert the resultant expression into postfix form by following algorithm.
Initialize an empty stack.
While not to end of infix expression
Scan the expression from left to right.
Get the input token in the infix expression.
a) A left parenthesis then push it onto the stack
b) A right parenthesis then Pop and display stack elements until a left parenthesis is encountered.
Note: Do not display parenthesis. Parenthesis has least priority in stack but highest priority when in input expression.
c) An operator: If the stack is empty or input token has higher priority than the top stack, push onto the stack. Otherwise, pop and display the top stack element. Repeat the comparison of input token with the new top stack element.
d) An operand: Just display it.
When end of infix expression is reached, pop and display stack elements until the stack is empty.
Reverse the resultant expression.
Eg. (A-(B/C))*((D*E)-F)
Step 1: Reverse the given expression
Original expression is (A-(B/C))*((D*E)-F) By reversing we get )F-)E*D((*))C/B(-A(
Step 2: Convert every opening bracket( into closing bracket ) and vice versa.
(F-(E*D))*((C/B)-A)
Step 3:Convert the resultant expression in postfix form
Infix | Stack | Postfix |
(F-(E*D))*((C/B)-A) |
|
|
F-(E*D))*((C/B)-A) | ( |
|
-(E*D))*((C/B)-A) | ( | F |
(E*D))*((C/B)-A) | (- | F |
E*D))*((C/B)-A) | (-( | F |
*D))*((C/B)-A) | (-( | FE |
D))*((C/B)-A) | (-(* | FE |
))*((C/B)-A) | (-(* | FED |
)*((C/B)-A) | (- | FED* |
*((C/B)-A) |
| FED*- |
((C/B)-A) | * | FED*- |
(C/B)-A) | *( | FED*- |
C/B)-A) | *(( | FED*- |
/B)-A) | *(( | FED*-C |
B)-A) | *((/ | FED*-C |
)-A) | *((/ | FED*-CB |
-A) | *( | FED*-CB/ |
A) | *(- | FED*-CB/ |
) | *(- | FED*-CB/A |
| * | FED*-CB/A- |
|
| FED*-CB/A-* |
Step 4:Reverse the postfix expression
*-A/BC-*DEF
Hence the prefix expression is *-A/BC-*DEF
Eg.2 4*(2-(6*3+4)*2)+1
Step 1: Step 1: Reverse the given expression
Original expression is 4*(2-(6*3+4)*2)+1
By reversing we get 1+)2*)4+3*6(-2(*4
Step 2: Convert every opening bracket( into closing bracket ) and vice versa.
1+(2*(4+3*6)-2)*4
Step 3:Convert the resultant expression in postfix form
Infix | Stack | Postfix |
1+(2*(4+3*6)-2)*4
|
|
|
+(2*(4+3*6)-2)*4 |
| 1 |
(2*(4+3*6)-2)*4 | + | 1 |
2*(4+3*6)-2)*4 | +( | 1 |
*(4+3*6)-2)*4 | +( | 12 |
(4+3*6)-2)*4 | +(* | 12 |
4+3*6)-2)*4 | +(*( | 12 |
+3*6)-2)*4 | +(*( | 124 |
3*6)-2)*4 | +(*(+ | 124 |
*6)-2)*4 | +(*(+ | 1243 |
)-2)*4 | +(*(+* | 1243 |
-2)*4 | +(*(+* | 12436 |
2)*4 | +(* | 12436*+ |
)*4 | +(- | 12436*+* |
*4 | +(- | 12436*+*2 |
4 | + | 12436*+*2- |
| +* | 12436*+*2- |
| +* | 12436*+*2-4 |
|
| 12436*+*2-4*+ |
Step 4:Reverse the postfix expression
+*4-2*+*63421
Hence the prefix expression is +*4-2*+*63421
***program to convert infix to prefix**************
#include <iostream.h>
#include <string.h>
#include <ctype.h>
#define int MAX = 50 ;
Class stack
{
Private :
Char S[MAX], A[MAX] ;
Char *s, *t ;
Int top, len ;
Public :
Stack( ) ;
Void exprn ( char *str ) ;
Void push ( char c ) ;
Char pop( ) ;
Void convert( ) ;
Int priority ( char c ) ;
Void display( ) ;
} ;
Stack :: stack( )
{
Top = -1 ;
Strcpy ( S, "" ) ;
Strcpy ( A, "" ) ;
Len = 0 ;
}
Void stack:: exprn ( char *str )
{
s = str ;
Strrev ( s ) ;
Len = strlen ( s ) ;
* ( S + len ) = '\0' ;
t = S + ( len - 1 ) ;
}
Void stack :: push ( char c )
{
If ( top == MAX - 1 )
Cout << "\nStack is full\n" ;
Else
{
Top++ ;
A[top] = c ;
}
}
Char stack :: pop( )
{
If ( top == -1 )
{
Cout << "Stack is empty\n" ;
Return -1 ;
}
Else
{
Char x = A[top] ;
Top-- ;
Return x ;
}
}
Void stack:: convert( )
{
Char opr ;
While ( *s )
{
If ( *s == ' ' || *s == '\t' )
{
s++ ;
Continue ;
}
If ( isdigit ( *s ) || isalpha ( *s ) )
{
While ( isdigit ( *s ) || isalpha ( *s ) )
{
*t = *s ;
s++ ;
t-- ;
}
}
If ( *s == ')' )
{
Push ( *s ) ;
s++ ;
}
If ( *s == '*' || *s == '+' || *s == '/' ||
*s == '%' || *s == '-' || *s == '^' )
{
If ( top != -1 )
{
Opr = pop( ) ;
While ( priority ( opr ) > priority ( *s ) )
{
*t = opr ;
t-- ;
Opr = pop( ) ;
}
Push ( opr ) ;
Push ( *s ) ;
}
Else
Push ( *s ) ;
s++ ;
}
If ( *s == '(' )
{
Opr = pop( ) ;
While ( ( opr ) != ')' )
{
*t = opr ;
t-- ;
Opr = pop ( ) ;
}
s++ ;
}
}
While ( top != -1 )
{
Opr = pop( ) ;
*t = opr ;
t-- ;
}
t++ ;
}
Int stack :: priority ( char c )
{
If ( c == '^' )
Return 3 ;
If ( c == '*' || c == '/' || c == '%' )
Return 2 ;
Else
{
If ( c == '+' || c == '-' )
Return 1 ;
Else
Return 0 ;
}
}
Void stack :: display( )
{
While ( *t )
{
Cout << " " << *t ;
t++ ;
}
}
Void main( )
{
Char C[MAX] ;
Stack O ;
Cout << "\nEnter an expression in infix form: " ;
Cin.getline ( C, MAX ) ;
O.exprn( C ) ;
O.convert( ) ;
Cout << "The Prefix expression is: " ;
O.display( ) ;
}
Postfix to Infix
Steps to convert postfix to infix are as follows
Scan the postfix expression from left to right.
If token is an operand push it into stack.
If token is an operator pop recent two operands. Form new subexpression with this operator and operands in infix form(operator between two operands).Place parentheses for subexpression to ensure proper order of evaluation in final expression.
Note: We place parenthesis only if it is required(operator in subexpression has lower precedence than operator used to merge two subexpressions ).Otherwise proper order of evaluation is maintained without any additional parentheses.
Push resulting subexpression in stack.
Move to next token.
Repeat steps 2 to 5 till the end of postfix expression.
Eg1.ab*cd*+e*
Postfix Expression | Stack | Description |
Ab*cd*+e* | Empty | Initially stack is empty |
b*cd*+e* | a | First token is operand hence push it to stack. |
*cd*+e* | a, b | Next token is an operand. Push it into stack. |
Cd*+e* | (a*b) | Next token is an operator ‘*’.Pop two recent operands(a,b) and form subexpression(a*b) in infix form. Place parentheses for Resultant subexpression(a*b).Push it into stack. |
d*+e* | (a*b), c | Next token is an operand c. Push it into stack |
*+e* | (a*b), c,d | Next token is an operand d. Push it into stack |
*+e* | (a*b), (c*d) | Next token is an operator ‘*’.Pop two recent operands(c,d) and form subexpression in infix form. Place parentheses for Resultant subexpression(c*d).Push it into stack. |
+e* | ((a*b)+ (c*d)) | Next token is an operator ‘+’.Pop two recent operands(a*b)and(c*d). Form subexpression in infix form. Place parentheses for Resultant subexpression((a*b)(c*d)).Push it into stack. |
e* | (a*b)+(c*d),e | Next token is an operand e. Push it into stack |
* | ((a*b)+(c*d))*e | Next token is an operator ‘*’.Pop two recent operands((a*b)+(c*d))and e. Form subexpression in infix form ((a*b)+(c*d))*e. Push it into stack. |
| ((a*b)+(c*d))*e |
|
Hence resultant infix expression is ((a*b)+(c*d))*e
Eg.2:Convert the following postfix expression to infix using stack.
Abcde^^*- May 2006
Postfix Expression | Stack | Description |
Abcde^^*- | Empty | Initially token is empty |
Bcde^^*- | A | Next token is an operand a. Push it into stack. |
Cde^^*- | a,b | Next token is an operand b. Push it into stack. |
De^^*- | a,b,c | Next token is an operand c. Push it into stack. |
e^^*- | a,b,c,d | Next token is an operand d. Push it into stack. |
^^*- | a,b,c,d,e | Next token is an operand e. Push it into stack. |
^*- | a,b,c,(d^e) | Next token is an operator ‘^’.Pop two recent operands(d)and(e). Form subexpression in infix form. Place parentheses for Resultant subexpression(d^e).Push it into stack. |
*- | a,b,c^(d^e) | Next token is an operator ‘^’.Pop two recent operands(c)and(d^e). Form subexpression in infix form. Push it into stack. |
- | a, b*c^(d^e) | Next token is an operator ‘*’.Pop two recent operands.Form subexpression in infix form. Push it into stack. |
| a-b*c^(d^e) | Next token is an operator ‘-’.Pop two recent operands. Form subexpression in infix form. Push it into stack. |
Hence resultant expression is a-b*c^(d^e)
Postfix to prefix
Postfix expression can be converted to prefix using following steps.
Scan the postfix expression from left to right.
If token is an operand push it into stack.
If token is an operator pop recent two operands. Form new subexpression with this operator and operands in prefix form(operator before two operands).
Push resulting subexpression in stack.
Move to next token.
Repeat step 2 to 5 till the end of postfix expression.
Eg.1: Convert the following postfix expression to prefix using stack.
Abcde^^*- May 2006
Postfix Expression | Stack | Description |
Abcde^^*- | Empty | Initially stack is empty |
Bcde^^*- | a | Next token is an operand a. Push it into stack. |
Cde^^*- | a,b | Next token is an operand b. Push it into stack. |
De^^*- | a,b,c | Next token is an operand c. Push it into stack. |
e^^*- | a,b,c,d | Next token is an operand d. Push it into stack. |
^^*- | a,b,c,d,e | Next token is an operand e. Push it into stack. |
^*- | a,b,c,^de | Next token is an operator ‘^’.Pop two recent operands(d)and(e). Form subexpression in prefix form. Push it into stack. |
*- | a,b,^c^de | Next token is an operator ‘^’.Pop two recent operands(c)and(^de). Form subexpression in prefix form. Push it into stack. |
- | a, *b^c^de | Next token is an operator ‘*’.Pop two recent operands.Form subexpression in prefix form. Push it into stack. |
| -a*b^c^de | Next token is an operator ‘-’.Pop two recent operands. Form subexpression in prefix form. Push it into stack. |
Hence resultant prefix expression is -a*b^c^de
Prefix to Infix
Steps to convert prefix to infix are as follows
Scan the prefix expression from right to left.
If token is an operand push it into stack.
If token is an operator pop recent two operands. Form new subexpression with this operator and operands in infix form(operator between two operands).Place parentheses for subexpression to ensure proper order of evaluation in final expression.
Note: We place parenthesis only if it is required(operator in subexpression has lower precedence than operator used to merge two subexpressions ).Otherwise proper order of evaluation is maintained without any additional parentheses.
Push resulting subexpression in stack.
Move to next token.
Repeat step 2 to 5 till the end of prefix expression.
Eg1. +/+AB-CDE
Prefix Expression | Stack | Description |
+/+AB-CDE | Empty | Initially stack is empty |
+/+AB-CD | E | Next token is an operand E. Push it into stack. |
+/+AB-C | E,D | Next token is an operand D. Push it into stack. |
+/+AB- | E,D,C | Next token is an operand C. Push it into stack. |
+/+AB | E,(C-D) | Next token is an operator ‘-’.Pop two recent operands(C)and(D). Form subexpression in infix form. Push it into stack. |
+/+A | E,(C-D),B | Next token is an operand B. Push it into stack. |
+/+ | E,(C-D),B,A | Next token is an operand A. Push it into stack. |
+/ | E,(C-D),(A+B) | Next token is an operator ‘+’.Pop two recent operands(A)and(B). Form subexpression in infix form. Push it into stack. |
+ | E,(A+B)/(C-D) | Next token is an operator ‘/’.Pop two recent operands(A+B)and(C+D). Form subexpression in infix form. Push it into stack. |
| (A+B)/(C-D)+E | Next token is an operator ‘+’.Pop two recent operands(A+B)/(C-D) and E. Form subexpression in infix form. Push it into stack. |
Hence resultant infix expression is (A+B)/(C-D)+E
Prefix to Postfix
Steps to convert prefix to postfix are as follows
Scan the prefix expression from right to left.
If token is an operand push it into stack.
If token is an operator pop recent two operands. Form new subexpression with this operator and operands in postfix form(operator after two operands).
Push resulting subexpression in stack.
Move to next token.
Repeat step 2 to 5 till the end of prefix expression.
Eg1. +/+AB-CDE
Prefix Expression | Stack | Description |
+/+AB-CDE | Empty | Initially stack is empty |
+/+AB-CD | E | Next token is an operand E. Push it into stack. |
+/+AB-C | E,D | Next token is an operand D. Push it into stack. |
+/+AB- | E,D,C | Next token is an operand C. Push it into stack. |
+/+AB | E,CD- | Next token is an operator ‘-’.Pop two recent operands(C)and(D). Form subexpression in postfix form. Push it into stack. |
+/+A | E,CD-,B | Next token is an operand B. Push it into stack. |
+/+ | E,CD-,B,A | Next token is an operand A. Push it into stack. |
+/ | E,CD-,AB+ | Next token is an operator ‘+’.Pop two recent operands(A)and(B). Form subexpression in postfix form. Push it into stack. |
+ | E,AB+/CD- | Next token is an operator ‘/’.Pop two recent operands(AB+)and(CD+). Form subexpression in postfix form. Push it into stack. |
| AB+/CD-E+ | Next token is an operator ‘+’.Pop two recent operandsAB+/CD- and E. Form subexpression in postfix form. Push it into stack. |
Hence resultant postfix expression is AB+/CD-E+
Queue
ADT of Queue
A Queue is a linear list in which data is inserted at one end called as rear and deleted from other end called as front. Queue removes elements in the same order in which they were inserted i.e. element inserted first is removed first. Hence they are called as First-in-First out( FIFO) data structure.
Imagine a queue of people waiting for a bus. The person in the front of queue will get a first chance to board a bus. The person at the rear will be last one to board a bus. Same case is of check out line in a grocery store or a cafeteria, list of jobs to be processed by computer or a list of calls on mobile phone.Fig.1 shows queue of alphabets. Alphabets are added at rear and removed from front end.
A Front | B | C | D | E | F Rear |
Fig 1. Queue of alphabets
We will see queue with respect to an example. Imagine queue of alphabets with size of three. Initially queue is empty.
Front |
|
Rear |
Now let us add an element in a queue. So queue becomes
Front |
| A Rear |
Add one more element ’B’ in a queue. Since element can only be inserted at rear, A progresses through queue and B is inserted at rear. Now queue becomes
Front | A | B Rear |
Adding one more element ‘C’ in queue
A Front | B | C Rear |
Now queue is full. If we try to insert one more element in queue then queue overflow occurs.
Now remove elements from queue. Element in queue is always removed from front end. Currently ‘A’ is at front end and hence will be removed first.
B Front | C |
Rear |
Removing ‘B’ and ‘C’ we get
Front |
|
Rear |
Now queue is empty. If we try to remove elements from queue, queue underflow occurs.
Operations on Queue:
Bool enqueue(TYPE in): Insert elements at rear of queue.
Bool dequeue(TYPE & out): Remove elements from front of queue.
Bool Front(TYPE& out): Determines element at the front of queue.
Bool Rear(TYPE& in): Determines element at the rear of queue.
Int Count():Determines total number of elements present in queue.
Bool isEmpty():Determines if queue is empty.
Bool isFull():Determines if queue is full.
Array Implementation of Queue
Template <class TYPE>
Struct Node //Node declaration
{
TYPE value; //data in a node
};
Template <class TYPE> //class template for queue
Class Queue
{
Private:
Node<TYPE> * P; //pointer to node
Int count;// number of elements present in queue
Int max; // maximum queue size
Int front; //index of element at front
Int rear // index of element at rear
Public:
Queue(int size=50);
~Queue();
Bool enqueue(TYPE in);
Bool dequeue(TYPE& out);
Bool QFront(TYPE& out);
Bool QRear(TYPE& out);
Int QCount();
Bool isEmpty();
Bool isFull();
};
We will see array implementation for
1. Linear Queue
2. Circular Queue
2.9.1 Array implementation for Linear Queue
Algorithms:
Create queue: Queue(int size)
Steps | Algorithm: Queue(int size) | Description
|
1 | Template<class TYPE> Queue<TYPE>::Queue(int size) { | Design constructor to create a queue with initial capacity. |
2 | Max=size; Front=-1; Rear=-1; Count=0; | Initially queue is empty so set front and rear to -1 and count to zero. |
3 | P=new Node<TYPE>[max] | Allocate memory to node P |
4 | If(!P) { Cout<<”Insufficient memory”; Exit(1); } } |
If memory cannot be allocated then print memory is unavailable. |
We assume queue of size 5.Initially queue is empty. So
Count=0
Front=rear=-1
Max=5
|
|
|
|
|
Data
Index 0 1 2 3 4
Enqueue: Insert element in queue
Steps | Algorithm: bool enqueue(TYPE in) | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::enqueue(TYPE in) { | Design function to insert element ‘in’ to queue. This function returns true if element is inserted successfully. |
2 | If(count==max) Return false | If queue is full then return false to indicate element cannot be inserted. |
3 | Rear++; | If queue is not full increment rear. |
5 | P[rear].value=in; | Insert data at rear |
6 | If(count==0) Front=0 | If count is 0 it means queue is empty. Set front pointer to 0. |
7 | Count++;
| Increment count |
8 | Return true } | Return true to indicate successful insertion of an element in queue. |
Let us add element ’10’ to queue. After adding an element in queue
Count =1
Front=rear=0
Max=5
10 |
|
|
|
|
 Data
Data
Index 0 1 2 3 4
Front rear
Add one more element ‘20’ to queue.
Count =2
Front=0
Rear=1
10 | 20 |
|
|
|
 Data
Data
Index 0 1 2 3 4
Front rear
Dequeue: Removes element from front of queue.
Steps | Algorithm: bool dequeue(TYPE& out) | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::dequeue(TYPE& out) { | Design function dequeue to remove element in queue. This function returns true if element is removed successfully. |
2 | If(count==0) Return false | If count is 0 return false to indicate queue underflow. |
3 | Out=P[front].value; | Pass data at front to reference parameter |
4 | Front++; | Increment front |
6 | If(count==1) Rear=front=-1; | If queue has only one element data set front and rear to -1. |
7 | Count--;
| Decrement count |
8 | Return true } | Return true to indicate successful removal of an element from queue. |
We continue with same example.
Count =2
Front=0
Rear=1
10 | 20 |
|
|
|
 Data
Data
Index 0 1 2 3 4
Front rear
Elements can be deleted only from front. Deleting an element ‘10’ from queue we get
Count =1
Front=1
Rear=1
| 20 |
|
|
|
 Data
Data
Index 0 1 2 3 4
Front rear
Now queue has only one element(20). Deleting it we get
Count=0
Front=rear=-1
|
|
|
|
|
Data
Index 0 1 2 3 4
QFront: Returns element at front of Queue.
Steps | Algorithm: bool QFront(TYPE& out) | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::QFront(TYPE& out) { | Design function QFront to find element at front . This function returns true if Queue front is found. |
2 | If(count==0) Return false | If count is 0 it means queue is empty. So return false. |
3 | Else { Out=P[front].value; Return true } } | If queue is not empty pass data at front of queue to calling function through reference parameter out. Return true to indicate success. |
QRear: Returns element at rear of Queue.
Steps | Algorithm: bool QRear(TYPE& out) | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::QRear(TYPE& out) { | Design function QRear to find element at rear . This function returns true if element at rear is found. |
2 | If(count==0) Return false | If count is 0 it means queue is empty. So return false. |
3 | Else { Out=P[rear].value; Return true } } | If queue is not empty pass data at rear of queue to calling function through reference parameter out. Return true to indicate success. |
IsEmpty():Determines if queue is empty
Steps | Algorithm: bool isEmpty() | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::isEmpty() { | Design function isEmpty() to find if queue is empty. This function returns true if queue is empty and false otherwise. |
2 | If(count==0) Return true; | If count is 0 it means queue is empty. So return true. |
3 | Else Return false; } | Else return false to indicate queue is not empty. |
IsFull():Determines if queue is full
Steps | Algorithm: bool isFull() | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::isFull() { | Design function isFull() to find if queue is full. This function returns true if queue is full and false otherwise. |
2 | If(count==max) Return true; | If count equals max then return true to indicate queue is full. |
3 | Else Return false | Else return false to indicate queue is not full |
QCount: Determines total number of elements present in queue. For this it simply returns the count in queue.
Steps | Algorithm: int QCount() | Description
|
1 | Template<class TYPE> Int Queue<TYPE>::QCount() { | Design function QCount() to return total number of elements in queue. |
2 | Return count; } | Return count . |
~Queue(): Destroy queue
Queue is destroyed using destructor.
Steps | Algorithm: ~Queue() | Description
|
1 | Template<class TYPE> Queue<TYPE>::~Queue() { | Design destructor to destroy queue. |
| Delete []P } } | Release array |
Write a Program to implement Linear Queue using array
#include<iostream>
#include<string>
#include<conio.h>
#include<process.h>
using namespace std;
template <class TYPE>
Struct Node //Node declaration
{
TYPE value; //data in a node
};
class Queue
{
Private:
Node<TYPE> * P; //
Int count;// number of elements present in queue
Int max; // maximum queue size
Int front; //index of element at front
Int rear // index of element at rear
Public:
Queue(int size=50)
{ max = x;
front=-1;
rear=-1;
Count=0
P = new TYPE[max];
}
~Queue();
Bool enqueue(TYPE in);
Bool dequeue(TYPE& out);
Bool QFront(TYPE& out);
Bool QRear(TYPE& out);
Int QCount();
Bool isEmpty();
Bool isFull();
};
Template <class TYPE>
Bool Queue<TYPE>:: isEmpty()
{
return (count==0);
}
template <class TYPE>
bool Queue<TYPE>::isFull()
{
return (rear==(max-1));
}
template <class TYPE>
bool Queue<TYPE>:: enqueue(TYPE in)
{
if(isFull())
Return false;
Rear++;
P[rear].value=in;
return true;
If(count==0)
Front=0;
Count++;
Return true;
}
template <class TYPE>
bool Queue<TYPE>::deQueue(TYPE & out)
{
if(isEmpty())
Return false;
|
Out=P[front].value;
|
Front++; |
If(count==1) Rear=front=-1; |
Count--;
|
Return true } |
Template <class TYPE>
Bool Queue<TYPE>::QFront(TYPE& out) { |
If(count==0) Return false |
Else { Out=P[front].value; Return true } } Template <class TYPE> |
Bool Queue<TYPE>::QRear(TYPE& out) { |
If(count==0) Return false |
Else { Out=P[rear].value; Return true } } |
Int Queue<TYPE>::QCount() { |
Return count; } |
template <class TYPE>
void Queue<TYPE>:: display()
{
for(int i=front;i<=rear;i++)
{
cout<<P[i]<<" <-- ";
}
cout<<endl;
}
}
void main(){
Queue<int> Q; //create queue of integers
int ch,x;
bool flag;
do{
cout<<"\nEnter your choice:\n1.enqueue\n2.dequeue\n3.queue front\
\n4.queue rear\n5.isfull\n6.isempty\n7.size\n8.display\n9.exit"<<endl;
cin>>ch;
switch(ch){
case 1:
Cout<<”Enter element to be inserted”;
Cin>>x;
flag=Q.enqueue(x)
If(flag==true)
cout<<"The queue is full"<<endl;
else
cout<<”element is inserted successfully ";
break;
case 2:
Flag=Q.dequeue(x);
if(flag==true)
cout<< "element is dequeued"<<endl;
else
cout<<"queue is empty"<<endl;
break;
case 3:TYPE y;
Flag=Q.QFront(y);
If(flag==true)
cout<<”Queue Front is”<<y<<endl;
Else
Cout<<"queue is empty"<<endl;
break;
case 4:TYPE z;
Flag=Q.QRear(z);
If(flag==true)
cout<<”Queue Rear is” <<z<<endl;
Else
Cout<<"queue is empty"<<endl;
break;
case 5:
Flag=Q.isFull();
If(flag==true)
cout<<Queue is full<<endl;
Else
Cout<<"queue is not full"<<endl;
Break;
Case 6:
Flag=Q.isEmpty();
If(flag==true)
cout<<Queue is empty<<endl;
Else
Cout<<"queue is not empty"<<endl;
Case 7:
Int c=Q.QCount();
Cout<<"size of queue is "<<c;
Break;
Case 8:
Q.display();
break;
case 9:exit(1);
}
}while(ch);
getch();
}
Limitation of Linear Queue:
Consider a linear queue of size 3.
Initially queue is empty.
So front,rear=-1
Max=3
|
|
|
Data
Index 0 1 2
Consider trace of operations on this queue.
A |
|
|
Enqueue A
 0 1 2
0 1 2
Front rear
A | B |
|
Enqueue B
 0 1 2
0 1 2
Front rear
| B |
|
Dequeue A
 0 1 2
0 1 2
Front rear
| B | C |
 enqueue C
enqueue C
 0 1 2
0 1 2
Front rear
| B | C |
 enqueue D
enqueue D
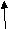 0 1 2
0 1 2
Front rear
Here when we try to insert D, overflow occurs as rear=max-1. But actually queue is not full as first location of queue is empty. Thus here memory is not utilized efficiently.
A more suitable method of representing a queue will be circular queue where all the elements are arranged in circular fashion .In circular queue last element is logically followed by first element. Fig- shows circular queue.
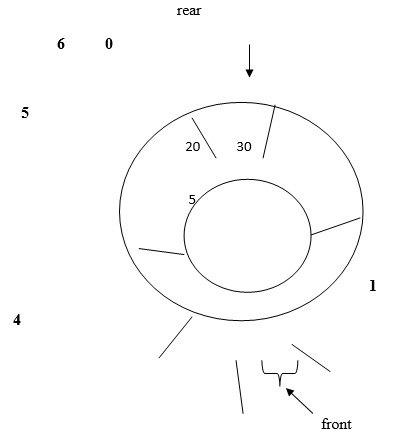
In above circular queue index 0 and 1 are vacant so we can insert element at these positions when rear=max-1.
We do this by wrapping rear to first index position.
Hence now rear=0. Inserting element ‘7’we get
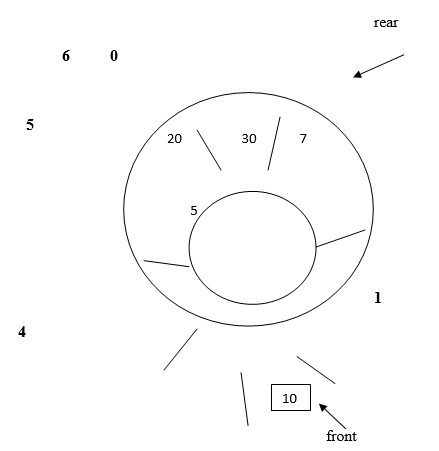
In this way memory can be utilized efficiently in circular queue.
2.9.2 Array implementation for Circular Queue
ALGORITHMS:
Queue():Create queue
Queue is created using constructor.
Steps | Algorithm: Queue(int size) | Description
|
1 | Template<class TYPE> Queue<TYPE>::Queue(int size) { | Design constructor to create a queue with initial capacity. |
2 | Max=size; Front=-1; Rear=-1; Count=0; | Initially queue is empty so set front and rear to -1 and count to zero. |
3 | P=new Node<TYPE>[max] | Allocate memory to node P |
4 | If(!P) { Cout<<”Insufficient memory”; Exit(1); } } |
If memory cannot be allocated then print memory is unavailable. |
We assume queue of size 7.Intially Queue is empty. So
Count=0
Front=rear=-1;
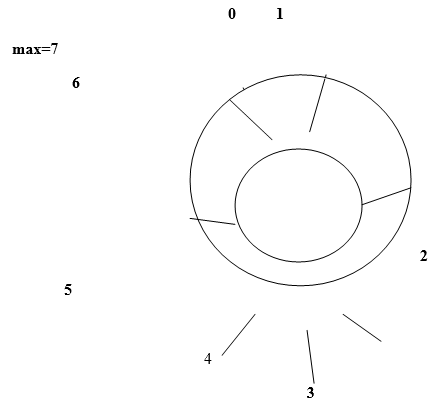
Enqueue: Insert element in queue
Steps | Algorithm: bool enqueue(TYPE in) | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::enqueue(TYPE in) { | Design function to insert element ‘in’ to queue. This function returns true if element is inserted successfully. |
2 | If(count==max) Return false | If queue is full then return false to indicate element cannot be inserted. |
3 | Rear++; | If queue is not full increment rear. |
4 | If(rear==max-1) Rear=0; | If rear is last element wrap to the first element of queue. |
5 | P[rear].value=in; | Insert data at rear |
6 | If(count==0) Front=0 | If count is 0 it means queue is empty. Set front pointer to 0. |
7 | Count++;
| Increment count |
8 | Return true } | Return true to indicate successful insertion of an element in queue. |
Let us add element to circular queue. After adding an element’10’ in queue
Count =1
Front=rear=0
Max=7
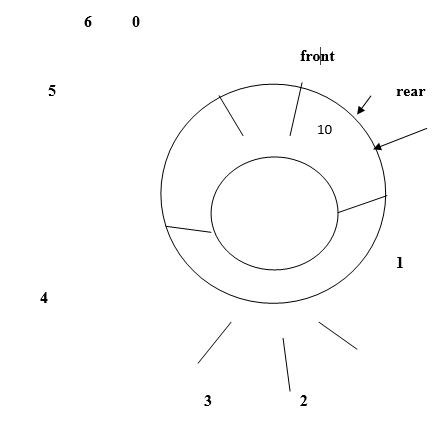
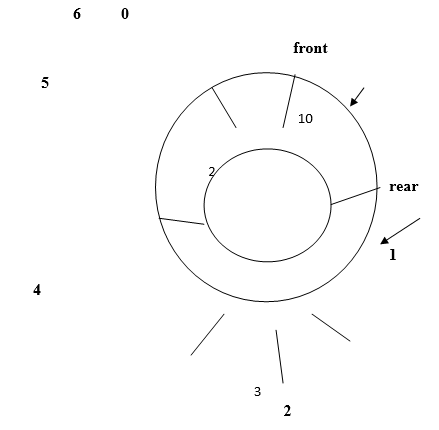
Add one more element ‘2’ to queue.
Count=2
Front=0
Rear=1
Dequeue: Removes element from front of queue.
Steps | Algorithm | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::dequeue(TYPE& out) { | Design function dequeue to remove element in queue. This function returns true if element is removed successfully. |
2 | If(count==0) Return false | If count is 0 return false to indicate queue underflow. |
3 | Out=P[front].value; | Pass element at front to reference parameter out |
4 | Front++; | Increment front |
5 | If(front==max-1) Front=0; | If front is last element wrap queue front to 0. |
6 | If(count==1) Rear=front=-1; | If queue has only one element data set front and rear to -1. |
7 | Count--;
| Decrement count |
8 | Return true } | Return true to indicate successful removal of an element from queue. |
QFront: Returns element at front of Queue.
Steps | Algorithm | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::QFront(TYPE& out) { | Design function QFront to find element at front . This function returns true if Queue front is found. |
2 | If(count==0) Return false | If count is 0 it means queue is empty. So return false. |
3 | Else { Out=P[front].value; Return true } } | If queue is not empty pass data at front of queue to calling function through reference parameter out. Return true to indicate success. |
QRear: Returns element at rear of Queue.
Steps | Algorithm | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::QRear(TYPE& out) { | Design function QRear to find element at rear . This function returns true if element at rear is found. |
2 | If(count==0) Return false | If count is 0 it means queue is empty. So return false. |
3 | Else { Out=P[rear].value; Return true } } | If queue is not empty pass data at rear of queue to calling function through reference parameter out. Return true to indicate success. |
10.isEmpty():Determines if queue is empty
Steps | Algorithm | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::isEmpty() { | Design function isEmpty() to find if queue is empty. This function returns true if queue is empty and false otherwise. |
2 | If(count==0) Return true; | If count is 0 it means queue is empty. So return true. |
3 | Else Return false; } | Else return false to indicate queue is not empty. |
IsFull():Determines if queue is full
Steps | Algorithm | Description
|
1 | Template<class TYPE> Bool Queue<TYPE>::isFull() { | Design function isFull() to find if queue is full. This function returns true if queue is full and false otherwise. |
2 | If(count==max) Return true; | If count equals max then return true to indicate queue is full. |
3 | Else Return false | Else return false to indicate queue is not full |
QCount: Determines total number of elements present in queue.
Steps | Algorithm | Description
|
1 | Template<class TYPE> Int Queue<TYPE>::QCount() { | Design function QCount() to return total number of elements in queue. |
2 | Return count; } | Return count . |
~Queue(): Destroy queue
Queue is destroyed using destructor.
Steps | Algorithm | Description
|
1 | Template<class TYPE> Queue<TYPE>::~Queue() { | Design destructor to destroy queue. |
| Delete []P } } | Release array |