UNIT-1
Ordinary differential equations
A differential equation is an equation with a function and one and more of its derivatives:
For example: y + 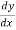 = 8x
= 8x
A differential equation with only single independent variable is known as ordinary differential equation.
Here we will learn about degree and order of an ordinary differential equation:
Order: the order is the highest derivative:
For example: (1) 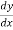 + y³ = 8x , here it has only first derivative so its ‘first order’.
+ y³ = 8x , here it has only first derivative so its ‘first order’.
(2) 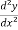 + y³ = 7x , here it has a second derivative so its ‘second order’ and so on.
+ y³ = 7x , here it has a second derivative so its ‘second order’ and so on.
Degree: Degree is known as the exponent of higher derivative.
For example: (1) 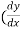 )² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
)² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
(2) 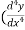 ) +
) +  y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
Note- A solution to a differential equation which contains one or more arbitrary constants of integration is called general solution.
If additional information is given so that constant may be calculated the particular solution . Additional informations are boundary conditions.
Let’s understand how to solve differential equations:
(1) The solution of equations of the form 
This type of equation can be solved by direction integration:
Y = 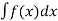
Example-1: Find the general solution of x 2 – 4x³
2 – 4x³
Solution: rearranging the given equation:
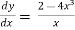 =
=  -
- 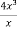 =
= 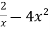
On integrating both sides,
y =  = 2 In x -
= 2 In x - 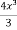 + c
+ c
This is the general solution.
Exampl-2: Find the particular solution of the differential equation 5 , given the boundary condition y = 1
, given the boundary condition y = 1 , when x = 2.
, when x = 2.
Solution: rearrange the diff. Equation,
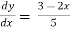 =
=  -
- 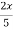
y = 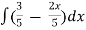 =
= 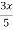 -
- 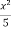 + c, which is the general solution.
+ c, which is the general solution.
Put the boundary conditions to find c,
1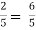 -
- 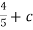 , which gives, c = 1
, which gives, c = 1
Hence the particular solution is,
y = 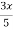 -
- 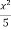 + 1.
+ 1.
(2) The solution of equation of the form 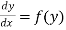 ,
,
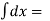
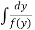
Example-1: Find the general solution of 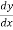 = 3 + 2y
= 3 + 2y
Solution: here, 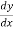 = 3 + 2y gives,
= 3 + 2y gives,

 ,
,
Integrating both sides,
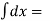
 ,
,
By substitution, u = (3 +2y),
X =  In(3 + 2y) + c.
In(3 + 2y) + c.
Example-2: Determine the particular solution of (y² - 1)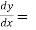 3y given that y =1 when x = 2
3y given that y =1 when x = 2 .
.
Solution: It gives,
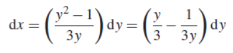
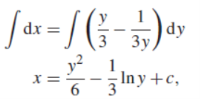
When putting the values, y =1 , x = 2 ,
,
The particular solution will be,
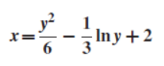
(3) The solution of equation of the form 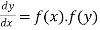
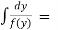
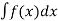
Example-1: Solve the equation 4xy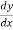 = y² - 1
= y² - 1
Solution: on separating variables, we get
(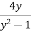 ) dy =
) dy =  dx
dx
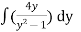 =
= 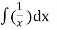
Using substitution, u = y² - 1
2In(y² - 1) = In x + c.
Example-2: Determine the particular solution of  = 2
= 2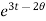 , given that t = 0, when θ = 0
, given that t = 0, when θ = 0
Solution: 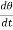 = 2
= 2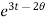 = 2
= 2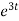
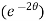 ,
,
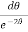 = 2
= 2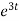 dt
dt
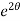 dθ =
dθ = 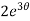 dt
dt
Now integrating both sides,
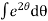 =
= 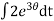
The general solution is ,
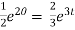 + c.
+ c.
When t = 0 and θ = 0, c = 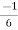
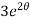 =
= 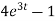
Definition- A differential equation M(x , y)dx + N(x , y)dy = 0 is said to be exact if there exist a function h( x, y) such that,
d h(x, y) = M(x , y)dx + N(x , y)dy
Note – before solving exact differential equations , first we test for exactness as mentioned below-
Any differential equation is exact if and only if-
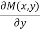 =
= 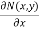
Working steps to solve exact differential equation:
(1) first we check the exactness of the differential equation.
(2) then we write the system of two differential equations that defines the function h(x,y)
h(x,y) : 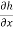 = P(x,y) ,
= P(x,y) , 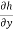 = Q(x,y)
= Q(x,y)
(3) integrate first equation over x , here we write a unknown function g(y) instead of constant C.
h(x,y) = 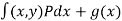
(4) differentiate with respect to y , we substitute the function h(x,y) as follows;
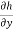 =
= 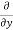 (
(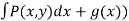 = Q(x,y)
= Q(x,y)
We get, g’(x) = Q(x,y) - 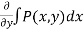 ,
,
Now integrate this function, we get
h(x,y) = 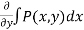 + g(x)
+ g(x)
Example-1: solve (6x² - y +3)dx + (3y² -x -2)dy = 0
Sol. First we check exactness,
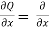 (3y² -x -2) = -1
(3y² -x -2) = -1
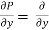 (6x² - y +3) = -1
(6x² - y +3) = -1
Hence this is an exact differential equation.
Write the system of equation to find h(x,y),
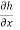 = P(x,y) = (6x² - y +3)
= P(x,y) = (6x² - y +3)
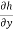 = Q(x,y) = (3y² -x -2)
= Q(x,y) = (3y² -x -2)
Integrate the first eq. w.r.t. x , assume y is constant,
h(x,y) = 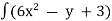 dx
dx
= 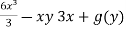
= 2x³ - xy +3x +g(y)
Here we have continuous differentiable function g(y) instead of C.
Now,
 =
= 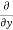 (2x³ - xy +3x +g(y))
(2x³ - xy +3x +g(y))
-x + g’(x) = 3y² - x – 2
We get,
g’(x) = 3y² – 2
Now integrate,
g(x) = 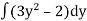 = y³ - 2y
= y³ - 2y
So,
h(x,y) = 2x³ -xy +3x +y³ -2y,
The general solution is defined by the following expression,
2x³ -xy +3x +y³ -2y = C
Example-2: Determine whether the differential function ydx –xdy = 0 is exact or not.
Solution. Here the equation is the form of M(x , y)dx + N(x , y)dy = 0
But, we will check for exactness,

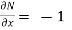
These are not equal results, so we can say that the given diff. Eq. Is not exact.
Bernoulli’s Equation:
A Bernoulli differential equation is an equation of the form
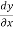 + p(x)y = q(x) yⁿ
+ p(x)y = q(x) yⁿ
When n = 1 or 0 , a Bernoulli eq. Reduces to a linear equation.
If n is real number then we make substitution,
Z = y¹‾ⁿ
Example-3: Solve 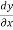 + xy = xy²
+ xy = xy²
Solution : Here , n =2, so me make substitution,
z =y¹‾² = y‾¹
y = 
y’ = 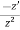
Now substitute these equations,
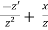 =
= 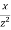
Or z’ – zx = -x -----------(1)
This is the linear form of unknown function f(z),
Integrating factor is,
I(x) = 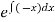 =
= 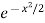
Multiply (1) by I(x), we get
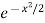
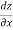 - x
- x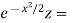 -x
-x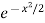
Or 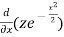 = -x
= -x
Integrating both sides,
 =
= 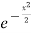 +c
+c
Z(x) = c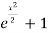
The solution for the original diff. Eq.
y = 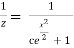 .
.
The basic equation of current I in a simple RLC, is given as below,
Where, R = resistance , L= inductor , E = electromotive force
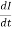 +
+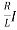 =
= 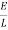
For an RC circuit which consist resistance and capacitance C and no inductance , then the equation for the electric charge q on the capacitor is given by,
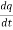 +
+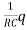 =
= 
The relationship between q and I is given by,
I = 
