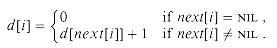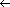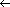Unit 8

PRAM Algorithms

8.1 Introduction

Here are a few simple details about general parallel processing. The following is one very simple fact that applies to parallel computation, irrespective of how it is implemented:

Suppose that T is the fastest sequential algorithm to perform a computation with parameter n. (n). Then, with m processors, the fastest parallel algorithm (each comparable to that of the sequential computer) has execution time / T(n)/m. The principle here is: If you could find a faster parallel algorithm, you could run it sequentially by simulating parallelism with a sequential machine and obtaining a faster sequential algorithm. This would contradict the fact that the sequential algorithm is the fastest possible.

We believe that the cost of sequential algorithms simulating parallel algorithms is negligible. The' Theory of Unitary Speedup' is called this assertion. As normal, the n parameter represents the relative size of the issue being considered as an example. For example, if the problem was that of sorting, n might be the number of items to be sorted and T(n) would be O(n lg n) for a comparison-based sorting algorithm.

As clear as this assertion is, it is a little controversial. It makes the tacit inference that deterministic is the algorithm in question. The algorithm, in other words, is like the normal computer programme definition – It conducts measurements and makes decisions based on the performance of these Calculations.

There is an important field of algorithm theory in which the assumption is not necessarily true; this is randomised algorithm theory. Here, at some point of the calculation, a solution to an issue could involve making random guesses. In this case, the parallel algorithm using m processors will run the sequential algorithm's speed faster than m. In certain problems in which random search is used, this phenomenon occurs and most guesses on a solution quickly lead to a valid solution, but there are a few guesses that run for a long time without producing any concrete results.

The sum of all these times, or 10.99 time-units, is the estimated execution time of a single (sequential) attempt to find a solution.

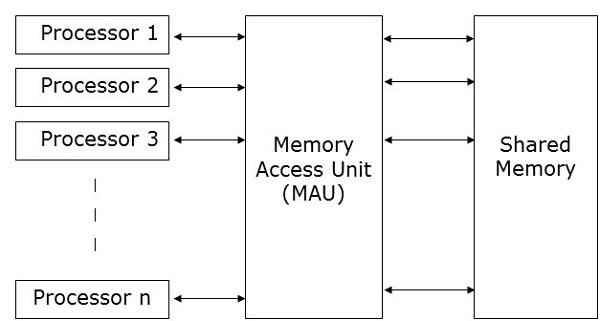
A model that is considered for most parallel algorithms is Parallel Random Access Machines (PRAM). Here, a single block of memory is connected to several processors.

A PRAM model requires −

●      A group of processors of a similar kind.

●      A common memory unit is shared by all the processors. Processors can only interact with each other via a shared memory.

●      A memory access unit (MAU) connects the processors to a single memory that is shared.

Fig 1: memory access unit

Here, on n number of data in a given unit of time, n number of processors may perform independent operations. This can result in simultaneous access by numerous processors to the same memory location.

Key takeaways

1. We believe that the cost of sequential algorithms simulating parallel algorithms is negligible.
2. The' Theory of Unitary Speedup' is called this assertion.
3. There is an important field of algorithm theory in which the assumption is not necessarily true; this is randomized algorithm theory.

8.2 Computational Model

Take into consideration some basic algorithms that can be used while using a SIMD

Machine where you can access common RAM from any processor. A machine in which several processors can access common RAM in a single programme phase is commonly referred to as the PRAM computer model. This is one of the oldest parallel processing models to be taken into account, but there have never been any large parallel computers implementing it. The PRAM model is a sort of parallel machine mathematical idealization that removes many of the low-level specifics and enables a researcher to focus on the strictly parallel aspects of a problem.

The PRAM model of computation has historically been considered to be of greater theoretical than practical importance. This is due to the fact that large numbers of processors are expected to be physically linked to the same memory location. An exception to this argument is not the two cases cited above: they have only a limited number of processors. Several researchers are investigating the possibility of using optical interfaces to physically grasp PRAM computers.

On a set (stream) of instructions called algorithms, both sequential and parallel computers work. The instruction set (algorithm) tells the machine what it has to do in each step.

Several different programme control models exist. There are several basic schemes described by Flynn:

●      Single Instruction stream, Single Data stream (SISD) computers

●      Single Instruction stream, Multiple Data stream (SIMD) computers

●      Multiple Instruction stream, Single Data stream (MISD) computers

●      Multiple Instruction stream, Multiple Data stream (MIMD) computers

SISD Computers

One control unit, one processing unit, and one memory unit are used in SISD computers.

The processor receives a single stream of instructions from the control unit for this type of device and runs with a single stream of data from the memory unit. The processor receives one instruction from the control unit at each stage during computation and operates on one single data received from the memory unit.

Fig 2: SISD computers

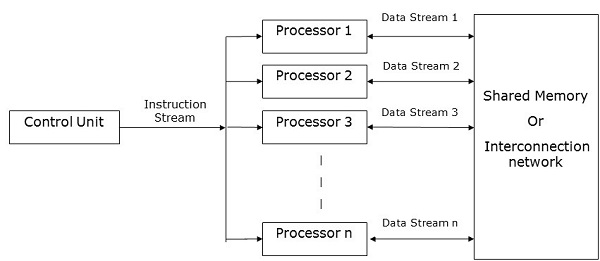
SIMD Computers

Single Multi Data Instruction. The processors in this model are managed by a programme whose instructions are applied simultaneously to all of them (with certain qualifications). Assume that each of the processors has a unique number that knows the processor in the sense that the parallel computer instructions may relate to the number of the processor.

An example of this type of machine is: Note that an algorithm like the one in the example's predicted runtime is the average of real running times, weighted by the likelihood that these running times will occur.

One control unit, multiple processing units, and a shared memory or interconnection network are used in SIMD computers.

Here, to all processing units, one single control unit sends instructions. All the processors receive a single set of instructions from the control unit at each stage during the computation process and work on different data sets from the memory unit.

To store both data and instructions, each of the processing units has its own local memory unit. In SIMD machines, processors need to connect with each other. This is done through shared memory or a network of interconnections.

When a set of instructions is being executed by some of the processors, the remaining processors wait for their next set of instructions. Control unit instructions determine which processor is active or inactive.

Fig 3: SIMD computers

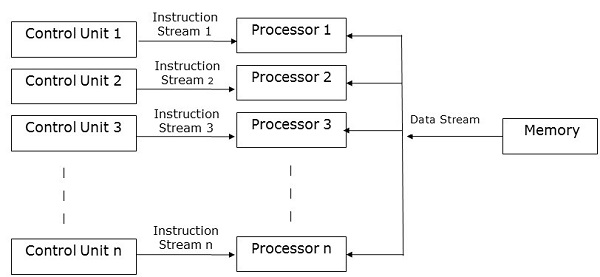
MISD Computers

MISD computers contain multiple control units, multiple processing units, and one common memory unit, as the name implies.

Fig 4: MISD computers

Each processor here has its own control unit and a common memory unit is shared by them. Both processors receive individual instructions from their own control unit and operate on a single data stream according to the instructions obtained from their respective control units. This processor runs concurrently.

This condition is also compared to the calculation used by Systolic Arrays. These are arrays of processors, typically on a single VLSI chip, designed to solve specific issues.

The data movement activities of all the processors are coordinated by a clock, and output from some processors is pipelined into other processors. The word Systolic comes from an analogy with the circulatory system of an animal, the knowledge in the systolic array that plays the blood part of the circulatory system. One can consider, in a way of speaking, the various processors in a systolic array consisting of several processors operating on one set of processor data.

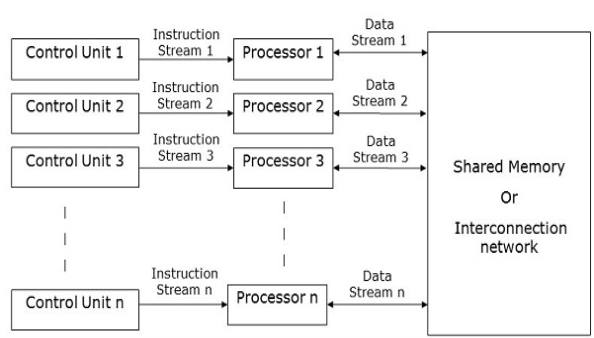
MIMD Computers

Multiple Multi-Data Instruction. Processors may each have autonomous programmes in this model that are read from the common RAM. In multiple environments, this model is used extensively:

The data-movement and communication issues that arise in all parallel computation are more important here since it is necessary to transfer the instructions to the processors and the data between the common memory and the processors. Commercial MIMD computers appear to have a relatively limited number of processors due to these data-movement problems . Generally, if one is only interested in a very restricted type of parallelism, namely the creation of processes, it is simpler to programme a MIMD computer.

MIMD computers have multiple control units, multiple processing units, and a shared memory or interconnection network.

Here, each processor has its own control unit, arithmetic and logic unit, and local memory unit. From their respective control units, they obtain various sets of instructions and work on different sets of data.

Fig 5: MIMD computers

Pure MIMD machines have no hardware features to ensure processor synchronisation. In general, simply loading several copies of a programme into all of the processors and starting all of these copies at the same time is not enough. In fact, many of these computers have hardware features that, once achieved, appear to eliminate synchronisation.

Key takeaways

1. Multiprocessors are known as MIMD computers that share a shared memory, whereas those that use an interconnection network are known as multi-computers.
2. The SIMD processors in this model are managed by a programme whose instructions are applied simultaneously to all of them.
3. In MISD Each processor here has its own control unit and a common memory unit is shared by them.
4. In SISD the processor receives a single stream of instructions from the control unit for this type of device and runs with a single stream of data from the memory unit.

8.3 Parallel Algorithms for Prefix Computation

PRAM Recursive Prefix Sum Algorithm

Key takeaways

1. The pointer jumping technique goes far beyond the application of list ranking.
2. In terms of a binary, associative operator 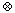, a prefix computation is specified.

8.4 List Ranking and Graph Problems

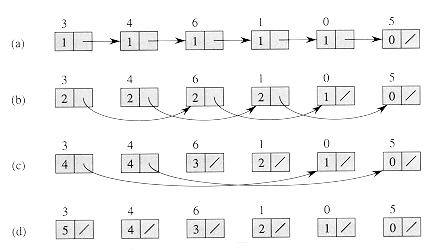
Lists are worked on by our first parallel algorithm. In a PRAM, we can store a list just like we store lists in an ordinary RAM. However, it is convenient to assign a "responsible" processor to each object in order to work parallel on list objects. We will presume that the ith processor is responsible for the ith object and that there are as many processors as list objects. For instance, it shows a linked list consisting of an object sequence of 3,4,6,1,0,5. Since there is one processor per list object, in O(1) time, an object in the list can be worked on by its responsible processor.

Suppose we are given a single connected list of L with n objects and want to measure its distance from the end of the list for each object in L. More formally, if the pointer field is next, we want to measure a value d[i] for each i-object in the list in such a way that

We name the list-ranking question the problem of calculating the d values.

Simply propagating distances back from the end of the list is one solution to the list-ranking problem. This approach takes (n) time as the kth object from the end must wait until the k-1 objects that follow it can decide their distances from the end before they can determine their own distances. A serial algorithm is basically this solution.

Fig 6 : linked list representation in PRAM

The following parallel pseudocode provides an effective parallel solution, requiring only O(lg n) time.

For all non-nil pointers next[i], we set next[i] next[next[i]], which is called pointer jumping. Note that the e-pointer fields are updated by jumping the pointer, thereby breaking the list structure. If it is important to maintain the list structure, then we make copies of the next pointers and use the copies to measure the distances.

Analysis :

The List-Rank procedure performs (n lg n) function, as n processors are needed and it runs in (lg n) time. In (n) time, the simple serial algorithm for the list-ranking problem runs, implying that List-Rank performs more work than is absolutely required, but only by a logarithmic factor.

If the work performed by A is within a constant factor of the work performed by B, we define a PRAM algorithm A to be work-efficient in relation to another (serial or parallel) algorithm B for the same problem. More simply, we also state that a PRAM algorithm A is work-efficient if it is work-efficient on a serial RAM with respect to the best possible algorithm.

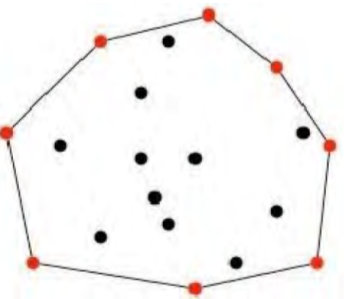
Convex hull problem

The smallest convex polygon encompassing all points S on the x-y plane is the planar convex hull of a set of points S ={p1, p2, ..., pn} of pi = (x,y) coordinates.

Fig 7: convex hull

Divide & conquer

●      Split S to S1 S2 and measure S1 and S2 UCH recursively

●      By computing the upper common tangent in O(1) time to form UCH(S) Repeat to compute the LCH(S) Repeat, combine UCH(S1) and UCH(S2)

Period in parallel  (assuming p = O(n) processors)

Key takeaways

1. Lists are worked on by our first parallel algorithm. In a PRAM, we can store a list just like we store lists in an ordinary RAM.
2. We will presume that the ith processor is responsible for the ith object and that there are as many processors as list objects.

References

1. Anany Levitin: Introduction to The Design & Analysis of Algorithms, 2nd Edition, Pearson Education, 2007.
2. Thomas H. Cormen, Charles E. Leiserson, Ronal L. Rivest, Clifford Stein: Introduction to Algorithms, 3rd Edition, PHI, 2010.