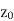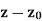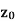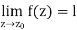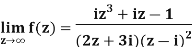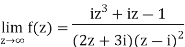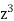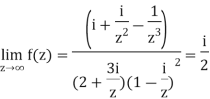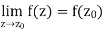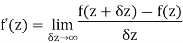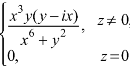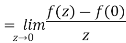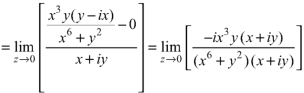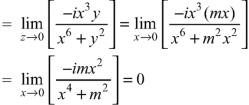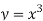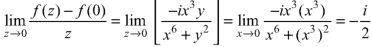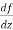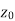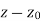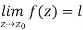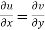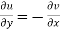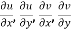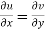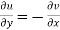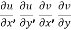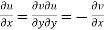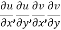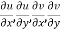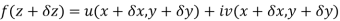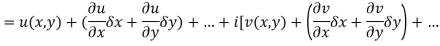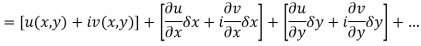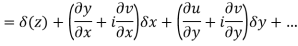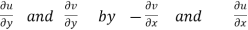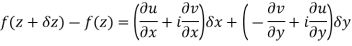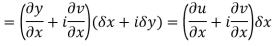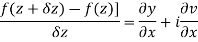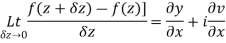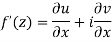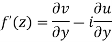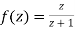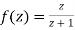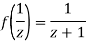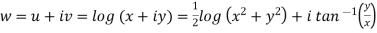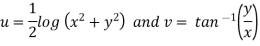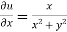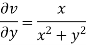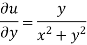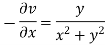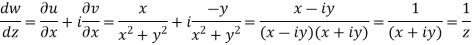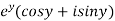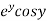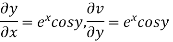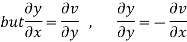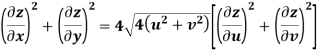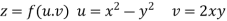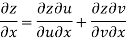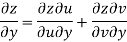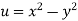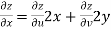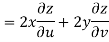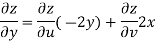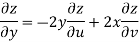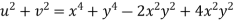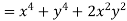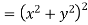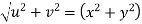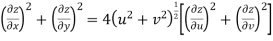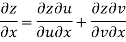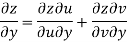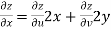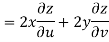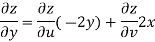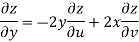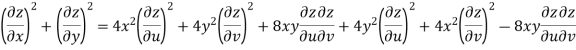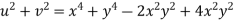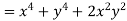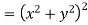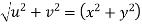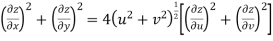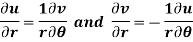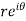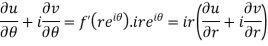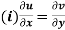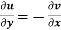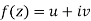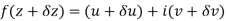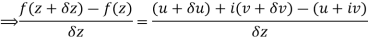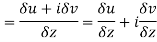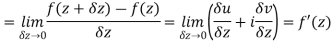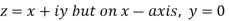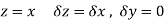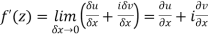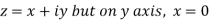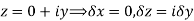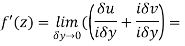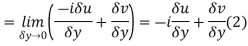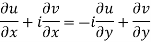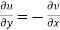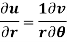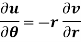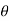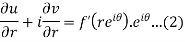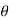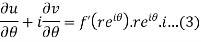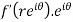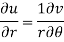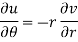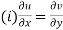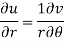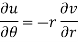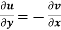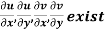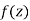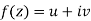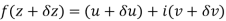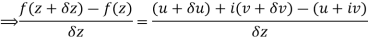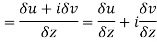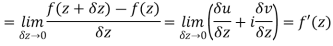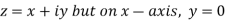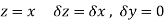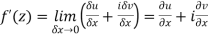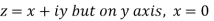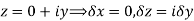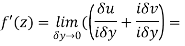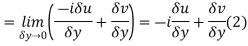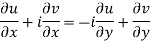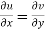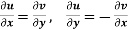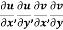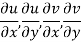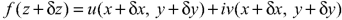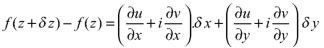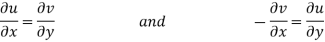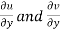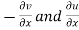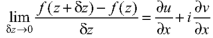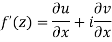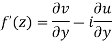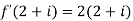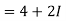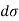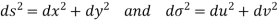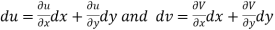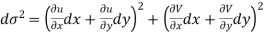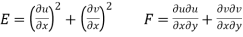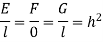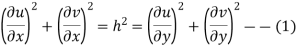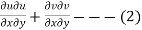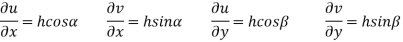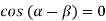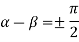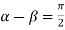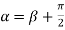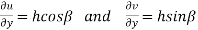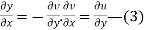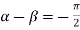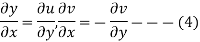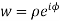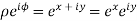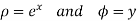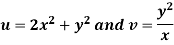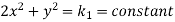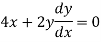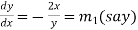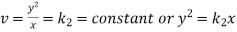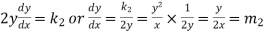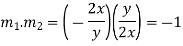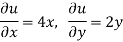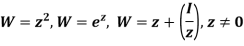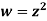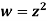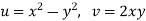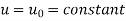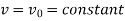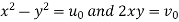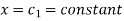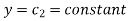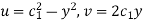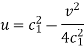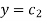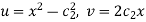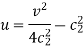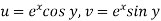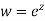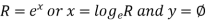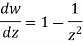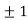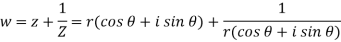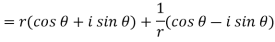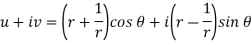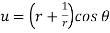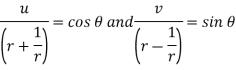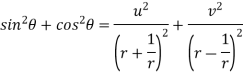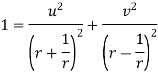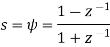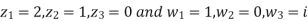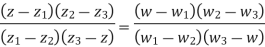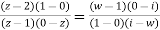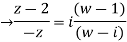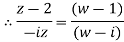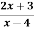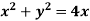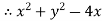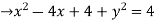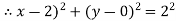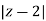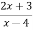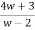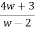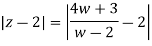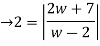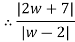2.1 Function of a complex variable Limit Continuity Differentiability – Definitions

EM-IV

Unit 2

Complex Variables

2.1 Function of a complex variable, Limit, Continuity Differentiability – Definitions

In the narrow sense of the term, the theory of function of a complex variable is the theory of analytic functions (cf. Analytic function) of one or several complex variables. As an independent discipline, the theory of functions of a complex variable took shape in about the middle of the 19th century as the theory of analytic functions.

Complex function-

x + iy is a complex variable which is denoted by z

If for each value of the complex variable z = x + iy in a region R, we have one or more than one values of w = u + iv, then w is called a complex function of z.

And it is denoted as-

w = u(x , y) + iv(x , y) = f(z)

Neighbourhood of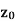

Let a point in the complex plane and z be any positive number, then the set of points z such that-

||<ε

Is called ε- neighbourhood of

Limit of a function of a complex variable-

Suppose f(z) is a single valued function defined at all points in some neighbourhood of point -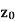

The-

Example-1: Find-

Sol.

Here we have-

Divide numerator and denominator by , we get-

Continuity- A function w = f(z) is said to be continuous at z = 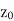, if

Also if w = f(z) = u(x , y) + iv(x , y) is continuous at z = 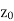then u(x , y), v(x , y) are also continuous at z = .

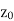Differentiability-

Let f(z) be a single valued function of the variable z, then

Provided that the limit exists and has the same value for all the different ways in which 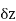approaches to zero.

Example-2: if f(z) is a complex function given below, then discuss

Sol.

If z→0 along radius vector y = mx

But along ,

In different paths we get different value of that means 0 and –i/2, in that case the function is not differentiable at z = 0.

Key takeaways

Neighbourhood of

||<ε

2. Limit of a function of a complex variable-

Suppose f(z) is a single valued function defined at all points in some neighbourhood of point -

The-

2.2 Analytic functions

A function 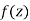is said to be analytic at a point 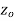if f is differentiable not only at 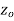but every point of some neighborhood at .

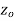Note-

1. A point at which the function is not differentiable is called singular point.

2. A function which is analytic everywhere is called an entire function.

3. An entire function is always analytic, differentiable and continuous function. (converse is not true)

4. Analytic function is always differentiable and continuous but converse is not true.

5. A differentiable function is always continuous but converse is not true.

The necessary condition for f(z) to be analytic-

f(z) = u + i(v) is to be analytic at all the points in a region R are-

1. …………. (1)

2. ……...…. (2)

Provided exists

Equation (1) and (2) are known as Cauchy-Riemann equations.

The sufficient condition for f(z) to be analytic-

f(z) = u + i(v) is to be analytic at all the points in a region R are-

1. …………. (1)

2. ……...…. (2)

are continuous function of x and y in region R.

Important note-

1. If a function is analytic in a domain D, then u and v will satisfy Cauchy-Riemann conditions.

2. C-R conditions are necessary but not sufficient for analytic function.

3. C-R conditions are sufficient if the partial derivative are continuous.

State and prove sufficient condition for analytic functions

Statement – The sufficient condition for a function 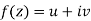to be analytic at all points in a region R are

2 are continuous function of x and y in region R.

Proof:

Let f(z) be a simple valued function having at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem

Ignoring the terms of second power and higher power

We know C-R equation

Replacing

Respectively in (1) we get

Show that is analytic at

Ans: The function f(z) is analytic at if the function is analytic at z=0

Since

Now is differentiable at z=0 and at all points in its neighbourhood Hence the function is analytic at z=0 and in turn f(z) is analytic at

Example-1: If w = log z, then find 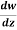. Also determine where w is non-analytic.

Sol.

Here we have

Therefore-

and

Again-

Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).

So that w is analytic everywhere but not at z = 0

Example-2: Prove that the function 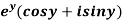is an analytical function.

Sol.

Let =u+iv

Let =u and =v

Hence C-R-Equation satisfied.

Example-3: Prove that

Sol.

Given that

Since

V=2xy

Now

But

Hence

Given that

Since

V=2xy

Now

But

Hence

Example-4: Show that polar form of C-R equations are-

Sol

. z = x + iy =

U and v are expressed in terms of r and θ.

Differentiate it partially w.r.t. r and θ, we get-

By equating real and imaginary parts, we get-

Key takeaways

A function 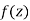is said to be analytic at a point 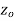if f is differentiable not only at 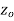but every point of some neighbourhood at .
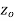A point at which the function is not differentiable is called singular point.
A function which is analytic everywhere is called an entire function.
If a function is analytic in a domain D, then u and v will satisfy Cauchy-Riemann conditions.
C-R conditions are necessary but not sufficient for analytic function.
C-R conditions are sufficient if the partial derivative are continuous

2.3 Cauchy – Riemann equations in cartesian and polar forms

In Cartesian form-

Theorem; The necessary condition for a function 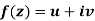to be analytic at all the points in a region R are

(ii)

Provided,

Proof:

Let be an analytic function in region R.

Along real axis

Then f’(z), becomes-

………… (1)

Along imaginary axis

From equation (1) and (2)

Equating real and imaginary parts

Therefore-

and

These are called Cauchy Riemann Equations.

C-R equation in polar from-

C-R equations in polar form are-

Proof:

As we know that-

x = r cos and u is the function of x and y

z = x + iy = r ( cos

Differentiate (1) partially with respect to r, we get-

Now differentiate (1) with respect to , we get-

Substitute the value of , we get-

Equating real and imaginary parts, we get-

Proved

Key takeaways

The necessary condition for a function to be analytic at all the points in a region R are

(ii)

2. C-R equations in polar form are-

2.4 Properties of analytic functions

Necessary condition for function f(z) to be analytic-

Theorem; The necessary condition for a function 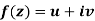to be analytic at all the points in a region R are

(ii)

Provided,

Proof:

Let be an analytic function in region R.

Along real axis

Then f’(z), becomes-

………… (1)

Along imaginary axis

From equation (1) and (2)

Equating real and imaginary parts

Therefore-

and

These are called Cauchy Riemann Equations.

Sufficient condition for function f(z) to be analytic-

Theorem-

The sufficient conditions of a function f(z) = u + iv to be analytic at all the points in the region R are-

2. are continuous functions of x and y in region R.

Proof:

Suppose f(z) be a single-valued function which has-

At each point in the R region, then the Cauchy-Reimann equations are satisfied.

By Taylor’s theorem-

Ignore the terms of higher power.

We know that from C-R equations-

Replace by

We get-

Proved

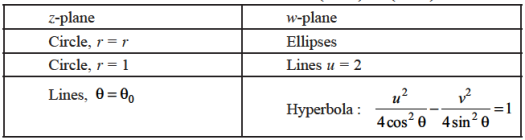
2.5 Conformal Transformation – Definition

Conformal mapping

If the sense of the relation as well as magnitude of the angle is preserved the transformation is said to be conformal.

Note-An analytic function f (z) is conformal everywhere except at its critical points where f (z) = 0.

Example-1: Find the conformal transformation of .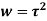

Answer. Let

Theorem: If W=f(z) represents a conformal transformation of a domain D in the z-plane into a domain D of the W plane then f(z) is an analytic function of z in D.

Proof:

We have u+iv=u(x,y)+iv(x,y)

So that u=u(x, y) and v=v(x,y)

Let ds and denote elementary arc length in the z-plane and w-plane respectively Then

Now

Hence

Where

Now is independent of direction if

Where h depends on x and y only and is not zero. Thus the conditions for an isogonal transformation

And

The equation are satisfied if we get

Then substituting these values in 2 we get

Taking i.e.

Also

Hence

Similarly i.e.

The equation (4) are the well-known Cauchy -Reimann

Conformal mapping

Example: Show that the mapping 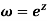is conformal in the whole of the z plane.

Sol.

Let z=x+iy

Then

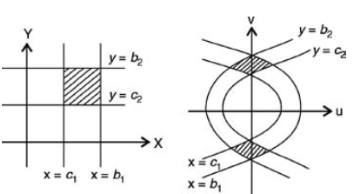
Consider the mapping of the straight-line x=a in z plane the w plane which gives 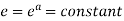which is a circle in the w plane in the anticlockwise direction similarly the straight-line y=b is mapped into 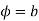which is a radius vector in the w plane.

The angle between the line x=a and y=b in the z plane is a right angle. The corresponding angle in the w plane between the circle e = constant and the radius vector 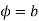is also a right angle which establishes that the mapping 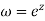is conformal.

Example: Show that the curve u = constant and v = constant cut orthogonally at all intersections but the transformation w = u + iv is not conformal. Where-

Sol.

Let …………. (1)

Differentiate (1), we get-

…………… (2)

Now-

…………….. (3)

Differentiate (3), we get-

………. (4)

As we know that for the condition for orthogonallity, from (2) and (4)

So that these two curves cut orthogonally.

Here,

And

Here the C-R equation is not satisfied so that the function u + iv is not analytic.

Hence the transformation is not conformal.

Key takeaways

If the sense of the relation as well as magnitude of the angle is preserved the transformation is said to be conformal.
An analytic function f (z) is conformal everywhere except at its critical points where f (z) = 0

2.6 Discussion of transformations:

Transformation:

Sol.

Now equating real and imaginary parts, we get-

Case-1: if and then shows equilateral hyperbolas with the lines y = ± x and the coordinate axes x = 0, y = 0 as asymptotes respectively) which are orthogonal trajectories of each other.

Case-2: if and then eliminating x and y, we get-

So that-

Which is a parabola with focus at origin, v = 0

As axis and open to the left. Similarly

So that-

These parabolas are orthogonal to each other.

w = z2 is conformal everywhere except at z = 0 where w = 2z = 0.

Transformation:

Now equating real and imaginary parts-

Again

Hence

Transformation:

At z =

So the transformation is not conformal at z =

and

Now

2.7 Bilinear transformations

Bilinear transformation is a correction of backwards difference method.

The bilinear transformation (also known as Tuatn’s method transformation) is defined as substitution:

Example 1:

Find the bi-linear transformation which aps points z=2,1,0 ontpo the points w=1,0,i

Sol.

Let

Thus we have

Example 2:

How that the bilinear transformation

w= transforms

in the z-plane to 4u+3=0 in w-plane.

Sol.

Consider the circle in z-plane

= 0

Thus, centre of the circle is (h,k)c(2,0) and radius r=2.

Thus in z-plane it is given as =2....(1)

Consider w=

W(z-4) = 2z+3

Wz-4w=2z+3

Wz-2z=4w+3

Z(w-2) = (4w+3)

z =

z-2 = - 2

References

E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
Higher engineering mathematics, HK Dass

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined