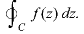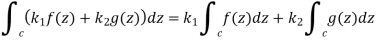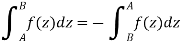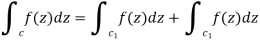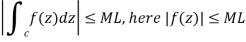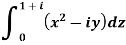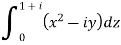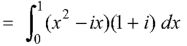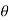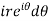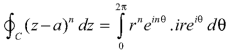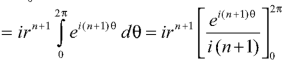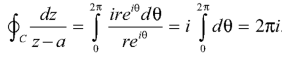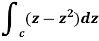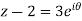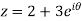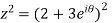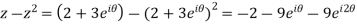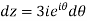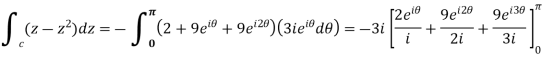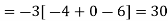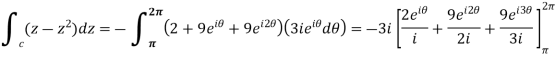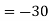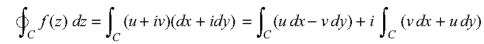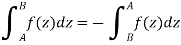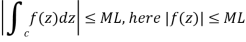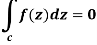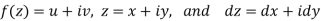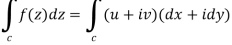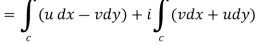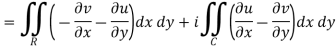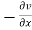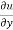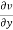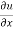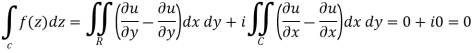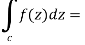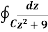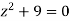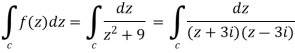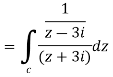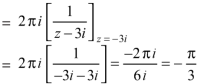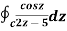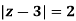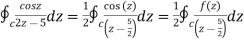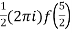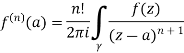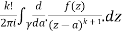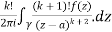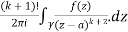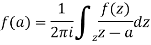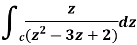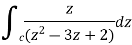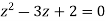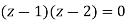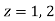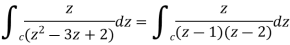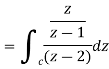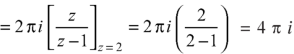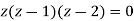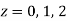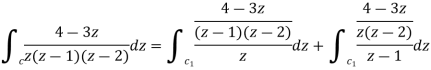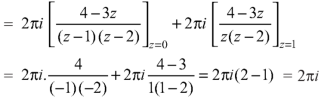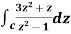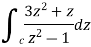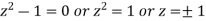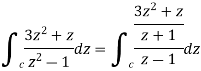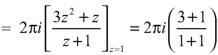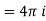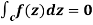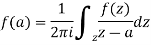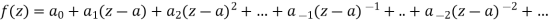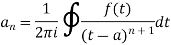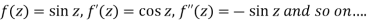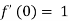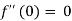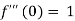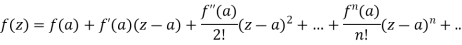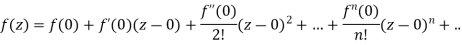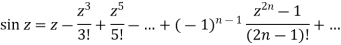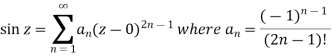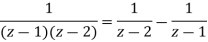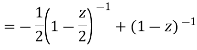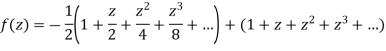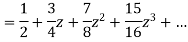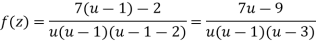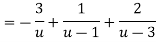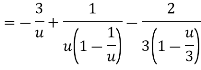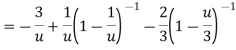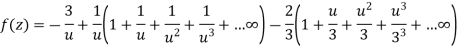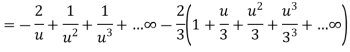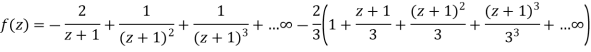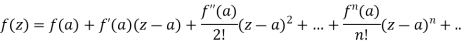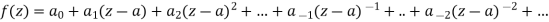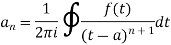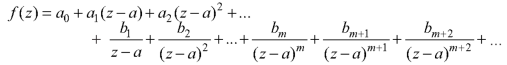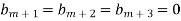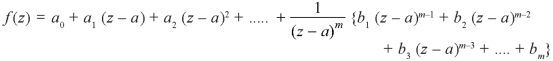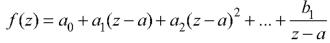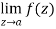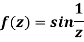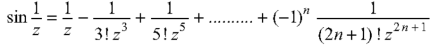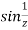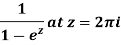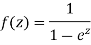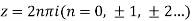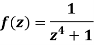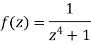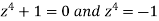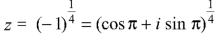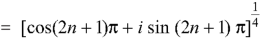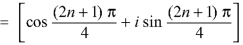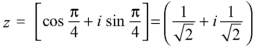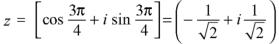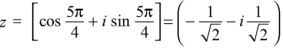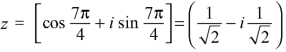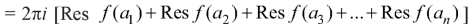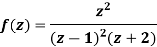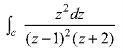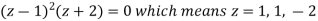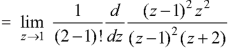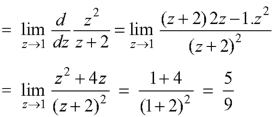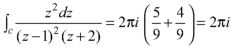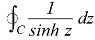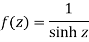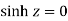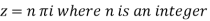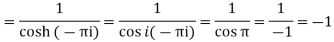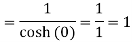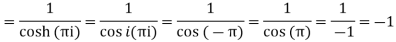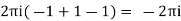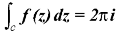Back to Study material
EM-IV

UNIT-3

Complex Integration

 

 


 

In case of a complex function f(z) the path of the definite integral 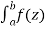can be along any curve from z = a to z = b.

In case the initial point and final point coincide so that c is a closed curve, then this integral called contour integral and is denoted by-

 

If f(z) = u(x, y) + iv(x, y), then since dz = dx + i dy

We have-

 

It shows that the evaluation of the line integral of a complex function can be reduced to the evaluation of two line integrals of real function.

 

Properties of line integral-

  1. Linearity-

2.     Sense reversal-

 

3.     Partitioning of path-

4.     ML – inequality-

 

 

Example: Evaluate

 along the path y = x.

Sol.

Along the line y = x,

dy = dx that dz = dx + i dy 

dz = dx + i dx = (1 + i) dx

On putting y = x and dz = (1 + i)dx

 

 

Example: Evaluate

where c is the circle with center a and r. What is n = -1.

Sol.

The equation of a circle C is |z - a| = r or z – a =

Where varies from 0 to 2π

dz =

Which is the required value.

When n = -1

 

 

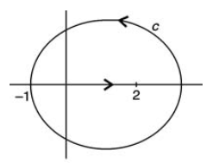
Example: Evaluate

where c is the upper half of the circle |z – 2| = 3.

Find the value of the integral if c is the lower half of the above circle.

Sol.

The equation of the circle is-

Or

 

 

 

Now for the lower semi circle-

 

 

Key takeaways-

  2. Linearity-

3.     Sense reversal-

 

4.     Partitioning of path-

5.     ML – inequality-

 

 

 


 

A function f(z) is analytic and its derivative f’(z) continuous at all points inside and on a closed curve c, then

 

Proof:

Suppose the region is R which is closed by curve c and let-

By using Green’s theorem-

Replace by and by -

 

So that-

 

 

Example-1: Evaluate

where C is |z + 3i| = 2

 

Sol.

Here we have-

Hence the poles of f(z),

Note- put determine equal to zero to find the poles.

Here pole z = -3i lies in the given circle C.

So that-


 

 

 

Example 2:

where C =

 

Sol.

where f(z) = cosz

           = by cauchy’s integral formula

                        =

 

 

Example 3:

Solve the following by cauchy’s integral method:

Solution:

Given,

                  =

          =

            =

 

Cauchy’s integral formula-

Cauchy’s integral formula can be defined as-

Where f(z) is analytic function within and on closed curve C, a is any point within C.

 

Example-1: Evaluate

 by using Cauchy’s integral formula.

Here c is the circle |z - 2| = 1/2

Sol. it is given that-

Find its poles by equating denominator equals to zero.

There is one pole inside the circle, z = 2,

So that-

Now by using Cauchy’s integral formula, we get-

 

Example-2: Evaluate the integral given below by using Cauchy’s integral formula-

 

Sol.

Here we have-

 

Find its poles by equating denominator equals to zero.

We get-

There are two poles in the circle-

Z = 0 and z = 1

So that-


 

 

 

Example-3: Evaluate

if c is circle |z - 1| = 1.

 

Sol.

Here we have-

 

Find its poles by equating denominator equals to zero.

The given circle encloses a simple pole at z = 1.

So that-


 

 

Key takeaways-

  1. A function f(z) is analytic and its derivative f’(z) continuous at all points inside and on a closed curve c, then
  2. Cauchy’s integral formula-

 


 

Taylor’s series-

If f(z) is analytic inside a circle C with centre ‘a’ then for z inside C,

 

Laurent’s series-

If f(z) is analytic in the ring shaped region R bounded by two concentric circles  C and 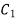of radii ‘r’ and 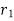where r is greater and with centre at’a’, then for all z in R

Where

 

Example: Expand sin z in a Taylor’s series about z = 0.

Sol.

It is given that-

Now-

We know that, Taylor’s series-

So that

 

Hence

 

Example: Expand

f(z) = 1/ [(z - 1) (z - 2)]

in the region |z| < 1.

Sol.

By using partial fractions-

Now for |z|<1, both |z/2| and |z| are < 1,

Hence we get from second equation-

Which is a Taylor’s series.

 

Example: Find the Laurent’s expansion of-

In the region 1 < z + 1< 3.

Sol.

Let z + 1 = u, we get-

Here since 1 < u < 3 or 1/u <  1 and u/3 < 1,

Now expanding by Binomial theorem-

Hence

Which is valid in the region 1 < z + 1 < 3

 

Key takeaways-

  1. Taylor’s series-

2.     Laurent’s series-

Where

 

 


 

A point at which a function f(z) is not analytic is known as a singular point or singularity of the function.

Isolated singular point- If z = a is a singularity of f (z) and if there is no other singularity within a small circle surrounding the point z = a, then z = a is said to be an isolated singularity of the function f (z); otherwise it is called non-isolated.

Pole of order m- Suppose a function f(z) have an isolated singular point z = a, f(z) can be expanded in a Laurent’s series around z = a, giving

…… (1)

In some cases it may happen that the coefficient , then equation (1) becomes-

Then z = a is said to be a pole of order m of the function f(z).

Note- The pole is said to be simple pole when m = 1.

In this case-

 

Working steps to find singularity-

Step-1: If exists and it is finite then z = a is a removable singular point.

Step-2: If does not exists then z = a is an essential singular point.

Step-3: If is infinite then f(z) has a pole at z = a. the order of the pole is same as the number of negative power terms in the series expansion of f(z).

 

Example: Find the singularity of the function-

Sol.

As we know that-

So that there is a number of singularity.

is not analytic at z = a

(1/z = ∞ at z = 0)

 

Example: Find the singularity of

 

Sol.

Here we have-

We find the poles by putting the denominator equals to zero.

That means-

 

Example: Determine the poles of the function-

Sol.

Here we have-

We find the poles by putting the denominator of the function equals to zero-

We get-

By De Moivre’s theorem-

If n = 0, then pole-

If n = 1, then pole-

If n = 2, then pole-

If n = 3, then pole-

 

Cauchy’s residue theorem-

If f(z) is analytic in a closed curve C, except at a finite number of poles within C, then-

 

;DOProof:

Suppose 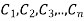be the non-intersecting circles with centres at respectively.

Redii so small that they lie within the closed curve C. then f(z) is analytic in the multipUYle connected region lying between the curves C and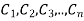

Now applying the Cauchy’s theorem-

 

 

Example: Find the poles of the following functions and residue at each pole:

and hence evaluate-

where c: |z| = 3.

 

Sol.

The poles of the function are-

The pole at z = 1 is of second order and the pole at z = -2 is simple-

Residue of f(z) (at z = 1)

Residue of f(z) ( at z = -2)

 

 

Example: Evaluate-

Where C is the circle |z| = 4.

Sol.

Here we have,

Poles are given by-

Out of these, the poles z = -πi , 0 and πi lie inside the circle |z| = 4.

The given function 1/sinh z is of the form

Its poles at z = a is

Residue (at z = -πi)

Residue (at z = 0)

Residue (at z = πi)

Hence the required integral is =

 

Key takeaways-

  1. The pole is said to be simple pole when m = 1.
  2. Cauchy’s residue theorem-

If f(z) is analytic in a closed curve C, except at a finite number of poles within C, then-

 

References

 

  1. E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
  2. P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
  3. S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
  4. W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
  5. N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
  6. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
  7. T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
  8. Higher engineering mathematics, HK Dass

 

 

 


Zoom Out
Zoom In
Sign Up
0 matching results found
Index
Notes
Highlighted
Underlined
:
Browse by Topics
:
Notes
Highlighted
Underlined
Loading ....