UNIT – 4
Optimization and Matching
Dijkstra's calculation is fundamentally the same as Prim's calculation for least spreading over tree. Like Prim's MST, we produce a SPT (most limited way tree) with given source as root. We keep two sets, one set contains vertices remembered for most brief way tree, other set incorporates vertices not yet remembered for most brief way tree. At each progression of the calculation, we discover a vertex which is in the other (set of not at this point included) and has a base separation from the source.
The following are the itemized steps utilized in Dijkstra's calculation to locate the most limited way from a solitary source vertex to any remaining vertices in the given diagram.
4.1.1 Calculation
1) Create a set sptSet (Shortest path tree set) that monitors vertices remembered for briefest way tree, i.e., whose base separation from source is determined and finished. At first, this set is vacant.
2) Assign a distance an incentive to all vertices in the information diagram. Instate all distance esteems as INFINITE. Allot distance an incentive as 0 for the source vertex so it is picked first.
3) While sptSet does exclude all vertices
a) Pick a vertex u which isn't there in sptSet and has least distance esteem.
b) Include u to sptSet.
c) Update distance estimation of all contiguous vertices of u. To refresh the distance esteems, repeat through all neighbouring vertices. For each neighbouring vertex v, if amount of distance estimation of u (from source) and weight of edge u-v, is not exactly the distance estimation of v, at that point update the distance estimation of v.
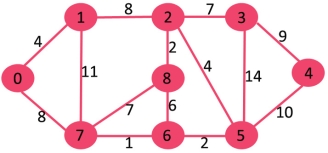
Example 1:
|
Figure 1
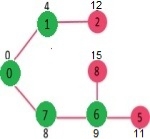
Initially, the sptSet set is empty and the distances allocated to the vertices are {0, INF, INF, INF, INF, INF, INF, INF} where infinity is implied by INF. Now choose the vertex with the lowest value for the size. Vertex 0 is chosen and included in sptSet. Therefore, sptSet becomes {0}. Update the distance values of its neighboring vertices after including 0 to sptSet. The adjacent vertices of 0 are 1 and 7. The distance values 1 and 7 are changed as 4 and 8 respectively. Only the vertices with finite distance values are displayed after the subgraph shows the vertices and their distance values. The vertices contained in the SPT are shown in green.
|
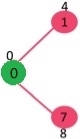
Figure 2
Select the minimum distance value of the vertex that is not already found in SPT (not in sptSET). Vertex 1 is chosen and sptSet is added. So, sptSet becomes {0, 1} now. Update the distance values of vertices adjacent to 1. The vertex 2 distance meaning becomes 12.
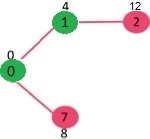
|
Figure 3
Select the minimum distance value of the vertex that is not already found in SPT (not in sptSET). Vertex 7 was chosen. So sptSet is now translated into {0, 1, 7}. Update the distance values of the vertices adjacent to 7. Vertex 6 and 8's gap value becomes a finite value (15 and 9 respectively).
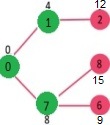
|
Figure 4
Select the minimum distance value of the vertex that is not already found in SPT (not in sptSET). Vertex 6 was chosen. So sptSet now transforms into {0, 1, 7, 6}. Update the distance values of the vertices adjacent to 6. The distance value is modified for vertex 5 and vertex 8.
|
Figure 5
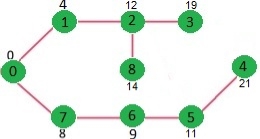
We repeat the steps above until all vertices of the given graph are covered by sptSet. Finally, we got the following Tree of the Shortest Route (SPT).
|
Figure 6
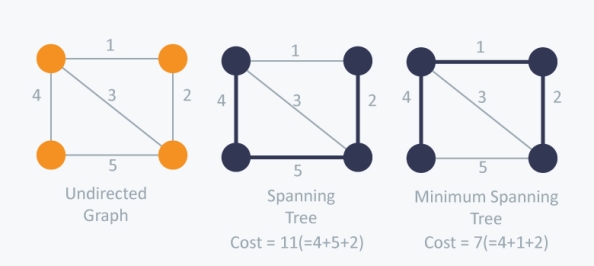
Given an undirected and connected graph G=(V,E), a spanning tree of the graph G is a tree that spans G (that is, it includes every vertex of G) and is a subgraph of G (every edge in the tree belongs to G)
The sum of the weights of all the edges in the tree is the expense of the spanning tree. There could be several trees spanning it. The minimal spanning tree is the spanning tree where all the spanning trees have the minimum cost. There can also be several trees with a minimal time.
The minimal spanning tree is directly used in network architecture. It is used in algorithms that approximate the problem of the travelling salesman, multi-terminal minimum cut problem and perfect matching weighted at minimum cost. Such implementations that are realistic are:
- Analysing the Clusters
- Recognition for handwriting
- Segmentation of Image
|
Figure 7
Algorithms to find Minimum Spanning Tree
Kruskal's Algorithm assembles the spanning tree by adding edges individually into a developing crossing tree. Kruskal's calculation follows a greedy approach as in every cycle it finds an edge which has least weight and add it to the developing traversing tree.
4.3.1 Calculation Steps:
Sort the chart edges concerning their loads.
Begin adding edges to the MST from the edge with the littlest load until the edge of the biggest weight.
Just add edges which doesn't frame a cycle, edges which interface just separated parts.
So now the inquiry is the means by which to check if vertices are associated or not?
This could be done using DFS which starts from the first vertex, then check if the second vertex is visited or not. But DFS will make time complexity large as it has an order of O(V+E) where V is the number of vertices, E is the number of edges. So the best solution is "Disjoint Sets":
Disjoint sets will be setting whose crossing point is the unfilled set so it implies that they don't share any component practically speaking.
Think about after model:
|
Figure 8
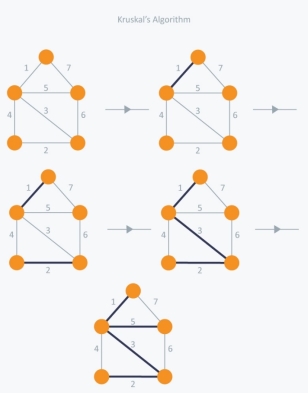
In Kruskal's algorithm, we pick the edge with the lowest weight for each iteration. So, first of all, we will start with the lowest weighted edge, i.e. the edges with weight 1. We would choose the second lowest weighted edge after that, i.e. the edge with weight 2. Notice that these two edges are absolutely disjointed. The third lowest weighted edge will now be the next edge, i.e. the edge with weight 3, which connects the two disjoint parts of the graph. Still, with weight 4, we are not able to choose the edge that will create a loop and we can't get any cycles. But we are going to pick the fifth lowest weighted edge, i.e. the 5th weighted edge. Now the other two sides are trying to build loops, so we're going to forget them. In the end, we end up with a minimum spanning tree with total cost 11 ( = 1 + 2 + 3 + 5).
4.3.2 Time Complexity:
In Kruskal’s algorithm, most time consuming operation is sorting because the total complexity of the Disjoint-Set operations will be O(ElogV), which is the overall Time Complexity of the algorithm.
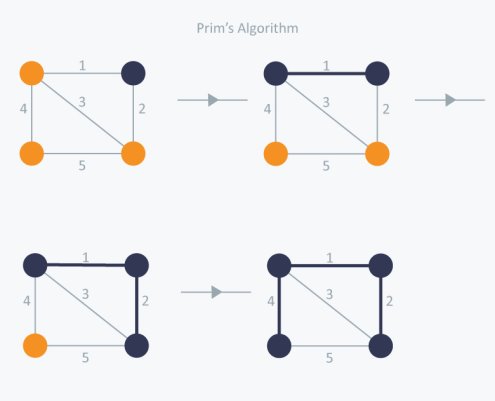
Prim's Algorithm additionally utilize Greedy way to deal with locate the base crossing tree. In Prim's Algorithm we become the crossing tree from a beginning position. In contrast to an edge in Kruskal's, we add vertex to the developing traversing tree in Prim's.
4.4.1 Calculation Steps:
Keep two disjoint arrangements of vertices. One containing vertices that are in the developing spreading over tree and other that are not in the developing traversing tree.
Select the least expensive vertex that is associated with the developing crossing tree and isn't in the developing traversing tree and add it into the developing spreading over tree. This should be possible utilizing Priority Queues. Addition the vertices, that are associated with developing traversing tree, into the Priority Queue.
Check for cycles. To do that, mark the hubs which have been now chosen and addition just those hubs in the Priority Queue that are not checked.
Consider the model underneath:
|
Figure 9
We will begin with an arbitrary node in Prim's Algorithm (it doesn't matter which one) and mark it. We will mark a new vertex in each iteration that is adjacent to the one we have identified already. Prim's algorithm would pick the cheapest edge as a greedy algorithm and name the vertex. But we're clearly going to pick the edge with weight 1. We have three choices in the next version, edges measuring 2, 3 and 4. So, we're going to pick the weight-2 edge and mark the vertex. We have three choices now again, edges measuring 3, 4 and 5. But with weight 3, we can't pick the edge as it produces a cycle. So we will select the edge with weight 4 and we end up with the minimum spanning tree of total cost 7 ( = 1 + 2 +4).
4.4.2 Time Complexity:
The time complexity of the Prim’s Algorithm is O((V+E)logV) because each vertex is inserted in the priority queue only once and insertion in priority queue take logarithmic time.
A transportation network with the following properties is a connected, weighted, directed graph.
- One source, a vertex with no incoming edges, exists. [The vertex has an indegree of 0 in other languages].
- One sink is there, a vertex with no outgoing edges. [The vertex has an outdegree of 0 in another language].
- A nonnegative weight Cuv, called the capacity of that edge, is allocated to each edge (u,v). [Notice that I wrote the edge rather than a set as an ordered pair. This is because an original vertex and a terminal vertex are on each edge, so the order matters.]]
Let G be a Cij-capable transport network on the edge (i,j) . A flow F on G assigns a non-negative number Fij, called the flow on edge (i,j) with the following properties to each edge (i,j).
|
What in terms do these two conditions mean? The first says that the power on an edge cannot surpass the flow. We can see why this requirement is important - we can't put more oil through a pipeline, for instance, than it can accommodate. The second notes that the IN flow to a vertex must be equal to the same vertex's OUT flow (except at the source or the sink). Again, this scenario makes sense: if oil flows through a system of pipelines, between the source of the oil and the location to which we deliver it, we do not receive or waste oil.
Offer each edge a pair of numbers with the power of an edge preceding the flow along that edge to compose a flow on a transportation network: Cij,Fij
4.5.1 Maximal Flow
A flow's value is the total flow out of the sink (or into the source). A maximal flow is a flow which has the greatest value possible.
S={A,B} and T={C,D,E,Z}, for instance, are a cut at the beginning of the section for the transport network.
4.5.2 Minimal cut
The capacity of the cut S,T is the sum of the capacities of all edges starting at a vertex in SS and ending at a vertex in TT. Equivalently, it is the number ∑i∈S, j∈TCij. A minimal cut is a cut with the least possible capacity.
4.5.3 Max Flow Algorithim
|
Que) Use the max flow algorithm to determine a maximal flow, the value of the maximal flow, and a minimal cut for the transportation network below.
|
Ans)
|
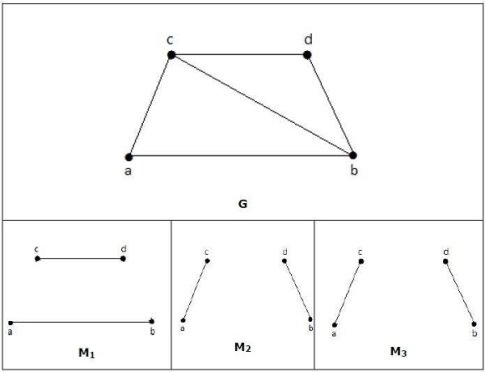
Let 'G' = (V, E) be a diagram. A subgraph is known as a coordinating M(G), if every vertex of G is episode with at most one edge in M, i.e., deg(V) ≤ 1 ∀ V ∈ G which implies in the coordinating diagram M(G), the vertices ought to have a level of 1 or 0, where the edges ought to be episode from the chart G. Documentation − M(G) |
Example 1:
|
Figure 10
In a coordinating,
on the off chance that deg(V) = 1, at that point (V) is supposed to be coordinated in the event that deg(V) = 0, at that point (V) isn't coordinated.
|
In a coordinating, no two edges are adjoining. It is since, in such a case that any two edges are nearby, at that point the level of the vertex which is joining those two edges will have a level of 2 which disregards the coordinating principle.
References
1. D.S. Chandrasekharaiah: Graph Theory and Combinatorics, Prism,2005.
2. Chartrand Zhang: Introduction to Graph Theory, TMH, 2006.
3. Richard A. Brualdi: Introductory Combinatorics, 4th Edition, Pearson Education, 2004.
4. Geir Agnarsson & Raymond Geenlaw: Graph Theory, Pearson Education, 2007.