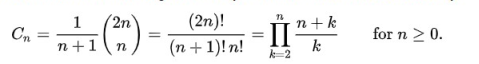UNIT – 5
Fundamental Principles of Counting
5.1.1 Rule of Sum - Statement:
In the event that there are n decisions for one activity, and mm decisions for another activity and the two activities is impossible simultaneously, at that point there are n+mn+m approaches to pick one of these activities.
5.1.2 Rule of Product - Statement:
On the off chance that there are n methods of accomplishing something, and mm methods of doing something else from that point onward, at that point there are n\times mn×m approaches to perform both of these activities.
Example 1:
Calvin needs to go to Milwaukee. He can browse 33 transport administrations or 22 train administrations to head from home to downtown Chicago. From that point, he can browse 2 transport administrations or 3 train administrations to go to Milwaukee. What number of ways are there for Calvin to get to Milwaukee?
He has 3 + 2=53+2=5 ways to get to downtown Chicago. (Rule of sum) |
A permutation of a set is, loosely speaking, an assembly of its members into a sequence or a linear order, or a rearrangement of its elements if the set is already arranged. The term "permutation" often refers to an ordered set's act or method of modifying the linear order.
Permutation: It is the various configurations taken one by one, or any, or all at a time, of a given number of elements. If we have two parts, for instance, A and B, so there are two potential configurations, AB and BA.
When 'r' elements are ordered out of a total of 'n' elements, the number of permutations is n Pr = n! / (n)-r) !. Let n = 4, for instance, (A, B, C and D) and r = 2 (All permutations of size 2). Answer is 4! /(4-2)! = 12. AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB and DC are among the twelve permutations. |
Combination: These are the various choices taken one by one, or several, or all at a time, of a given number of elements. For instance, if we have two objects, A and B, then there is only one way to pick two items, both of which are chosen.
When 'r' elements are chosen from a total of 'n' elements, the number of combinations is n C r = n! / [(r !) x (n-r)! ]. Let n = 4, for instance, (A, B, C and D) and r = 2 (All combinations of size 2). Answer is 4! /((2-4)! To *2! ) = 6. The six combinations are AB, AC, AD, BC, BD, CD. n C r = n C (n – r) |
NOTE: We have separate cases for permutation and combination in the same example. AB and BA are two separate elements for permutation, but AB and BA are the same for collection.
The Binomial Theorem is a simple way of extending (or multiplying) a binomial expression that has been elevated to some (usually inconveniently large) power (okay, it's a less sluggish way). The phrase (3x-2)10, for example, would be very painful to multiply by hand. Thankfully, somebody has worked out a formula for this extension, and to get the extended (multiplied-out) shape, we can plug the binomial 3x-2 and the power 10 into that formula.
The formal expression of the Binomial Theorem is as follows:
The parenthetical bit above has these equivalents:
|
![(a + b)^n = sum[k=0,n][(n over k)a^(n-k)b^k]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642930212_8886838.png)
![(n over k) = nCk = n!/[(n-k)!k!]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642930212_9471726.png)
Recall that the factorial notation "n!" "means "the product of all the numbers between 1 and n", so, for example, 6! = 1×2×3×4×5×6. Then the "10C7" (often pronounced as "ten, choose seven") means:
|
![10_C_7 = 10! / [(10 - 7)! 7!] = 10! / [3!7!] = 120](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642930213_0016673.png)
Assume we've got a Set A to the elements n. Any selection of r objects from A, where each object is selected,
The object can be selected more than once, referred to as the n combination. Objects taken at a time of repetition with r. The combinations, for example, The letters a, b, c, d taken 3 at a time with repetition are: aaa, aab, aaa, aab, Aac, aad, abb, abc, abd, acc, acd, add, bbb, bbc, bbc, bcc, bcd, bdd, ccc, ccd, add, bbb, bbc, bcc, bcd, bcd, bdd, ccc, ccc, ccd, Ddd, cdd. Two repetition combinations are considered identical, If the same elements are repeated an equal number of times, independent of their order.
Note that there are equivalents to the following:
1. The number of n-object combinations taken by r at a time with r repeating.
2. The number of ways r identical objects can be spread among the same objects N Separate Containers.
3. The number of the equation's nonnegative integer solutions:
For x1 + x2 + · · · + xn = r.
The Catalan numbers in combinatorial mathematics form a set of natural numbers that appear in different counting problems, frequently involving objects that are recursively described. They are named after Eugène Charles Catalan, the Belgian mathematician.
In terms of binomial coefficients, the nth Catalan number is directly given by
|
The first Catalan numbers for n = 0, 1, 2, 3, ... are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ... |
References
1. D.S. Chandrasekharaiah: Graph Theory and Combinatorics, Prism,2005.
2. Chartrand Zhang: Introduction to Graph Theory, TMH, 2006.
3. Richard A. Brualdi: Introductory Combinatorics, 4th Edition, Pearson Education, 2004.
4. Geir Agnarsson & Raymond Geenlaw: Graph Theory, Pearson Education, 2007.
