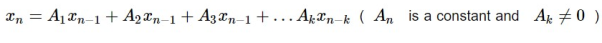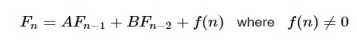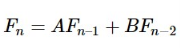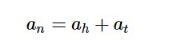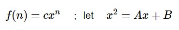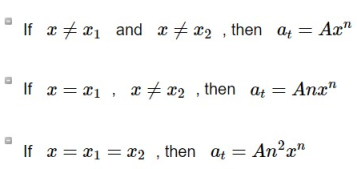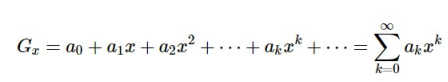Unit-8
Recurrence Relations
The process for recursively finding the terms of a sequence is called the recurrence relation.
8.1.1 Definition:
A recurrence relationship is an equation that represents a series recursively where a function of the previous terms is the next term (Expressing Fn as some combination of Fi with i<n).
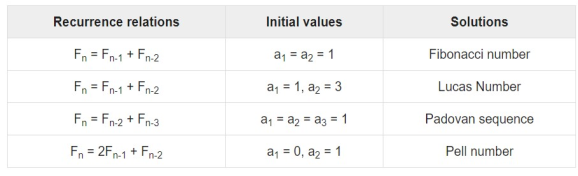
Example − Fibonacci series − Fn=Fn−1+Fn−2 Tower of Hanoi − Fn=2Fn−1+1 |
A degree k or order k linear recurrence equation is a recurrence equation that is in the format of
|
on a sequence of numbers as a first-degree polynomial.
Examples:
|
A linear homogeneous recurrence relation of the second-order with. A recurrence relationship of the form is the constant coefficients.
ak = Aak−1 + Bak−2 for all integers k greater than some fixed integer, where A and B are fixed real numbers with B ≠ 0. Following given are examples of linear second-order Homogeneous relationship of recurrence with constant coefficients: A) ak=3ak-1 + 2ak+2 ; A=3 & B=2 B) ek=2ek-2 ; A=0 & B=2 C) gk=gk-1 + gk-2 ; A=1 & B=1 |
A relationship of recurrence is considered non-homogeneous if it is in the form of
Its associated homogeneous recurrence relation is Its associated homogeneous recurrence relation is
The solution (an)of a non-homogeneous recurrence relation has two parts. First part is the solution (ah)of the associated homogeneous recurrence relation and the second part is the particular solution (at).
The solution (an)of a non-homogeneous recurrence relation has two parts. First part is the solution (ah)of the associated homogeneous recurrence relation and the second part is the particular solution (at).
The first element of the approach is carried out using the protocols described in the previous section.
Let be the characteristic equation of the associated homogeneous recurrence relation and let x1 and x2 be its roots.
|
Generating functions are sequences in which each sequence term is expressed in a formal power series as a coefficient of a variable x.
Mathematically, the generating function would be − for an infinite number, say a0,a1,a2,...,ak,...
|
Some Domain Fields
For the following reasons, generating functions may be used −
- For solving a number of problems with counting. For instance, the number of ways to modify a note of Rs. 100 with denominations of Rs.1, Rs.2, Rs.5, Rs.10, Rs.20 and Rs.50 notes
- To solve relationships with recurrence
- Any of the combinatorial identities to prove
- For the finding of asymptotic formulas for sequence words
References
1. D.S. Chandrasekharaiah: Graph Theory and Combinatorics, Prism,2005.
2. Chartrand Zhang: Introduction to Graph Theory, TMH, 2006.
3. Richard A. Brualdi: Introductory Combinatorics, 4th Edition, Pearson Education, 2004.
4. Geir Agnarsson & Raymond Geenlaw: Graph Theory, Pearson Education, 2007.