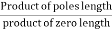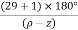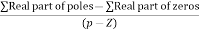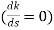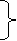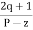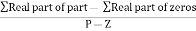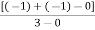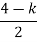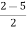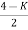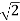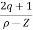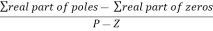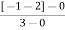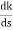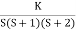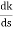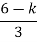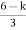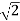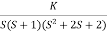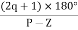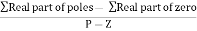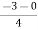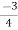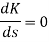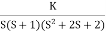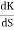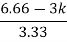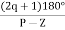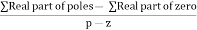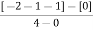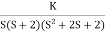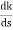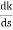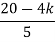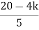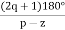UNIT-5:
Root–Locus Techniques
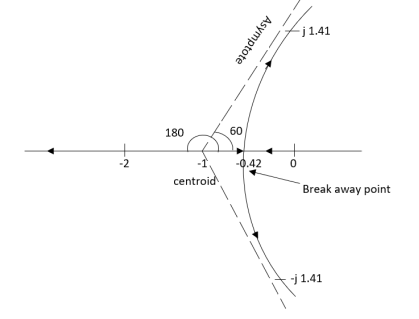
The root locus is a graphical produce for determining the stability of a control system which is determined by the location of the poles. The poles are nothing but the roots of the characteristic equation.
Features of Root Locus
(open loop poles) (open loop zeros) 4. A point on the real axis lies on the root locus if number of open loop poles or zero to the right side of that point is odd in number. 5. Value of K anywhere on the root locus is given as K = 6. I)If poles > zeros then (Þ-z) branches will terminate at ∞ (where k=∞) II)If Z > P, then (Z-P) branches will start from ∞ (K = 0) 7. When P>Z, (P-Z) branches will terminate at ∞ (open loop zeros). But by which path. So the path is shown by asymptotes and this asymptote is given by
Asymptote = 8. There asymptotes intersect the real axis at a single point and this point is known as centroid. Centroid = 9. Break away and break in point when root locus lies between two poles it’s called break in point.
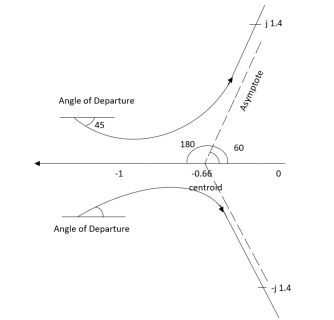
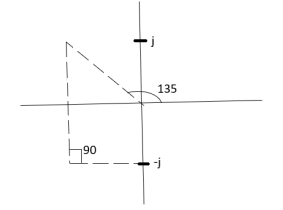
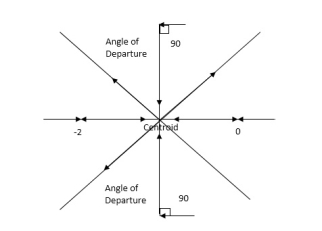
10. Angle of arrival and angle of departure this print is used when the roots are complex. Angle of departure - for complex poles Angle of arrival – for complex zero.
øA = (2q+1) 180° - ø = ∠Z– ∠P.
|
11. Intersection of root locus with imaginary axis can be calculated by Routh Hurwitz. By calculating valve of k at intersection point (we can comment about system stability) so by knowing values of k at intersection point (imaginary axis) the valve of s at that point can also be calculated.
Absolutely stable: If the root low (all the branches) lies within the left side of S-plane.
Conditionally Stable: - If some part of the root locus lies on the left half and same
Part on the right of S-plane then it is conditionally stable.
Unstable: If the root locus lies completely on right side of S-plane then it is unstable.
Key takeaways
- The values of S which satisfy both the angle and magnitude conditions are the roots of the characteristic equation.
- Angle condition:
LG(S)H(S) = +-1800(2 KH) (K = 1,2,3, --)
If angle is odd multiple of 1800 it satisfies above condition.
3. Magnitude condition:
| G(S)H(S) = 1 | at any point on root locus. The magnitude condition can be applied only if angle condition is satisfied.
Q1. Sketch the root locus for given open loop transfer function:
G(S) = 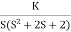 .
.
Soln:1) G(s) = 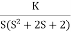
Number of Zeros = 0 Number of polls S = (0, -1+j, -1-j) = (3). 1) Number of Branches = max (P, Z) = max (3, 0) = 3.
2) As there are no zeros in the system so, all branches terminate at infinity. 3) As P>Z, branches terminate at infinity through the path shown by asymptotes Asymptote = P=3, Z=0. q= 0, 1, 2. For q=0 Asymptote = 1/3 × 180° = 60° For q=1 Asymptote = = 180° For q=2 Asymptote = Asymptotes = 60°,180°,300°.
4) Asymptote intersects real axis at centroid Centroid = = Centroid = -0.66 5) |
6) As poles are complex so angle of departure
øD = (2q+1)×180°+ø
ø = ∠Z –∠P.
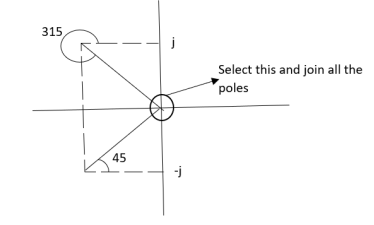
Calculating ø for S=0
|
Join all the other poles with S=0
ø = ∠Z –∠P.
= 0-(315°+45°)
= -360°
ØD = (2q + 1)180 + ø.
= 180° - 360°
ØD = -180° (for q=0)
= 180° (for q=1)
=540° (for q=2)
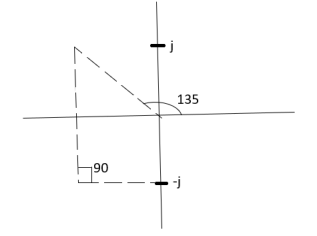
Calculation ØD for pole at (-1+j)
|
ø = ∠Z –∠P.
= 0 –(135°+90°)
= -225°
ØD = (2q+1) 180°+ø.
= 180-225°
= -45°
ØD = -45° (for q = 0)
= 315° (for q = 1)
= 675° (for q =2)
7) The crossing point on imaginary axis can be calculated by Routh Hurwitz the characteristic equation is.
1+G(s) H (s) = 0
1+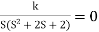
S (S2+2s+2)+k = 0
S3+2s2+2s+K = 0
S3 | 1 | 1 | 0 |
| 2 | K | 0 |
S1 |
| 0 |
|
S0 | K |
|
|
For stability 0<K<2. So, when K=2 root locus crosses imaginary axis S3 + 2S2 + 2S + 2 =0 For k Sn-1 = 0 n : no. of intersection S2-1 = 0 at imaginary axis S1 = 0
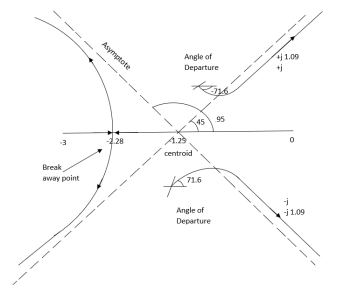
K<4 For Sn = 0 for valve of S at that K S2 = 0 2S2 + K = 0 2S2 + 2 = 0 2(S2 +1) = 0 32 = -2 S = ± j The root locus plot is shown in figure 1. |
|
Fig 1 Root Locus for G(S) = 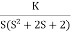
Q2. Sketch the root locus plot for the following open loop transfer function
G(s) = 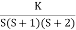
- Number of zero = 0, number of poles = 3
- As P>Z, branches will terminates at infinity
- There are no zeros so all branches will terminate at infinity.
- The path for the branches is shown by asymptote
Asymptote = P=3, Z=0 q= 0,1,2. For q = 0 Asymptote = For q=1 Asymptote = For q=2 Asymptote = |
5. Asymptote intersect real axis at centroid
Centroid =
= |
6. As root locus lies between poles S= 0, and S= -1 So, calculating breakaway point.
The characteristic equation is 1+ G(s) H (s) = 0. 1+ K = -(S3+3S2+2s)
3s2+6s+2 = 0 S = -0.423, -1.577. So, breakaway point is at S=-0.423 because root locus is between S= 0 and S= -1 |
7. The intersection of root locus with imaginary axis is given by Routh criterion.
Characteristics equation is
|
Fig 2 Root Locus for G(s) = 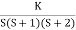
The root locus plot is shown in fig. 2.
Q3. Plot the root locus for the given open loop transfer function
G(s) =
P = (S=0,-1,-1+j,-1-j) = 4 2. As P>Z all the branches will terminated at infinity. 3. As no zeros so all branches terminate at infinity. 4. The path for branches is shown by asymptote.
Asymptote =
q=0,1,2,3. (P-Z = 4-0) for q=0 Asymptote = For q=1 Asymptote = For q=2 Asymptote = For q=3 Asymptote = 5. Asymptote intersects real axis at unmarried Centroid = Centroid = 6) As poles are complex so angle of departure is ØD = (2q+1) ×180 + ø ø = ∠Z –∠P. |
A) Calculating Ø for S=0
|
ø = ∠Z –∠P.
= 0 –[315° + 45°]
Ø = -360°
For q = 0
ØD = (2q+1) 180° + Ø
= 180 - 360°
ØD = -180°
b) Calculating Ø for S=-1+j
ø = ∠Z –∠P.
= 0-[135° + 90° + 90°]
Ø = -315°
For q=0
ØD= (2q+1) 180° +Ø
= 180° -315°
ØD = -135°
ØD for S=1+j will be ØD = 45°
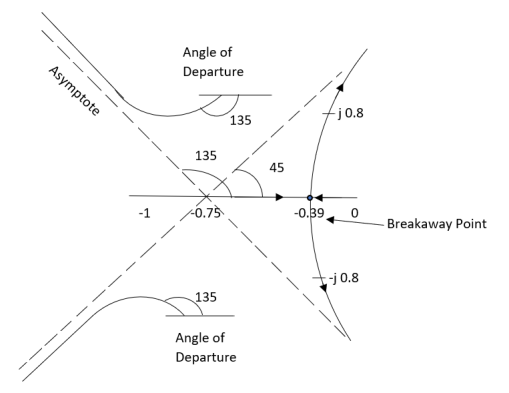
7) As the root locus lie between S=0 and S=-1 So, the breakaway point is calculated
1+ G(s)H(s) = 0 1+ (S2+S)(S2 +2S+2) + K =0 K = -[S4+S3+2s3+2s2+2s2+2s]
S = -0.39, -0.93, -0.93. The breakaway point is at S = -0.39 as root locus exists between S= 0 and S=-1
|
8) Intersection of root locus with imaginary axis is given by Routh Hurwitz
I + G(s) H(s) = 0 K+S4+3S3+4S2+2S=0
|
For system to be stable
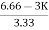 >0
>0
6.66>3K
0<K<2.22.
For K = 2.22
3.3352+K =0
3.3352 + 2.22 = 0
S2 = -0.66
S = ± j 0.816.
The root locus plot is shown in figure 3.
|
Fig 3 Root Locus for G(s) = 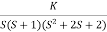
Q4. Plot the root locus for open loop system
G(s) = 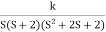
1) Number of zero = 0 number of poles = 4 located at S=0, -2, -1+j, -1-j. 2) As no zeros are present so all branches terminated at infinity. 3) As P>Z, the path for branches is shown by asymptote Asymptote = q = 0,1,2……p-z-1 For q = 0 Asymptote = 45° q=1 Asymptote = 135° q=2 Asymptote = 225° q=3 Asymptote = 315° 4) Asymptote intersects real axis at centroid.
Centroid = = Centroid = -1. 5) As poles are complex so angle of departure is ØD=(2q+1)180° + Ø ø = ∠Z –∠P = 0-[135°+45°+90°] = 180°- 270° ØD = -90° 6) As root locus lies between two poles so calculating point. The characteristic equation is 1+ G(s)H(s) = 0 1+ K = -[S4+2S3+2S2+2S3+4S2+4S] K = -[S4+4S3+6S2+4S]
S = -1 So, breakaway point is at S = -1 7) Intersection of root locus with imaginary axis is given by Routh Hurwitz.
K≤5. For K=5 valve of S will be. 5S2+K = 0 5S2+5 = 0 S2 +1 = 0 S2 = -1 S = ±j. |
The root locus is shown in figure 4.
|
Fig 4 Root Locus For G(s) = 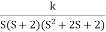
Q5. Plot the root locus for open loop transfer function
G(s) = 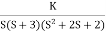
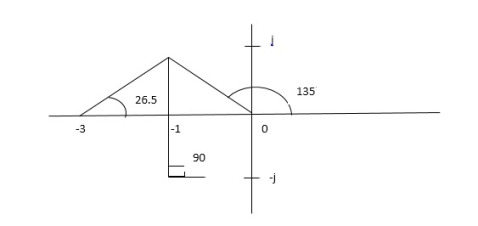
Asymptote = For q = 0 Asymptote = 45 For q = 1 Asymptote = 135 For q = 2 Asymptote = 225 For q = 3 Asymptote = 315 (4). The asymptote intersects real axis at centroid. Centroid = ∑Real part of poles - ∑Real part of zero / P – Z = [-3-1-1] – 0 / 4 – 0 Centroid = -1.25 (5). As poles are complex so angle of departure φD = (29 + 1)180 + φ |
|
ø = ∠Z –∠P. = 0 – [ 135 + 26.5 + 90 ] = -251.56 For q = 0 φD = (29 + 1)180 + φ = 180 – 215.5 φD = - 71.56 (6). Break away point dk / ds = 0 is at S = -2.28. (7). The intersection of root locus on imaginary axis is given by Routh Hurwitz. 1 + G(S)H(S) = 0 K + S4 + 3S3 + 2S3 + 6S2 + 2S2 + 6S = 0 S4 1 8 K S3 5 6 S2 34/5 K S1 40.8 – 5K/6.8 K ≤ 8.16 For K = 8.16 value of S will be 6.8 S2 + K = 0 6.8 S2 + 8.16 = 0 S2 = - 1.2 S = ± j1.09
|
The plot is shown in figure 20.
|
Fig 5 Root Locus for G(s) = 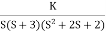
Q.6. Sketch the root locus for open loop transfer function.
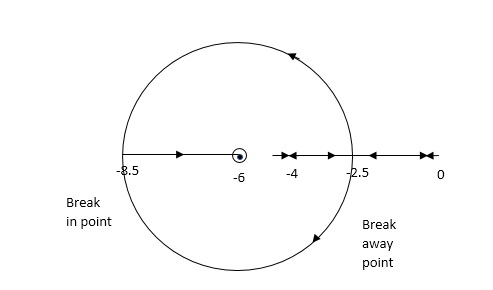
G(S) = K (S + 6)/S (S + 4)
Number of poles = 2(S = 0, -4) 2. As P > Z one branch will terminate at infinity and the other at S = -6. 3. For Break away and breaking point 1 + G(S)H(S) = 0 1 + K (S + 6)/S (S + 4) = 0 dk/ds = 0 S2 + 12S + 24 = 0 S = -9.5, -2.5 Breakaway point is at -2.5 and Break in point is at -9.5. 4. Root locus will be in the form of a circle. So finding the center and radius. Let S = + jw. G( + jw) = K( + jw + 6)/( + jw)( + jw + 4 ) = +- π tan-1 w/ + 6 - tan-1 w/ – tan-1 w / + 4 = - π taking tan of both sides. w/ + w/ + 4 / 1 – w/ w/ + 4 = tan π + w / + 6 / 1 - tan π w/ + 6 w/ + w/ + 4 = w/ + 6[ 1 – w2 / ( + 4) ] (2 + 4)( + 6) = (2 + 4 – w2) 2 2 + 12 + 4 + 24 = 2 + 4 – w2 22 + 12 + 24 = 2 – w2 2 + 12 – w2 + 24 = 0 Adding 36 on both sides ( + 6)2 + (w + 0)2 = 12 |
The above equation shows circle with radius 3.46 and centre (-6, 0) the plot is shown in figure 6
|
Fig 6 Root locus for G(S) = K (S + 6)/S (S + 4)
1. “Modern Control Engineering “, K. Ogata, Pearson Education Asia/
PHI, 4th Edition, 2002.
2. “Automatic Control Systems”, Benjamin C. Kuo, John Wiley India
Pvt. Ltd., 8th Edition, 2008.
3. “Feedback and Control System”, Joseph J Distefano III et al.,
Schaum’s Outlines, TMH, 2nd Edition 2007.
4. J. Nagarath and M. Gopal, “Control Systems Engineering”, New Age
International (P) Limited, Publishers, Fourth edition – 2005