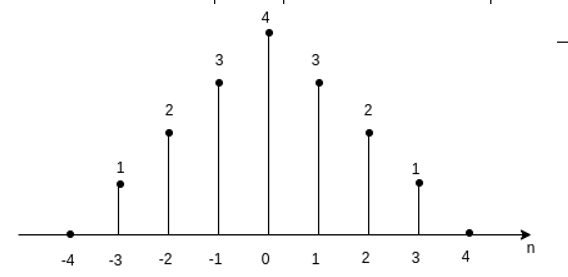
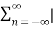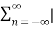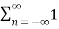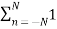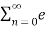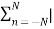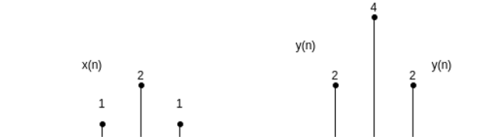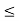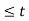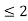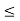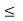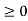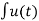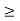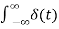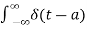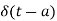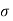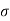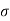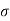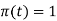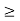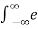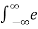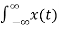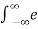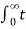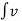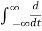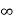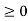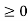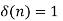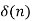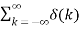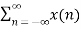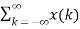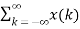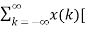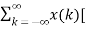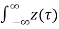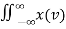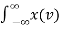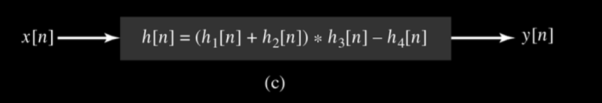Unit -1
Introduction
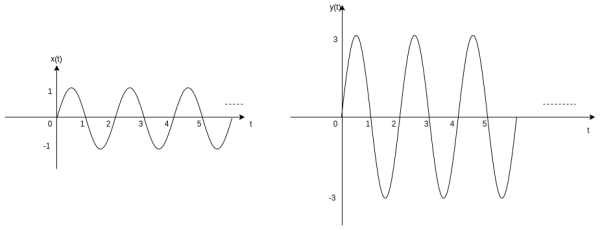
A signal is a description of how one parameter varies with another parameter. For instance, voltage changing over time in an electronic circuit, or brightness varying with distance in an image.
Figure 1. Voltage change Figure 2. Picture Brightness |
Picture brightness: A camera senses the incoming light and records the light reflectivity as a function of space onto a magnetic film.
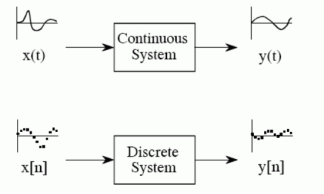
A system is any process that produces an output signal in response to an input signal. This is illustrated by the block diagram in Figure.
Figure3 . System |
Continuous systems input and output continuous signals, such as in analog electronics. Discrete systems input and output discrete signals, such as computer programs that manipulate the values stored in arrays.
Key Takeways:
- The fundamental quantity of representing some information is called a signal.
Deterministic
A signal is said to be deterministic if there is no uncertainty with respect to its value at any instant of time or the signals which can be defined exactly by a mathematical formula are known as deterministic signals.
Figure 4. Deterministic signal |
Random
A signal is said to be non-deterministic if there is uncertainty with respect to its value at some instant of time. Non-deterministic signals are random in nature hence they are called random signals. Random signals cannot be described by a mathematical equation. They are modelled in probabilistic terms.
Figure5 . Random signal |
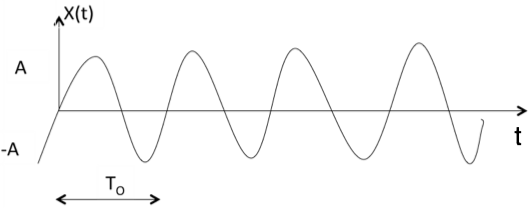
Periodic
A signal is said to be periodic if it satisfies the condition x(t) = x(t + T) or x(n) = x(n + N).
Where
T = fundamental time period,
1/T = f = fundamental frequency.
|
Figure6 . Random signal
The above signal will repeat for every time interval T0 hence it is periodic with period T0.
Non-periodic
Non-periodic signals (also known as aperiodic signals), unlike periodic signals, do not have just one particular frequency. Instead, they are spread out over a continuous range of frequencies. For example, a speech signal
Energy
A signal is said to be energy signal when it has finite energy
Energy E = 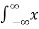 2(t) dt
2(t) dt
Power:
A signal is said to be power signal when it has finite power.
Power P = lim T-> ∞ 1/2T 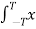 2 (t) dt
2 (t) dt
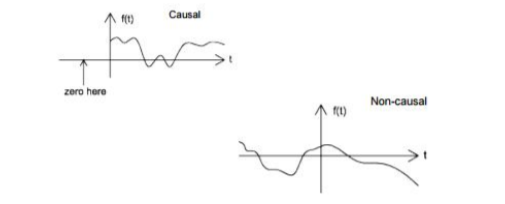
Causal and Non-casual
A system is said to be causal if its output depends upon present and past inputs, and does not depend upon future input. For non- causal system, the output depends upon future inputs also.
|
Figure 7. Casual and Non casual system
Even and odd signal.
A signal is said to be even when it satisfies the condition x(t) = x(-t)
Example 1: t2, t4… cost etc.
Let x(t) = t2
x(-t) = (-t)2 = t2 = x(t)
∴,∴, t2 is even function
Example 2: As shown in the following diagram, rectangle function x(t) = x(-t) so it is also even function.
Figure . Even signal |
A signal is said to be odd when it satisfies the condition x(t) = -x(-t) Example: t, t3 ... And sin t Let x(t) = sin t x(-t) = sin(-t) = -sin t = -x(t) ∴,∴, sin t is odd function. Any function ƒ(t) can be expressed as the sum of its even function ƒe(t) and odd function ƒo(t). ƒ(t ) = ƒe(t ) + ƒ0(t ) where ƒe(t ) = ½[ƒ(t ) +ƒ(-t )] |
Problems :
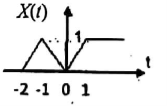
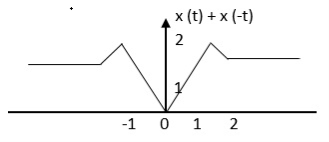
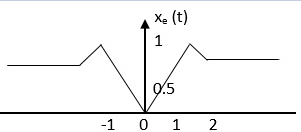
Find the even and odd of the signal as shown in the figure
Step 1: Find the signal x(-t)
The even signal is xe(t) = x(t) +x(-t)
Therefore
xe(t) = ½ x(t) +x(-t)/2
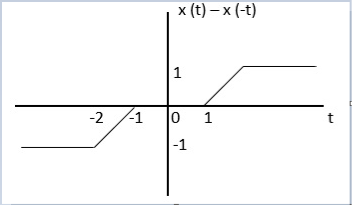
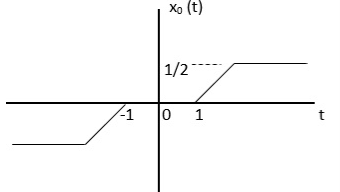
For odd the signal is
xo(t)
If f(t) = cos w1t + cos w2t . Find its period f(t) = cos w1t + cos w2t = cosw1(t+T) + cos w2(t+T) w1T = 2mπ w2T = 2nπ w1/w2 = m/n = rational number f(t) = cos 10t + cos(10+π) t w1 =10 t w2= (10+π) t w1/w2 = 10/10+π which is not a rational number hence non periodic Find whether the following signals are periodic or not. Find its fundamental frequency. a) x1(t) = sin3t + sin πt b) x2(t) = 1.2 + sin3t c) x3(t) = 1.2 + sin πt d) x4(t) = -1.2 -2 sin 2.1t + 3 cos 2.8 t
a) T1 = 2π/w1 = 2π/3 T2 = 2π/w2 = 2π/π=2
T1/T2 = 2π/3 / 2 = π/3 Irrational number hence aperiodic
b) Clamped sinusoidal wo= 3rad/sec c) Clamped sinusoidal wo=π rad/sec d) T1 = 2π/w1 = 2π/2.1 = 20π/21 T2 = 2π/w2 = 2π/2.8 = 20π/28 = 5π/7
T1/T2 = 20π/21/5π/7 = 4/ 3 LCM = 3. Hence it is periodic To = LCM x T1 = 3 x 20π/21 = 20π/7 wo = 2π/20π/7 = 7/10 = 0.7 rad/sec Problem: Determine the values of power and energy of the signals : x(n) = sin(π/4n) Energy is given by x(n) E= |x(n)| 2 E = = = P = lim N->∞ 1/ 2N+1 The energy is infinite, and the power is finite. Therefore, the signal is a power signal. x(n) = e 2n u(n) E = E= |x(n)| 2 = 1 P = lim N->∞ 1/2N+1 = lim N->∞ 1/2N+1 [ e 4(N+1) -1 / e 4 -1 ] = ∞ The signal is neither power or energy signal.
Key Takeaways:
|
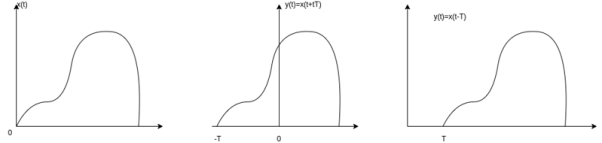
Time Shifting Let us consider a signal x(t) as shown in figure. The time shifting of x(t) may delay or advance the signal in time. Mathematically this can be represented by y(t) = x(t-T) ------------------------------------------(1) If T is positive the shifting delays the signal as shown in figure. If T is negative the shifting advances the signal as shown in figure.
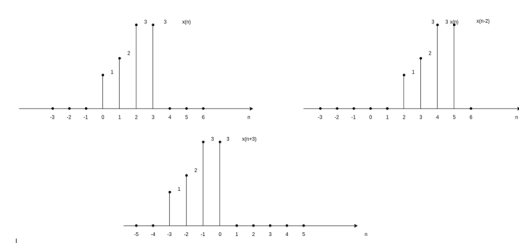
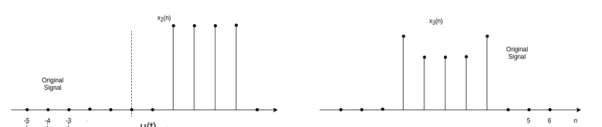
Figure8. Time Shifting Similarly, the time shifting operation of discrete time signals is represented by y(n) = x(n-k) which shows that the signal y(n) can be obtained by shifting x(n) by k units. If k is positive the shift is to the right (delay) and if k is negative the shift is to the left . Let us consider a signal x(n) as shown in figure. The signal x(n-2) is obtained by shifting x(n-2) is obtained by shifting x(n) right by 2 units of time. The result is shown in fig (b). On the other hand x(n+3) is obtained by shifting x(n) left by three units of time.
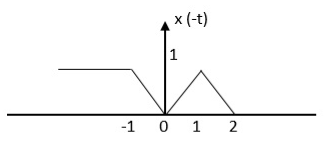
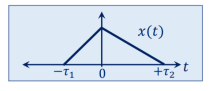
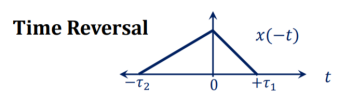
Figure . Time shifting using discrete signal Time Reversal The time-reversal of signal x(t) can be obtained by folding the signal about t=0. It is denoted by x(-t). The signal x1(t) and its reflection x(-t) are illustrated in fig a and b respectively.
Figure9. Time Reversal for continuous time
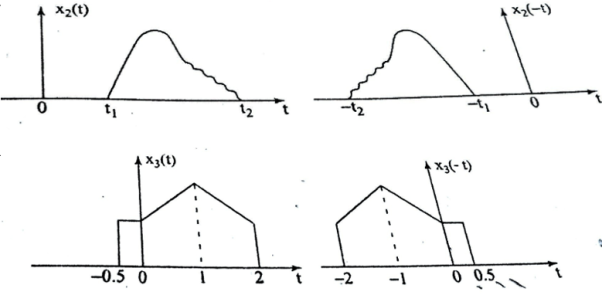
The signal x(-t+2) is obtained by delaying x1(-t) by two units of time and x1(-t-2) is obtained by advancing x1(-t) by two units of time. The signals x1(-t+2) and x1(-t-2) are shown in figure ( c) and (d).
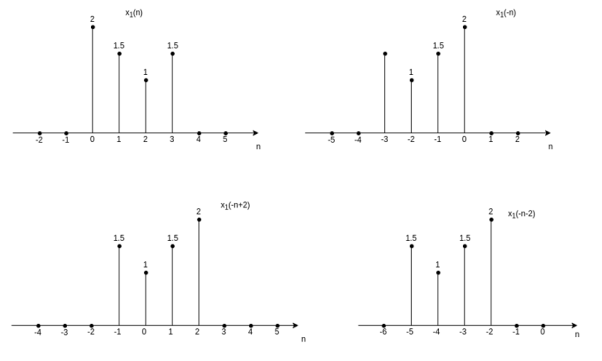
Figure 10. Time reversal for x2(t) and x3(t) The time-reversal of the discrete-time signal can be obtained by folding the sequence x(n) about n=0. For signal x1(n) in fig, the time-reversal signal x1(-n) is shown in fig (b).
Figure 11. Time reversal for discrete time signal The signal x1(-n+2) is obtained by delaying x1(-n) by two units of time and x1(-n-2) is obtained by advancing x1(-n) by two units of time. The other examples for time-reversal of discrete-time signal are obtained by fig (a) and (b).
Problem: Sketch the following signals (i) u(-t+1)
Step 1: draw the unit step signal
Figure . Unit step signal
Step 2: Fold the signal about t-0 as shown in fig (b)
Figure .Folding of unit step signal u(t)
Step 3: Shift the signal u(-t) right by one unit as shown in fig(c )
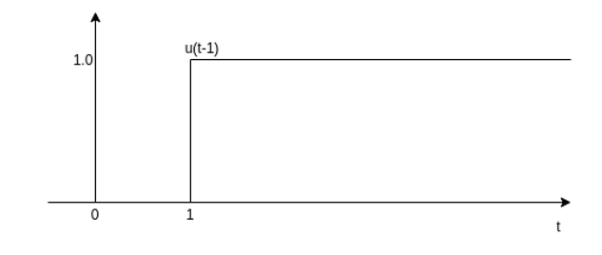
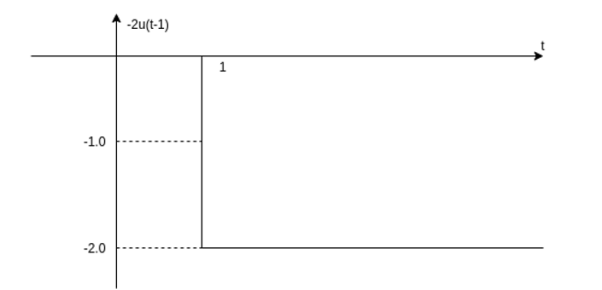
Figure . Shifting the signal by one unit (ii) x(t) = -2 u(t-1) Step 1: Draw the unit step signal
Fig . Unt step signal Step 2: Shift the signal u(t) right by one unit of time as shown in the figure.
Fig . Delayed unit step signal Step3: Multiply the signal u(t-1) with -2
Figure . Multiply with -2 units Amplitude Scaling: Consider a signal x(t) that is fed to an amplifier with a gain of 3 then the output of an amplifier can be represented by y(t) = 3 x(t) That is the output y(t) is identical in shape to the input signal x(t) but its amplitude is thrice everywhere. This concept is illustrated in the figure.
Figure 12. Amplitude Scaling
From fig 1.48 we find that the amplitude is rescaled hence the name amplitude scaling. Similarly, the amplitude scaling of a discrete-time signal can be represented by y(n) = a x(n) If x(n) is as shown in figure and a=2 then y(n) is as shown in figure(b).
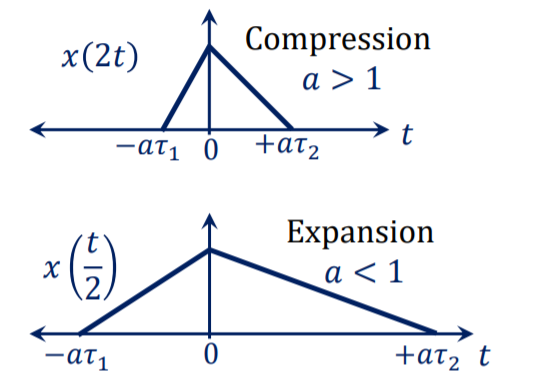
Figure13 . Amplitude scaling in discrete domain Time scaling: Let us consider a signal x(t) as shown in figure(a). The time scaling of the signal can be accomplished by replacing t by at in signal x(t). If a=2 we get new signal y(t) = x(2t) Observe that x(t) is switching from 0 to 1 at t=-1 and switching from 1 to 0 at t=3. . When y(t) = 2t, y(t) = x(2t), y(t) switches from 0 to 1 at t=0.5 and switches from 1 to 0 at t=1.5. In the original signal x(t) magnitude is equal to 1 at t=0 and t=2 . But in a time-scaled signal y(t) magnitude is equal to 1 at t=0 and t=2. But in a time-scaled signal y(t) magnitude is equal to 1 at t=0 and t=1. This behavior shows that x(t) is compressed in time by factor 2.
Figure 14. Time Scaling The resulting signal x(2t) is shown in fig(b). Let x(t) be an audio signal. If x(t) were recorded on a magnetic tape then x(2t) is the signal played back twice the recording speed. Now consider another signal y(t) = x(at) with a=1/2. Figure ( c ) shows x(1/2) which is expanded in time by factor 2. In discrete- time signal y(n) = x(2n) Let x(n) be a sequence as shown in figure. Then we plot time scaled signal y(n) by substituting different values of n. For n =-1 y(-1) = x(-2) =2 ….. y(0) = x(0) =4 y(1) = x(2) =2 y(2) = x(4) = 0
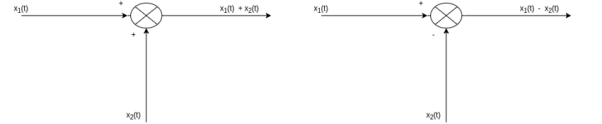
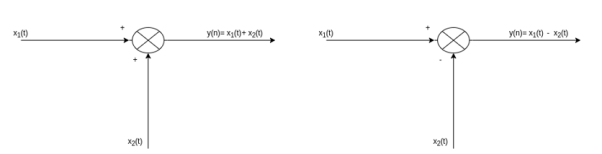
Figure 15. Discrete time signal Signal addition: The sum of two continuous-time signals can be obtained by adding their values at every instant. Similarly, the subtractions of two continuous-time signals can be obtained by subtracting their values at every instant.
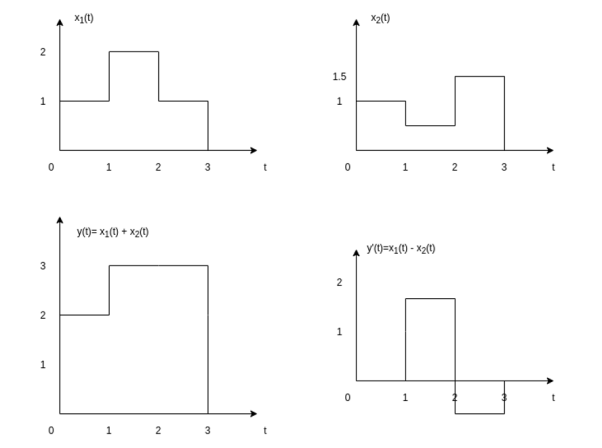
Figure16 . Signal addition Let us consider the addition and subtraction of two signals x1(t) and x2(t) as shown in Figures (a) and (b).
Figure 17. Resultant for addition of signals The addition of signals of two signals x1(t) and x2(t) can be obtained by considering each time interval separately as follows: x1(t) = 1 for 0 x2(t) =1 for 0 Hence x1(t) + x2(t) = 2 for 0 x1(t) = 2 for 1 x2(t) =0.5 for 1 Hence x1(t) + x2(t) = 2.5 for 1 x1(t) = 1 for 2 x2(t) =1.5 for 2 Hence x1(t) + x2(t) = 2.5 for 2 The sketch for y(t) = x1(t) + x2(t) as shown in fig ( c ) In the same way the subtraction of x2(t) from x1(t) can be obtained. By inspection we can find y’(t) = x1(t) – x2(t) = 0 for 0 = 1.5 for 1 = -0.5 for 2 For discrete-time signals, the sum of two sequences can be obtained by adding the sequence values at the same index n for which the sequences are defined.
Figure 18. Addition in discrete time signals If x1(n) = {1, 3, 2, 1} and x2(n) = {1, -2, 3, 2} then x1(n) + x2(n) = { 1+1, 3-2, 2+3, 1+2}= {2, 1, 5, 3} x1(n) – x2(n) = { 1-1, 3-(-2), 2-3, 1-2} = { 0, 5, -1, -1}
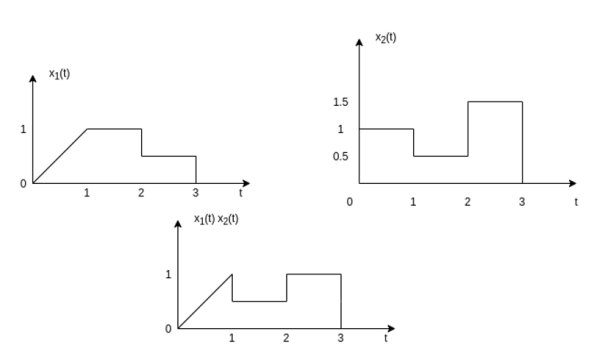
Signal multiplication The multiplication of two signals can be obtained by multiplying their values at every instant. The multiplication process is illustrated in the figure. In the interval 0 x1(t) = t; x2(t) = 1. Therefore y(t) = x1(t) x2(t) Therefore y(t) = x1(t) x2(t)=t In in the interval 1 x1(t) =1; x2(t) = 0.5. Therefore y(t) = 0.5 In in the interval 2 x1(t) =0.5; x2(t) = 1.5. Therefore y(t) = 0.75
Figure19 . Signal Multiplication
If x1(n) = { 1, 2, -2, 3} and x2(n) = {1, 0.5, 0.5, 1} then y(n) = x1(n) . x2(n) ={ 1.1, 2.(0.5), -2(0.5), 3.1} ={1, 1, -1, 3}
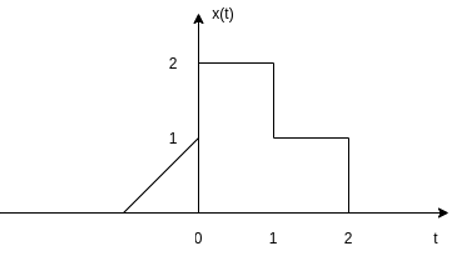
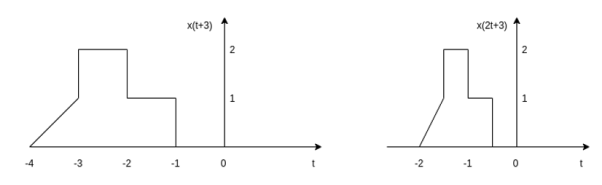
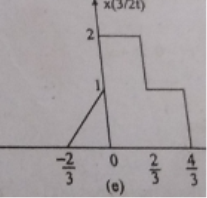
Problem: For the signal x(t) as shown in figure find : (i) x(t-2) (ii) x(2t +3) (iii) x(3/2t)
x(t-2) This signal can be obtained by delaying the signal by 2 units of time.
x(2t+3) This signal can be obtained first shifting the sequence x(t) left by 3 units of time as shown in fig and then by applying time scaling by factor 2. The resultant signal is shown in the figure.
x(3/2t) The signal x(3/2t) can be obtained by compressing the signal x(t) by 2/3 times.
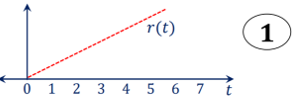
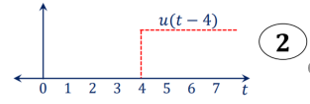
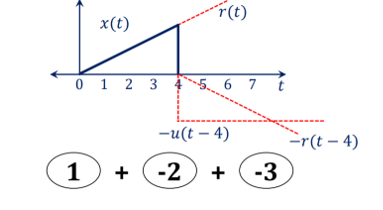
x(t) = r(t) – [ u(t-4) + r(t-4)]
Key Takeaways:
|
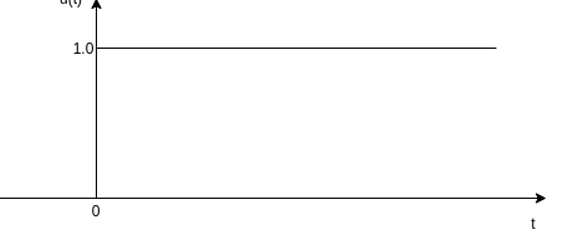
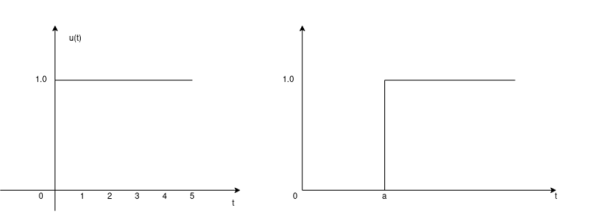
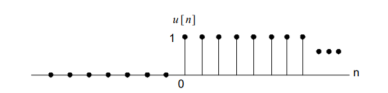
The unit step sequence is defined as: u(t) = 1 for t = 0 for t<0 From the above equation we find the when the argument t in u(t) is less than zero then the unit step function is zero and when the argument t in u(t) is greater than or equal to zero then the unit step function is unity Similarly, for a shifted unit step function u(t-a) is zero if the argument (t-a) <0 or t<a and is one if the argument (t-a) > 0 or t>a. That is u(t-a) = 1 for t>a =0 for t<a
Figure20. Step function Unit ramp function The unit ramp function is defined as: r(t) = t for t =0 for t<0 or r(t) = t u(t)
Figure21. Ramp function The ramp function can be obtained by applying unit step function to an integrator. r(t) = The unit step function can be obtained by differentiating the unit ramp function Thus u(t) = d/dt r(t) Unit parabolic function The unit parabolic function is given by p(t) = t 2 / 2 for t = 0 for t<0
Figure22. Unit parabolic function Or p(t) = t2/2 u(t)
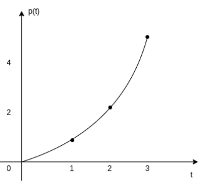
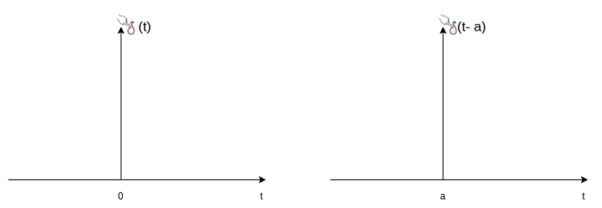
Impulse function The impulse function occupies an important place in signal analysis. It is defined as
and δ(t) =0 for t The impulse function has zero amplitude everywhere except at t=0. At t=0 the amplitude is infinity such that the area under the curve is equal to one. The unit impulse function can be obtained by using limiting process on the rectangular pulse as shown in figure. Note that the area under the rectangular pulse is equal to unity.
Figure 23. Impulse function
The rectangular pulse function of the figure can be expressed as x(t) = 1/ ∆ [ u(t) – u(t-∆)] …………………………………..(1) The impulse function can be obtained when the width ∆ ->0 that is δ(t) = lim ∆-> 0 x(t) = lim ∆-> 0 1/ ∆ [ u(t) – u(t-∆)]
Figure 24. Delayed impulse function
The delayed unit impulse function is defined as
and
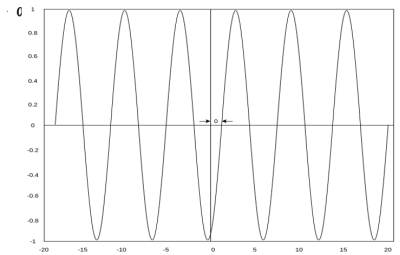
Figure 25. Unit impulse function Sinusoidal signal A continuous time sinusoidal signal is given by x(t) = A sin ( where A is the amplitude, Ω is the frequency in radians per second, and Figure shows the waveform of sinusoidal signal with A=1,
Figure 26. Sinusoidal signal Real exponential and complex exponential Real exponential
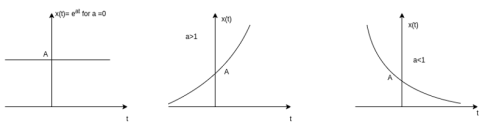
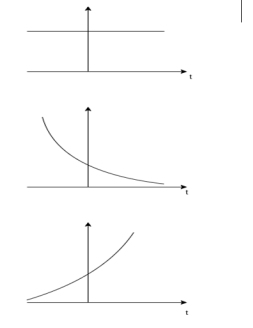
Figure27. Real exponential signals A real exponential signal is defined as x(t) = A e at --------------------------------(1) where both A and a are real. Depending on the value of ‘a’ we get different signals. It ‘a’ is positive the signal x(t) is growing exponential as shown in fig(b) If ‘a’ is negative then x(t) is decaying exponential as shown in fig(c). For a=0 x(t) is constant. Complex exponential signal. The most general for of complex exponential signal is given by x(t) = e st ---------------------------------------(1) where s is a complex variable defined as s = Therefore x(t) = e st = e s( Using Euler identity, we can expand e j Ωt = cos Ω t + j sin Ωt substituting in eq(1) we get x(t) = e Depending on the values of
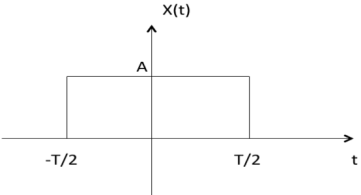
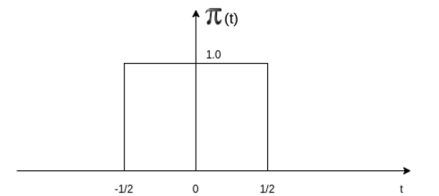
Figure 28. Complex exponential signal Rectangular Pulse: The rectangular pulse function is defined as
Figure 29. Rectangular pulse
=0 otherwise
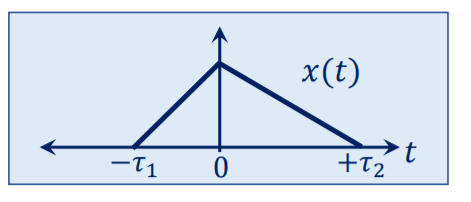
Triangular pulse function The unit triangular function is defined as ∆a(t) = 1 - |t|/a |t| 0 |t|
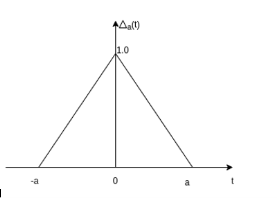
Figure30. Triangular pulse function Signum function The sinc function is defined by the expression sinc(t) = sin t/t -∞ < t < ∞
Figure 31.sinc function
The sinc function oscillates with period 2π and decays with increasing t. Its value is zero at nπ, n = ±1, ±2, …………………….. It is an even function of t. Gaussian function:
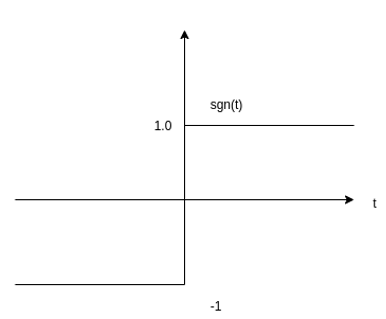
Figure 32. Gaussian function
The Gaussian function is defined by the expression ga(t) = e – at ^2 - ∞ <t<∞ This function is extensively used in probability theory. Problems: Sketch the continuous time signal x(t) = 2 sin πt for interval 0
Solution: Given: x(t) = 2 sin πt To sketch the signal we have values x(t) for different values of t, that is x(0) = 2 sin π (0) = 0. x(0.25) = 2 sin π (0.25) = √2 x(0.5) = 2 sin π (0.5) = 2 x(0.75) = 2 sin π (0.75) = √2. x(1) = 2 sin π (1) = 0 x(1.25) = 2 sin π (1.25 = -√2 x(1.5) = 2 sin π (1.5) = -2. x(0.25) = 2 sin π (1.75) = - √2 x(2) = 2 sin 2π =0 Take t on x-axis and x(t) on y-axis. Mark the above points and join all the points by a smooth curve to get continuous signal as shown in fig (a) . Given sampling period T =0.2 Sketch the signal x(t) = e -t for an interval 0 Sample the signal with a sampling period T=0.2 second and sketch the discrete time signal. Solution: Given x(t) = e -t ; x(0) =1; x(0.5) = 0.606, x(1)= 0.36768; x(1.5) = 0.2237, x(2) = 0.1353 To get signal x(t) mark the above points and draw a smooth curve joining all points as shown in figure (a) x(nT) = x(t) | t =nT = x(t) | t=0.2n x(0.2n) = e -0.2 n x(0) =1 x(1) = e – 0.2 = 0.818 x(2) = e – 0.4 = 0.67 x(3) = e – 0.6 = 0.5488 x(2) = e – 0.8 = 0.449 x(2) = e – 1 = 0.3678 x(2) = e – 1.2 = 0.3012 x(2) = e – 1.4 = 0.2466 x(2) = e – 1.6 = 0.2022 x(2) = e – 1.8 = 0.1653 x(2) = e – 2 = 0.1353
Evaluate the following integrals: (i)
Given (i) From the property
We have
e-100 α δ(t-10) =1 for t=10 = 0 otherwise
Given
δ(t-3) = 1 for t=3 =0 otherwise
Let u=x(t) dv = d/dt δ(t) v = δ(t)
du = dx/dt
Elementary Discrete Time Signals Unit step sequence: The unit step sequence is defined as: u(n) = 1 for n =0 for n<0
Figure 33. Unit step sequence
Unit ramp sequence: The unit ramp sequence is defined as r(n) = n for n =0 for n<0
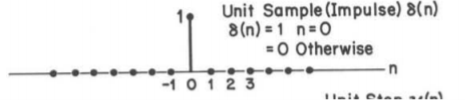
Figure 34. Unit ramp sequence Unit sample sequence The unit sample sequence is defined as
=0 for n The graphical representation of
Figure 35. Unit sample sequence
The unit impulse function has the following properties:
u(n) = =
Exponential sequence The exponential sequence is a sequence of the form x(n) = a n for all n. Figure illustrates different types of discrete time exponential signals. When the value of α > 1 the sequence grows exponentially and when the value is 0<a<1 the sequence decay exponentially. When a<0 the discrete time signal takes alternating signs.
Figure 36. Exponential sequence
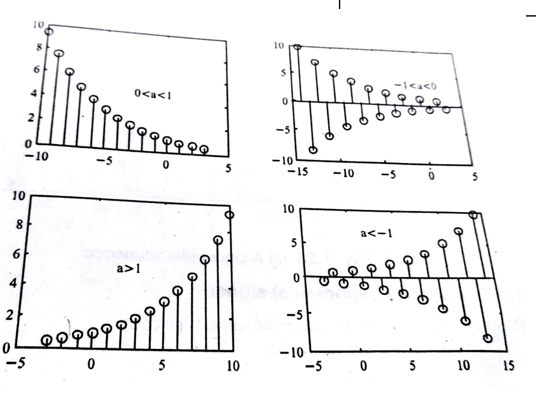
Sinusoidal signal The discrete time sinusoidal signal is given by x(n)= A cos (won + ɸ)---------------------------(1) where wo is the frequency and ɸ is the phase Using Euler’s identity we can write A cos(won + ɸ) = A/2 e jɸ . e j won + A/2 e-jɸ e -jwon ---------------------(2) Since | e jwon | 2 =1 The energy of the signal is infinite and the average power of the signal is 1. An example of discrete time sinusoidal signal is shown in figure.
Figure 37. Sinusoidal sequence
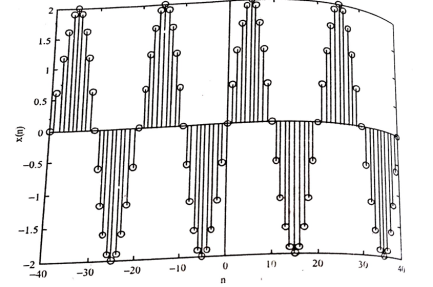
Complex exponential signals. The discrete time complex exponential signal is given by x(n) = a n e j (won + ɸ) ------------------------------------(1) = a n cos (wo + ɸ) + j a n sin (won + ɸ) . For |a| =1 the real and imaginary parts of complex exponential sequence are sinusoidal. For |a| < 1 the amplitude of sinusoidal sequence decays exponentially For |a| > 1 the amplitude of the sinusoidal sequences increases exponentially . Examples of these signals are given in figure.
Figure 38. Complex exponential sequence
Key Takeaways:
|
(i) Parallel Connection of Systems Consider two LTI systems with impulse responses h1(n) and h2(n) connected in parallel as shown in fig(a)
Figure 39. Parallel connection From the figure the output of the system1 is y1(n) = x(n) * h1(n) and the output of system 2 is y2(n) = x(n) * h2(n) = = = = x(n) * h(n) where h(n) = h1(n) + h2(n) Thus, if the two systems are connected in parallel then the overall impulse responses is equal to the sum of the two impulse responses.
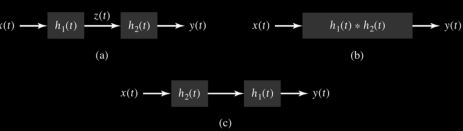
(ii) Cascade connection of two systems Consider the cascade connection of two LTI systems, as illustrated in Fig. (a). Let z(t) be the output of the first system and therefore the input to the second system in the cascade. The output is expressed in terms of z(t) as 𝑦 (𝑡) = 𝑧(𝑡) ∗ ℎ2(𝑡) Substituting for z(t), we get y(t) = Putting for z(t) we get y(t) = = = h(t) * h(t)
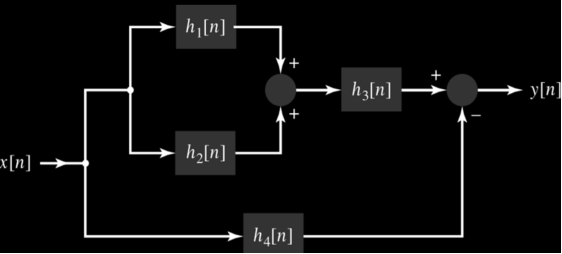
Figure 40. Cascade connection Interconnection of two LTI systems. (a) Cascade connection of two systems. (b) Equivalent system. (c) Equivalent system: Interchange system order. Problem: Consider the interconnection of four LTI systems as shown in figure. The impulse responses of the systems are h1[n] = u[n] h2[n] = u[n+2] – u[n] h3[n] = δ[n-2] and h4[n] = α n u[n] Find the impulse response h[n] of the overall system.
Figure 41. Impulse response h[n] We first derive the expression for the overall impulse response in the terms of impulse response of each system. The parallel com0bination h1[n] and h2[n] . The distributive property implies that the equivalent system h12[n] = h1[n] + h2[n] as shown in figure 1.
Figure 42. Reduction This system is in series with h3[n] so the associative property implies that the equivalent system for the upper branch has the impulse response h123[n] = h12[n] * h3[n] Substituting for h12[n] in this expression we have h123[n] = (h1[n] + h2[n] * h3[n]) as shown in fig(b) . Last the upper branch is in parallel with the lower branch characterized by h4[n] ; hence application of the distributive property gives the overall system impuse response as h[n] = h123[n] – h4[n] Substituing for h123[n] in this expression yields H[n] = ( h1[n] + h2[n] ) * h3[n] – h4[n] As shown in fig ( c) Now substitute the specified forms h1[n] and h2[n] to obtain h12[n] = u[n] + u[n+2] – u[n] =u[n+2] Convolving h12[n] with h3[n] gives h123[n] = u[n+2] * δ[n-2] = u[n] Finally, we sum h123[n] and -h4[n] to obtain the overall impulse response h[n] = { 1- α n } u{n}
Figure43 . Output response
Key Take Aways: Systems can be combined to form more complex systems otherwise known as the interconnection of systems. |
Constitutes two properties: Additivity/ Super position If x1(t) -> y1(t) and x2(t) -> y2(t) then x1(t) + x2(t) -> y1(t) + y2(t) Property of scaling if x1(t) -> y1(t) a * x1(t) -> a * y1(t) If both are satisfied then system is linear y(t) = x2(t) The responses due to inputs x1(t) and x2(t) are given by y1(t) = x1 2(t) y2(t) = x2 2(t) The output due to weighted sum of inputs is y3(t) = T[ax1(t) + bx2(t)] = [ax1(t) + bx2(t)]2 The weighted sum of inputs a y1(t) + by2(t) = ax12(t) + b x2 2(t) y3(t) ≠ ay1(t) + by2(t) System is non-linear.
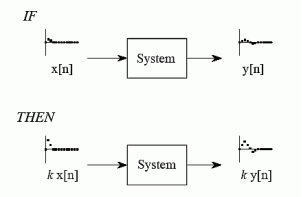
Homogeneity Homogeneity means change in input signals amplitude results in a corresponding change in the output signal’s amplitude. That is a change in x[n] will result in a change in y [n] Also, a change in k x[n] will result in a change in k y[n]
Figure 44. Homogenity
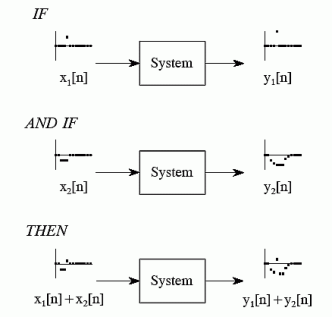
Additivity Consider a system where input x1[n] produces an output y1[n]. Similarly x2[n] produces y2[n]. The system is additive when x1[n] + x2[n] = y1[n] + y2[n] In other words signals added at the input will produce signals added at the output.
Figure45. Additivity
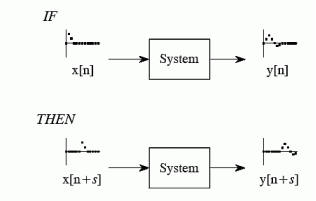
Shift invariance means that a shift in the input signal will result in an identical shift in the output signal If x[n] -> y[n] Then x[n+s] -> y[n +s] for any constant s
Figure.46 Shift Invariance
Examples of casual system: y(t) = x(t) + x(t-1) y(n) = n x(n) + x(n-3)
Examples of non-casual system y(t) = x(t+3) + x 2 (t) y(n) = x(2n)
For example y(t) = 2 x(t) + 3 x(t-3) let t=1 therefore y (1) = 2 x(1) + 3 x(-2) The system output only depends upon present and past inputs. Hence, the system is causal. y(t) = 2 x(t) + 3 x(t – 3) + 6 x( t+3) let t=1 the system output is y(1) = 2x(1) + 3 x(-2) + 6 x( 4) Here the output depends future input. Hence non –casual.
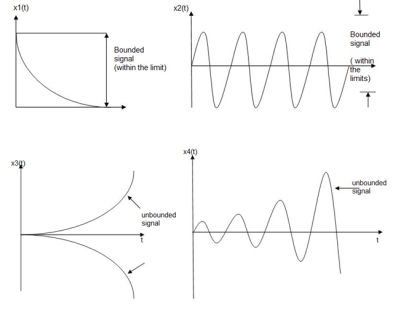
Figure 47. Stability of the system An input signal x(t) is said to be bounded if it satisfies the condition |x(t) |≤Mx < ∞ for all t. Similarly, the output signal is bounded if it satisfies the condition |y(t)| ≤My < ∞ The example for bounded and unbounded signals is as shown in the figure. Note: For a bounded signal, the amplitude is finite. Example 1: y (t) = x2(t) Let the input is u(t) that is unit step then output y(t) = u2(t) = u(t) = bounded output. Hence, the system is stable. Example 2: y (t) = ∫x(t)dt∫x(t)dt Let the input be u (t) then output y(t) = ∫u(t)dt but ∫ u(t)dt = ramp signal It is unbounded because the amplitude of ramp is not finite and tends to become infinite when t →infinite Hence, the system is unstable.
y(t)=x(t−1)y(t)=x(t−1) is a causal system, because its output is a time-delayed version of the original signal. On the other hand, the second system y(t)=x(t+1)y(t)=x(t+1), is non-causal. This system returns a time-advanced version of the input signal. This means, that for example at the output time t=0, the system requires access to the value of the input signal at time t=1. Clearly, this is impossible in a realizable system, as nobody can predict the future.
Key Takeaways:
|
References:
1 Signals and Systems by Simon Haykin
2 Signals and Systems by Ganesh Rao
3 Signals and Systems by P. Ramesh Babu
4 Signals and Systems by Chitode