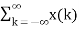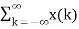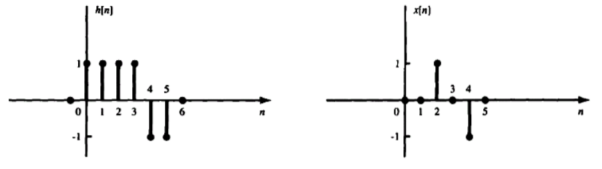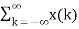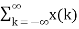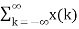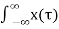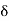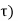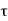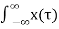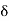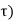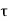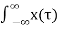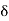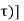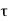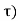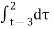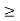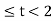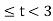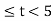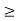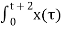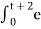Convolution is a formal mathematical operation, just as multiplication, addition, and integration. Addition takes two numbers and produces a third number, while convolution takes two signals and produces a third signal. Convolution is used in the mathematics of many fields, such as probability and statistics.

   y(t) = x(t) *h(t) where

y(t) = output of LTI system

x(t) = input of LTI system

h(t) = impulse response of LTI system.

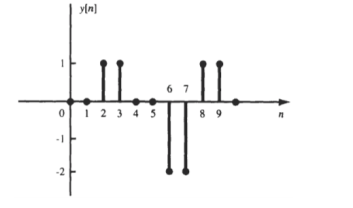
If the input to the system is unit impulse response, then the output of the system is known as impulse response of the system denoted by h(n). That is

h(n) = T [ δ(n)]…………………………………………………………..(1)

The arbitrary sequence x(n) can be represented as weighted sum of discrete impulses given by

x(n) =    δ(n-k) --------------------------------------------(2)

Then the output

y(n) = T [     δ(n-k)] -----------------------------------------------------(3)

The impulse response h[n] of a discrete-time LTI system. Determine and sketch the output y[n] of this system to the input x[n]

h[n] = δ[n] + δ[n-1] + δ[n-2]+ δ[n-3]+ δ[n-4]+ δ[n-5]

x[n] = δ[n-2] - δ[n-4]

x[n] * h[n] = x[n] * { δ[n] + δ[n-1] + δ[n-2]+ δ[n-3]+ δ[n-4]+ δ[n-5]}

= x[n] + x[n-1] + x[n-2]+ x[n-3]+ x[n-4]+ x[n-5]

y[n] =  δ[n-2]- δ[n-4]+ δ[n-3]- δ[n-5] + δ[n-4]- δ[n-6]+ δ[n-5]- δ[n-7] - δ[n-6]+ δ[n-8]- δ[n-7]+ δ[n-9]}

= δ[n-2]+ δ[n-3]-2 δ[n-6]-2 δ[n-7] + δ[n-8]+ δ[n-9]

y[n] = {0,0,1,1,0,0,-2,-2,1,1}

Key Takeaways:

1. The impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse.

Using linear property of the system the interchange operator T with the summation k to obtain

y(n) =  [    T δ(n-k)] ----------------------------------------------(4)

The response to the shifted impulses is represented as h(n,k)

h(n,k) = T[ δ(n-k)]

Now

y(n) =    h(n,k)   -----------------------------------------------------------(5)

For time-invariant system

h(n,k) =h(n-k) ----------------------------------------------------------------------(6)

Substituting (6) in (5) we get

y(n) =    h(n-k)   ------------------------------------------------------------------(7)

Thus, the output of the LTI system is given by the weighted sum of time-shifted responses.

The sum in eq(7) is termed as convolution sum which is given by

y(n) = x(n) * h(n)   -----------------------------------------------------------------------------(8)

* denotes convolution operation.

Key Take Aways:

1. CONVOLUTION SUM or superposition sum of the sequences x[n] and h[n].

Consider an LTI system which is initially related at t=0. If the input of the system is an impulse, then the output of the system is denoted by h(t) is called the impulse response of the system.

 We can denote

h(t) = T [ δ(t)]

 We know that any arbitrary signal x(t) can be represented as

x(t) = ( t-d           ------------------------------------------------------(1)

 The system output is given by

y(t) = T[x(t)]   --------------------------------------------------------------------------------(2)

Substituting (1) in (2)

y(t) = T [   ( t-d      --------------------------------------------------------(3)

For linear system

  y(t) =  [ T[ ( t-d  --------------------------------------------(4)

If the response of the system due to impulse δ(t) is h(t) then the response of the system due to delayed impulse is

h(t,  = T [ δ(t-T)] --------------------------------------------------------------(5)

Substituting (5) in (4) we get

 y(t) =  [ h(t,τ) dτ  -------------------------------------------------------(6)

For a time invariant system the output due to the delayed input by T is equal to delayed output by T, That is

 h(t,τ) = h(t-τ) ---------------------------------------------------------------(7)

Substituting (7) in (6) we get

y(t) =   h(t-τ) dτ   -----------------------------------------------------------(8)

This is called convolution Integral. The convolution of two signal x(t) and h(t) can be represented as

y(t) = x(t) * h(t)

Computation of convolution integral using graphical method

The procedure is as follows:

1. For the given signals x(t) and h(t) graph the signals x(τ) and h(τ) as a function of independent variable τ.
2. Obtain the signal h(t-τ) by folding h(τ) about τ=0 and then time shifting by time t.
3. Graph both signals x(τ) and h(t-τ) on the same τ-axis beginning with very large negative time shift t.
4. Multiply the two signals x(τ) h(t-τ) and integrate over the overlapping interval of  two signals to obtain y(t)
5. Increase the time shift and take the new interval whenever the function of either x(τ) and h(t-τ) changes. The value of t at which the change occurs defines the end of the current interval and beginning of a new interval. Calculate y(t) using step 4.
6. Repeat steps 5 and 4 for all intervals.

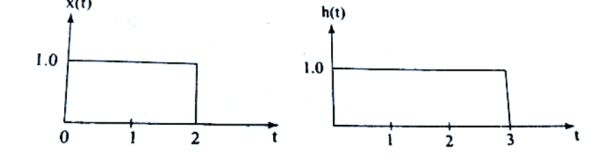
unit step to rectangular:

Find the convolution of x(t) and h(t)

x(t) =1                                    0

       = 0                                   otherwise

Fig 2. x(t) and h(t)

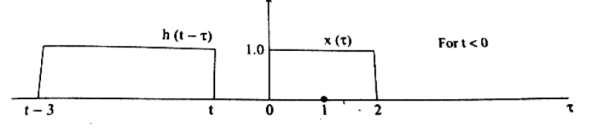
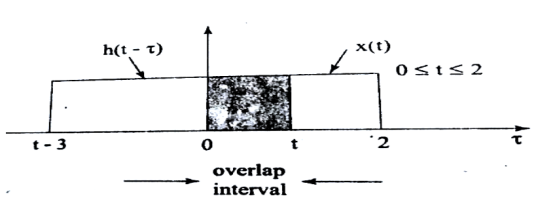
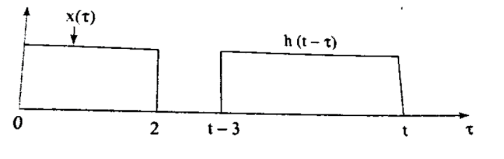
Figure 3: x(τ) and h(t-τ)

As shown in Figure the signals x(τ) and h(t-τ) does not overlap for t<0. Therefore the product x(τ) h(t-τ) is zero.

That is,

y(t) = h(t-τ) =0            for t<0

Now the shift the signal h(t-τ) right until the right edge of the signal h(t-τ) intersects left edge of x(τ).

In the interval 0

y(t) = = t

Figure 4. Product of x(t) and h(t-τ)

In the interval 2 

y(t) = = 2

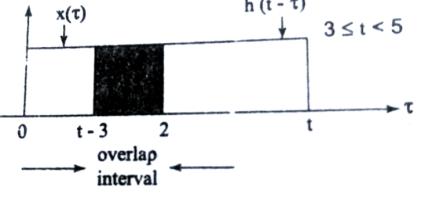
In the interval 3

Figure 5. Product of h(t-τ) x(τ)

y(t) =  = 2 – (t-3)

= 5-t.

For t

Figure6. Product of x(τ) h(t-τ) for t 5

The signals x(τ) and h(t-τ) do not overlap. Therefore y(t)=0.

y(t) = 0   for t<0

       =  t     for 1

       = 2     for  2

       = 5-t   for 3

       =0       for t 5.

The sketch y(t) is as shown in figure

Figure 7. The output waveform

Unit Step to Exponential

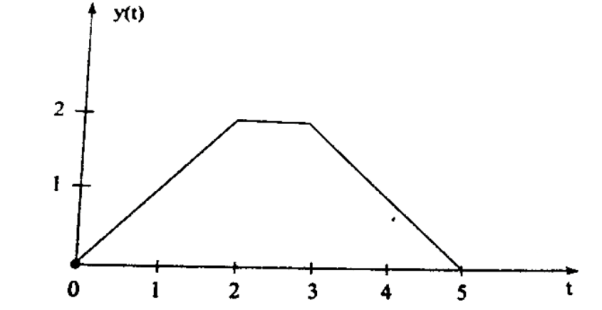
Given:

x(t) = e -2 u(t)                                            h(t) = u(t+2)

Figure 8. x(t) and h(t)

Figure 9. Product exponential signal and unit step signal

Figure10. Product of exponential signal and delayed unit step signal

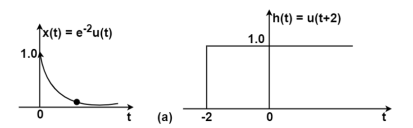
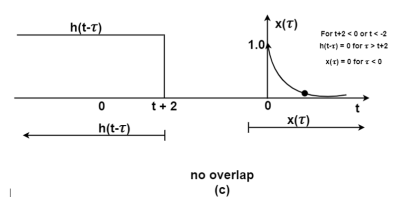
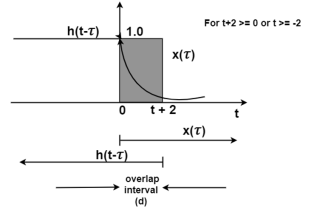
Figure 11. The output waveform

Figure (a) shows x(t) and h(t) . Fig (b) shows x(τ) and h(-τ) as functions of τ. The function h(-τ) can be obtained by folding the signal h(τ) about τ=0.

Figure (c ) shows that signal h(t-τ) is sketched for t<-2 by shifting h(τ) to left. For t<-2 x(τ) and h(t-τ) does not overlap and the product x(τ) h(t-τ) =0 that is

y(t) =0 for t<-2

Now increase the time shift until the signal h(t-τ) intersects x(τ). Figure (d) shows the situation for t>-2.

Here x(τ) =0   for τ <0  and h(t-τ) does not overlap and the product x(τ) h(t-τ) =0 that is

y(t)=0      for t<-2

Now increase the time shift t until the signal h(t-τ) intersects x(τ).

Figure (d) shows the situation for t>-2. Here x(τ) and h(t-τ) overlapped. But x(τ) =0 for τ<0 and h(t-τ) = 0 for τ > t+2. Therefore, the integration interval is from τ=0 to τ=t+2

y(t) =   h(t-τ) dτ

= =   -2τ  dτ

= -1/2  e -2 τ    | 0 t+2

= -1/2 [ e -2 (t+2) -1]

= 1 – e -2(t+2)   /2

y(t) = 0         for t<-2 

= 1 – e-2(t+2)/2                                 for t -2

Key Takeaways:

1. The convolution operation is given by the integral over the product of two functions, where one function is flipped and shifted in time.