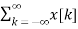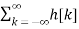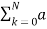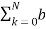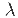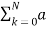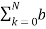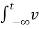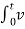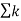A system is memoryless if its output depends on the current input only. From the expression

y[n] = x[n] *h[n]

=   h[n-k]

It is easily seen that y[n] depends only on x[n] only if h[n] =0 for n0

h[n] = k δ[n]

Hence

y[n] =   x[n] *h[n]

       = x[n] * k δ[n]

 = (k* δ) [n]

= k x[n]

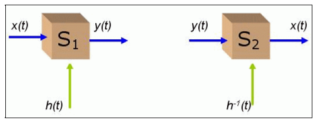
Invertibility :

A system is said to be invertible if there exists an inverse system which when connected in series with the original system produces an output identical to input.

(x *δ) [n] = x[n]

(x*h*h-1 ) [n] = x[n]

(h*h-1) [n] = δ[n]

Figure 1. Invertibilty

Casuality :

y[n]  = h[n-k] = x[n-k]

In order for discrete LTI system be casual y[n] must not depend on x[k] for k>n. For this to be true h[n-k] corresponding to the x[k]’s for k>n must be zero. This then requires the impulse response of casual discrete time LTI system satisfy the following conditions

h[n] =0   .

Essentially the system output depends on the past and present values of the input

Key Takeaways:

1. Any LTI filter may be represented in the time domain by its response to a specific signal called the impulse. 

The general form of differential equation is

  kd k / d t k y(t) =   k d k / d t k x(t)

Where ak and bk are coeffecients

An LTI system is specified by equation

 d 2 y(t)/ dt 2 + 5 d y(t) /dt + 6 y(t) = dx(t) / dt + 4 x(t)

The input is x(t) = e -t u(t)

Find the natural response for initial conditions:

y (0+) = 3       d y(0+)/dt =0

Forced response

Total response.

Given d 2 y(t) / dt 2 + 5 d y(t)/dt + 6 y(t) = d x(t)/dt + 4 x(t)

The natural response can be obtained by equating input terms in differential equation to zero.

d 2 y(t) / dt 2 + 5 d y(t)/dt + 6 y(t)=0

The characteristic equation is

• 2 + 5 + 6=0

• 1=-2 and 2 = -3

The homogenous solution is

yh(t) = c1 e -2t + c2 e -3t

y (0+) = c1 + c2

d y (0+)/dt = 2 c1 e -2t + (-3) c2 e -3t |t=0

= 2c1 – 3c2

From initial conditions

y (0+) = 3

dy (0+)/dt =0

Comparing we get c1 + c2 =3

                                     2c1 + 3c2 =0.

c2 =-6 and c1=9

yn(t) = 9 e -2t – 6 e -3t

Forced response:

The homogeneous solution is given by

yn(t) = c1 e -2t + c2 e -3t

for input x(t) = e -t  

The particular solution is of the form

yp(t) = k e -t

from which

dyp(t)/dt = -k e-t

d2 yp(t)/dt2 = k e-t

Therefore,

 d 2 yp(t)/dt2 + 5 d yp(t)/dt + 6 yp(t) = dx(t)/dt + 4 x(t)

k e -t – 5 k e-t + 6 k e-t = - e-t + 4 e-t

2k = 3

K=1.5

yp(t) = 1.5 e -t.

The forced response is the sum of homogeneous solution for particular solution.

yf(t) = c1 e -2t + c2 e -3t + 1.5 e -t

y(0+) = c1 + c2 +1.5

dy(0+)/dt = -2c1 e -2t -3 c2 e -3t – 1.5 e -t |t=0

To obtain forced response equate initial conditions to zero

C1 + C2 = -1.5

2C1 + 3C2 = -1.5

Solving for c1 and c2 we get

C2 = 1.5

C1 =-3

 y(t) = yn(t) + yf(t)

Substituting yn(t) and yf(t) we get

  y(t) = 6 e -2t – 4.5 e -3t + 1.5 e -t

 y(0) = c1 + c2 + 1.5 =3

dy(0+)/dt = -2c1 -3c2 -1.5 =0

c1 =6 and c2 =-4.5

y(t) = 6 e -2t -4.5 e -3t + 1.5 e -t

Problem:

Consider the difference equation given by

y[n] + 0.5 y[n-1] = (-0.8) n u[n]

The solution is composed of natural response and forced response of the system.

y[n] = yh[n]+yp[n]

Where the particular solution satisfies for n≥0 and the homogeneous solution satisfies

yh[n] + 0.5 yh[n-1] = 0

for n ≥0 yp(n) = y (-0.8) n

Then we get

Y (-0.8) n + 0.5Y(-0.8) n-1 = (-0.8) n

Y [ 1+0.5(-0.8) -1] = 1

Y=8/3

which yields yp(n) = 8/3 (-0.8) n

To determine yh(n)

Yh[n] = A z n

1+ 0.5 z -1 =0

z=-0.5

y[n] = yh[n]+yp[n] = A(-0.5) n + 8/3 (-0.8) n

y[n] = -0.5 y[n-1] + (-0.8) n u[n] -- n=0

y[0] = -0.5y[-1] + (-0.8) n =0+1=1

y[0] = 1=A(-0.5) 0 + 8/3 (-0.8) 0 = A+8/3 = 1

A=-5/3

y[n] = 5/3 (-0.5) n + 8/3 (-0.8) n

Key Takeaways:

1. They are used in circuit analysis, filter design, controller design, process modeling, and in many other applications.

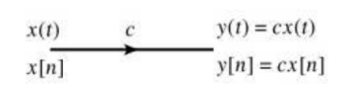
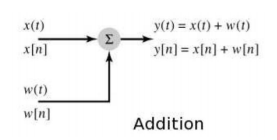
A block diagram is an interconnection of elementary operations that act on the input signal.

The impulse response and differential /difference equation descriptions represent only the input -output behaviour of the system, block diagram representation describes how the operations are ordered.

Each block diagram representation describes a different set of internal computations used to determine the system output.

Scalar Multiplication:

y(t) = cx(t) or

y[n] = x[n] where c is scalar

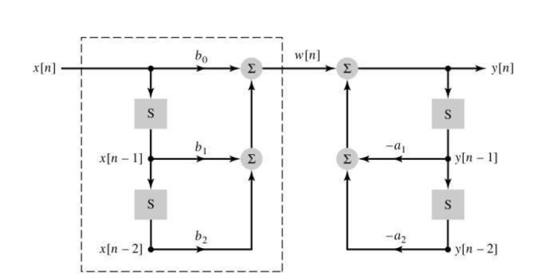
Figure 2. Parameters for block diagram

Direct Form-1

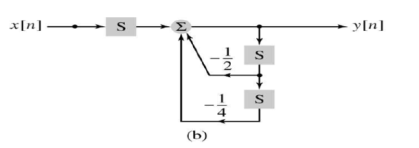
Figure3 . Direct Form -I

Consider the system described by the block diagram as shown in figure.

The part within the dashed box is the input x[n] which is time shifted by 1 to get x[n-1] and again time shifted by 1 to get x[n-1] and again time shifted to get x[n-2]. These scalar multiplications are carried out and added to get

w[n] = bo x[n] + b1 x[n-1] + b2 x[n-2] 

Put the value of w[n] and we get

y[n] = -a1y[n-1] – a2y[n-2] + bo x[n] + b1 x[n-1] + b2 x[n-2] 

Consider the system described by the block diagram and its difference equation by

y[n] + ½ y[n-1] + ¼ y[n-2] = x[n-1]  . Obtain direct form1

Rewrite the differential equation we get

  kd k / d t k y(t) =   k d k / d t k x(t)

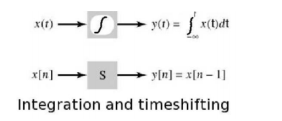
As an integral equation . Let v(o) (t) = v(t) be an arbitrary signal and set

v (n) (t) = (n-1) (τ) dτ                               n = 1,2,3

where v (n) (t) is the n-fold integral of v(t) with respect to time

Rewrite in terms of initial condition on the integrator as

v (n) (t) = (n-1) (τ) dτ  + v (n) (0)              n=1,2,3               

If we assume zero ICs then differentiation and integration are inverse operations

d/dt v(n) (t) = v (n-1) (t)           t> 0  and n=1,2,3…………………..

Thus, if N M and integrate N times we get the integral description of the system

= 0 N a ky (N-k) (t) = = 0 M a ky (N-k) (t) 

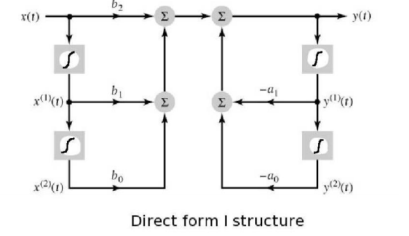
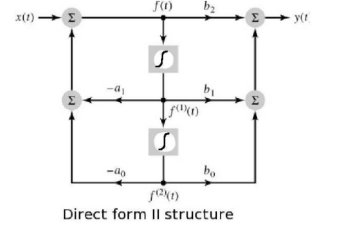
For the second order system with ao=1 the differential equation can be

Written as

y (t) = -a1 y(1) (t) – ao y(2) (t) + b2 x(t) + a1 x(1) (t) + bo x(2) (t)

   Figure 4. Direct form

Figure 5. Direct form-II