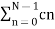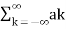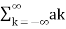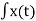The Fourier series represents periodic, continuous-time signals as a weighted sum of continuous-time sinusoids. It is widely used to analyze and synthesize periodic signals.

Key Takeaways

1. A Fourier series is a way of representing a periodic function as a (possibly infinite) sum of sine and cosine functions.

Given a periodic sequence x[k]  with period N the Fourier series representation for x[k] uses N harmonically related exponential functions

 e j2πkn/N                    k=0,1,………….. N-1

The Fourier series is expressed as

x[k] =    e j2πnk/N

The Fourier co-effecients cn are given gy

cn = 1/N   e- j2πnk/N

Key Takeaways:

1. The discrete-time Fourier series representation provides notions of frequency content of discrete-time signals

A signal is said to be periodic if it satisfies the condition x (t) = x (t + T) or x (n) = x (n + N).

Where T = fundamental time period,

ω0= fundamental frequency = 2π/T

There are two basic periodic signals:

x(t)=cosω0t

x(t)=cos foωot (sinusoidal) &

x(t)=ejω0t

These two signals are periodic with period T=2π/ω0T=2π/ω0.

A set of harmonically related complex exponentials can be represented as {ϕk(t)}

ϕk(t)={ejkω0t}={ejk(2πT)t} where k=0±1,±2..n.....(1)

All these signals are periodic with period T

According to orthogonal signal space approximation of a function x (t) with n, mutually orthogonal functions is given by

x(t) = e jkwot  -----------------------------------------------(2)

= k e jkwot

Where ak= Fourier coefficient = coefficient of approximation.

This signal x(t) is also periodic with period T.

Equation 2 represents Fourier series representation of periodic signal x(t).

The term k = 0 is constant.

The term k=±1 having fundamental frequency ω0, is called as 1st harmonics.

The term k=±2 having fundamental frequency 2ω0, is called as 2nd harmonics, and so on...

The term k=±n having fundamental frequency nω0, is called as nth harmonics.

Key Takeaways

1. The continuous-time Fourier series expresses a periodic signal as a lin- ear combination of harmonically related complex exponentials. 

Linearity Property

If x(t) -- fxn

y(t) - fyn

then linearity property states that

a x(t) + by(t) - a fxn + b fyn

Time Shifting Property

If x(t) ------------ fxn

Then time shifting property states that

x(t-to)  -------- e -jnwot fxn

Frequency Shifting Property

If x(t) -- fxn

Then frequency shifting property states that

e jnwoto . x(t) ----- fx(n-no)

Time Reversal Property

If x(t) -- fxn

Then time reversal property states that

If x(-t) --- f-xn

Time Scaling Property

If x(t) -- fxn

Then time scaling property states that

If x(at) -- fxn

Time scaling properties changes frequency components from wo to awo

Differentiation and Integration Properties

If x(t) -- fxn

Then differentiation property states that

If dx(t)/dt -- jnwo.fxn

And integration property states that

If dt --- fxn/jnwo

Multiplication and Convolution Properties

If x(t) -- fxn

Then multiplication  property states that

x(t) y(t) -- T fxn * fyn

and the convolution property states that

x(t) * y(t) -- T fxn.fyn

Conjugate and Conjugate Symmetry Properties

If x(t)  fxn

Then the conjugate property states that

x*(t)  f*xn x*(t)

Conjugate symmetry property for real valued time signal states that f*xn = f-xn

Key Takeaways:

1. The Fourier series representation possesses a number of important properties that are useful for various purposes during the transformation of signals from one form to other .