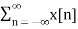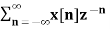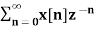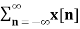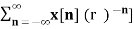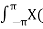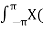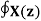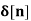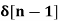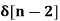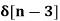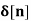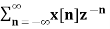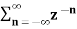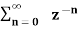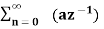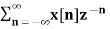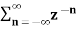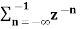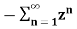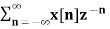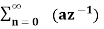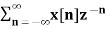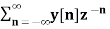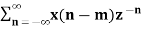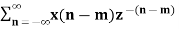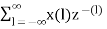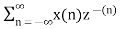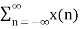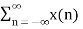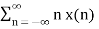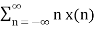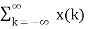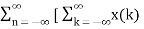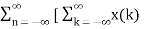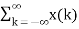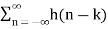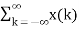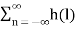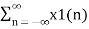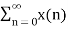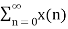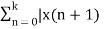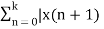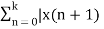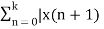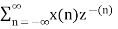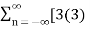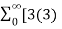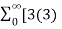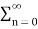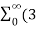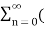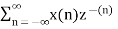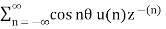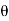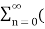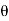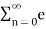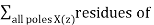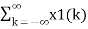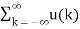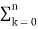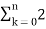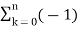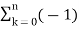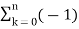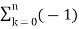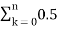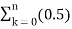The z-transform is a mathematical process from the discrete time domain to the z domain known as the complex frequency domain.

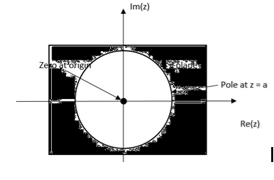
In the discrete time- domain the signal is defined as a sequence of real or complex numbers which is then converted to the z-domain by the process of z-transform.

The z-transform is important technique, used in areas of signal processing, system design and analysis and control theory.

The formula used to convert a discrete time signal x[n] to X[z] is as follows:

X(z) =   z-n

where x[n] is the discrete time signal and X[z] is the z-transform of the discrete time signal.

Z-transform comes in two parts.

The first part is the formula as shown above

The second part is to define a region of convergence for the z-transform.

Both parts are needed for a complete z-transform as a z-transform without a ROC would not be of much help in signal processing.

Key Takeaways:

1. Analysis of continuous time LTI systems can be done using z-transforms.

The Z transform for discrete time system x(n ) is defined as

X(z) =    ------- (1) where z is a complex variable.

In polar form z can be expressed as

z  = r e jw  ---------------(2) where r is the radius of a circle.

 For n≥ 0

X(z ) =        --------- (3)which is called one-sided z-transform.

By substituting z = r e jw

X(r e jw)  =    (r e jw) –n     ------- (4)

     e- jwn       ----- (5)

Equation(5) represents the Fourier transform of the signal x(n) r-n

Hence the inverse DTFT  X(r ejw) must be x(n) r-n.

x(n) r-n = 1/2π r e jw )  e jwn dw

On multiplying both sides by rn  we get

x(n) = 1/ 2 π   r ejw) (r ejw ) n dw                  [ z = r ejw

Let z= r e jw  and dw= dz/jz 

dz = r ejw dw

dw = dz/jre jw

x[n] = 1/ 2πj   z n-1 dz

Example

Find the z-transform for the sequence

x[n] = 2 + 3 + 5 + 2

Solution:

          X(z) = 2 + 3 z-1 + 5 z -2 + 2 z -3   

 Example

 If X(z)= 4 – 5 z-2 + z-3 – 2z -4    then find x[n]

 Solution:

 x[n] = 4 - 5 + - 2

Key Takeaways:

1. The Z transform is the discrete time analog of the Laplace transform

1. The ROC is a ring or disk in z-plane centered at the origin.
2. The ROC cannot contain any poles.
3. If x(n) is finite duration casual sequence then the ROC is the entire z-plane except at z=0.
4. If x(n) is a finite duration anti-casual sequence then the ROC is the entire z-plane except at z=∞.
5. If x(n) is a finite duration two- sided sequence the ROC is entire z-plane except at z=0 and z=∞.
6. If x(n) is infinite duration two- sided sequence ROC will consist of a ring in z-plane bounded on the interior and exterior by a pole not containing any poles.
7. The ROC of an LTI stable system contains the unit circle
8. ROC must be connected region.

Find the z-transform and ROC of the signal

 x(n) = an u(n)

 Solution: 

  X(z) = 

         = an u(n) -----(1)    u(n) = 0 for n<0

          1 for n≥0

  = an ------- (2)

 = n   ------- (3)

 This is a geometric series of infinite length that is

 a + ar + ar2 + ………….. ∞ = a /1-r if |r| <1

          Then from equation (3) it converges when |az-1| < 1 or |z| >|a|

 Therefore

 X(z) = 1/ 1-az-1:  ROC    |z| > |a|

   Figure 1. ROC |z| > |a|

Find the z-transform of the signal x(n) =-b n u(-n-1). Find ROC

X(z) = 

X(z) =  bn u(-n-1)                                                                u(-n-1) =0 for n ≥0

            = 1 for n                

                                                                                                                                     ≤ -1

= bn   = b-1  =

= b-1z/1- b-1z = z/ z-b = 1/ 1-bz-1                                                               |z| < |b|

Figure 2

. ROC |z| < |b|

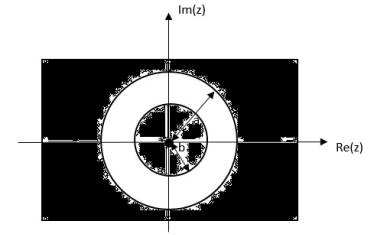
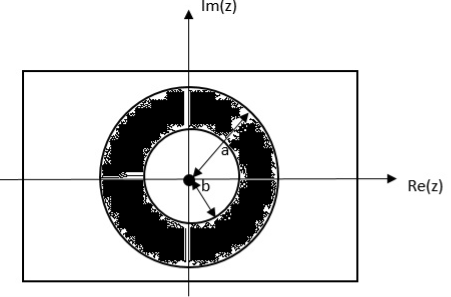
Find the z-transform of x(n) = an u(n) – bn u(-n-1)

 X(z) = 

=  n  + b-1

= z/z-a + z/z-b       ROC |a| < |z| < |b|

   Figure 3. |a|<|z|<|b|

|b|< |a|

                                      Figure 4. |b| >|a|

Key Takeaways:

1. Region of convergence (ROC) is the region (regions) where the z-transform X(z)or H(z) converges . 

• Linearity

If x(n)       Z.T        X(Z)

    y(n)         Z.T      Y(Z) then

It states that

a x(n) + b y(n)        Z.T      a X(Z) + b Y(Z)

Proof:

Z{ a a x(n) + b y(n)} = a x(n) + b y(n)] z -1

= a   + b

= a X(z) + b Y(z)

• Time Shifting Property

If X(z) = Z{x(n)} and the initial conditions for x(n) are zeros then

Z{ x(n-m)} = z -m X(z)

Where m is positive or negative integer

Proof:

Z{x(n-m)} =

= z -m

Let (n-m) =l then we have

Z{x(n-m) = z -m

= z -m X(z)

Multiplication by an exponential sequence

If X(z) = Z{x(n)} then

Z{ a n x(n) } = X ( a-1 z)

Proof :

Z{ a n x(n) } =     a n  

( a -1 z) -n = X(a -1 z)
 

Differentiation in Z-Domain OR Multiplication by n Property

If X(z) = Z{x(n)} then

Z{ n x(n)} = -z d/dz X(z)

Proof:

X(z) =

Differentiating the z-transform we get

X(z) = d/dz  z -n

  (-n) z -n-1

= -1/z z -n

Multiplying both sides we get

-z dX(z) /dz =  z -n    = Z{nx(n)}

Convolution Theorem:

If X(z) = Z{x(n)}

H(z) = Z{h(n)} then

Z{x(n) * h(n) } = X(z) H(z)

Where x(n) * h(n) = convolution

Proof:

We have y(n) = x(n) * h(n)

= h(n-k)

And

Y(z) = Z{y(n)} = h(n-k)] z -n

=    z-k h(n-k)] z –(n-k)

Interchange the order of summation

Y(z)  = z -k    z –(n-k)

Replace (n-k) by l in summation we get

Y(z) = z -k    z –(l)

= X(z) H(z)

    Correlation Property

If X1(z) = Z{x1(n)} and X2(z) = Z{x2(n)} then

Z{ x1 x2(l)} = Z{ x2(n-l)}

= x1x2(z) = X1(z) X2(z -1 )

Initial Value Theorem

If  X+(z) = Z{x(n)} then x(0) = lim z->∞ X+(z)

Proof:

X+(z) = z-n

As z-> ∞ all the terms vanish except x(0) which proves the theorem

Ie

Lim z-> ∞ X+(z) = lim z-> ∞ z-n = x(0)

Final Value Theorem

If X+(z) = Z{x(n)} where ROC for X+(z) includes but is not necessarily confined to |z| >1 and (z-1) X+(z) has no poles on or outside the unit circle then

x(∞) = Lim z->1 (z-1) X+(z)

Z{ x(n+1) – Z{x(n)} = Lim k-> ∞   - x(n)]z-n

Z X+(z) – z x(0) – X+(z) = Lim k-> ∞   - x(n)]z-n

(z-1) X+(z) – zx(0) =  Lim k-> ∞   - x(n)]z-n

Let z-> 1 we get

Lim z->1 (z-1) X+(z) – zx(0) = Lim k-> ∞   - x(n)]

Lim z->1 (z-1) X+(z) – x(0) = Lim n-> ∞ { [x(1) -x(0)] + [x(2) -x(1)] +……+[x(n+1)-x(n)]}

= x(∞) – x(0)

Therefore,

x(∞) = limz->1 (z-1) X+(z)

this can be written as

x(∞) = lim z->1 (1-z-1) X(z)

This theorem enables us to find the steady state of x(n) without solving the entire sequence.

Find the z-transform of x(n) = [3(3) n – 4(2) n ] u(n)

X(z) =

= n – 4(2) n ] u(n) z -n

= n – 4(2) n ] u(n) z -n

= n z -n   - 4(2) n ]  z -n

= 3  z -1 ) n – 4    2 z -1 ) n

The first power series converges when |3z -1| <1 that is |z| > 3 . The second power series converges when |2z-1| <1 or |z| >2. Hence X(z) converges for |z|>3 .

Now X(z) = 3/1-3z-1 -4/1-2z-1

= 3z/z-3 – 4z/z-2 .

Find the z transform of x(n) = cos n u(n)

X(z) =

=

= ejn + e-jn/2] z -n 

= ½ [    e j z -1 ) n += -j   z -1 ) n ]

Both the series converges if [ e j  z-1| <1  and | e j z -1 | <1 which implies |z|>1 

Now X(z) = ½ [ 1/1 – e j  z -1   + 1/ 1 – e -j z -1 ]

= ½ [ 1 – e -j z -1 + 1 – e j  z -1   / 1 – e j  z -1    – e -j z -1 + z -2  

e j  + e -j  = 2 cos

= ½ [ 2 – 2 z -1 cos / 1 – 2 z-1 cos + z -2 ]

= 1-z-1 cos / 1 – 2 z-1 cos   + z -2

• Find the z transform of the sequence x(n) = n u(n)

The z-transform of unit step sequence is given by

Z{u(n)} = z/z-1

Z{ n u(n)} = -z d/dz (z/z-1)

= z/(z-1)2    

• Determine the z-transform of the signal

 x(n ) = rn (sin w0n ) u(n)

Z{(sin w0n ) u(n)}  = sin w0 z-1/ 1 -2 (cos w0) z-1 + z-2

Z{ an x(n)} = X(a-1 z)

Therefore

Z{ rn sin(w0n) u(n) } = (sin w0) (r-1 z)-1/ 1- 2 (cos w0)(r-1z)-1 + (r-1z)-2  

= r(sinw0) z-1/ 1-2r(cos w0) z-1 + r2 z-2

• Determine the signal x(n) whose z-transform is given by

X(z) = log(1- az-1)

X(z)= log(1-az-1)

Differentiating both sides we get

d/dz X(z) = 1/1-az-1 (a z-2) = az-2/1- az-1

-z d/dz { X(z)} = -az-1/1-az-1

= -az-1[ 1/1-az-1]

= -a Z[ a n-1 u(n-1)]                           -------- (1)

From differentiation property

Z{ n x(n)} = -z d/dz [ X(z)]            ------- (2)

Comparing (1) and (2) we get

n  x(n) = -a [ a n-1 u(n-1)]

or x(n) = -a [a n-1 u(n-1)]/n

• Determine the z-transform of the signal

x(n) =1/2 (n2 + n) (1/3) n-1 u(n-1)

=½ n2 (1/3) n-1 u(n-1) +1/2 n (1/3) n-1 u(n-1)

We know that

Z[(1/3) n u(n)] = z/ z-1/3

Using time-shifting property

Z{(1/3) n-1 u(n-1)] = 1/ z- 1/3

Z [ n (1/3) n-1 u(n-1)] = -z d/dz [1/z-(1/3)]

=-z d/dz( 1/z-1/3)= -z [-1/(z-1/3) 2]= z/ (z-1/3)2

Z [ n2 (1/3) u(n-1)] = -z d/dz [ z/(z-1/3)2]

= z(z+1/3)/(z-1/3)2 

= -z [ (z-1/3)2 -2z(z-1/3)/(z-1/3)4

= z(z+1/3)/(z-1/3)3 

X(z) = ½[z(z+1/3)/(z-1/3)3 + z/ (z-1/3)2]

= z2/(z-1/3)3

Key Takaways:

1. The z-transform has a set of properties in parallel with that of the Fourier transform

When analysis is required in discrete format, we convert   frequency domain signal back into discrete format through inverse Z-transformation. There are four ways to determine the inverse Z-transformation.

• Long Division Method
• Partial Fraction expansion method
• Residue or Contour integral method

Long Division Method

In this method, the Z-transform of the signal x (z) can be represented as the ratio of polynomial as shown below;

x(z)=N(Z)/D(Z)

Now, if we go on dividing the numerator by denominator, then we will get a series as shown below

X(z)=x(0)+x(1)z−1+x(2) z−2+.........

The above sequence represents the series of inverse Z-transform of the given signal for n≥ and the above system is causal.

However, for n<0 the series can be written as;

x(z)=x(−1)z1+x(−2)z2+x(−3)z3+.........

Partial Fraction Expansion Method

Here also the signal is expressed first in N (z)/D (z) form.

If it is a rational fraction it will be represented as follows;

x(z)=(b0+b1z−1+b2 z-2 + …… + bm z -m ) / ( a0 + a1 z-1 + a2 z-2 + ……….an z-n )

The above one is improper when m<n and an≠0

If the ratio is not proper i.e. Improper then we have to convert it to the proper form to solve it.

Residue or Contour Integral Method

In this method, we obtain inverse z-transform x(n) by summing residues of [x(z)Zn−1] at all poles.

Mathematically, this may be expressed as

x(n)=[x(z) Z n-1}

Here, the residue for any pole of order m at z=β is

Residues = 1/ (m-1) ! lim { d m-1 / dZ m-1 { (z-β) m X(z) Z n-1 }

Convolution Method

In this method given X(z) is divided into X1(z) and X2(z) such that X(z) = X1(z) X2(z). Next we find x1(n) and x2(n) by taking inverse z transform of X1(z) and X2(z) . From convolution property we know that

Z[ x1(n) *x2(n)] = X1(z) X2(z) = X(z)

Problems :

Find the inverse z transform of X(z) = z+0.2/ (z+0.5) (z-1)   |z|>1

X(z) = z+0.2 / z2 -0.5z -0.5

Divide the numerator by denominator

                                            z-1 + 0.7 z-2 + 0.85 z-3 + 0.775 z-4

     x2 -0.5z -0.5     

                                  z+0.2

                                 z -0.5 -0.5 z -1

                                0.7 + 0.5 z-1

                                0.7 -0.35 z-1 -0.35 z-2

                                        0.85 z -1 + 0.35 z-2

                                        0.85 z-1 -0.42 z-2 -0.425 z-3

                                                                      0.775 z -2 + 0.425 z-3

                                                                     0.775 z-2  -0.387 z-3 – 0.3875 z-4

X(z) = z-1 + 0.7 z-2 + 0.85 z-3 + 0.775 z -4 + …………………………….   

Using long division method Find the inverse z-transform of the sequence of

X(z) = z+1

 z2 +3z + 2

    z-1 + 4z-2 + 10 z-3 +22 z-4

z2 -3z +2                                z+1

 z- 3 + 2z-1

   4 – 2z-1

   4 – 12 z-1 + 8 z-2

          10z-1 – 8z-2

           10 z-1 – 30z-2 +20 z-3

               22 z-2 – 20 z-3

     22 z-2 -66 z-3 +44 z-4

      46 z-3 – 44 z-4

X(z) = z-1 + 4 z-2 + 10 z-3 + 22z-4

x(n) = { 0,1,4,10,22………}

Find the inverse z transform of

X(z) = 1+3 z-1 / 1 + 3 z-1 + 2 z-2  by partial fraction method.

X(z) = z(z+3)/ z2 + 3z+2 = z(z+3)/ (z+1)(z+2)

X(z)/z = z+3/ (z+1)(z+2)

X(z)/z = C1/z+1 + C2/ z+2

By solving we get C1 =2 and C2 =-1

X(z)/z = 2/ z+1 -1/z+2

X(z) = 2 . z/z+1 – z/z+2

x(n) = 2(-1) n u(n) – (-2) n u(n)

Find the partial fraction method of

X(z) = ¼ z-1

  (1 – ½ z-1)(1-1/4 z-1)

X(z) =         A                +          B

      Z (1-1/2z-1)      (1 – ¼ z-1)

By solving A= 1 and B=-1

Therefore,

X(z) =   z     -       z 

 z-1/2 z-1/4

x(n) = (1/2) n u(n) – (1/4) n u(n)

Find the partial fraction of

X(z) =           1

  1+ z-1 + z-2

X(z) =   z

  z2 + z + 1

=  z

(z + 0.5 +j 0.866)(z+0.5 – j0.866)

X(z)    =      c                      +                      c* 

  z    z-(-0.5 +j0.866) z – (- 0. 5 – j 0.866)

X(z)    =      0.5+j0.288                      +          0.5 – j 0.288 

  z    z-(-0.5 +j0.866)  z – (- 0. 5 – j 0.866)

X(z)  =       0.5+j0.288  z                    +          0.5 – j 0.288  z

     z-(-0.5 +j0.866)  z – (- 0. 5 – j 0.866)

By taking inverse z-transform both sides we get

= (0.5+j0.288)( (-0.5 +j0.866) n u(n) +(0.5+j0.288)( (-0.5 -j0.866) n u(n

Find the inverse z transform of

X(z) = 1/ 1-3z-1 + 2z-2 using convolution method.

X(z) = 1/ 1-3z-1 + 2z-2

X1(z) = 1/ 1-z-1 X2(z) = 1/ 1-2z-1

We know that u(n) = 1/ 1-z-1

x2(n) = 2 n u(n) we know that

x(n) = x1(n) * x2(n)

= x2(n-k)

= 2 n-k u(n-k)

 = 2 n-k = 2 n   -k

= 2 n [ 1 – (1/2) n+1 / 1-1/2 ] u(n)

= [2 n+1 – 1] u(n)

If x(n) = x1(n) * x2(n) where x1(n) = (1/3)n u(n) and x2(n) = (1/5)n u(n). Find X(z) by using convolution property.

X1(z) = 1/ 1- (1/3)z-1         X2(z) = 1/1- (1/5) z-1 

 X(z) = 1/1-(1/3)z-1 . 1/1-(1/5) z-1  

Using z-transform find the convolution of two sequences.

x1(n) = {1,2,-1,0,3}        x2(n) = { 1,2,-1}

Z{ x1(n) * x2(n)} = X1(z) . X2(z)

X1(z) = 1 + 2z-1 – z-2 + 3 z-4

X2(z) = 1 + 2z-1 – z-2 

(1 + 2z-1 – z-2 + 3 z-4  )  (1 + 2z-1 – z-2  )

= 1 + 4z-1 + 2z-2 – 4 z- 3 + 4 z-4 + 6 z- 5 – 3 z-6 

Using convolution method  find

X(z) = 1 + 3z-1

   1 + 3z-1 + 2z-2

= z(z+3)

   (z+1)(z+2)  

X1(z) =     z       X2(z) = z+3     =  z       + z-1 3z

     z+1     z+2     z+2            z+2

x1(n) = (-1) n u(n)

 x2(n) = (-2) n u(n) + 3 (-2) n-1 u(n-1)

x(n) = x1(n) * x2(n)

      = (-1) n u(n) * [ (-2) n u(n) + 3 (-2) n-1 u(n-1)]

   = (-1) n u(n) *  (-2) n  u(n) + 3 (-1) n u(n) * (-2) n-1 u(n-1)

= k u(k) (-2) n-k  u(n-k) + 3 k u(k) (-2) n-k-1  u(n-k-1)

= (-2)n k (-2) –k + 3(-2) n-1 k (-2) –k

= (-2) n     k  + 3 (-2) n-1   k  

= (-2) n  [ 1-(0.5) n+1 ]   + 3 (-2) n-1 [ 1- (0.5) n]

      1 – 0.5   1 – 0.5

x(n)  = [ 2(-1)n – (-2)n]  u(n)

Key Takeaways:

1. If we want to analyze a system, which is already represented in frequency domain, as discrete time signal then we go for Inverse Z transform.