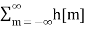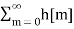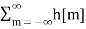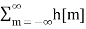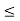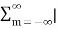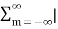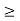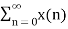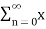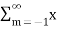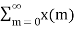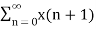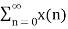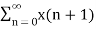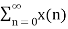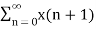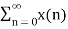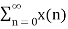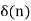Due to its convolution property, the z-transform is a powerful tool to analyze LTI systems

y[n] = h[n] * x[n] - Y(z) = H(z) X(z)

When the input is the eigenfunction of all LTI system, i.e x[n] = e sn = z n

the operation on this input by the system can be found by multiplying the system's eigenvalue H(z)  to the input:
 

y[n] = O[z n] = h[n] * z n = H(z) z n

• Causal LTI systems

An LTI system is causal if its output y[n] depends only on the current and past input x[n] but not the future.

Assuming the system is initially at rest with zero output y[n] | n<0 =0 then its response y[n] = h[n] to an impulse x[n] = δ[n] at n=0 is at rest for n<0 that is h[n] = h[n] u[n]

 Its response to a general input x[t]  is:

y[n] = h[n] * x[n] =   x[n-m] = x[n-m]

Due to the properties of the ROC, we know that

If an LTI system is causal (with a right sided impulse response function h[n]=0  for  n<0, then the ROC of its transfer function H(z)  is the exterior of a circle including infinity.

In particular, when H(z)  is rational, then the system is causal if and only if its ROC is the exterior of a circle outside the out-most pole, and the order of numerator is no greater than the order of the denominator.

• Stable LTI systems

An LTI system is stable if its response to any bounded input is also bounded for all n:

if |x[n]| < Bx then |y[n]| < ∞

As the output and input of an LTI is related by convolution, we have:

y[n] = h[n] * x[n] =   x[n-m] <∞

and

|y[n]| = |   x[n-m]| Bx h[m]| <∞

which obviously requires:

h[m]| <∞

In other words, if the impulse response function h[m] of an LTI system is absolutely integrable, then the system is stable. We can show that this condition is also necessary that is all stable LTI systems' impulse response functions are absolutely integrable.

• The Unilateral z-transform is also called as one-sided z- transform.
• It is defined for n  0 that is causal sequences.
• The unilateral z- transform is used to solve difference equations with initial conditions.

X(z) = z-n

• Unilateral and bilateral transforms are same for causal signals.

Properties of Unilateral Z transform

Time Shift

x(n) -> X(z)

x(n-1) => z -k X(z) + z -k+1 x(-1) + --------------+ z-1 x(-k+1) + x(-k)

x(n)  X(z)

x(n-1) -> Y(z)

Y(z) = (n-1) z -n

Let n-1=m

Y(z) = (m) z m+1

Y(z) = x(-1) + z -1 z -m

x(n-1) - z-1 X(z) + x(-1)

x(n-2) -> z -2 X(z) + z-1 x(-1) + x(-2)

Final Value Theorem

x(∞) = lim n->∞ (1-z-1) X(z)

Final value and initial value theorems are valid only for causal and stable system.

x(n +1) -> z X(z) – z x(0)

x(n) -> X(z)

z -n = z X(z) – z x(0)

x(n)  X(z)

X(z) =    z -n

Subtracting these two equations

z -n  -    z -n = (z-1) X(z) – z x(0)

Taking the limit as    

   -   =   lim z->∞(z-1) X(z) 

Let us expand the LHS os the above equation as   n->∞

x(∞) = lim n->∞ (1-z-1) X(z)

or

x(∞) = lim n->∞ (z-1) X(z)

Initial Value Theorem

x(n) -> X(z)

x(0) = lim z-> ∞ X(z)

X(z) = z -n

X(z) = x(0) + x(1)/z+x(2)/z2 +--------

Lim z->∞ X(z) = x(0)

The z-transform can be used to convert a difference equation into an algebraic equation in the same manner that the Laplace converts a differential equation into an  algebraic equation

The difference equation DE contains the unknown function x(n) and shifted versions of it such as x(n−1) or x(n+3).  The solution of the equation is the determination of x(t). A linear DE has only simple linear combinations of x(n) and its shifts.

Z transform converts the difference into algebraic equation in z-domain.

Find the impulse response and step response for the following systems:

y(n) = -  ¾ y(n-1) + 1/8 y(n-2) = x(n)

y(n)  - ¾ y(n-1) + 1/8 y(n-2) = x(n)

Taking z-transform on both sides we get

Y(z) – ¾ [ z-1 Y(z) + y(-1) ] +1/8 [ z-2 Y(z) + z-1 y(-1)+y(-2)] = X(z)

Substituting y(-1)=y(-2)= 0

Y(z) -3/4 z-1 Y(z) + 1/8 z-2 Y(z) = X(z)

Y(z) =     1____________

1-     ¾ z-1 + 1/8 z-2

 Impulse response

 x(n) =        X(z) =1

 Y(z) =    1____________           =      1____________ 

1-     ¾ z-1 + 1/8 z-2                 1-  ¾ z-1 + 1/8 z-2  

Y(z)  =  z__________       =        A___        +    B__

  X(z) (z-1/2)(z-1/4)  (z-1/2)            (z-1/4)

  By solving A=2 and B=-1.

  Y(z) = 2 z          -       z

   z-1/2       (z-1/4)

            y(n) = 2 (1/2)n u(n) – (1/4) n u(n).

Step Response

x(n) = u(n)   X(z) = z/z-1

Y(z)  =         1_______

X(z)   1-3/4 z-1 + 1/8 z-2

Y(z) = z  z2___________

 z-1  z2 -3/4 z +1/8

Y(z)   =    z2___________

z     z2 -3/4 z +1/8

Y(z)   =    z2___________

z     (z-1)(z-1/2)(z-3/4)

=               A       +     B   +      C

          z-1        z-1/2      z- 1/4

By solving A=8/3   B= -2  C= 1/3

Therefore

Y(z) = 8 . z      -2  z   + 1/3 z

 3     z-1      z-1/2 z-1/4

y(n) = 8/3 u(n) – 2(1/2)n u(n) +1/3 (1/4) n u(n)