3.1 Arrays 1D 2D | unit 3 arrays

Back to Study material

C PPS

UNIT 3

ARRAYS

3.1 Arrays (1-D, 2-D)

One Dimensional Array:

The array which is used to represent and store data in a linear form is called as 'single or one dimensional array.'

Syntax:

data-type array_name[size];

Example 2:

int a[3] = {2, 3, 5};

char ch[10] = "Data" ;

float x[3] = {2.5, 3.50,489.98} ;

Total Size of an array (in Bytes) can be calculated as follows:

total size(in bytes) = length of array * size of data type

In above example, a is an array of type integer which has storage size of 3 elements. One integer variable occupies 2 bytes. Hence the total size would be 3 * 2 = 6 bytes.

Memory Allocation:

Index/Subscript 0 1 2 3 4

Address 1000 1002 1004 1006 1008

Fig 1 : Memory allocation for one dimensional array

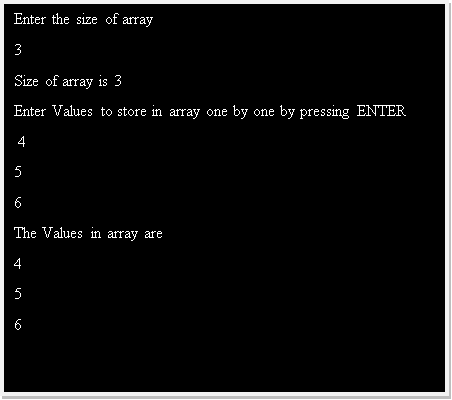
P1: Program to display all elements of 1-D array.

#include<stdio.h>
#include<conio.h>
void main()
{
int a[20];
int n,i;
printf("\n Enter the size of array :");
scanf("%d",&n);
printf("size of array is %d",n);
printf("\n Enter Values to store in array one by one by pressing ENTER :");
for(i=0;i<n;i++)
{
scanf("%d",&a[i]);
}
printf("\n The Values in array are..");

for(i=0;i<n;i++)
{
printf("\n %d",a[i]);
}
getch();
}

P2: Program to copy 1-D array to another 1-D array

#include <stdio.h>

#include<conio.h>

void main()

{

int n, i, j, a[100], b[100];// a is original array and b is copied array

printf("Enter the number of elements in array a\n");

scanf("%d", &n);

printf("Enter the array elements in a\n");

for (i= 0; i < n ; i++)

scanf("%d", &a[i]);

Copying elements from array a into array b */

for (i =0;i<n;i++)

b[i] = a[i];

Printing copied array b

printf("Elements of array b are\n");

for (i = 0; i < n; i++)

printf("%d\n", b[i]);

getch();

}

Output:

P3:Program to find reverse of 1-D array

#include <stdio.h>

#include<conio.h>

void main()

{

int n, i, j, a[100], b[100];// a is original array and b is reversed array

printf("Enter the number of elements in array\n");

scanf("%d", &n);

printf("Enter the array elements\n");

for (i= 0; i < n ; i++)

scanf("%d", &a[i]);

* Copying elements into array b starting from end of array a

for (i = n - 1, j = 0; i >= 0; i--, j++)

b[j] = a[i];

Printing reversed array b

printf("Reverse array is\n");

for (i = 0; i < n; i++)

printf("%d\n", a[i]);

getch();

}

Output:

2. Multi Dimensional Array

1-D array has 1 row and multiple columns but multidimensional array has of multiple rows and multiple columns.

Two Dimensional array:

It is the simplest multidimensional array. They are also called as matrix.

Declaration:

data-type array_name[no.of rows][no. of columns];

Total no of elements= No.of rows * No. of Columns

Example 3: int a[2][3]

This example illustrates two dimensional array a of 2 rows and 3 columns.

Col 0 Col 1 Col 2

Row 0

a[0][0]

a[0][1]

a[0][2]

a[1][0]

a[1][1]

a[1][2]

Row 1

Fig.2: Index positions of elements of a[2][3]

Total no of elements: 2*3=6

Total no of bytes occupied: 6( total no.of elements )*2(Size of one element)=12

Initialization and Storage Representation:

In C, two dimensional arrays can be initialized in different number of ways. Specification of no. of columns in 2 dimensional array is mandatory while no of rows is optional.

int a[2][3]={{1,3,0}, // Elements of 1st row

{-1,5,9}}; // Elements of 2nd row

int a[][3]={{1,3,0}, // Elements of 1st row

{-1,5,9}}; // Elements of 2nd row

int a[2][3]={1,3,0,-1,5,9};

Fig. 3 gives general storage representation of 2 dimensional array

Col 0 Col 1 Col n

Row 0

a[0][0]

a[0][1]

---

a[0][n]

a[1][0]

a[1][1]

---

a[1][n]

a[m][0]

a[m][1]

a[m][n]

Row 1

Row m

Fig.3 General Storage Representation of 2 dimensional array.

Eg 4. int a[2][3]={1,3,0,-1,5,9}

-1

Row 0

Row 1

Col 0 col1 col2

Accessing Two-Dimensional Array Elements:

An element in 2-dimensional array is accessed by using the subscripts i.e. row index and column index of the array. For example:

int val = A[1][2];

The above statement will access element from the 2nd row and third column of the array A i.e. element 9.

3.2 Character arrays and Strings

If the size of array is n then index ranges from 0 to n-1. There can be array of integer, floating point or character values. Character array is called as String.

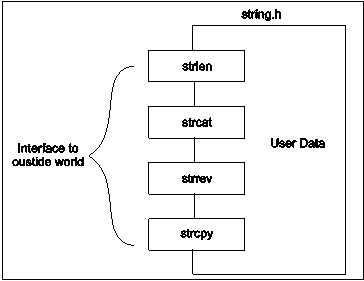
The abstract model of string is implemented by defining a character array data type and we need to include header file ‘string.h’, to hold all the relevant operations of string. The string header file enables user to view complete string and perform various operation on the string. E.g. we can call ‘strlen’ function to find length of string, ‘strcat’ to concatenate two string, ‘strcpy’ to copy one string to another, ‘strrev’ to reverse the string. The definitions of all these functions are stored in the header file ‘string.h’. So string functions with the user provided data becomes the new data type in ‘C’.

Fig. 3.1: String data type

To use the functions related to strings, user only need to include ‘string.h’ header file. All the definitions details of these functions are keep hidden from the user, user can directly use these function without knowing all the implementation details. This is known as abstraction or hiding.

String Manipulation in C Language

Strings are also called as the array of character.

A special character usually known as null character (\0) is used to indicate the end of the string.
To read and write the string in C program %s access specifier is required.
C language provides several built in functions for the manipulation of the string
To use the built in functions for string, user need to include string.h header file.
Syntax for declaring string is

Char string name[size of string];

Char is the data type, user can give any name to the string by following all the rules of defining name of variable. Size of the string is the number of alphabet user wants to store in string.

Example:

Sr. No.	Instructions	Description
	#include<stdio.h>	Header file included
2.	#include<conio.h>	Header file included
3.	void main()	Execution of program begins
4.	{	String is declare with name str and size of storing 10 alphbates
5.	char str[10];
6.	clrscr();	Clear the output of previous screen
7.	printf("enter a string");	Print “enter a string”
8.	scanf("%s",&str);	Entered string is stored at address of str
9.	printf("\n user entered string is %s",str);	Print: user entered string is (string entered by user)
10.	getch();	Used to hold the output screen
11.	}	Indicates end of scope of main function

Following are the list of string manipulation function

Sr. No.	String Function	Purpose
	strcat	use to concatenate (append) one string to another
2.	Strcmp	use to compare one string with another. (Note: The comparison is case sensitive)
3.	strchr	use to locate the first occurrence of a particular character in a given string
4.	Strcpy	use to copy one string to another.
5.	Strlen	use to find the length of a string in bytes,

3.3 Basic Algorithms: Searching and Sorting Algorithms (Linear Search, Binary Search, Bubble sort and Selection sort)

Sorting and Searching are fundamental operations in computer science. Sorting refers to the operation of arranging data in some given order. Searching refers to the operation of searching the particular record from the existing information.

Consider a database of banking system where information of all customers such as name, contact number, address, account number is stored. If a manager wants to search for a record of a particular customer, he has to look for that record from among all records that has been stored in a database. This process of looking up for a particular record in a database is referred as searching.

If records in a banking database are not ordered properly it will be very difficult for a manager to search for a specific record. On the contrary if all record are arranged in order according to some criteria like names in alphabetical order or account numbers in ascending order, searching becomes easy and fast. The process of ordering the records in a data base is called sorting. Thus for efficient searching sorting is necessary.

Linear Search

Given a collection of objects, the goal of search is to find a particular object in this collection. The objects have key values on which search is performed and data values which correspond to the information one wishes to retrieve once an object is found. For example, a telephone book is a collection of names on which one searches and telephone numbers which correspond to the data being sought. The collection of objects is often stored in a list or an array. Given a collection of objects in an array A[1.. n], the ith element A[i] corresponds to the key value of the ith object in the collection. The input to a search algorithm is an array of objects A, the number of objects n, and the key value being sought x.

Thus Algorithm for Linear Search is

1. start at one end of the list

2. if the current element is not equal to the search target, move to the next element,

3. stop when a match is found or the opposite end of the list is reached.

Function for Linear search is

find(values, target)

{

for( i = 0; i < values.length; i++)

{

if (values[i] == target)

{ return i; }

}

return –1;

}

If element is found this function returns index of that element otherwise it returns –1.

Example : we have an array of integers, like the following:

Elements 	9	6	7	12	1	5
Index 	0	1	2	3	4	5

Let’s search for the number 7. According to function for linear search index for element 7 should be returned. We start at the beginning and check the first element in the array.

First element is 9.Match is not found and hence we move to next element i.e 6.

Again match is not found so move to next element i.e.7.

9	6	7	12	1	5
0	1	2	3	4	5

We found the match at the index position 2. Hence output is 2.

If we try to find element 10 in above array, it will return –1,as 10 is not present in the array.

Complexity Analysis of Linear Search:

Let us assume element x is to be searched in array A of size n.

An algorithm can be analyzed using following three cases.

1. Worst case

2. Average case

3. Best case

1. Worst case : In Linear search worst case happens when element to be searched is not present. When x is not present, the linear search function compares it with all the elements of A one by one. The size of A is n and hence x is to be compared with all n elements. Thus, the worst case time complexity of linear search would be O(n).

2. Average case : In average case analysis, we take all possible inputs and calculate computing time for all of the inputs. Sum all the calculated values and divide the sum by total number of inputs. Following is the value of average case time complexity.

Average Case Time = =

= O (n)

3. Best Case : In linear search , the best case occurs when x is present at the first location. So time complexity in the best case would be O(1).

P1 : Program for Linear Search

#include<stdio.h>
#include<conio.h>

int search(int [],int, int);
void main()
{
int a[20],k,i,n,m;
clrscr();
printf(“\n\n ENTER THE SIZE OF ARRAY”);
scanf(“%d”,&n);
printf(“\n\nENTER THE ARRAY ELEMENTS\n\n”);
for(i=0;i<n;i++)
{
scanf(“%d”,&a[i]);
}
printf(“\n\nENTER THE ELEMENT FOR SEARCH\n”);
scanf(“%d”,&k);
m=search(a,n,k);
if(m==–1)
{
printf(“\n\nELEMENT IS NOT FOUND IN LIST”);
}
else
{
printf(“\n\nELEMENT IS FOUND AT LOCATION %d”,m);
}
}
getch();
}

int search(int a[],int n,int k)
{
int i;
for(i=0;i<n;i++)
{
if(a[i]==k)
{
return i;
}
}
if(i==n)
{
return –1;
}
}

Merits :

1. Simple and easy to implement

2. It works well even on unsorted arrays.

3. It is memory efficient as it does not require copying and partitioning of the array being searched.

Demerits :

Suitable only for small number of values.
It is slow as compared to binary search.

Binary Search

Binary Search requires sorted array.

Steps to perform binary search on sorted array A of size n are as follows.

1. Initialize lower and upper limit of array to be searched Low=0,High= n–

2. Find the middle position

Mid=(Low + High)/2

3. Compare the input key value with the key value of the middle element of the array. It has 3 possibilities.

Case 1 : If keys match then return mid and print element found.

if(key==A[mid])

return mid

Case 2 : If key is less than middle element then element is present in left half of array. Update High and goto step 2.

if(key<A[mid])

High= Mid–1

goto step 2

Case 3 : If key is greater than middle element then element is present in right half of array. Update Low and goto step 2.

if(key>A[mid])

Low= Mid+1

goto step 2

Case 4: if(Low>High)

Print element not found.

Iterative algorithm for Binary Search

int BinarySearch( int A[],int x)

{

int mid,n;

int Low = 0;

int High = n–1;

while ( Low <= High )

{

mid = (Low + High) / 2;

if ( A[mid] == x )

return mid;

if ( A[mid] > x )

High = mid – 1;

else Low = mid + 1;

}

return –1;

}

Example 1 : Let array A= {–1, 5, 6, 18, 19, 25, 46, 78, 102, 114}. We want to find element ‘6’ using binary search.

–1	5	6	18	19	25	46	78	102	114
0	1	2	3	4	5	6	7	8	9

Solution:

Step 1 : Low=0, High= 9

Step 2 : Mid=(Low + High)/2

Mid = (0+9)/2 =4.5 i.e 4. It means middle element is located at position 4. So A[Mid] is 19.Thus

Low=0

Mid=4

High=9

Low				Mid					High
–1	5	6	18	19	25	46	78	102	114
0	1	2	3	4	5	6	7	8	9

Step 3 : Compare 6 with 19. It satisfies case 2 of step 3. so High= 4–1=3 and element is present in left half of array. We can ignore right half of array.

Repeat step 2. So mid= (0+3)/2 = 1.5 i.e 1. mid is at position 1. Element 5 is present at position 1.

Low = 0

Mid = 1

High = 3

Low	Mid		High
–1	5	6	18	19
0	1	2	3	4

Again compare 5 with 6. It satisfies case 3 of step 3. so

Low = 1+1=2.

Repeat step 2. Mid= (2+ 3)/2= 2.5 i.e 2 .Mid is at position 2. Element 6 is at position 2.

Low=2

Mid=2

High=3

		Low, Mid	High

–1	5	6	18	19
0	1	2	3	4

Compare 6 with 6.

Match is found. Return the position and print element found.

Example 2 : Find 103 in {–1, 5, 6, 18, 19, 25, 46, 78, 102, 114} using Binary Search.

Low				Mid					High
–1	5	6	18	19	25	46	78	102	114
0	1	2	3	4	5	6	7	8	9

Step 1 : Low=0

High=9

Step 2 : Mid=(0+9)/2=4

So middle element is 19.

Step 3 : Compare(103,19)

103>19 hence element is located at right half of array and we can ignore left half of array. Update Low and recalculate mid.

Low = 4+1=5

High = 9

Mid = (5+9)/2=7

Low		Mid		High
25	46	78	102	114
5	6	7	8	9

Middle element is 78. Compare(103,78)

103>78. Recalculate Low and Mid

Low = 7+1=8

High = 9

Mid = (8+9)/2=8

Low, Mid	High
102	114
8	9

Middle element is 102. Compare(103,102)

103>102. Recalculate Low and Mid.

Low = 8+1=9

High = 9

Here Low=High and match is not found hence we conclude that element is not

Example 3 : Find 44 in A={5,12,17,23,38,44,77,84,90} using binary search.

Step 1: Low=0

High=8

Mid=(0+8)/2=4

Low				Mid				High
5	12	17	23	38	44	77	84	90
0	1	2	3	4	5	6	7	8

Middle element is 38. Compare(44,38)

44>38.Thus element is located at right half of array and we can ignore left half of array. Recalculate Low and Mid.

Low = (4+1)= 5

High = 8

Mid = (5+8)/2=6.5 i.e 6

Low	Mid		high
44	77	84	90
0	1	2	3

Middle element is 77. Compare(44,77)

44<77. Recalculate High and Mid.

Low=5

High = 6–1=5

Mid = (5+5)/2=5

Low, Mid, high
44	77	84	90
0	1	2	3

Middle element is 44. Compare(44,44)

Match is Found. Return index and print “Element Found.”

present in array.

Algorithm for Recursive Binary Search

int BinarySearch (int A[], int x, int Low, int High)
{

if (High > Low)

return –1;

int mid = (High + Low) / 2;

if (A[mid] == x)

return mid;

if (A[mid] < x)

return BinarySearch(A, x, mid+1, High);

return BinarySearch(A, x, Low, mid–1);

}

P2 : Program for Binary Search

#include<stdio.h>
#include<conio.h>
void main()
{
int n,i,search,f=0,low,high,mid,a[20];
clrscr();
printf("Enter the number of elements:");
scanf("%d",&n);
for(i=1;i<=n;i++)
{
printf("Enter the number in ascending order a[%d]=",i);
scanf("%d",&a[i]);
}
printf("Enter the element to be searched:");
scanf("%d",&search);
low=0;
high=n–1;
while(low<=high)
{
mid=(low+high)/2;
if(search<a[mid])
{
high=mid–1;
}
else if(search>a[mid])
{
low=mid+1;
}
else
{
f=1;
printf("Element is found at the position %d:",mid);
exit();
}
}
if(f==0)
{
printf("Element not found");
}
getch();
}

Complexity Analysis of Binary Search :

Assume our array size is 16.

When n= 16 BinarySearch is called to reduce size to n=8.

When n= 8 BinarySearch is called to reduce size to n=4.

When n= 4 BinarySearch is called to reduce size to n=2.

When n= 2 BinarySearch is called to reduce size to n=1 .

Thus we see that BinarySearch function is called 4 times

i.e. 4 elements of the array were examined for n =16.

Note that 16 = 24

Let us consider a more general case where

n is still a power of 2. Let us say n =2k

After k searches, the while loop is executed k times and n reduces to size 1. Let us assume that each run of the while loop involves at most 4 operations.

Thus total number of operations: 4k.

The value of k can be determined from the expression

2k = n

Taking log of both sides

k = log n

Thus total number of operations = 4 log n.

We conclude that the time complexity of the Binary search method is O(log n), which is much more efficient than the Linear Search method.

Merits :

Binary Search is fast and efficient.

Suitable for large number of values.

Demerits :

Binary search works only on sorted array or list.

Bubble Sort

Steps to perform Bubble sort are as follows.

Assume we want to sort the elements in ascending order and no two elements are equal.

1. Compare first element with second element. If first element is greater than next element, we interchange their position accordingly. i.e first element is moved to second element’s position and second element is moved to first element’s position. If No, then we don’t interchange any elements.

2. The element in second position is compared with element in third position and the process of interchanging elements is performed if second is greater than third element. The whole process of comparing and interchanging is repeated till last element. When the process gets completed, the largest element in array will get placed in the last position of the array.

Let us consider array A of size n. Then Algorithm for Bubble sort is

1. Set i to 0.

2. Set j to 0.

3. if(A[j]>A[j+1])

swap A[j],A[j+1]

4. Increment j

5. if j<(n–1–i) goto step 3

6. Increment i

7. if(i<n–1) goto step 2.

Example 1 : Suppose the following numbers are stored in an array A:

32	51	27	85	66	23	13	57
j = 0	1	2	3	4	5	6	7

We apply bubble sort to array A. We discuss each pass separately.

Pass 1

1. Compare j[0] and j[1]. Since 32 < 51, the list is not altered.

2. Compare j[1] and j[2] Since 51 > 27, interchange 51 and 27 as follows:

32	51	27	85	66	23	13	57
j = 0	1	2	3	4	5	6	7

Array A becomes

32	27	51	85	66	23	13	57
j = 0	1	2	3	4	5	6	7

3. Compare j[2] and j[3]. Since 51 < 85, array is not altered.

4. Compare j[3] and j[4]. Since 85 > 66, interchange 85 and 66 as follows:

32	27	51	85	66	23	13	57
j = 0	1	2	3	4	5	6	7

Array A becomes

32	27	51	66	85	23	13	57
j = 0	1	2	3	4	5	6	7

5. Compare j[4] and j[5]. Since 85 > 23, interchange 85 and 23 as follows:

32	27	51	66	85	23	13	57
j = 0	1	2	3	4	5	6	7

Array A becomes

32	27	51	66	23	85	13	57
j = 0	1	2	3	4	5	6	7

6. Compare j[5] and j[6]. Since 85 > 13, interchange 85 and 13 as follows:

32	27	51	66	23	85	13	57
j = 0	1	2	3	4	5	6	7

32	27	51	66	23	13	85	57
j = 0	1	2	3	4	5	6	7

7. Compare j[6] and j[7]. Since 85 > 57, interchange 85 and 57 as follows:

32	27	51	66	23	13	85	57
j = 0	1	2	3	4	5	6	7

Array A becomes

32	27	51	66	23	13	57	85
j = 0	1	2	3	4	5	6	7

At the end of this first pass, the largest number, 85, has moved to the last position. However, the rest of the numbers are not sorted, even though some of them have changed their positions.

Pass 2 will move second last number at second last position, Pass 3 will move third last number at third last position and so on. Here we show array after every pass.

Pass 2 :

27	33	51	23	13	57	66	85
j = 0	1	2	3	4	5	6	7

Pass 3 :

27	33	23	13	51	57	66	85
j = 0	1	2	3	4	5	6	7

Pass 4:

27	23	13	33	51	57	66	85
j = 0	1	2	3	4	5	6	7

Pass 5 :

23	13	27	33	51	57	66	85
j = 0	1	2	3	4	5	6	7

Pass 6 :

13	23	27	33	51	57	66	85
j = 0	1	2	3	4	5	6	7

Hence the array is sorted in 6 passes.

We will see one more example

Example 2 : Apply Bubble Sort on array A= {5,3,1,9,8,2,4,7}.

j =0	5	3	1	9	8	2	4	7
j =1	3	5	1	9	8	2	4	7
j =2	3	1	5	9	8	2	4	7
j =3	3	1	5	9	8	2	4	7
j =4	3	1	5	8	9	2	4	7
j =5	3	1	5	8	2	9	4	7
j =6	3	1	5	8	2	4	9	7
j =7	3	1	5	8	2	4	7	9

Pass 2 : i=2

3	1	5	8	2	4	7	9
1	3	5	8	2	4	7	9
1	3	5	8	2	4	7	9
1	3	5	8	2	4	7	9
1	3	5	2	8	4	7	9
1	3	5	2	4	8	7	9
1	3	5	2	4	7	8	9

Pass 3 :

1	3	5	2	4	7	8	9
1	3	5	2	4	7	8	9
1	3	5	2	4	7	8	9
1	3	2	5	4	7	8	9
1	3	2	4	5	7	8	9

Pass 4 :

1	3	2	4	5	7	8	9
1	3	2	4	5	7	8	9
1	2	3	4	5	7	8	9

This array gets sorted in 4 passes only.

Example : Apply Bubble Sort on array A= {23,78,45,8,32,56}

Pass 1 :

23	78	45	8	32	56
23	78	45	8	32	56
23	45	78	8	32	56
23	45	8	78	32	56
23	45	8	32	78	56
23	45	8	32	56	78

Pass 2 :

23	45	8	32	56	78
23	45	8	32	56	78
23	8	45	32	56	78
23	8	32	45	56	78

Pass 3 :

23	8	32	45	56	78
8	23	32	45	56	78

This array is sorted in 3 passes.

P3: Write a Program for Bubble sort in C

#include <stdio.h>

#include<conio.h>

void bubble_sort(int A[], int n);

int main()

{

int A[100], n, i, j, swap;

printf("Enter number of elements\n");

scanf("%d", &n);

printf("Enter the elements\n", );

for (i = 0; i < n; i++)

scanf("%d", &A[i]);

bubble_sort(A, n);

printf("Sorted list in ascending order:\n");

for ( i = 0 ; i < n ; i++ )

printf("%ld\n", A[i]);

return 0;

}

void bubble_sort(int A[], int n)

{

int i, j, t;

for (i = 0 ; i < ( n – 1 ); i++)

{

for (j = 0 ; j < (n – i – 1); j++)

{

if (A[j] > list[j+1])

{

/* Swapping */

t = A[j];

A[j] = A[j+1];

A[j+1] = t;

}

Complexity Bubble sort:

Suppose we have a list with n elements, and each element perform n – 1 comparisons with elements to its left, and swap, if necessary.

Best Case: If the list is already sorted, only one iteration is performed and complexity is O(1).

Average and Worst case: For n elements at most n – 1 swap operations is performed in each pass. The worst and average case complexity is O(n2).

Selection Sort

Assume we want to sort list in ascending order. Selection sort finds the smallest element from unsorted list and swap it with the element in first position. Then it finds second smallest element and swap it with element at second position. This process is repeated till entire list is sorted in ascending order. Each time we swap elements, we say that we have completed a sort pass. A list of n elements requires n–1 passes to completely rearrange the data.

Procedure for every pass is as follows.

Pass 1 : Find the position P of the smallest in the list of N elements A[l], A[2], . . . , A[N], and then interchange A[P] and A[1] . Then A[1] is sorted.

Pass 2 : Find the position P of the smallest in the sublist of N –1 elements A[2], A[3],. . . , A[N], and then interchange A[P]and A[2]. Then A[l], A[2] is sorted.

Pass 3 : Find the position P of the smallest in the sublist of N–2 elements A[3], A[4], . . . , A[N], and then interchange A[P] and A[3]. Then: A[l], A[2] , A[3] is sorted.

Pass N –1 : Find the position P of the smaller of the elements A[N –1), A[N], and then interchange A[P] and A[N–1]. Then: A[l], A[2], . . . , A[N] is sorted. Thus A is sorted after N –1 passes.

Example 1 :

Fig. 4.2 : Original List

We will apply selection sort on this list.

Pass 1 :

Here smallest element is 9 and 25 is located at first position. so we swap 9 with 25.

After Pass 1

Sorted Unsorted sublist

Now we find smallest element from unsorted sublist and place it in second position.

Pass 2 :

Unsorted sublist has 25 as a smallest element and 79 is located at second position. Hence we swap 25 and 79.

After Pass 2 :

Sorted Unsorted sublist

Pass 3 :

After Pass 3 :

Sorted Unsorted sublist

Pass 4 :

After Pass 4 :

Sorted Unsorted sublist

Pass 5 :

After Pass 5 :

Thus list is sorted.

We will see one more example.

Apply selection sort on array A= {77,30,40,10,88,20,65,56}

Pass 1 :

After Pass 1

Pass 2 :

After Pass 2

Pass 3 :

After Pass 3

Pass 4 :

After Pass 4

Pass 5 :

After Pass 5

Pass 6 :

After Pass 6

Hence the list is sorted in ascending order by applying selection sort.

Function for Selection Sort

void selectionSort(int A[], int n)

{

int i, j, s, temp;

for (i= 0; i <= n; i ++)

{

s = i;

for (j=i+1; j <= n; j++)

if(A[j] < A[s])

s= j;

// Smallest selected; swap with current element

temp = A[i];

A[i] = A[s];

A[s] = temp;

}

P4 : Program to perform Selection Sort.

#include <stdio.h>

int main()

{

int A[100], n, i, j, s, temp;

/* n=total no. of elements in array

s= smallest element in unsorted array

temp is used for swapping */

printf("Enter number of elements\n");

scanf("%d", &n);

printf("Enter %d integers\n", n);

for ( i = 0 ; i < n ; i++ )

scanf("%d", &A[i]);

for ( i = 0 ; i < ( n – 1 ) ; i++ )

{

s = i;

for ( j = i + 1 ; j < n ; j++ )

{

if ( A[s] > A[j] )

s = j;

}

if ( s != i )

{

temp = A[i];

A[i] = A[s];

A[s] = temp;

}

printf("Sorted list in ascending order:\n");

for ( i = 0 ; i < n ; i++ )

printf("%d\n", A[i]);

return 0;

}

Output:

Enter number of elements

Enter 5 integers

Sorted list in ascending order

Complexity of Selection Sort :

In selection sort outer for loop is executed n–1 times. On the kth time through the outer loop, initially the sorted list holds

k–1 elements and unsorted portion holds n–k+1 elements. In inner for loop 2 elements are compared each time.

Thus, 2*(n–k) elements are examined by the inner loop during the k th pass through the outer loop. But k ranges from 1 to n–1.

Total number of elements examined is:

T(n) = 2*(n –1) + 2*(n–2) + 2*(n–3) + .. + 2*(n–(n–2))

+ 2*(n–(n–1))

= 2*((n–1) + (n–2) + (n–3) + ... + 2 + 1)

(or 2*(sum of first n–1 integers)

= 2*((n–1)*n)/2)

= n2 – n, so complexity of algorithm is O(n2).

References:

The C programming language by Dennis Ritchie
C programming by K.N. King
The Complete Reference C Fourth Edition by Herbert Schilt
Computer Fundamentals and Programming in C by Reema Theraja.
C in a nutshell by Peter Prinz.

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined