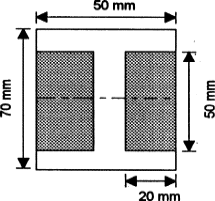
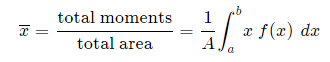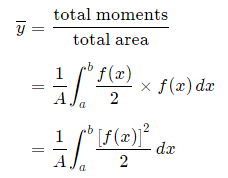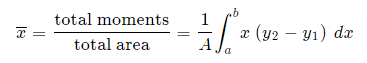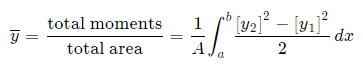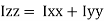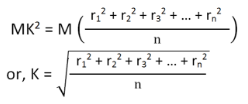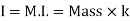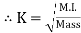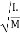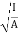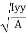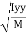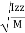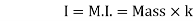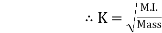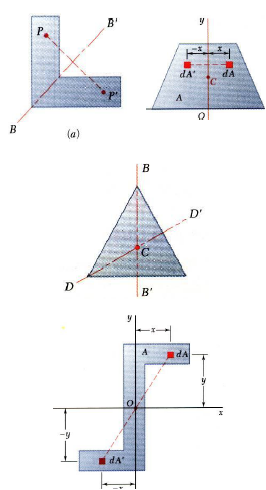
| unit 4 centroid

ECEM

UNIT-4CENTROID

4.1 Centroid of simple figure from first principle

CentroidIn Geometry, the centroid is an important concept related to a triangle. A triangle is a three-sided bounded figure with three interior angles. Based on the sides and angles, a triangle can be classified into different types such as

Scalene triangle

Isosceles triangle

Equilateral triangle

Acute-angled triangle

Obtuse-angled triangle

Right-angled triangle

Centroid DefinitionThe centroid is the centre point of the object. The point in which the three medians of the triangle intersect is known as the centroid of a triangle. It is also defined as the point of intersection of all the three medians. The median is a line that joins the midpoint of a side and the opposite vertex of the triangle. The centroid of the triangle separates the median in the ratio of 2: 1. It can be found by taking the average of x- coordinate points and y-coordinate points of all the vertices of the triangle.

Centroid TheoremThe centroid theorem states that the centroid of the triangle is at 2/3 of the distance from the vertex to the mid-point of the sides.

Centroid theorem

Fig 1Suppose PQR is a triangle having a centroid V. S, T and U are the midpoints of the sides of the triangle PQ, QR and PR, respectively. Hence as per the theorem;QV = 2/3 QU, PV = 2/3 PT and RV = 2/3 RS

Centroid of a Right Angle TriangleThe centroid of a right angle triangle is the point of intersection of three medians, drawn from the vertices of the triangle to the midpoint of the opposite sides.

Centroid of right angle triangle

Fig 2

Centroid of a SquareThe point where the diagonals of the square intersect each other is the centroid of the square. As we all know, the square has all its sides equal. Hence it is easy to locate the centroid in it. See the below figure, where O is the centroid of the square.

Centroid of the square

Fig 3

Properties of centroidThe properties of the centroid are as follows:

The centroid is the centre of the object.

It is the centre of gravity.

It should always lie inside the object.

It is the point of concurrency of the medians.

Centroid FormulaLet’s consider a triangle. If the three vertices of the triangle are A(x1, y1), B(x2, y2), C(x3, y3), then the centroid of a triangle can be calculated by taking the average of X and Y coordinate points of all three vertices. Therefore, the centroid of a triangle can be written as:Centroid of a triangle = ((x1+x2+x3)/3, (y1+y2+y3)/3)

Centroid of a Triangle

Fig 4

Centroid Formula for Different ShapesHere, the list of centroid formula is given for different geometrical shapes.

Shapes	Figure	x̄	ȳ	Area
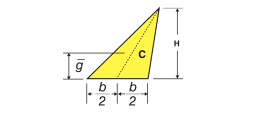
Triangular area		–	h/3	bh/2
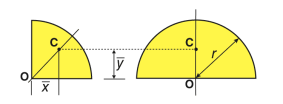
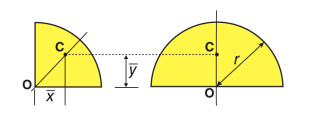
Quarter-circular area		4r/3π	4r/3π	πr2/4
Semi-circular area		0	4r/3π	πr2/2
Quarter-elliptical area		4a/3π	4b/3π	πab/4
Semi elliptical area		0	4b/3π	πab/2
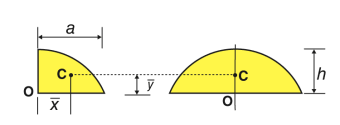
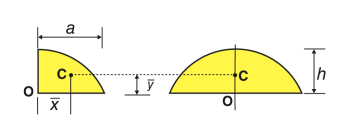
Semi parabolic area		3a/8	3h/5	2ah/3
Parabolic area		0	3h/5	4ah/3
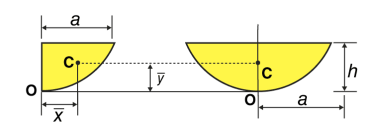
Parabolic spandrel		3a/4	3h/10	ah/3

Key takeaways:1) Centroid of a triangle = ((x1+x2+x3)/3, (y1+y2+y3)/3)2) The centroid is the centre point of the object. The point in which the three medians of the triangle intersect is known as the centroid of a triangle.

4.2 Centroid of composite/build up sectionTaking the simple case first, we aim to find the centroid for the area defined by a function f(x), and the vertical lines x = a and x = b as indicated in the following figure.

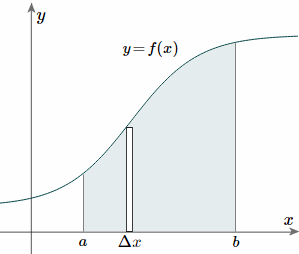
Finding x-centroid

Fig 5To find the centroid, we use the same basic idea that we were using for the straight-sided case above. The "typical" rectangle indicated is x units from the y-axis, and it has width Δx (which becomes dx when we integrate) and height y = f(x)Generalizing from the above rectangular areas case, we multiply these 3 values x, f(x) and Δx, which will give us the area of each thin rectangle times its distance from the x-axis), then add them. If we do this for infinitesimally small strips, we get the x-coordinates of the centroid using the total moments in the x-direction, given by:

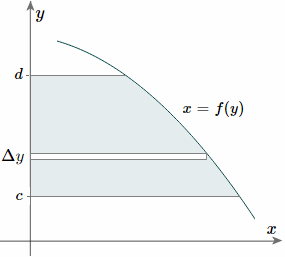
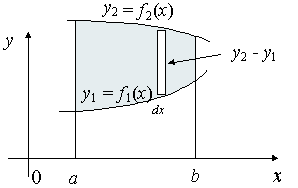
And, considering the moments in the y-direction about the x-axis and re-expressing the function in terms of y, we have:

Finding y-centroid

Fig 6Notice this time the integration is with respect to y, and the distance of the "typical" rectangle from the x-axis is y units. Also note the lower and upper limits of the integral are c and d, which are on the y-axis.Of course, there may be rectangular portions we need to consider separately. (I've used a different curve for the y case for simplification.)Alternate method: Depending on the function, it may be easier to use the following alternative formula for the y-coordinate, which is derived from considering moments in the x-direction (Note the "dx" in the integral, and the upper and lower limits are along the x-axis for this alternate method).

This is true since for our thin strip (width dx) the centroid will be half the distance from the top to the bottom of the strip. Another advantage of this second formula is there is no need to re-express the function in terms of y.

Centroids for Areas Bounded by 2 Curves

Area bounded by 2 curves

Fig 7We extend the simple case given above. The "typical" rectangle indicated has width Δx and height y2 − y1, so the total moments in the x-direction over the total area is given by:

For the y coordinate, we have 2 different ways we can go about it.Method 1: We take moments about the y-axis and so we'll need to re-express the expressions x2 and x1 as functions of y.

Method 2: We can also keep everything in terms of x by extending the "Alternate Method" given above:

Centroids of Composite sections ( 1D, 2D)

First Moments of Areas and Lines •An area is symmetric with respect to an axis BB’ if for every point P there exists a point P’ such that PP’ is perpendicular to BB’ and is divided into two equal parts by BB’. •The first moment of an area with respect to a line of symmetry is zero. •If an area possesses a line of symmetry, its centroid lies on that axis •If an area possesses two lines of symmetry, its centroid lies at their intersection. •An area is symmetric with respect to a center O if for every element dA at (x,y) there exists an area dA’ of equal area at (-x,-y). •The centroid of the area coincides with the center of symmetry.

Fig 8 Key takeaways:Centroid formula:

4.3 Moment of inertia introduction Moment of inertia in physics quantitative measure of the rotational inertia of a body i.e the opposition that the body exhibits to having its speed of rotation about an axis altered by the application of a torque (turning force) The axis may be internal or external and may or may not be fixed. The moment of inertia (I), however, is always specified with respect to that axis and is defined as the sum of the products obtained by multiplying the mass of each particle of matter in a given body by the square of its distance from the axis. In calculating angular momentum for a rigid body, the moment of inertia is analogous to mass in linear momentum. For linear momentum, the momentum p is equal to the mass m times the velocity v; whereas for angular momentum, the angular momentum L is equal to the moment of inertia I times the angular velocity ω.The figure shows two steel balls that are welded to a rod AB that is attached to a bar OQ at C. Neglecting the mass of AB and assuming that all particles of the mass m of each ball are concentrated at a distance r from OQ, the moment of inertia is given by I = 2mr2.

Fig 9The unit of moment of inertia is a composite unit of measure. In the International System (SI), m is expressed in kilograms and r in metres, with I (moment of inertia) having the dimension kilogram-metre square. In the U.S. customary system, m is in slugs (1 slug = 32.2 pounds) and r in feet, with I expressed in terms of slug-foot square.The moment of inertia of anybody having a shape that can be described by a mathematical formula is commonly calculated by the integral calculus. The moment of inertia of the disk in the figure about OQ could be approximated by cutting it into a number of thin concentric rings, finding their masses, multiplying the masses by the squares of their distances from OQ, and adding up these products. Using the integral calculus, the summation process is carried out automatically; the answer is I = (mR2)/2. For a body with a mathematically indescribable shape, the moment of inertia can be obtained by experiment. One of the experimental procedures employs the relation between the period (time) of oscillation of a torsion pendulum and the moment of inertia of the suspended mass. If the disk in the figure were suspended by a wire OC fixed at O, it would oscillate about OC if twisted and released. The time for one complete oscillation would depend on the stiffness of the wire and the moment of inertia of the disk; the larger the inertia, the longer the time.Key takeaways:Moment of inertia formula= I = (mR2)/2.

4.4 Second moment of area of plane section from first principles

Second moment of areaThe integral ∫ y2 dA defines the second moment of area I about an axis and can be obtained by considering a segment of area δA some distance y from the neutral axis, writing down an expression for its second moment of area and then summing all such strips that make up the section concerned, i.e. integrating. As indicated in the discussion of the general bending equation, the second moment of area is needed if we are to relate the stress produced in a beam to the applied bending moment.As an illustration of the derivation of a second moment of area from first principles, consider a rectangular cross-section of breadth b and depth d . For a layer of thickness δy a distance y from the neutral axis, which passes through the centroid, the second moment of area for the layer is:Second moment of area of strip=y2δA=y2b δyThe total second moment of area for the section is thus:Second moment of area=∫limits from −d/2 to d/2) y2bdy=bd3/12

Fig 10Determine the second moment of area about the neutral axis of the I-section shown in Figure 11.

Fig 11We can determine the second moment of area for such a section by determining the second moment of area for the entire rectangle containing the section and then subtracting the second moments of area for the rectangular pieces ‘missing’

Fig12Thus for the rectangle containing the entire section, the second moment of area is given by I = bd3/12 = (50 × 703)/12 = 1.43 × 106mm4. Each of the ‘missing’ rectangles will have a second moment of area of (20 × 503)/12 = 0.21 × 106 mm4. Thus the second moment of area of the I-section is 1.43 × 106 − 2 × 0.21 × 106 = 1.01 × 106mm4 Moment of Inertia for Composite AreasA composite area consists of a series of simpler parts or shapes such as rectangle, triangle and circles. Provided the moment of inertia of each of these parts is known or can be determined about a common axis, then the moment of inertia for the composite area about this axis equals the algebraic sum of the moments of inertia for all its parts. Procedure for Analysis The moment of inertia for a composite area about a reference axis can be determined using the following steps 1. Using a sketch divided the area into its composite parts and indicates the perpendicular distance from the centroid of each part to the reference axis. 2.If the centroid axis for each part does not coincide with the reference axis, the parallel axis theorem, should be used to determine the moment of inertia about the reference axis. 3. The moment of inertia of entire area about the reference axis is determined by the summing the results of its composite parts about this axis. 4. If a composite part has an empty region (hole),its moment of inertia is found by subtracting the moment of inertia of this region from the moment of inertia of the entire part including the region.

4.5 Parallel axes and perpendicular axesParallel axis theorem states thatThe moment of inertia of a body about an axis parallel to the body passing through its centre is equal to the sum of moment of inertia of body about the axis passing through the centre and product of mass of the body times the square of distance between the two axes.

Parallel Axis Theorem FormulaParallel axis theorem statement can be expressed as follows:I = Ic + Mh2Where,

I is the moment of inertia of the body

Ic is the moment of inertia about the centre

M is the mass of the body

h2 is the square of the distance between the two axes

Parallel Axis Theorem DerivationLet Ic be the moment of inertia of an axis which is passing through the center of mass (AB from the figure) and I be the moment of inertia about the axis A’B’ at a distance of h.Consider a particle of mass m at a distance r from the center of gravity of the body.
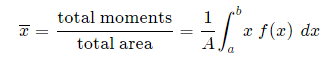
Then,
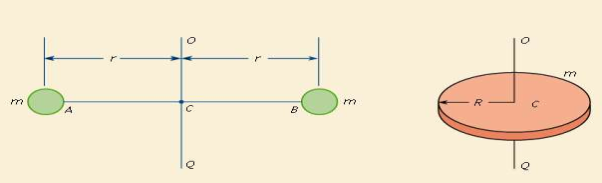
Distance from A’B’ = r + hI = ∑m (r + h)2I = ∑m (r2 + h2 + 2rh)I = ∑mr2 + ∑mh2 + ∑2rhI = Ic + h2∑m + 2h∑mrI = Ic + Mh2 + 0I = Ic + Mh2Hence, the above is the formula of parallel axis theorem.

Perpendicular axes theoremsIt states that , if

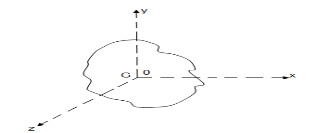
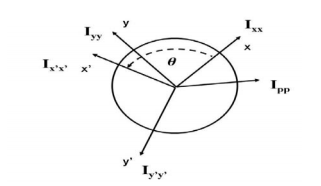
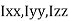be the moments of inertia of figure or plane section about two axis x and y which are perpendicular to each other at point O, then moment of Inertia of that plane section about Z axis which is perpendicular to the plane [&(

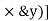is given by :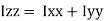

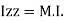Description: S 23.png

Fig 13

of plane area about Z axis passing through C.G.

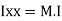of plane area about X axis passing through C.G

of plane area about Y axis passing through C.G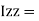

Is also called as polar moment of Inertia (J) Key takeaways:

1) Parallel Axis Theorem Formula

I = Ic + Mh22)

Perpendicular axes theorems formula

4.6 Radius of gyrationThe moment of inertia of a body about an axis is sometimes represented using the radius of gyration. We can define the radius of gyration as the imaginary distance from the centroid at which the area of cross-section is imagined to be focused at a point in order to obtain the same moment of inertia. It is denoted by k.

Radius of Gyration FormulaThe formula of moment inertia in terms of the radius of gyration is given as follows:I = mk2 (1)Where I is the moment of inertia and m is the mass of the bodyAccordingly, the radius of gyration is given as followsk=√ I/m (2)The unit of the radius of gyration is mm. By knowing the radius of gyration, one can find the moment of inertia of any complex body equation (1) without any hassle.Consider a body having n number of particles each having a mass of m. Let the perpendicular distance from the axis of rotation be given by r1, r2, r3,…,rn. We know that the moment of inertia in terms of radius of gyration is given by the equation (1). Substituting the values in the equation, we get the moment of inertia of the body as follows

………… (3)

If all the particles have the same mass then equation (3) becomes

Radius of Gyration

We can write mn as M which signifies the total mass of the body. Now the equation becomes

Radius of Gyration

………… (4)

From equation (4), we get

Radius of Gyration

From the above equation, we can infer that the radius of gyration can also be defined as the root-mean-square distance of various particles of the body from the axis of rotation.

What is the use of radius of gyration?

The radius of gyration is used to compare how various structural shapes will behave under compression along an axis. It is used to predict buckling in a compression beam or member.

OR If entire mass of body be assumed to be concentrated at a certain point which is located at a distance K from given axis such that

Then

Distance K is known as Radius of Gyration

Thus Radius of Gyration is defined as the Distance from the axis of reference where whole mass of the body is assumed to be concentrated

For plane figure having negligible mass, we can consider area for finding radius of gyration

Thus

M.I. of an area (plane figure)

K =

where, Kxx, Kyy, Kzz is radius of gyration of any area ir body about X, y, z, axis respectively

Kxx = =

Kyy = =

Kzz = =

Key takeaways:

1) Distance K is known as Radius of Gyration

Then

2) Radius of Gyration is defined as the Distance from the axis of reference where whole mass of the body is assumed to be concentrated

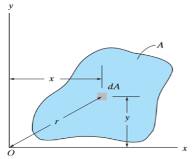
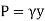4.7 Moment of inertia of composite area and build up sections.When a distributed loading whose intensity varies linearly acts perpendicular to an area, the computation of the moment of the loading distribution about an axis involves a quantity called the moment of inertia of the area or simply area moment of inertia.Consider a differential plate, subjected to fluid pressure P that varies linearly with depth, as shown in fig, such that

, where,

is the specific weight of fluid.The force acting on a acting on the differential area of the plate is given by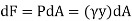

The moment of this this force about the x-axis is

Integrating

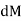over the entire area of the plate yields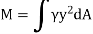

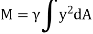The integral part of the moment equation is called area moment of inertia about x-axis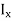

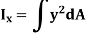Similarly, area moment of inertia about y-axis is given as,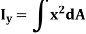

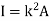Fig 14Moment of Inertia for area can also be given as

Where, A is the total areaAnd k is referred as radius of gyrationRadius of gyration for area of a plate about an axis is defined as the radial distance to a point which would have a same moment of inertia as the plate’s actual distribution of area, if the total area of the plate were concentrated.It is given by,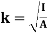

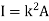
Moment Of Inertia of CylinderThe moment of inertia of cylinder about a perpendicular axis passing through its centre is determined by;Ix = ¼ MR2 + 1/12 ML2

Moment Of Inertia Of Cylinder About Perpendicular Axis

Fig 15 We will look at the derivation of this formula below.Generally, the derivation involves 3 primary steps. It includes;

Splitting the cylinder into infinitesimally thin disks and stating the moment of inertia.

Using both parallel and perpendicular axis theorems to determine the expression.

Integrating over the length of the cylinder.

1. Cutting the cylinder into infinitesimally thin disksWe will consider the cylinder having mass M, radius R, length L and the z-axis which passes through the central axis.Here,Density ρ = M / VNext, we will consider the moment of inertia of the infinitesimally thin disks with thickness dz.First, we assume that dm is the mass of each disk, We get;dm = ρ X Volume of diskdm = M / V X (πr2.dz)We take V = area of circular face X length which is = πr2L. Now we obtain;dm = M / πr2L X (πr2.dz)dm = M / L X dzThe moment of inertia about the central axis is given as;dlz = ½ dmR2 Use of Perpendicular Axis TheoremWe now apply the perpendicular axis theorem which gives us;dlz = dlx + dlyHere, if we need to consider that both x and y moments of inertia are equal by symmetry.dlx = dlyWe need to combine the equations for the perpendicular axis theorem and symmetry. We get;dlx = dlz / 2Now we substitute lz from the equation above.dlx = ½ x ½ dmR2dlx = ¼ dmR2Alternatively, for the x-axis, we use the parallel axis theorem to find the moment of inertia. We get;dlx = ¼ dmR2 + dmz2 IntegrationNow we conduct integration over the length of the cylinder to express the mass element dm in terms of z. We take the integral from z=0 to z=L.Ix = o∫L dlxIx = o∫L ¼ dzR2 + o∫L ¼ z2 m / l dzIx = ¼ M / L R2z + M / L Z3 / 3]0LSince it is a definite form of integral we ignore the constant. We will now have;Ix = ¼ M / L R2 L + M / 3L 2L3 / 23Ix = ¼ MR2 + 1/12 ML2Therefore,

=1/2 MR2 Moment Of Inertia of Sphere

Moment Of Inertia Of Sphere

Fig 16First, we take the moment of inertia of a disc that is thin. It is given as;I = ½ MR2In this case, we write it as;dI (infinitesimally moment of inertia element) = ½ r2dmFind the dm and dv using;dm = p dVp = moment of a thin disk of mass dmdv = expressing mass dm in terms of density and volumedV = π r2 dxNow we replace dV into dm. We get;dm = p π r2 dxAnd finally, we replace dm with dIdI = ½ p π r4 dxThe next step involves adding x to the equation. If we look at the diagram we see that r, R and x form a triangle. Now we will use Pythagoras theorem which gives us;r2 = R2 – x2Now if we substitute the values we get;dI = ½ p π (R2 – x2)2 dxThis leads to:I = ½ p π -R∫R (R2 – x2)2 dxAfter integration and expanding we get;I = pπ 8/15 R5Additionally, we have to find the density as well. For that we use;P (density) = M (mass) / V (volume)p = M (mass) / (4/3 πR3)If we substitute all the values;I = 8/15 π [M / (4/3 πR3)] R5I = ⅖ MR2

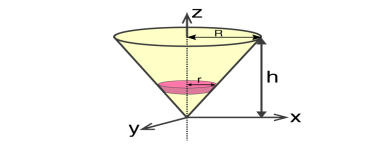
Moment of inertia of Solid ConeWe will take a solid cone where its axis will pass through the centre with radius = r, height = h. We will need to determine the mass though.

Moment Of Inertia Of Solid Cone

Fig 17We take the elemental disc whose mass is given by;dm = ρ⋅ π r2dzDensity is given as;ρ = M / V = M / (⅓π R2h)With this, we will calculate the dm.dm = [M / (⅓π R2h)] X π r2dzdm = (3M / R2h) X r2 dzIf we consider the similarity of the triangle, then we have;R / r = h / zr = R .z / hNow,dm = (3M / R2h)⋅( R2 / h2) ⋅ z2dzdm = (3M / h3). z2dzIf we consider z-axis, the moment of inertia of the elemental disk will be;dI = ½ dmr2dI = ½ ⋅ (3M / h3). z2 ⋅ (z2 R2 / h2) dzdI = 3 / 2 ⋅ M R2 / h5 X z4dzNow we will follow the integration process. Here;I = 3 / 2 ⋅ M R2 / h5 o∫h z4dzI = 3 / 2 ⋅ M R2 / h5 [z5 / 5 ]ohI = 3 / 2 ⋅ M R2 / h5 ⋅ h5 / 5Therefore, I = 3/10 MR2 Key takeaways:1) Moment of Inertia for area can be given as

2) Moment of inertia of Solid Cone = I = 3/10 MR2

3) Moment Of Inertia of Sphere = I = ⅖ MR2

4.8 Concept of product of inertiaThe product of inertia is defined as The x and y terms inside the integral denote the centroidal position of the differential area measured from the y and x axes, respectively. Similar to moments of inertia discussed previously, the value of product of inertia depends on the position and orientation of selected axes. It is possible for the product of inertia to have a positive, negative, or even a zero value.

Fig 18 For example, either x or y represents an axis of symmetry, then the product of inertia Ixy would be zero. To see why this is the case, take a look at the figure to the right. Consider the small area A1 to the right of y axis at the distance of x1. Then consider a similar area to the left of this axis of symmetry at the distance of -x1. Since both areas are at the same vertical position from the x-axis, they have the same value of y. The contribution from the left area is -x1yA1 and that from the right is x1yA1 which add up to zero. Since every point on one side of the axis of symmetry has an equal counterpart on the other side, the total value of the integral would be zero. However, if we were to consider the product of inertia with respect to the x' and y' axes, then Ix'y' would not be zero. We will have more discussion about the product of inertia in the section on principal axes.For a general three-dimensional body, it is always possible to find 3 mutually orthogonal axes (an x, y, z coordinate system) for which the products of inertia are zero, and the inertia matrix takes a diagonal form. In most problems, this would be the preferred system in which to formulate a problem. For a rotation about only one of these axis, the angular momentum vector is parallel to the angular velocity vector. For symmetric bodies, it may be obvious which axis is principle axis. However, for an irregular-shaped body this coordinate system may be difficult to determine by inspection; we will present a general method to determine these axes in the next section. But, if the body has symmetries with respect to some of the axis, then some of the products of inertia become zero and we can identify the principal axes. For instance, if the body is symmetric with respect to the plane

then, we will have

and

will be a principal axis. This can be shown by looking at the definition of the products of inertia.

Fig 19The integral for, say,

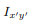can be decomposed into two integrals for the two halves of the body at either side of the plane

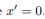. The integrand on one half

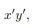will be equal in magnitude and opposite in sign to the integrand on the other half (because

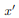will change sign). Therefore, the integrals over the two halves will cancel each other and the product of inertia

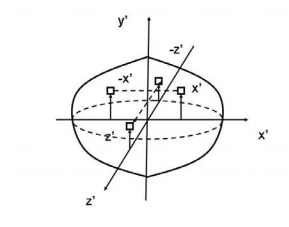
will be zero. (As will the product of inertia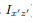

) Also, if the body is symmetric with respect to two planes passing through the center of mass which are orthogonal to the coordinate axis, then the tensor of inertia is diagonal, with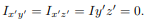

Fig 20Another case of practical importance is when we consider axisymmetric bodies of revolution. In this case, if one of the axes coincides with the axis of symmetry, the tensor of inertia has a simple diagonal form. For an axisymmetric body, the moments of inertia about the two axis in the plane will be equal. Therefore, the moment about any axis in this plane is equal to one of these. And therefore, any axis in the plane is a principal axis. One can extend this to show that if the moment of inertia is equal about two axis in the plane (IP P = Ixx), whether or not they are orthogonal, then all axes in the plane are principal axes and the moment of inertia is the same about all of them. In its inertial properties, the body behaves like a circular cylinder.

Fig 21The tensor of inertia will take different forms when expressed in different axes. When the axes are such that the tensor of inertia is diagonal, then these axes are called the principal axes of inertia. References:

Andy Ruina and Rudra Pratap , Introduction to Statics and Dynamics, Oxford University Press.

Reddy Vijaykumar K. and K. Suresh Kumar, Singer's Engineering Mechanics.

F. P. Beer and E. R. Johnston, Mechanics for Engineers, Statics and Dynamics,

McGraw Hill. Irving H. Shames, Engineering Mechanics, Prentice Hall.

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined