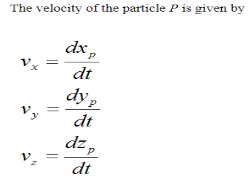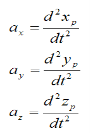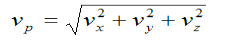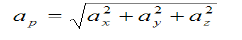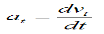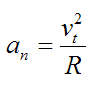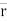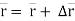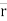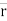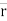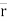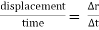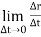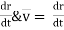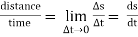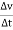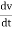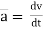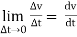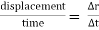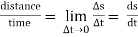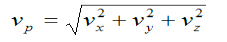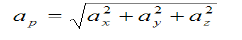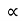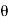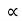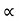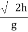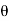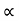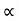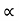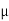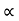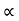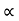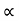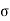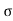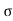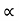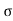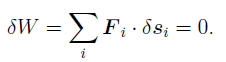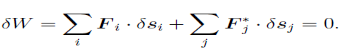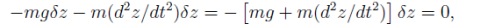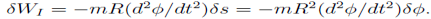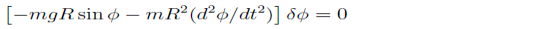UNIT-5
KINEMATICS
Kinematics, the part of physics we have studied up to this point, deals with describing motion. We have looked at position, velocity and acceleration as the three basic properties of a particle in motion. In Dynamics, we look at the causes of the motion that we have already studied. In studying these causes, which we shall call forces, we can get a more complete picture of a given physical situation. Starting with a given set of forces, through dynamics we are able to describe all resulting motion. Dynamics is thus the basis for the rest of the study of classical mechanics, and is applied in every branch of physics.
The study of Dynamics begins with an introduction of the concepts of force and mass, then goes on to introduce the basic laws of Dynamics, Newton's Three Laws. From here, we will look at how Newton's Laws are applied to a variety of forces, including tension, friction, and gravity. We will also examine the Dynamics of uniform circular motion.
Studying Newton's Laws is perhaps the most important part of classical mechanics. Kinematics, which you have already studied, lays the groundwork for Newton's laws. For the most part, the subject matter studied after Newton's laws simply applies the laws to a variety of physical situations, and derives further concepts from them. Newton's laws are the axioms of classical mechanics; brilliant not only in their applicability, but in their simplicity.
Kinematics, branch of physics and a subdivision of classical mechanics concerned with the geometrically possible motion of a body or system of bodies without consideration of the forces involved (i.e., causes and effects of the motions).
Kinematics aims to provide a description of the spatial position of bodies or systems of material particles, the rate at which the particles are moving (velocity), and the rate at which their velocity is changing (acceleration). When the causative forces are disregarded, motion descriptions are possible only for particles having constrained motion—i.e., moving on determinate paths. In unconstrained, or free, motion, the forces determine the shape of the path.
When a particle moves on a curved path, a description of its position becomes more complicated and requires two or three dimensions. In such cases continuous descriptions in the form of a single graph or mathematical formula are not feasible. The position of a particle moving on a circle, for example, can be described by a rotating radius of the circle, like the spoke of a wheel with one end fixed at the centre of the circle and the other end attached to the particle. The rotating radius is known as a position vector for the particle, and, if the angle between it and a fixed radius is known as a function of time, the magnitude of the velocity and acceleration of the particle can be calculated. Velocity and acceleration, however, have direction as well as magnitude; velocity is always tangent to the path, while acceleration has two components, one tangent to the path and the other perpendicular to the tangent.
Displacement
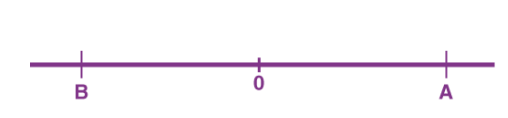
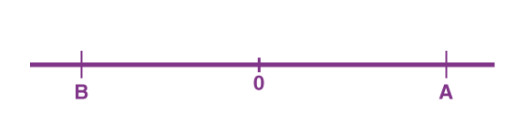
Distance is defined as, The total path length covered during a journey While displacement is defined as, The path length from final position of the particle to the origin O. Consider the following figure:
|
Fig 1
We have an origin O, measurements to the right of O are taken as a positive while to the left are taken as negative. Suppose a person, who starts from origin O reaches point A,
Distance = OA
Displacement = OA
Now he turns and reaches point B,
Distance = OA + AB
Displacement = -OB
As we can see, displacement is negative since it is measured to the left of the origin. From the above example, we can infer that distance is always positive while displacement can either be positive or negative.
Average velocity
Average velocity = total distance travelled in a particular direction/
total time taken
Example 1: A man walks 500 m due east in 300 s and then a further 400 m in 320 s in the same direction. Determine his velocities for the 500 m, the 400 m and his average velocity for the whole journey.
For the 500 m:
v = 500/300 which gives 1.67 m/s due east
For the 400 m:
v = 400/320 which gives 1.25 m/s due east
Average velocity = 500 + 400
300 + 320
= 1.45 m/s due east
Note that in this case the average speed will also be 1.45 m/s due to the same direction travelled in each instance.
Example 2: A man walks 500 m due east in 300 s followed by 400 m due west in 320 s. Determine:
A) his average velocity for i) 500 m, ii) 400 m
B) his average velocity for the whole journey
Consider the direction east to be positive and the direction west to be negative. Therefore there will be no need to write the directions for distance and velocity as these will be shown as positive or negative numbers.
A) i) for 500 m: v = 500/300
v = 1.67 m/s
ii) for 400m: v = -400/320
v = -1.25 m/s
B) The actual distance travelled in a particular direction in 620 seconds (300+320) is 500 +(-400) = 100 m in an easterly direction.
Although the man has walked a total distance of 900 m, he has effectively only walked 100 m east because he changed direction in the lat 400 m.
Therefore the actual distance travelled in a particular direction is called a displacement.
And the average velocity of the man = 100/(300 + 320)
= 0.16 m/s
Note that the average speed of the man will be:
900/620 = 1.45 m/s as the man has still walked 900 m in 620 s.
Instantaneous velocity
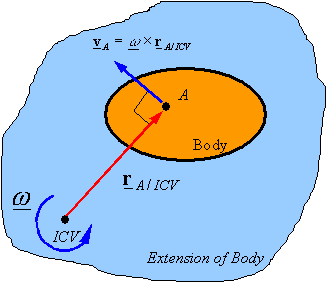
Instantaneous Center of Velocity (ICV): Any point on a rigid body or on its extension that has zero velocity is called the Instantaneous Center of Velocity of the body. Assuming one knows the ICV of a body, one can calculate the velocity of any point A on the body using the equation
VA = VA/ICV + VICV and recognizing that be definition
VICV = 0. This gives
VA = ω x rA/ICV
|
Fig 2
In 2-D motion, if rA/ICV is in the plane of motion and ω is perpendicular to this plane, then one can use the scalar relation
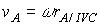
Methods of finding the ICV:
|
Fig 3
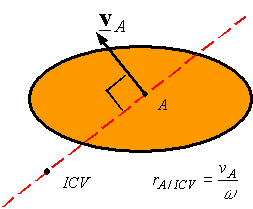
Given the velocity VA of point A on a rigid body and the angular velocity of the rigid body one can use the above equation to find the distance rA/ICV between the point A and the ICV. One can then draw a line perpendicular to the velocity and passing through A, and move along this line a distance rA/ICV to get to the ICV. The side on which the ICV is can be determined by the direction of the angular velocity.
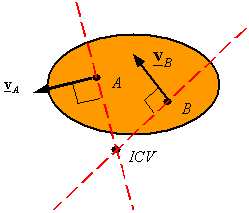
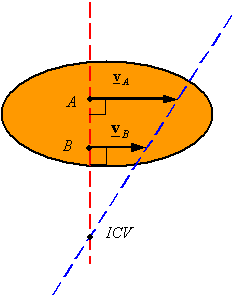
Given the velocity of points A and B on a rigid body one can find the ICV by drawing a line perpendicular to VA and passing through A, and by drawing a line perpendicular to VB and passing through B. One of the following three cases will result
The lines intersect at one point: The point of intersection is the ICV. The angular velocity can be calculated once the ICV is determined using the velocity of both point and its corresponding distance from the ICV.
|
Fig 4
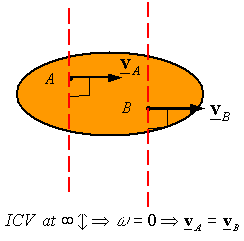
The lines are parallel (they intersect at infinity): The ICV is at infinity, and the angular velocity is zero since infinity times zero is the only way one can get velocities other than infinite. Therefore, the body is in pure translation and the velocity of the two points must be the same.
|
Fig 5
The two lines fall on top of each other: One can find the location of the ICV using the proportionality of velocity and distance from the ICV to create similar triangles. This follows from
|
Fig 6
ω = VA / rA/ICV = VB/rB/ICV
Key takeaways:
1) Average velocity = total distance travelled in a particular direction/
total time taken
2) Any point on a rigid body or on its extension that has zero velocity is called the Instantaneous Center of Velocity of the body
We know velocity of a body is V = (ds/dt) OR V = (dx / dt) & Acceleration A =dv / dt a = dx /dt = d/dt (ds/dt) | = d / dt (dx / dt) A = d2s/ dt2 | a = d2x/ dt2 = V. dv/ds | = V.dv/dx
|
A body or particle sometimes moves along the straight line with variable acceleration .
This variable acceleration may be the function of time or position or velocity .
(1) When acceleration is function of time (t) [ a= f(t) ]
a= dv /dt) = f (t)
∴dv= f(t) dt
Integrating both sides, we got
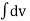 =
= 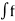 (t) dt
(t) dt
This will give us equation for velocity as a function of time
V = f (t)
Velocity,
V = ds /dt = f (t)
∴ds = f (t) dt
Integrating above equation we get S ( displacement ) in terms of ‘t’.
While solving the problems on variable acceleration , following cases will arise :-
(1)Given equation of motion is in terms of displacement (s) & time (t)
S = f (t) or x = f (t)
Differentiating both sides will give (w.r.t. Time t)
V = ds / dt = f(t) or V = dx / dt = f (t)
Again differentiating above equation, w.r.t. (t)
A= dv /dt = d2s / dt2 = v.dv/ds = f (t) OR
∴ a= dv/dt = d2x/dt2 =v. dv/dx = f (t)
(2) given equation is in terms of acceleration (a) & time (t) .
A = f (t)
Integrating once will give us velocity & Integrating again willgive us the displacement.
(3) Given equation is in terms of acceleration (a) & displacement ( x or s)
A = f(s) or a = f(x)
Integrating once will give us velocity equation Integrating twice will give the equation of motion for displacement
(4) Given equation is in terms of velocity (v) & time (t)
V = f (t)
Integrate above equation to get displacement. Differentiate above equation to get acceleration .
Examples based on variable acceleration -
(Equation in terms of s & t or x & t – given)
Question 1 ) the position of a particle which moves along a straight line is defined by the relation S= t3 - 6t2 - 15 + 40 , where S is in meters and t in sec ;
Determine :- a) time at which velocity will be zero .
b) position & distance travelled by particle at that time .
c) Acceleration at that time.
d) Distance travelled by particle from t= 4 sec to t= 6sec
→ s = t3 - 6t2 -15t +40
Differentiating w.r.t. Time‘t’
ds/dt = 3t2 -12t - 15
∴ v = ds/dt =3t2 -12 t -15
Again differentiating w.r.t. time ‘t’
a= dv/dt = d2s/ dt2 = 6t -12
a) Time at which velocity will be zero
for V =0
∴ v = 3t2 – 12t -15
∴ 0 =3t2 - 12t -15
Solving the equation
[t = 5 sec]
B) t= 5 sec. At this time Displacement will be,
∴ Ss= t2-6t2 – 15t +40
∴ Ss= (5)2 - (6 x 52) - (15 x 5 )+ 40
∴ Ss= -60 m.
At t = 0 sec; displacement will be
S0 = t2 - 6t2 – 15t + 40
∴ S0 = 40 m.
Question 2 ) the motion of particle is defined by x = t3 - 6t2 - 36 t - 40 in meter Determine (1) when the velocity is zero. (2) velocity , acceleration & total distance travelled when x = 0 .
→given,
X=t3 - 6t2 -36t- 40
Differentiating w.r.t t we get
∴ v =dx /dt =3t2 – 12t - 36
Again differentiating w.r.t. ‘t’
∴a= dv/dt =d2x/ d2t= 6t – 12
(1) When the velocity is zero.
For, v= 0
V= 3t2-12t - 36
0 = 3t2 - 12t - 36
Solving above equation, we get
[t = 6 sec.]
( 2) velocity , acceleration & total distance travelled at x=0 .
For x = 0,
x =t3 - 6t2 – 36t – 40
O =t3- 6t2 – 36t -40
Solving above equation, we get
T = 10sec.
∴velocity (for t =0)
V10 = 3t2 – 12 t – 36
= (3x102) - (12x10)-36
V10 = 144m/sec
∴acceleration (for t = 10)
A= 6t – 12
= (6x10)-12
A = 48m/sec2
Distance travelled =|x10 – x6| + |x6 –x0|
∴ x10 = 103 – ( 6 x 102)- ( 36 x 10 ) – 40
= 1000 – 600 – 360- 40
X10 = 0m
∴ x6 = 63 – (6x62) –(36x6) – 40
X6 = -256m
∴ x0 = 03 – 6 x 02 -36x 0 -40
X0 =-40 m
∴distance travelled = |0 – (-256)| +|-256 –(-40)|
=256 + 216
= 472m
Distance travelled = |ss- s0
= |-60-40|
=100m
(c) Acceleration at t = 5 sec
A = 6t-12
= (6 x 5) -12
A = 18 m/s2
(d) Distance travelled from 4 to 6 sec
As at t= 5sec, v = 0
Thus,
Distance travelled = distance travelled from 4 to 5 sec + distance travelled from 5 to 6 sec.
= |s5 – s4|+ |s6 – s5|
∴at t = 6,
s6 = 63 - (6 x 62) – (15 x 6) + 40
=-50m
At t =4,
s4 = 43 - (6 x 42) – (15 x 4) + 40
= -52m
Distance travelled = | -60 – (-52)|+|-50 – (-60)|
= 8+10
= 18m
Key takeaways:
1) Velocity of a body is
V = (ds/dt)
2) Acceleration
A =dv / dt
Acceleration due to gravity is the acceleration that is gained by an object due to the gravitational force. Its SI unit is ms². It has a magnitude as well as direction. Thus it is a vector quantity.
We represent acceleration due to gravity by the symbol g. Its standard value on the surface of the earth at sea level is 9.8 ms². Its computation formula is based on Newton’s Second Law of Motion and Newton’s Law of Universal Gravitation.
Near the surface of Earth, the acceleration due to gravity is approximately constant. But, at large distances from the Earth, or around other planets or moons, it is varying. The acceleration due to gravity depends on the terms as the following:
Mass of the body,
Distance from the center of mass,
Constant G i.e. Universal gravitational constant
g = GM/r2
Where,
g= Acceleration due to gravity (unitsms−1)(unitsms−1)
G= The universal gravitational constant =6.673×10−11Nm2Kg2
m=Mass of a very large body like Earth.
r=The distance from the center of mass of the large body
Acceleration due to gravity varies with the height from the surface of the earth. Its computation can be done as follows:
gh =g(1+hR)−2gh=g(1+hR)−2
Where,
g=Acceleration due to gravity at the surface.
gh =Acceleration due to gravity at the height h.
R=The radius of the earth.
h=Height from the earth’s surface.
It is clear that the value of g decreases with an increase in height of an object. Hence the value of g becomes zero at infinite distance from the earth.
Example: The radius of the moon is 1.74×106m1.74×106m. The mass of the moon is taken as 7.35×10227.35×1022 kg. Find out the acceleration due to gravity on the surface of the moon.
Solution: On the surface of the moon, the distance to the center of mass will be the same as the radius.
Thus, r = 1.74×106m1.74×106m.
Mass of the object i.e. moon,
m = 7.35×10227.35×1022 kg
As we know that, universal gravitational constant G = 6.673×10−116.673×10−11
The acceleration due to gravity on the surface of the moon can be computed by using the formula as below:
g = GM / r2
Substituting the values
g = 6.673×10−11×7.35×1022 / (1.74×106)2
g = 1.620ms−2
Hence, value of the acceleration due to gravity is 1.620ms−2
Newton’s law of motion
|
The first law of motion implies that things cannot start, stop, or change direction all by themselves. It requires some force from the outside to cause such a change. This property of massive bodies to resist changes in their state of motion is called inertia. Newton’s first law is also known as the law of inertia.
Newton’s 1st law states that a body at rest or uniform motion will continue to be at rest or uniform motion until and unless a net external force acts on it.
The second law of motion describes what happens to the massive body when acted upon by an external force. The 2nd law of motion states that the force acting on the body is equal to the product of its mass and acceleration.
Newton’s 2nd law states that the acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.
Newton’s second law describes precisely how much an object will accelerate for a given net force.
Mathematically, we express the second law of motion as follows:
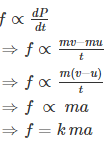
In the equation, k is the constant of proportionality, and it is equal to 1 when the values are taken in SI unit. Hence, the final expression will be,
F=ma
|
The third law of motion describes what happens to the body when it exerts a force on another body.
The Newton’s 3rd law states that for every action there is an equal and opposite reaction.
When two bodies interact, they apply force on each other that are equal in magnitude and opposite in direction. To understand Newton’s third law with the help of an example, let us consider a book resting on a table. The book applies a downward force equal to its weight on the table. According to the third law of motion, the table applies an equal and opposite force on the book. This force occurs because the book slightly deforms the table; as a result, the table pushes back on the book like a coiled spring.
Key takeaways:
1) Constant G i.e. Universal gravitational constant = g = GM/r2
2) Newton’s 2nd law states that the acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.
Motion is one of the most common phenomena we come across in our daily lives. For example, a moving car, a kid running on the road or a fly moving in the air are all said to be in motion. So, in general terms, a body is said to be in motion if it changes its position with respect to a reference point and time. Depending upon the path taken by the particle the motion can be of different types like projectile motion, rectilinear motion, rotational motion, etc. For now, we will only focus on the rectilinear motion which is also known as linear motion.
When we require only one co-ordinate axis along with time to describe the motion of a particle it is said to be in linear motion or rectilinear motion. Some examples of linear motion are a parade of soldiers, a train moving along a straight line, and many more.
So now that we have learned about linear motion we will discuss two terms related to change in position. These are called – ‘Distance’ and ‘Displacement’.
Distance is defined as, The total path length covered during a journey While displacement is defined as, The path length from final position of the particle to the origin O. Consider the following figure:
|
Fig 7
We have an origin O, measurements to the right of O are taken as a positive while to the left are taken as negative. Suppose a person who starts from origin O reaches point A,
Distance = OA
Displacement = OA
Now he turns and reaches point B,
Distance = OA + AB
Displacement = -OB
As we can see, displacement is negative since it is measured to the left of the origin. From the above example, we can infer that distance is always positive while displacement can either be positive or negative.
These terms are used to describe the rate of change of position. Speed is the rate of change of distance while velocity is the rate of change of displacement. Comparing from above as distance can never be negative so the speed is never negative while velocity can be both positive and negative. In mathematical terms, these are defined as follows:
Speed = Distance Travelled Time Taken
Velocity = (Final position–Initial position) / Time Taken
Examples for Rectilinear Motion
Following are the rectilinear motion examples:
- The use of elevators in public places is an example of rectilinear motion.
- Gravitational forces acting on objects resulting in free fall is an example of rectilinear motion.
- Kids sliding down from a slide are a rectilinear motion.
- The motion of planes in the sky is a rectilinear motion.
Key takeaways:
1) Speed = Distance Travelled Time Taken
2) Velocity = (Final position–Initial position) Time Taken
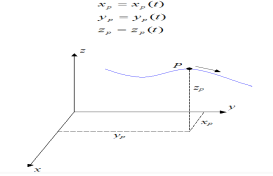
Curvilinear motion is defined as motion that occurs when a particle travels along a curved path. The curved path can be in two dimensions (in a plane), or in three dimensions. This type of motion is more complex than rectilinear (straight-line) motion.
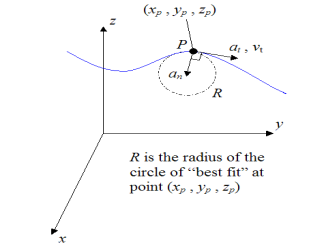
Three-dimensional curvilinear motion describes the most general case of motion for a particle.To find the velocity and acceleration of a particle experiencing curvilinear motion one only needs to know the position of the particle as a function of time.
Let’s say we are given the position of a particle P in three-dimensional Cartesian (x,y,z) coordinates, with respect to time, where
|
Fig 8
The acceleration of the particle P is given by
As you can see, if we know the position of a particle as a function of time, it is a fairly simple exercise to find the velocity and acceleration. You simply take the first derivative to find the velocity and the second derivative to find the acceleration.
Note that the direction of velocity of the particle P is always tangent to the curve (i.e. the path travelled, denoted by the blue curve in the figure above). But the direction of acceleration is generally not tangent to the curve.
Fig 9
Fig 10
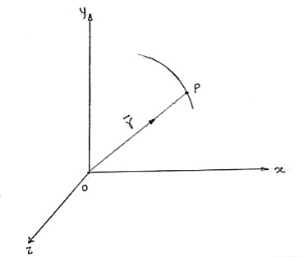
b. Let ‘P’ is the position of particle at any time instant ‘t’. c. Let we have fixed reference axes x,y,z as shown. d. The line ‘OP’ represents the position of particle &it is known as position vector of particle at time‘t’.
e.
2. Displacement and distance:
Fig 11
Position of particle at point P is given by vector
∆ ∆
3. Velocity : In above figure ∆ ∆r = displacement of particle (magnitude). ∆t = time taken by particle to move from P to P’. Avg. velocity =
Instantaneous velocity at P will be, V = V = Speed =
4. Acceleration: - Avg. acceleration a = For very small interval of time ∆t → 0 Thus a = The acceleration at point P = (Instantaneous acceleration) Key takeaways: 1) Avg. velocity = 2) Speed = 3) The magnitude of the velocity of particle P is given by
4) The magnitude of the acceleration of particle P is given by
|
When a particle is freely thrown in the air along any direction other than vertical it follows it follows the parabolic path .The motion of a particle along this parabolic path is called as projectile motion.
i.e. when we project the particle in the space, its motion is a combination of horizontal & vertical motion. This motion is called as projectile Motion.
Wind Resistance, curvature & rotation of the earth affects the actual path.
But these parameters are neglected.
- The path Traced by projectile is called as Trajectory.”
- The motion of projectile in Horizontal direction is uniform motion.
- Ax = Horizontal component of acceleration = 0
- The acceleration in vertical direction is affected by gravity. Thus motion in y direction is considered as “Motion under gravity.”
:.  y = -
y = -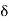
Basic Terms involved in the projectile Motion
1) Time of flight :- (t)
- The time by the projectile to move from point of projection to the point of target is called as “Time of flight.”
- It is the total time during which projectile remains in space.
2) “Horizontal Range” :- (R)
It is Horizontal distance from point of projection the point of target. OR It is Horizontal distance bet/n point of projection & point of landing.
3) Maximum Height :- (H) or (Hmax)
It is the vertical distance bet/n the point of projection and the point © where the vertical component of velocity is zero.
4) Angle of projection :( 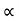 )
)
- It is the angle made by velocity with the Horizontal.
- If velocity is directed up the horizontal, then it is called as angle of elevation.
-If the velocity is directed down the Horizontal, then it is called as angle of depression.
5) Trajectory:-
It is the path traced by a projectile during its motion. It is parabolic in nature.
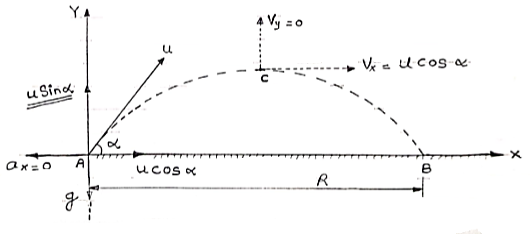
Projectile on Horizontal plane
Consider a projectile projected from point A with
u= initial velocity of projection &
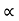 = Angle of projection.
= Angle of projection.
Let t = total time of flight.
Thus projectile will land at point b after time‘t’ Both point A& B are Qn H.P
Diagram
|
Fig 12
As the air resistance is neglected, the motion in X-direction is uniform motion & y dirn motion is Motion under Gravity”.
a) Time of flight (t)
t 2 u sin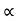 /
/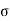
b) Horizontal Range (R)
R = u2. Sin2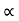 /
/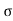
c) Maximum Range (R max)
For maximum Range angle of projection must be 45
R max = u2/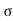
d) Maximum Height
H = u2. Sin2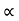 /2
/2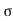
Derivation of path Equation
[Eqn of Trajectory]
Vx= u cos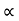 = constant.
= constant.
Vy = u sin 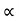
|
Fig 13
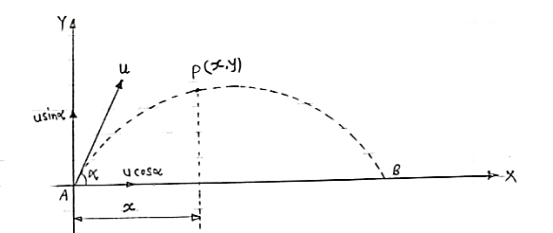
Consider a particle projected from A with initial velocity ‘u’ & angle of projection ‘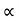 ’.
’.
Let after time‘t’ the particle has reached at point p (x,y).
Consider the motion of projectile in X dirn (VM) :- [ A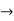 p]
p]
S= velocity * time
X = u cos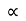 . t1
. t1
:. t1 = X/ u cos 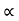 . t1
. t1
:. t1 = X/ u cos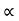 . --------- (1)
. --------- (1)
Consider the motion of projectile in y dir/n (m. U.G) [ A  p]
p]
:. Sy= uyt1- ½  t2
t2
Y = u sin  .t1 – 1/2
.t1 – 1/2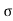 t12
t12
From eqn (1), put the value of time t1
:. y = usin 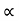 .(x/ucos
.(x/ucos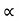 .) – ½
.) – ½ 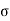 (x/ u-cos
(x/ u-cos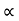 .)2
.)2
:. y = X. tan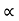 - gx2/u2 cos2
- gx2/u2 cos2 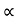
:. y X. tan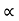 - gX2/2u2 cos2
- gX2/2u2 cos2 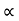
Eqn of Trajectory
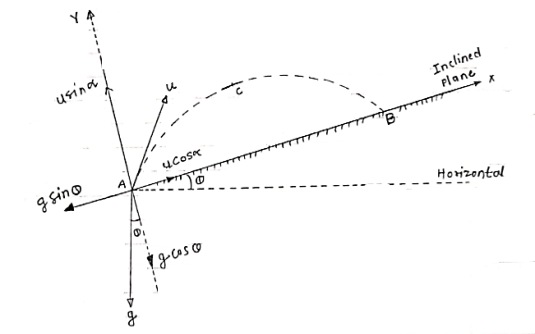
Projectile on Inclined plane
|
Fig 14
Let projectile is projected from point A. let
Now let us select X axis along the inclined plane and y –axis perpendicular to the inclined plane. :. X component of velocity = u cos :. Y - ----- -------------------- u sin Similarly for gravitation Acc/n ‘g’ X component = g sin y component = g cos
a) Time of flight (t) b) Range along the plane (R) t= 2u. sin
c) Maximum Range (Rmax) d)Max. Height (lar to plane) Rmax = u2/g (1+sin
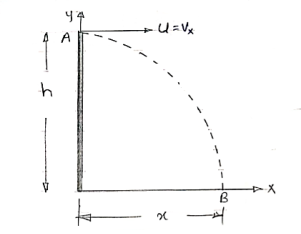
*Special cases of projectile* *projectile projected with Horizontal velocity:-*
X motion Consider motion A
Fig 15 X = u*t Consider Motion (y- motion) From A S = ut + ½ gt2 h= 0 + ½gt2 :. t= :. Horizontal distance, = X = u Y = x tanx - gx2/u2 cos 2 But :. –h = -y = 0 - gx2/2u2 :. h = gx2 / 2u2
*for given values of u, two angle gives us the same Range.
Numerical on projectile Motion. (Projectile on Horizontal plane) Question) A projectile is fired with a velocity of 60 m/s on Horizontal plane. Find its time of flight in the following 3 cases. a) is Range is 4 times the max . Height b) Its max height is 4 times Horizontal range. c) Its max. Height & Horizontal range are equal. Answer)
a) When R = 4 H u2 sin 2 :. u2/g 2sin :. Cos :. Cos Time of flight t= 2usin b) When H = 4R :. u2sin2 :. Sin2 :. sin :. sin :. tan t= 2usin c) When H = R u2sin2 :.Sin2 :. Sin :.tan t= 2usin = 2*60*sin75.96/9.81 t = 11.87 sec.
Range = R -8 :. u2* sin (2*15)/g = (R-8) :. Multiply both sides by 2 :. Cos (2) Range = R +18 u2 sin2 u2/g. sin 90 = R +18 :. 42/g = R =18------------ (2) From (1) & (2) R +18 = 2 R- 16 :. 2R – R = 18+16 = 34. :. 2R = 34m ---- Actual Range to hit the object Actual Range R (42/g) sin 2 34 = (R +18) sin2 34 = (34+18) sin2 34 = 52 sin 2 :. Sin 2
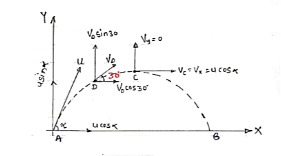
Question) A shot is fired from the gun .After 2 sec. the velocity of shot is inclined at 30 Answer) Let, u = initial velocity & Let after one more second, shot attains max , Height at point C as shown in figure.
At point D, V0 makes 30 :. X component of velocity at ‘D’ = VD cos 30 But we know that velocity in X dirn is constant (U.m.) :. VD cos 30 = u cos :. 0.87 VD cos 30 = ucos Consider y-Motion from A to D. By substituting the value of VD in eqn (1) & (2) This is Motion under gravity 0.87 VD = u cos :. V = u +at : U cos :. VD sin 30 = usin :. 0.5 VD = usin :.0.5 VD = usin Now Consider y motion from D-c ,(M.V.G) Also, usin V = u +at = 0.5*19.62+ 19.62 0 = VD sin30 – g*tDC =u sin 0= 0.5 VD – 9.81 *1 from eqn (3) & (4) :. 0.5 VD = 9.81 usin :. VD = 19.62 m/s : tan :.
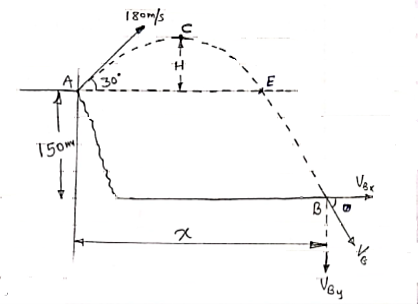
Question) A projectile is fired from the edge of 150 m cliff an initial velocity of 180 m/s at 30
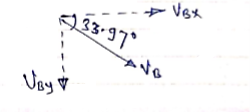
Answer) Let X= Horizontal distance between A& B A= point of projection B= point of striking. We can see from the fig that A& B are not on same level. TAB = time Req = tAB Consider the Horizontal motion from A to B (U.M) :. Distance = velocity * time X = 180 cos 30 * tAB X= 155.88 tAB ------ (1) Consider vertical motion from A to C, H+ 150+ ½*9.81* t2CB : V = u + at 412.84+ 150 = 4.905 +tCB Vcy = 180sin30- g*tAC : t2CB = 562.84/4.905 :0 = 90 – 9.81 tAC :. t2CB = 114.748 :tAC = 90/9.81 :. tCB = 10.71 sec :tAC = 9.17 sec. tAB = 9.17 + 10.71 = 19.88 sec H = u2sinsin2 X = 3098.9 m H = 412.84 m. :. Now using. Eqn of motion S = ut + ½ gt2 Horizontal distance from the to the point of striking is X = 3098.9 m Time req. from A to B = tAB = 19.88 sec. Greatest Height Reached by projectile above the ground is Hmax H + 150 = 412.84+150 Hmax = 562.84 m Now, Consider that VB = striking velocity. & Ø = angle made by striking velocity with Horizontal. As shown. Let VBX = X component of VB. VBy = y component of VB. But we know that, in X dirn, motion is uniform. Thus VBX = u cos To find VBy consider the motion from C to B. :. V = u + gt VBy = Vcy + g * tCB VBy = 0 + 9.81 * 10.71 VBy = 105.06 m/sec :. VB =
VB = 187.9 m/sec Tanø = VBy/ VBX = 105.06/155.88 :. Ø = 33.97 Key points 1) Time of flight (t) t 2 u sin 2) Horizontal Range (R) R = u2. Sin2 3) Maximum Range (R max) For maximum Range angle of projection must be 45 R max = u2/ 4) Maximum Height H = u2. Sin2
|
Whenever a body is released from a height, it travels vertically downward towards the surface of earth. This is due to the force of gravitational attraction exerted on body by the earth.
The acceleration produced by this force is called acceleration due to gravity and is denoted by ‘g’. Value of ‘g’ on the surface of earth is taken to the 9.8 m/s2 and it is same for all the bodies.
It means all bodies (whether an iron ball or a piece of paper), when dropped (u=0) from same height should fall with same rapidity and should take same time to reach the earth. Our daily observation is contrary to this concept. We find that iron ball falls more rapidly than piece of paper. This is due to the presence of air which offers different resistance to them. In the absence of air both would have taken same time to reach the surface of earth.
When a body is dropped from some height (earth's radius = 6400 km), it falls freely under gravity with constant acceleration g (= 9.8 m/s2) provided the air resistance is negligible small. The same set of three equations of kinematics (where the acceleration 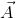 remains constant) are used in solving such motion. Here, we replace
remains constant) are used in solving such motion. Here, we replace 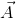 by
by 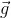 and choose the direction of y-axis conveniently. When the y-axis is chosen positive along vertically downward direction, we take
and choose the direction of y-axis conveniently. When the y-axis is chosen positive along vertically downward direction, we take 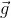 as positive and use the equation as
as positive and use the equation as
v = u + gt, v2 = u2 + 2gh,
and h = ut + 1/2gt2
Where h is the displacement of the body and u is initial velocity of projection in the vertically downward direction. However, if an object is projected vertically upward with initial velocity u, we can take y-axis positive in the vertically upward direction and the set of equations reduces to
v = u - gt, v2 = u2 - 2gh, and h = ut - 1/2gt2
In order to avoid confusion in selecting 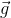 as positive or negative, it is advisable to take the y-axis as positive along vertically upward direction and point of projection as the origin. We can now write the set of three equations in the vector form:
as positive or negative, it is advisable to take the y-axis as positive along vertically upward direction and point of projection as the origin. We can now write the set of three equations in the vector form:
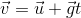 ,
,
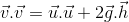
And
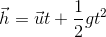
Where h is the displacement of the body.
The motion of a particle is described by the equation u = at. The distance travelled by the particle in the first 4 second.
Because for the motion u = at. So acceleration is uniform which is equal to a.
Therefore, Distance travelled = 1/2[(a)(4)2] = 8a
A body moving with a constant retardation in straight line travels 5.7 m and 3.9 m in the 6th and 9th second, respectively. When will the body come momentarily to rest?
A body moving with initial velocity u and acceleration a, traverses distance Sn in nthsecond of its motion.
Sn = u + (1/2) x (2n - 1) a
=> 5.7= u + (1/2) x (2 x 6 – 1) a
And 3.9 = u + (1/2)(2 x 9 - 1)a
or,
3.9 = u + (17/2) a
Solving eqns. (1) and (2) we get,
u = 9 m/s and a = -0.6 m/s2.
If the body stops moving after t seconds, then from the relation v=u+at
Thus, 0 = 9 + (-0.6)t
or
t = (9/0.6)s = 15s
A stone, thrown up is caught by the thrower after 6s. How high did it go and where was it 4 s after start? g = 9.8 m/s2
Time to go up and come back = 6s
Thus, time to reach the highest point = (6/2) s = 3s
From point of projection to the highest point we have
u =?, v = 0, a = -9.8 m/s2, t = 3s
Using the relation, v = u + at
0= u – 9.8 3
3
Thus, u = 29.4 m/s2
Maximum height, H = u2/2g
= [(29.4)2/2(9.8)]
m =44.1 m
Let h = height of stone at 4s.
Using the relation, S = ut + ½ at2
So, h = [(29.4) x (4)-1/2 (9.8) (4)2]m
= [117.6-78.4] m = 39.2 m
From the above observation we conclude that, the height would be 39.2 m.
Kinetics
The principle of virtual work states that the sum of the incremental virtual works done by all external forces Fi acting in conjunction with virtual displacements _si of the point on which the associated force is acting is zero:
|
This technique is useful for solving statics problems, with static forces of constraint. A static force of constraint is one that does no work on the system of interest, but merely holds a certain part of the system in place. In a statics problem there are no accelerations. We can extend the principle of virtual work to dynamics problems, i.e., ones in which real motions and accelerations occur, by introducing the concept of inertial forces. For each parcel of matter in the system with mass m, Newton’s second law states that
F=ma:
We can make this dynamics problem look like a statics problem by defining an inertial force
F* = - ma
And rewriting equation (1.1.2) as
F total = F + F* = 0
D’Alembert’s principle is just the principle of virtual work with the inertial forces added to the list of forces that do work:
|
|
Fig 16
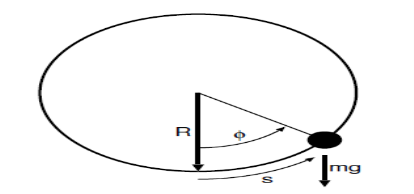
Figure 1.1.1: Sketch of bead of mass m sliding frictionless on a vertical hoop of radius R under the influence of gravity.
Mass falling under gravity
A trivial example would be a mass m falling under the effect of a constant gravitational field g. With z positive upward, the force on the mass is -mg and the work due to this force under vertical displacement 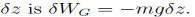
The inertial force is 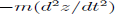 and the work is
and the work is 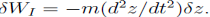
Setting the sum of the two to zero gives us
|
From which we infer the expected result
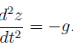
D’Alembert’s principle offers no advantages over normal procedures in this case. However, it becomes more economical in problems with constraints.
Bead on frictionless vertical hoop
Figure 1.1.1 illustrates the slightly more interesting problem of a bead sliding frictionless around a vertically oriented hoop of wire. Here the force of gravity is not in the direction of motion. The component of gravity normal to the hoop does no work on the bead. Nor does the force of the hoop on the bead that constrains the bead to move in a circle. The work on the bead due to gravity for a small displacement 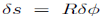 along the wire
along the wire 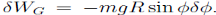
The acceleration of the bead also has two components, a radial component
 Where the tangential velocity is
Where the tangential velocity is  and a tangential component
and a tangential component 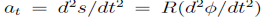
The radial component of the inertial force mv2=R does no work. However, the tangential component 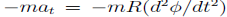
Does:
|
D’Alembert’s principle thus gives us
|
|
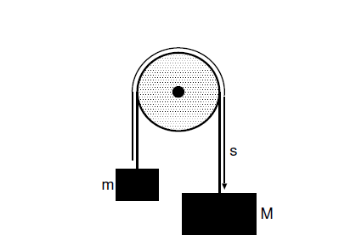
Fig 18 sketch of Atwood’s machine
from which we get the governing equation
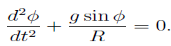
(This could equally well have been expressed in terms of s rather than _.)
References:
- Andy Ruina and Rudra Pratap , Introduction to Statics and Dynamics, Oxford University Press.
- Reddy Vijaykumar K. and K. Suresh Kumar, Singer's Engineering Mechanics.
- F. P. Beer and E. R. Johnston, Mechanics for Engineers, Statics and Dynamics,
- McGraw Hill. Irving H. Shames, Engineering Mechanics, Prentice Hall.