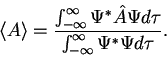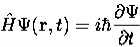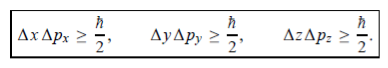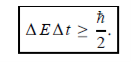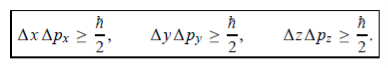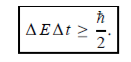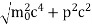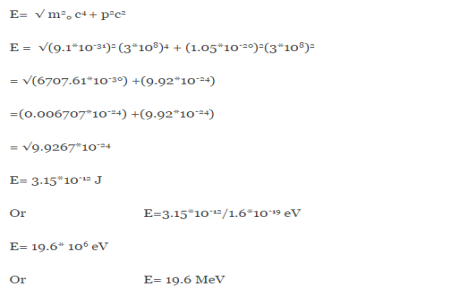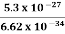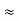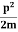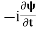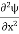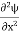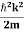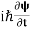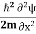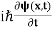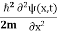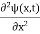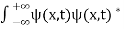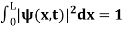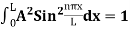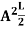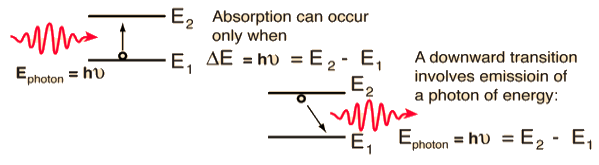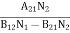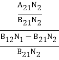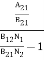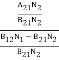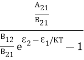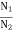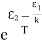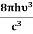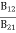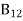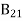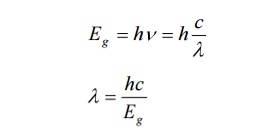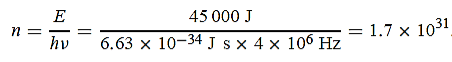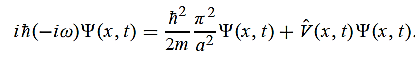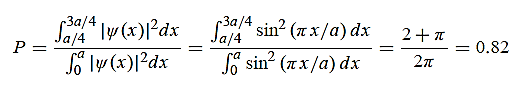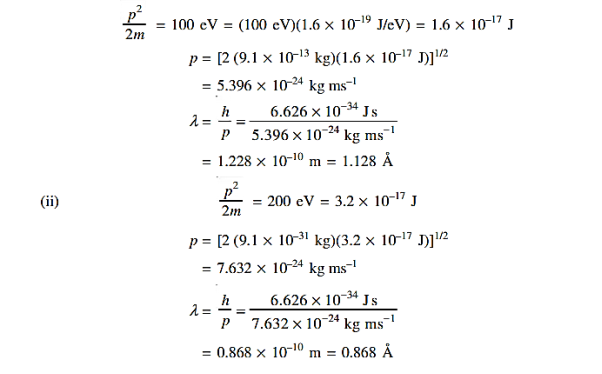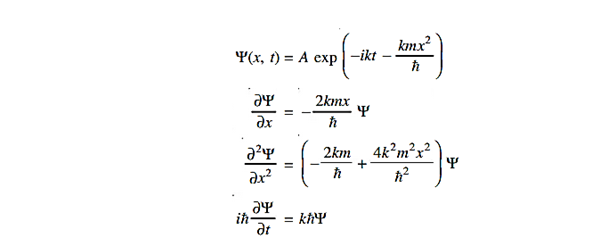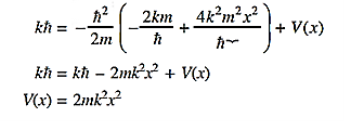UNIT- 4
QUANTUM MECHANICS AND LASERS
If the systems of quantum theory are thought of as elementary information carriers in the first place, rather than elementary constituents of matter, and their connections are logical connections within a given algorithm, rather than space-time relations, then we need to find the origin of mechanical concepts that characterise quantum mechanics as a theory of physical systems. To this end, we will illustrate how physical laws can be viewed as algorithms for the update of memory registers that make a physical system.
The term "quantum mechanics" was first coined by Max Born in 1924.
Quantum mechanics is the branch of physics dealing with the behaviour of matter and light on the atomic and subatomic level. . It attempts to describe and account for the properties of molecules and atoms and their constituents—electrons, protons, neutrons, and other more particles such as quarks and gluons.
At the scale of atoms and electrons, many of the equations of classical mechanics which describe how things move at everyday sizes and speeds cease to be useful.
In classical mechanics objects exist in a specific place at a specific time. However, in quantum mechanics, objects instead exist in a haze of probability they have a certain chance of being at point A another chance of being at point B and so on. It results some very strange conclusions about the physical world.
At the turn of the twentieth century, however, classical physics not able to explain some of the phenomena.
Relativistic domain: Einstein’s 1905 theory of relativity showed that the validity of
Newtonian mechanics ceases at very high speeds i.e. Speeds comparable to that of light.
Microscopic domain: As soon as new experimental techniques were developed to the point of searching atomic and subatomic structures, it turned out that classical physics fails miserably in providing the proper explanation for several newly discovered phenomena. It thus became evident that the validity of classical physics ceases at the microscopic level and that new concept had needed to describe.
The classical physics fails to explain several microscopic phenomena such as blackbody radiation, the photoelectric effect, atomic stability and atomic spectroscopy
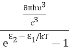
In 1900 Max Planck introduced the concept of the quantum of energy. He successfully explained the phenomenon of blackbody radiation .He introduced the concept of discrete or quantized Energy. He also explained that the energy exchange between an electromagnetic wave of frequency ν and matter occurs only in integer multiples of hν, which he called the energy of a quantum, where h is called Planck’s constant.
In 1905 Einstein provided a powerful consolidation to Planck’s quantum concept. In trying to understand the photoelectric effect, Einstein recognized that Planck’s idea of the quantization of the electromagnetic waves must be valid for light as well.
So, He Gave light itself is made of discrete bits of energy or tiny particles, called photons, each of energy hν, ν being the frequency of the light. The introduction of the photon concept enabled Einstein to give an elegantly accurate explanation to the photoelectric problem.
Bohr introduced in 1913 his model of the hydrogen atom. He explained that atoms can be found only in discrete states of energy and the emission or absorption of radiation by atoms, takes place only in discrete amounts of hν.This successfully explained to problems such as atomic stability and atomic spectroscopy
Then in 1923 Compton made an important discovery of scattering X-rays with electrons, he confirmed that the X-ray photons behave like particles with momenta hν/c, ν is the frequency of the X-rays.
Planck, Einstein, Bohr, and Compton gave the theoretical and experimental confirmation for the particle aspect of wave that means that waves exhibit particle behaviour at the microscopic scale.
Some of the most prominent scientists to subsequently contribute in the mid-1920s to what is now called the "new quantum mechanics" or "new physics" were Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, and Erwin Schrödinger.
Through a century of experimentation and applied science, quantum mechanical theory has proven to be very successful and practical.
Historically, there were two independent formulations of quantum mechanics. The first formulation, called matrix mechanics, was developed by Heisenberg (1925) to describe atomic structure starting from the observed spectral lines.
The second formulation, called wave mechanics, was due to Schrödinger (1926).
It is a generalization of the de Broglie postulate. This method describes the dynamics of microscopic matter by means of a wave equation, called the Schrodinger equation.
Dirac derived in 1928 an equation which describes the motion of electrons. This equation, known as Dirac’s equation, predicted the existence of an antiparticle.
In short, quantum mechanics is the founding basis of all modern physics: solid state, molecular, atomic, nuclear, and particle physics, optics, thermodynamics, statistical mechanics, and so on. Not only that, it is also considered to be the foundation of chemistry and biology.
Postulates of Quantum Mechanics
- The state of a quantum mechanical system is completely specified by a function (r,t) that depends on the coordinates of the particle(s) and on time. This function, called the wave function or state function, has the important property that *(r,t) (r,t)d
is the probability that the particle lies in the volume element d
located at r at time t
The wave function must satisfy certain mathematical conditions because of this probabilistic interpretation. For the case of a single particle, the probability of finding it somewhere is 1, so that we have the normalization condition
|
It is customary to also normalize many-particle wavefunctions to 1. The wave function must also be single-valued, continuous, and finite.
2. To every observable in classical mechanics, there corresponds a linear, Hermitian operator in quantum mechanics. For example, in coordinate space, the momentum operator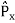 
corresponding to momentum px in the 
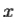direction for a single particle is -iℏ
.
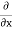3. The average value of the observable corresponding to operator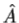 
is given by
|
4. The wavefunction evolves in time according to the time-dependent Schrödinger equation
|
5. In any measurement of the observable associated with operator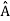 
, the only values that will ever be observed are the eigenvalues a which satisfy 
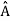= a. Although measurements must always yield an eigenvalue, the state does not originally have to be in an eigen state of 
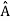. An arbitrary state can be expanded in the complete set of eigenvectors of 
(
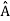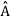= a) as, = 
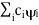where the sum can run to infinity in principle. The probability of observing eigenvalue ai is given by ci*ci.
6. The total wavefunction must be antisymmetric with respect to the interchange of all coordinates of one fermion with those of another. Electronic spin must be included in this set of coordinates. The Pauli Exclusion Principle is a direct result of this antisymmetry principle.
Key Takeaways
- The term "quantum mechanics" was first coined by Max Born in 1924.
- Quantum mechanics is the branch of physics dealing with the behaviour of matter and light on the atomic and subatomic level. .
- It attempts to describe and account for the properties of molecules and atoms and their constituents—electrons, protons, neutrons, and other more particles such as quarks and gluons.
- The introduction of the photon concept enabled Einstein to give an elegantly accurate explanation to the photoelectric problem.
- The state of a quantum mechanical system is completely specified by a function.
Einstein Equation
Quantum mechanics began with two deceptively simple formulas
E=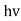
and p= h/λ
These are the Einstein and de Broglie relations, respectively.
De Broglie Hypothesis of Matter Waves
As we know in the Photoelectric Effect, the Compton Effect, and the pair production effect—radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal.
In 1923, the French physicist Louis Victor de Broglie (1892-1987) put forward the bold hypothesis that moving particles of matter should display wave-like properties under suitable conditions.
All material particles should also display dual wave–particlebehaviour. That is, the wave–particle duality present in light must also occur in matter.
So, starting from the momentum of a photon p = hν/c = h/λ.
We can generalize this relation to any material particle with nonzero rest mass. Each material particle of momentum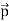 
behaves as a group of waves(matter waves) whose wavelength λand wave vector 
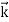are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed.
λ= 
=
…….(1) 
= 
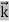…….(2)
Where ℏ = h/2π. The expression known as the deBroglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle.The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation.
λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment.
However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c.
Therefore
= 
= λ
Matter waves: According to De-Broglie, a wave is associated with each moving particle which is called matter waves.
That is, the wave–particle duality present in light must also occur in matter. So, starting from the momentum of a photon p= hν /c =h/λ, we can generalize this relation to any material particle with nonzero rest mass: each material particle of momentum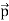
behaves as a group of waves (matter waves) whose wavelength λand wave vector
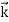are governed by the speed and mass of the particle.
λ = 
= 
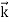Wave has wavelength λ here h is Planck's constant and p is the momentum of the moving particle.
We have seen that microscopic particles, such as electrons, display wave behaviour. What about macroscopic objects? Do they also display wave features? They surely do. Although macroscopic material particles display wave properties, the corresponding wavelengths are too small to detect; being very massive, macroscopic objects have extremely small wavelengths.
At the microscopic level, however, the waves associated with material particles are of the same size or exceed the size of the system. Microscopic particles therefore exhibit clearly noticeable wave-like aspects.
The general rule is: whenever the de Broglie wavelength of an object is in the range of, or exceeds, its size, the wave nature of the object is detectable and hence cannot be neglected.
But if its de Broglie wavelength is much too small compared to its size, the wave behaviour of this object is undetectable.
For a quantitative illustration of this general rule, let us calculate in the following example the wavelengths corresponding to two particles, one microscopic (electron) and the other macroscopic (ball).
Key Takeaways
- Quantum mechanics began with two deceptively simple formula E=
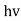and p= h/λ. These are the Einstein and de Broglie relations respectively. - De Broglie (1892-1987) put forward the bold hypothesis that moving particles of matter should display wave-like properties under suitable conditions.
- All material particles should also display dual wave–particlebehaviour. That is, the wave–particle duality present in light must also occur in matter.
- The expressions known as the de Broglie relation
λ = 
=
= 
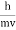
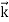Where ℏ = h/2π. The expression known as the de Broglie relation
According to classical physics, given the initial conditions and the forces acting on a system, the future behaviour (unique path) of this physical system can be determined exactly. That is, if the initial coordinates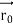
, velocity 
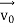, and all the forces acting on the particle are known, the position 
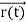, and velocity 
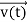are uniquely determined by means of Newton’s second law. So by Classical physicsit can be easily derived.
Does this hold for the microphysical world?
Since a particle is represented within the context of quantum mechanics by means of a wave function corresponding to the particle’s wave, and since wave functions cannot be localized, then a microscopic particle is somewhat spread over space and, unlike classical particles, cannot be localized in space. In addition, we have seen in the double-slit experiment that it is impossible to determine the slit that the electron went through without disturbing it. The classical concepts of exact position, exact momentum, and unique path of a particle therefore make no sense at the microscopic scale. This is the essence of Heisenberg’s uncertainty principle.
In its original form, Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x =ℏ/(2∆px). The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:
|
This principle indicates that, although it is possible to measure the momentum or position of a particle accurately, it is not possible to measure these two observables simultaneously to an arbitrary accuracy. That is, we cannot localize a microscopic particle without giving to it a rather large momentum.
We cannot measure the position without disturbing it; there is no way to carry out such a measurement passively as it is bound to change the momentum.
To understand this, consider measuring the position of a macroscopic object (you can consider a car) and the position of a microscopic system (you can consider an electron in an atom). On the one hand, to locate the position of a macroscopic object, you need simply to observe it; the light that strikes it and gets reflected to the detector (your eyes or a measuring device) can in no measurable way affect the motion of the object.
On the other hand, to measure the position of an electron in an atom, you must use radiation of very short wavelength (the size of the atom). The energy of this radiation is high enough to change tremendously the momentum of the electron; the mere observation of the electron affects its motion so much that it can knock it entirely out of its orbit.
It is therefore impossible to determine the position and the momentum simultaneously to arbitrary accuracy. If a particle were localized, its wave function would become zero everywhere else and its wave would then have a very short wavelength. According to de Broglie’s relation p =ℏ /λ,
Time Energy Uncertainty Relation
The momentum of this particle will be rather high. Formally, this means that if a particle is accurately localized (i.e., ∆x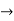 
0), there will be total uncertainty about its momentum (i.e., ∆px
∞).
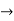Since all quantum phenomena are described by waves, we have no choice but to accept limits on our ability to measure simultaneously any two complementary variables.
Heisenberg’s uncertainty principle can be generalized to any pair of complementary, or canonically conjugate, dynamical variables: it is impossible to devise an experiment that can measure simultaneously two complementary variables to arbitrary accuracy .If this were ever achieved, the theory of quantum mechanics would collapse.
Energy and time, for instance, form a pair of complementary variables. Their simultaneous measurement must obey the time–energy uncertainty relation:
|
This relation states that if we make two measurements of the energy of a system and if these measurements are separated by a time interval ∆t, the measured energies will differ by an amount ∆E which can in no way be smaller than ℏ /∆t. If the time interval between the two measurements is large, the energy difference will be small. This can be attributed to the fact that, when the first measurement is carried out, the system becomes perturbed and it takes it a long time to return to its initial, unperturbed state. This expression is particularly useful in the study of decay processes, for it specifies the relationship between the mean lifetime and the energy width of the excited states.
In contrast to classical physics, quantum mechanicsis a completely in deterministic theory. Asking about the position or momentum of an electron, one cannot get a definite answer; only a probabilisticanswer is possible.
According to the uncertainty principle, if the position of a quantum system is well defined its momentum will be totally undefined.
Key Takeaways
- Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x =ℏ/(2∆px).
- The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:
|
- This principle indicates that, although it is possible to measure the momentum or position of a particle accurately, it is not possible to measure these two observables simultaneously to an arbitrary accuracy. That is, we cannot localize a microscopic particle without giving to it a rather large momentum.
- Energy and time, for instance, form a pair of complementary variables. Their simultaneous measurement must obey the time–energy uncertainty relation:
|
The Heisenberg uncertainty principle based on quantum physics explains a number of facts which could not be explained by classical physics.
- Non-existence of electrons in the nucleus or Non-confinement of electron in the nucleus)
One of the applications is to prove that electron cannot exist inside the nucleus.
But to prove it, let us assume that electrons exist in the nucleus.
As the radius of the nucleus in approximately 10-14m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given by
According to uncertainty principle
∆x ∆p =h/2π
Thus ∆p=h/2π∆x
Or ∆p=6.62 x10-34/2 x 3.14 x 10-14
Or ∆p=1.05 x 10-20 kg m/ sec
If this is p the uncertainty in the momentum of electron then the momentum of electron should be at least of this order that is p=1.05*10-20 kg m/sec.
An electron having this much high momentum must have a velocity comparable to the velocity of light. Thus, its energy should be calculated by the following relativistic formula
E =
|
Therefore, if the electron exists in the nucleus, it should have an energy of the order of 19.6 MeV.
However, it is observed that beta-particles (electrons) ejected from the nucleus during b – decay have energies of approximately 3 Me V, which is quite different from the calculated value of 19.6 MeV.
Another reason that electron cannot exist inside the nucleus is that experimental results show that no electron or particle in the atom possess energy greater than 4 MeV.
Therefore, it is confirmed that electrons do not exist inside the nucleus.
2. Ground State Energy of A Harmonic Oscillator or Calculation of zero point energy
Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly fluctuate in their lowest energy state as described by the Heisenberg uncertainty principle. As well as atoms and molecules, the empty space of the vacuum has these properties. According to quantum field theory, the universe can be thought of not as isolated particles but continuous fluctuating fields: matter fields, whose quanta are fermions and force fields, whose quanta are bosons. All these fields have zero-point energy.
The minimum energy of a system at o k (zero kelvin) is called zero point energy.
Consider a particlewhichis confined to move under the influence of potential of dimensions a. Since the particlemay be present anywhere in these dimensions, so uncertainty in position
∆x = a/2 (half thediameter).
According to uncertainty principle
∆x∆px = ℏ/2
or
Thus ∆px=ℏ /2∆x
∆px=ℏ /2a/2 = ℏ /a
Uncertainty in momentum of particle along x-axis is
∆px=ℏ /a
Assuming the momentum of particle to be at least equal to uncertainty in it, the lowest possible value of K.E. of particle is given by
K.E. =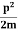
= 
=
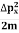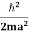
Where mis the mass of the particle.
Energy even at O K is given by the above equation. This minimum energy is called the zero-point energy.
This implies that even at zero kelvin, the particle is never at rest. If it is so, then ∆pX = 0, which is not possible. [It gives ∆x =∞]
3. Existence of proton, neutron and alpha particles within the nucleus.
We know that the rest mass of the protons and neutron is of the order of
1.67x 10-27 kg. Hence, the value of momentum 5.27 x 10-21 kg.m/sec from calculation and also the value of v come out to be 3x 105m/sec.
The corresponding value of kinetic energy of a neutron or a proton is
E=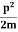
= 
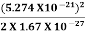=8.33 x 10-15J =
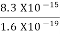eV
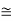52.05 keV
Since the rest mass of the a-particle is nearly four times the proton mass, therefore the alpha particle should have a minimum kinetic energy of one fourth of 52.05 keV, or about 13 keV. Since the energy carried by the protons or neutrons emitted by the nuclei are greater than 52 keV and for a-particle more than 13 keV, these particles can exist in the nuclei.
4. Size of Elementary cell in Phase space
We have studied in our previous class that state of a microsystem is defined by six variables – three are due to position and three due to momentum.
Hence, a system of N particles needs 6 N variables
If ∆ x and ∆px be the uncertainly in position and in momentum measurements then
∆ x ∆ px = 
;
Similarly ∆ y ∆ py = 
,
And ∆ z ∆ pz = 
,
Multiplying these three equations, we get
∆ x ∆ y ∆ z ∆ px ∆ py ∆ pz = (
)3 in the units (J3 S3).
The above product is called the volume of elementary cell in phase space.
So, volume of an elementary cell in phase space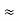 
10-101 units, (for quantum statistics) being 
.
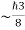5. Accurate limit of frequency of radiation emitted by an atom
Consider the radiation emitted from an excited atom. The energy of this atom will decrease when it emits one or more photons of characteristic frequency.
The average period between excitation of the atom and the release of energy is about 10-8 seconds.
Thus, uncertainly in energy is
∆ E 
Or ∆ E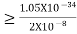 
J
Or ∆ E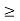 
5.3 x 10-27 J
Frequency of light is uncertain by
∆ν =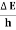 
= 
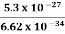Hz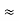 
0.8 x 107 Hz
As a result, the radiation from an excited atom does not have the noted precise frequency new ν - ∆ν and ν + ∆ν.
Key Takeaways
- Electron cannot exist inside the nucleus because experimental results show that no electron or particle in the atom possess energy greater than 4 MeV.
- Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly fluctuate in their lowest energy state as described by the Heisenberg uncertainty principle.
- Heisenberg uncertainty principle proves proton, neutron and alpha particles exists within the nucleus.
- Size of Elementary cell in Phase space is given by Heisenberg uncertainty principle
- Frequency of light is uncertain by
∆ν = |
Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory.
Let us consider a particle of mass m and classically the energy of a particle is the sum of the kinetic and potential energies. We will assume that the potential is a function of only x.
So We have E= K+V =
By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk. Using this equation (1) for the energy will become ℏω =
A wave with frequency ω and wave number k can be written as usual as ψ(x, t) =Aei(kx−ωt) ……….. (3)
the above equation is for one dimensional and for three dimensional we can write it as ψ(r, t) =Aei(k·r−ωt) ……….. (4) But here we will stick to one dimension only.
If we multiply the energy equation in Eq. (2) by ψ, and using(5) and (6) , we obtain ℏ(ωψ) = This is the time-dependent Schrodinger equation. If we put the x and t in above equation then equation (7) takes the form as given below
In 3-D, the x dependence turns into dependence on all three coordinates (x, y, z) and the
|
The term |ψ(x)|2 gives the probability of finding the particle at position x.
Let us again take it as simply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this function ψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7)
But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
= - 
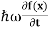+ V(x) f(x) ……….. (9)
We already know that E=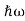
. However ψ(x, t) is general convention to also use the letter ψto denote the spatial part. So we will now replace f(x) with ψ(x)
Eψ = -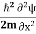 
+ V(x)ψ ……….. (10)
This is called the time-independent Schrodinger equation.
Key Takeaways
Schrodinger wave equation, is the fundamental equation of quantum mechanics
The time-dependent Schrodinger equation is given by
⇒
= - 
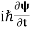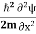+ V(x)ψ
The time-independent Schrodinger equation is given by
Eψ = -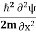 
+ V(x)ψ
Quantum theory and determinism usually do not go together. A natural combination is quantum theory and randomness. Indeed, when in the end of 19th century physics seemed to be close to provide a very good deterministic explanation of all observed phenomena, Lord Kelvin identified “two clouds” on “the beauty and clear-ness of the dynamical theory”. One of this “clouds” was the quantum theory which brought a consensus that there is randomness in physics. Recently we even “certify” randomness using quantum experiments
The quantum theory of the wave function of the Universe is a very successful deterministic theory fully consistent with our experimental evidence. However, it requires accepting that the world we experience is only part of the reality and there are numerous parallel worlds. The existence of parallel worlds allows us to have a clear deterministic and local physical theory.
Wave Function
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as
ψ(x, y, z, t) = a + ib
and its complex conjugate as
ψ*(x, y, z, t) = a – ib.
The product of wave function and its complex conjugate is
ψ(x, y, z, t)ψ*(x, y, z, t) =
(a + ib) (a – ib) = a2 + b2
a2 + b2 is a real quantity.
However, this can represent the probability density of locating the particle at a place in a given instant of time.
The positive square root of ψ(x, y, z, t) ψ*(x, y, z, t) is represented as |ψ(x, y, z, t)|, called the modulus of ψ. The quantity |ψ(x, y, z, t)|2 is called the probability. This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number.
We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one.
For the probability interpretation to make sense, the wave function must satisfy certain conditions.
- The wave function must be single valued at each point.
- The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1.
- ψ must be finite everywhere.
- ψ must be continuous everywhere and
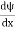must also be continuous everywhere except where V(x) is infinite. - ψ (x) must vanish ψ
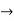0 as x
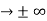. - The wave function should satisfy the normalization condition. Normalization condition of a wave function ψ is mathematical statement of existence of the particle somewhere so that if we sum up all possible values ∑|ψ(xi,t)|2∆xi we must obtain 1. The total probability of finding the particle anywhere must be one. Normalization condition is given as
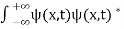dx =1
Only wave function with all these properties can yield physically meaningful result.
Physical significance of wave function
- The wave function ‘Ѱ’ has no physical meaning. it is a complex quantity representing the variation of a matter wave.
- The wave function Ѱ(r,t) describes the position of particle with respect to time .
- It can be considered as ‘probability amplitude’ since it is used to find the location of the particle.
- The square of the wave function gives the probability densityof the particle which is represented by the wave function itself.
- More the value of probability density, more likely to find the particle in that region.
The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation.
All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics.
Statistical Interpretation
It is not possible to measure all properties of a quantum system precisely. Max Born suggested that the wave function was related to the probability that an observable has a specific value.
In any physical wave if ‘A’ is the amplitude of the wave, then the energy density i.e., energy per unit volume is equal to ‘A2’. Similar interpretation can be made in case of mater wave also. In matter wave, if ‘Ψ‘is the wave function of matter waves at any point in space, then the particle density at that point may be taken as proportional to ‘Ψ2’ . Thus Ψ2 is a measure of particle density.
According to Max Born ΨΨ*=Ψ2gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume (dv=dxdydz) is given by
= 
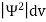Since the particle has to be present somewhere, total probability of finding the particle somewhere is unity i.e., particle is certainly to be found somewhere in space. i.e.
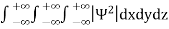=1
Or 
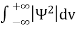=1
This condition is called Normalization condition. A wave function which satisfies this condition is known as normalized wave function.
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
Key Takeaways
- Quantum theory and determinism usually do not go together. A natural combination is quantum theory and randomness.
- The wave function, at a particular time, contains all the information that anybody at that time can have about the particle.
- The wave function itself has no physical interpretation. It is not measurable.
- The square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
- Normalization condition is given as
|
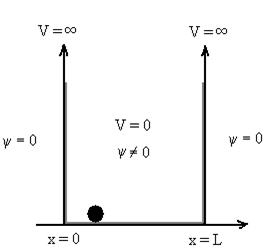
Let us consider a particle of mass ‘m’ in a deep well restricted to move in a one dimension (say x). Let us assume that the particle is free inside the well except during collision with walls from which it rebounds elastically.
The potential function is expressed as
V= 0 for 0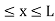
………. (1)
V=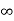 
for x <0, x>L ………. (2)
|
Figure 1: Particle in deep potential well
The probability of finding the particle outside the well is zero (i.e. Ѱ =0)
Inside the well, the Schrödinger wave equation is written as
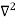ψ +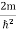
Eψ =0 …………….(2)
Substituting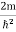 
E = k2 …………….(3)
writing the SWE for 1-D we get
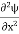+ k2ψ =0 …………….(4)
The general equation of above equation may be expressed as
ψ = Asin (kx + ϕ) …………….(5)
Where A and ϕ are constants to be determined by boundary conditions
Condition I: We have ψ = 0 at x = 0, therefore from equation
0 = A sinϕ
As A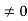 
then sinϕ =0 or ϕ=0 …………….(6)
Condition II:Further ψ = 0 at x = L, and ϕ=0, therefore from equation (5)
0 = Asin kL
As A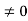 
then sinkL =0 or kL=nπ
k =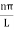 
…………….(7)
where n= 1,2,3,4………
Substituting the value of k from (7) to (3)
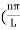)2 = 
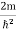E
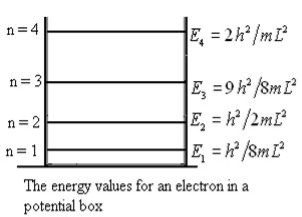
This gives energy of level
En =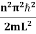
n=1,2,3,4…so on …………….(8)
From equation En is the energy value (Eigen Value) of the particle in a well.
It is clear that the energy values of the particle in well are discrete not continuous.
|
Figure 2: The energy values for an electron in a potential box
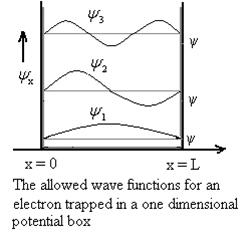
Using (6) and (7) equation (5) becomes, the corresponding wave functions will be
ψ =ψn= Asin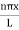
…………….(9)
The probability density
|ψ(x,t)|2 =ψψ*
|ψ(x,t)|2= A2sin2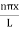
…………….(10)
The probability density is zero at x = 0 and x = L. since the particle is always within the well
A = |
Substituting A in equation (9) we get
ψ =ψ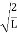n= 
sin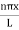
n=1,2,3,4….. …………….(12)
The above equation (12) is normalized wave function or Eigen function belonging to energy value En
|
F
Figure 3: Wave function for Particle
Key Takeaways
- It is assume that the particle is free inside the well except during collision with walls from which it rebounds elastically.
- The probability of finding the particle outside the well is zero (i.e. Ѱ =0)
- The energy values of the particle in well are discrete not continuous and Energy of level is given by
- En =
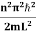n=1,2,3,4…so on - The probability density is given by
|ψ(x,t)|2 = A2sin2
Introduction
LASER stands for “Light Amplification by Stimulated Emission of Radiation” .
L = Light
A = Amplification (by)
S = Stimulated
E = Emission (of)
R = Radiation
Stimulated Absorption:
Let E1 and E2be the energies of the ground and excited states of an atom. Suppose, if a photon of energy hν= E1−E2interacts with an atom present in the ground state, the atom gets excitation from ground state E1 to excited state E2. This process is called stimulated absorption. Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.
Stimulated absorption rate ∝ Number of atoms in the ground state
∝The density of photons Spontaneous emission
|
Figure 4:Interaction of Radiation with Matter
Spontaneous Emission:
Let E1and E2 be the energies of the ground and excited states of an atom. Suppose, if a photon of energy hν= E1−E2interacts with an atom present in the ground state, the atom gets excitation from ground stateE1 to excited state E2. The excited atom does not stay a long time in the excited state. The excited atom gets de-excitation after its lifetime by emitting a photon of energy hν= E1−E2. This process is called spontaneous emission. Also Spontaneous means by its own. Here excited atom comes to the ground state on its own so it is named as spontaneous emission.
The spontaneous emission rate depends upon the number of atoms present in the excited state.
Spontaneous emission ∝rate number of atoms in the excited state
Stimulated Emission:
This phenomenon is responsible for producing laser light. Let E1and E2be the energies of the ground and excited states of an atom. Suppose, if a photon of energy hν= E1−E2 interacts with an atom present in the ground state, the atom gets excitation from ground stateE1 to excited state E2. Let, a photon of energy hν= E1−E2interacts with the excited atom within their lifetime; the atom gets de-excitation to the ground state by emitting another photon. These photons have the same phase and it follows coherence. This phenomenon is called stimulated emission.
Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.
Stimulated emission rate ∝ number of atoms in the excited state
∝Density of photons
Key Takeaways
- LASER stands for “Light Amplification by Stimulated Emission of Radiation”.
- Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.
- The spontaneous emission rate depends upon the number of atoms present in the excited state.
- Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.
EINSTEIN’S COEFFICIENTS
The distribution of atoms in the two energy levels will change by absorption or emission of radiation. Einstein introduced three empirical coefficients to quantify the change of population of the two levels. Let N1be the number of atoms per unit volume with energy E1and N2be the number of atoms per unit volume with energy E2. Let ‘n’ be the number of photons per unit volume at frequency ‘υ’ such that hυ= E1− E2.
Then, the energy density of photons ρ(υ) = nhυ
|
Figure 5: Interaction of photons with atoms
When these photons interact with atoms, both upward (absorption) and downward (emission) transition occurs.
At the equilibrium the upward transitions must be equal downward transitions.
Upward Transition
Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.
We have seen above that
Stimulated absorption rate ∝N1 i.e. Number of atoms in the ground state
∝ρ(υ) i.e. Density of photons spontaneous emission
Stimulated absorption rate= B12N1ρ(υ) ………(1)
Where B12 is the Einstein coefficient of stimulated absorption.
Downward transition
The spontaneous emission rate depends up on the number of atoms present in the excited state.
Spontaneous emission rate∝ N2 i.e. number of atoms in the excited state
Spontaneous emission rate = A21N2 ………(2)
Where A21 is the Einstein coefficient of spontaneous emission.
Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.
Stimulated emission rate ∝N2 i.e. number of atoms in the excited state
∝ρ(υ) i.e. Density of photons
Stimulated emission rate = B21N2ρ(υ) ………(3)
If the system is in equilibrium the upward transitions must be equal downward transitions.
upward transitions = downward transitions B12N1ρ(υ) = A21N2 + B21N2ρ(υ) ………(4) B12N1ρ(υ) - B21N2ρ(υ) = A21N2 (B12N1- B21N2)ρ(υ) = A21N2 ρ(υ) = Divide with B21N2 in numerator and denominator in right side of the above equation, ρ(υ) = ρ(υ) = = We know from Maxwell Boltzmann distribution law
And also from Planck’s law, the radiation density ρ(υ) = Comparing the two equations (7) and (9)
The above relations referred to as Einstein relations. From the above equation for non degenerate energy levels the stimulated emission rate is equal to the stimulated absorption rate at the equilibrium condition.
|
Key Takeaways
- Einstein gave his theory of the interaction of electromagnetic radiation with matter. He proposed that electromagnetic radiation interacts with matter in the following three steps. Stimulated Absorption, Spontaneous Emission and Stimulated Emission.
- Stimulated absorption rate = B12N1ρ(υ)
- Spontaneous emission rate = A21N2
- Stimulated emission rate = B21N2ρ(υ)
- If the system is in equilibrium the upward transitions must be equal downward transitions.
- The Einstein relations is given as
=
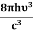and 
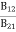=1
Every LASER consists of three basic components. These are –
- Lasing material or active medium.
- External energy source.
- Optical resonator.
|
Figure 6: Components of laser
- Lasing Material or Active Medium
The active medium is excited by the external energy source (pump source) to produce the population inversion. In the gain medium that spontaneous and stimulated emission of photons takes place, leading to the phenomenon of optical gain, or amplification. Semiconductors, organic dyes, gases (He, Ne, CO2, etc), solid materials (YAG, sapphire (ruby) etc.) are usually used as lasing materials and often LASERs are named for the ingredients used as a medium.
- External Energy Source
The excitation source, pump source provides energy which is needed for the population inversion and stimulated emission to the system. Pumping can be done in two ways – electrical discharge method and optical method. Examples of pump sources are electrical discharges, flash lamps, arc lamps, light from another laser, chemical reactions etc.
- Optical Resonator
Resonator guide basically provides the guidance about the simulated emission process. It is induced by high-speed photons. Finally, a laser beam will be generated.
In most of the systems, it consists of two mirrors. One mirror is fully reflective and other is partially reflective. Both the mirrors are set up on optic axis, parallel to each other. The active medium is used in the optical cavity between the both mirrors. This arrangement only filters those photons which came along the axis and others are reflected by the mirrors back into the medium, where it may be amplified by stimulated emission.
Key Takeaways
- Every LASER consists of three basic components. These are Lasing material or active medium, External energy source, Optical resonator.
- The active medium is excited by the external energy source (pump source) to produce the population inversion
- The excitation source, pump source provides energy which is needed for the population inversion and stimulated emission to the system.
- Resonator guide basically provides the guidance about the simulated emission process. It is induced by high-speed photons. Finally, a laser beam will be generated.
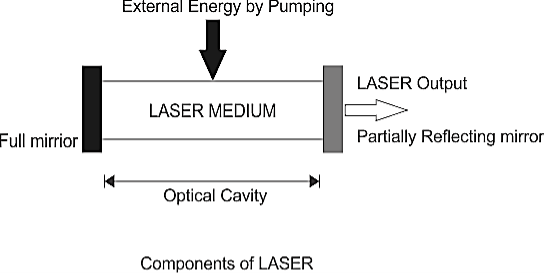
Definition
The number of atoms present in the excited state or higher energy state is greater than the number of atoms present in the ground state or lower energy state is called population inversion.
Population inversion as name suggests that this is inverted phenomena. In general lower energy level is more populated that means it have more number of atoms in lower energy level as compared to higher energy level. But by pumping we will obtain a state when the number of atoms present in the higher energy state is greater than the number of atoms present in lower energy state.
Let us consider two level energy system of energies E1 and E2 as shown in figure.
Let N1 and N2 be the populations that means number of atoms per unit volume of energy levels E1 andE2 respectively.
According to Boltzmann’s distribution the population of an energy level E, at temperature T is given by
Ni=N0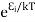
Where N0 is the population of the lower level or ground state and k is the Boltzmann’s constant.
From the above relation, the population of energy levels E1 andE2 are
N1=N0
N2=N0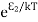
At ordinary conditionsN1>N2 i.e., the population in the ground or lower state is always greater than the population in the excited or higher states. The stage of making, population of higher energy level is greater than the population of lower energy level is called population inversion i.e. N1< N2
|
Figure 7: Population Inversion
When population inversion method is used to enforce more and more atoms to give up photons. This initiates a chain reaction and releasing massive amount of energy.
This results in rapid build-up of energy of emitting one particular wavelength traveling coherently in fixed direction. This process is called amplification by stimulated emission using population inversion.
This population inversion situation is essential for a laser action. For any stimulated emission, It is necessary that the upper energy level or meta stable state should have a long life time, i.e., the atoms should pause at the meta stable state for more time than at the lower level.
Pumping mechanisms of population inversion
Thus for laser action, pumping mechanism (exciting with external source) maintain a higher population of atoms in the upper energy level relative to that in the lower level.
A system in which population inversion is achieved is called as an active system. The method of raising the particles from lower energy state to higher energy state is called pumping.
The process of achieving of population inversion is called pumping.
This can be done by number of ways.
The most commonly used pumping methods are
- Optical pumping
- Electrical discharge pumping
- Chemical pumping
- Thermal Pumping
- Injection current pumping
- Inelastic Atom-Atom Collisions
Optical pumping As the name suggests, in this method, light is used to supply energy to the laser medium. Optical pumping is used in solid laser. Xenon flash tubes are used for optical pumping. Since these materials have very broad band absorption, sufficient amount of energy is absorbed from the emission band of flash lamp and population inversion is created. So xenon flash lamp is used to produce more electrons in the higher energy level of the laser medium.
Examples of optically pumped lasers are ruby, Nd: YAG Laser(Neodymium: Yttrium Aluminum Garnet).
Electrical discharge pumping Electrical discharge pumping is used in gas lasers. Since gas lasers have very narrow absorption band pumping then any flash lamp is not possible. Electric discharge refers to flow of electrons or electric current through a gas, liquid or solid.
In this method of pumping, electric discharge acts as the pump source or energy source. A high voltage electric discharge (flow of electrons, electric charge, or electric current) is passed through the laser medium or gas. The intense electric field accelerates the electrons to high speeds and they collide with neutral atoms in the gas. As a result, the electrons in the lower energy state gains sufficient energy from external electrons and jumps into the higher energy state
Examples of Electrical discharge pumped lasers are He-Ne laser, CO2 laser, argon-ion laser etc.
Chemical pumping Chemical reaction may also result in excitation and hence creation of population inversion in few systems.
If an atom or a molecule is produced through some chemical reaction and remains in an excited state at the time of production, then it can be used for pumping. The hydrogen fluoride molecule is produced in an excited state when hydrogen and fluorine gas chemically combine. The number of produced excited atoms or molecules is greater than the number of normal state atoms or molecules. Thus, population inversion is achieved.
Examples H2 + F2→ 2HF, in this chemical reaction, hydrogen (H2) and fluorine (F2) molecules are chemically combined to produce hydrogen fluoride molecule (2HF) in an excited state.
Thermal Pumping: Sometimes we can achieve population inversion by heating the laser medium. In thermal pumping, heat acts as the pump source or energy source. In this method, population inversion is achieved by supplying heat into the laser medium.
When heat energy is supplied to the laser medium, the lower energy state electrons gains sufficient energy and jumps into the higher energy level.
The process of achieving population inversion in thermal pumping is almost similar to the optical pumping or electric discharge method, except that in this method heat is used as pump source instead of light or electric discharge.
Injection current pumping In semiconductors, injection of current through the junction results in creates of population inversion among the minority charge carriers.
Examples of such systems are InP and GaAs.
Inelastic Atom-Atom Collisions: Like the electric discharge method, here also a high voltage electric discharge acts as a pump source. However, in this method, a combination of two types of gases, say X and Y are used. The excited state of gas X is represented as X+ whereas gas Y is represented as Y+. Both X and Y gases have the same excited states (X+ and Y+).
When high voltage electric discharge passes through a laser medium having two types of gases X and Y, the lower energy state electrons in gas X will move to the excited state X+ similarly the lower energy state electrons in gas Y moves to the excited state Y+.
Initially, during electric discharge, the lower energy state electrons in gas X or atom X gets excited to X+ due to continuous collision with electrons. The excited state electrons in gas X+ now collide with the lower energy state electrons in gas Y. As a result, the lower energy state electrons in gas Y gains sufficient energy and jump into the excited state Y+. This method is used in the Helium–Neon (He-Ne) laser.
Key Takeaways
- The number of atoms present in the excited state or higher energy state is greater than the number of atoms present in the ground state or lower energy state is called population inversion.
- The condition of population inversion is given as N1< N2
- The population inversion results in a rapid build-up of the energy of emitting one particular wavelength traveling coherently in a fixed direction. This process is called amplification by stimulated emission using population inversion.
- For laser action, the pumping mechanism (exciting with external source) maintain a higher population of atoms in the upper energy level relative to that in the lower level.
- A system in which population inversion is achieved is called an active system.
- The process of achieving population inversion is called pumping.
- Pumping can be done in several ways. The most commonly used pumping methods are Optical pumping, Electrical discharge pumping, Chemical pumping Thermal Pumping, Injection current pumping , Inelastic Atom-Atom Collisions
CO2 LASER
In a molecular gas laser, laser action is achieved by transitions between vibrational and rotational levels of molecules. Its construction is simple and the output of this laser is continuous.
In CO2 molecular gas laser, transition takes place between the vibrational states of Carbon dioxide molecules.
CO2 Molecular gas laser
It was the first molecular gas laser developed by Indian born American scientist Prof.C.K.N.Pillai.
It is a four level laser and it operates at 10.6 μm in the far IR region. It is a very efficient laser.
Energy states of CO2 molecules.
A carbon dioxide molecule has a carbon atom at the center with two oxygen atoms attached, one at both sides. Such a molecule exhibits three independent modes of vibrations. They are
a) Symmetric stretching mode.
b) Bending mode
c) Asymmetric stretching mode.
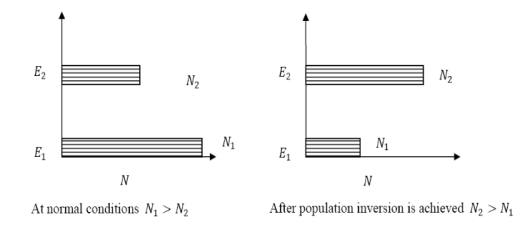
a. Symmetric stretching mode
In this mode of vibration, carbon atoms are at rest and both oxygen atoms vibrate simultaneously along the axis of the molecule departing or approaching the fixed carbon atoms.
|
Figure 8:Symmetric stretching mode
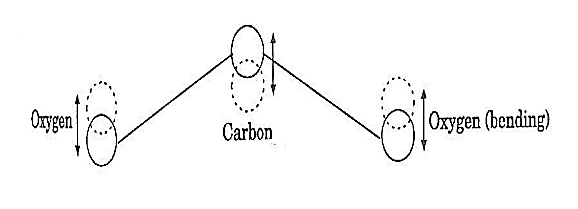
b. Bending mode:
In this mode of vibration, oxygen atoms and carbon atoms vibrate perpendicular to molecular axis.
|
Figure 9:Bending mode
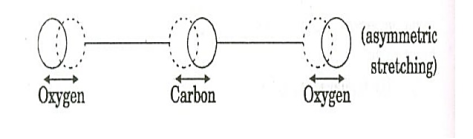
c. Asymmetric stretching mode:
|
Figure 10: Asymmetric stretching mode
In this mode of vibration, oxygen atoms and carbon atoms vibrate asymmetrically, i.e., oxygen atoms move in one direction while carbon atoms in the other direction.
PRINCIPLE:
The active medium is a gas mixture of CO2, N2 and He. The laser transition takes place between the vibrational states of CO2 molecules.
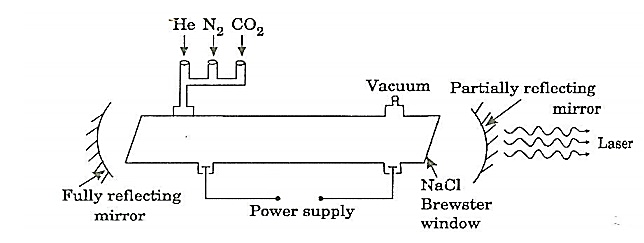
CONSTRUCTION:
It consists of a quartz tube 5 m long and 2.5 cm in the diameter. This discharge tube is filled with gaseous mixture of CO2 (active medium), helium and nitrogen with suitable partial pressures.
|
Figure 11:Construction of CO2
The terminals of the discharge tubes are connected to a D.C power supply. The ends of the discharge tube are fitted with NaCl Brewster windows so that the laser light generated will be polarized.
WORKING:
|
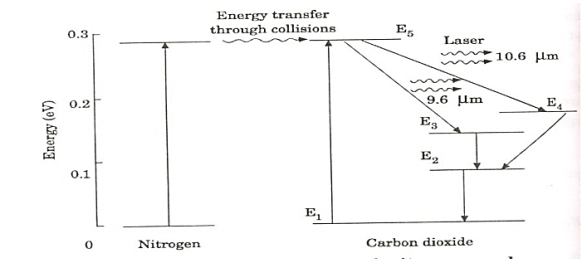
Figure 12: energy levels of nitrogen and carbon dioxide molecules
When an electric discharge occurs in the gas, the electrons collide with nitrogen molecules and they are raised to excited states. This process is represented by the equation
N2 + e* = N2* + e
N2 = Nitrogen molecule in ground state
e* = electron with kinetic energy
N2* = nitrogen molecule in excited state
e= same electron with lesser energy
Now N2 molecules in the excited state collide with CO2 atoms in ground state and excite to higher electronic, vibrational and rotational levels.
This process is represented by the equation
N2* + CO2 = CO2* + N2
N2* = Nitrogen molecule in excited state.
CO2 = Carbon dioxide atoms in ground state
CO2* = Carbon dioxide atoms in excited state
N2 = Nitrogen molecule in ground state.
Since the excited level of nitrogen is very close to the E5 level of CO2 atom, population in E5 level increases.
As soon as population inversion is reached, any of the spontaneously emitted photon will trigger laser action in the tube. There are two types of laser transition possible.
1. Transition E5 to E4
This will produce a laser beam of wavelength 10.6μm
2. Transition E5 to E3
This transition will produce a laser beam of wavelength 9.6μm. Normally 10.6μm transition is more intense than 9.6μm transition. The power output from this laser is 10kW.
Characteristics:
1. Type: It is a molecular gas laser.
2. Active medium: A mixture of CO2 , N2 and helium or water vapour is used as active medium
3. Pumping method: Electrical discharge method is used for Pumping action
4. Optical resonator: Two concave mirrors form a resonant cavity
5. Power output: The power output from this laser is about 10kW.
6. Nature of output: The nature of output may be continuous wave or pulsed wave.
7. Wavelength of output: The wavelength of output is 0.6μm and 10.6μm.
ADVANTAGES:
1. The construction of CO2 laser is simple
2. The output of this laser is continuous.
3. It has high efficiency
4. It has very high output power.
5. The output power can be increased by extending the length of the gas tube.
DISADVANTAGES:
1. The contamination of oxygen by carbon monoxide will have some effect on laser action
2. The operating temperature plays an important role in determining the output power of laser.
3. The corrosion may occur at the reflecting plates.
4. Accidental exposure may damage our eyes, since it is invisible (infra-red region) to our eyes.
APPLICATIONS:
1. High power CO2 laser finds applications in material processing, welding, drilling, cutting soldering etc.
2. The low atmospheric attenuation (10.6μm makes CO2 laser suitable for open air communication.
3. It is used for remote sensing
4. It is used for treatment of liver and lung diseases.
5. It is mostly used in neuro surgery and general surgery.
6. It is used to perform microsurgery and bloodless operations.
Key Takeaways
- In a molecular gas laser, laser action is achieved by transitions between vibrational and rotational levels of molecules.
- Its construction is simple and the output of this laser is continuous.
- In CO2 molecular gas laser, transition takes place between the vibrational states of Carbon dioxide molecules.
- It is a four level laser and it operates at 10.6 μm in the far IR region. It is a very efficient laser.
- The active medium is a gas mixture of CO2, N2 and He. The laser transition takes place between the vibrational states of CO2 molecules.
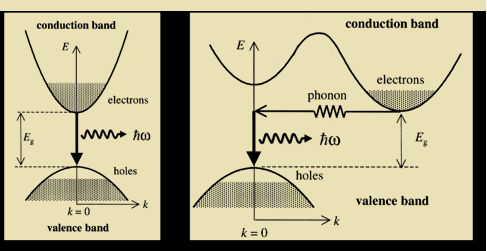
Semiconductor Laser
It is a solid state semiconductor laser. It is specifically fabricated p-n junction diode. This diode emits laser light when it is forward biased. A semiconductor laser is a device that causes laser oscillation by flowing an electric current to semiconductor. The mechanism of light emission is the same as a light-emitting diode (LED). Light is generated by flowing the forward current to a p-n junction. In forward bias operation, the p-type layer is connected with the positive terminal and the n-type layer is connected with the negative terminal, electrons enter from the n-type layer and holes from the p-type layer. When the two meet at the junction, an electron drops into a hole and light is emitted at the time.
Semiconductor lasers represent one of the most important class of lasers in use today, not only because of the large variety of direct applications in which they are involved but also because they have found a widespread use as pumps for solid state lasers.
Semiconductor lasers require, for the active medium, a direct gap material and accordingly, the normal elemental semiconductors like Si or Ge cannot be used. The majority of semiconductor-laser materials are based on a combination of elements belonging to the third group of the periodic table such as Al, Ga, In with elements of the fifth group such as N, P,As, Sb. Examples include the best known GaAs as well as some ternary AlGaAs, InGaAs and quaternary InGaAsP alloys.
InGaN semiconductor lasers the best candidates for semiconductor laser emission in the very important blue-green spectral region. Semiconductor laser materials are not limited to III–V compounds, however. For the blue-green end of the spectrum we note that there are wide-gap semiconductors using a combination between elements of the second group (such as Cd and Zn) and of the sixth group (S, Se).
PRINCIPLE
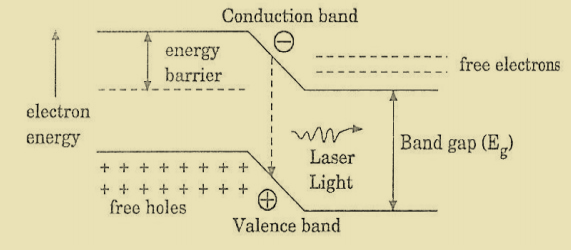
When a p-n junction diode is forward biased, the electrons from n – region and the holes from the p- region cross the junction and recombine with each other.
During the recombination process, the light radiation (photons) is released from a certain specified direct band gap semiconductors like Ga-As. This light radiation is known as recombination radiation.
The photon emitted during recombination stimulates other electrons and holes to recombine. As a result, stimulated emission takes place which produces laser.
|
Figure 13: Semiconductor Laser
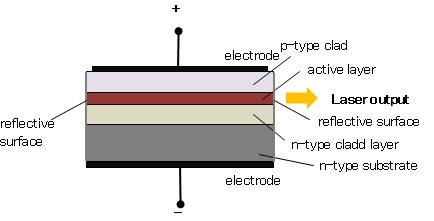
CONSTRUCTION
The basic structure of a semiconductor laser is shown in Figure. The active medium is a p-n junction diode made from the single crystal of gallium arsenide. The active layer called as light emission layer sandwiched between the p- and n-type clad layers i.e. double hetero structure is formed on an n-type substrate and voltage is applied across the p-n junction from the electrodes. This crystal is cut in the form of a platter having thickness of 0.5μmm. Both edges of the active layer has mirror-like surface. When forward voltage is applied, electrons combine with holes at the p-n junction, and emit the light.
This light is not a laser yet; it is confined within the active layer because the refractive index of the clad layers is lower than that of the active layer. In addition both ends of the active layer act as a reflecting mirror where the light reciprocates in the active layer. Then, the light is amplified by the stimulated emission process and laser oscillation is generated.
The photon emission is stimulated in a very thin layer of PN junction (in order of few microns). The electrical voltage is applied to the crystal through the electrode fixed on the upper surface. The end faces of the junction diode are well polished and parallel to each other. They act as an optical resonator through which the emitted light comes out.
|
Figure 14: Construction of semiconductor Laser
WORKING
When the PN junction is forward biased with large applied voltage, the electrons and holes are injected into junction region in considerable concentration
The region around the junction contains a large amount of electrons in the conduction band and a large amount of holes in the valence band.
If the population density is high, a condition of population inversion is achieved. The electrons and holes recombine with each other and this recombination’s produce radiation in the form of light.
When the forward – biased voltage is increased, more and more light photons are emitted and the light production instantly becomes stronger. These photons will trigger a chain of stimulated recombination resulting in the release of photons in phase.
|
Figure 15:Energy Level diagram of Semiconductor Laser
The photons moving at the plane of the junction travels back and forth by reflection between two sides placed parallel and opposite to each other and grow in strength.
After gaining enough strength, it gives out the laser beam of wavelength 8400Å. The nature of output is continuous wave or pulsed output. The power output from this laser is 1mW. The wavelength of laser light is given by
|
Where Eg is the band gap energy in joule.
ADVANTAGES
- It is very small in dimension.
- The arrangement is simple and compact.
- It exhibits high efficiency.
- It is operated with lesser power than ruby and CO2 laser.
- The laser output can be easily increased by controlling the junction current
- It requires very little auxiliary equipment
- It can have a continuous wave output or pulsed output.
DISADVANTAGES
- It is difficult to control the mode pattern and mode structure of laser.
- The output is usually from 5 degree to 15 degree i.e., laser beam has large divergence.
- The purity and monochromacity are power than other types of laser
- Threshold current density is very large (400A/mm2).
- It has poor coherence and poor stability.
APPLICATION
- It is widely used in fibre optic communication
- It is used to heal the wounds by infrared radiation
- It is also used as a pain killer
- It is used in laser printers and CD writing and reading.
Key Takeaways
- It is a solid-state semiconductor laser. It is a specifically fabricated p-n junction diode.
- Semiconductor laser is based on the principle that when a p-n junction diode is forward biased, the electrons from the n – region and the holes from the p- region cross the junction and recombine with each other.
- During the recombination process, the light radiation (photons) is released from a certain specified direct bandgap semiconductor like Ga-As. This light radiation is known as recombination radiation.
- The photon emitted during recombination stimulates other electrons and holes to recombine. As a result, stimulated emission takes place which produces laser.
- A semiconductor laser is a device that causes laser oscillation by flowing an electric current to the semiconductor.
- Semiconductor lasers require, for the active medium, a direct gap material, and accordingly, the normal elemental semiconductors like Si or Ge cannot be used.
Applications of lasers because of unique property of laser beam such as coherence, monochromacity, directionality, and high intensity, they are widely used in various fields like
1. Communication
2. Computers
3. Chemistry
4. Photography
5. Industry
6. Medicine
7. Military
8. Scientific Research
1. Communication
In case of optical communication semiconductors laser diodes are used as optical sources and its band width is (1014Hz) is very high compared to the radio and microwave communications. More channels can be sent simultaneously Signal cannot be tapped as the band width is large, more data can be sent. A laser is highly directional and less divergence, hence it has greater potential use in space crafts and submarine.It is used in optical fiber communications to send information over large distances with low loss. Laser light is used in underwater communication networks. Lasers are used in space communication, radars and satellites.
2. Computers
In LAN (local area network), data can be transferred from memory storage of one computer to other computer using laser for short time. Lasers are used in CD-ROMS during recording and reading the data. Lasers are used in computer printers.
3. Chemistry
Lasers are used in molecular structure identification Lasers are also used to accelerate some chemical reactions. Using lasers, new chemical compounds can be created by breaking bonds between atoms are molecules.
4. Photography
Lasers can be used to get 3-D lens less photography. Lasers are also used in the construction of holograms.
5. Industry
Lasers can be used to blast holes in diamonds and hard steel. Lasers are also used as a source of intense heat Carbon dioxide laser is used for cutting drilling of metals and non-metals, such as ceramics plastics glass etc. High power lasers are used to weld or melt any material. Lasers are also used to cut teeth in saws and test the quality of fabric. It is used to cut glass and quartz, used in electronic industries for trimming the components of Integrated Circuits (ICs).Lasers are used for heat treatment in the automotive industry. Laser light is used to collect the information about the prefixed prices of various products in shops and business establishments from the bar code printed on the product. Ultraviolet lasers are used in the semiconductor industries for photolithography. Photolithography is the method used for manufacturing printed circuit board (PCB) and microprocessor by using ultraviolet light. It is also used to drill aerosol nozzles and control orifices within the required precision.
6. Medicine
Pulsed neodymium laser is employed in the treatment of liver cancer. Argon and carbon dioxide lasers are used in the treat men of liver and lungs. Lasers used in the treatment of Glaucoma.
Lasers used in endoscopy to scan the inner parts of the stomach. Lasers used in the elimination of moles and tumors which are developing in the skin tissue and hair removal. It is also used for bloodless surgery.
Lasers are used to destroy kidney stones, in cancer diagnosis and therapy also used for eye lens curvature corrections. Lasers are used to study the internal structure of microorganisms and cells. It is used to create plasma. Lasers are used to remove the caries or decayed portion of the teeth.
7. Military
Lasers can be used as a war weapon. High energy lasers are used to destroy the enemy air-crofts and missiles. Lasers can be used in the detection and ranging likes RADAR. Laser range finders are used to determine the distance to an object. The ring laser gyroscope is used for sensing and measuring very small angle of rotation of the moving objects.
Lasers can be used as a secretive illuminators for reconnaissance during night with high precision.
8. Scientific research
Lasers are used in the field of 3D-photography Lasers used in Recording and reconstruction of hologram. Lasers are employed to create plasma. Lasers are used in Raman spectroscopy to identify the structure of the molecule and to count the number of atoms in a substance. Lasers are used in the Michelson- Morley experiment. A laser beam is used to confirm Doppler shifts in frequency for moving objects. A laser helps in studying the Brownian motion of particles. With the help of a helium-neon laser, it was proved that the velocity of light is same in all directions. Lasers are used to measure the pollutant gases and other contaminants of the atmosphere. Lasers help in determining the rate of rotation of the earth accurately. Lasers are used for detecting earthquakes and underwater nuclear blasts. A gallium arsenide diode laser can be used to setup an invisible fence to protect an area.
1 Question:What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?
Solution:
(a)For the electron:
Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s.
Then, momentum
p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s)
p = 4.92 × 10–24 kg m/s
de Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24 kg m/s
λ= 0.135 nm
(b)For the ball:
Mass m’ = 0.150 kg,
Speed v ’= 30.0 m/s.
Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s)
p’= 4.50 kg m/s
de Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50 kg m/s =1.47 ×10–34 m
The de Broglie wavelength of electron is comparable with X-ray wavelengths. However, for the ball it is about 10–19 times the size of the proton, quite beyond experimental measurement.
2 Question:What is the de Broglie wavelength associated with an electron, accelerated through a potential difference of 100 volts?
Solution:
Accelerating potential V = 100 V. The de Broglie wavelength λis
λ= h /p = 1 227/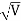
nm
λ.1 227/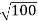
nm = 0.123 nm
The de Broglie wavelength associated with an electron in this case is of the order of x ray wavelengths.
3 Question: The uncertainty in the momentum of a ball travelling at 20m/s is 1×10−6 of its momentum. Calculate the uncertainty in position? Mass of the ball is given as 0.5kg.
Solution:
Given
v = 20m/s,
m = 0.5kg,
h = 6.626 × 10-34 m2 kg / s
Δp =p×1×10−6
As we know that,
P = m×v = 0.5×20 = 10kgm/s
Δp = 10×1×10−6
Δp = 10-5
Heisenberg Uncertainty principle formula is given as,
∆x∆p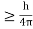 
∆x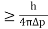 
∆x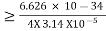 
∆x =0.527 x 10-29 m
4 Question: The mass of an electron is 9.1×10–31 kg. Its uncertainty in velocity is 5.7×105 m/sec. Calculate uncertainty in its position?
Solution:
Given m= 9×10–31
ΔV= 5.7×105 m/sec
Δx=?
h= 6.6×10–34 Joule-Sec.
Δx.Δv ≥h/4πm
Δx≥h/4πmΔv
≥6.6×10–34/9×3.14×9.1×10–31×5.7×105
≥ 0.010×10–8
≥ 1×10–10m
5 Question: The mass of a ball is 0.15 kg & its uncertainty in position to 10–10m. What is the value of uncertainty in its velocity?
Solution:
Given
m=0.15 kg.
h=6.6×10-34 Joule-Sec.
Δx = 10 –10 m
Δv=?
Δx.Δv ≥h/4πm
Δv≥h/4πmΔx
≥6.6×10-34/4×3.14×0.15×10–10
≥ 3.50×10–24m
6 Question: The mass of a bullet is 10gm & uncertainty in its velocity is 5.25×10–26 cm/sec. Calculate the uncertainty in its position?
Solution:
m=10 gm. h=6.6×10–27 erg-sec
Δv= 5.25×10–26 cm
Δx=?
Δx.Δv ≥h/4πm
Δx≥h/4πmΔv
≥6.6×10-34/4×3.14×10×5.25×10–26
≥ 0.10×10–2m
≥ 1×10–3 cm
7 Question: A 45 kW broadcasting antenna emits radio waves at a frequency of 4 MHz.
(a) How many photons are emitted per second?
(b) Is the quantum nature of the electromagnetic radiation important in analyzing the radiation emitted from this antenna?
Solution:
(a) The electromagnetic energy emitted by the antenna in one second is E = 45 000 J. Thus, the number of photons emitted in one second is
|
(b) Since the antenna emits a huge number of photons every second, 1.7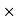
1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism.
8 Question: Consider a one-dimensional particle which is confined within the region 0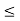 
x
a and whose wave function is (x, t) =sin(πx/a) exp-iωt.
(a) Find the potential V(x).
(b) Calculate the probability of finding the particle in the interval a/4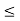 
x 
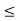3a/4.
Solution:
Since the first time derivative and the second x derivative of (x, t), are given by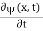 
=-iω (x, t) and 
=-(π2/a2) (x, t)the Schrödinger equation yields
|
Hence V(x,t) is time independent and given by
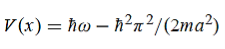
(b) The probability of finding the particle in the interval a/4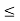 
x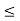 
3a/4.can be obtained from
|
9 Question: Calculate the de Broglie wavelength of an electron having a kinetic energy of 1000 eV. Compare the result with the wavelength of x-rays having the same energy?
Solution:
The kinetic energy
|
10 Question:Determine the de Broglie wavelength of an electron that has been accelerated through a potential difference of (i) 100 V, (ii) 200 V.
Solution:
(i)The energy gained by the electron = 100 eV. Then
|
11 Question: The wave function of a particle of mass m moving in a potential V (x) is
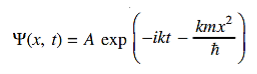
where A and k are constants. Find the explicit form of the potential V (x).
Solution:
|
Substituting these values in the time dependendent Schrödinger equation, we have
|
12 Question: Calculate the wavelength of radiation emitted by an LED made up of a semiconducting material with band gap energy 2.8eV.
Solution:
E = hc/ʎ
Therefore, ʎ = hc/E
ʎ = 4430.8 Å.
13Question:Calculate the number of photons, from green light of mercury (ʎ = 4961 Å), required to do one joule of work.
Solution:
E = hc/ʎ
E = 4.006×10-19 Joules
Number of photons required = (1 Joule)/(4.006×10-19)
N = 2.4961×1018/m3.
14 Question:What is the relationship between B21 and B12?
a) B12> B21
b) B12< B21
c) B12 = B21
d) No specific relation
Solution:
C is the correct answer.
B21 is the coefficient for the stimulated emission while B12 is the coefficient for stimulated absorption. Both the processes are mutually reverse processes and their probabilities are equal. Therefore, B12 = B21.
Reference
- Griffiths-introduction-to-quantum-mechanics
- Quantum-physics-H.C. Verma
- Quantum Mechanics Concepts and Applications Second Edition Nouredine Zettili
- Engineering physics- Gaur and Gupta, & S.Chand Publication
- Engineering physics - Avadhanalu and Kshirsagar, S.Chand Publication
- Lasers and Non Linear Optics, BB laud, 3rd Ed, New Age International Publishers 2011.
