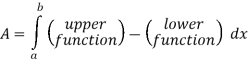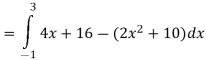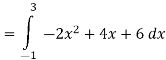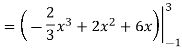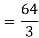Unit IV

Double Integral

Q 1:

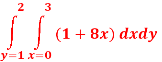
Solution: In this example the “inner integral” is 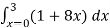with y treated as a constant.

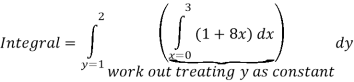
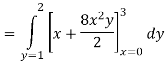
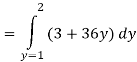
Q 2:

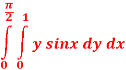
Solution:

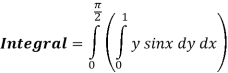
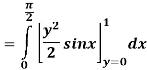
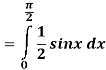
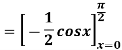
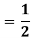
Q 3: Find the volume of the solid bounded above by the plane z = 4-x-y and below by the rectangle R = {(x,y): 0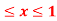  0}.

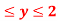Solution:  The volume under any surface z = f(x, y) and above a region R is given by

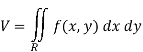
In our case

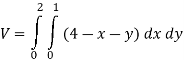
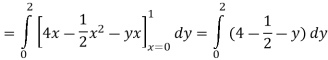
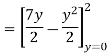
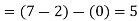
Q 4: Evaluate

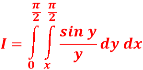
By changing the order of integration.

Solution:  The given limits are (inner) y from x to 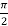; (Outer) x from 0 to .

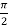We use these to sketch the region of integration.

The given limits have inner variable y. To reverse the order of integration we use horizontal stripes. The limits in this order are

(inner) x from 0 to y;   (outer) y from 0 to .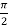

So the integral becomes

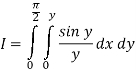
We compute the inner, then the outer integrals.

Inner:

Q 5: Change the order of integration in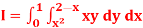

Of hence evaluate the same.

Solution:

Pt. Of interaction:

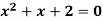
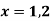
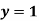
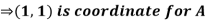
Region of interaction is divided into 2 parts OAM and MAB

For region OAM:

For region MAB:

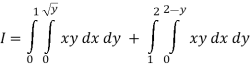
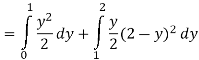
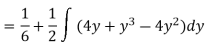
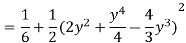
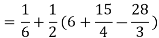
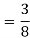
Q 6: Change the order of integration of evaluate

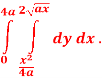
Solution:

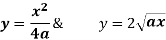
Pt. Of intersection

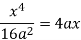
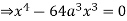
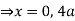
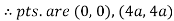
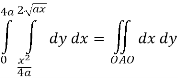
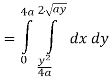
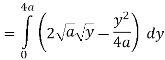
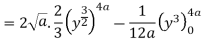
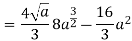
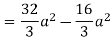
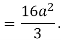
Q 7: is the portion of the circles of radius 2 and radius 5 cantered at the origin that line in the first quadrant.

Solution:  First let’s get D terms of polar coordinates. The circle of radius 2 is given by r =2 and the circle of radius 5 is given by r =5. We want the region between the two circles, so we will have the following inequality for r.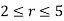
 

Also, since we only want the portion that in the first quadrant, we get following range of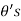

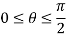
Now that we’ve got these we can do the integral

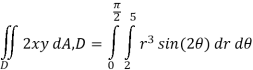
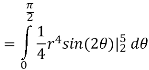
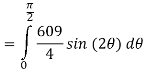
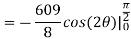
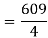
Q 8: 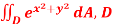is the unit centered at the origin.

Solution: In this case we can’t do this integral in terms of cartesian coordinates. We will however be able to do it in polar coordinates. First, the region D is defined by 

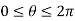
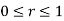
In terms of polar coordinates, the integral is then,

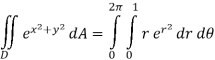
Notice that the addition of the r is given us an integral that we can now do. Here is the work for this integral.

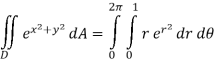
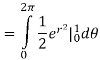
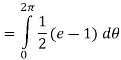
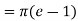
Q 9: Determine the area of the region bounded by

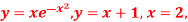and the y-axis.

Solution:  In this case the last two pieces of 8information, x =2 and the y-axis, tell us the right and left boundaries of the region. Also, recall that the y-axis is given by the line x =0. Here is the graph with the enclosed region shaded in.

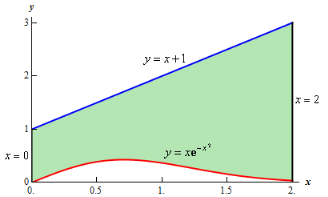
Here, unlike the first example, the two curves don’t meet. Instead we rely on two vertical lines to bound the left and right sides of the region as we noted above.

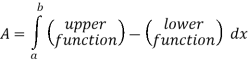
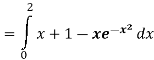
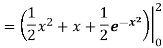
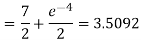
Q 10: Determine the area of the region bounded

Solution: In this case the intersection points (which we’ll need eventually) are not going to be easily identified from the graph so let’s go ahead and get them now. Note that for most of these problem’s you’ll not be able to accurately identify the intersection points from the graph and so you’ll need to be able to determine them by hand. In this case we can get the intersection points by setting the two equations equal.

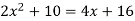
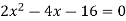
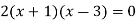
So, it looks like the two curves will intersect at x = -1 and x=3. If we need them we can get the y values corresponding to each of these by plugging the values back into either of the equations. We’ll leave it to you to verify that the coordinates of the two intersection points on the graph are(-1, 12) and (3, 28).

Note as well that if you aren’t good at graphing knowing the intersection points can help in at least getting the graph started. Here is a graph of the region.

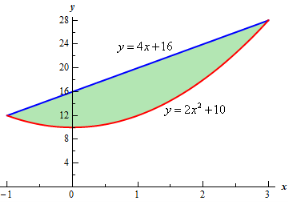
With the graph we can now identify the upper and lower function and so we can now find the enclosed area.

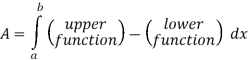
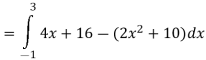
Unit IV

Double Integral

Q 1:

Solution: In this example the “inner integral” is 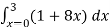with y treated as a constant.

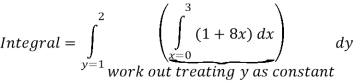
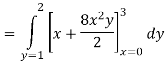
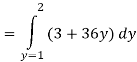
Q 2:

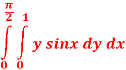
Solution:

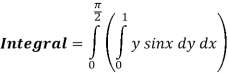
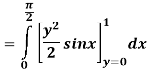
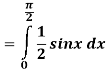
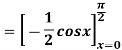
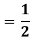
Q 3: Find the volume of the solid bounded above by the plane z = 4-x-y and below by the rectangle R = {(x,y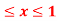): 0  0}.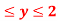

Solution:  The volume under any surface z = f(x, y) and above a region R is given by

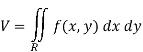
In our case

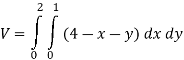
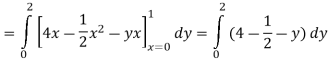
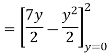
Q 4: Evaluate

By changing the order of integration.

Solution:  The given limits are (inner) y from x to ; (Outer) x from 0 to .

We use these to sketch the region of integration.

The given limits have inner variable y. To reverse the order of integration we use horizontal stripes. The limits in this order are

(inner) x from 0 to y;   (outer) y from 0 to .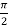

So the integral becomes

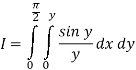
We compute the inner, then the outer integrals.

Inner:

Q 5: Change the order of integration in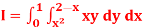

Of hence evaluate the same.

Solution:

Pt. Of interaction:

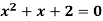
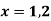
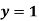
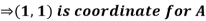
Region of interaction is divided into 2 parts OAM and MAB

For region OAM:

For region MAB:

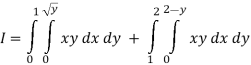
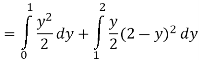
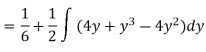
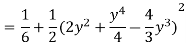
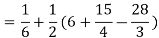
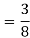
Q 6: Change the order of integration of evaluate

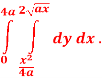
Solution:

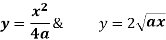
Pt. Of intersection

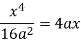
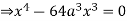
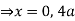
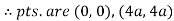
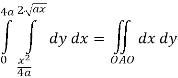
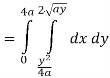
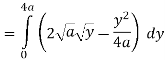
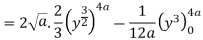
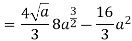
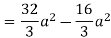
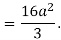
Q 7: is the portion of the circles of radius 2 and radius 5 cantered at the origin that line in the first quadrant.

Solution:  First let’s get D terms of polar coordinates. The circle of radius 2 is given by r =2 and the circle of radius 5 is given by r =5. We want the region between the two circles, so we will have the following inequality for r.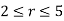
 

Also, since we only want the portion that in the first quadrant, we get following range of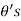

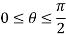
Now that we’ve got these we can do the integral

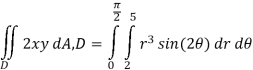
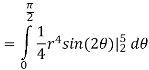
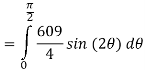
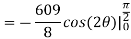
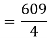
Q 8: 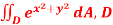is the unit centered at the origin.

Solution: In this case we can’t do this integral in terms of cartesian coordinates. We will however be able to do it in polar coordinates. First, the region D is defined by 

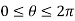
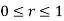
In terms of polar coordinates, the integral is then,

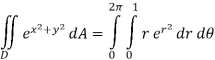
Notice that the addition of the r is given us an integral that we can now do. Here is the work for this integral.

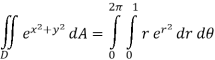
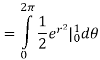
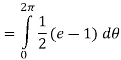
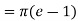
Q 9: Determine the area of the region bounded by

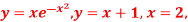and the y-axis.

Solution:  In this case the last two pieces of 8information, x =2 and the y-axis, tell us the right and left boundaries of the region. Also, recall that the y-axis is given by the line x =0. Here is the graph with the enclosed region shaded in.

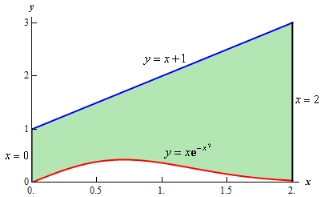
Here, unlike the first example, the two curves don’t meet. Instead we rely on two vertical lines to bound the left and right sides of the region as we noted above.

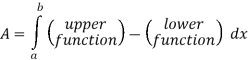
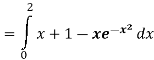
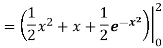
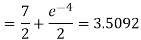
Q 10: Determine the area of the region bounded

Solution: In this case the intersection points (which we’ll need eventually) are not going to be easily identified from the graph so let’s go ahead and get them now. Note that for most of these problem’s you’ll not be able to accurately identify the intersection points from the graph and so you’ll need to be able to determine them by hand. In this case we can get the intersection points by setting the two equations equal.

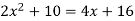
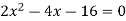
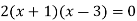
So, it looks like the two curves will intersect at x = -1 and x=3. If we need them we can get the y values corresponding to each of these by plugging the values back into either of the equations. We’ll leave it to you to verify that the coordinates of the two intersection points on the graph are(-1, 12) and (3, 28).

Note as well that if you aren’t good at graphing knowing the intersection points can help in at least getting the graph started. Here is a graph of the region.

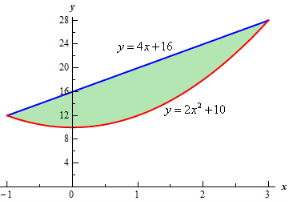
With the graph we can now identify the upper and lower function and so we can now find the enclosed area.