Unit V
Multiple Integral and special function
Q1) Evaluate the following:
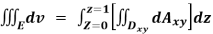
A1)
= 
= 
= 
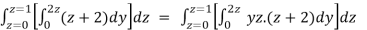
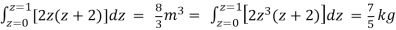
Q2) Evaluate the following:
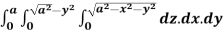
A2) let I =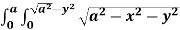 
.dxdy
= 
= 
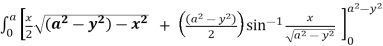
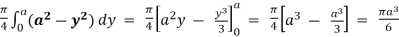
Q3) Evaluate the following triple integral
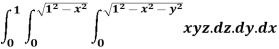
A3) let I =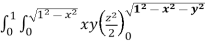 
.dzdydx
= 
= 
= 
= 
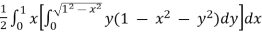
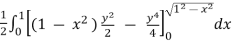
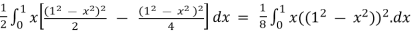
Q4) Evaluate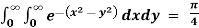 
by changing to polar co-ordinates hence evaluate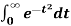 
A4) let I =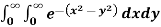 
Polar form: x = rcos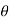
, y= rsin
dx dy = r. Dr d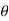
= 
= 
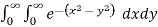
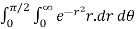
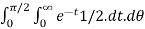
= ½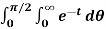 
= -1/2 
= - ½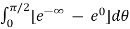 
= -1/2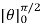 
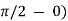
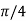= ½ (
= 
…(1)
To find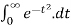 
By equation 1.,
= 
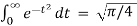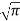/2.
Q5) Express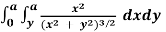 
in polar cartesian form hence evaluate it
A5) let cartesian form I=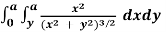 
where
X varies from x = y to x = a
Y varies from y = 0 to y = a
Polar form: x = rcos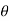
, y= rsin
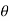dx dy = r. Dr d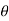
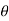varies from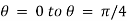 
I =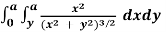 
= 
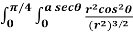r.dr. d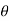
= 
=
= 
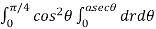
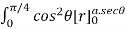
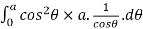
=a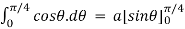
= a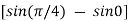
= 
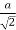
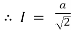
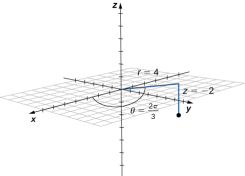
Q6) Plot the point with cylindrical co-ordinates (4, 2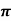
/3, -2) and express its location in rectangular coordinates.
A6) conversion from cylindrical to rectangular coordinates requires a simple application.
x = r cos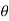
= 4 cos (2
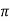/3) = -2
y = r sin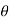
= 4sin (2
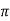/3) = 2/
.
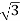Z = -2
The point with cylindrical co-ordinates (4, 2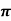
/3, -2) has rectangular coordinates (-2, 2/
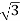, -2) seen in the diagram.
Q7) Convert the rectangular co-ordinates (1, -3, 5) to cylindrical co-ordinates.
A7) use the second set of equations from note to translate from rectangular to cylindrical co-ordinates
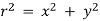
r =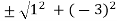 
= 
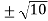
We choose the positive square root, so r =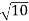 
. Now, we apply the formula to find 
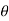. In this case, y is negative and x is positive, which means we must select the value 
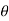between 
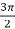and 2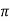
Tan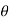
= 
= 
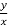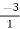
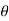= arctan (-3) 
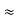5.03 rad.
In this case the z-coordinates are the same in both rectangular and cylindrical coordinates: z = 5.
The point with rectangular co-ordinates (1, -3, 5) has cylindrical coordinates approximately equal to (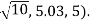
Q8) f(B) =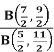 
Solve the given function.
A8)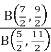 
= 
= 
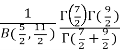
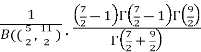[Recursive function for the gamma function]
= 
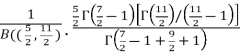[Recursive formula for the gamma function]
=
=
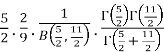
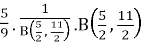[By the definition of Beta function]
= 
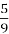
Q9) B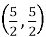
=
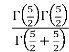
A9) =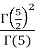 
= 
=
= 
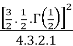
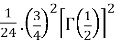
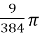[because 
]
Q9) Evaluate I =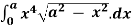 
A10) let x2 = a2 y, we get
I =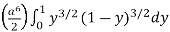 
= 
)
= 
.
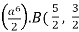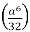Q10) Evaluate I =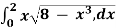 
A11) let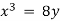 
I =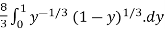 
= 
= 
.
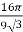Q11) Prove that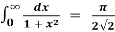 
A12) let I =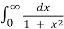 
Put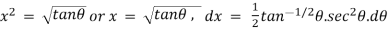 
= 
= 
.
= 
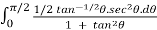
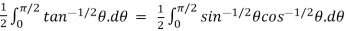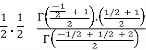= ¼. 
= 
.
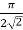