Unit II

Mean value theorems

Q1) Verify Rolle’s theorem for the function f(x) = x(x+3) 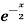in interval [-3, 0].

A1) First we will differentiate the given function with respect to x, we get

f’(x) = (x²+3x) 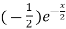+ (2x + 3)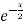

=

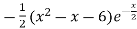
This shows that f’(x) exists for all x, therefore f(x) is continuous for all x.

Now, f(-3) = 0 and f(0) = 0 , so that f(-3) = f(0).

Here f(x) satisfies all the conditions of Rolle’s theorem,

Then,

f’(x) = 0  , which gives

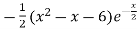= 0

We get,

X = 3 and x = -2

Here we can see that clearly -3<-2<0 , therefore there exists   -2 ∈ (-3,0) such that

f’(-2) = 0

That means the Rolle’s theorem is true for the given function.

Q2) Verify Rolle’s theorem for the given functions below-

1.  f(x) = x³ - 6x²+11x-6 in the interval [1,3]

2. f(x) = x²-4x+8 in the interval [1,3]

A2)  (1) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]

Also, f(1) = f(3) = 0

Now we find f’(x) = 0

3x² - 12x +11 = 0

We get, x = 2+ 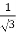and 2 -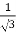

Hence both of them lie in (1,3).

Hence the theorem holds good for the given function in interval [1,3]

(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]

Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5

Hence f(1) = f(3)

Now the first derivative of the function,

f’(x) = 0

2x – 4 = 0 , gives

X = 2

We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.

This means that the Rolle’s theorem holds good for the given function and given interval.

Q3) Verify the Rolle’s theorem for sin x in the interval []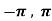

A3) Suppose f(x) = sin x

We know that sin x is continuous for all x.

Now, f’(x) = cos x exists for all x in (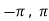) and

f(0

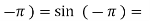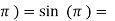f(0

Thus f(x) satisfies all the conditions of Rolle’s theorem.

Now,

f’(x) = 0 that gives, cos x = 0

x =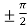  

Here we notice that both intervals lie in (.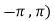

There exists, c =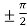

So that, f’(c) = 0

The Rolle’s theorem has been verified.

Q4) Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].

A4) polynomial is continuous in [0,4] and differentiable in (0,4).

f(x) = (x-1)(x-2)(x-3)

f(x) =  x-6x²+11x-6

Now at x = 0, we get

f(0) = -6  and

At x = 4, we get.

f(4) = 6

Diff. The function w.r.t.x , we get

f’(x) = 3x²-6x+11

Suppose x = c, we get

f’(c) = 3c²-6c+11

By Lagrange’s mean value theorem,

f’(c) = 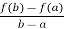   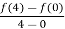 =     =   = 3                                                                                                                        

Now we get,

3c²-6c+11 = 3

3c²-6c+8 = 0

On solving the quadratic equation, we get

C = 2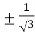

Here we see that the value of c lies between 0 and 4

Therefore, the given function is verified.

Q5) Verify Lagrange’s mean value theorem for f(x) = log xin [1,e].

A5) We already know that the function which is log x is continuous for all x>0.

So that this is the continuous function In [1,e]

Now,

f’(x) = 1/x

Which is exists for all x in (1,e)

So that f(x) is differentiable in (1,e).

By Lagrange’s mean value theorem, we get

f’(c) = 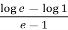, let x = c,

Then ,

f’(c) =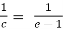

We get,

c = e-1

e-1 will always lies between 1 and e .

Hence the function is verified by Lagrange’s mean value theorem

Q6) Verify Cauchy’s mean value theorem for the function f(x) = sin x and g(x) = cosx in [ 0, π/2]

A6) It is given the,

f(x) = sin x and g(x) = cos x

Now,

f’(x) = cos x and g’(x) = - sin x

We know that both the functions are continuous in [ 0 , π/2] and differentiable in     ( 0 , π/2 )

Also, g’(x) = -sin x  ≠ 0 for all x ϵ( 0 , π/2 )

By Cauchy’s mean value theorem, we get

for some c: 0< c <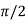

That means

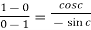which gives,

Cot c = 1

C =

Now we see that lies between 0 and

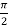
Q7) Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]

A7) We are given, f(x) = x⁴ and g(x) = x

Derivative of these functions,

f’(x) = 4x³ and g’(x) = 2x

Put these values in Cauchy’s formula, we get

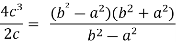
2c² =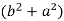

c² =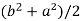

c =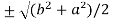

Now put the values of a = 1 and b = 2 ,we get

c = 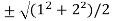= =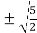 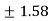(approx)

Hence the Cauchy’s theorem is verified.

Q8) Express the polynomial 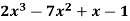in powers of (x-2).

A8)  Here we have,

f(x) =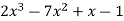

Differentiating the function w.r.t.x-

f’(x) =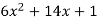

f’’(x) = 12x + 14

f’’’(x) = 12

f’’’’(x)=0

Now using Taylor’s theorem-

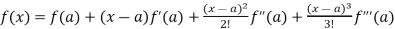+ …….     (1)

Here we have, a = 2,

Put x = 2 in the derivatives of f(x), we get-

f(2) = 

f’(2) =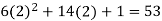

f’’(2) = 12(2)+14 = 38

f’’’(2) = 12   and f’’’’(2) = 0

Now put a = 2 and substitute the above values in equation (1), we get-

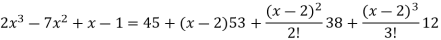
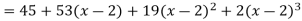
Q9) Expand sin x in powers of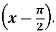

A9)  Let f(x) = sin x

Then,

=

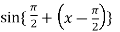
By using Taylor’s theorem-

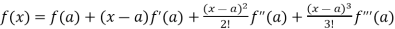+ …….     (1)

Here f(x) = sin x and a = π/2

f’(x) = cosx, f’’(x) = - sin x, f’’’(x) = - cos x and so on.

Putting x = π/2, we get

f(x) = sin x = 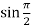= 1

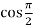f’(x) = cos x = = 0

f’’(x) = -sin x = 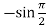= -1

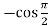f’’’(x) = -cos x = = 0

From equation (1) put a = 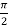and substitute these values, we get-

+ …….    

= ………………………..

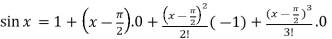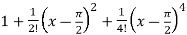Unit II

Mean value theorems

Q1) Verify Rolle’s theorem for the function f(x) = x(x+3) in interval [-3, 0].

A1) First we will differentiate the given function with respect to x, we get

f’(x) = (x²+3x) 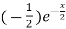+ (2x + 3)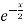

=

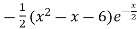
This shows that f’(x) exists for all x, therefore f(x) is continuous for all x.

Now, f(-3) = 0 and f(0) = 0 , so that f(-3) = f(0).

Here f(x) satisfies all the conditions of Rolle’s theorem,

Then,

f’(x) = 0  , which gives

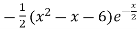= 0

We get,

X = 3 and x = -2

Here we can see that clearly -3<-2<0 , therefore there exists   -2 ∈ (-3,0) such that

f’(-2) = 0

That means the Rolle’s theorem is true for the given function.

Q2) Verify Rolle’s theorem for the given functions below-

1.  f(x) = x³ - 6x²+11x-6 in the interval [1,3]

2. f(x) = x²-4x+8 in the interval [1,3]

A2)  (1) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]

Also, f(1) = f(3) = 0

Now we find f’(x) = 0

3x² - 12x +11 = 0

We get, x = 2+ and 2 -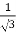

Hence both of them lie in (1,3).

Hence the theorem holds good for the given function in interval [1,3]

(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]

Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5

Hence f(1) = f(3)

Now the first derivative of the function,

f’(x) = 0

2x – 4 = 0 , gives

X = 2

We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.

This means that the Rolle’s theorem holds good for the given function and given interval.

Q3) Verify the Rolle’s theorem for sin x in the interval []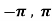

A3) Suppose f(x) = sin x

We know that sin x is continuous for all x.

Now, f’(x) = cos x exists for all x in () and

f(0

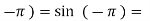f(0

Thus f(x) satisfies all the conditions of Rolle’s theorem.

Now,

f’(x) = 0 that gives, cos x = 0

x =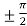  

Here we notice that both intervals lie in (.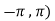

There exists, c =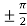

So that, f’(c) = 0

The Rolle’s theorem has been verified.

Q4) Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].

A4) polynomial is continuous in [0,4] and differentiable in (0,4).

f(x) = (x-1)(x-2)(x-3)

f(x) =  x-6x²+11x-6

Now at x = 0, we get

f(0) = -6  and

At x = 4, we get.

f(4) = 6

Diff. The function w.r.t.x , we get

f’(x) = 3x²-6x+11

Suppose x = c, we get

f’(c) = 3c²-6c+11

By Lagrange’s mean value theorem,

f’(c) = 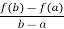   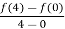 =  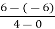   =   = 3                                                                                                                        

Now we get,

3c²-6c+11 = 3

3c²-6c+8 = 0

On solving the quadratic equation, we get

C = 2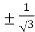

Here we see that the value of c lies between 0 and 4

Therefore, the given function is verified.

Q5) Verify Lagrange’s mean value theorem for f(x) = log xin [1,e].

A5) We already know that the function which is log x is continuous for all x>0.

So that this is the continuous function In [1,e]

Now,

f’(x) = 1/x

Which is exists for all x in (1,e)

So that f(x) is differentiable in (1,e).

By Lagrange’s mean value theorem, we get

f’(c) = , let x = c,

Then ,

f’(c) =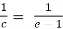

We get,

c = e-1

e-1 will always lies between 1 and e .

Hence the function is verified by Lagrange’s mean value theorem

Q6) Verify Cauchy’s mean value theorem for the function f(x) = sin x and g(x) = cosx in [ 0, π/2]

A6) It is given the,

f(x) = sin x and g(x) = cos x

Now,

f’(x) = cos x and g’(x) = - sin x

We know that both the functions are continuous in [ 0 , π/2] and differentiable in     ( 0 , π/2 )

Also, g’(x) = -sin x  ≠ 0 for all x ϵ( 0 , π/2 )

By Cauchy’s mean value theorem, we get

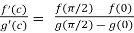for some c: 0< c <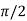

That means

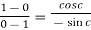which gives,

Cot c = 1

C =

Now we see that lies between 0 and

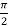
Q7) Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]

A7) We are given, f(x) = x⁴ and g(x) = x

Derivative of these functions,

f’(x) = 4x³ and g’(x) = 2x

Put these values in Cauchy’s formula, we get

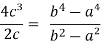
2c² =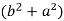

c² =

c =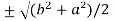

Now put the values of a = 1 and b = 2 ,we get

c = 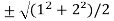= =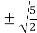 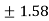(approx)

Hence the Cauchy’s theorem is verified.

Q8) Express the polynomial 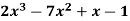in powers of (x-2).

A8)  Here we have,

f(x) =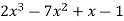

Differentiating the function w.r.t.x-

f’(x) =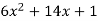

f’’(x) = 12x + 14

f’’’(x) = 12

f’’’’(x)=0

Now using Taylor’s theorem-

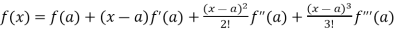+ …….     (1)

Here we have, a = 2,

Put x = 2 in the derivatives of f(x), we get-

f(2) =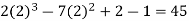 

f’(2) =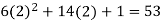

f’’(2) = 12(2)+14 = 38

f’’’(2) = 12   and f’’’’(2) = 0

Now put a = 2 and substitute the above values in equation (1), we get-

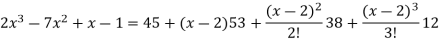
Q9) Expand sin x in powers of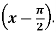

A9)  Let f(x) = sin x

Then,

=

By using Taylor’s theorem-

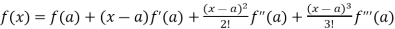+ …….     (1)

Here f(x) = sin x and a = π/2

f’(x) = cosx, f’’(x) = - sin x, f’’’(x) = - cos x and so on.

Putting x = π/2, we get

f(x) = sin x = 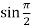= 1

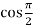f’(x) = cos x = = 0

f’’(x) = -sin x = 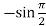= -1

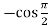f’’’(x) = -cos x = = 0

From equation (1) put a = 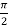and substitute these values, we get-

+ …….    

= ………………………..
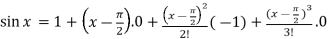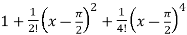