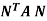Unit I
Matrix operations and solving systems of linear equations
Q1) Find the rank of a matrix M by echelon form.
M = 
A1) First we will convert the matrix M into echelon form,
M = 
Apply,  , we get
, we get
M = 
Apply  , we get
, we get
M = 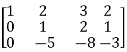
Apply 
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Q2) Find the rank of a matrix A by echelon form.
A = 
A2) Convert the matrix A into echelon form,
A = 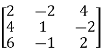
Apply 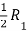
A = 
Apply  , we get
, we get
A = 
Apply  , we get
, we get
A = 
Apply  ,
,
A = 
Apply  ,
,
A = 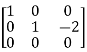
Therefore, the rank of the matrix will be 2.
Q3) Find the rank of a matrix A by echelon form.
A = 
A3) Transform the matrix A into echelon form, then find the rank,
We have,
A = 
Apply, 
A = 
Apply  ,
,
A = 
Apply 
A = 
Apply 
A = 
Hence the rank of the matrix will be 2.
Q4) Find the rank of the following matrices by echelon form?
A4) Let A = 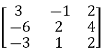
Applying 
A 
Applying 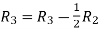
A 
Applying 
A 
Applying 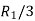
A 
It is clear that minor of order 3 vanishes but minor of order 2 exists as 
Hence rank of a given matrix A is 2 denoted by 
2. 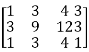
Let A = 
Applying 

Applying 

Applying 

The minor of order 3 vanishes but minor of order 2 non zero as 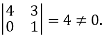
Hence the rank of matrix A is 2 denoted by 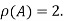
3. 
Let A = 
Apply 

Apply 

Apply 

It is clear that the minor of order 3 vanishes whereas the minor of order 2 is non zero as 
Hence the rank of given matrix is 2 i.e. 
Q5) Find the solution of the following homogeneous system of linear equations,



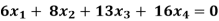
A5) The given system of linear equations can be written in the form of matrix as follows,

Apply the elementary row transformation,

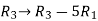
 , we get,
, we get,


 , we get
, we get

Here r(A) = 4, so that it has trivial solution,

Q6) Find out the value of ‘b’ in the system of homogeneous equations-
2x + y + 2z = 0
x + y + 3z = 0
4x + 3y + bz = 0
Which has
(1) Trivial solution
(2) Non-trivial solution
A6) (1) For trivial solution, we already know that the values of x , y and z will be zero, so that ‘b’ can have any value.
Now for non-trivial solution-
(2)
Convert the system of equations into matrix form-
AX = O
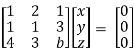
Apply  Respectively , we get the following resultant matrices
Respectively , we get the following resultant matrices


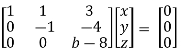
For non-trivial solutions, r(A) = 2 < n
b – 8 = 0
b = 8
Q7) check whether the following system of linear equations is consistent of not.
2x + 6y = -11
6x + 20y – 6z = -3
6y – 18z = -1
A7) Write the above system of linear equations in augmented matrix form,

Apply  , we get
, we get

Apply 

Here the rank of C is 3 and the rank of A is 2
Therefore, both ranks are not equal. So that the given system of linear equations is not consistent.
Q8) Check the consistency and find the values of x , y and z of the following system of linear equations.
2x + 3y + 4z = 11
X + 5y + 7z = 15
3x + 11y + 13z = 25
A8) Re-write the system of equations in augmented matrix form.
C = [A, B]
That will be,

Apply 

Now apply ,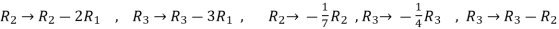
We get,
 ~
~ ~
~
Here rank of A = 3
And rank of C = 3, so that the system of equations is consistent,
So that we can solve the equations as below,

That gives,
x + 5y + 7z = 15 ……………..(1)
y + 10z/7 = 19/7 ………………(2)
4z/7 = 16/7 ………………….(3)
From eq. (3)
z = 4,
From 2,

From eq.(1), we get
x + 5(-3) + 7(4) = 15
That gives,
x = 2
Therefore the values of x , y , z are 2 , -3 , 4 respectively.
Q9) solve the following system of linear equations by using Guassseidel method-
6x + y + z = 105
4x + 8y + 3z = 155
5x + 4y - 10z = 65
A9) The above equations can be written as,
 ………………(1)
………………(1)
 ………………………(2)
………………………(2)
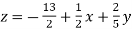 ………………………..(3)
………………………..(3)
Now put z = y = 0 in first eq.
We get
x = 35/2
Put x = 35/2 and z = 0 in eq. (2)
We have,

Put the values of x and y in eq. 3

Again start from eq.(1)
By putting the values of y and z
y = 85/8 and z = 13/2
We get
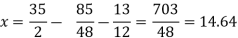
The process can be showed in the table format as below
Iterations | 1 | 2 | 3 | 4 |
 | 32/2=17.5 | 14.64 | 15.12 | 14.98 |
 | 85/8=10.6 | 9.62 | 10.06 | 9.98 |
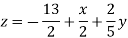 | 13/2=6.5 | 4.67 | 5.084 | 4.98 |
At the fourth iteration, we get the values of x = 14.98, y = 9.98, z = 4.98
Which are approximately equal to the actual values?
As x = 15, y = 10 and y = 5 (which are the actual values)
Q10) Solve the following system of linear equations by using Guassseidel method-
5x + 2y + z = 12
x + 4y + 2z = 15
x + 2y + 5z = 20
A10) These equations can be written as ,
 ………………(1)
………………(1)
 ………………………(2)
………………………(2)
 ………………………..(3)
………………………..(3)
Put y and z equals to 0 in eq. 1
We get,
x = 2.4
Put x = 2.4, and z = 0 in eq. 2 , we get
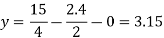
Put x = 2.4 and y = 3.15 in eq.(3) , we get

Again start from eq.(1), put the values of y and z , we get
 = 0.688
= 0.688
We repeat the process again and again,
The following table can be obtained –
Iterations | 1 | 2 | 3 | 4 | 5 |
 | 2.4 | 0.688 | 0.84416 | 0.962612 | 0.99426864 |
 | 3.15 | 2.448 | 2.09736 | 2.013237 | 2.00034144 |
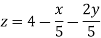 | 2.26 | 2.8832 | 2.99222 | 3.0021828 | 3.001009696 |
We see that the values are approx. Equal to exact values.
Exact values are, x = 1, y = 2, z = 3.
Q11) Are the vectors  ,
,  ,
, 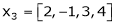 linearly dependent. If so, express x1 as a linear combination of the others.
linearly dependent. If so, express x1 as a linear combination of the others.
A11) Consider a vector equation,

i.e. 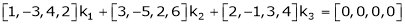
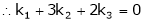

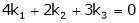

Which can be written in matrix form as,


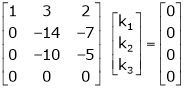




Here 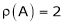 & no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
& no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
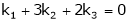

Put 
 and
and
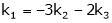



Thus 
i.e. 
i.e. 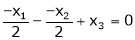


Since F11k2, k3 not all zero. Hence  are linearly dependent.
are linearly dependent.
Q12) Examine whether the following vectors are linearly independent or not.
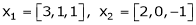 and
and 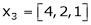 .
.
A12) Consider the vector equation,

i.e. 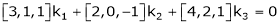 … (1)
… (1)



Which can be written in matrix form as,

R12
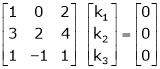
R2 – 3R1, R3 – R1



R3 + R2

Here Rank of coefficient matrix is equal to the no. Of unknowns. i.e. r = n = 3.
Hence the system has unique trivial solution.
i.e. 
i.e. vector equation (1) has only trivial solution. Hence the given vectors x1, x2, x3 are linearly independent.
Q13) At what value of P the following vectors are linearly independent.

A13)
Consider the vector equation.
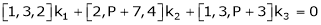
i.e.



This is a homogeneous system of three equations in 3 unknowns and has a unique trivial solution.
If and only if Determinant of coefficient matrix is non zero.
 consider
consider  .
.
 .
.
i.e.






Thus for  the system has only trivial solution and Hence the vectors are linearly independent.
the system has only trivial solution and Hence the vectors are linearly independent.
Q14) Determine the Eigen values of Eigen vector of the matrix.

A14) Consider the characteristic equation as, 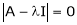
i.e. 
i.e. 



i.e. 
Which is the required characteristic equation.


 are the required Eigen values.
are the required Eigen values.
Now consider the equation
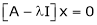 … (1)
… (1)
Case I:
If 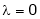 Equation (1) becomes
Equation (1) becomes

R1 + R2





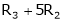

Thus 
 independent variable.
independent variable.
Now rewrite equation as,
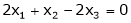

Put x3 = t
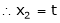 &
&



Thus  .
.
Is the eigen vector corresponding to  .
.
Case II:
If 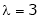 equation (1) becomes,
equation (1) becomes,

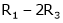
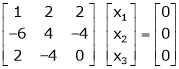

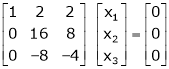



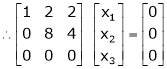
Here 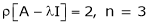
 Independent variables
Independent variables
Now rewrite the equations as,


Put 
 &
&



 .
.
Is the eigen vector corresponding to 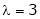 .
.
Case III:
If 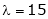 equation (1) becomes,
equation (1) becomes,









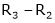
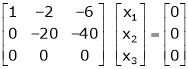
Here rank of 
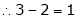 independent variable.
independent variable.
Now rewrite the equations as,
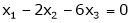

Put 

Thus  .
.
Is the eigen vector for  .
.
Q15) Find the Eigen values of Eigen vector for the matrix.

A15) Consider the characteristic equation as 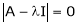
i.e. 
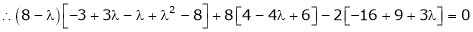


i.e. 


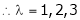 are the required eigen values.
are the required eigen values.
Now consider the equation
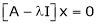 … (1)
… (1)
Case I:
 Equation (1) becomes,
Equation (1) becomes,
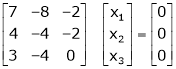

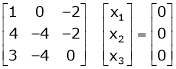


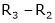

Thus  and n = 3
and n = 3
 3 – 2 = 1 independent variables.
3 – 2 = 1 independent variables.
Now rewrite the equations as,
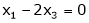

Put 
 ,
, 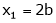
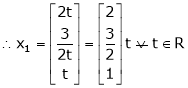
I.e.
The Eigen vector for 
Case II:
If 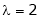 equation (1) becomes,
equation (1) becomes,

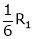



Thus 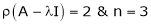

Independent variables.
Now rewrite the equations as,
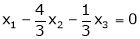

Put 

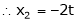


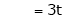
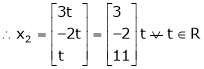
Is the Eigen vector for
Now
Case III:-
If  equation (1) gives,
equation (1) gives,

R1 – R2
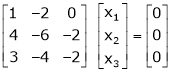




Thus 

Independent variables
Now 

Put 
Thus
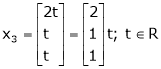
Is the Eigen vector for
Q16) Find the characteristic equation of the matrix A =  andVerify cayley-Hamlton theorem.
andVerify cayley-Hamlton theorem.
A16) Characteristic equation of the matrix, we can be find as follows-

Which is,
( 2 - , which gives
, which gives
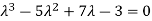
According to cayley-Hamilton theorem,
1  …………(1)
…………(1)
Now we will verify equation (1),


Put the required values in equation (1) , we get




Hence the cayley-Hamilton theorem is verified.
Q17) Find the characteristic equation of the the matrix A and verify Cayley-Hamilton theorem as well.
A = 
A17) Characteristic equation will be-
 = 0
= 0
( 7 -
(7-
(7-
Which gives,
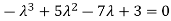
Or

According to cayley-Hamilton theorem,
 …………………….(1)
…………………….(1)
In order to verify cayley-Hamilton theorem , we will find the values of 
So that,

Now
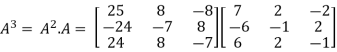


Put these values in equation(1), we get

 = 0
= 0
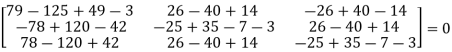

Hence the cayley-hamilton theorem is verified.
Q18) Using Cayley-Hamilton theorem, find  , if A =
, if A =  ?
?
A18) Let A =
The characteristics equation of A is 

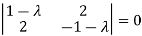
Or 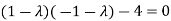
Or 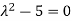
By Cayley-Hamilton theorem 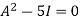
L.H.S. 
=
By Cayley-Hamilton theorem we have 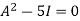
Multiply both side by 
 .
.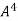
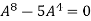
Or 
=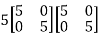
=
Q19) Find the inverse of matrix A by using Cayley-Hamilton theorem.
A = 
A19) The characteristic equation will be,
|A - 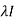 | = 0
| = 0

Which gives,
(4-

According to Cayley-Hamilton theorem,

Multiplying by 

That means

On solving,
11
= 
= 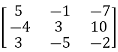
So that,

Q20) Find the inverse of matrix A by using Cayley-Hamilton theorem.
A = 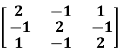
A20) The characteristic equation will be,
|A -  | = 0
| = 0
= 
= (2-
= (2 - 
= 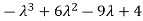
That is,

Or

We know that by Cayley-Hamilton theorem,
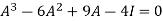 …………………….(1)t,
…………………….(1)t,
Multiply equation (1) by  , we get
, we get

Or
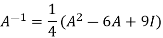
Now we will find 
= 

= 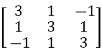
Hence the inverse of matrix A is,

Q21) Verify the Cayley-Hamilton theorem and find the inverse.
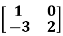 ?
?
A21) Let A =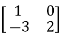
The characteristics equation of A is 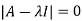

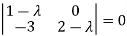
Or 
Or 
Or 
By Cayley-Hamilton theorem 
L.H.S: 


=  =0=R.H.S
=0=R.H.S
Multiply both side by  on
on 

Or 
Or 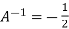 [
[
Or 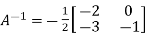
Q22) Diagonalise the matrix 
A22) Let A= 
The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values  .
.
Then  and
and 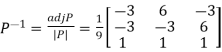
Also, we know that 




Q23) Diagonalise the matrix
A23) Let A =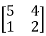
The Eigen vectors are (4,1),(1,-1) corresponding to Eigen values  .
.
Then  and also
and also 
Also, we know that 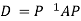
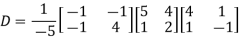


Q24) Consider the function  .Determine whether q(0,0) is the global minimum.
.Determine whether q(0,0) is the global minimum.
A24) Based on matrix technique
Rewrite the above equation

=
Note that we split the contribution -4 equally among the two components.
equally among the two components.
More succinctly, we can write

Or

The matrix A is symmetric by construction. By the spectral theorem, there is an orthonormal eigen basis 

With associated eigenvalues 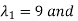
 .
.
Let  can express the value of the function as follows:
can express the value of the function as follows:

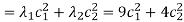
Therefore,  is the global minimum if the function.
is the global minimum if the function.
Q25) The matrix A= has row vectors.
has row vectors.
A25)  ,
, 
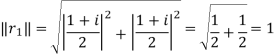



Orthogonal matrix: An orthogonal matrix is the real specialization of a unitary matrix, and thus always a normal matrix. Although we consider only real matrices here, the definition can be used for matrices with entries from any field.
Suppose A is a square matrix with real elements and of n x n order and AT is the transpose of A. Then according to the definition, if, AT = A-1 is satisfied, then,
A AT = I
Where ‘I’ is the identity matrix, A-1 is the inverse of matrix A, and ‘n’ denotes the number of rows and columns.
Q26) prove Q= 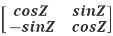 is an orthogonal matrix
is an orthogonal matrix
A26) Given Q = 
So, QT =  …..(1)
…..(1)
Now, we have to prove QT = Q-1
Now we find Q-1
Q-1 = 
Q-1 = 
Q-1 = 
Q-1 =  … (2)
… (2)
Now, compare (1) and (2) we get QT = Q-1
Therefore, Q is an orthogonal matrix.
Q27) Reduce the following quadratic form to canonical form by orthogonal transformation. Also, find rank, index, signature and nature of quadratic form.
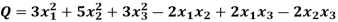
A27) 
Characteristic eq, of matrix A is



For  , Eigen Vector,
, Eigen Vector, 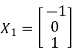
For  , Eigen Vector,
, Eigen Vector, 
For 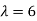 , Eigen Vector,
, Eigen Vector, 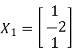
Length of eigen vector, 
Length of eigen vector, 
Length of eigen vector, 
Normalised eigen vectors are:

Modal matrix P (Normalised Eigen vector as its column vectors)
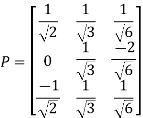


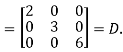
Hence, the canonical form is
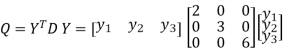
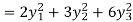
Rank (r) = 3 (No. Of non-zero eigen values)
Index = 3 (no. Of positive eigen values)
Q28) Reduce the quadratic form  to the canonical form through an orthogonal transformation.
to the canonical form through an orthogonal transformation.
A28) 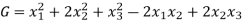

To find the characteristic equation.,
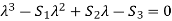
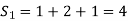
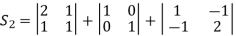
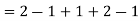


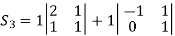



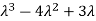 = 0 ,
= 0 , 
To find the eigenvectors,
Case-1,
If 
(A- )X=0
)X=0








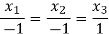
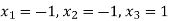

Case(2),
If 
(A- )X = 0.
)X = 0.




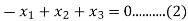

From equation ….(1)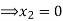
Put  in equation …(2)
in equation …(2)



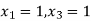


Case (3),
If 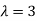
(A- )X = 0
)X = 0


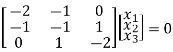


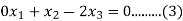


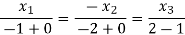






D =