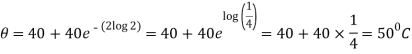Question Bank
Unit-1
Differential equation of first order and first degree
Question-1: Solve-
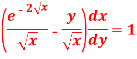
Sol. We can write the given equation as-
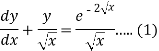
So that-
I.F. = 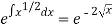
The solution of equation (1) will be-
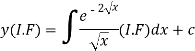
Or
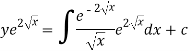
Or
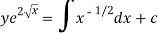
Or

Question-2: Solve-
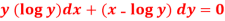
Sol.
We can write the equation as-

We see that it is a Leibnitz’s equation in x-
So that-
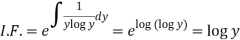
Therefore the solution of equation (1) will be-

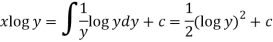
Or
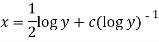
Question-3: : Solve 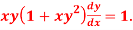
Sol.
We can write the equation as-
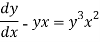
On dividing by 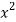 , we get-
, we get-

Put 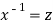 so that
so that 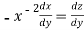
Equation (1) becomes,
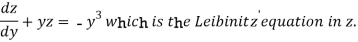
Here,
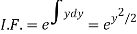
Therefore the solution is-
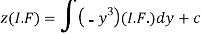
Or
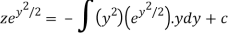
Now put 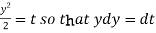
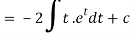
Integrate by parts-
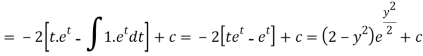
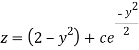
Or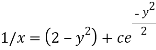
Question-4: Solve 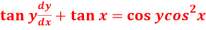
Sol. Here given,
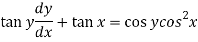
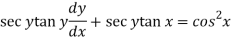
Now let z = sec y, so that dz/dx = sec y tan y dy/dx
Then the equation becomes-
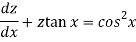
Here,
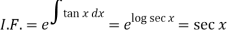
Then the solution will be-

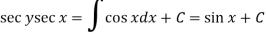
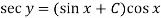
Question-5: Solve- 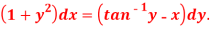
Sol. Here given-
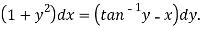
We can re-write this as-
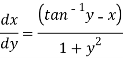
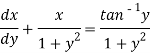
Which is a linear differential equation-
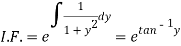
The solution will be-
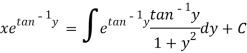
Put 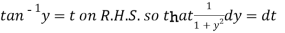
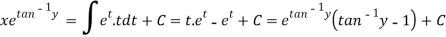
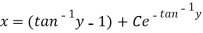
Question-6: Solve-
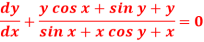
Sol. We can write the equation as below-
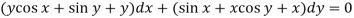
Here M = 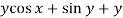 and N =
and N = 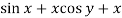
So that-

The equation is exact and its solution will be-
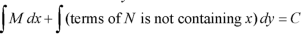
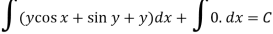
Or
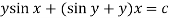
Question-7: Solve-
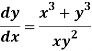
Sol.
We can write the given equation as-
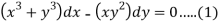
Here,
M = 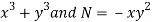
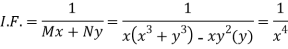
Multiply equation (1) by 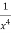 we get-
we get-
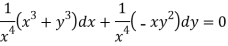
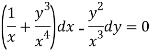
This is an exact differential equation-
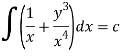
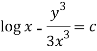
Question-8: Solve-
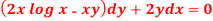
Sol.
Here given,
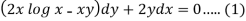
M = 2y and N = 2x log x - xy
Then-
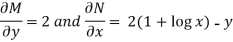
Here,

Then,
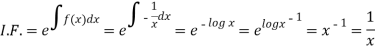
Now multiplying equation (1) by 1/x, we get-
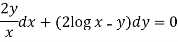
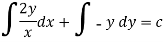
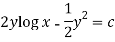
Question-9: Solve-

Sol.
We can write the equation as below-
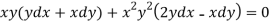
Now comparing with-
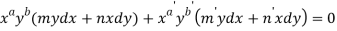
We get-
a = b = 1, m = n = 1, a’ = b’ = 2, m’ = 2, n’ = -1
I.F. = 
Where-
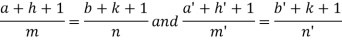
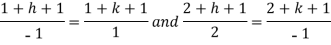
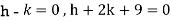
On solving we get-
h = k = -3

Multiply the equation by 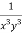 , we get-
, we get-
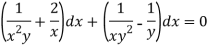
It is an exact equation.
So that the solution is-
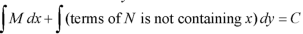

Question-10: if the family of curves is xy = c , then find its orthogonal trajectory.
Sol. First we will differentiate the given equation with respect to x,
We get,
y + x 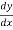 = 0
= 0
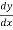 =
= 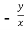
Replace 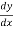 by
by 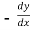
 =
= 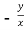
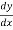 =
= 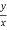
We get,
Ydy = x dx
Now integrate this equation, we get
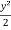 =
= 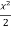 + c
+ c
y² - x² = 2c. Ans.
Question-11: find the orthogonal trajectory of the family of curves x² - y² = c
Sol. Here we will follow same procedure as we did in above example,
Diff. The given equation w.r.t. x, we get
2x – 2y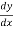 = 0
= 0
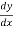 =
= 
Replace 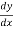 by
by 
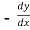 =
= 
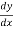 = -
= - 
Ydy = - xdx
Now integrate the above eq.
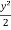 =
= 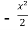 + c
+ c
On solving we get,
x² + y² = 2c.
Question-12: A body originally at  cools down to
cools down to  in 20 minutes. The temperature of the air being
in 20 minutes. The temperature of the air being 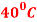 . What will be the temperature of the body after 40 minutes from the original?
. What will be the temperature of the body after 40 minutes from the original?
Sol.
If 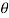 is the temperature of the surroundings and
is the temperature of the surroundings and 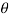 that of the body at any time t, then-
that of the body at any time t, then-
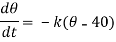
On integrating-
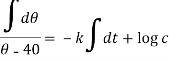
Or
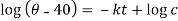
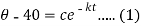
When t = 0 and 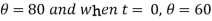
So that-

Then equation-1 becomes-
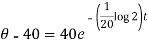
When t = 40 min, then-