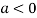Question Bank
Unit–3
Partial Differentiation
Question-1: Calculate 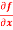 and
and  for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
Sol. To calculate 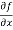 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
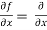 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)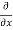 (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50)cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,
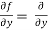 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)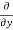 (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xycos(y²x + 5x – 8)
Question-2: if 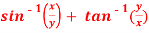 , then show that-
, then show that- 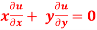
Sol. Here we have,
u = 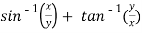 …………………..(1)
…………………..(1)
Now partially differentiate eq.(1) w.r to x and y , we get

= 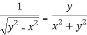
Or
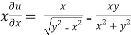 ………………..(2)
………………..(2)
And now,
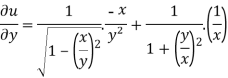
= 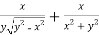
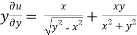 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
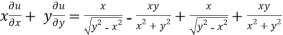 = 0
= 0
Hence proved.
Question-3: If u = x²(y-x) + y²(x-y), then show that 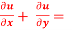 -2 (x – y)²
-2 (x – y)²
Solution - here, u = x²(y-x) + y²(x-y)
u = x²y - x³ + xy² - y³,
Now differentiate u partially with respect to x and y respectively,
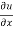 = 2xy – 3x² + y² --------- (1)
= 2xy – 3x² + y² --------- (1)
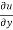 = x² + 2xy – 3y² ---------- (2)
= x² + 2xy – 3y² ---------- (2)
Now adding equation (1) and (2), we get
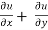 = -2x² - 2y² + 4xy
= -2x² - 2y² + 4xy
= -2 (x² + y² - 2xy)
= -2 (x – y)²
Question-4: Find  if u = x³y⁴ where x = t³ and y = t².
if u = x³y⁴ where x = t³ and y = t².
Sol. As we know that by definition, 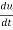 =
= 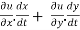
 3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
Example-3: if w = x² + y – z + sintand x + y = t, find
(a) 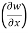 y,z
y,z
(b) 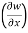 t, z
t, z
Sol. With x, y, z independent, we have
t = x + y, w = x²+ y - z + sin (x + y).
Therefore,
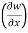 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y)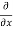 (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
Thus t, z = 2x - 1
t, z = 2x - 1
Question-5: If z is the function of x and y , and x = 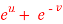 , y =
, y =  , then prove that,
, then prove that,
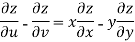
Sol. Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
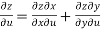 ……………….(1)
……………….(1)
And,
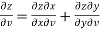 ………………..(2)
………………..(2)
Also there is,
x = 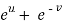 and y =
and y = 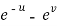 ,
,
Now,
 ,
, 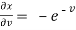 ,
, 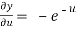 ,
, 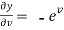
From equation(1) , we get
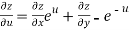 ……………….(3)
……………….(3)
And from eq. (2) , we get
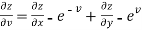 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get
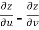 =
= 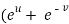 )
)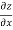 – (
– (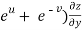
= x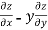
Hence proved.
Question-6: If  where
where  then find the value of
then find the value of 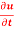 ?
?
Sol.
Given 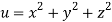
Where 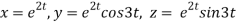
By chain rule
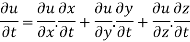
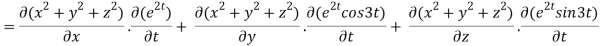
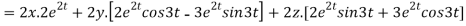

Now substituting the value of x ,y,z we get
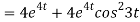 -6
-6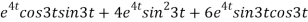
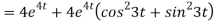
 8
8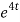
Question-7:If 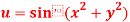 where the relation is
where the relation is 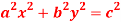 .
.
Find the value of 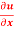
Let the given relation is denoted by 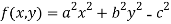
We know that
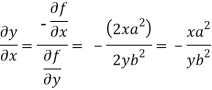
Differentiating u with respect to x and using chain rule
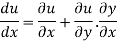
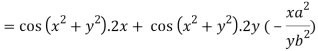
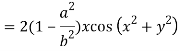
Question-8: If x = r sin , y = r sin
, y = r sin , z = r cos
, z = r cos , then show that
, then show that
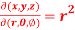 sin
sin also find
also find 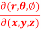
Sol.
We know that,
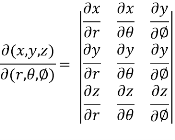
= 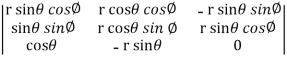
= 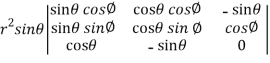
= 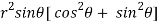 ( on solving the determinant)
( on solving the determinant)
= 
Now using first propert of Jacobians, we get
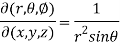
Question-9: Find the Taylor’s expansion of 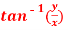 about (1 , 1) up to second degree term.
about (1 , 1) up to second degree term.
Sol. We have,
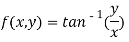
At (1 , 1)
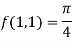

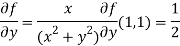
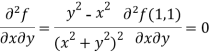
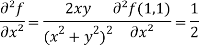
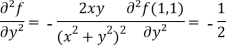
Now by using Taylor’s theorem-
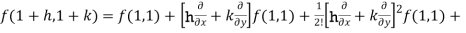 ……
……
Suppose 1 + h = x then h = x – 1
1 + k = y then k = y - 1
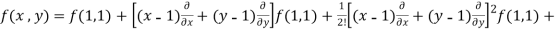 ……
……
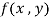 =
= 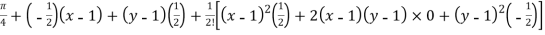
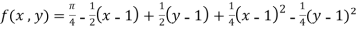 ……..
……..
Question-10: Find out the maxima and minima of the function
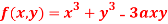
Sol.
Given 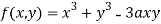 …(i)
…(i)
Partially differentiating (i) with respect to x we get
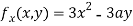 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
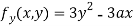 ….(iii)
….(iii)
Now, form the equations 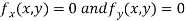
Using (ii) and (iii) we get
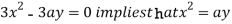

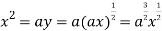 using above two equations
using above two equations
Squaring both side we get
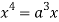
Or 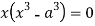
This show that 
Also we get 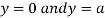
Thus we get the pair of value as 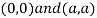
Now, we calculate
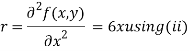

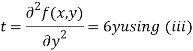
Putting above values in
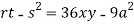
At point (0,0) we get
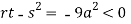
So, the point (0,0) is a saddle point.
At point 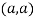 we get
we get

So the point 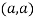 is the minimum point where
is the minimum point where 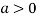
In case 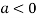
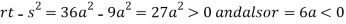
So the point  is the maximum point where
is the maximum point where