Question Bank
Unit 1
Q1. What are the Maxwell equation in vacuum?
Answer:
Maxwell's equations represent one of the most elegant and concise ways to state the fundamentals of electricity and magnetism. From them one can develop most of the working relationships in the field. Because of their concise statement, they embody a high level of mathematical sophistication and are therefore not generally introduced in an introductory treatment of the subject, except perhaps as summary relationships.
These basic equations of electricity and magnetism can be used as a starting point for advanced courses, but are usually first encountered as unifying equations after the study of electrical and magnetic phenomena.
Integral form in the absence of magnetic or polarizable media:
I. Gauss' law for electricity | 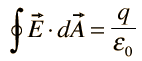 |
II. Gauss' law for magnetism |  |
III. Faraday's law of induction |  |
IV. Ampere's law | 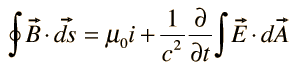 |
Q 2 Define Stokes theorem?
Answer:
Stokes Theorem (also known as Generalized Stoke’s Theorem) is a declaration about the integration of differential forms on manifolds, which both generalizes and simplifies several theorems from vector calculus. As per this theorem, a line integral is related to a surface integral of vector fields.
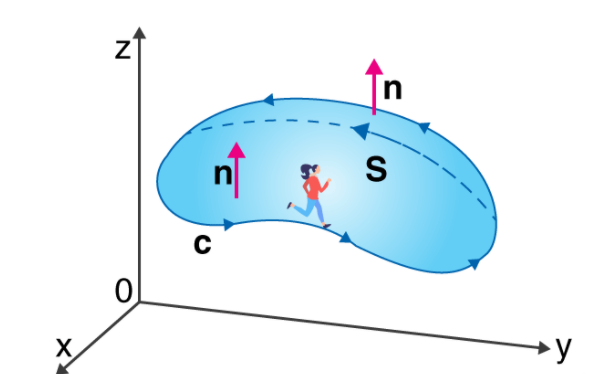
The Stoke’s theorem states that “the surface integral of the curl of a function over a surface bounded by a closed surface is equal to the line integral of the particular vector function around that surface.”
∮CF⃗.dr→=∬S(▽×F⃗ )dS→
Where,
C = A closed curve.
S = Any surface bounded by C.
F = A vector field whose components have continuous derivatives in an open region of R3 containing S.
This classical declaration, along with the classical divergence theorem, fundamental theorem of calculus, and Green’s theorem are exceptional cases of the general formulation specified above.
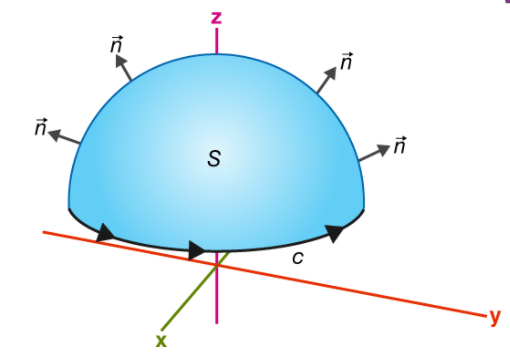
If you walk in the positive direction around C with your head pointing in the direction of n, the surface will always be on your left.
S is an oriented smooth surface bounded by a simple, closed smooth-boundary curve C with positive orientation.
Q 3. Give the formulation of Gauss Theorem?
Answer:
According to Gauss’s theorem the net-outward normal electric flux through any closed surface of any shape is equivalent to 1/ε0 times the total amount of charge contained within that surface
Proof of Gauss’s Theorem Statement:
- Let the charge be = q
- Let us construct the Gaussian sphere of radius = r
Now, Consider, A surface or area ds having ds (vector)
Normal having the flux at ds:
Flux at ds:
d e = E (vector) d s (vector) cos θ
But, θ = 0
Therefore, Total flux:
C = f d Φ
E 4 π r2
Therefore,
σ = 1 / 4πɛo q / r2 × 4π r2
σ = q / ɛo
Q4 What is Faraday law?
Answer:
Faraday’s law of electromagnetic induction, also known as Faraday’s law is the basic law of electromagnetism which helps us to predict how a magnetic field would interact with an electric circuit to produce an electromotive force (EMF). This phenomenon is known as electromagnetic induction.
Faraday’s Laws of Electromagnetic Induction
Faraday’s Laws of Electromagnetic Induction consists of two laws. The first law describes the induction of emf in a conductor and the second law quantifies the emf produced in the conductor. In the next few sections, let us learn these laws in detail.
Faraday’s First Law of Electromagnetic Induction
The discovery and understanding of electromagnetic induction are based on a long series of experiments carried out by Faraday and Henry. From the experimental observations, Faraday arrived at a conclusion that an emf is induced in the coil when the magnetic flux across the coil changes with time. With this in mind, Faraday formulated his first law of electromagnetic induction as,
Whenever a conductor is placed in a varying magnetic field, an electromotive force is induced. If the conductor circuit is closed, a current is induced which is called induced current.
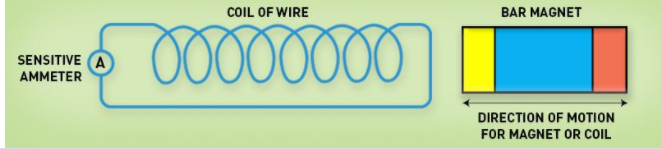
Mentioned here are a few ways to change the magnetic field intensity in a closed loop:
- By rotating the coil relative to the magnet.
- By moving the coil into or out of the magnetic field.
- By changing the area of a coil placed in the magnetic field.
- By moving a magnet towards or away from the coil.
Faraday’s Second Law of Electromagnetic Induction
Faraday’s second law of electromagnetic induction states that
The induced emf in a coil is equal to the rate of change of flux linkage.
The flux is the product of the number of turns in the coil and the flux associated with the coil. The formula of Faraday’s law is given below:

Where,
- ε is the electromotive force
- Φ is the magnetic flux
- N is the number of turns
The negative sign indicates that the direction of the induced emf and change in the direction of magnetic fields have opposite signs.
Additionally, there is another key law known as Lenz’s law that describes electromagnetic induction as well.
Q 5 What do you mean by hysteresis curve?
Answer:
The hysteresis loop shows the relationship between the intensity of magnetization and the magnetizing field. The loop is generated by measuring the magnetic flux coming out from the ferromagnetic substance while changing the external magnetizing field.
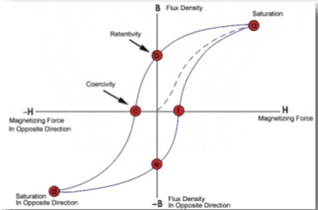
Looking at the graph, if B is measured for various values of H and if the results are plotted in graphic forms then the graph will show a hysteresis loop.
- The intensity of the magnetism (B) is increased when the magnetic field (H) is increased from 0 (zero).
- With increasing the magnetic field there is an increase in the value of magnetism and finally reaches point A which is called saturation point where B is constant.
- With a decrease in the value of the magnetic field, there is a decrease in the value of magnetism. But at B and H are equal to zero, substance or material retains some amount of magnetism is called retentivity or residual magnetism.
- When there is a decrease in the magnetic field towards the negative side, magnetism also decreases. At point C the substance is completely demagnetized.
- The force required to remove the retentivity of the material is known as Coercive force (C).
- In the opposite direction, the cycle is continued where the saturation point is D, retentivity point is E and coercive force is F.
- Due to the forward and opposite direction process, the cycle is complete and this cycle is called the hysteresis loop.
Q6 Define magnetization?
Answer:The magnetization of a given sample material M can be defined as the net magnetic moment for that material per unit volume.
Mathematically,
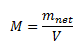
Let us now consider the case of a solenoid. Let us take a solenoid with n turns per unit length and the current passing through it be given by I, then the magnetic field in the interior of the solenoid can be given as,
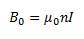
Now, if we fill the interior with the solenoid with a material of non-zero magnetization, the field inside the solenoid must be greater than before. The net magnetic field B inside the solenoid can be given as,
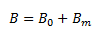
Where Bm gives the field contributed by the core material. Here, Bm is proportional to the magnetization of the material, M. Mathematically,
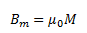
Here, µ0 is the constant of permeability of a vacuum.
The magnetic intensity of a material can be given as,
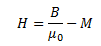
From this equation, we see that the total magnetic field can also be defined as,
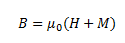
Here, the magnetic field due to the external factors such as the current in the solenoid is given as H and that due to the nature of the core is given by M. The latter quantity, that is M is dependent on external influences and is given by,
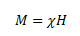
Where χ is the magnetic susceptibility of the material. It gives the measure of the response of a material to an external field. The magnetic susceptibility of a material is small and positive for paramagnetic materials and is small and negative for diamagnetic materials.
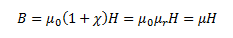
Q 7 Define ampere law?
Answer:
The magnetic field in space around an electric current is proportional to the electric current which serves as its source, just as the electric field in space is proportional to the charge which serves as its source. Ampere's Law states that for any closed loop path, the sum of the length elements times the magnetic field in the direction of the length element is equal to the permeability times the electric current enclosed in the loop.
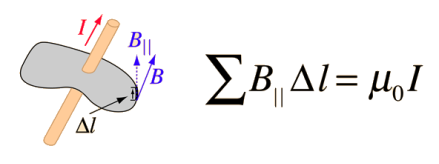
In the electric case, the relation of field to source is quantified in Gauss's Law which is a very powerful tool for calculating electric fields
Q8 Explain Magnetic permeability?
Answer:
Magnetic permeability is defined as the ratio of the magnetic induction to the magnetic intensity. It is a scalar quantity and denoted by the symbol μ. Magnetic permeability helps us measure a material’s resistance to the magnetic field or measure of the degree to which magnetic field can penetrate through a material.
If the material has greater magnetic permeability, greater will be the conductivity for magnetic lines of force.
Factors Affecting Magnetic Permeability
Permeability also depends on several factors such as the nature of the material, humidity, position in the medium, temperature, and frequency of the applied force. Magnetic permeability is always positive and can vary with a magnetic field. Meanwhile, the opposite of magnetic permeability is magnetic reluctivity.
Magnetic Permeability Formula
Magnetic permeability formula is given as;
Magnetic permeability (u) = B/H
Where B = magnetic intensity and H = magnetising field.
The SI unit of magnetic permeability is henries per meter (H/m) or newtons per ampere squared (N⋅A−2).
Q 9 Introduce Gausslaw of electrostatics?
Answer:
Gauss’s law for the electric field describes the static electric field generated by a distribution of electric charges. It states that the electric flux through any closed surface is proportional to the total electric charge enclosed by this surface. By convention, a positive electric charge generates a positive electric field. The law was published posthumously in 1867 as part of a collection of work by the famous German mathematician Carl Friedrich Gauss.
Integral Equation
Gauss’s law in integral form is given below:

Where:
e is the electric field
Q is the enclosed electric charge
ε0 is the electric permittivity of free space
n^ is the outward pointing unit-normal
Flux is a measure of the strength of a field passing through a surface. Electric flux is defined in general as
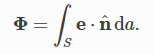
Gauss’s law tells us that the net electric flux through any closed surface is zero unless the volume bounded by that surface contains a net charge.
Q 10 Explain Gauss law for magnetism?
Answer:
Gauss’ Law for Magnetic Fields states that the flux of the magnetic field through a closed surface is zero.
This is expressed mathematically as follows:
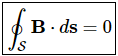
Where B is magnetic flux density and S is a closed surface with outward-pointing differential surface normal ds. It may be useful to consider the units. B has units of Wb/m2; therefore, integrating B over a surface gives a quantity with units of Wb, which is magnetic flux, as indicated above.
GLM can also be interpreted in terms of magnetic field lines. For the magnetic flux through a closed surface to be zero, every field line entering the volume enclosed by S must also exit this volume – field lines may not begin or end within the volume. The only way this can be true for every possible surface S is if magnetic field lines always form closed loops.
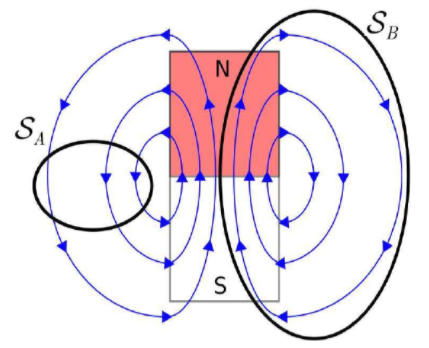
GLM implies there can be no particular particle or structure that can be the source of the magnetic field (because then that would be a start point for field lines). This is one way in which the magnetic field is very different from the electrostatic field, for which every field line begins at a charged particle.