Unit – 1

Calculus

Q1) Prove that the evolute of parabola 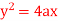is given by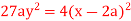

A1) It is given that-

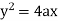
If (X, Y) are the coordinates of the centre of curvature at any point P (x, y) on the curve y = f(x), then X and Y are given as-

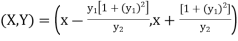  …………….. (1)

Now consider the equation of parabola (given)

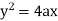
On differentiating w.r.t x-

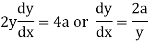
Again differentiating w.r.t. x-

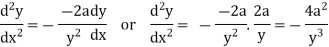
Put these derivatives in (1), we get-

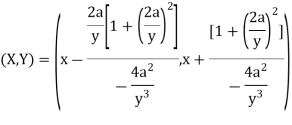
Now consider X,

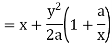
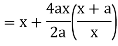
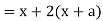
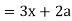
Here we get-

Now consider,

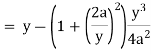
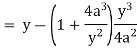
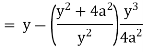
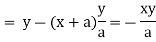
Here we get-

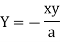
Now

Taking L.H.S of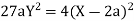

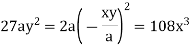
Taking R.H.S of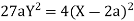

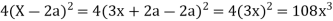
Hence proved.

Q2) Evaluate.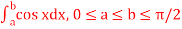

A2) Here we notice that f:x→cos x is a decreasing function on [a, b],

Therefore, by the definition of the definite integrals-

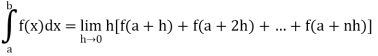
Then

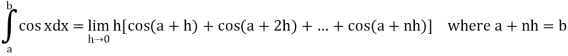
Now,

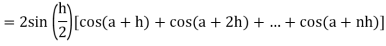
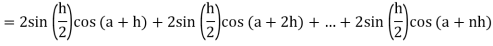
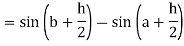
Here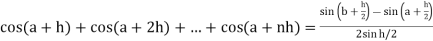

Thus

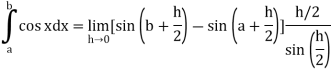
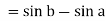
Q3) Evaluate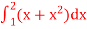

A3) Here 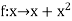is an increasing function on [1, 2]

So that,

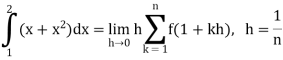
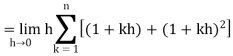
  …. (1)

We know that-

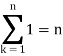
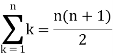
And

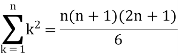
Then equation (1) becomes-

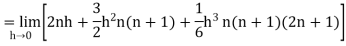
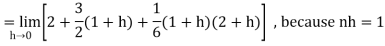
Q4) Evaluate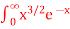 dx

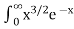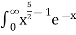A4) dx = dx

= Γ (5/2)

= Γ (3/2+ 1)

= 3/2 Γ (3/2)

= 3/2.  ½ Γ (½)

= 3/2. ½ π

=    ¾ π

Q5) Evaluate 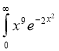  dx.

A5)   Let 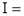 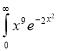 dx.

x	0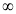
t	0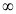

Put 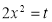or 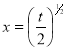 ;             4x dx = dt

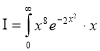dx

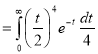
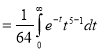
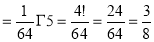
Q6) Determine the area enclosed by the curves-

 A6) We know that the curves are equal at the points of interaction, thus equating the values of y of each curve-

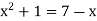
Which gives-

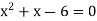
By factorization,

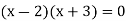
Which means,

x = 2 and x = -3

By determining the intersection points the range the values of x have been found-

x	-3	-2	-1	0	1	2
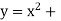1	10	5	2	1	2	5

And

We get the following figure by using above two tables-

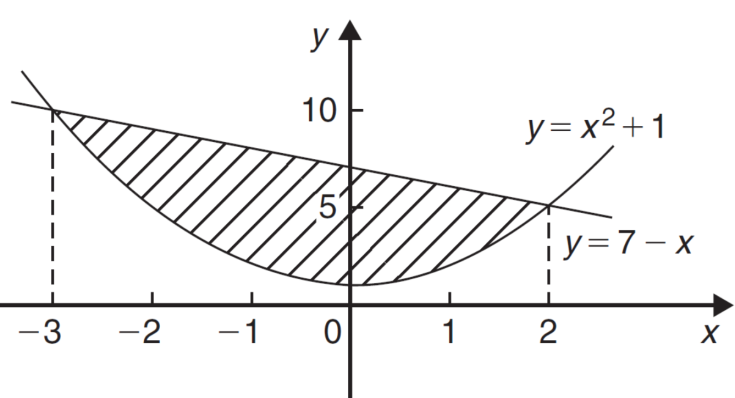
Area of shaded region =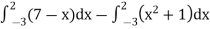

=

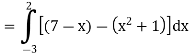
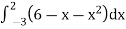
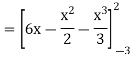
= (12 – 2 – 8/3) – (-18 – 9/2 + 9)

=

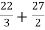
= 125/6 square unit

Q7) Find the area enclosed by the curves and if the area is rotated about the x-axis, then determine the volume of the solid of revolution.

A7) We know that, at the point of intersection the coordinates of the curve are equal. So that first we will find the point of intersection-

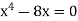
We get,

x = 0 and x = 2

The curve of the given equations will look like as follows-

Then,

The area of the shaded region will be-

A =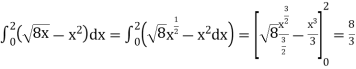

So that the area will be 8/3 square unit.

The volume will be

= (volume produced by revolving 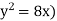– (volume produced by revolving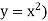

=

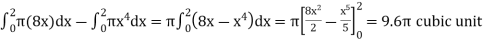
Q8) Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1, 3].

A8) The graph of the function f(x) = 1/x will look like-

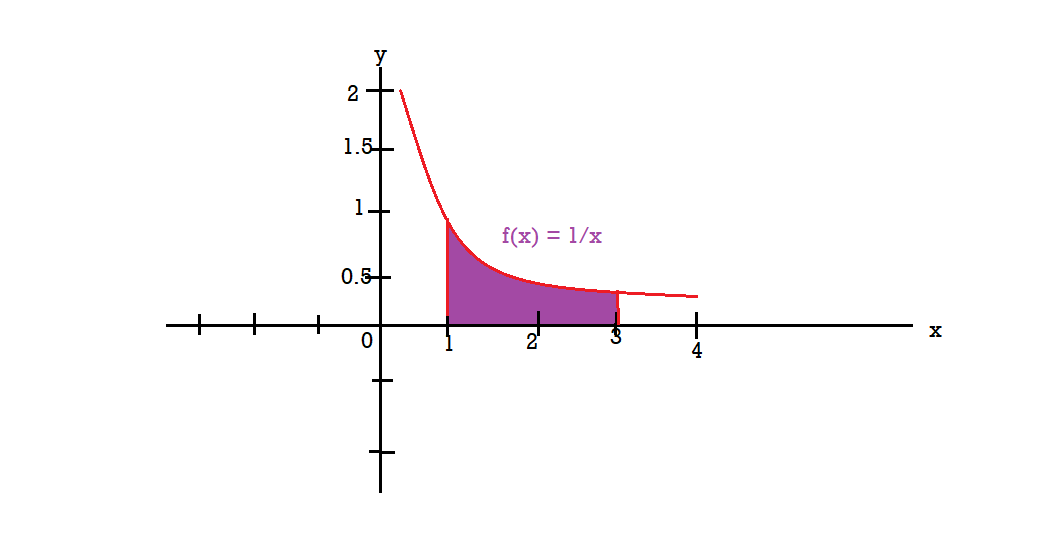
The volume of the solid of revolution generated by revolving R (violet region) about the y-axis over the interval [1, 3]

  Then the volume of the solid will be-

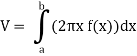
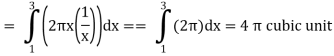
Q9) Verify Rolle’s theorem for the function f(x) = x2 for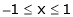

A9)

Here f(x) = x2;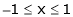

i)      Since f(x) is algebraic polynomial which is continuous in [-1, 1]

ii)    Consider f(x) = x2

Diff. w.r.t. x we get

f'(x) = 2x

Clearly f’(x) exists in (-1, 1) and does not become infinite.

iii)  Clearly

f (-1) = (-1)2 = 1

f (1) = (1)2 = 1

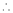f (-1) = f (1).

Hence by Rolle’s theorem, there exist 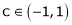such that

f’(c) = 0

i.e., 2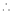c = 0

c = 0

Thus 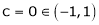such that

f'(c) = 0

Hence Rolle’s Theorem is verified.

Q10) Verify whether Rolle’s theorem is applicable or not for

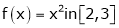
A10)

Here f(x) = x2;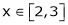

i)      X2 is an algebraic polynomial hence it is continuous in [2, 3]

ii)    Consider

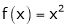
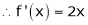
F’(x) exists for each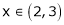

iii)  Consider

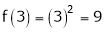
Thus .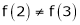

Thus, all conditions of Rolle’s theorem are not satisfied Hence Rolle’s theorem is not applicable for f(x) = x2 in [2, 3]

Q11) Verify the Lagrange’s mean value theorem for

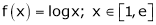
A11)

Here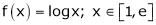

i)      Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]

ii)    Consider f(x) = log x.

Diff. w.r.t. x we get,

Clearly f’(x) exists for each value of 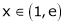& is finite.

Hence all conditions of LMVT are satisfied Hence at least

Such that

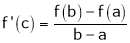
i.e.,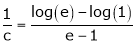

i.e.,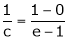

i.e.,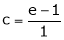

i.e.,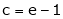

since e = 2.7183

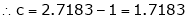
Clearly c = 1.7183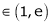

Hence LMVT is verified.

Q12) Verify Cauchy mean value theorems for 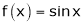&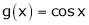in

A12)

Let &;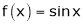

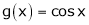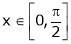
i)       Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in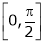

ii)    Since &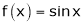

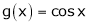
Diff. w.r.t. x we get,

&

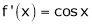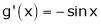
Clearly both f’(x) and g’(x) exist & finite in 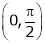. Hence f(x) and g(x) are derivable in 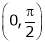and

iii)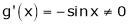   

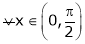
Hence by Cauchy mean value theorem, there exist at least 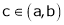such that

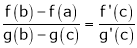
i.e.,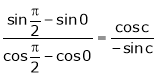

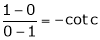
i.e., 1 = cot c

i.e.,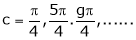

Clearly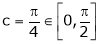

Hence Cauchy mean value theorem is verified.

Q13) Using Taylors series method expand

in powers of (x + 2)

A13)

Here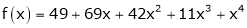

a = -2

By Taylors series,

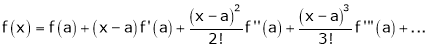   … (1)

Since

,  , …..

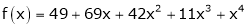
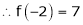
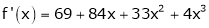
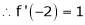
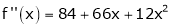
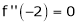
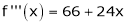
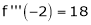
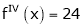
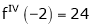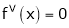Thus equation (1) becomes

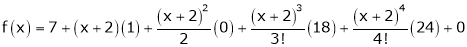
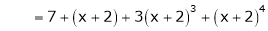
Q14) Evaluate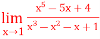

A14) Let f(x) = 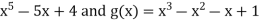, then

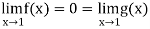
And

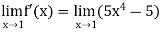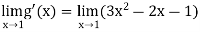= 0

= 0

But if we use L’Hospital rule again, then we get-

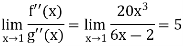
Q15) Find out the maxima and minima of the function

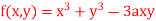
A15) Given …(i)

Partially differentiating (i) with respect to x we get

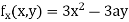….(ii)

Partially differentiating (i) with respect to y we get

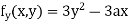….(iii)

Now, form the equations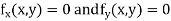

Using (ii) and (iii) we get

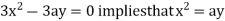
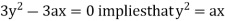
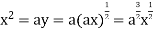using above two equations

Squaring both side we get

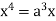
Or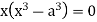 

This show that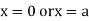

Also, we get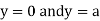

Thus, we get the pair of value as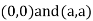

Now, we calculate

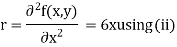
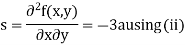
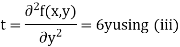
Putting above values in

At point (0,0) we get

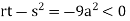
So, the point (0,0) is a saddle point.

At point 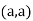we get

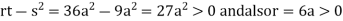
So, the point 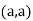is the minimum point where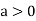

In case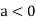 

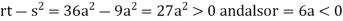
So, the point 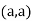is the maximum point where