Unit – 2

Sequence and series

Q1) Check whether the series 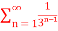 is convergent or divergent. Find its value in case of convergent.

A1) The general formula for this series is given by,

Sn =  = )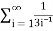

           We get,

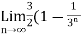) = 3/2

Hence the series is convergent and its values is 3/2.

Q2) Check whether the following series is convergent or divergent. If convergent, find its value.

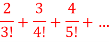
A2) n’th term of the series will be,

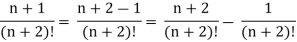
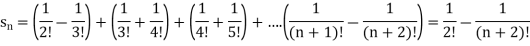
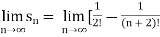] = ½

Q3) Test the convergence of the following series:

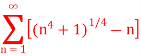
A3)

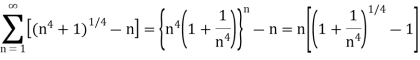
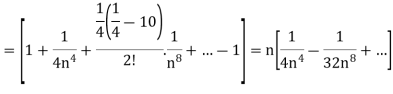
Here we take,

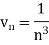
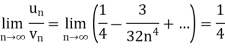
Which not zero and finite,

So, by comparison test, and both converges or diverges, but by p-series test

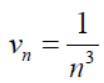
Is convergent. so that  is convergent.

Q4) Test the convergence of the following series.

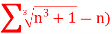
A4) We have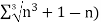  

First, we will find  and the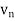

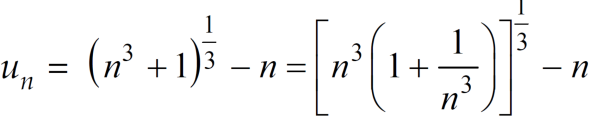
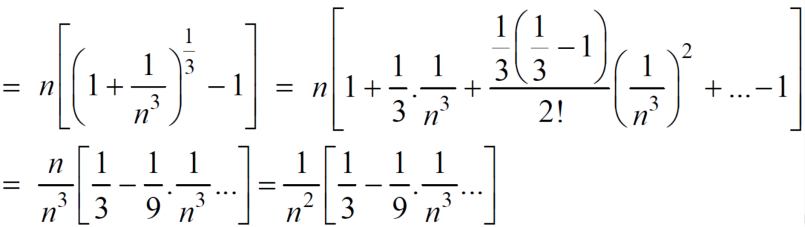
And

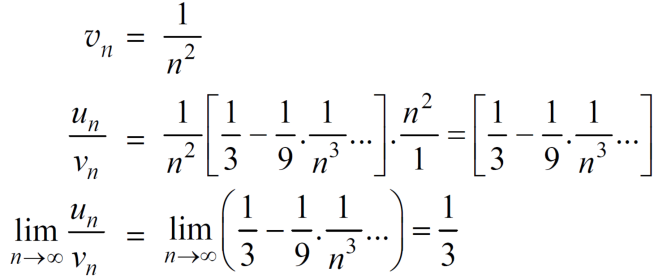
Here, we can see that, the limit is finite and not zero,

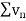Therefore, and converges or diverges together.

Since is of the form 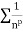 where p = 2>1

So that, we can say that,

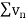is convergent, so that 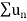will also be convergent.

Q5) Test the series:

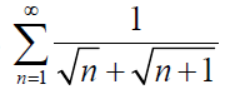
A5) The series is,

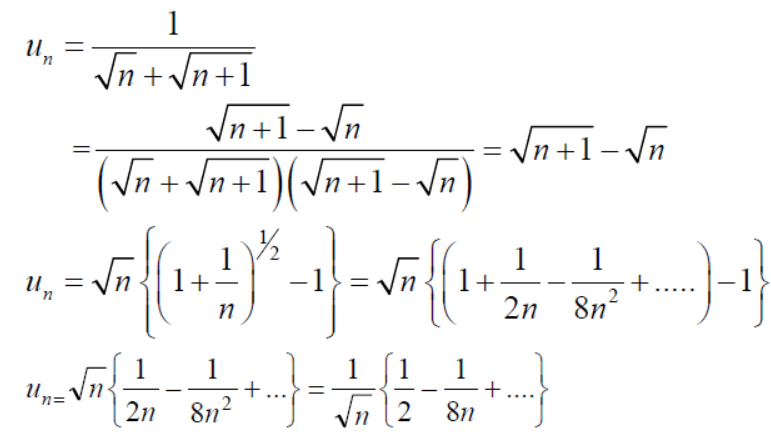
Now,

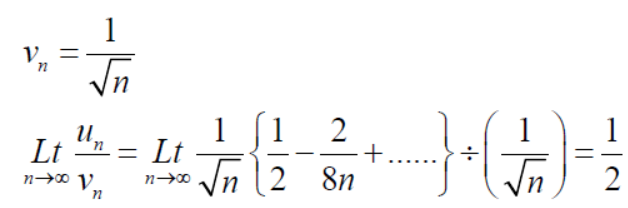
Take,

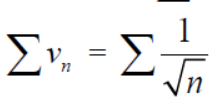
Which is finite and not zero.

Which is finite and not zero.

By comparison test and 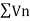converge or diverge together.

But,

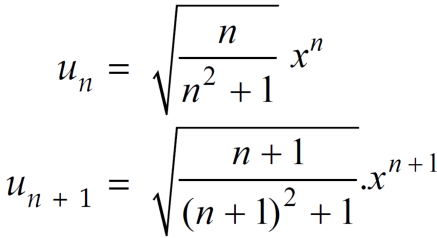
Is divergent. (p = ½)

 So that is divergent.

Q6) Test for the convergence of the n’th term of the series given below-

A6) We have,

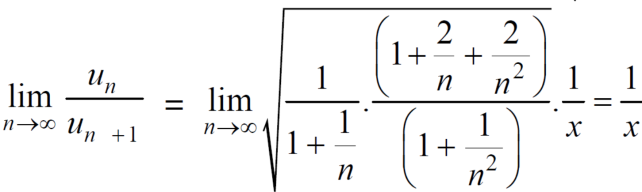
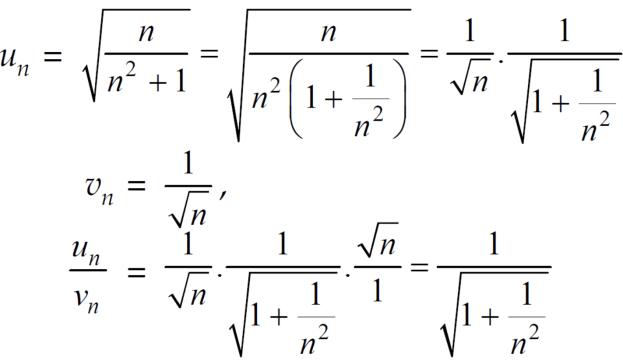
Now, by D’Almbert ratio test 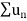converges if 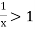and diverges if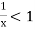 

At x = 1, this test fails.

Now, when x = 1

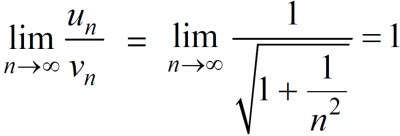
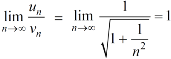
The limit is finite and not zero.

Then by comparison test, 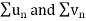converges or diverges together.

Since 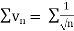is the form of 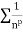, in which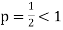

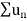Hence diverges then will also diverge.

Therefore, in the given series 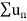converges if x<1 and diverges if x≥1

Q7) If the series converges, then find the value of x.

A7) Here

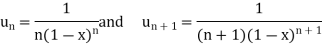
Then,

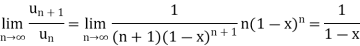
By D’Almbert’s ratio test the series is convergent for |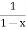|<1 or |1-x|>1

Or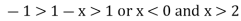

At x = 0, the series becomes- 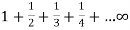 which is divergent harmonic series.

At x = 2, the series becomes-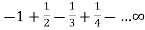 

It is an alternate series which is convergent by Leibnitz rule.

So that the series  .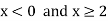

Q8) Express the polynomial 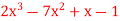in powers of (x-2).

A8)

Here we have,

f(x) =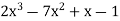

Differentiating the function w.r.t. x-

f’(x) =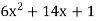

f’’(x) = 12x + 14

f’’’(x) = 12

f’’’’(x)=0

now using Taylor’s theorem-

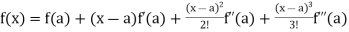+ …….     (1)

Here we have, a = 2,

Put x = 2 in the derivatives of f(x), we get-

f (2) =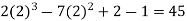 

f’ (2) =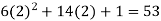

f’’ (2) = 12(2) +14 = 38

f’’’ (2) = 12   and f’’’’ (2) = 0

now put a = 2 and substitute the above values in equation (1), we get-

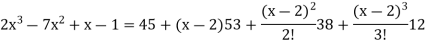
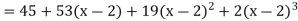
Q9) Expand as far as the term in .

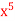A9) We know that the power series for is-

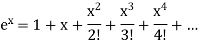
Here we have to find-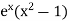 

So that-

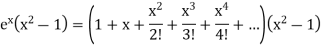
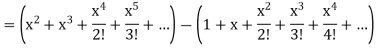
On solving, we get-

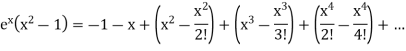
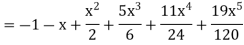
Q10) Find half range cosine series of 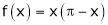in the interval 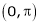and hence deduce that

a)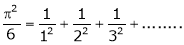    

b)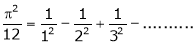   

A10)

Here

; 

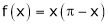Hence, it’s half range cosine series is,

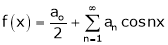       … (1)

Where

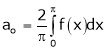
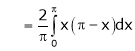
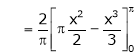
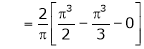
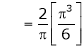
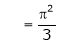
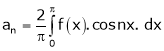
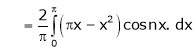
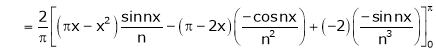
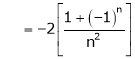
Hence equation (1) becomes,

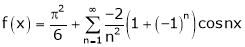
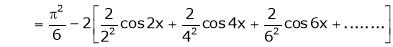
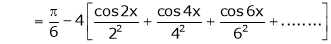    … (2)

Put x = 0, we get

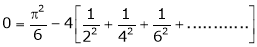
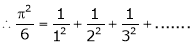
Hence the result

Put 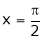 we get,

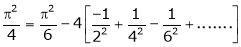
i.e.,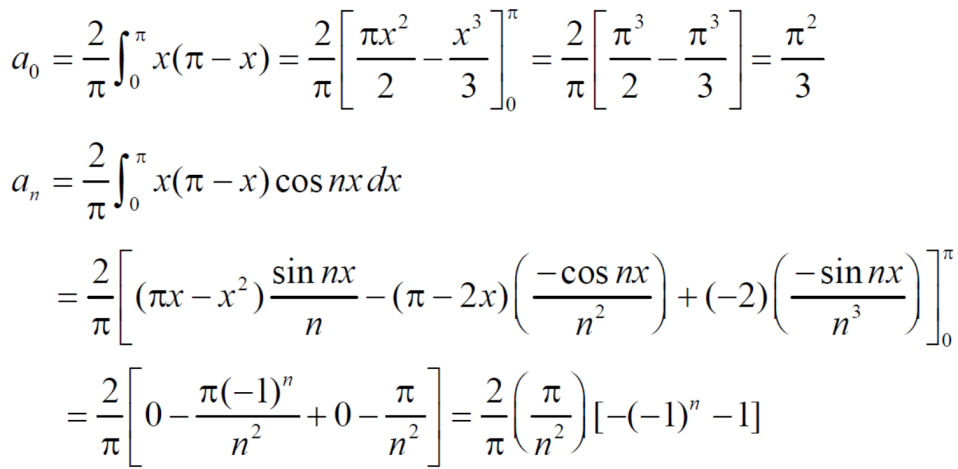

Q11) Prove that for 0 < x <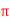

1.

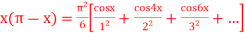
2.

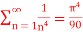
A11)

1. Half range series,

=

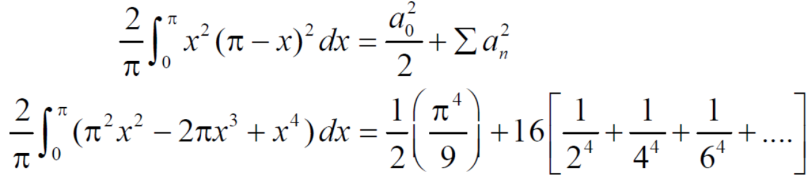
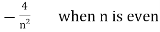
= 0            when n is odd

So that-

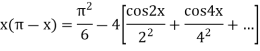
Now by Parseval’s formula-

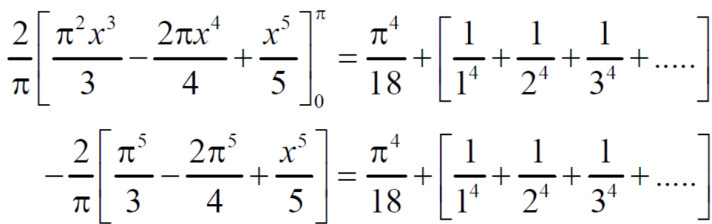
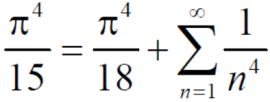
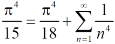
So that-